1 Introduction

Limestone quarries are multifaceted resources serving various purposes in construction, cement production, water purification, and the mining sector. They serve as a source of construction materials, furnishing stones for building applications, and raw materials for mortar and plaster [1,2,3]. Additionally, limestone is a key component in the production of cement, supplied to cement factories [4, 5], and can be utilized for sulfate sorption in treating mine waters with high sulfate concentrations [6]. Situated in karst landscapes, limestone quarries contribute to groundwater flow through joints, fractures, and conduits [7]. The extraction of limestone from these quarries involves significant drilling and blasting operations, a predominant excavation method compared to mechanical methods. This process breaks down the rock material into the desired size, known as fragmentation [8]. However, challenges such as oversize fragmented material, small-sized blasts, indirect cost escalation, unmanageable digging, transportation of blasted muck pile, improper throw of fragmented rock material, ground vibration, fly rock during blasting, and the generation of overbreak are associated concerns [9].

The mining industry, various processing industries, and the building industry all place a significant emphasis on the process of fragmentation, which involves breaking down materials into smaller pieces. According to experts like Roy et al. [10] and Mackenzie [11], the art of strategic blasting is emerging as a transformative force in mining and construction. Their research illuminates the profound impact of rock fragmentation on critical facets like loading, hauling, crushing rates, grinding capabilities, and ore recovery in mining and processing plants. Mackenzie, in particular, advocates for a blasting approach that aligns with the lowest unit cost across drilling, loading, conveying, and crushing activities. The ripple effect of rock fragmentation extends downstream, influencing crucial processes like crushing and grinding, and subsequently sha** the entire mine-to-mill process and product size distribution [12]. Implementing optimized blasting practices and refining comminution circuit operations, as emphasized in various studies [13], holds the key to substantial enhancements in productivity and overall plant performance. This comprehensive approach not only optimizes processes but also becomes a beacon for enhanced crusher efficiency, reduced maintenance and repair expenses, and cost savings in drilling and blasting operations [14,15,16]. In the dynamic landscape of mining, strategic rock fragmentation emerges not only as a science but as an art that unlocks efficiency and cost-effectiveness, resha** the very foundation of mining operations [16,17,18].

Prediction of rock fragmentation can play a significant role in the optimization of rock blasting, increasing productivity, reduces operational costs, better utilization of available resources, lowering energy consumption in down streams, and it enhances production and increases the profitability of mining. Understanding the blasting process and its costs necessitates the prediction and evaluation of the rock size distribution that results [19]. Mining activities have recently been improving with the use of machine learning (ML) techniques for evaluating and optimizing rock fragmentation. Through the utilization of extensive datasets and computational methodologies, machine learning models have the capability to reveal complex patterns and correlations between blasting parameters and geological attributes. This, in turn, facilitates the generation of more precise forecasts regarding powder factors and fragmentation consequences [20], which leads blasting techniques to sustainability [21].

This work is centered on the utilization of machine learning and deep learning techniques for the purpose of forecasting the degree of fragmentation in open-pit mining situations. The research endeavors to construct robust models that can reliably predict fragmentation percentages by considering a complete range of elements, such as rock mass characteristics, blast geometry, and explosive properties. The impact of several parameters, including spacing, drill hole diameter, burden, powder factor, and others, on fragmentation is thoroughly examined in order to determine their influence on the predictive models. The research aims to reveal valuable insights that help improve blasting procedures and enhance overall operational performance through careful data collecting and rigorous model construction.

Our study is structured logically. After this introduction, in Sect. 2 a comprehensive literature review is presented, wherein pertinent earlier research is scrutinized and the contextual framework for our study is established. Following this, Sect. 3 details the methodology, datasets, models created, and performance evaluation criteria employed. In addition, we offer the results and discussion of our research in Sect. 4, which encompass an examination of the influence of numerous parameters on the prediction of fragmentation and the effectiveness of several machine learning methods within this domain. Section 5 of our study discusses the constraints and shortcomings that we encountered. Additionally, it suggests potential directions for further investigation. The last section serves to summarize crucial discoveries and delineate prospective avenues for future investigation.

2 Literature review

Rock fragmentation assessment plays a crucial role in optimizing blasting operations within mining activities, directly impacting productivity, cost efficiency, and safety. Traditional approaches to rock fragmentation assessment have relied heavily on empirical methods, often limited by their inability to account for the complex interplay of geological factors, blast design parameters, and explosive properties. Over the years, numerous studies have investigated various aspects of rock fragmentation in mining operations, striving to enhance understanding and improve assessment techniques. Concurrently, recent advancements in computational techniques, particularly the integration of machine learning (ML) algorithms, have presented promising avenues for revolutionizing the assessment and optimization of rock fragmentation. This section of the literature review explores the factors affecting rock fragmentation, the challenges inherent in traditional approaches, and the emergence of machine learning as a transformative tool in this domain.

Dynamic blasting stands as a refined art, delicately breaking rocks into controlled fragments through meticulous drilling and strategic explosive placement. Beginning with deliberate drilling and meticulous placement of explosives, the detonation initiates a powerful shockwave, fracturing rocks along inherent vulnerabilities, with configurations of the blast, rock characteristics, and explosive properties collectively crafting fragmented rock masses vital in mining and construction. The process of dynamic blasting within mining and construction operations has been the subject of extensive study and refinement over the years. Researchers have meticulously explored the intricate interplay of drilling techniques, explosive properties, and blast configurations in sha** the resultant rock fragmentation. For instance, studies by [22, 23]. Decoupled charge blasting, as suggested by [24], enhances fragmentation while optimizing for reduced size ranges with lower decoupling ratios or different coupling media. This intricate dance of forces is governed by factors like specific charge, material properties, and debris, sha** the complex process of blasting-induced fragmentation [25,26,27].

Researchers such as Jimeno [28], Kanchibotla [29], and Changyou [30] examined the shock wave interaction in the presence of a short delay for the improvement of fragmentation; when the delays were in the range of the contacts, compared with no shock wave interactions, the results showed no clear differences or significant improvements in the fragmentation. Johansson and Ouchterlony [31] claimed that shock wave interactions are always extremely limited, affecting just a small portion of the rock. Aside from proper blast geometry and effective stemming, the different properties of an explosive play a role in achieving optimal fragmentation [32].

Different factors affect rock fragmentation. Based on this point, different researchers explained that fragmentation is the breakage of rock material using either mechanical excavation or drilling and blasting operations. This outcome of blasting, which is called fragmentation, is influenced by several factors. Some are well-known, while others are more difficult to grasp. Factors affecting rock fragmentation include rock properties (e.g., brittleness, fracture toughness, hardness, compressive strength, and tensile strength), cutting parameters (e.g., cutting depth, attack angle, wedge angle, cutting velocity), confining stress, joint parameters (e.g., inclination, orientation, spacing), and blast-induced wetness of blast holes [33,34,35,36,37,38]. The conditions of the rock are of great importance, which means that the influence of changes in other factors can vary considerably from one place to another. A change in a parameter in one type of rock, for instance, can make an important difference in the result, whereas the same change in other places may not be noticed at all. Researchers classified the factors into two main categories: controllable and uncontrollable parameters as shown in Fig. 1.

Fig. 1
figure 1

Factors affecting rock fragmentations

Full size image

The main controllable parameters are blast design parameters, which can differ from one blasting operation to the next and are used to modify and adjust the output of the operations to yield preferable results. They stated that the controllable parameters are classified into various groups. These groups are geometric parameters, which include burden, spacing between boreholes, bench height, drill hole diameter, hole length, charge depth, stemming height, sub-drilling, the drilling pattern, hole inclination (vertical or inclined), blasting direction, explosive parameters (types of explosives, energy, strength, priming systems, etc.), and time (delay timing and initiation sequence) [39]. Design parameters for open-pit bench blasting are depicted in Fig. 2. Other parameters include confinement of the explosive, i.e., properties of the rock, hole diameter, and degree of coupling. The more predictable fragmentation results in high values for the explosive velocity of detonation (VOD). This is achieved due to an increase in explosive energy, which corresponds to an increase in fragmentation [32]. Jimeno [28] observed that the results of blasting operations are determined by a different parameter. Jimeno stated that poor fragmentation, insufficient swelling of the muck pile, uncontrolled fly rock, high vibration levels, and low-frequency vibrations are the results of blasting if the delay timing and the initiation sequence of blasting are not adequate.

Fig. 2
figure 2

Design parameters for open-pit bench blasting

Full size image

Uncontrolled parameters include, but are not limited to, the geology of the rock, the strength of the rock, the properties of the rock, the presence of water, and the structure of the rock, which is usually shown by the way the cracks are distributed [40]. According to Hagan [41], rock properties have a significant effect on the output of blasting when they are compared to other variables. Hagan stated the relationship between the importance of rock material strength and the rock mass strength relied on the mean spacing between the fissures, cracks, or joints. Moreover, he explained that blasting operations are required in a rock mass with widely spaced joints to create new cracks in the rock mass to form fragmentation. Cunningham [42] also stated that the relation between the tensile strength of the rock and the fragmentation was that a tensile strength of more than 15 MPa should tend to give a rough fragmentation, whereas a tensile strength of less than 6 MPa is supposed to give a fine fragmentation.

Chakraborty et al. [39] conducted extensive research on overburden blasting and fragmentation in three large opencast coal mines. They used rock quality designation (RQD) to represent all the rock mass structure parameters. Based on RQD, the rock masses were investigated and divided into massive and jointed branches [43]. After the division, they considered the observed mean fragment size as the dependent variable and different rock mass properties, blast design parameters, explosive properties, firing sequence, and drilling error as independent variables. Separate multiple linear regression analyses were performed for massive and joint formations. The structural features of the rocks, such as bedding planes, fractures, and faults, have significant influences on the responses of the rock mass, as well as the blasting results, and those features should not be ignored during blast design. Researchers who studied the response of the rock structure to blasting results stated that structural features have a greater influence on blasting results than explosive properties and blast geometry [44].

Different researchers have developed different empirical methods, such as the Kuz–Ram model, Kuznetsov’s equation, Rosin–Rammler’s equation, Cunningham’s uniformity index, and the Modified Kuz–Ram model, which have been used to predict and improve the prediction of the fragments resulting from blasting [45,46,47]. The Kuz–Ram model is an approach used for the prediction of rock fragmentation due to blasting. In the Kuz–Ram model, the input data consists of the relevant blast design parameters. Three key equations are the backbone of this model, and these equations are Kuznetsova’s equation, the Rosin–Rammler equation, and the uniformity index. The formula was created by Kuznetsov and further developed by Cunningham as Adebola [48] stated it. As Engin [45] explained that Cunningham [42] used the Kuz–Ram model not as a quantitative prediction model, but as a tool to examine how different parameters could influence blast fragmentation. A uniformity index was introduced later due to the deficiency of the model in describing the distribution of fine fragments that are below the mean size. It is hypothesized that the finer fractions are produced by the pulverizing or crushing action of the explosive in a blast hole. The crushing zone radius around each blast hole is determined based on the peak blast-hole pressure and the strength of the rock [49].

It is hard for empirical methods to predict rock fragmentation during blasting because they cannot handle the nonlinear relationship between input and output parameters. This makes it harder to get accurate predictions of fragment size [50, 51]. Common models like the Kuznetsov model may yield unsatisfactory results, and the Kuznetsov–Cunningham–Ouchterlony (KCO) model, though useful for limestone mine sites, still exhibits errors between expected and actual outcomes [52, 53]. The limitations in accurately predicting fragment size arise from the nonlinear relationship between input and output parameters, insufficient investigation into parameter combinations, and errors in existing models [50]. As such, addressing these limitations in empirical methods is imperative for advancing accurate rock fragmentation prediction in blasting [52, 54].

In addition to empirical models the existing methods for assessing rock fragmentation, including physical screening and image analysis, are hindered by challenges such as time consumption and subjectivity [55, 56]. Manual inspection and sieving tests, relying on human judgment, are neither real-time nor effective in capturing the diverse size distribution and complex patterns of rock fragments [57, 58]. The limitations extend to the measurement of rock mass properties, impacting the accuracy of fragmentation prediction models, while environmental concerns with conventional techniques prompt the need for more efficient and real-time methods that can accurately recognize and measure rock fragments.

In the realm of modern mining operations, the quest for precision and efficiency has led researchers to harness the power of machine learning predictive modeling techniques. Machine learning (ML) is a computational approach that empowers systems to automatically learn and improve from experience without being explicitly programmed. In the field of rock mechanics and blasting, ML techniques have emerged as invaluable tools for optimizing performance, enhancing decision-making, and improving safety [59]. Studies have shown that ML methods, including hybrids and ensembles, outperform other approaches in various tasks, such as predicting blast-induced ground vibration and forecasting the elastic properties of rocks [60, 61], slope stability predictions [62], strength prediction for recycling waste tailing [63], predicting fly rock distance [64]. These advancements underscore the potential of ML techniques to revolutionize practices within the realm of rock mechanics and blasting, offering more accurate predictions and deeper insights into the underlying processes.

Shams et al. [65] pioneered the development of a predictive model aimed at forecasting rock fragmentation during blasting operations in open pit mines. Utilizing a combination of fuzzy inference systems (FIS) and multiple regression analysis (MRA), their model provided invaluable insights into the intricate dynamics of rock fragmentation. Furthermore, Sheykhi et al. [66] introduced a hybrid model integrating support vector regression (SVR) and fuzzy C-means clustering (FCM) techniques to estimate ground vibration resulting from such operations. Their findings highlighted the superiority of SVR over traditional empirical equations, emphasizing the pivotal role of data clustering in achieving accurate predictions of blast-induced ground vibration. Meanwhile, Ghasemi [67] delved into the prediction of peak particle velocity (PPV) at the Sarcheshmeh copper mine, employing ANFIS–PSO and SVR models. Their study underscored the superior performance of the ANFIS–PSO model, showcasing a remarkable root mean square error (RMSE) value of 1.83 compared to SVR. These advancements underscore the critical importance of precise prediction in optimizing blasting operations, as elucidated by Bahrami et al. [68]. Accurate forecasts of rock fragmentation not only enhance operational efficiency but also contribute to minimizing environmental impact and ensuring the safety of mining personnel. Thus, the integration of sophisticated modeling techniques represents a significant stride towards sustainable and efficient mining practices in the twenty-first century.

A systematic summery of previous studies on the application of soft computing techniques in blasting is presented in Table 1. In this research, an artificial neural network (ANN), in comparison with different machine learning models, i.e., random forest regression (RF), support vector regression (SVR), and XGBoost regression, is used for the prediction of fragmentation. Based on different soft computing evaluation metrics, the ANN has shown superior results compared to the other machine learning techniques. Researchers such as Fissha et al. [61] and Taiwo et al. [69], concluded that the prediction models based on ANN have significant implications for the accuracy and perfect estimation of the blasting phenomena. Additionally a machine learning models like XGBoost-PSO model were used to accurately predict tunnel deformation in squeezing prone grounds [70] and tunnel face conditions [71]. Random forest model has also shown its accuracy in predicting blast ground vibrations [72] and hazard level of water inrush in tunnel [73].

Table 1 Summary of selected previous studies on application of machine learning to blasting
Full size table

The significance and importance of this research lies in its potential for transforming rock fragmentation assessment practices in the mining industry by implementing machine learning algorithms. A precise and effective evaluation of rock fragmentation is crucial for enhancing mining operations, as it has direct effects on subsequent procedures and resource utilization. This study pioneers a data-driven, machine learning-based solution to overcome the limitations of manual measurements and image analysis. Traditional approaches struggle to anticipate rock fragmentation in open pit mining due to subjectivity, time, and scalability. This project aims to automate, objectively, and scalable prediction by using cutting-edge machine learning and deep learning algorithms. Combining these modern technologies provides for a complete grasp of the complex relationship between rock fragmentation factors. The study seeks to shift from labor-intensive, subjective methods to a sophisticated, data-driven framework that improves accuracy and allows the incorporation of more influencing factors, enabling more efficient and effective blasting operations in open-pit mining environments. The ability of the developed model to predict fragmentation results based on key blasting parameters and rock properties will allow mining companies to make informed decisions and customize blast designs to achieve the desired fragmentation results. Implementing this effective strategy can result in significant benefits for the mining industry, such as increased productivity, decreased energy consumption during downstream processes, and reduced environmental impact. In addition, by utilizing historical blasting data and perpetually learning from new data, the machine learning model is anticipated to evolve and adapt to a wide range of geological conditions and blasting scenarios. Ultimately, this research has the potential to revolutionize how rock fragmentation is evaluated in mining blasting, contributing to more sustainable mining practices and enhanced resource extraction efficiency.

3 Research methodology

3.1 Data collection

The focus of this study is the development of a prediction model for fragmentation in a limestone quarry located in the Baloda Bazaar district of Chhattisgarh state/province in India. The purpose of the study is to create a predictive tool that can estimate rock fragmentation, a critical factor in the mining process. The limestone mine, situated in this specific district, plays a crucial role in providing insights into the optimization of subsequent operations such as crushing and milling. Rock fragmentation, referring to the size distribution of broken rock pieces after blasting, is a key parameter influencing mining efficiency. Our study area predominantly involves conventional drill and blast techniques, where the integration of blasting systems, particularly the electric initiation system and power deck, plays a pivotal role in our operations. The electric initiation system serves as a foundational component, providing the necessary infrastructure for initiating explosives with precision. Seamlessly complementing this system, the power deck enhances our blasting operations by offering precise timing control for each detonator. The central control unit, which serves as the heart of the system, was strategically positioned in a centralized location to ensure efficient communication with all detonators. Detonators were then securely connected to the central control unit using reliable wiring systems, adhering to safety protocols and best practices. Delay times for each detonator were used based on the geological characteristics of the limestone formations and the desired blasting objective.

The data used for the study was obtained as secondary data from the limestone quarry in the Baloda Bazaar district of Chhattisgarh. The dataset comprises a total of 219 data points, each characterized by 11 features. These features consist of ten input parameters, namely drill diameter (mm), spacing (m), burden (m), average bench height (m), number of holes, specific drilling (m/m3), powder factor (PF), compressive strength (kgf/cm2), stemming, and charge per delay. Additionally, there is one output feature, rock fragmentation, which serves as the target variable for the prediction model. The 219 data points provide a comprehensive view of the quarry's operational conditions, allowing for a detailed analysis of the factors influencing rock fragmentation in the Baloda Bazaar district of Chhattisgarh. The inclusion of various input features related to drilling and blasting parameters enables a nuanced understanding of the complex interplay between these variables and the resulting fragmentation. Figure 3 showcases the histogram distributions for both input and output data, offering graphical insights into the distribution patterns and interrelationships among the variables.

Fig. 3
figure 3figure 3

Histogram plots of input and output datasets

Full size image

3.2 Data analysis

A database with a constrained quantity of data was constructed using the Python programming language to implement multiple machine learning and deep learning methods. The outcomes of these methods are compared in terms of performance. In this study, a total of ten input parameters (drill hole diameter (mm), spacing (m), burden (m), average bench height (m), number of holes, specific drilling (m/m3), powder factor (PF), compressive strength (kg/cm2), stemming, the charge per delay), and one output parameter (fragmentation) were used. The descriptive statistical summary of the datasets is presented in Table 2. The datasets were grouped into training and testing datasets; 199 data points were considered for training the network, 9 data points (approximately 3.8% of total data) were kept for cross-validation, and 11 data points (approximately 5% of total data) were considered for testing the model. In the dataset, out of ten input features, nine have decimal values, and the remaining feature has integer values (number of holes). The output feature, which is rock fragmentation, is also expressed in terms of decimal values. By looking at the data in its raw format, the drill diameter does not change significantly with the change in the value of rock fragmentation (most of the time the value is only 114.3). This means it may not contribute to the variability of our output feature and hence can be eliminated to reduce model complexity. The same is the case with compressive strength. However, we established it with the help of a correlation plot and eliminated the unwanted features accordingly.

Table 2 Descriptive statistics of the input and output parameters
Full size table

The presentation of data in a graphical or pictorial format is named “data visualization.” Violin plots to show the input and output dataset distribution with quartiles at 25–75% (Q1 and Q3) are depicted in Fig. 4, which also shows the median of each dataset. To obtain insights, the violin plot enables decision makers to view analytics that are displayed visually. Visualization is the act of using visual representations of the data to identify trends and relationships. A variety of Python data visualization libraries, such as Matplotlib and Seaborn, were used to conduct data visualization in this work. Statistical parameters, correlation plots, scatter plots, and histograms are used to visualize and recognize the relationship between the inputs and outputs of the datasets.

Fig. 4
figure 4figure 4

Violin plots to show the input and output dataset distribution with quartiles at 25–75% (Q1 and Q3) and the median of each dataset

Full size image

3.3 Pre-processing

Data pre-processing is a technique that involves transforming raw data into a more coherent format. After data collection, the basic data pre-processing procedures are conducted to more efficiently train the ANNs and MLs. The data pre-processing involves identifying missing values, splitting the data into training and testing sets, and finally undertaking feature scaling to limit the range of variables so that they can be compared and worked on in common. In our investigation, we have implemented various preprocessing methodologies to adequately prepare our input characteristics for the machine learning frameworks. These approaches are imperative for enhancing data integrity and optimizing model effectiveness. The overall methodology is shown in Fig. 5.

Fig. 5
figure 5

Schematic diagram of the overall study

Full size image
  1. (A)

    Data cleaning: The initial stage entailed finding and addressing missing or inaccurate data pieces. Missing values in the dataset were addressed by imputing them using suitable approaches to avoid any impact on the model's performance.

  2. (B)

    Feature scaling: feature scaling was applied to standardize the range of the features. This ensures that each feature contributes equally to the model's learning process and prevents features with larger scales from dominating the model.

  3. (C)

    Data splitting: The datasets divided into training set (was used to train the models), cross validation set (was used to tune hyperparameter and evaluate model performance during training), and test set (used to assess the final performance of the trained model). The data splitting into training, validation, and testing was more on the basis of hit and trail to accommodate adequate training while at the same time validating and testing the mode. The splitting approach was dynamically adjusted to ensure adequate training while maintaining robust validation and testing procedures.

  4. (D)

    Data normalization and preparation: Data normalization techniques were applied to ensure adherence to a predefined distribution, bolstering stability in the machine learning process. Additionally, correlation analysis helped classify input features based on their relationship with the output, facilitating the removal of insignificant features.

3.4 Proposed machine learning techniques

According to Abu-Mostafa [83], “A neural network is often defined as a massively parallel distributed processor made from neurons that features a natural propensity for storing experimental knowledge and making it available for use.” This technique can extrapolate a result from the pattern that was performed during training. The network with enough input data can be trained, and the test can be conducted based on previous learning with new inputs having similar patterns [80]. A neural network is an intelligent hub that is ready to predict an output pattern when it recognizes a given input pattern. The input layer contains input neurons (nodes) that send information to the hidden layer. Outputs are produced using hidden layers through the output layer. Every neuron has weighted inputs (synapses in biological neurons), an activation function (defines the output given an input), and one output. ANNs are capable of learning, but they must be trained. The learning strategies of an ANN are supervised learning, unsupervised learning, and reinforcement learning. The way the neurons of a neural network are structured is intimately linked with the training algorithm used to train the network with a different class of network architecture, i.e., single-layer feed-forward networks, multilayer feed-forward networks, and recurrent networks [84].

Artificial neural networks (ANNs) were used by [85,86,87,88] to predict ground vibration, forecast back break, evaluate the effects of design parameters in fly rock, and predict and optimize blast-induced impacts. The study experimented with several hidden layers and neurons before settling on a network with a topology of 10-7-7-1 as the best option. Using mean square error (MSE), variance account for (VAF), and coefficient of determination (R2) as comparison metrics, the ANN model outperformed traditional regression analysis. Sensitivity analysis showed that water content is the least effective parameter in the study, while weight is the parameter that has the biggest impact on the back break. Monjezi et al. [89] also addressed the simultaneous prediction of rock fragmentation and back break, using a radial basis function neural network (RBFNN) and a backpropagation neural network (BPNN). A network with the architecture 6-10-2 was determined to be ideal for BPNN modeling, while RBFNN’s architecture of 6-36-2 with a spreading factor of 0.79 offered the best predictive ability. As a result, it was found that the BPNN model is the most desirable since it offers the highest accuracy and lowest error.

The backpropagation (BP) network is the most popular network architecture today as it contains the highlights of the neural network theory is simple in structure and is clear in mathematical meaning. It has been proven that any continuous function is often uniformly approximated by the BP network model with just one hidden layer used for backpropagation network to predict the mean particle size of a rock fragmentation resulting from blasting. The backpropagation method was found to be optimal for predicting fragmentation.

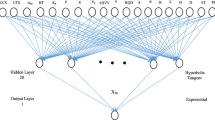
In an artificial neural network model, the number of hidden layers, neurons in each layer, activation function in each layer, training function, weight/bias learning function, and performance function are specified. The input layer contains input neurons (nodes) that send information to the hidden layer. The activation functions in each layer, training function, weight/bias learning function, and performance function are specified. The input layer contains input neurons (nodes) that send information to the hidden layer. The full structure of artificial neural network is depicted in Fig. 6.

Fig. 6
figure 6

Artificial neural network (ANN) structure

Full size image

Supervised machine learning algorithms such as support vector machine, random forest regression, and XGBoost have shown remarkable prediction efficiency in many disciplines due to their ability to generalize. The overall schematic diagram of the machine learning techniques and ANN of this study is shown in Fig. 5. Different scholars [90,91,92,93] used a powerful machine learning method known as SVM to address classification and regression issues based on mathematical statistics. Regression issues can be resolved with SVM using the insensitive loss function. Random forest regression is a non-parametric regression method that has proven its high accuracy and superiority. According to [94], random forests construct K regression trees and average the outcomes of regression. The outputs of all individual trees are combined to provide the final anticipated values.

In our study, we employed a range of hyperparameters tailored to each regression model, including artificial neural network (ANN), support vector regression (SVR), random forest regression (RFR), and extreme gradient boosting (XGBoost) as shown in Table 3. To refine these parameters for optimal performance, we utilized two primary methods: an iterative process and grid search. Initially, the iterative process involved setting initial hyperparameter values based on common defaults and empirical knowledge. Subsequently, we trained each model, assessed performance metrics, and systematically adjusted hyperparameters based on observed results. This iterative approach continued until satisfactory performance levels were achieved. Furthermore, we implemented grid search for hyperparameter tuning. This involved defining a grid of hyperparameter values to explore for each model. By systematically evaluating model performance using different combinations of hyperparameters, the algorithm selected the combination yielding the best results based on predefined evaluation metrics.

Table 3 Summary of the hyperparameter of the machine learning models used in this study
Full size table

4 Results and discussion

In our investigation, we explore the intricate relationship between rock fragmentation and a multitude of influencing parameters, including the critical factor of powder factor. In our study area, the powder factor serves as a pivotal metric, quantifying the ratio of rock volume to the amount of explosive used in blasting operations. We examine how variations in powder factor, alongside other pertinent parameters such as geological properties, blasting parameters, and rock characteristics, intricately shape the fragmentation process. Through rigorous correlation analysis, we elucidate the significance of these diverse parameters which drive fragmentation dynamics in our study area. Using the pearson correlation plot shown in Fig. 7, spearman correlation plot (Fig. 8), Kendall correlation heatmap (Fig. 9), and 2D kernel density plot we found the relationship between different input parameters and the output parameter, which is fragmentation. We observed that certain features exhibit limited variability and weak correlations with rock fragmentation. Drill diameter, for instance, predominantly maintains a value of 114.3 across all cases, indicating minimal variability concerning rock fragmentation. Its correlation coefficient of 0.32 suggests a weak association with fragmentation outcomes, thus contributing insignificantly to the predictive model. Similarly, compressive strength showcases uniformity across all samples in our dataset, lacking significant variability and displaying a weak correlation with fragmentation. Conversely, features such as burden, specific drilling, and spacing demonstrate a normal distribution of values, albeit with marginal effects on model performance.

Fig. 7
figure 7

Pearson correlation heatmap plot

Full size image
Fig. 8
figure 8

Spearman correlation plot of input and output parameters

Full size image
Fig. 9
figure 9

Kendall correlation heatmap

Full size image

The feature that has the most powerful correlation with rock fragmentation is the powder factor having Pearson correlation of − 0.82, spearman correlation − 0.85, and Kendall correlation − 0.68. Its value ranges from 1.82 to 16.25 with a mean value of 8.55 as shown in Fig. 10. The negative value of the correlation indicates that the powder factor is showing a reverse relationship with fragmentation. The rationale behind the observed decrease in powder factor with increasing rock fragmentation is rooted in the definition used in our study. The powder factor is defined as the ratio of unit volume of rock to the amount of explosive energy applied. A higher powder factor signifies a larger unit volume of rock per unit of explosive energy, indicating that less energy is available to break each unit volume of rock. This leads to a less concentrated distribution of energy within the blast area, resulting in a reduced efficiency of energy transfer to the rock mass. Consequently, the process of fragmentation tends to produce coarser outcomes, characterized by larger particle sizes and diminished rock breakage.

Fig. 10
figure 10figure 10

2D kernel density plot of all variables

Full size image

Unlike features such as drill diameter, average bench height, compressive strength, stemming, and charge per delay, all other features display strong correlations with rock fragmentation. Thus, eliminating these weakly correlated features promises to streamline model complexity and enhance predictive accuracy. The input features (drill diameter, average bench height, compressive strength, stemming, and charge per delay) showed a weak correlation with rock fragmentation are eliminated to reduce model complexity in all models we trained.

Sensitivity analysis was used to assess the effects of different blasting parameters on fragmentation by determining how different parameters affected the way rocks broke apart. To solve this issue, the Shapely effects were recently developed. They divide the mutual contribution of a group of inputs (owing to correlation and interaction) among all the inputs in the group. Permutation importance and shapely values were used as feature importance measures to identify the sensitivity analysis in this work. The shapely value is a tool used in machine learning for data valuation, ensemble pruning, multi-agent reinforcement learning, explanation, and feature selection [95]. Based on Enming et al. [95], stated that the shapely value has been used as the foundation for many techniques that link a machine learning model’s predictions based on inputs to its underlying features.

Mean absolute error (MAE), mean absolute percentage error (MAPE), mean square error (MSE), root mean square error (RMSE), and the determination coefficient (R2) were used to compare the performance of the machine learning analysis and ANN models.

4.1 Results of random forest regression

The mean squared error values for training and testing data are 12.37 and 9.89, respectively (see Fig. 11). Similarly, the R2 value for both the training and testing data is 94%. This means there are no issues of underfitting or overfitting with this model. It shows that the random forest regression has the potential to perform well on this kind of data (from varied distributions).

Fig. 11
figure 11

Performance model of random forest regression (RFR)

Full size image

According to the feature importance in Fig. 12 the random forest regression model shows the powder factor (PF) is the most important feature and the burden is the least important feature in the determination of rock fragmentation. All other features are not as significant as the powder factor and have scores of 0.8 or less on the feature importance scale.

Fig. 12
figure 12

Feature importance of the random forest regression (RFR) model

Full size image

4.2 Results of support vector regression (SVR)

The above figure shows the mean squared error values for training and test data are 0.339 and 0.124, respectively, which seem small because of data scaling. Similarly, the R2 values for both the training and test data are 66% and 87%, respectively. With this model, there is an issue with over- and underfitting. Because the variability of training data is low, this model was unable to investigate the variance between input features and output features. Moreover, it shows that support vector regression has no potential to perform using this kind of data (from varied distributions). The overall performance model for SVR is depicted in Fig. 13.

Fig. 13
figure 13

Performance model of support vector regression (SVR)

Full size image

According to the feature importance Fig. 14 for the support vector regression model, the powder factor is the most important feature, but instead of the burden, spacing is the least important feature in the determination of rock fragmentation. All other features show more significance compared to the results of the random forest regression model. This is because of the bad fit of the SVR on the dataset.

Fig. 14
figure 14

Feature importance of the support vector regression (SVR) model

Full size image

4.3 Results of XGBoost regression (XGBR)

As you can see from Fig. 15, the mean squared error values for training and test data are 21.03 and 9.78, respectively, which are slightly higher than the results of the RFR model. Similarly, the R2 values for the training and test data are 91% and 94%, respectively.

Fig. 15
figure 15

Performance model of XGBoost regression

Full size image

Since the difference between the two is significant, this model probably suffers from underfitting, i.e., the variability of input variables with the output variable is not able to be studied. Based on the feature importance analysis in Fig. 16 the powder factor is the most important feature and burden is the second most important feature.

Fig. 16
figure 16

Feature importance of XGBoost regression model

Full size image

This shows that XGBoost regression has the potential to perform using this kind of data (from varied distributions), but more data are needed for better performance.

Features show the same significance as for the random forest regression model. Again, this is because of the bad fit of the XGBoost regression on the dataset.

4.4 Results of artificial neural network (ANN)

Structure of the neural network with the input and output layers (see Fig. 17).

Fig. 17
figure 17

Structure of the developed neural network model

Full size image

The mean squared error values for training and test data are 41.31 and 28.58, respectively. Similarly, the R2 value for training and test data is near 80%. This means that there is no issue of underfitting or overfitting with this model. The performance of the model can still be improved if more data are obtained, but it does not provide any unrealistic figures, which was the case with the random forest regression model. The performance model of ANN based on the test data, and the epoch with accuracy and loss is depicted in Fig. 18. This shows that the neural network has the greatest potential for performing using this kind of data (from varied distributions) if collected in large quantities.

Fig. 18
figure 18

Performances model of ANN on training and test data

Full size image

Feature Importance: The intuition behind permutation importance is straightforward. The only requirement is to have fitted a model, either for regression or classification. If a feature is deemed unimportant by the model, it can be shuffled (rearrange the rows) with little effect on the model’s performance. On the other hand, if the feature is relevant, shuffling its rows will negatively affect the prediction accuracy.

According to the feature importance of the neural network model (Fig. 19), the powder factor is the most important feature in the RFR, SVR, and XGBR models. The burden is the least important feature in the determination of rock fragmentation, as found in the RFR model. Other features show more significance compared to the results of the other models.

Fig. 19
figure 19

Feature importance of ANN model

Full size image

4.5 Residual plots

The model behaves as expected and in accordance with the NN concepts. According to the histogram generated shown in Fig. 20 residuals follow a normal distribution with a mean of 0. This means the residuals satisfy the constant variance assumption for the unbiasedness of ordinary least squares estimators (mean squared error) and show that the selected features are optimal for the prediction of rock fragmentation.

Fig. 20
figure 20

Residual plots: a histogram of residuals and b kernel density estimation

Full size image

The second graph is a kernel density estimate (KDE) plot, which is a method for visualizing the distribution of actual and predicted values, analogous to a histogram. It shows that the predicted values of rock fragmentation are in line with the corresponding actual values. The range covered is 25 to 100 for predicted values and 25 to 90 for corresponding actual values. The central tendency for both values is near 45, which shows that the model provides the same statistical observations as the actual rock fragmentation value for the predicted rock fragmentation value.

Partial dependence plots: Permutation importance allowed us to identify the most important variables in terms of predicting rock fragmentation. The next question comes naturally: What is the effect of such variables on the value of rock fragmentation? In the world of linear models, this question is answered by looking at the coefficients. In the black-box world, we look at the partial dependence plots (PDPs).

The underlying idea behind these plots is to marginalize the effect of one or two variables over the predicted values. When a neural network has several features and layers, it is hard or even impossible to assess the impact of a single feature on the outcome by simply looking at the coefficients. Instead, the marginal effect is approximated by a Monte Carlo approach. We run predictions for a set of features and then average them over the features whose effects we are interested in. The partial dependence plot is depicted in Fig. 21.

Fig. 21
figure 21figure 21

Partial dependence plot of powder factor, spacing, number of holes, burden, and specific drilling

Full size image

From the following figures, we can draw several conclusions:

  • Higher values of spacing, burden, and specific drilling lead to higher values of rock fragmentation.

  • The change in the number of holes has a negligible impact when there are more than 40 holes. There are some cases (number of holes less than 40) where the relationship with rock fragmentation is positive. This means the effect of the number of holes on rock fragmentation stabilizes after a value of 40.

  • The powder factor has a decreasing effect on the value of rock fragmentation with its increasing value, which was also confirmed earlier with a correlation plot.

Shapely values: Shapely values contribute to understanding the model in an analogous way to coefficients in a linear model. Given a prediction, how much of it is affected by the explanatory variables? What features contribute positively and negatively?

The Shapely value is the average marginal contribution of a feature value over all possible combinations of the other features. Shapely values are useful for understanding the contributions of the features of the model when we produce a prediction. Shapely values answer “why” the prediction is different from the mean prediction. As you can see in Fig. 22, it shows the feature importance of the input and output parameters of the study. Based on the shapely value the powder factor (PF) is the most important feature. Figure 23 shows the future importance of combined support vector regression, random forest regression, XGBoost regression, and ANN results.

Fig. 22
figure 22

Shapely values for the input parameters based on their future importance

Full size image
Fig. 23
figure 23

Future importance of combined support vector regression, random forest regression, XGBoost regression, and ANN results

Full size image

Each row corresponds to a feature, the colour represents the feature value (red high, blue low), and each dot corresponds to a training sample.

From the combined Shapely plot values, we conclude the following points:

  • The powder factor is the feature with the highest impact. We discovered this previously when calculating the permutation importance. Nevertheless, it is always a good idea to double-check the conclusions. The effect of specific drilling is opposite to that of the powder factor: higher specific drilling levels imply more rock fragmentation.

  • Burden and spacing seem somewhat irrelevant because these factors have the least impact, unlike the value of powder factor. They may also be removed from the model.

4.6 Combined support vector regression, random forest regression, XGBoost regression and ANN results

In our investigation, we utilized a combination of support vector regression, random forest regression, XGBoost regression, and artificial neural networks (ANN) future importance to analyze the factors influencing rock fragmentation (see Fig. 23). Across all models, the powder factor consistently emerged as the most influential factor sha** fragmentation outcomes. But the importance of other variables varied depending on the model used.

  1. 1.

    Random forest regression and ANN: Random forest regression and ANN excel at capturing complex relationships and nonlinear dependencies within the data. In our analysis, specific drilling exhibited higher importance in these models due to its potential nonlinear relationship with fragmentation. Conversely, burden had relatively lower importance in these models, as it was highly correlated with spacing, which the models deemed more crucial. In such cases, the models prioritized capturing the variability introduced by other variables over burden.

  2. 2.

    Support vector machine and XGBoost: Support vector machines (SVM) and XGBoost are two widely recognized machine learning models renowned for their ability to handle high-dimensional data and capture complex decision boundaries. We observed that specific drilling exhibited less importance compared to burden in these models. This observation aligns with the notion that SVM is particularly well-suited for capturing linear relationships within the data. Upon closer examination of our dataset, we noted that specific drilling and the number of holes exhibited nonlinear relationships with the output variable. XGBoost prioritize variables that directly contribute to minimizing the loss function.

Overall, the differing importance of specific drilling and burden in feature importance analysis across different machine learning models reflects their distinct capabilities in capturing and prioritizing different types of relationships and patterns in the data.

The training and testing results of random forest regression, support vector regression, XGBoost regression, and neural network are summarised in Fig. 24.

Fig. 24
figure 24

The training and testing results of random forest regression, support vector regression, XGBoost regression, and neural network

Full size image

This research has huge implications for the mining industry. Machine learning can measure rock fragmentation after blasting to increase mining efficiency and productivity. Precise, real-time fragmentation data can enhance blasting configurations and ore extraction, decreasing operating costs and enhancing profitability. Rock fragmentation improves mining design, resource use, and environmental impact. This research can improve mining practices.

5 Limitations and future works

Despite the promising results obtained from our study on predicting rock fragmentation in open pit mining through machine learning algorithms, it is crucial to acknowledge certain limitations that may impact the generalizability and application of our findings. First and foremost, the dataset used in this study consisted of 219 data sets, which, while sufficient for our purposes, could be considered relatively small in the broader context of machine learning. Future research endeavors should aim to expand the dataset to improve the robustness of the predictive models and enhance their applicability across various geological and operational conditions. Additionally, the decision to eliminate certain parameters, such as drill diameter, average bench height, compressive strength, stemming, and charge per delay, was made to simplify the model. However, it is essential to recognize that these factors may still influence rock fragmentation under specific geological circumstances, suggesting avenues for further exploration. Because those parameters exhibited nearly identical values across the dataset, indicating constrained variability and that is the one of the reasons for eliminating them. This restricted range of variation is indicative of the specific geological conditions and operational constraints inherent to our study area. Future research endeavors may benefit from exploring alternative datasets or incorporating additional geological and operational factors to provide a more nuanced understanding of these parameters and their implications for blasting outcomes.

Moreover, the complexity of the chosen neural network architecture should be noted, and a balance between model complexity and interpretability should be considered. Future studies might explore simpler architectures for practical implementation. Another consideration is the applicability of the developed models to different mining conditions. Our study focused on open pit mining with specific parameters, and future research could investigate the transferability of the models to diverse operational environments. Exploring the integration of sensor data for real-time monitoring and adaptation of blasting operations could also be a promising avenue for future research, enabling more dynamic and responsive predictive models. Lastly, efforts should be directed toward collaborative initiatives with industry stakeholders to integrate the developed models into existing operational practices, fostering practical tools for optimizing blasting operations in real-world mining scenarios. Addressing these limitations and pursuing these future research directions will contribute to the continued advancement of rock fragmentation prediction in mining operations.

6 Conclusions

This study demonstrates the potential of machine learning algorithms to greatly improve the assessment of rock fragmentation in mining blasting operations. The findings of our research indicate that the utilization of these algorithms provides a reliable and effective method for predicting and evaluating fragmentation patterns. Our employed approach deviates from conventional techniques utilized in fragmentation evaluation, as it leverages the computational power and predictive capabilities of machine learning. A Python programming tool is used to pre-process the data and train the model. In this study, various ANNs and machine learning models were tested for predicting rock fragmentation in limestone mine blasting. A database with 219 datasets was used to train the ANN model and various machine learning models. The factors burden, spacing, number of holes, powder factor, and specific drilling were considered as model input parameters to anticipate output fragmentation, and thereby produce more accurate prediction models, i.e., the same independent and dependent variables were subjected to ANN, RFR, SVR, and XGBoost regression analysis. Networks with designs of 5-64-32-16-1 were discovered to be ideal for ANN modeling. Testing datasets were used to evaluate the effectiveness of the developed models. To compare anticipated outputs from ANN and machine learning models with actual outputs, the metrics MAE, MAPE, RMSE, R2, and MSE were calculated. It was discovered that the ANN model performs better than the support vector regression, XGBoost regression, and random forest regression models in terms of accuracy and general fitting on the dataset. From the permutation importance and Shapely values, it can be deduced that input features such as powder factor and features such as burden are the most and least effective parameters, respectively, for predicting the outputs. Finally, for future research, it is advised that more data be obtained with prescribed input features to create a more complex model that can outperform the models proposed here in terms of data fitting.

The results obtained in this study show promise and indicate a level of performance that is comparable to, if not superior to, the findings documented in previous research. Other conclusions can be summarized as follows:

  • The study has substantial implications for the mining industry. By incorporating machine learning techniques into their operational processes, businesses can potentially achieve enhanced accuracy in managing blasting outcomes, reduce operational expenses, and enhance worker safety.

  • Moreover, the application of the machine learning methodology for evaluating fragmentation can function as a valuable decision-making instrument during the initial phases of mining endeavours.

  • Future investigations could potentially explore alternative machine learning algorithms or hybrid models to further improve the optimization of fragmentation assessment with more datasets.

Additionally, the methodologies utilized in this study possess the capacity to be extended to diverse domains within the mining industry, thus presenting new opportunities for the application of machine learning methods in mining operations. In conclusion, this study demonstrates the efficacy of machine learning algorithms in improving the assessment of rock fragmentation in mining blasting activities.