1 Introduction

Hyperthermia is one of the cancer treatment processes, which involves increasing the temperature of tumor-containing tissues, usually up to more than 42 degrees Celsius, to destroy cancer cells. Usually used in combination with other cancer treatment method, hyperthermia direct heats and destroys surface tumors on the skin. By increasing the temperature and metabolism of the target cell and tissue, this technique can significantly improve the performance of radiotherapy and chemotherapy [1].

Owing to the increase of blood circulation and oxygen in the tumoral tissue and stabilization of the damages applied to the DNA of the tumoral tissue, it is important to reduce the length of radiotherapy treatment in hyperthermia, e.g. once per week. This is critical for recurrent patients who cannot receive a high dose of radiation. On the other hand, the effectiveness of chemotherapy related drugs can be increased by increasing blood circulation in the target tissue through hyperthermia [2, 3]. Different methods of hyperthermia currently under study include whole-body, regional and local hyperthermia. In local hyperthermia, heat radiates to a small area such as a tumor through various energy transfer techniques to heat the tumor. Different types of energy are used to produce heat, including microwave energy, radio frequency, and ultrasound. Depending on the tumor location, different methods are available for treatment of local hyperthermia. One of the methods is applying an external heat to treat tumors just below the skin. External heat-generating devices are placed above an appropriate area, and energy is focused on the tumor to increase the applied temperature [4,5,6]. Hyperthermia is useful when only heat is delivered to the target tissue locally without affecting adjacent healthy tissues. This is similar to radiotherapy in which a high dose of waves must be radiated to the tumoral tissue, while ensuring a minimal dose to adjacent healthy tissues. Non-homogeneous distribution of heat to all tumor cells, an insufficient amount of heat, and unwanted heat treatment of healthy cells are the fundamental challenges of current hyperthermia methods [7]. In this respect, current active research studies on hyperthermia are focused on designing suitable heat-generating devices to focus the heat on the tumoral tissue and kee** other healthy tissues away from the heat, as well as preventing burning of the skin surface [8]. In the existing literature, the design of antennas normally considers resonance at the desired frequency, and no specific solutions are available to focus on a target region [9,10,11]. In some studies, array antennas are used to prevent further damage to healthy tissues. By changing the input phase between the elements of an array antenna, the radiation beam can be controlled properly [12,13,14]. There are various issues with hyperthermia antenna design, which can be classified as follows: (a) The antenna size may not be suitable for the size of the target tissue. (b) The presence of unwanted radiation, which can sometimes be strong, on the healthy tissue adjacent to the target tissue. (c) The failure to optimize the characteristics of the interface layers used to protect the skin surface from damage. (d) Simulation of the moment method and the absence of time analysis in the simulation field.

In recent years, several studies have been conducted to address these issues. The design of very small antennas capable of being arrayed in the desired dimensions [15, 16], focusing hyperthermia energy to prevent damage to healthy tissues [17, 18], optimizing the water bolus layer to avoid burns on the skin surface [19, 20], and carrying out time analysis of hyperthermia have been part of these studies [21]. However, a review of these studies reveals that each article only investigated and sometimes optimized one problem area. The modified parameters in each study may not be compatible, which means that achieving one goal can result in the violation of other goals. Achieving a compromise between different antenna parameters requires a comprehensive study of an antenna in the field of hyperthermia.

In this paper, we present the design of an antenna that is specifically tailored for chest hyperthermia. The antenna is equipped with an Artificial Intelligence (AI)-based system that helps to localize heat on specific areas that contain tumoral tissues. Optimization has been done in such a way that to ensure that the interface layers of water bolus and silicone are of the highest quality to prevent any superficial skin burns. On the other hand, During the energy application process, FDTD analysis provides the entire time profile of hyperthermia. The antenna radiation and body tissue reaction are simulated using the Finite Difference Time Domain (FDTD) method, while the Particle Swarm Optimization (PSO) algorithm is leveraged to optimize the antenna parameters such that the spatial error with respect to the location of thermal focus is minimized. In our study, the necessary large number of computations justifies the use of the PSO algorithm, which has a higher convergence speed as compared with other algorithms such as the genetic algorithm. Based on our previous studies [22,23,24,25,26], a microstrip antenna with parametric physical characteristics is selected in this work. The associated antenna parameters are optimized such that the antenna resonance occurs at the desired frequency. In addition, heat transfer to the tumoral site located at a depth of three centimeters of the muscle needs to take place in the best possible way. We design the antenna and evaluate its usefulness with simulations, and compare the results with actual laboratory experimental outcomes. In addition to lightweight and small size of the antenna design, one of the important factors in hyperthermia antennas is to maximize the ratio of electric fields parallel to the skin surface with respect to electric fields perpendicular to it. By maximizing this ratio, the penetration depth of electromagnetic waves inside the tissue is optimized [27]. Avoiding excessive proximity between the antenna and the skin surface, on the one hand, and reducing the thickness of the water bolus to prevent energy loss in the water, on the other hand, are among the challenges in designing effective hyperthermia antennas [28]. These issues are considered in our work.

In Sect. 2, we delve into the initial antenna design and its interaction with body tissue. The propagation of waves within these mediums is simulated employing the FDTD method. Additionally, we introduce the PSO algorithm and its associated fitness function. Section 3 examines the performance of the proposed antenna utilizing the outcomes derived from the PSO. Subsequently, this section showcases the experimental findings from the fabricated antenna, compared to the simulation results. An analysis and discussion follow. Finally, Sect. 4 offers concluding remarks.

2 Methodology

Hyperthermia techniques have gained attention as a therapeutic process for malignant tumors, and they can be used in two different ways. The first method, which has recently faced serious criticism, involves the creation of intense heat in the area of malignant tumors with the aim of burning them. In this method, horn antennas are widely used since they have high directivity and can provide concentrated heat to burn the targeted tissue section.

Horn antennas for hyperthermia also have significant drawbacks: 1- The large and non-flat size of these antennas results in a bulky stature for hyperthermia applicators. 2- The very narrow bandwidth of horn antennas can be seen as their most critical flaw when used as hyperthermia antennas. The expected differences in the thickness of skin and fat of tissues facing these antennas create changes in the radiation characteristics of the antenna and the narrow bandwidth will cause problems in these cases. 3- Compared to antennas like microstrip antennas, horn antennas are considered to be high-cost.

The second area of hyperthermia technique applications involves generating heat, not necessarily intense, but merely to warm the targeted tissue area to 42 degrees Celsius. In this scenario, hyperthermia is used as an adjunctive therapeutic method along with chemotherapy. Given the drawbacks mentioned for horn antennas on one hand, and the lack of need for intense heat at a specific location on the other, antennas other than horn antennas, such as microstrip antennas, have become suitable candidates for use in hyperthermia.

Another important reason for the use of microstrip antennas is the simplicity of creating array combinations from this category of antennas. Microstrip array antennas offer capabilities such as more precise adjustment of the heating location or creating thermal scans for tissue. According to the authors, with the aim of extending the current research to the future use of optimized array microstrip antennas, a microstrip antenna has been considered for this article.

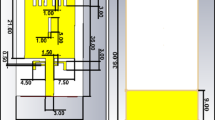
The frequency range for hyperthermia applications is between 300 and 600 MHz. In this study, the antenna is designed to operate at a resonant frequency of 433 MHz, i.e., the Industrial, Scientific, and Medical (ISM) band. This is the most utilized frequency band in hyperthermia technology across many country [29, 30]. Figure 1 depicts the base shape of our antenna design.

Fig. 1
figure 1

Geometry of the proposed hyperthermia antenna a Top plane, b Bottom plane

Full size image

The dimensions and parameters specified in Fig. 1 are optimized such that the antenna resonant frequency is set at 433 MHz, while meeting other desired hyperthermic characteristics of antenna.

It has been decided to use aluminum as the conductive material for the patch and ground sections of the antenna, based on the satisfactory results obtained in the previous study [23]. However, simulations have shown that copper can also be used without any significant difference. The permittivity of the antenna substrate has been taken into account for optimization purposes. By combining Teflon with materials like alumina, glass powder, etc., the permittivity can be altered effectively within the range of 1.8 to 4.2. The range of permittivity variations has been chosen within this same range.

Our previous studies have proven that the existence of a silicon layer can improve penetration of the electric fields into the muscle tissue [24]. As such, a silicon layer is added to our antenna structure. The thickness of this layer is one of the parameters for optimization. Figure 2 shows the layer structure of our proposed antenna.

Fig. 2
figure 2

Layers of the proposed hyperthermia applicator

Full size image

The antenna is fed by a 50-Ω coaxial cable. As shown in Fig. 1b, the connection point of the coaxial cable's inner conductor has been considered in the optimization process. The materials for both the inner and outer conductors of the coaxial cable have been selected as copper. (There was no access to coaxial cables with aluminum conductors in the laboratory). The inner and outer diameters of this cable are considered equal to 0.6 and 3 mm. Additionally, the insulating material used in the coaxial cable is polyethylene. Coding the FDTD for the coaxial feed line was one of the significant challenges in this article. For accurate simulation, the metal sheath of the cable and the electromagnetic field outside the metal sheath are solved using the FDTD method, and the wave phenomena inside the metal sheath are solved based on transmission line theory. Therefore, the effects of the coaxial cable’s metal sheath, the transmitted wave inside the cable, and the wires connected to the cable’s inner conductor are considered simultaneously. Despite the simulations carried out, to prevent signal attenuation, SMA connectors with gold plating were used in practice to connect the coaxial cable to the antenna. The length of the coaxial cable in the laboratory for practical results assessment was 80 cm. Employing a microstrip feeding line for the antenna, in addition to its great simplicity compared to the coaxial feeding line, would also provide more possibilities for impedance matching. However, due to the lack of laboratory facilities for microstrip line feeding, a coaxial feeding line was used.

After determining the main shape of the antenna structure, its dimensions and various parameters need to be optimized such that the resonant frequency is at 432 MHz and the target tumoral tissues are exposed to maximum heating. We employ the FDTD method to solve Maxwell's equations of the electromagnetic fields. With a properly-defined fitness function, the PSO algorithm is used to optimize the antenna parameters. Figure 3 illustrates a block diagram of the implemented solution for designing our hyperthermia antenna and optimizing its parameters.

Fig. 3
figure 3

Block diagram of our solution for designing the antenna and optimizing its parameters

Full size image

2.1 FDTD analysis of the antenna electromagnetic fields

According to the cubic structure of the antenna proposed in this study, the analysis of electromagnetic fields is formulated in a Cartesian coordinate system. The FDTM method is utilized to solve Maxwell's equations. The main features of our implemented method are as follows:

  • Cubical of the body tissue pertaining to the antenna, despite its heterogeneity, is assumed to have a fixed grid step size in accordance with the X, Y, and Z dimensions. Both X and Y dimensions have the same setting, which is different from that in the z dimension;

  • A Transverse Electromagnetic (TEM) wave is set up in the feed point of the antenna, along with consideration of the power supply. Using the technique proposed in [31, 32] for tackling the scattering problems, the electric and magnetic fields are computed.

  • To model the absorbed waves propagating in the z direction inside the applicator, the Bayliss-Turkel boundary conditions are applied. In addition, to model the reflected waves propagating in the z direction outside the applicator, the Moore condition is used [33, 34].

  • Using the Pennes bioheat equation, the temperature analysis associated with the two-dimensional tissue sections is conducted [35].

Figure 4 shows the placement of the body tissue, water bolus and silicon layers above the antenna.

Fig. 4
figure 4

Placement of the body tissue, water bolus and silicon layers above the antenna

Full size image

The thickness of various tissue layers in the body, such as skin, fat, and muscle, and the thickness of the water bolus are essential parameters in determining the resonance frequency of an antenna and the level of heat penetration into the tissue. In studies on hyperthermia, skin thickness has been considered to range from zero (ignoring the presence of skin) to three millimeters. Additionally, different articles show that the thickness of fat in the body can vary between one to three centimeters. Depending on the target location for hyperthermia, varying fat thicknesses are taken into account. For neck hyperthermia, the minimum possible thickness is considered, while for abdominal organ hyperthermia, the maximum possible thickness of fat is taken into account.

It’s important to note that muscle thickness can vary slightly when measured in simulation conditions compared to natural scales. In simulation environments, the end of the muscle section is also the end of the simulation structure. Therefore, if the muscle thickness is not considered sufficiently thick, reflected waves from the end of the structure towards the target space can occur. This results in a higher heating level than what would be seen in reality. To avoid this issue, the muscle should be considered to be thick enough. In laboratory conditions, the space behind the muscle is free space, allowing possible waves exiting the muscle to flow into it.

In this article, to create consistency in simulation results, the thickness of skin and fat is assumed to be equal to the thickness of laboratory-tested tissue (chicken breast). The skin thickness is assumed to be 2 mm, and the fat thickness is assumed to be 1.4 cm. Also, due to the reasons mentioned, the muscle thickness is assumed to be 20 cm. In superficial hyperthermia, the thickness of the water bolus is typically a few millimeters to one centimeter. However, in deep hyperthermia, the thickness can range from one to several centimeters. If the water bolus thickness increases, there will be a significant decrease in the transfer of thermal energy into the tissue. This article focuses on simulations where the water bolus thickness is precisely one centimeter, which closely aligns with the experimental value.

2.2 PSO for optimization of the antenna parameters

Among many evolutionary algorithms, the PSO algorithm is capable of achieving a balance between local and global exploitation and exploration in the search space, in addition to having a high speed of convergence [36,37,38,39]. This unique property of PSO overcomes the problem of premature convergence and increases the search capacity, making PSO different from the GA and other heuristic algorithms.

The PSO algorithm is inspired by the social behaviors of living organisms such as flocks of birds and schools of fish. In this algorithm, the particles (which encodes the problem variables) conduct multi-dimensional searches through the problem solution space. During the search process, each particle adjusts its location according to its previous positions and the best particle’s position [40]. The particle momentary motion relationship is defined as follows:

$$v\left( {t + 1} \right) = w\left( t \right)v\left( t \right) + c_{1} r_{1} \left[ {P_{Personal - Best} \left( t \right) - x\left( t \right)} \right] + c_{2} r_{2} \left[ {P_{Global - Best} \left( t \right) - x\left( t \right)} \right]$$
(1)

where \(v\left( {t + 1} \right)\) and \(v\left( t \right)\) are the particle's new and previous motion vectors, respectively. \(w\left( t \right)\) is the weight of the previous motion direction. Personal-Best indicates the best position among the particle’s previous positions Global-Best indicates the current best particle position. \(x\left( t \right)\) is the previous particle location. \(c_{1}\) and \(c_{2}\) are coefficients of motion acceleration with respect to the direction of the best position among the particle’s previous positions and the direction of the current best particle, respectively. while \(r_{1}\) and \(r_{2}\) are two random numbers to prevent the algorithm’s pre-mature convergence toward the best local position too quickly [41, 42]. All the parameters in Eq. (1) are considered in an N-dimensional space. The PSO parameters ranges are listed in Table 1. Owing to the difference in the variable limits, it is inappropriate to consider the same acceleration for their movement.

Table 1 Parameters of implemented PSO algorithm
Full size table

According to Fig. 5, the PSO fitness function includes two main elements:

  1. 1.

    DHotSpot: spatial distance between the hot spot in the layers of muscle tissue and the target location

  2. 2.

    DS11: the difference in the return loss of the antenna at the resonant frequency of 434 (MHz) with respect to the reference value of − 20 (dB).

Fig. 5
figure 5

Two elements of the PSO fitness function: a spatial distance between the hot spot and the target location, b the difference of the return loss at the resonant frequency of 434 MHz with respect to -20 dB

Full size image

The fitness functions can be formulated as:

$${\text{Fitness}}\,{\text{Function}} = \alpha_{1} {\text{D}}_{{{\text{HotSpot}} \to {\text{Target}}\,{\text{(Tumoral Tissue Location) }}}} { + }\alpha_{{2}} {\text{D}}_{{{\text{S}}_{{{11}}} {\text{ at 434 MHz }} \to {\text{ - 20 dB Line }}}}$$
(2)

where α1 and α2 are the weight parameters.

The return loss graph presented in Fig. 5b was extracted using the initial parameters of the antenna structure (unoptimized) with the aid of the full-wave analysis software CST. Two main resonances occurred at frequencies of 310 (0.31*10^9) and about 430 (0.43*10^9) MHz. The optimization objectives are: 1- Stabilizing the frequency at 433 MHz, and 2- Achieving a return loss value of -20 dB at this specified frequency. The following reasons justify why the elimination or suppression of the 310 MHz resonance frequency has not been set as an optimization goal:

  • Increasing the number of optimization goals could reduce the precision of the optimization algorithm. Adding a third goal may result in the resonance frequency not being fully stabilized at 433 MHz or the return loss value not settling near − 20 dB.

  • According to the authors' previous study [23], the proposed antenna structure has the potential for dual-frequency resonance. Therefore, completely suppressing the second resonance frequency may not be feasible. Defining the suppression of the unwanted resonance frequency (310 MHz) as an optimization goal will likely lead to suboptimal performance of the optimization function in reducing the fitness value.

  • It is likely that by optimizing the antenna parameters to transfer the main resonance frequency to 434 MHz, the effect of the subsequent resonance frequency will be reduced. This is expected as dual-resonance antennas generally have a strong primary resonance and a weaker secondary resonance compared to the first one.

3 Results and discussion

As can be observed from Fig. 6, the PSO algorithm is able to minimize its fitness function, after about 80 iterations of particle movement. The decreasing trend of the fitness function indicates convergence of the search performance, while flatness of the curve toward the final steps indicates that the best possible solution is achieved. After the search process, the position of the best particle, which include the optimized parameters of the antenna, is obtained, as presented in Table 2.

Fig. 6
figure 6

Decreasing curve of the PSO fitness function, which indicates convergence of the search process toward the best position

Full size image
Table 2 The optimized parameters of hyperthermia applicator
Full size table

3.1 Specific absorption rate (SAR)

The SAR is used to determine the amount of heat created in the tissue. It indicates the amount of energy absorbed in the tissue and its conversion into heat, and can be obtained as:

$$SAR = \frac{{\sigma E^{2} }}{\rho }$$
(3)

where E is the absorbed electric field by the tissue, σ and ρ are the conductivity and density of the tissue, respectively [24]. Considering the optimized parameters of the antenna, its return loss and the cell SAR in different layers cut to a depth of three centimeters from the muscle, are shown in Figs. 7 and 8, respectively.

Fig. 7
figure 7

Return loss of the optimized antenna in simulation with the FDTD method

Full size image
Fig. 8
figure 8

Cell SAR in different layers of the muscle tissue: a K = 113, Depth = 30 mm, b K = 75, Depth = 20 mm, c K = 37, Depth = 10 mm, d K = 18, Depth = 5 mm

Full size image

As depicted in Fig. 7, the resonant frequency occurs at 434 MHz. Its good accuracy, along with the good performance of the PSO algorithm, is due to the following reasons. Firstly, according to previous studies, the ranges of antenna dimensions are selected such that the resonant frequency range is close to the desired frequency. Secondly, by choosing a suitable value of α2 (higher than α1), the weight of the resonant frequency in the fitness function is increased; therefore, the PSO algorithm is able to act rapidly to achieve the good result.

The relatively good performance of the PSO algorithm in determining the hotspot can be observed in Fig. 8. As expected, the hotspot occurs in the first layer of the muscle tissue; while the optimized x and y coordinates of the hotspot are acceptable. The structure of the applicator and tissue are simulated using the Ansoft software. The outcomes are used for comparison with the results of FDTD-based simulations.

In FDTD analysis, the cells created in the structure along the x, y, and z directions have specific dimensions. The height of the dividing cells in the z dimension of the structure is assumed to be 0.265 mm. Therefore, the accuracy of the structural height, which indicates the level of heat penetration into the tissue, will be 0.265 mm. In Fig. 8, both the precise height and the cell number in the height dimension of the structure are simultaneously presented. It is evident that the thermal map applied in this figure also has the same 0.265 mm accuracy. It can be said that cell 'k' represents a height of k * 0.265 mm from the ground surface of the antenna. Reducing cell length improves accuracy but increases computation and execution times based on FDTD simulations.

The SAR from Ansoft, which uses the Moment Method, is shown in Fig. 9. The results from Ansoft confirm the accuracy from the FDTD method. It should be noted that the SAR in Fig. 9 is related to a side view of the tissue. The presence of two parts of the muscle under more heat, on the one hand, and one of them being hotter than the other, on the other hand, confirms the accuracy of the FDTD-based method.

Fig. 9
figure 9

Simulated SAR in the tissue using the Ansoft software

Full size image

3.2 Temperature analysis

Using the Pennes bioheat transfer equation, the temperature of different areas of the target layer can be determined, which yields:

$$\rho c\frac{dT}{{dt}} = \nabla k\,\nabla T + Q_{r} + Q_{m} - \rho_{b} c_{b} w_{b} (T - T_{b} )$$
(4)

where \(\rho\) is the tissue density, \(c\) is the specific heat capacity, T is the tissue temperature, k is the thermal conductivity, Qr is the regional heat generated by SAR and Qm is the power generated by metabolism; while \(\rho_{b}\), \(c_{b}\), \(w_{b}\), and \(T_{b}\) are the blood density, specific heat capacity of the blood, blood perfusion, and blood temperature, respectively.

In Table 3, the parameters in Eq. (4) are presented for different environmental settings. The SAR results are used to replace the heat sources in the Pennes bioheat equation. In addition to the values in Table 3, the amount of blood perfusion equals to 0.03 ml/(100 g.min) and the initial blood temperature equals to 36.8 degrees Celsius [35].

Table 3 The values of the parameters in Pennes bioheat equation presented for different environments [43]
Full size table

By using Eq. (4), the cell temperature of the three-centimeter depth layer of the muscle (the target layer) is calculated. Figure 10 shows the results after iterating the Pennes bioheat equation until approximately 1288 s.

Fig. 10
figure 10

Cell temperature of the target layer after about 1088 s from the start of hyperthermia

Full size image

In the optimization objectives pursued, three main goals have been considered:

  • Stabilizing the resonance frequency at 434 megahertz.

  • Ensuring a return loss of less than − 20 decibels at the target resonance frequency.

  • Generating maximum SAR (Specific Absorption Rate) at the target location (tumor).

Considering that achieving the third goal without accomplishing the first and second objectives would be futile, each objective has been assigned a weight based on its impact. As shown in Fig. 6, the PSO algorithm’s convergence function varies and eventually reaches a certain level of error. While it’s possible to minimize this error by adjusting the weights assigned to objectives, it’s impractical to adjust them in a way that precisely places the maximum SAR at the tumor location while also maintaining the stability of the resonance frequency at 434 megahertz and reducing the return loss.

In order to make the optimization process as clear as possible, the paper assumes that the tumor dimensions are 1 * 1 * 1 cubic centimeters. Considering the diverse dimensions of actual tumors, employing larger dimensions allows disregarding any observed simulation errors to a significant extent.

3.3 Linear SAR

As mentioned earlier, the amount and manner of heat penetration into the tissue is one of the challenges in designing hyperthermia antennas. By using a linear SAR, a better understanding of this penetration can be obtained. Linear SAR is the maximum amount of SAR in the tissue along a straight line towards its interior.

Figure 11 shows the linear SAR results from Ansoft (with the Moment Method) and FDTD-based method. A good match between the two linear SAR results can be observed. The proposed structure (with a silicone layer next to the water bolus layer) is able to direct as much heat energy into the muscle as possible, which is in agreement with the observation in our previous studies.

Fig. 11
figure 11

Simulated linear SAR results from by the Ansoft software and the FDTD method

Full size image

It is important to note that the skin and fat are located closest to the antenna, which means that the highest SAR (specific absorption rate) will always be generated in these two mediums, regardless of the antenna type or technique used. However, it’s crucial to understand that the highest SAR doesn’t necessarily equate to the highest heat generation in these two mediums. This is because the skin, fat, and muscle have different thermal capacities, which result in different heat distributions.

Previous studies [23, 24] have demonstrated that adding a silicon layer with a water bolus reduces the amount of heat generated in the skin and fat layers. This was observed in a linear SAR graph that shows a decrease in the amount of heat present in the skin and fat layers when compared to previous studies that did not use silicon layers. It’s important to note that the reduced SAR in the skin and fat tissues does not necessarily mean a lower SAR compared to the muscle tissue. Instead, it means a lower SAR compared to the existing SAR in these layers when silicon layers are not used.

Figure 12a shows a view of the constructed antenna according to the specifications listed in Table 2, while Fig. 12b depicts the measured return loss of the constructed antenna. For obtaining measurement of the hyperthermia antenna in a laboratory experiment, it is necessary to place the tissue on the antenna. The characteristics of the body tissue undergo non-linear changes with respect to temperature variations. Therefore, the tissue temperature is raised to the human body temperature. Note that the differences between living and non-living tissues should be taken into account in laboratory measurement.

Fig. 12
figure 12

a The view of the constructed applicator (Antenna + silicon layer + water bolus), b Measured return loss of the constructed antenna

Full size image

In this study, chicken breast tissue is used to simulate human body tissue. To prevent the field reflection of the end of tissue, the muscle thickness is set to a high value during the simulation. Note that the end of tissue is considered a 100% reflective layer during the simulation. This is to ensure that the electric field drops sharply and reaches zero at the end of tissue if thickness of the muscle tissue is high. In the laboratory experiment, it is not necessary for considering thickness of the muscle tissue. However, thickness of the experimental muscle tissue (as well as the fat tissue) is approximately the same as the one considered in the simulation. In this respect, the skin is not very important in influencing the results due to its thinness.

The temperature of about 32 – 34 degrees Celsius is known as the standard temperature of non-living tissue in hyperthermia experiments. As such, before hyperthermic heating, a controlled temperature bath is used to stabilize the initial temperature of the tissue at about this temperature range. This initial temperature must be maintained in the outer area of the tissue until the end of experiment. Control of the temperature at the outer surface of tissue is accomplished manually. Temperature of the muscle target section is measured by using two Copper-nickel thermocouple sensor with a diameter of 50 mm, and the LABVIEW software is used for analysis. It is important to measure the temperature on both sides of the tumor site as uneven temperatures can complicate the treatment process. Therefore, two sensors are used to determine the temperature.

The study conducted in this article, as well as prior works, focuses on hyperthermia of the glands located in the chest (breast cancer). Therefore, to align with real conditions, the dimensions of the tissue under study are considerably larger than the antenna dimensions. The antenna dimensions of 128*121 square millimeters compared to the simulated tissue dimensions of 400*400*216 cubic millimeters are significantly smaller. The tissue height of 216 mm is important to ensure that the muscle tissue is deep enough to prevent the creation of reflective waves at its end. In laboratory settings, it may not be necessary to strictly adhere to this height due to the presence of enough free space at the end of the muscle tissue. However, if the lateral and longitudinal dimensions of the surface are not large enough, leakage waves from the antenna (waves not located on the antenna’s surface) will not be considered when calculating the heat generated within the tissue. Based on the information provided, the laboratory tissue considered with dimensions of 232*288*184 cubic millimeters, along with the coverage of the antenna’s lateral and upper waves and a relatively accurate simulation of real chest tissue, causes the antenna becomes hidden from both the top and side views.

Figure 13 shows the reported temperatures from two thermocouples placed at three-centimeter depth in the tissue. The sampling frequency is set to one Hertz, i.e. Fs = 1 Hz, with a duration of 30 min. The temperature data was recorded every one second, thus each sample will represent the temperature value for one second.

Fig. 13
figure 13

Temperatures reported from two thermocouples placed at 3 cm deep in the tissue

Full size image

As can be seen from Fig. 13, after about 12 min, the tissue starts to heat up and reaches a stable state at approximately 42 degrees Celsius. An influential issue in the laboratory test of hyperthermia antenna is the absence of blood perfusion in non-living tissue. Due to the lack of blood circulation in non-living tissue, radiant heat is able to heat the target area faster as compared with that in living tissue, which could burn the tissue. Therefore, with living tissue, the tissue heating time should be more than 12 min. In this respect, the time and amount of heat can be controlled by using an amplifier with a suitable output power.

In this article, the design of hyperthermia antennas has been carried out in such a way that there is virtually no air gap between the antenna structure and the tissue under study. The presence of an air gap causes a significant decrease in the thermal efficiency of the antenna in the tissue. For this reason, in almost all cases studied in the field of hyperthermia, the antenna structure (antenna along with water bolus and other related surfaces) is considered to be fully tangent to the tissue surface. On the other hand, the antenna's resonance frequency has been calculated under conditions where the tissue adheres tangentially to the antenna structure. Only Slight variations in the positions of the antenna and tissue are negligible in the resonance bandwidth. Significant changes in the location of the antenna and the tissue will change the frequency characteristics of the antenna drastically. Considering the points mentioned, placing the antenna perpendicular to the tissue (or at any other angle relative to the tissue), in addition to drastically reducing the thermal efficiency due to creating an air gap, will also cause a change in the antenna’s resonance frequency. Due to the relatively high power transmitted towards the antenna, a change in resonance frequency and subsequently creating a high-amplitude reflected wave can damage the source. Therefore, positioning the antenna in different states relative to the tissue has been avoided.

Tumor tissue has some distinctive thermal features compared to healthy muscle tissue, mainly due to having more blood vessels. The reason for these differences lies in the blood flow within the vessels of the tumor tissue, which experiences higher flow intensity with increased heat, leading to slightly more efficient cooling compared to healthy tissue. It is important to note that in all reported hyperthermia studies, non-living tissue has been used. Non-living tissue has different characteristics compared to living tissue due to the absence of blood flow. This results in higher heat generation within it. The reported outcome in this article, which achieved a temperature of 42 degrees Celsius over a 12-min duration, was based on non-living tissue. Therefore, if living tissue were used, it would require a slightly longer duration to achieve the same temperature. Using non-living tissue leads to a similar thermal profile between healthy and tumor tissues. The main difference between these two tissues is the increased blood flow in the tumor tissue, which is not present in the non-living tissue. Therefore, the experiment used healthy tissue instead of tumor tissue. It is expected that if living tissue with a tumor was used, it would take more than 12 min to raise the temperature within the tumor.

4 Conclusions

In this paper, we have presented a preliminary design of an antenna structure for hyperthermia applications. The FDTM method has been employed to analyze the propagation of waves inside the antenna structure and the tissue placed on the antenna. The PSO algorithm has been utilized to optimize the antenna parameters in such a way maximum heating is delivered to the tumoral section of the muscle tissue at the antenna resonant frequency of 432 MHz. The error in the resonant frequency of the antenna is a few kilohertz (Return loss measured − 22 dB at 432.6 MHz), which can be ignored due to the resonance bandwidth. The target point has been heated only with a distance of a few cells (4 horizontal cells and 5 vertical cells), and favorable outcome has been achieved. The laboratory results using two temperature sensors indicate that after about 12 min, the temperature of the target area stabilizes at 42 degrees Celsius. The temperature recorded by the sensors is very close, indicating a homogeneous temperature distribution in the target area. In addition, according to the simulation results, other parts of the body tissue (non-target) suffer the lowest possible amount of heating. The simulation and laboratory results have indicated appropriate accuracy. The results are acceptable, even in the presence of unavailable errors from multiple sources, which include the use of non-living tissue in laboratory measurement, the construction of applicator especially the layer thickness, and the material composition for constructing the substrate with optimized relative permittivity.

For further research, several ways to further improve the proposed method are suggested as:

  • use an array antenna structure and optimize the phase difference of its array elements to heat the target tissue area.

  • use the shift antenna and optimize its shape to heat the target tissue areas.

  • use metamaterial layers and optimize their characteristics to achieve the best heating effect.