1 Introduction

In recent years, with China’s economy’s continuous development and Comprehensive National Power’s continuous improvement, tunnel engineering construction has developed rapidly [1, 2]. Deep-buried tunnels often face various geological hazards when crossing complex geological conditions, such as rock bursts, collapse, and large deformation of soft rock [3,4,5,6]. Tunnel engineering in the southwestern region of China is generally located in the Qinghai Tibet Plateau and its adjacent areas. This area is compressed by plate tectonics, which results in high tectonic stress [7], and the hydrogeological and geological conditions of the strata are complex. When constructing tunnels, it is inevitable to cause large deformation disasters [8]. The application of advanced stress release technology in advanced center drift can transform high-stress surrounding rock into low-stress surrounding rock by releasing in-situ stress in advance, thereby reducing rock deformation, which is of great significance for solving the problem of large deformation in tunnels [9].

Up to now, many scholars have conducted research on advanced stress-release technology. Under high ground stress, the Muzhailing Tunnel of the Lanzhou–Chongqing railway experienced severe large deformation during tunnel excavation. Yan et al. [10] analyzed the deformation of tunnel surrounding rock under the excavation of advanced pilot tunnel and bench method relying on the Muzhailing Tunnel. They concluded that the pilot tunnel during excavation is an effective method to control tunnel deformation. However, due to the large horizontal ground stress, the effect of the advanced pilot tunnel on controlling tunnel horizontal convergence is better than that of vault settlement. **a et al. [11] established a two-stage mechanical model for advanced center drift excavation based on the Lianchengshan Tunnel and derived the elastic–plastic solutions for excavating the middle and main tunnel. Liu [12] studied the application effect of the advanced center drift advance method in large cross-section mountain tunnels based on a particular railway tunnel. Guo et al. [13] analyzed and studied the deformation release law of surrounding rock under different sizes and positions of advanced center drifts through numerical simulation and proposed reasonable parameters corresponding to the advanced center drift when achieving an ideal stress release effect. Yan [14] conducted a field experiment on the advanced center drift in the Maoyushan Tunnel of the Lanzhou-Chongqing Railway and proposed a reasonable design scheme for the advanced center drift. Zhou et al. [15] obtained the deformation characteristics of the surrounding rock after excavating the advanced center drift through numerical simulation. The results showed that compared to three-step excavation, the advanced center drift method has a better control effect on the deformation of the surrounding rock. Zhang et al. [16] conducted stress release tests on the Muzhailing Tunnel and Maoyushan Tunnel using the advanced center drift method, and the results showed that compared to not using the advanced center drift method, the deformation during the expansion of the main tunnel can be reduced by about 30% to 40%. The above studies have all researched advanced stress-release technology. Among them, there is a comparison between the stress-release technology of the advanced center drift and the non-use of the advanced stress-release technology, and there is less research on the reasonable vertical position of the advanced center drift.

Therefore, this paper investigates the reasonable vertical position of the advanced center drift in response to the significant deformation issues encountered during the construction of the Haba Snow Mountain Tunnel in the Lijiang Section of the Yunnan Tibet Railway. The engineering overview is presented in Sect. 2, followed by the establishment of the numerical calculation model and condition design in Sect. 3. Section 4 analyzes the numerical calculation results, including tunnel deformation, initial support structure stress and plastic zone of surrounding rock, ultimately determining the reasonable vertical position of the advanced center drift. In Sect. 5, the field-measured tunnel deformations and support structure stresses are analyzed, clarifying the practical effectiveness of the advanced center drift. The research findings can serve as a reference for similar projects in the future.

2 Project overview

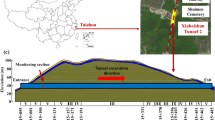
The Haba Snow Mountain Tunnel is a crucial control project of the Yunnan Tibet Railway Lijiang **angtan Line, which belongs to the mountain crossing tunnel. The tunnel is located in the middle of the Hengduan Mountains on the southeast edge of the Qinghai Tibet Plateau northwest of Yunnan Province, on the left bank of the **sha River. The mountain is located on the Chongjiang River and **sha River's eroded terrace, as shown in Fig. 1a.

Fig. 1
figure 1

Basic engineering information. a Landform of the Haba Snow Mountain Tunnel. b Section of Haba Snow Mountain Tunnel. c Geological Profile of Haba Snow Mountain Tunnel

Full size image

The starting and ending mileage of the tunnel is DK52 + 183 ~ DK61 + 706, with a total length of 9523 m. The maximum burial depth is DK58 + 900, with a maximum burial depth of 1155 m and a design speed of 140 km/h. The geological structure is complex, and the neotectonic movement is strong, making it a Class I high-risk tunnel. The main fault that passes through is the Natianzeng Fault, with an inclination angle of 35°–60°. The upper wall is schistose basalt, and the lower wall is sandy slate, slate mixed with limestone. The geological profile of the tunnel is shown in Fig. 1c, the central tunnel section is shown in Fig. 1b, and the composite lining parameters are shown in Table 1.

Table 1 Parameters for the composite lining of the main tunnel
Full size table

The Haba Snow Mountain Tunnel is deeply buried, and the geological structure and stress environment are complex. Serious large deformation problems occurred during the construction process, as shown in Fig. 2.

Fig. 2
figure 2

Large deformation of Haba Snow Mountain Tunnel. a Tunnel deformation due to overall squeezing. b The overall collapse of tunnel secondary lining

Full size image

3 Numerical model and condition design

3.1 Modeling

Establish a model using FLAC 3D finite element software [17, 18] with a model size of 120 m × 100 m × 80 m, Z direction as the direction of gravity. The average burial depth of the tunnel in this model is about 850 m, and the calculation model is shown in Fig. 3.

Fig. 3
figure 3

Calculation model

Full size image

The surrounding rock in the model adopts a joint model that can simultaneously consider the mechanical properties of the surrounding rock mass and joints [19,20,21]. The failure mode of surrounding rock mainly depends on its stress state and mechanical properties, such as joints, and may occur in the rock mass, along the joint surface, or simultaneously [22]. Tunnel support includes anchor rods, steel arches, and sprayed concrete. In the calculation process of this model, the anchor rods are simulated using the cable element in FLAC 3D and are made of elastic materials [23,24,25]. The values of parameters related to rock mass and structural planes are shown in Table 2. The physical and mechanical parameters of sprayed concrete, steel arch frame, and anchor rod are shown in Table 3.

Table 2 Physical and mechanical parameters of rock mass and structural planes
Full size table
Table 3 Physical and mechanical parameters of support structure
Full size table

The boundary conditions of the model adopt two types: displacement and stress. Establish a 3D model, as shown in Fig. 4. Conducting geo-stress regression analysis, it can be concluded that within the burial depth range of 800 m to 900 m, the average σx' is 19.7875 MPa, the average σy' is 21.7327 MPa, and the average τxy' is 19.9559 MPa. Apply it to the outer surface of the model in Fig. 3 to restore the initial stress field of the study area.

Fig. 4
figure 4

Geo-stress inversion model

Full size image

The displacement boundary condition adopts the method of zeroing the velocity of grid nodes, zeroing the nodes on the left and right sides of the model in the X direction, zeroing the velocity of grid nodes on the front and back surfaces of the model in the Y direction, and zeroing the velocity of grid nodes on the bottom surface of the model in the Z direction, thereby achieving displacement constraints on the model boundary.

3.2 Model validation

Select the displacement changes during the expansion of the main tunnel to verify the model. Assuming that the on-site excavation step corresponds to the excavation step in numerical simulation, only the mechanical behavior caused by excavation is considered in numerical simulation, and the impact of blasting on surrounding rock disturbance is ignored. The main tunnel expansion section with mileage DK55 + 740 was selected as the research section and the comparison between numerical simulation and on-site monitoring results is shown in Fig. 5.

Fig. 5
figure 5

Comparison of numerical simulation and on-site measurement values

Full size image

From Fig. 5, it can be seen that the difference between the numerical simulation scheme calculation results and the on-site monitoring of arch settlement and horizontal convergence values at the side wall is slight. After calculation, the differences in settlement of the arch crown and the horizontal convergence values of the left and right side walls are 9.52%, 10.76%, and 9.69%, respectively. The model can effectively simulate the construction methods used on site. The calculation results are relatively accurate, which can ensure the accuracy of the subsequent calculation results under different conditions.

Condition design. The design section area of the Haba Snow Mountain Tunnel is 115.98 m2, the width is 11.68 m, and the height is 12.49 m. The design’s cross-sectional area of the advanced center drift is 73.03 m2, with a width of 10.27 m and a height of 8.71 m. When designing the conditions for the position of the advanced center drift, the advanced center drift remains unchanged at the center line of the main tunnel, and the advanced center drift expansion is carried out after the advanced center drift is connected during simulation construction. Choose five conditions: the distance H between the advanced center drift and the arch top of the main tunnel is 1.0 m, 1.5 m, 2.0 m, 2.5 m, and 3.0 m, respectively. The position relationship between the advanced center drift and the main tunnel is shown in Fig. 6. The parameters of each condition are shown in Table 4.

Fig. 6
figure 6

The position relationship between the advanced center drift and the main tunnel

Full size image
Table 4 Parameters of various conditions
Full size table

4 Analysis of numerical calculation results

4.1 Vault settlement

During the model calculation process, the average settlement of the arch crown at the longitudinal mileage of Y = 30 m, Y = 40 m, and Y = 50 m sections was extracted, and the settlement values of the arch crown under different conditions were obtained as shown in Fig. 7a. From Fig. 7a, it can be seen that as the H value increases, i.e., the distance between the advanced center drift arch and the main tunnel arch increases, the final settlement value of the main tunnel arch generally shows a significant decrease and tends to stabilize. When H increases from 1.0 to 2.0 m, the settlement of the main tunnel arch decreases significantly from 0.482 to 0.374 m, and when H increases from 2.0 to 3.0 m, the settlement of the main tunnel arch decreases slightly from 0.374 to 0.362 m.

Fig. 7
figure 7

Tunnel deformation under different conditions. a Settlement value of arch crown under different conditions. b Horizontal convergence of steps under different conditions. c Horizontal convergence of steps under different conditions

Full size image

4.2 Horizontal convergence

During the model calculation process, the horizontal convergence values of the upper and lower steps of the longitudinal mileage Y = 30 m, Y = 40 m, and Y = 50 m sections were extracted and averaged to obtain the horizontal convergence values of the upper and lower steps under different conditions, as shown in Fig. 7b and c.

From Fig. 7b, it can be seen that when H = 1.0 m ~ 2.0 m, the average horizontal convergence value of the upper stage decreases due to the stress release effect of the advanced center drift. When H = 2.0 m ~ 3.0 m, the stress release effect on the upper step decreases as the position of the advanced center drift becomes lower, increasing the average horizontal convergence value of the upper step. When H = 2.0 m, the average horizontal convergence value of 0.830 m in the upper stage is the minimum. From Fig. 7c, it can be seen that as H increases, i.e., the position of the advanced center drift moves downwards, the stress release effect on the lower steps of the main tunnel becomes more and more apparent, and the average horizontal convergence value of the lower steps of the main tunnel shows a decreasing trend. When H increases from 1.0 to 2.0 m, the settlement of the main tunnel arch decreases significantly from 0.750 to 0.584 m, and when H increases from 2.0 to 3.0 m, the settlement of the main tunnel arch decreases slightly from 0.584 to 0.554 m.

In summary, by analyzing the arch crown's settlement and horizontal convergence values under different conditions, the most reasonable distance between the advanced center drift arch crown and the main tunnel is H = 2.0 m.

4.3 Initial support stress

Initial Support Stress. After tunnel excavation, the surrounding rock continuously undergoes deformation, and the support and surrounding rock will work together, gradually changing the stress on the support. When the tensile and compressive stresses of sprayed concrete support exceed the concrete's ultimate tensile or compressive strength, tensile cracking and fracturing failure will occur. The initial support adopts C30 sprayed concrete, with a compressive strength design value of fc = 14.3 N/mm2 and a tensile strength design value of ft = 1.43 N/mm2. To study the influence of different advanced center drift positions on the support stress of the main tunnel, this section further analyzes the initial support stress of the third layer under different conditions. The FLAC 3D numerical calculation software specifies that the tensile stress is positive and the compressive stress is negative.

The average maximum principal stress curve at each position of the initial support of the Y = 30 m, Y = 40 m, and Y = 50 m sections under different conditions is shown in Fig. 8a. From Fig. 8a, it can be seen that the maximum principal stress of the arch under all conditions is negative. As the H-value increases, the maximum principal stress of the arch first decreases and then slightly increases. The compressive stress at other positions gradually decreases and develops into a continuous increase in tensile stress. The average maximum principal stress values of the arch crown and left arch waist under different conditions do not exceed the tensile strength design value ft = 1.43 N/mm2. When the distance between the arch top of the advanced center drift and the arch top of the main tunnel is H = 2.0 m, the maximum principal stress at each position of the initial support of the main tunnel does not exceed the tensile strength design value. When H is more significant than 2.0 m, the maximum principal stress of the right arch waist and left and right side walls exceeds the tensile strength design value. Therefore, the distance between the advanced center drift’s arch top and the main tunnel’s arch top should be taken as H = 2.0 m.

Fig. 8
figure 8

Main stress curve of initial support under different conditions. a Maximum principal stress at different conditions. b Minimum principal stress at different conditions

Full size image

The average minimum principal stress curve at each position of the initial support of the Y = 30 m, Y = 40 m, and Y = 50 m sections under different conditions is shown in Fig. 8b. As shown in Fig. 8b, the minimum principal stress at each position of the initial support of the main tunnel is compressive. As the H value increases, the minimum principal stress at the arch crown first decreases and then increases, and only when H = 2.0 m does the minimum principal stress not exceed the compressive strength design value, which is 12.744 MPa. The minimum principal stresses at other positions show a gradually decreasing trend, with H > 2.0 m decreasing to less than the compressive strength design value. Therefore, the reasonable value of H should be 2.0 m.

4.4 Plastic zone of surrounding rock

This section is solved by FLAC 3D and compared with the final plastic zone distribution after excavation at different positions of the advanced center drift. To quantitatively describe the size of the plastic zone of the surrounding rock, CAD software was used to calculate the area of the plastic zone. The comparison of the plastic zone area of the Y = 40 m section under different conditions is shown in Fig. 9.

Fig. 9
figure 9

Plastic zone area under different conditions

Full size image

From Fig. 9, it can be seen that under different conditions, after the expansion of the main tunnel is completed, the plastic zone area first decreases and then increases. The slight difference indicates that different positions of the advanced center drift have little impact on the distribution of the plastic zone in the surrounding rock. The plastic zone of the surrounding rock is relatively small when the distance between the arch top of the advanced center drift and the arch top of the main tunnel is 2.0 m, indicating that the position of the advanced center drift section above or below the main tunnel section is unreasonable. The excavation of the advanced center drift and the expansion of the main tunnel significantly impact the surrounding rock, leading to a larger plastic zone of the surrounding rock. Therefore, the reasonable value of H should be 2.0 m, and the plastic zone area of the surrounding rock is 398.184 m2, which is approximately 3.1 times the area of the main tunnel.

5 On-site application effect

The central line of the Haba Snow Mountain Tunnel’s advanced center drift coincides with the main tunnel’s central line. The vault is 2.0 m away from the arch crown of the main tunnel. The ratio of the advanced center drift section area to the main tunnel section area is 0.62, and the leading distance is twice the advanced center drift diameter. This section analyzes the deformation and support stress of the Haba Snow Mountain Tunnel after adopting an advanced center drift. It analyzes the application effect of an advanced center drift.

5.1 Tunnel deformation control effect

The deformation time history curve of each position before and after the advanced center drift is adopted in the Haba Snow Mountain Tunnel is shown in Fig. 10. Among them, “1” represents before using the advanced center drift, and “2” represents after using the advanced center drift. The final deformation amount and reduction rate at each position are shown in Table 5.

Fig. 10
figure 10

Time history curve of tunnel deformation before and after adopting the advanced center drift

Full size image
Table 5 Deformation at each position
Full size table

After the middle pilot tunnel is adopted in the Haba Snow Mountain Tunnel, the deformation at each position is reduced by 44.52% on average, and the deformation control effect is significant, significantly reducing the damage to the support structure.

5.2 Support structure stress

After adopting the advanced center drift, the initial support of the main tunnel was subjected to stress monitoring. The time history curves of surrounding rock pressure, steel stress, and shotcrete stress at each structure position are shown in Fig. 11.

Fig. 11
figure 11

Time history curve of support structure stress. a Time history curve of surrounding rock pressure. b Time history curve of steel bar stress. c Time history curve of shotcrete stress

Full size image

It can be seen from Fig. 11 that after the advanced center drift is adopted for the Haba Snow Mountain Tunnel, the stress of the initial support structure is minor. The surrounding rock pressure at each location is less than 0.4 MPa, which is lower than the bearing capacity of the support structure (0.5 MPa). The steel bars are all in a compressive state, and the maximum stress occurs at the left wall foot, with a maximum value of − 210.41 MPa, 52.6% of the designed compressive strength of the steel bars. The shotcrete stress at each position is negative (under compression), and the maximum shotcrete stress is at the left arch waist, which is − 13.34 MPa and does not exceed the designed compressive strength value of concrete (C35). The deformation of the Haba Snow Mountain Tunnel after adopting the advanced center drift and the stress of the initial support structure were monitored and analyzed. It can be seen that the deformation of each position of the tunnel decreased by 44.52% on average, and the stress of the initial support was minor, which can ensure the safety of the initial support structure.

6 Conclusion

The stress on the support structure, the plastic zone of the surrounding rock, and the deformation of the tunnels at various vertical positions of the advanced center drift were all analyzed. As the distance H between the arch top of the advanced center drift and the main tunnel grows, the settlement of the main tunnel's arch top and the horizontal convergence of the lower steps diminish at first and subsequently stabilize. The upper stage's horizontal convergence diminishes before increasing. Based on a comprehensive analysis H should be setting to 2.0 m. When H = 2.0 m, the maximum and minimum principal stresses of the main tunnel’s initial support do not exceed the concrete’s tensile and compressive strength design values. As H grows, the difference in the surrounding rock’s plastic zone area decreases, followed by an increase. When H = 2.0 m, the plastic zone area is the smallest, about 3.1 times the main tunnel. On-site tests revealed that using a advanced center drift reduced the Haba Snow Mountain Tunnel’s deformation by an average of 44.52%. The initial support force is small, ensured the stability of the support structure.

Based on the Haba Snow Mountain Tunnel, this article discusses the advanced center drift’s suitable vertical position. However, the use of the advanced center drift in large deformation tunnels is limited, and the Haba Snow Mountain Tunnel’s engineering requirements may not be directly applicable to other tunnels. As a result, there are certain limitations to the conclusions presented in this article. The stress release effects of advanced center drift on large deformation tunnels will require quite a lot of engineering applications in the future.