Abstract
Let \(X\) be a smooth \(p\)-adic formal scheme. We show that integral crystalline local systems on the generic fiber of \(X\) are equivalent to prismatic \(F\)-crystals over the analytic locus of the prismatic site of \(X\). As an application, we give a prismatic proof of Fontaine’s \(\mathrm {C}_{{\mathrm {crys}}}\)-conjecture, for general coefficients, in the relative setting, and allowing ramified base fields. Along the way, we also establish various foundational results for the cohomology of prismatic \(F\)-crystals, including various comparison theorems, Poincaré duality, and Frobenius isogeny.

Similar content being viewed by others
Notes
In [28, Def. 1.1] such objects are called completed prismatic \(F\)-crystals. To see that their notion is compatible with ours, note that by [28, Prop. 4.13] and Beauville–Laszlo gluing, the restriction of a completed prismatic \(F\)-crystal to the open subset \(\operatorname{Spec}(\mathfrak {S})\setminus V(p,E)\) of a Breuil–Kisin prism \((\mathfrak {S},E)\) is a vector bundle. Moreover, the global sections of a vector bundle over \(\operatorname{Spec}(A)\setminus V(p,I)\) are a finitely presented module over \(A\) (cf. Lemma 5.8).
For any multiindex \(\alpha \in \mathbf {Z}^{d}_{\ge 0}\), we use the customary notation
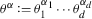 ,
, 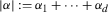 , and
, and 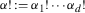 .
.Here we use that the ramification index of \(V_{0}\) is \(1 \le p-1\); when it is \(\ge p\), the analogous limit \(\lim _{n \to \infty} \lvert \pi ^{n}/n!\rvert = \infty \) for a uniformizer \(\pi \in V_{0}\).
To see this, we recall from Definition 2.23 and Remark 2.24 that there are natural injections \(\operatorname{gr}^{\bullet }\mathbb{B}_{{\mathrm {crys}}}(S,S^{+})\to \operatorname{gr}^{\bullet }\mathbb{B}_{{\mathrm {crys}}, K}(S,S^{+}) \to \operatorname{gr}^{\bullet }\mathbb{B}_{{\mathrm {dR}}}(S,S^{+})\). Thus, the claimed isomorphism follows from the fact that the composed map is a graded isomorphism, thanks to [63, Cor. 2.25].
We warn the reader that our construction of \(\mathcal {O}\mathbb{A}_{{\mathrm {crys}}}\) is ad hoc and different from that of [63], where \(\mathcal {O}_{K}\) is assumed to be unramified.
More conceptually, (10) forms a diagram of objects in an appropriately defined infinitesimal site and there is a natural infinitesimal crystal associated to ℰ that can evaluate on the diagram.
The uniqueness follows from the fact that the set of elements \(\{e\otimes f \mid e\in E(R[1/p]),~f\in \mathbb{B}^{+}_{{\mathrm {dR}}}(S,S^{+}) \}\) is dense in \(\mathcal {O}\mathbb{B}_{{\mathrm {dR}}}^{+}(S,S^{+})\), thanks to the explicit formula in [57, Prop. 6.10].
Let \(d\) be a generator of
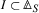 . Then \(\delta (d)+p^{p-1} \cdot (d/p)^{p}\) is invertible in
. Then \(\delta (d)+p^{p-1} \cdot (d/p)^{p}\) is invertible in 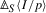 , so the element \(\varphi (d)=d^{p}+p\delta (d) = p(\delta (d)+p^{p-1} \cdot (d/p)^{p})\) is automatically invertible in
, so the element \(\varphi (d)=d^{p}+p\delta (d) = p(\delta (d)+p^{p-1} \cdot (d/p)^{p})\) is automatically invertible in 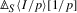 .
.The fact that the vanishing locus of \(V(\mu )\) in \(\mathcal {Y}_{[0,\infty )}\) is the union \(\bigcup _{n>0} V(\varphi ^{-n}(I))\) follows from the intersection formula \(\bigcap _{r} \frac{\mu}{\varphi ^{-r}(\mu )}\mathrm {A}_{\inf}= \mu \mathrm {A}_{ \inf}\) in [22, Lem. 3.23]: for fixed \(s\in \mathbf {N}\) and \(m \gg 0\), the ideal \(\varphi ^{-m}(I)\) is invertible in \(\mathcal {O}_{\mathcal {Y}_{[0,s]}}\), so the sequence of ideals \(\frac{\mu}{\varphi ^{-r}(\mu )}\cdot \mathcal {O}_{\mathcal {Y}_{[0,s]}}= \varphi ^{-1}(I) \cdots \varphi ^{-r}(I) \cdot \mathcal {O}_{\mathcal {Y}_{[0,s]}}\) eventually stabilizes for large enough \(r\).
To see the injectivity, we note that for the Breuil–Kisin prism \((\mathfrak{S},I=(E(u))\) one has the injections \(\mathfrak{S} \to \mathfrak{S}\langle \varphi ^{n}(I)/p\rangle \to \mathfrak{S}\langle I/p \rangle \). So the case of \(S'\) follows by taking the \(p\)-complete flat base change along
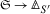 and a further localization.
and a further localization.This is a Breuil–Kisin prism in the sense of [28, Ex. 3.4].
More precisely, given a divided power thickening \((A,J)\) of \(R\), we can lift the composition \(P \twoheadrightarrow R \to A/J\) to a map \(\mathbf {Z}_{p}[ x_{s}]\to A\) by the freeness of \(P\). The base change of \((A,J)\) along the quasi-syntomic cover \(A\to (A\otimes _{\mathbf {Z}_{p} [ x_{s}]} \mathbf {Z}_{p} [x_{s}^{1/p^{\infty}}])^{ \wedge}_{p}\) forms a divided power thickening of \(R\otimes _{P} P^{0}\), and thus admits a map from \(\mathrm {A}_{{\mathrm {crys}}}(R\otimes _{P} P^{0})\).
This is possible by the \(p\)-completeness of \(B\) and the observation that any lift of a unit of \(B/(J,p^{n})\) is a unit in \(B/p^{n}\), since \(J\) is a divided power ideal.
To reduce to the setting of [61, Cor. 2.37], it suffices to notice that each cohomology sheaf \(H^{i}(\mathcal {E}'[1/p])\) is an isocrystal in vector bundles, which produces a finite filtration on \(Rf_{s,{\mathrm {crys}},*} \mathcal {E}'[1/p]\) such that each graded piece is a perfect complex.
Using the perspective on symmetric monoidal \(\infty \)-categories as certain coCartesian fibrations \(\mathcal {C}^{\otimes} \to \mathrm {Fin}_{*}\) (see e.g. [46, Def. 2.0.0.7]), recall that a functor \(F^{\otimes} \colon \mathcal {C}^{\otimes} \to \mathcal {D}^{\otimes}\) over \(\mathrm {Fin}_{*}\) is lax symmetric monoidal if it preserves locally coCartesian lifts of inert maps ([46, Def. 2.1.1.8]) and symmetric monoidal if it preserves all locally coCartesian lifts. It is an equivalence if it is additionally an equivalence on the underlying \(\infty \)-categories ([46, § 2.1.3]). One can check easily that if \(F\) is lax symmetric monoidal and has a homotopy inverse \((F^{\otimes})^{-1}\) which is a symmetric monoidal equivalence, then \(F\) must also preserve all locally coCartesian lifts and hence be a symmetric monoidal equivalence.
The statement in [28] contains the assumption that the \(\varphi \)-module is torsionfree, which is not used in the proof.
The tensor product is automatically complete because
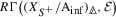 is perfect (Proposition 5.11).
is perfect (Proposition 5.11).Let \(S=\overline{A}/p\) be the quasiregular semiperfect ring. As in [15, Thm. 4.6.1, Ex. 4.6.9], the surjection from \(\mathrm {A}_{{\mathrm {crys}}}(\overline{A}/p) \to \overline{A}/p\) can be understood via the diagram of prismatic cohomology:
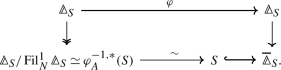
By the triviality of the Kähler differential, we identify this de Rham complex with a Koszul complex.
References
Andreatta, F., Iovita, A.: Semistable sheaves and comparison isomorphisms in the semistable case. Rend. Semin. Mat. Univ. Padova 128, 131–285 (2012)
Andreatta, F., Iovita, A.: Comparison isomorphisms for smooth formal schemes. J. Inst. Math. Jussieu 12(1), 77–151 (2013)
Anschütz, J., Le Bras, A.-C.: Prismatic Dieudonné theory. Forum Math. Pi 11, Paper No. e2, 92 (2023)
Antieau, B., Mathew, A., Morrow, M., Nikolaus, T.: On the Beilinson fiber square. Duke Math. J. 171(18), 3707–3806 (2022)
Beilinson, A.: On the crystalline period map. Camb. J. Math. 1(1), 1–51 (2013)
Berkovich, V.G.: Étale cohomology for non-Archimedean analytic spaces. Publ. Math. Inst. Hautes Études Sci. 78, 5–161 (1994)
Berthelot, P.: Cohomologie cristalline des schémas de caractéristique \(p>0\). Lecture Notes in Mathematics, vol. 407. Springer, Berlin (1974)
Berthelot, P.: Cohomologie rigide et cohomologie rigide à supports propres, Première partie (version provisoire 1991), Prépublication IRMAR (1996). https://perso.univ-rennes1.fr/pierre.berthelot/publis/Cohomologie_Rigide_I.pdf
Berthelot, P., Ogus, A.: Notes on Crystalline Cohomology. Princeton University Press, Princeton; University of Tokyo Press, Tokyo (1978)
Bhatt, B.: \(p\)-adic derived de Rham cohomology. Preprint (2012). https://arxiv.org/abs/1204.6560
Bhatt, B.: Algebraization and Tannaka duality. Camb. J. Math. 4(4), 403–461 (2016)
Bhatt, B.: Specializing varieties and their cohomology from characteristic 0 to characteristic \(p\). In: Algebraic Geometry: Salt Lake City 2015. Proc. Sympos. Pure Math., vol. 97, pp. 43–88. Am. Math. Soc., Providence (2018)
Bhatt, B.: Cohen-Macaulayness of absolute integral closures. Preprint (2020). https://arxiv.org/abs/2008.08070
Bhatt, B., de Jong, A.J.: Crystalline cohomology and de Rham cohomology. Preprint (2011). https://arxiv.org/abs/1110.5001
Bhatt, B., Lurie, J.: Absolute prismatic cohomology. Preprint (2022). https://arxiv.org/abs/2201.06120
Bhatt, B., Lurie, J.: The prismatization of \(p\)-adic formal schemes. Preprint (2022). https://arxiv.org/abs/2201.06124
Bhatt, B., Mathew, A.: The arc-topology. Duke Math. J. 170(9), 1899–1988 (2021)
Bhatt, B., Scholze, P.: The pro-étale topology for schemes. Astérisque 369, 99–201 (2015)
Bhatt, B., Scholze, P.: Projectivity of the Witt vector affine Grassmannian. Invent. Math. 209(2), 329–423 (2017)
Bhatt, B., Scholze, P.: Prisms and prismatic cohomology. Ann. Math. (2) 196(3), 1135–1275 (2022)
Bhatt, B., Scholze, P.: Prismatic \(F\)-crystals and crystalline Galois representations. Camb. J. Math. 11(2), 507–562 (2023)
Bhatt, B., Morrow, M., Scholze, P.: Integral \(p\)-adic Hodge theory. Publ. Math. Inst. Hautes Études Sci. 128, 219–397 (2018)
Bhatt, B., Morrow, M., Scholze, P.: Topological Hochschild homology and integral \(p\)-adic Hodge theory. Publ. Math. Inst. Hautes Études Sci. 129, 199–310 (2019)
Bogdan, Z.: Mod-\(p\) Poincaré duality in \(p\)-adic analytic geometry. Preprint (2021). https://arxiv.org/abs/2111.01830
Bosch, S., Güntzer, U., Remmert, R.: Non-Archimedean Analysis. Grundlehren der Mathematischen Wissenschaften, vol. 261. Springer, Berlin (1984)
Brinon, O.: Représentations \(p\)-adiques cristallines et de Rham dans le cas relatif. Mém. Soc. Math. Fr. (N. S.), no. 112, vi+159 (2008)
Česnavičius, K., Scholze, P.: Purity for flat cohomology. Ann. Math. (2) 199(1), 51–180 (2024)
Du, H., Liu, T., Suk Moon, Y., Shimizu, K.: Completed prismatic \(F\)-crystals and crystalline \(\mathbf{Z}_{p}\)-local systems. Preprint (2022). https://arxiv.org/abs/2203.03444
Faltings, G.: Crystalline cohomology and \(p\)-adic Galois-representations. In: Algebraic Analysis, Geometry, and Number Theory (Baltimore, MD, 1988), pp. 25–80. Johns Hopkins University, Baltimore (1989)
Fontaine, J.-M.: Sur certains types de représentations \(p\)-adiques du groupe de Galois d’un corps local; construction d’un anneau de Barsotti-Tate. Ann. Math. (2) 115(3), 529–577 (1982)
Fontaine, J.-M., Messing, W.: \(p\)-Adic periods and \(p\)-adic étale cohomology. In: Current Trends in Arithmetical Algebraic Geometry (Arcata, Calif., 1985). Contemp. Math., vol. 67, pp. 179–207. Am. Math. Soc., Providence (1987)
Guo, H.: Crystalline cohomology of rigid analytic spaces. Preprint (2021). https://arxiv.org/abs/2112.14304
Guo, H., Petrov, A., Yang, Z.: Pointwise criteria of \(p\)-adic local systems (2023, in preparation)
Harris, M.E.: Some results on coherent rings. Proc. Am. Math. Soc. 17, 474–479 (1966)
Hollander, S.: A homotopy theory for stacks. Isr. J. Math. 163, 93–124 (2008)
Huber, R.: A generalization of formal schemes and rigid analytic varieties. Math. Z. 217(4), 513–551 (1994)
Huber, R.: Étale cohomology of rigid analytic varieties and adic spaces. Aspects of Mathematics, vol. E30. Friedr. Vieweg & Sohn, Braunschweig (1996)
Ivanov, A.B.: Arc-descent for the perfect loop functor and \(p\)-adic Deligne-Lusztig spaces. J. Reine Angew. Math. 794, 1–54 (2023)
Kato, K., Messing, W.: Syntomic cohomology and \(p\)-adic étale cohomology. Tohoku Math. J. (2) 44(1), 1–9 (1992)
Katz, N.M.: \(p\)-Adic properties of modular schemes and modular forms. In: Modular Functions of One Variable, III (Proc. Internat. Summer School, Univ. Antwerp, Antwerp, 1972). Lecture Notes in Math., vol. 350, pp. 69–190. Springer, Berlin (1973)
Kedlaya, K.S.: A \(p\)-adic local monodromy theorem. Ann. Math. (2) 160(1), 93–184 (2004)
Kedlaya, K.S.: Some ring-theoretic properties of \(\mathrm{A}_{\mathrm{inf}}\), \(p\)-adic Hodge theory. In: Simons Symp., pp. 129–141. Springer, Cham (2020)
Kedlaya, K.S., Liu, R.: Relative \(p\)-adic Hodge theory: foundations. Astérisque 371, 239 (2015)
Liu, R., Zhu, X.: Rigidity and a Riemann-Hilbert correspondence for \(p\)-adic local systems. Invent. Math. 207(1), 291–343 (2017)
Lurie, J.: Higher Topos Theory. Annals of Mathematics Studies, vol. 170. Princeton University Press, Princeton (2009)
Lurie, J.: Higher Algebra (2017). https://www.math.ias.edu/~lurie/papers/HA.pdf
Mann, L.: A \(p\)-adic 6-functor formalism in rigid-analytic geometry. Preprint (2022). https://arxiv.org/abs/2206.02022
Mathew, A.: The Galois group of a stable homotopy theory. Adv. Math. 291, 403–541 (2016)
Mathew, A.: Faithfully flat descent of almost perfect complexes in rigid geometry. J. Pure Appl. Algebra 226(5), Paper No. 106938, 31 (2022)
Min, Y., Wang, Y.: Relative \((\varphi ,\Gamma )\)-modules and prismatic \(F\)-crystals. Preprint (2021). https://arxiv.org/abs/2110.06076
Morrow, M., Tsuji, T.: Generalised representations as q-connections in integral \(p\)-adic Hodge theory. Preprint (2020) https://arxiv.org/abs/2010.04059
Nie, T.: Absolute Hodge cycles in prismatic cohomology. Ph.D. thesis (2021). https://dash.harvard.edu/handle/1/37370189
Nizioł, W.: Crystalline conjecture via \(K\)-theory. Ann. Sci. Éc. Norm. Supér. (4) 31(5), 659–681 (1998)
Ogus, A.: \(F\)-Isocrystals and de Rham cohomology. II. Convergent isocrystals. Duke Math. J. 51(4), 765–850 (1984)
Ogus, A.: The convergent topos in characteristic \(p\). In: The Grothendieck Festschrift, Vol. III. Progr. Math., vol. 88, pp. 133–162. Birkhäuser, Boston (1990)
Ogus, A.: Crystalline prisms: reflections on the present and past. Preprint (2023). https://arxiv.org/abs/2204.06621
Scholze, P.: \(p\)-Adic Hodge theory for rigid-analytic varieties. Forum Math. Pi 1, e1, 77 (2013)
Scholze, P.: \(p\)-Adic Hodge theory for rigid-analytic varieties—corrigendum. Forum Math. Pi 4, e6, 4 (2016)
Scholze, P.: Étale cohomology of diamonds. Preprint (2017). https://arxiv.org/abs/1709.07343
Scholze, P., Weinstein, J.: Berkeley Lectures on \(p\)-Adic Geometry. Annals of Mathematics Studies, vol. 207. Princeton University Press, Princeton (2020)
Shiho, A.: Relative log convergent cohomology and relative rigid cohomology I. Preprint (2007). https://arxiv.org/abs/0707.1742
Shimizu, K.: A \(p\)-adic monodromy theorem for de Rham local systems. Compos. Math. 158(12), 2157–2205 (2022)
Tan, F., Tong, J.: Crystalline comparison isomorphisms in \(p\)-adic Hodge theory: the absolutely unramified case. Algebra Number Theory 13(7), 1509–1581 (2019)
Tang, L.: Syntomic cycle classes and prismatic Poincaré duality. Preprint (2022). https://arxiv.org/abs/2210.14279
The Stacks Project Authors: Stacks Project (2022). https://stacks.math.columbia.edu
Tian, Y.: Finiteness and duality for the cohomology of prismatic crystals. J. Reine Angew. Math. 800, 217–257 (2023)
Tsuji, T.: \(p\)-Adic étale cohomology and crystalline cohomology in the semi-stable reduction case. Invent. Math. 137(2), 233–411 (1999)
Vasconcelos, W.V.: On finitely generated flat modules. Trans. Am. Math. Soc. 138, 505–512 (1969)
Xu, D.: On higher direct images of convergent isocrystals. Compos. Math. 155(11), 2180–2213 (2019)
Zhu, X.: Affine Grassmannians and the geometric Satake in mixed characteristic. Ann. Math. (2) 185(2), 403–492 (2017)
Acknowledgements
The influence of the work of Bhatt–Scholze [20, 21] on our article is obvious, and we thank them heartily for their pioneering work. We initiated our project during the fall of 2021 after several conversations with Peter Scholze. We are grateful for his support and his many patient explanations throughout the writing of this project, especially his suggestion of the gluing construction in Theorem 4.15 using both the local system and its associated \(F\)-isocrystal. We are indebted to Bhargav Bhatt for many illuminating explanations and suggestions throughout the genesis of this paper. We are also thankful to the anonymous referee for countless remarks and corrections, which substantially enhanced the quality of our manuscript. Further thanks go to Sasha Petrov for suggesting that we should be able to prove the Frobenius isogeny property via Poincaré duality and to Guido Bosco, David Hansen, Hiroki Kato, Shizhang Li, Samuel Marks, Akhil Mathew, Yuchen Wu and Bogdan Zavyalov for helpful discussions and correspondence. We gratefully acknowledge funding through the Max Planck Institute for Mathematics in Bonn, Germany, during the preparation of this work. Additional support came from the University of Chicago (H.G.) and the National Science Foundation under Grant No. DMS-1926686 and the IAS School of Mathematics (E.R.) in the revision stage of the project.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Guo, H., Reinecke, E. A prismatic approach to crystalline local systems. Invent. math. 236, 17–164 (2024). https://doi.org/10.1007/s00222-024-01238-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00222-024-01238-4



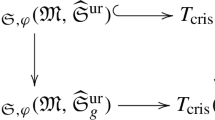
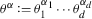 ,
, 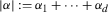 , and
, and 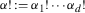 .
.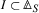 . Then
. Then 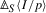 , so the element
, so the element 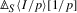 .
.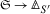 and a further localization.
and a further localization.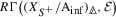 is perfect (Proposition
is perfect (Proposition 