Introduction

In quantum mechanics, the study of relativistic and nonrelativistic wave equations arouse the interest of different researchers [1,2,3,4,5]. Schrӧdinger equation is the nonrelativistic wave equation, while Dirac and Klein–Gordon equations are relativistic wave equation describing spin-half and spinless particles, respectively [6,7,8,9,10]. The total wave function provides implicitly the information about the quantum mechanical system. [11]. Researchers have adopted many methods in providing solutions to both relativistic and nonrelativistic wave equations. Among them are Nikiforov–Uvarov method [12,13,14,15,16], supersymmetric quantum mechanics approach [17], exact proper quantization [18] asymptotic iteration method [19], Wentzel–Kramers–Brillouin (WKB) approach [20] and many others [21,22,23,24,25,26,27,28,29]. These techniques have been used to solve some quantum mechanical potentials, like Hulthen, Yukawa, Poschl–Teller, Tietz–Wei, Tietz–Hua, exponential-type potentials, hyperbolic potentials, Kratzer potentials, screened-Kratzer potential, Mobius square, Hellmann, coulomb, Cornel, Killingbeck, Woods–Saxon, Deng-Fan, Hylleraas, Eckart, pseudoharmonic, Poschl–Teller, modified Yukawa potential and many others [30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48]. Yukawa potential which is otherwise known as screened Coulomb potential is a short-range potential with application in particle, high energy and molecular physics which is basically used for the description of interaction existing between atoms of diatomic molecules [49]. A lot of research work has been carried out on thermodynamic properties of some considerable potentials. Okon et.al [50] studied spin and pseudospin solutions of Dirac equation and its thermodynamic properties using hyperbolic Hulthen plus hyperbolic exponential inversely quadratic potential where they obtained numerical bound state solutions for both spin and pseudospin symmetries. Using nonrelativistic limit, they also obtain nonrelativistic energy eigenequation presented in a close form to study partition function and other thermodynamic properties. Okon et al. [51] studied thermodynamic properties and bound state solutions of Schrӧdinger equation using Mobius square plus screened-Kratzer potential within the framework of parametric Nikiforov–Uvarov (NU) method. In their study, they applied NU and semi-classical WKB to obtain bound state solutions and thermodynamic properties for two diatomic molecules (Carbon (II) oxide and Scandium Fluoride). Okorie et al. [52] studied energy spectra and thermodynamic properties of hyperbolic Poschl–Teller potential model. In that work, they solved Dirac equation using modified factorization method to obtain both relativistic and nonrelativistic ro-vibrational energy spectra and thermodynamic properties as applied to some diatomic molecules: Hydrogen chloride (HCl), chlorine (Cl2), carbon (II) oxide and lithium hydride (LiH). The potential they used is reduced to screened-Kratzer and Kratzer potential as special cases. Onate et al. [53] studied bound state solutions and thermal properties of modified Tietz–Hua potential using supersymmetric quantum mechanics approach where they study ro-vibrational energy spectra and thermodynamic properties as applicable to some diatomic properties. Purohit et al. [54] studied eigensolutions and various properties of the screened cosine Kratzer potential in D-dimension via relativistic and nonrelativistic treatment. Here, the screened-Kratzer potential model was extended to study rotational and vibrational energies for few heterogeneous diatomic molecules. They authors also extend the potential model to study the partition function as well as information theoretic measures like Tsallis, Renyi, Shannon and Fisher information entropies. Recently, researchers have studied potential model under the influence of Aharonov–Bohm flux and external magnetic field. Purohit et al. [55] studied the thermomagnetic properties of the screened-Kratzer potential under the influence of Aharonov–Bohm flux and external magnetic field where the obtained thermomagnetic properties as well as persistent current, magnetization and magnetic susceptibility. Okon et al. [56] investigated the effect of Aharonov–Bohm and external magnetic field on Hellmann plus screened-Kratzer potential where the energy equation was presented in a closed form and applied to study thermomagnetic properties as applicable to some diatomic molecules. Here, the authors obtained a normalized wave function expressed in terms of Jacobi polynomials as well as the wave function and probability density plots for some selected diatomic molecules. They also obtained other thermomagnetic properties including partition function, vibrational mean energy, vibrational heat capacity, magnetization, persistent current and magnetic susceptibility. Based on this motivation, in this paper, we study an approximate bound state solutions of Schrӧdinger equation and thermodynamic properties of newly proposed potential called modified exponential screened plus Yukawa potential (MESPYP) within the framework of parametric Nikiforov–Uvarov method. This is a new potential model that has not yet been studied to the best of our knowledge. This article is divided into seven sections. Section one gives the brief introduction of the article. Parametric Nikiforov–Uvarov method is presented in section two. The radial solution of the proposed potential is presented in section three. Numerical computation of energy eigenvalues is carried out in section four. Thermodynamic properties are presented in section five. Results and discussion are presented in section 6, while the article is concluded in section seven.

Review of parametric Nikiforov–Uvarov method

The NU method was proposed to solve the second-order linear differential equation by reducing it to a generalized equation of hypergeometric type of the form

$$\psi^{\prime\prime}(s) + \frac{{\tilde{\tau }(s)}}{\sigma (s)}\psi^{\prime}(s) + \frac{{\tilde{\sigma }(s)}}{{\sigma^{2} (s)}}\psi (s) = 0,$$
(1)

where \(\sigma (s)\) and \(\sigma^{2} (s)\) are polynomials at most second degree, and \(\tilde{\tau }(s)\) is a first degree polynomial.

According to Tezcan and Sever [57], the parametric Nikiforov–Uvarov method is given as

$$\psi^{\prime\prime}(s) + \frac{{C_{1} - C_{2} S}}{{S\left( {1 - C_{3} S} \right)}}\psi^{\prime}(s) + \frac{1}{{S^{2} \left( {1 - C_{3} S} \right)^{2} }}\left[ { - \chi_{1} S^{2} + \chi_{2} S - \chi_{3} } \right]\psi (s) = 0$$
(2)

The total wave function is given as

$$\psi (s) = N_{nl} S^{{C_{12} }} \left( {1 - C_{3} S} \right)^{{ - C_{12} - \left( {{\raise0.7ex\hbox{${C_{13} }$} \!\mathord{\left/ {\vphantom {{C_{13} } {C_{3} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${C_{3} }$}}} \right)}} P_{n}^{{\left( {c_{10} - 1,\frac{{C_{11} }}{{C_{3} }} - C_{10} - 1} \right)}} \left( {1 - 2S} \right)$$
(3)

, while the total energy eigenequation is given as

$$C_{2} n - \left( {2n + 1} \right)C_{5} + \left( {2n + 1} \right)\left( {\sqrt {C_{9} } + C_{3} \sqrt {C_{8} } } \right) + n\left( {n - 1} \right)C_{3} + C_{7} + 2C_{3} C_{8} + 2\sqrt {C_{8} C_{9} } = 0,$$
(4)

where the parametric constants can be obtained as follows:

$$\left. \begin{gathered} C_{4} = \frac{1}{2}\left( {1 - C_{1} } \right) \hfill \\ C_{5} = \frac{1}{2}\left( {C_{2} - 2C_{3} } \right) \hfill \\ C_{6} = C_{5}^{2} + \chi_{1} \hfill \\ C_{7} = 2C_{4} C_{5} - \chi_{2} \hfill \\ C_{8} = C_{4}^{2} + \chi_{3} \hfill \\ C_{9} = C_{3} C_{7} + C_{3}^{2} C_{8} + C_{6} \hfill \\ C_{10} = C_{1} + 2C_{4} + 2\sqrt {C_{8} } \hfill \\ C_{11} = C_{2} - 2C_{5} + 2\left[ {\sqrt {C_{9} } + C_{3} \sqrt {C_{8} } } \right] \hfill \\ C_{12} = C_{4} + \sqrt {C_{8} } \hfill \\ C_{13} = C_{5} - \left[ {\sqrt {C_{9} } + C_{3} \sqrt {C_{8} } } \right] \hfill \\ \end{gathered} \right\}$$
(5)

The Jacobi polynomial can be expressed in terms of Laguerre polynomial for a special case where \(C_{3} = 0\) [32]

$$\lim P_{n}^{{\left( {c_{10} - 1,\frac{{c_{11} }}{{c_{3} }} - c_{10} - 1} \right)}} \left( {1 - 2c_{3} s} \right) = L_{n}^{{c_{10} - 1}} \left( {c_{11} s} \right)$$
(6)

and

$$\lim_{{C_{3 \to 0} }} \left( {1 - C_{3} S} \right)^{{ - C_{12} - \frac{{C_{13} }}{{C_{3} }}}} = e^{{C_{13} S}} .$$
(7)

Hence, the solution given by Eq. (3) becomes

$$\psi_{\left( s \right)} = S^{{C_{12} }} e^{{C_{13} S}} L_{n}^{{C_{10} - 1}} \left( {C_{11} S} \right).$$
(8)

Radial solution of Schrӧdinger equation with modified exponential screened plus Yukawa potential

The modified exponential screened plus Yukawa potential is given as

$$V(r) = D_{0} \left( {\frac{{1 + e^{ - 2\alpha r} }}{{1 - e^{ - 2\alpha r} }}} \right) + \frac{{D_{1} e^{ - \alpha r} }}{r},$$
(9)

where \(D_{0} = \frac{{D_{e} }}{2} > 0\), \(D_{e}\) is the dissociation energy that describes the depth of the potential well, \(\alpha\) is the screening parameter which characterizes the strength of the potential. \(D_{1}\) is a real constant which also serve as a control parameter for the potential model, while \(r\) is the internuclear distance between the atoms of diatomic molecules.

The Schrödinger wave equation is given as:

$$\frac{{{\text{d}}^{2} R}}{{{\text{d}}r^{2} }} + \left\{ {\left. {\frac{2\mu }{{\hbar^{2} }}\left[ {E - V(r)} \right] - \frac{\lambda }{{r^{2} }}} \right\}} \right.R(r) = 0.$$
(10)

Substituting the potential of Eq. (9) into Eq. (10) gives

$$\frac{{{\text{d}}^{2} R}}{{{\text{d}}r^{2} }} + \left\{ {\left. {\frac{2\mu }{{\hbar^{2} }}\left[ {E - D_{0} \left( {\frac{{1 + e^{ - 2\alpha r} }}{{1 - e^{ - 2\alpha r} }}} \right) - \frac{{D_{1} e^{ - \alpha r} }}{r}} \right] - \frac{\lambda }{{r^{2} }}} \right\}} \right.R(r) = 0,$$
(11)

where \(\lambda = l\left( {l + 1} \right)\).

Let us use Greene–Aldrich approximation to the centrifugal term as [24]

$$\frac{1}{{r^{2} }} = \frac{{4\alpha^{2} e^{ - 2\alpha r} }}{{\left( {1 - e^{ - 2\alpha r} } \right)^{2} }} \Rightarrow \frac{1}{r} = \frac{{2\alpha e^{ - \alpha r} }}{{\left( {1 - e^{ - 2\alpha r} } \right)}}.$$
(12)

Substituting Eq. (12) into (11) gives

$$\frac{{{\text{d}}^{2} R}}{{{\text{d}}r^{2} }} + \left\{ {\left. {\frac{2\mu }{{\hbar^{2} }}\left( {\left. {E - D_{0} \left( {\frac{{1 + e^{ - 2\alpha r} }}{{1 - e^{ - 2\alpha r} }}} \right) - \frac{{2\alpha D_{1} e^{ - 2\alpha r} }}{{1 - e^{ - 2\alpha r} }}} \right) - \frac{{4\alpha^{2} e^{ - 2\alpha r} \lambda }}{{\left( {1 - e^{ - 2\alpha r} } \right)^{2} }}} \right.} \right\}} \right.R(r) = 0.$$
(13)

Using \(s = e^{ - 2\alpha r}\) , Eq. (13) can be transform from r to s-dimensions as

$$\frac{{{\text{d}}^{2} R(s)}}{{{\text{d}}s^{2} }} + \frac{{\left( {1 - s} \right)}}{{s\left( {1 - s} \right)}}\frac{{{\text{d}}R(s)}}{{{\text{d}}s}} + \frac{1}{{s^{2} \left( {1 - s} \right)^{2} }}\left\{ {\left( { - \xi^{2} + A + B} \right)s^{2} + \left( {2\xi^{2} - B - \lambda } \right)s + \left( { - \xi^{2} - A} \right)} \right\}R(s) = 0,$$
(14)

where \(\xi^{2} = - \frac{\mu E}{{2\alpha^{2} \hbar^{2} }}\begin{array}{*{20}c} , & {A = \frac{{\mu D_{0} }}{{2\alpha^{2} \hbar^{2} }}} \\ \end{array} \begin{array}{*{20}c} , & {B = \frac{{\mu D_{1} }}{{\alpha \hbar^{2} }}} \\ \end{array}\),

Comparing Eq. (14) with Eq. (2) gives

$$\chi_{1} = - \xi^{2} + A + B\begin{array}{*{20}c} , & {\chi_{2} = 2\xi^{2} - B - \lambda \begin{array}{*{20}c} , & {\chi_{3} = \xi^{2} + A} \\ \end{array} } \\ \end{array} .$$
(15)

Using Eq. (6), other parametric constants can be obtained as

$$\begin{aligned} & C_{1} = C_{2} = C_{3} = 1\begin{array}{*{20}c} , & {C_{4} = 0} \\ \end{array} \begin{array}{*{20}c} , & {C_{5} = - \frac{1}{2}} \\ \end{array} \begin{array}{*{20}c} , & {C_{6} = \frac{1}{4} + \xi^{2} - A - B} \\ \end{array} \\ & C_{7} = - 2\xi^{2} + B + \lambda \begin{array}{*{20}c} , & {C_{8} = \xi^{2} + A} \\ \end{array} \begin{array}{*{20}c} , & {C_{9} = \lambda + \frac{1}{4}} \\ \end{array} \begin{array}{*{20}c} , & {C_{10} = 1 + 2\sqrt {\xi^{2} + A} } \\ \end{array} \\ & C_{11} = 2 + 2\left( {\sqrt {\lambda + \frac{1}{4}} + \sqrt {\xi^{2} + A} } \right)\begin{array}{*{20}c} , & {C_{12} = \sqrt {\xi^{2} + A} } \\ \end{array} \begin{array}{*{20}c} , & {C_{13} = - \frac{1}{2} - \sqrt {\lambda + \frac{1}{4}} - \sqrt {\xi^{2} + A} } \\ \end{array} . \\ \end{aligned}$$
(16)

Using Eq. (5), the energy eigenequation for the proposed potential is given as

$$E_{nl} = - \frac{{2\alpha^{2} \hbar^{2} }}{\mu }\left\{ {\frac{{n^{2} + n + \frac{1}{2} + \left( {n + \frac{1}{2}} \right)\sqrt {4l\left( {l + 1} \right) + 1} + l\left( {l + 1} \right) + \frac{{\mu D_{1} }}{{\alpha \hbar^{2} }} + \frac{{\mu D_{e} }}{{2\alpha^{2} \hbar^{2} }}}}{{2n + 1 + \sqrt {4l\left( {l + 1} \right) + 1} }}} \right\}^{2} + \frac{{D_{e} }}{2}.$$
(17)

Using Eq. (4), the total unnormalized wave function is given as

$$\Psi_{nl} (s) = N_{nl} s^{{\sqrt {\frac{{\mu D_{0} }}{{2\alpha^{2} \hbar^{2} }} - \frac{{\mu E_{nl} }}{{2\alpha^{2} \hbar^{2} }}} }} \left( {1 - s} \right)^{{\frac{1}{2} + \sqrt {\frac{1}{4} + \lambda } }} P_{n}^{{\left[ {\left( {2\sqrt {\frac{{\mu D_{0} }}{{2\alpha^{2} \hbar^{2} }} - \frac{{\mu E_{nl} }}{{2\alpha^{2} \hbar^{2} }}} } \right),\left( {2\sqrt {\frac{1}{4} + \lambda } } \right)} \right]}} (1 - 2s)$$
(18)

Equation (18) can further be simplified as

$$\Psi_{nl} (s) = N_{nl} s^{{\chi_{1} }} \left( {1 - s} \right)^{{\chi_{2} }} P_{n}^{{\left[ {\left( {2\chi_{1} } \right),\left( {2\chi_{2} - 1} \right)} \right]}} (1 - 2s)$$
(18a)

where \(\chi_{1} = \sqrt {\frac{{\mu D_{0} }}{{2\alpha^{2} \hbar^{2} }} - \frac{{\mu E_{nl} }}{{2\alpha^{2} \hbar^{2} }}} \begin{array}{*{20}c} , & {\chi_{2} = } \\ \end{array} \frac{1}{2} + \sqrt {\frac{1}{4} + \lambda } .\)

Numerical computation of energy eigenvalues

Using Eq. (17), the numerical bound state solutions were carried out for fixed principal quantum number (n) with varying orbital angular quantum number \(l\) = 0, 1, 2 and 3.

Thermodynamic properties

In this section, we present the thermodynamic properties for the potential model. The thermodynamic properties of quantum systems can be obtained from the exact partition function given by [53, 54]

$$Z\left( \beta \right) = \sum\limits_{n = 0}^{\lambda } {e^{{ - \beta E_{n} }} } ,$$
(19)

where \(\lambda\) is an upper bound of the vibrational quantum number obtained from the numerical solution of \(\frac{{{\text{d}}E_{n} }}{{{\text{d}}n}} = 0\), \(\beta = \frac{1}{kT}\) where \(k\) and T are Boltzmann constant and absolute temperature, respectively. In the classical limit, the summation in Eq. (19) can be replaced with an integral:

$$Z(\beta ) = \int\limits_{0}^{\lambda } {e^{{ - \beta E_{n} }} {\text{d}}n} .$$
(20)

In order to obtain the partition function, energy equation (17) can be presented in a close and compact form as

$$E_{nl} = \frac{{D_{e} }}{2} - \frac{{\alpha^{2} \hbar^{2} }}{2\mu }\left\{ {n + \frac{1}{2} + \frac{1}{2}\sqrt {4l\left( {l + 1} \right) + 1} + \frac{{\frac{{\mu D_{1} }}{{\alpha^{2} \hbar^{2} }} + \frac{{\mu D_{e} }}{{2\alpha^{2} \hbar^{2} }}}}{{n + \frac{1}{2} + \frac{1}{2}\sqrt {4l\left( {l + 1} \right) + 1} }}} \right\}^{2} .$$
(21)

The energy equation of (21) can be presented in a compact form as

$$E_{nl} = K_{1} - 2K_{2} K_{3} - \left\{ {K_{2} \rho^{2} + \frac{{K_{2} K_{3}^{2} }}{{\rho^{2} }}} \right\},$$
(22)

where

$$K_{1} = \frac{{D_{e} }}{2},K_{2} = \frac{{\alpha^{2} \hbar^{2} }}{2\mu },K_{3} = \frac{{\mu D_{1} }}{{\alpha^{2} \hbar^{2} }} + \frac{{\mu D_{e} }}{{2\alpha^{2} \hbar^{2} }}$$
(23)
$$\rho = n + \frac{1}{2} + \frac{1}{2}\sqrt {4l\left( {l + 1} \right) + 1}$$
(24)

Using Eq. (20), the partition function can be expressed as

$$Z(\beta ) = e^{{\beta \left( {2K_{2} K_{3} - K_{1} } \right)}} \int\limits_{0}^{\lambda } {e^{{\beta \left( {K_{2} \rho^{2} + \frac{{K_{2} K_{3}^{2} }}{{\rho^{2} }}} \right)}} } {\text{d}}\rho .$$
(25)

Using Maple 10.0 version, the partition function of equation (25) can be evaluated as

$$Z(\beta ) = \frac{{\frac{1}{4}e^{{\beta \left( {2K_{2} K_{3} - K_{1} } \right)}} \sqrt \pi \left( {e^{{2\beta K_{2} K_{3} }} erf\left( {\sqrt { - \beta K_{2} } \lambda + \frac{{K_{3} \sqrt { - \beta K_{2} } }}{\lambda }} \right) + e^{{ - \beta K_{2} K_{3} }} erf\left( {\sqrt { - \beta K_{2} } \lambda - \frac{{K_{3} \sqrt { - \beta K_{2} } }}{\lambda }} \right)} \right)}}{{\sqrt { - \beta K_{2} } }}.$$
(26)

Other thermodynamic properties can be obtained using the partition function.

  1. (a)

    Vibrational mean energy: The vibrational mean energy \(U(\beta )\) is

    $$U(\beta ) = - \frac{\partial \ln Z(\beta )}{{\partial \beta }} \Rightarrow - \frac{1}{2}\left( {\frac{A + B + C + D}{{\sqrt \pi \beta \lambda \left( {e^{{2\beta K_{2} K_{3} }} erf\left( {\frac{{\sqrt { - \beta K_{2} } \left( {\lambda^{2} + K_{3} } \right)}}{\lambda }} \right) + e^{{ - 2\beta K_{2} K_{3} }} erf\left( {\frac{{\sqrt { - \beta K_{2} } \left( {\lambda^{2} - K_{3} } \right)}}{\lambda }} \right)} \right)}}} \right),$$
    (27)

    where

    $$\begin{aligned} & A = 8\sqrt \pi \beta \left( {2K_{2} K_{3} e^{{2\beta K_{2} K_{3} }} } \right)erf\left( {\frac{{\sqrt { - \beta K_{2} } \left( {\lambda^{2} + K_{3} } \right)}}{\lambda }} \right) - 2\sqrt \pi \beta \lambda K_{1} e^{{2\beta K_{2} K_{3} }} erf\left( {\sqrt { - \beta K_{2} } \left( {\lambda^{2} + K_{3} } \right)} \right) \\ & B = - 2\sqrt \pi \beta \lambda K_{1} e^{{ - 2\beta K_{2} K_{3} }} erf\left( {\left( {\frac{{\sqrt { - \beta K_{2} } \left( {\lambda^{2} + K_{3} } \right)}}{\lambda }} \right)} \right) + 2\sqrt { - \beta K_{2} } e^{{\frac{{\beta K_{2} \left( {4K_{3} \lambda^{2} + \lambda^{4} + K_{3}^{2} } \right)}}{{\lambda^{2} }}}} \lambda^{2} + 2\sqrt { - \beta K_{2} } e^{{\frac{{\beta K_{2} \left( {4K_{3} \lambda^{2} + \lambda^{4} + K_{3}^{2} } \right)}}{{\lambda^{2} }}}} \\ & C = K_{3} + 2\sqrt { - \beta K_{2} } e^{{\frac{{\beta K_{2} \left( { - 4K_{3} \lambda^{2} + \lambda^{4} + K_{3}^{2} } \right)}}{{\lambda^{2} }}}} \lambda^{2} - 2\sqrt { - \beta K_{2} } e^{{\frac{{\beta K_{2} \left( { - 4K_{3} \lambda^{2} + \lambda^{4} + K_{3}^{2} } \right)}}{{\lambda^{2} }}}} K_{3} - \sqrt \pi \lambda e^{{2\beta K_{2} K_{3} }} erf\left( {\sqrt { - \beta K_{2} } \left( {\lambda^{2} + K_{3} } \right)} \right) \\ & D = - \sqrt \pi \lambda e^{{ - 2\beta K_{2} K_{3} }} erf\frac{{\left( {\sqrt { - \beta K_{2} } \left( {\lambda^{2} - K_{3} } \right)} \right)}}{\lambda } \\ \end{aligned}$$
    (28)
  2. (b)

    Vibrational specific heat capacity: The vibrational specific heat capacity \(C(\beta )\) is

    $$\begin{aligned} C(\beta ) & = k\beta^{2} \left( {\frac{{\partial^{2} \ln Z(\beta )}}{{\partial \beta^{2} }}} \right) \\ & = \frac{1}{2}\left[ {K\left( {\frac{\begin{gathered} E + F + G + H + I + J + L + M + N + \hfill \\ O + P + Q + R + S + T + U + V + W + X \hfill \\ \end{gathered} }{{\left( {\sqrt { - \beta K_{2} } \lambda^{3} \pi \left[ {e^{{2\beta K_{2} K_{3} }} erf\left( {\frac{{\sqrt { - \beta K_{2} } \left( {\lambda^{2} + K_{3} } \right)}}{\lambda }} \right) + e^{{ - 2\beta K_{2} K_{3} }} erf\left( {\frac{{\sqrt { - \beta K_{2} } \left( {\lambda^{2} - K_{3} } \right)}}{\lambda }} \right)} \right]^{2} } \right)}}} \right)} \right], \\ \end{aligned}$$
    (29)

    where

    $$\begin{aligned} E & = 4K_{2} \lambda^{3} \beta \sqrt { - \beta K_{2} } e^{{\frac{{2\beta K_{2} \left( {4K_{3} \lambda^{2} + \lambda^{4} + K_{3}^{2} } \right)}}{{\lambda^{2} }}}} K_{3} - 4K_{2} \lambda^{3} \beta \sqrt { - \beta K_{2} } e^{{\frac{{2\beta K_{2} \left( { - 4K_{3} \lambda^{2} + \lambda^{4} + K_{3}^{2} } \right)}}{{\lambda^{2} }}}} \\ & \quad + 2K_{2} \lambda \beta \sqrt { - \beta K_{2} } e^{{\frac{{2\beta K_{2} \left( {4K_{3} \lambda^{2} + \lambda^{4} + K_{3}^{2} } \right)}}{{\lambda^{2} }}}} \\ F & = K_{3}^{2} - 4K_{2} \lambda \beta \sqrt { - \beta K_{2} } e^{{\frac{{2\beta K_{2} \left( {4K_{3} \lambda^{2} + \lambda^{4} + K_{3}^{2} } \right)}}{{\lambda^{2} }}}} K_{3}^{2} \\ & \quad + 2K_{2} \lambda \beta \sqrt { - \beta K_{2} } e^{{\frac{{2\beta K_{2} \left( { - 4K_{3} \lambda^{2} + \lambda^{4} + K_{3}^{2} } \right)}}{{\lambda^{2} }}}} K_{3}^{2} \\ G & = \sqrt \pi \beta e^{{\frac{{\beta K_{2} \left( {6K_{3} \lambda^{2} + \lambda^{4} + K_{3}^{2} } \right)}}{{\lambda^{2} }}}} K_{3} K_{2} \lambda^{2} erf\left( {\left( {\frac{{\sqrt { - \beta K_{2} } \left( {\lambda^{2} + K_{3} } \right)}}{\lambda }} \right)} \right) \\ & \quad - \sqrt \pi \beta \,e^{{\frac{{2\beta K_{2} \left( { - 6K_{3} \lambda^{2} + \lambda^{4} + K_{3}^{2} } \right)}}{{\lambda^{2} }}}} K_{3} K_{2} \lambda^{2} erf\left( {\left( {\frac{{\sqrt { - \beta K_{2} } \left( {\lambda^{2} - K_{3} } \right)}}{\lambda }} \right)} \right) \\ H & = - 22\sqrt \pi \beta^{2} K_{2}^{2} K_{3} e^{{\frac{{\beta K_{2} \left( {\lambda^{2} + K_{3} } \right)^{2} }}{{\lambda^{2} }}}} \lambda^{4} erf\left( {\left( {\frac{{\sqrt { - \beta K_{2} } \left( {\lambda^{2} - K_{3} } \right)}}{\lambda }} \right)} \right) \\ & \quad - 22\sqrt \pi \beta^{2} K_{2}^{2} K_{3}^{2} e^{{\frac{{\beta K_{2} \left( {\lambda^{2} + K_{3} } \right)^{2} }}{{\lambda^{2} }}}} \lambda^{2} erf\left( {\left( {\frac{{\sqrt { - \beta K_{2} } \left( {\lambda^{2} - K_{3} } \right)}}{\lambda }} \right)} \right) \\ I & = 2\sqrt \pi \beta^{2} K_{2}^{2} e^{{\frac{{2\beta K_{2} \left( { - 6K_{3} \lambda^{2} + \lambda^{4} + K_{3}^{2} } \right)}}{{\lambda^{2} }}}} K_{3}^{3} erf\left( {\left( {\frac{{\sqrt { - \beta K_{2} } \left( {\lambda^{2} - K_{3} } \right)}}{\lambda }} \right)} \right) \\ & \quad + 22K_{2}^{2} \lambda^{4} \beta^{2} \sqrt \pi K_{3} e^{{\frac{{\beta K_{2} \left( {\lambda^{2} - K_{3} } \right)^{2} }}{{\lambda^{2} }}}} \,erf\left( {\left( {\frac{{\sqrt { - \beta K_{2} } \left( {\lambda^{2} - K_{3} } \right)}}{\lambda }} \right)} \right) \\ J & = - 22K_{2}^{2} \lambda^{2} \beta^{2} \sqrt \pi K_{3}^{2} e^{{\frac{{\beta K_{2} \left( {\lambda^{2} + K_{3} } \right)^{2} }}{{\lambda^{2} }}}} erf\left( {\left( {\frac{{\sqrt { - \beta K_{2} } \left( {\lambda^{2} + K_{3} } \right)}}{\lambda }} \right)} \right) \\ \end{aligned}$$
    (30)
    $$\begin{aligned} L & = \sqrt \pi \beta e^{{\frac{{\beta K_{2} \left( {\lambda ^{2} + K_{3} } \right)^{2} }}{{\lambda ^{2} }}}} K_{3} K_{2} \lambda ^{2} erf\left( {\left( {\frac{{\sqrt { - \beta K_{2} } \left( {\lambda ^{2} - K_{3} } \right)}}{\lambda }} \right)} \right) - \sqrt \pi \beta e^{{\frac{{\beta K_{2} \left( {\lambda ^{2} - K_{3} } \right)^{2} }}{{\lambda ^{2} }}}} K_{3} K_{2} \lambda ^{2} erf\left( {\left( {\frac{{\sqrt { - \beta K_{2} } \left( {\lambda ^{2} + K_{3} } \right)}}{\lambda }} \right)} \right) \\ M & = 2\sqrt { - \beta K_{2} } \lambda ^{3} \pi erf\left( {\left( {\frac{{\sqrt { - \beta K_{2} } \left( {\lambda ^{2} + K_{3} } \right)}}{\lambda }} \right)} \right)erf\left( {\left( {\frac{{\sqrt { - \beta K_{2} } \left( \begin{gathered} \lambda ^{2} - \hfill \\ K_{3} \hfill \\ \end{gathered} \right)}}{\lambda }} \right)} \right) \\ N & = 2\sqrt { - \beta K_{2} } \lambda ^{3} \pi erf\left( {\left( {\frac{{\sqrt { - \beta K_{2} } \left( {\lambda ^{2} + K_{3} } \right)}}{\lambda }} \right)} \right)erf\left( {\left( {\frac{{\sqrt { - \beta K_{2} } \left( \begin{gathered} \lambda ^{2} - \hfill \\ K_{3} \hfill \\ \end{gathered} \right)}}{\lambda }} \right)} \right) + 2K_{2} \lambda ^{5} \beta \sqrt { - \beta K_{2} } e^{{\frac{{2\beta K_{2} \left( {4K_{3} \lambda ^{2} + \lambda ^{4} + K_{3}^{2} } \right)}}{{\lambda ^{2} }}}} \\ \end{aligned}$$
    (31)
    $$\begin{aligned} O & = 4K_{2} \lambda^{5} \beta \sqrt { - \beta K_{2} } e^{{\frac{{2\beta K_{2} \left( {\lambda^{4} + K_{3} } \right)}}{{\lambda^{2} }}}} + 2K_{2} \lambda^{5} \beta \sqrt { - \beta K_{2} } e^{{\frac{{2\beta K_{2} \left( { - 4K_{3} \lambda^{2} + \lambda^{4} + K_{3}^{2} } \right)}}{{\lambda^{2} }}}} \\ & \quad + \sqrt { - \beta K_{2} } \lambda^{3} \pi e^{{4\beta K_{2} K_{3} }} erf\left( {\left( {\frac{{\sqrt { - \beta K_{2} } \left( {\lambda^{2} - K_{3} } \right)}}{\lambda }} \right)} \right)^{2} \\ Q & = \beta K_{2} \lambda^{4} \sqrt \pi e^{{\frac{{\beta K_{2} \left( {6K_{3} \lambda^{2} + \lambda^{4} + K_{3}^{2} } \right)}}{{\lambda^{2} }}}} erf\left( {\frac{{\sqrt { - \beta K_{2} } \left( {\lambda^{2} + K_{3} } \right)}}{\lambda }} \right) \\ P & = \sqrt { - \beta K_{2} } \lambda^{3} \pi e^{{4\beta K_{2} K_{3} }} erf\left( {\left( {\frac{{\sqrt { - \beta K_{2} } \left( {\lambda^{2} - K_{3} } \right)}}{\lambda }} \right)} \right)^{2} \\ S & = - 2\sqrt \pi \beta^{2} K_{2}^{2} e^{{\frac{{\beta K_{2} \left( {6K_{3} \lambda^{2} + \lambda^{4} + K_{3}^{2} } \right)}}{{\lambda^{2} }}}} erf\left( {\frac{{\sqrt { - \beta K_{2} } \left( {\lambda^{2} + K_{3} } \right)}}{\lambda }} \right) \\ & \quad + \sqrt { - \beta K_{2} } \lambda^{3} \pi e^{{ - 4\beta K_{2} K_{3} }} \\ T & = - 2\sqrt \pi \beta^{2} K_{2}^{2} e^{{\frac{{\beta K_{2} \left( { - 6K_{3} \lambda^{2} + \lambda^{4} + K_{3}^{2} } \right)}}{{\lambda^{2} }}}} \lambda^{6} erf\left( {\frac{{\sqrt { - \beta K_{2} } \left( {\lambda^{2} + K_{3} } \right)}}{\lambda }} \right) \\ \end{aligned}$$
    (32)
    $$\begin{aligned} U & = - 6\sqrt \pi \beta^{2} K_{2}^{2} e^{{\frac{{\beta K_{2} \left( {6K_{3} \lambda^{2} + \lambda^{4} + K_{3}^{2} } \right)}}{{\lambda^{2} }}}} \lambda^{2} K_{3}^{2} erf\left( {\frac{{\sqrt { - \beta K_{2} } \left( {\lambda^{2} + K_{3} } \right)}}{\lambda }} \right) \\ & \quad - 6\sqrt \pi \beta^{2} K_{2}^{2} e^{{\frac{{\beta K_{2} \left( {6K_{3} \lambda^{2} + \lambda^{4} + K_{3}^{2} } \right)}}{{\lambda^{2} }}}} \lambda^{4} K_{3} erf\left( {\frac{{\sqrt { - \beta K_{2} } \left( {\lambda^{2} + K_{3} } \right)}}{\lambda }} \right) \\ V & = 32\pi \beta^{2} K_{2}^{2} \lambda^{3} K_{3}^{2} erf\left( {\frac{{\sqrt { - \beta K_{2} } \left( {\lambda^{2} + K_{3} } \right)}}{\lambda }} \right)\sqrt { - \beta K_{2} } erf\left( {\frac{{\sqrt { - \beta K_{2} } \left( {\lambda^{2} - K_{3} } \right)}}{\lambda }} \right) \\ & \quad + \beta K_{2} \lambda^{4} \sqrt \pi e^{{\frac{{\beta K_{2} \left( {\lambda^{2} - K_{3} } \right)^{2} }}{{\lambda^{2} }}}} erf\left( {\frac{{\sqrt { - \beta K_{2} } \left( {\lambda^{2} + K_{3} } \right)}}{\lambda }} \right) \\ W & = - 2\sqrt \pi \beta^{2} K_{2}^{2} e^{{\frac{{\beta K_{2} \left( {\lambda^{2} - K_{3} } \right)^{2} }}{{\lambda^{2} }}}} \lambda^{6} erf\left( {\frac{{\sqrt { - \beta K_{2} } \left( {\lambda^{2} + K_{3} } \right)}}{\lambda }} \right) \\ & \quad + 2\sqrt \pi \beta^{2} K_{2}^{2} e^{{\frac{{\beta K_{2} \left( {\lambda^{2} - K_{3} } \right)^{2} }}{{\lambda^{2} }}}} \lambda^{6} erf\left( {\frac{{\sqrt { - \beta K_{2} } \left( {\lambda^{2} + K_{3} } \right)}}{\lambda }} \right) \\ X & = 2\sqrt \pi \beta^{2} K_{2}^{2} e^{{\frac{{\beta K_{2} \left( {\lambda^{2} - K_{3} } \right)^{2} }}{{\lambda^{2} }}}} K_{3}^{2} erf\left( {\frac{{\sqrt { - \beta K_{2} } \left( {\lambda^{2} + K_{3} } \right)}}{\lambda }} \right) \\ \end{aligned}$$
    (33)
  3. (c)

    Vibrational Entropy: The vibrational entropy is given as

    $$\begin{aligned} S(\beta ) & = k\ln Z(\beta ) - k\beta \frac{\partial \ln Z(\beta )}{{\partial \beta }} \\ & = - \frac{1}{2}k\left[ {\frac{A + B + C + D + E}{{\sqrt \pi \beta \lambda e^{{2\beta K_{2} K_{3} }} erf\left( {\frac{{\sqrt { - \beta K_{2} } \left( {\lambda^{2} + K_{3} } \right)}}{\lambda }} \right) + e^{{ - 2\beta K_{2} K_{3} }} erf\left( {\frac{{\sqrt { - \beta K_{2} } \left( {\lambda^{2} - K_{3} } \right)}}{\lambda }} \right)}}} \right], \\ \end{aligned}$$
    (34)

    where

    $$\begin{aligned} A & = 4\ln 2 - \ln \pi - 2\ln \left( {e^{{ - \beta \left( { - 2K_{2} K_{3} + K_{1} } \right)}} erf\left( {\frac{{\sqrt { - \beta K_{2} } \left( {\lambda^{2} + K_{3} } \right)}}{\lambda }} \right)} \right) \\ & \quad + e^{{\left( { - 2\beta K_{2} K_{3} } \right)}} erf\left( {\frac{{\sqrt { - \beta K_{2} } \left( {\lambda^{2} - K_{3} } \right)}}{\lambda }} \right) \\ B & = 2\beta \left( { - \frac{1}{2}\left( { - 8\sqrt \pi \beta K_{2} \lambda K_{3} e^{{2\beta K_{2} K_{3} }} erf\left( {\frac{{\sqrt { - \beta K_{2} } \left( {\lambda^{2} + K_{3} } \right)}}{\lambda }} \right)} \right)} \right) \\ & \quad + 2\sqrt \pi \beta \lambda K_{1} e^{{2\beta K_{2} K_{3} }} erf\left( {\frac{{\sqrt { - \beta K_{2} } \left( {\lambda^{2} + K_{3} } \right)}}{\lambda }} \right) \\ C & = 2\sqrt \pi \beta \lambda K_{1} e^{{ - 2\beta K_{2} K_{3} }} erf\left( {\frac{{\sqrt { - \beta K_{2} } \left( {\lambda^{2} - K_{3} } \right)}}{\lambda }} \right) \\ & \quad - 2\sqrt { - \beta K_{2} } e^{{\frac{{\beta K_{2} \left( {4K_{3} \lambda^{2} + \lambda^{4} + K_{3}^{2} } \right)}}{{\lambda^{2} }}}} \lambda^{2} - 2\sqrt { - \beta K_{2} } e^{{\frac{{\beta K_{2} \left( {4K_{3} \lambda^{2} + \lambda^{4} + K_{3}^{2} } \right)}}{{\lambda^{2} }}}} K_{3} \\ D & = - \sqrt { - \beta K_{2} } e^{{\frac{{\beta K_{2} \left( { - 4K_{3} \lambda^{2} + \lambda^{4} + K_{3}^{2} } \right)}}{{\lambda^{2} }}}} \lambda^{2} + 2\sqrt { - \beta K_{2} } e^{{\frac{{\beta K_{2} \left( {4K_{3} \lambda^{2} + \lambda^{4} + K_{3}^{2} } \right)}}{{\lambda^{2} }}}} K_{3} \\ E & = \sqrt \pi \lambda e^{{2\beta K_{2} K_{3} }} erf\left( {\frac{{\sqrt { - \beta K_{2} } \left( {\lambda^{2} + K_{3} } \right)}}{\lambda }} \right) + \sqrt \pi \lambda e^{{ - 2\beta K_{2} K_{3} }} erf\left( {\frac{{\sqrt { - \beta K_{2} } \left( {\lambda^{2} - K_{3} } \right)}}{\lambda }} \right) \\ \end{aligned}$$
    (35)
  4. (d)

    Vibrational free energy: The vibrational free energy \(F(\beta )\) is given as

    $$\begin{aligned} F(\beta ) & = - \frac{1}{\beta }\ln Z(\beta ) \\ & = - \frac{1}{\beta }\left[ {\ln \left( {\frac{1}{4}\frac{1}{{\sqrt { - \beta K_{2} } }}\left( \begin{gathered} e^{{\beta \left( {2K_{2} K_{3} - K_{1} } \right)}} \sqrt \pi \left( {e^{{2\beta K_{2} K_{3} }} erf\left( {\sqrt { - \beta K_{2} } \lambda + \frac{{K_{3} \sqrt { - \beta K_{2} } }}{\lambda }} \right)} \right) \hfill \\ + e^{{ - 2\beta K_{2} K_{3} }} erf\left( {\sqrt { - \beta K_{2} } \lambda - \frac{{K_{3} \sqrt { - \beta K_{2} } }}{\lambda }} \right) \hfill \\ \end{gathered} \right)} \right)} \right], \\ \end{aligned}$$
    (36)

Results and discussion

The numerical bound state energy for the selected diatomic molecules (HgH, ZnH, CdH, HBr and HF) has been computed. The spectroscopic constants of the five selected diatomic molecules used for the numerical computation are presented in Table 1.

Table 1 Spectroscopic constants for five selected diatomic molecules (Refs [58, 59])
Full size table

Table 2 shows the numerical bound state solution of HgH with fixed screening parameter \(\alpha = 0.312\). The numerical table shows both monotonous increment and decrement with respect to quantum state for various orbital angular quantum number \(l\) = 0, 1, 2 and 3. The trend given in Tables 3, 4, 5 and 6 with screening parameters \(\alpha\) = 0.25, 0.218, 0.226 and 0.77 are spectroscopic constants for ZnH, CdH, HBr, and HF molecules, respectively, taken from Refs. [38, 48] for different values of the reduced mass (\(\mu\)) and dissociation energy (\(D_{e}\)). Throughout our computation, \(D_{1}\) is a control and optimizing parameter which is fixed to a value of 0.5, while \(\hbar\) takes a unitary value of 1.

Table 2 Numerical solutions for HgH molecule \(\mu = 1.0031\begin{array}{*{20}c} , & {D_{e} = 0.46130} \\ \end{array} \begin{array}{*{20}c} {\begin{array}{*{20}c} , & {D_{1} = 0.5} \\ \end{array} } & {\hbar = 1.0} \\ \end{array}\)
Full size table
Table 3 Numerical solutions for ZnH molecule \(\mu = 0.9928\begin{array}{*{20}c} , & {D_{e} = 0.950352} \\ \end{array} \begin{array}{*{20}c} {\begin{array}{*{20}c} , & {D_{1} = 0.5} \\ \end{array} } & {\hbar = 1.0} \\ \end{array}\)
Full size table
Table 4 Numerical solutions for CdH molecule \(\mu = 0.9992\begin{array}{*{20}c} , & {D_{e} = 0.766272} \\ \end{array} \begin{array}{*{20}c} {\begin{array}{*{20}c} , & {D_{1} = 0.5} \\ \end{array} } & {\hbar = 1.0} \\ \end{array}\)
Full size table
Table 5 Numerical solutions for HBr molecule \(\mu = 0.9956\begin{array}{*{20}c} , & {D_{e} = 3.916848} \\ \end{array} \begin{array}{*{20}c} {\begin{array}{*{20}c} , & {D_{1} = 0.5} \\ \end{array} } & {\hbar = 1.0} \\ \end{array}\)
Full size table
Table 6 Numerical solutions for HF molecule \(\mu = 0.9573\begin{array}{*{20}c} , & {D_{e} = 6.6456} \\ \end{array} \begin{array}{*{20}c} {\begin{array}{*{20}c} , & {D_{1} = 0.5} \\ \end{array} } & {\hbar = 1.0} \\ \end{array}\)
Full size table

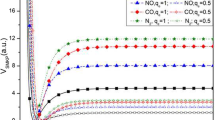
Figure 1a, b shows the variation of partition function (\(Z(\lambda ,\beta )\)) which increases exponentially with respect to \(\beta\) and decreases to -0.5 with respect to \(\lambda\). Figure 2a, b shows variation of vibrational mean energy (\(U(\lambda ,\beta )\)) with respect to \(\beta\) in Fig. 2a and variation with respect to \(\lambda\) as shown in Fig. 2b. In Fig. 2a, the vibrational mean energy increases with an increase in energy-dependent parameter but monotonically decreases with respect to \(\lambda\). The variation of vibrational specific heat capacity \(C(\lambda ,\beta )\) with respect to \(\beta\) is shown in Fig. 3a where there are several minimum turning points between \(\beta = 0.1\) and 0.2. In Fig. 3b, the vibrational specific heat capacity with respect to \(\lambda\) reproduces the same characteristics of vibrational mean energy with respect to \(\lambda\). In Fig. 4a, the vibrational entropy increases exponentially with respect to \(\beta\) but display an hyperbolic nature with respect \(\lambda\) as shown in Fig. 4b. The vibrational free energy decreases monotonically to a constant value of 0.08 with respect to \(\beta\) as shown in Fig. 5a but exhibits an hyperbolic nature with multiple maximum points at \(\lambda = - 1\) with respect to \(\lambda\) as shown in Fig. 5b. The trend of partition function and other thermodynamic properties obtained in this work is in excellent agreement with researches of refs [50,51,52,53,54] which affirm the accuracy of the work.

Fig. 1
figure 1

a, b Variation of partition function with \(\beta\) and \(\lambda\) for thermodynamic properties

Full size image
Fig. 2
figure 2

a, b Variation of vibrational mean energy with \(\beta\) and \(\lambda\) for thermodynamic properties

Full size image
Fig. 3
figure 3

a, b Variation of specific heat capacity with \(\beta\) and \(\lambda\) for thermodynamic properties

Full size image
Fig. 4
figure 4

a, b Variation of vibrational mean entropy with \(\beta\) and \(\lambda\) for thermodynamic properties

Full size image
Fig. 5
figure 5

a, b Variation of vibrational free energy with \(\beta\) and \(\lambda\) for thermodynamic properties

Full size image

Conclusion

In this work, we study an approximate bound state solutions of Schrӧdinger wave equation with MESPYP potential model using parametric Nikiforov–Uvarov method where we obtain energy eigenequation and total unnormalized wave function expressed in terms of associated Jacobi polynomial. We obtained numerical bound state energies for five selected diatomic molecules. The resulting energy eigenequation was presented in a compact form and employed to study partition function and other thermodynamic properties. The numerical bound state solutions were carried out with a fixed control and optimizing parameter. The thermodynamic curves obtained are in excellent agreement to work of an existing literature.