The Elastic Properties of Dilute Solid Suspensions with Imperfectly Bonded Inclusions of Ellipsoidal Shape: Bounds, Asymptotics, Approximations

Abstract

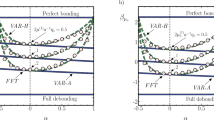
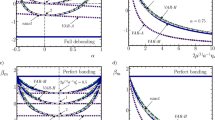
The elastic properties of dilute solid suspensions with imperfectly bonded inclusions of ellipsoidal shape are estimated. The imperfect bonding is regarded as a sharp interface across which the displacement jumps in proportion to the surface traction. Elastic compliances of the matrix and inclusion phases can exhibit arbitrary anisotropy while that of the bonding exhibits an anisotropy that depends on the interface normal only. A variational framework is employed to generate pairs of elementary bounds, asymptotically exact results, and approximations for the effective elasticity tensor. Each member of the pair differs in the way the bonding compliance is averaged over the interfacial surface: an ‘arithmetic’ mean in one case and a ‘harmonic’ mean in the other case. The results are used to infer the most convenient approximation for a given range of material parameters.

Appendices

Appendix A: Some Useful Identities for Ellipsoidal Inclusions

• 1. The identity

  $$\begin{aligned} \ell ^{-1}\langle \overline{{\mathbf {x}}}\otimes {\mathbf {n}}\rangle ^{(1,2)} = {\mathbf {I}} \end{aligned}$$

  (82)

  follows from the sequence of identities

  

  (83)

  The third identity follows from the change of variables , while the last identity follows from the fact that the integral is an isotropic symmetric function of the symmetric tensor ${\mathbf {A}}$, that it therefore shares the same eigenvectors of ${\mathbf {A}}$, and that it therefore has eigenvalues $e_{i}$ given by

  

  (84)

• 2. The identity

  

  (85)

  follows from the fact that the integral is an isotropic symmetric function of ${\mathbf {A}}$, that it therefore shares the same eigenvectors ${\mathbf {a}}_{i}$ ($i=1,2,3$) of ${\mathbf {A}}$, and that it therefore has eigenvalues $e_{i}$ given by

  

  (86)

  where $\alpha _{i}$, $\alpha _{j}$ and $\alpha _{k}$ ($i\neq j\neq k$) are the three eigenvalues of ${\mathbf {A}}$. The second identity follows from expressing the integration vector as with and .

Appendix B: Auxiliary Problem

Consider the displacement field ${\mathbf {v}}({\mathbf {x}})$ that solves the set of equations

(87)

(88)

$$\begin{aligned} &{\mathbf {v}}({\mathbf {x}}) = {\mathbf{0}} \quad \text{on} \quad \partial \Omega , \end{aligned}$$

(89)

for prescribed tensors , and ${\mathbf {D}}^{(1,2)}$. The tensors and are symmetric but the tensor ${\mathbf {D}}^{(1,2)}$ need not be. These equations can be recast into the single equation

(90)

with

(91)

which should be understood in the sense of distributions. Here, $\mathbb{E}({\mathbf {x}}) = {\mathbf {I}}\boxtimes ({\mathbf {n}}({\mathbf {x}}) \otimes {\mathbf {x}})$, and

$$\begin{aligned} \delta ^{(1,2)}({\mathbf {x}}) = |{\mathbf {A}}^{-2}{\mathbf {x}}|\ \delta \left ( |{\mathbf {A}}^{-1} {\mathbf {x}}| - 1 \right ) \end{aligned}$$

(92)

refers to the Dirac delta function with support on the interface $\Gamma ^{(1,2)}$. Making use of the Radon transform of equation (90) and its inverse we can write the strain field as

(93)

where is given by (32)₂ and is the Radon transform of the polarization field given by

(94)

Given that inclusions are well separated, the strain field within any particular inclusion can be computed by neglecting the presence of all the other inclusions. This amounts to identifying the functions $\chi ^{(2)}({\mathbf {x}})$ and $\delta ^{(1,2)}({\mathbf {x}})$ in (91) with those of a single inclusion centered at the origin of an infinite medium. In that case,

(95)

where

(96)

(97)

and the sets and are the intersections of a rotated Radon plane with a unit sphere and with its surface, respectively; the second identities follow from the change of variables ${\mathbf {y}}= {\mathbf {A}}^{-1}{\mathbf {x}}$; computations give

(98)

(99)

where $H(\cdot )$ is the Heaviside step function. Therefore, when

(100)

Introducing this expression into (93) and making use of the identity (85) then gives an expression for the strain field within the inclusion ($|{\mathbf {A}}^{-1}{\mathbf {x}}|<1$) of the form

(101)

where ℙ is the microstructural tensor given by (32). Thus, the strain field within every inclusion of the suspension is uniform and given by (101). The procedure based on Radon transforms pursued above was initially advocated by Willis [15] for inclusion problems with perfect interfacial bonding.