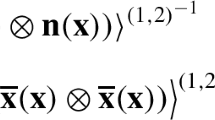Improved estimates for the elastic properties of dilute composites with imperfect interfacial bondings of moderate anisotropy

Abstract

Estimates are proposed for the linearly elastic properties of dilute composites reinforced by either spherical particles or circular fibers that are imperfectly bonded to the surrounding matrix. This imperfection is represented via interfacial bonding conditions requiring continuity of tractions but permiting discontinuities of displacements that are proportional to the tractions. Elastic anisotropy of the matrix and the reinforcements can be arbitrary, but that of the interfacial bond is restricted to a particular form of common use. Like the variational estimates of Gallican et al. (J Elast 153:373–398, 2023), the new estimates incorporate a dependence on bonding compliance through an equivalent stiffness tensor for the reinforcing phase. But instead of depending on either the arithmetic or harmonic mean of the bonding compliance, the equivalent stiffness tensor is made to depend on a function of the degree of bonding compliance anisotropy chosen in such a way that certain conditions for the elastic neutrality of rigid reinforcements are recovered exactly. The resulting estimates can be cast in variational form and interpreted as an interpolation between estimates of the arithmetic and harmonic type. Explicit expressions for effective shear moduli of isotropic composites are provided and confronted to exact results for assessment. Predictions are asymptotically exact when bonding compliance is weakly anisotropic, and are found to improve on earlier predictions of the arithmetic and harmonic type when bonding compliance is moderately anisotropic.

Appendices

Appendix 1: A procedure to determine elastic moduli of isotropic composites

Making use of the overall balance of average strains over each phase and of the divergence theorem within the inclusions, the free-energy density of a suspension can be written as

$$\begin{aligned} \frac{1}{2}\overline{\varvec{\varepsilon }}\cdot \widetilde{\mathbb {C}}\overline{\varvec{\varepsilon }}&= \frac{1}{2}\overline{\varvec{\varepsilon }}\cdot \mathbb {C}^{(1)}\overline{\varvec{\varepsilon }}+ \frac{1}{2} c\ \ell ^{-1} \nonumber \\&\quad \left[ \left\langle (\mathbb {C}^{(2)}\overline{\varvec{\varepsilon }}){\textbf{n}} \cdot {\textbf{u}} ^{(2)}\right\rangle ^{(1,2)}-\left\langle (\mathbb {C}^{(1)}\overline{\varvec{\varepsilon }}){\textbf{n}}\cdot {\textbf{u}}^{(1)}\right\rangle ^{(1,2)}\right] , \end{aligned}$$

(28)

where $\overline{\varvec{\varepsilon }}$ is the macroscopic strain tensor, $\widetilde{\mathbb {C}}$ is the effective stiffness tensor, $\textbf{u}$ is the displacement field, the superscripts (1) and (2) refer to the limiting values at the interface evaluated from the matrix side and from the particle side, respectively, and $\ell$ is the volume to surface ratio of inclusions. The effective elastic moduli of the suspension can then be determined from knowledge of these displacement fields for particular macroscopic deformations. In the case of isotropic suspensions of spherical particles, the effective stiffness tensor is isotropic and fully characterized by the effective bulk $\widetilde{\kappa }$ and shear $\widetilde{\mu }$ moduli. The effective bulk modulus has been given by Hashin [13]. The effective shear modulus can be determined by considering axisymmetric strains of the form $\overline{\varvec{\varepsilon }}= \overline{\varepsilon }(3 \textbf{e}\otimes \textbf{e} - \textbf{I})$ and solving for the local mechanical fields. The components of the stress and displacement fields in a spherical coordinate system centered at the particle admit a separated solution of functions of the radial coordinate multiplied by Legendre polynomials as in expressions (37) of [13]. Once computed, expression (12) for the effective shear moduli is obtained by introducing the displacement fields in (28) and performing the required integrations over the interface.

Appendix 2: A variational format for the new estimates

The effective mechanical response of a dilute composite can be written as

$$\begin{aligned} \overline{\varvec{\sigma }}= \frac{\partial \widetilde{w}}{\partial \overline{\varvec{\varepsilon }}}(\overline{\varvec{\varepsilon }}), \end{aligned}$$

(29)

where $\overline{\varvec{\varepsilon }}$ and $\overline{\varvec{\sigma }}$ are the macroscopic strain and stress tensors, and $\widetilde{w}$ is the homogenized or effective free-energy density of the composite given by [4]

$$\begin{aligned} \widetilde{w}(\overline{\varvec{\varepsilon }})&= \min _{\textbf{d}} \left[ \min _{\varvec{\varepsilon }\in \mathchoice{\text{ K }}{\text{ K }}{\text{ K }}{\text{ K }}(\overline{\varvec{\varepsilon }},\textbf{d})} \sum _{r=1}^2 c^{(r)}\left\langle w^{(r)}\left( \varvec{\varepsilon }(\textbf{x})\right) \right\rangle ^{(r)}\right. \nonumber \\&\quad \left. + c^{(2)} \ell ^{-1} \Big \langle \textrm{w}^{(1,2)}\left( \textbf{n}(\textbf{x}),\textbf{d}(\textbf{x})\right) \Big \rangle ^{(1,2)} \right] . \end{aligned}$$

(30)

Here, $w^{(r)}$ and $\textrm{w}^{(1,2)}$ are the free-energy densities of each constituent phase and of the bonding, respectively, $c^{(r)}$ and $\langle \cdot \rangle ^{(r)}$ refer to the volume fraction of phase r and the volume average over the subdomain $\Omega ^{(r)}$ occupied by that phase, respectively, $\mathchoice{\text{ K }}{\text{ K }}{\text{ K }}{\text{ K }}(\overline{\varvec{\varepsilon }},\textbf{d})$ is the set of kinematically compatible strain fields of the form $\varvec{\varepsilon }(\textbf{x}) = \overline{\varvec{\varepsilon }}+ \nabla \otimes _s\textbf{v}(\textbf{x})$ with $\textbf{v}:\Omega \rightarrow \mathbb {R}^3$ square-integrable with compact support and such that its gradient is also square-integrable in each subdomain $\Omega ^{(r)}$ and the interfacial jump is $\llbracket \textbf{v}(\textbf{x}) \rrbracket = \textbf{d}(\textbf{x})$ on the surface $\Gamma ^{(1,2)}$ occupied by the bonding.

Making use of the Legendre transform, we decompose the free-energy density of linearly elastic bondings as

$$\begin{aligned} \textrm{w}^{(1,2)}(\textbf{n},\textbf{d})&= \frac{1}{2} \textbf{d}\cdot \varvec{\eta }(\textbf{n})^{-1} \textbf{d}= (1-\beta ) \frac{1}{2} \textbf{d}\cdot \varvec{\eta }(\textbf{n})^{-1} \textbf{d}\nonumber \\&\quad + \beta \max_{\textbf{t}}\left[ \textbf{t}\cdot \textbf{d}- \frac{1}{2} \textbf{t}\cdot \varvec{\eta }(\textbf{n})\textbf{t}\right] , \end{aligned}$$

(31)

where $\beta \in [0,1]$ is a dimensionless parameter to be chosen. Introducing this decomposition into (30) we obtain the alternative representation

$$\begin{aligned} \widetilde{w}(\overline{\varvec{\varepsilon }})&= \min _{\textbf{d}} \max_{\textbf{t}} \left[ \min _{\varvec{\varepsilon }\in \mathchoice{\text{ K }}{\text{ K }}{\text{ K }}{\text{ K }}(\overline{\varvec{\varepsilon }},\textbf{d})} \sum _{r=1}^2 c^{(r)}\left\langle w^{(r)}\left( \varvec{\varepsilon }(\textbf{x})\right) \right\rangle ^{(r)}\right. \\&\quad \left. + c^{(2)} (1-\beta ) \ell ^{-1} \Big \langle \frac{1}{2} \textbf{d}\cdot \varvec{\eta }(\textbf{n})^{-1} \textbf{d}\Big \rangle ^{(1,2)} \right. \\&\quad \left. + c^{(2)} \beta \ell ^{-1} \Big \langle \textbf{t}\cdot \textbf{d}- \frac{1}{2} \textbf{t}\cdot \varvec{\eta }(\textbf{n})\textbf{t}\Big \rangle ^{(1,2)} \right] . \end{aligned}$$

A variational approximation for composites reinforced by spherical particles or circular fibers can now be derived by considering the trial fields

$$\begin{aligned} \textbf{d}(\textbf{x}) = \textbf{D}^{(1,2)} \textbf{x}\quad \text{ and } \quad \textbf{t}(\textbf{x}) = \textbf{S}^{(1,2)}\textbf{n}(\textbf{x}), \end{aligned}$$

(32)

so that

$$\begin{aligned} \widetilde{w}(\overline{\varvec{\varepsilon }})&\approx \min _{\textbf{D}^{(1,2)}} \max_{\textbf{S}^{(1,2)}} \left[ \min _{\varvec{\varepsilon }\in \mathchoice{\text{ K }}{\text{ K }}{\text{ K }}{\text{ K }}(\overline{\varvec{\varepsilon }},\textbf{D}^{(1,2)})} \sum _{r=1}^2 c^{(r)}\left\langle w^{(r)}\left( \varvec{\varepsilon }(\textbf{x})\right) \right\rangle ^{(r)}\right. \nonumber \\&\quad \left. + c^{(2)} (1-\beta ) \frac{1}{2} \textbf{D}^{(1,2)} \cdot \mathbb {R}^{(1,2)}_H \textbf{D}^{(1,2)} + \right. \nonumber \\&\quad \left. c^{(2)} \beta \left( \textbf{S}^{(1,2)}\cdot \textbf{D}^{(1,2)} - \frac{1}{2} \textbf{S}^{(1,2)} \cdot \mathbb {R}^{(1,2)^{-1}}_A \textbf{S}^{(1,2)} \right) \right] \nonumber \\&= \min _{\textbf{D}^{(1,2)}} \left[ \min _{\varvec{\varepsilon }\in \mathchoice{\text{ K }}{\text{ K }}{\text{ K }}{\text{ K }}(\overline{\varvec{\varepsilon }},\textbf{D}^{(1,2)})} \sum _{r=1}^2 c^{(r)}\left\langle w^{(r)}\left( \varvec{\varepsilon }(\textbf{x})\right) \right\rangle ^{(r)}\right. \nonumber \\&\quad \left. + c^{(2)} \frac{1}{2} \textbf{D}^{(1,2)} \cdot \left[ (1-\beta ) \mathbb {R}^{(1,2)}_H + \beta \mathbb {R}^{(1,2)}_A\right] \textbf{D}^{(1,2)} \right] \nonumber \\&= \min _{\textbf{D}^{(1,2)}} \left[ \min _{\varvec{\varepsilon }\in \mathchoice{\text{ K }}{\text{ K }}{\text{ K }}{\text{ K }}(\overline{\varvec{\varepsilon }},\textbf{D}^{(1,2)})} \sum _{r=1}^2 c^{(r)}\left\langle w^{(r)}\left( \varvec{\varepsilon }(\textbf{x})\right) \right\rangle ^{(r)} \right. \nonumber \\&\quad \left. + c^{(2)} \frac{1}{2} \textbf{D}^{(1,2)} \cdot \mathbb {R}^{(1,2)}_{M} \textbf{D}^{(1,2)} \right] , \end{aligned}$$

(33)

where $\mathbb {R}^{(1,2)}_H$ and $\mathbb {R}^{(1,2)}_A$ are the harmonic and arithmetic mean tensors, respectively, as given by expressions (4), and

$$\begin{aligned} \mathbb {R}^{(1,2)}_{M} = (1-\beta ) \mathbb {R}^{(1,2)}_H + \beta \mathbb {R}^{(1,2)}_A. \end{aligned}$$

(34)

It is shown in [4] that when the constituent phases are linearly elastic and the free-energy densities $w^{(r)}$ are thus quadratic functions of strain, the minimizing strain in the approximation (33) is uniform within the reinforcements, and the resulting approximation for the effective stiffness tensor is of the form (1) with the equivalent stiffness tensor for the reinforcing phase given by (3) but with the interfacial tensor $\mathbb {R}^{(1,2)}$ given by the modified tensor (34). Thus, a variational estimate for the effective stiffness tensor has been generated, for any choice of parameter $\beta$. The extreme choices $\beta =0$ and $\beta =1$ generate the variational estimates of the harmonic and arithmetic type derived by [4]. On the other hand, the choice

$$\begin{aligned} \beta = \left\{ \begin{array}{ll} \displaystyle \frac{5+\alpha }{432 \alpha ^2} \left( 25 + 17\alpha - 5 \sqrt{25 + 34\alpha -23\alpha ^2} \right) &{} \quad \text{ spherical } \text{ particles } \\ \\ \displaystyle \frac{\sqrt{4-3{\alpha '}^2} - 2 + 3 {\alpha '}^2}{3{\alpha '}^2} &{} \quad \text{ circular } \text{ fibers } \end{array} \right. \end{aligned}$$

(35)

generates the modified estimates proposed in this work, given that the interfacial stiffness tensor (34) agrees exactly with the modified stiffness tensor (8) in this case.