Introduction

Hydrogen bonding plays a critical role in how water is sequestered, often as hydroxyl units, within minerals. The response of hydrogen bonding to compression has long been understood in a general sense, with high pressures often favoring stronger hydrogen bonding within single phases, as manifested by negative pressure shifts of the hydroxyl stretching vibrations (e.g., Moon and Drickamer 1974; Lutz 1995). In turn, the minerals in which hydroxyls have extremely weak or non-existent hydrogen bonding often undergo positive pressure shifts (e.g., Kruger et al. 1989; Duffy et al. 1995a, b; Williams et al. 2012; Thompson et al. 2016). A general increase in hydrogen bonding as progressively higher pressure polymorphs are accessed has also been suggested (Faust and Williams 1996). Beyond general conceptual viewpoints, overarching systematics for how hydrogen bonding in materials is impacted by pressure have long been sought. For example, Moon and Drickamer (1974) analyzed the pressure dependence of a simple modified Lippincott-potential to semi-quantitatively demonstrate that lower frequency zero pressure O–H stretching vibrations (those with stronger hydrogen bonds) are generally expected to trend towards more negative pressure shifts relative to those with higher frequencies and weaker hydrogen bonding. This loose correlation was shown by Moon and Drickamer (1974) to hold for a range of hydroxyl-bearing organic materials under compression. This semi-theoretic correlation has been commonly deployed for hydrous minerals of possible mantle/subduction relevance (e.g., Hofmeister et al. 1999; Thompson et al. 2016; Liu et al. 2021). Importantly, as recognized by these authors, different structural/bonding environments of the oxygens involved in the hydrogen bonds generate different trends in frequency−pressure shift space. Thus, those materials with similar local bonding environments near the hydroxyl ion, like amphiboles and micas, plot on a similar trend; dissimilar minerals, like brucite and the dense hydrous magnesium silicate (DHMS) phases, do not.

One intent here is to examine if, beyond the semi-theoretic and conceptual frequency-mode shift correlations, there might be any other systematics that could be deployed that might provide a correlation with the observed pressure dependences of hydroxyl mode shifts. In particular, the degree to which there might be semi-predictive, rather than simply correlative, relations between hydroxyl mode pressure shifts and spectroscopically derived physical properties is of primary interest. Among physical properties (other than simple mode frequency) that likely correlate with mode shifts, hydroxyl and hydrogen bond lengths certainly play a major role. This dependence is implicit in the long-recognized correlation between hydroxyl stretching frequencies and O–O distances (e.g., Nakamoto et al. 1955; Novak 1974; Libowitzky 1999; Friedrich et al. 2007; Mitev et al. 2009). Yet, precise locations of hydrogen in hydrated minerals at high pressures are challenging to determine. Although structural correlations are likely to ultimately provide the most robust correlations with hydroxyl mode shifts, the paucity of accurate hydrogen location data under compression makes such an effort premature at this juncture. Accordingly, a prospective correlation between pressure shifts of hydroxyl bands and spectroscopically determined parameters (beyond mode frequency) is examined here. Beyond this possible correlation, multiple spectroscopic probes of anharmonicity provide complementary experimental information on the shape of the hydroxyl potential in (for example) high-pressure hydrous phases. Such improved constraints on the shape of this potential are critical for both how hydrogen is bound and retained in minerals, and how hydrogen might diffuse (via escape from the potential well) under extreme conditions.

As a starting point, it is worth recalling that fully harmonic potential wells are characterized by zero pressure shifts of their vibrational modes in response to changes in bond distance: as has been discussed in detail (e.g., Sherman 1980; Lucazeau 2003), pressure-induced mode shifts (and, of course, non-zero mode Grüneisen parameters) are a direct consequence of the anharmonicity of the potential well. For context, the classical definition of a harmonic oscillator is V = k(r–r0)2, where V is the potential energy, r0 is the equilibrium oscillator length, and k is the force constant which is, in the harmonic model, independent of the oscillator length, r. Clearly, this classical definition is unrealistic for essentially all real-world situations (including bonds): no compaction or expansion-induced shift in the force constant is present, and the oscillator is completely decoupled from any other vibrations. Anharmonicity is typically included via either higher order potential (e.g., cubic, quartic, etc.) terms, or modifying the form of the potential itself: often (for bonding) an exponential function is deployed. For hydrogen-bonded systems, double-welled potentials also generate strongly anharmonic effects (e.g., Konwent et al. 1998; Goryainov 2012). Hence, anharmonicity can be viewed as any deviation from harmonic/quadratic behavior, whether expressed by higher order terms in the potential, different potential shapes, or simply by a separation/distance-dependent force constant. A distant-dependent force constant is, of course, tantamount to adding higher order terms into the potential.

Anharmonic effects are also, at times, divided into mechanical anharmonicity and electrical anharmonicity (e.g., di Paolo et al. 1972; Balan et al. 2021). Electrical anharmonicity is generated by higher order dependences of the dipole moment on distance, and its effects are important, as expected for alterations of the dipole moment, for determining the intensities of overtones. Here, mechanical anharmonicity is the principal focus.

Hence, pressure- or temperature-induced mode shifts are signatures of anharmonicity: measurements of both thermal and compression-induced shifts allows the separation of the anharmonicity into volumetrically-dependent and volume-independent components via

$$(\partial {\text{ln}}\omega/\partial T)_P = - \alpha K_T (\partial {\text{ln}}\omega/\partial P)_T + \, (\partial {\text{ln}}\omega/\partial T)_V .$$
(1)

Here, ω is the frequency, α is the thermal expansion, and KT is the isothermal bulk modulus (e.g., Lowndes 1971; Peercy and Morosin 1973; Zallen and Slade 1978; Gillet et al. 1989a; Lan et al. 2012). The term on the left hand side reflects the thermal shifts of modes; the first term on the right hand side reflects the pressure shifts (and is simply the product of the thermal expansion and the mode Grüneisen parameter); and the final, constant-volume term is termed as either the explicit (Wallace 1965; Zallen and Slade 1978; Perakis et al. 1999; Lan et al. 2012) or intrinsic (Gillet et al. 1989a) anharmonicity. The origin of the non-volumetric term lies in anharmonic coupling with other phonon modes, as permitted by the presence of higher order/anharmonic terms within the potential (Balkanski et al. 1983; Tang and Herman 1991; Lan et al. 2012). As such, the final term tends to be highly temperature dependent (Balkanski et al. 1983; Tang and Herman 1991). Coupling with other modes is a manifestation of anharmonicity that further deviates from the standard, isolated harmonic oscillator.

Importantly, Eq. 1 is, sensu stricto, only applicable to cubic or isotropic materials (e.g., Samara and Peercy 1973); Perakis et al. (1999) illustrate the importance of the elastic compliance tensor in producing a substantially more complex version of Eq. 1 that is applicable to tetragonal crystals. However, perhaps most importantly for a discussion of hydroxyl mode shifts, the deployment of Eq. 1 as an approximation to lower symmetry, hydroxyl-bearing phases has generally produced small values for the explicit anharmonicity of the hydroxyl stretch (e.g., Mernagh et al. 1999; Comodi et al. 2007; Ott and Williams 2020; Liu et al. 2021). This is generally consistent with the high frequency of the hydroxyl stretching band, and thermal occupancy of lower-lying vibrational modes being relatively decoupled from these high lying vibrations.

In addition to pressure- (or temperature-) induced mode shifts (and, less commonly within the mineral sciences, isotopic mode shifts (e.g. Berglund et al. 1978) or linewidths (e.g. Ipatova et al. 1967)), there are other spectroscopic observations that directly constrain vibrational anharmonicity. The planetary science/remote sensing communities have extensively probed the near-infrared spectra of a broad suite of minerals (e.g., Salisbury et al. 1991; Clark et al. 2007; Gavin et al. 2013; Kokaly et al. 2017). These measurements provide, in tandem with the fundamental vibrational frequencies, an absolute constraint on the degree of anharmonicity within the hydroxyl potential well between the fundamental frequency and its first overtone. Thus, the correlation between anharmonicity as derived from overtone/combination bands, and mode Grüneisen parameters is examined here. As part of assessing how anharmonic parameters might change under pressure, the behavior under pressure of the anharmonicity of the hydroxyl unit of the amphibole glaucophane is examined as a very weakly hydrogen-bonded test case.

The instructive illustration of the Morse potential

As a guide to approaches to correlations between mode shifts and other parameters, we briefly examine the properties of the Morse potential (Fig. 1). The Morse potential has been widely deployed as a model for the vibrations of weak or intermediate-strength hydrogen-bonded hydroxyl units (e.g., Johannsen et al. 1999; Rong et al. 2003; Tosoni et al. 2005; Greathouse et al. 2009; Boyer et al. 2019). Indeed, Morse potential-based models of the hydroxyl unit have been shown to be accurate and transferable between a wide range of mineral-associated hydrogen-bonding environments (Baram and Parker 1996). Here, weak/intermediate-strength hydrogen bonding refers to the terminology of Novak (1974), in which weak/intermediate-strength hydrogen bonds are those associated with hydroxyl stretching vibrations above ~ 2800 cm−1—this range encompasses both structural and defect hydroxyl units in the vast majority of minerals. Here, structural hydroxyl denotes those phases that have hydroxyl units regularly incorporated within their unit cell (and their stoichiometry), while defect hydroxyl indicates phases (like the so-called nominally anhydrous magnesium silicates (NAMS): e.g., Williams and Hemley 2001) in which hydroxyl often substitutes into crystals via a substitution such as xO2− + Mx+—> xOH− + a vacancy, where M is a cation, and x is its typical valence.

Fig. 1
figure 1

Schematic illustration of the Morse potential relative to a harmonic potential; vertical bars illustrate the range of the potential over which the Gruneisen parameter of the fundamental O–H vibration samples, relative to that over which anharmonicity factors derived from the 1st overtone and the fundamental sample

Full size image

The Morse potential, in detail, likely has limitations in describing the precise character of hydrogen bonds (e.g., Szalay et al. 2002), but it provides a generally instructive potential model that can be analytically deployed to evaluate the role of anharmonicity in mode shifts. Within the Morse potential,

$$V\left(r\right)= {{D}_{e}\left[1-{e}^{-a\left(r-{r}_{e}\right)}\right]}^{2},$$
(2)

the potential as a function of distance, V(r), is dictated by two parameters: the dissociation energy De, and a parameter governing the curvature of the potential well, a.

The eigenvalues of the Morse potential are

$$E_n = \, \left( {n \, + { 1/2}} \right){\hbar}\omega_e - \, \left( {n \, + { 1/2}} \right)^{2} {\hbar}x_e \omega_e ,$$
(3)

where ωe is the frequency produced by the quadratic term of the expansion of the potential (often termed the harmonic stretching vibration) (e.g., Morse 1929). Both ωe and xeωe, the anharmonicity factor, are simply related to the parameters of the Morse potential:

$$\omega_e = a({2}D_e /\mu_m )^{{1}/{2}} ,$$
(4)

where μm is the reduced mass of the diatomic (hydroxyl) unit (ωe is also equal to three times the frequency of the fundamental minus the frequency of the first overtone, 3ω0->1 – ω0->2), and

$$x_e \omega_e = a^{2}\hbar /{2}\mu_m .$$
(5)

Unsurprisingly, the anharmonicity depends primarily on the curvature parameter (a) within the Morse potential, while the frequency derived from the quadratic portion of the potential depends on both Morse parameters. In practice, the anharmonicity factor (xeωe) is typically experimentally determined from the difference ω0->2/2 – ω0->1. Here, ω0->2 is the frequency of the first overtone, and ω0->1 is the frequency of the fundamental vibration. Sensu stricto, this is the anharmonicity factor relevant to the portion of the potential well between the fundamental and first overtone (or x1,2), but this part of the potential well overlaps with that part of the well that dictates the frequency shift of the fundamental vibration under pressure.

Equation 3 implicitly results in the relation, ω0->n = nωe – (n2 + n) xeωe, and the pressure derivatives of the fundamental stretching vibration and its overtones are

$$d\omega_{0 - > n} /{\text{dP }} = {\text{ nd}}\omega_e /{\text{d}}P- \, \left( {n^{2} + n} \right){\text{d}}(x_e \omega_e )/{\text{dP}}.$$
(6)

Similarly, for each energy level, the derivative with respect to pressure can be expressed as

$${\text{d}}E_n /{\text{d}}P = \, \left( {n + { 1/2}} \right){\hbar}({\text{d}}\omega_e /{\text{d}}P) \, -{2}\hbar\left( {n \, + { 1/2}} \right)^{2} [x_e ({\text{d}}\omega_e /{\text{d}}P) - { 2}/{\hbar}x_e^{2} ({\text{d}}D_e /{\text{d}}P)].$$
(7)

Therefore, measurements of the pressure dependence of the fundamental and an overtone (or of two overtones) can constrain the pressure dependence of both the quadratic component of the potential (dωe/dP) and the anharmonicity factor. This relation has been deployed by a number of investigators in a range of different systems under pressure (Ben-Amotz et al. 1988; Luck and Mentel 1990; Johannsen et al. 1999; Shinoda et al. 2000). These studies have yielded divergent results on the importance of the pressure derivatives in Eq. 7. Shinoda et al. (2000) calculate that the anharmonicity coefficient in Ca(OH)2-portlandite increases by ~ 12% between 0 and 8 GPa from measurements of the pressure dependence of what they interpreted to be the hydroxyl unit’s first infrared overtone, and Nguyen et al. (1994) report that the anharmonicity of Co(OH)2 increases by a factor of two between 0 and 20 GPa based on the behavior of a hot band (a difference band between the first overtone and fundamental). However, as is discussed below, the selection rules for overtones/combinations in centrosymmetric materials (such as brucite-structured materials) may not be simple, and whether the hot band observed by Nguyen et al. (1994) reflects a difference of ungerade (out-of-phase) vibrations of the two hydroxyl units within the unit cell or a combination of gerade and ungerade vibrations is unclear. If the latter, then an assessment of the pressure dependence of anharmonicity would need to incorporate the pressure shift of the principal Raman-active symmetric stretch, which is markedly different from the infrared shift for brucite-structured hydroxides (e.g., Kruger et al. 1989; Duffy et al. 1995a,b; Shinoda et al. 2002). With respect to the Shinoda et al. (2000) result, the principal infrared absorption in the n = 0—> 2 region in portlandite is a combination band of the infrared and Raman hydroxyl stretches (Martens and Freund 1976; Weckler and Lutz 1996) and is not (as they considered) a simple infrared overtone. A re-analysis of the pressure dependence of Shinoda et al. (2000) combination band using their data on the infrared fundamental and the pressure dependence of the Raman fundamental of portlandite (Duffy et al. 1995a) yields a net increase in anharmonicity of ~ 7% across 8 GPa, or slightly over half the rate of change in anharmonicity proposed by Shinoda et al. (2000).

For comparison, Ben-Amotz et al. (1988) observed no change in the anharmonicity under compression for iodine in organic solutions over 1.2 GPa (but ~ 15% volume compression) from measurements of the Raman fundamental and its first and second resonance-enhanced overtones. Luck and Mentel (1990) similarly derived a zero shift in the anharmonicity of the hydroxyl unit in an organic solvent to 9 GPa. Lastly, and perhaps most directly relevant to the behavior of hydroxyl in minerals, the pressure shift of a in Eq. 5 was constrained to be “constant within experimental accuracy” for proton-exchanged hydroxyls in LiNbO3 up to ~ 15 GPa (p. 588 of Johannsen et al. 1999). Thus, the stated analysis in Johannsen et al. (1999), as per Eq. 5, is that the anharmonicity of the hydroxyl units in this material is constant under compression. A re-analysis of the data presented on proton-exchanged LiNbO3 in Johannsen et al. (1999) indicates that an increase in magnitude of ~ 4–6% in the anharmonicity may occur over 6 GPa (or ~ − 0.66 to − 1%/GPa), depending on whether a zero-pressure anharmonicity factor of − 86 cm−1, as derived from a fit to the pressure-dependent data or the Johannsen et al. (1999) preferred value of − 88.5 cm−1, is used. That said, the robustness of this re-analysis is unknown, since the resolution of their spectroscopic data is not stated (Johannsen et al. 1999).

Notably, if the anharmonicity is constant within a given pressure range, and the Morse potential (Eq. 2) is viewed as accurate, then the a term that governs the curvature of the Morse potential is also invariant over that pressure range, and the entirety of the pressure dependence of the hydroxyl potential would be associated with pressure-induced shifts in De, the dissociation energy. Hence, a goal of this study is to assess the magnitude of any pressure-induced shift in anharmonicity in another geologically relevant, hydroxyl-bearing material: the amphibole glaucophane.

Another goal of this study is to probe whether there is a correlation between the anharmonicity of the hydroxyl bond and its pressure shift. That such a general correlation might exist can be anticipated from a combination of Eq. 2 and simple scaling relations. The force constant of a bond (k) is proportional to the second derivative of the potential d2V/dr2. By the same token, mode Grüneisen parameters (γi), which are equal to K/ω(dω/dP), where K is the bulk modulus, thus scale to first order as (1/k)dk/dr (Sherman 1980); phrased another way, Grüneisen parameters scale as the third derivative of the potential. For comparison, Zallen (1974), using a somewhat similar analysis, proposed that γi scales as 1/k.

If there exists a scaling between γi and either the force constant or a derivative of the force constant (and hence a derivative of Eq. 2), then we expect a variation driven by either the exponential term of Eq. 2, or (for the (1/k)dk/dr proportionality) a power of a and hence of the anharmonicity. In either instance, we would expect a scaling between the logarithm of the mode Grüneisen parameters and the anharmonicity factor (which scales as a in Eq. 2). As an aside, a non-linear relation between the anharmonicity factor and force constant for hydroxyl units in ice has been proposed by Sceats and Rice (1979): this is in general accord with the conceptual approach here. Moreover, Szalay et al. (2002) and Balan et al. (2007) have each noted that the harmonic frequency is correlated, in some measure, with the anharmonicity parameter in hydroxides and phyllosilicates, respectively.

As an important aside, the single-well Morse potential does not, of course, fully capture the deviation from anharmonicity associated with the well-known double-well potential proposed to describe hydrogen bonding; rather, it is limited to describing the asymmetric bonding potential of a single bond. In some instances, the deviation between single-well approximations and double-well treatments has been argued to be small for weakly hydrogen-bound systems (Johannsen 1998). Nevertheless, the eigenvalues of asymmetric double-well potentials, while not as analytically straightforward (e.g., Ulyanov and Zaslavskii 1992; Konwent et al. 1998), do share characteristics of the single-well potential: a harmonic frequency term that depends on dV2/dr2, with negative terms that are proportional to the third and fourth (or higher, depending on the truncation) derivatives of the potential (e.g., Krobok and Holzapfel 1994). Thus, given the curvature of the double-well potentials, the anharmonicity derived from overtones might be anticipated to exceed that derived from the pressure dependence of the n = 0—> 1 transition. This is simply because higher-lying vibrational transitions in the double-well potential are more likely to deviate from harmonic behavior due to the effects of the second well.

Nevertheless, there are scaling relations that can be generated from the double Morse potential model. For example, a symmetric double Morse potential yields a dependence on frequency of

$$\omega_{0 - > 1} = \omega_e \left[ {{1} - {\text{4exp}}\left( { - {2}a*R_1 } \right)} \right]^{{1}/{2}} ,$$
(8)

(e.g., Goryainov 2012). In Eq. 8, R1 represents the distance between the hydrogen atom and the mid-point between the two oxygens involved in the hydrogen bond. The pressure derivative of this expression yields a sum of terms involving dωe/dP, da/dP and dR1/dP. If da/dP is negligible, as has been proposed (Ben-Amotz et al. 1988; Luck and Mentel 1990; Johannsen et al. 1999), and 4a*dR1/dP > dωe/dP, then this relation has intuitive structural implications, as pressure-induced contraction of the hydroxyl bond relative to the mid-point between the oxygens generates a positive Grüneisen parameter. Correspondingly, expansion of this distance (as would be generated by increased hydrogen bonding) produces negative Grüneisen parameter values. This attaches a direct structural significance to the Grüneisen parameter of hydroxyl mode shifts. However, it is difficult to assess the accuracy or applicability of such a relationship because of the limited data set on hydrogen positions under pressure: a fundamental limitation in correlating spectroscopic and structural data on hydroxyl units. Indeed, the ability to evaluate pressure-associated correlations derived from either general concepts of hydrogen bonding (as in the frequency-dω/dP systematics of Moon and Drickamer (1974), Hofmeister et al. (1999) and Thompson et al. (2016)) or from simple potentials (as in Fig. 1) hinges on the ability of hydrogen bonding to provide a largely complete description of the system. In this context, it is important to note that surrounding cations also play a role in the strength of hydrogen bonding. For example, Hermansson (1991) has reviewed the role of electrostatic forces surrounding cations producing upshifts and down-shifts of the hydroxyl stretching band relative to the estimated stretching value of the free hydroxyl ion (which she estimates as near 3560 cm−1). Most critically, Hermansson (1991) noted that lowered values of the O–H stretching vibrations need not be indicative of hydrogen bonding, nor raised values with the lack of hydrogen bonding (Beckenkamp and Lutz 1992), if strongly polarizing fields are generated by the local cation environment.

Experiments

Experiments were conducted on natural glaucophane from Sonoma County, California. The average composition of this amphibole, as determined by the Lawrence Livermore National Laboratory Cameca electron microprobe, is approximately Na1.74Ca0.12(Mg1.8Fe1.2)(Al1.7Fe0.3)Si8O22(OH)2, with the oxygen and hydroxyl content assumed to be ideal. Infrared experiments were conducted using a Bruker IFS-66v interferometer, coupled with an infrared microscope, CaF2 beamsplitter, globar source and a liquid-nitrogen cooled layered InSb/MCT detector. All spectra were measured with 4 cm−1 resolution. Peak locations were determined by peak-fitting using the Levenberg–Marquardt algorithm. Gasketted samples were compressed in Merrill-Bassett type diamond anvil cells equipped with type I diamonds. Both the comparatively low concentration of hydroxyl units within amphiboles and the small thickness of diamond cell samples resulted in most ambient temperature runs being conducted with a mixture of (by weight) ~ 10 wt% glaucophane and KBr for the fundamental vibrations, with the salt serving as a pressure medium. The combination vibrations are quite weak (greater than an order of magnitude weaker than the fundamentals), and hence were not resolved in many spectra (for comparison, Shinoda et al. (2000) were unable to resolve the combination bands of portlandite above 5.2 GPa). The glaucophane overtones were observed in runs with extended collection times and more concentrated suspensions of glaucophane (~ 40 wt% in KBr) to maximize their signal to noise.

Results

Figure 2 shows the pressure-dependent infrared spectrum of glaucophane in the hydroxyl stretching region. The oxygen of the hydroxyl unit in the amphibole stucture is coordinated by three octahedral cations, with different occupancies of the 2 M1 and the M3 octahedra generating splitting of the hydroxyl stretching vibration (e.g., Bancroft and Burns 1969). In the case of glaucophane, the highest frequency of these four peaks (3662 cm–1) is generated by all three of the neighboring octahedral sites being occupied by magnesium cations, the second highest frequency peak (3649 cm–1) corresponding to one octahedral iron neighbor, that at 3636 cm–1 to two iron neighbors, and the lowest frequency peak (3618 cm–1) to the hydroxylated oxygen being entirely coordinated by neighboring iron ions (e.g., Bancroft and Burns 1969). The zero-pressure locations of the fundamentals are in accord with those of Bancroft and Burns (1969) and Gillet et al. (1989b).

Fig. 2
figure 2

Representative infrared spectrum of the four fundamental hydroxyl stretching bands of glaucophane

Full size image

In order to examine the role of compression in altering the bonding of the hydroxyl unit in glaucophane, both the pressure shift of the hydroxyl fundamentals (Figs. 2 and 3), and the pressure dependence of the overtones of the hydroxyl stretching vibration of glaucophane (Figs. 4 and 5) were measured. The shifts of the fundamental vibrations agree with those measured by Thompson et al. (2016) on a more iron-rich glaucophane. Due to their composition, Thompson et al. (2016) only reported peak locations of the three lower frequency components. Above ~ 10 GPa, deconvolution of the spectra was required to accurately locate this highest frequency band in our data. The high-pressure overtone data are confined to the overtones of the 2Mg/1Fe and the 1Mg/2Fe hydroxyl stretching bands (the lowest frequency 3 Fe overtone is observed in the lower pressure spectra, but cannot be consistently tracked). These bands occur at 7126 and 7097 cm−1 at ambient pressure in our sample: our locations of these bands are approximately 10 cm−1 lower in frequency than corresponding bands observed in a glaucophane with somewhat higher Mg content (Bancroft and Burns 1969).

Fig. 3
figure 3

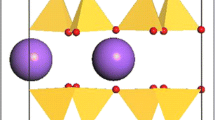
Mode shifts of the fundamental hydroxyl stretching vibrations of glaucophane. Inset shows the local structure around hydrogen (small black central circle) in the amphibole structure: open circles are oxygens, shaded circles are silicons, and different neighboring divalent cation sites are labeled M1, M2 and M3 (after Sheu and McMillan 1989)

Full size image
Fig. 4
figure 4

Representative spectra of the first set of hydroxyl stretching overtone/combination bands in glaucophane under pressure

Full size image
Fig. 5
figure 5

Mode shifts of principal hydroxyl stretching combination bands within glaucophane

Full size image

The positive mode shifts observed for these hydroxyl bands are not uncommon for weakly hydrogen-bonded minerals, and such shifts have been typically attributed to cation-hydrogen repulsion or shifts in hydrogen orientation (e.g., Williams et al. 2012; Noguchi et al. 2012). Within glaucophane, these positive mode shifts could result from one of several possible effects. First, either enhanced repulsion between the hydrogen cations and the silicons of the six-membered tetrahedral ring lying above the hydroxyl site at high pressures could increase the energy of the hydroxyl stretching vibration (see Fig. 1 inset). This effect produces the predicted positive initial mode shift in cluster simulations of the hydroxyl environment of tremolite (Sheu and McMillan 1989). Second, structural constraints associated with the tetrahedral double chains could cause the distance between the closest (hydrogen-bonded) oxygen and the hydroxyl group to increase as a function of compression. A straightening of the tetrahedral double chains of glaucophane has been observed to pressures of 3.5 GPa (Comodi et al. 1991): the net effect of such straightening will be to increase the distance of the nearest oxygen (O7) from the hydroxyl unit (Fig. 3 inset). Third, the bond strength of the hydroxyl ion may simply increase with compression, due to either a pressure-induced increase in the polarizability of the oxygen ion (e.g., Larsen and Williams 1998) and a commensurate pressure-induced decrease in the electronegativity of the M1 and M3 cations. Indeed, the frequencies of the hydroxyl vibrations in amphiboles have been demonstrated to decrease by as much as ˜70 cm−1 as the electronegativity of the M1 and M3 cations increases (Hawthorne 1981). To 3.7 GPa, the M3-O(H) and M1-O(H) bond distances in glaucophane are virtually unchanged by compression (Comodi et al. 1991), implying that such pressure-induced decreases in electronegativity may occur.

Each of these possible explanations may play a role in the positive frequency shifts with pressure of the hydroxyl bands, which certainly reflect a complex sum of the changing attractive and repulsive forces on the hydroxyl unit. Yet, the last of these effects, a general pressure-induced weakening of the octahedral cation-hydroxyl bonds and strengthening of the hydroxyl bond, may play a dominant role in the positive mode shifts. The pressure shifts of the different hydroxyl vibrations depend strongly on the identity of the octahedral neighbors of the hydroxyl group (Table 1 and Fig. 3); hence, the positive shifts of these vibrations are plausibly a consequence of changes in the M3- and M1-oxygen bonds as a function of pressure. The differing pressure shifts of the bands are thus attributed to variations in the characteristics of the iron-oxygen bond relative to the Mg−O bond under pressure, rather than simply a differing local compressibility for the H−Mg and H−Fe configurations (Yang et al. 1998).

Table 1 Glaucophane Mode Shifts
Full size table

The observed pressure shifts of the n = 0—> n = 2 modes are slightly greater than twice the mode shifts of the primary n = 0—> n = 1 hydroxyl stretches (Table 1). Thus, the anharmonicity of the vibrations as derived from the first overtones, or 2 x ω0->1–ω0->2, decreases in magnitude on compression. Yet, this decrease is quite small–indeed, barely resolved: the zero pressure anharmonicity parameters (xeωe) at ambient pressure of these bands of − 87 to − 87.5 cm−1 shifts by an average of ~ 2.8 (± 3.5 cm−1), or 3.2% (± 4%), at the maximum pressure of the overtone measurements of 15 GPa, or ~ 0.2%/GPa. Notably, the error bars here could be viewed as generous: since peak locations are determined using peak fitting, and the formal resolution relative to the peak widths dictates that the peaks are reasonably well-sampled, the uncertainties in peak locations may be less than the formal resolution (e.g., Beechem et al. 2007; Saltonstall et al. 2019). If this is the case, then the robustness of the small decrease in the magnitude of the anharmonicity is greater than is reflected by the current errors.

The results thus demonstrate that the potential curve of the hydroxyl unit in glaucophane is quite insensitive to volume compressions of up to ~ 12%, as are generated at 15 GPa (Comodi et al. 1991; Jenkins et al. 2010), For comparison, the vibrational frequencies of the primary hydroxyl bands increase by ~ 1% in frequency over 33 GPa, and the anharmonicity of the hydroxyl bond decreases by about 3 (± 3)% over 15 GPa. The key point here is that the shift in anharmonicity is towards smaller absolute values, yet these changes are quite small, implying that the parameter a in Eq. (2) weakly decreases with pressure in glaucophane. This is in general accord with the inference that this parameter is nearly constant with pressure based on the pressure dependence of the fundamental and overtone of LiNbO3:OH (Johannsen et al. 1999), and the behavior of hydroxyl in an organic solvent to 9 GPa (Luck and Mentel 1990). This possible slight decrease in anharmonicity is plausibly a consequence of the increased strength of the hydroxyl bond under compression, and is thus consistent with the positive pressure shift of the hydroxyl stretching vibrations. For comparison, in portlandite (where the hydroxyl stretching vibration shifts negatively with pressure), our re-analysis of the data of Shinoda et al. (2000) in the context of observing a combination band rather than an overtone yields an increase in anharmonicity with pressure of ~ 0.9%/GPa. In both the cases of glaucophane and portlandite, the change in anharmonicity with pressure is slight. From a conceptual perspective, pressure-induced increases in hydrogen bonding (which are likely for minerals with lower frequency hydroxyl stretching vibrations) are likely to, because of the nature of a compacting double-well potential, produce increases in anharmonicity. This conceptual trend has, to date, not been conclusively observed in the three mineral-like oxide examples whose anharmonicity under pressure has been probed with clearly identified combinations/overtones: in portlandite, with a zero pressure hydroxyl stretching frequency of 3645 cm−1, anharmonicity is proposed to weakly increase (Shinoda et al. 2000); in LiNbO3 with OH impurities and a stretching frequency of 3504 cm−1, anharmonicity appears constant with pressure (Johannsen et al. 1999); and in glaucophane (stretching frequencies of 3636 cm−1 and 3650 cm−1), anharmonicity may slightly decrease under compression.

A correlation between Anharmonicity and the Grüneisen parameter?

The bonding environments of hydroxyls within minerals vary markedly, spanning from relatively strongly hydrogen bound (as in zoisite: Winkler et al. 2008), to within layer structures (e.g. Shinoda et al. 2002; Williams et al. 2012), to weakly- or non-hydrogen-bound hydroxyls sequestered within a framework structure (e.g., Fig. 3, inset). Similarly, the detailed structural responses of the hydroxyl groups to compression will also vary markedly between different phases. A question that arises is whether there are possible systematics (beyond the well-known zero-pressure frequency/pressure−shift correlation) that can span these different structural environments and corresponding responses to pressure. In this context, if the anharmonicity parameter of Eqs. 3–5 is not particularly sensitive to pressure then, as discussed in the section above on the Morse potential, the measured pressure shifts of hydroxyl vibrations (and their associated Grüneisen parameters) are expected to vary with the ambient pressure anharmonicity parameters. Indeed, a general correlation between the log of the Grüneisen parameters and anharmonicity parameters is anticipated. However, assessment of anharmonicity parameters for different hydroxyl-bearing minerals is, at times, challenging.

Given the occasionally complex structure of overtone/combination bands (e.g., Martens and Freund 1976; Balan et al. 2022), the materials included here are those with the most straightforward to assign combination band spectra. The phases that are incorporated in this analysis are those with one (or several easily-identifiable sharp, as in the case of amphiboles) or two peaks in the hydroxyl fundamental stretching region that are readily associated with clear, usually single, intense overtones/combinations. For example, partially fluorinated chondrodite is an example of a phase with multiple hydroxyl peaks, but with one O–H infrared stretching band that is clearly the highest amplitude, and sharp (Williams 1992; Kuribayashi et al. 2004): this is reflected in its overtone spectrum (Prasad and Sarma 2004). However, only partially fluorinated chondrodite has had its overtone spectrum characterized: overtone/combination data are not available on fully hydroxylated synthetic chondrodite. Hence, only the pressure shift of fluorinated chondrodite is included in the correlation with the anharmonicity parameter. Moreover, phases with multiple overlap** hydroxyl bands and a complex overtone region that is a mixture of both hydroxyl stretch combinations and overtones are not included. The overtone spectra of such phases produce ambiguity in clearly identifying an overtone/combination associated with a given fundamental, and hence an accurate calculation of the anharmonicity factor is precluded. Gibbsite is an example of such an excluded phase. Gibbsite has well-characterized mode shifts under pressure, but has multiple peaks of similar amplitude in its fundamental hydroxyl stretching spectrum, and hence a complex and challenging to assign overtone/combination spectrum (Liu et al. 2004; Kokaly et al. 2017). In a similar vein, some phases do not appear to have reliable overtone spectra available. For example, the reported near-infrared spectrum of chloritoid (Li et al. 2015) is, by comparison with the well-documented mid-infrared spectrum of this material (which includes pressure-induced mode shifts of the fundamentals: Koch-Muller et al. 2002), likely heavily contaminated by either talc or pyrophyllite (if the reported overtone spectrum were uncontaminated, then chloritoid would represent an extremely unusual example of a mineral with a positive anharmonicity factor associated with its hydroxyl unit—a notable and, if correct, probably unprecedented result). An additional example of a material which is excluded is proton-exchanged HxLi1-xNbO3 (Johannsen et al. 1999). In this material, multiple phases are observed in this centrosymmetric system (e.g., Korkishko et al. 1997) and the Raman spectra of this material show considerable variation depending on thermal history (Savatinova et al. 1999). As described next, the calculation of the anharmonicity of a centrosymmetric material from combination bands hinges on the Raman spectrum. Therefore, this material’s hydroxyl pressure shift is excluded, since no Raman spectrum is available for the proton-exchanged sample for which the pressure-dependent infrared spectrum was measured.

Table 2 compiles data on infrared fundamental frequencies, pressure shifts, Raman frequencies, anharmonicity factors and Grüneisen parameters for phases for which both pressure shifts and overtone/combination data are available. For overtones/combinations, the general assumption is made that the strongest single peak in the near-infrared represents the overtone/combination associated with the strongest single fundamental. There is a primary distinction which emerges between overtones and combinations: most minerals have centrosymmetric space groups (pyrophyllite and polytypes of antigorite are exceptions), which do not have allowed infrared first overtones of fundamentals (Mitra 1962; Weckler and Lutz 1996). Brucite-structured solids provide a simple example of this effect: as noted above, selection rules dictate that the primary peak in the first O–H stretching overtone region is a combination band of the Raman and infrared fundamental stretching vibrations (an A1g x A2u combination) (e.g., Martens and Freund 1976; Weckler and Lutz 1996). The key aspect here is that the principal band(s) in the n = 0—> 2 hydroxyl stretching region are combination band(s) between the Raman and infrared fundamental bands for centrosymmetric minerals. Hence, for such minerals, the anharmonicity is assessed from the difference between the principal hydroxyl stretching combination band and the sum of the Raman and infrared fundamentals; for non-centrosymmetric minerals, the principal band(s) in the n = 0—> 2 hydroxyl stretching region of the infrared spectrum is likely a true overtone of the infrared fundamental.

Table 2 Anharmonicity, pressure shifts and Grüneisen parameters of selected minerals
Full size table

The inclusion of the Raman frequency induces only a small effect for many phases, as the separation between the principal infrared and Raman fundamentals is small (on the order of 0.2% or less: Table 2). That these narrow (or negligible) splittings between infrared and Raman bands likely persist under pressure is illustrated by the negligible separation between the infrared and Raman stretching vibrations of tremolite under pressure. In this amphibole, the principal Ag-symmetry Raman-active hydroxyl stretching vibration is indistinguishable in frequency from the Bu-symmetry infrared-active hydroxyl stretch (at the 2 cm−1 or less level) to pressures of at least 45 GPa (Ott and Williams 2020; Thompson et al. 2016). Hence, while the first infrared-active ‘overtone’ in tremolite is actually a combination band between the Raman- and infrared-active fundamentals, the combination band frequency is indistinguishable from that of an overtone. Indeed, the hydroxyl units in most of the hydrous minerals interrogated under pressure are both sufficiently few in number within the unit cell, and distant from one another, that Davydov splitting between the principal Raman and infrared fundamental stretches (induced by hydroxyl-hydroxyl interactions) is anticipated to be small or negligible (e.g., Ott and Williams 2020)–here, brucite-structured phases are the exception (Table 2).

Figure 6 presents both a trend of log(− γ + 0.1) versus the anharmonicity factor (Fig. 6A), and the commonly-deployed initial hydroxyl mode frequency-pressure shift scaling (Fig. 6B). The rationale for adding 0.1 to the Grüneisen parameter is simply to ensure that the trend does not cross zero (which would preclude a logarithmic analysis): all Grüneisen parameters of the phases in Table 2 are less than 0.1. Such addition of a constant is well-precedented in logarithmic analyses of data sets with negative values (e.g., Aitchison and Brown 1957).

Fig. 6
figure 6

A Correlation between a normalized Grüneisen Parameter for hydroxyl stretching vibrations and the hydroxyl anharmonicity factor; B Correlation between the pressure shift of hydroxyl stretches and their ambient pressure frequency

Full size image

A key aspect of Fig. 6A involves the notably large number of phases that have Grüneisen parameters between − 0.1 and 0.1, and anharmonicity parameters between − 80 and − 100 cm−1; most amphiboles, layer silicates and hydroxides fall within this category. As such, these weakly hydrogen-bound phases form a cluster: although they have small (and generally similar) Grüneisen parameters, the log scale amplifies their separation. Indeed, almost all of these clustered points fall, in terms of their Grüneisen parameter, within ± 0.03 of the trend line. Much of the trend in Fig. 6A is derived largely from those phases with stronger hydrogen bonding and larger absolute values of their anharmonicity parameter: zoisite, clinozoisite and lawsonite. Nevertheless, an overarching trend does appear to emerge across this data set, although validation of this trend will hinge on further data on more strongly hydrogen-bound minerals (in terms of both well-characterized combination bands and pressure shifts of the fundamentals). Figure 6B illustrates the excellent correlation associated with the frequency-pressure shift correlation for micas and amphiboles, with the similar structural environment (with the oxygen of their hydroxyl with three neighboring octahedral cations, and weak hydrogen bonding) producing an overarching trend. What is also evident in Fig. 6B is that the frequency-pressure shift trend breaks down for other phases, and particularly those with stronger hydrogen bonding.

What are the possible shortcomings of the approach of Fig. 6A? A possible difficulty with the correlation between the mode Grüneisen parameters and the anharmonicity factors lies in the differing sampling of the compaction of the crystal structure associated with each parameter. The Grüneisen parameter, through the bulk modulus, incorporates the bulk crystal response to pressure, while the anharmonicity of the hydroxyl bond only reflects the local bonding environment of the hydroxyl unit. As such, the bulk volume dependence embedded within the Grüneisen parameter may not fully reflect the local deformation of the hydroxyl unit. By the same token, the anharmonicity factor is intrinsically a local probe of the O–H bonding potential. Hence, the deployment of the bulk Grüneisen parameter (as opposed to a dependence on local bond length) may not be entirely optimal for comparison with the hydroxyl anharmonicity parameter. It is possible that this effect, given (for example) the high compressibility along the c-axis in micas (e.g., Comodi et al. 2004) or the anisotropic compressibility of amphiboles (e.g., Yong et al. 2019; Ott et al. 2023), may contribute to the scatter observed for these weakly hydrogen-bound (and small Grüneisen parameter) phases in Fig. 6A. Indeed, were abundant data available on O–H distances under pressure for different phases, a local Grüneisen-like parameter defined using normalized changes in hydroxyl-bond length (or, if hydrogen bonds were consistently linear, O–O hydrogen-bond distances) could give rise to improved correlations.

Similarly, different or complex bonding configurations of hydrogen could produce separate trends on a Grüneisen parameter-anharmonicity parameter correlation. The deviation of prehnite from the overarching trend of Fig. 6A may hint at such an effect: prehnite has a bifurcated hydrogen bond (Detrie et al. 2008; Ross et al. 2020), and hence the shape of its potential curve is unlikely to be captured by a model that hinges on a linear hydrogen bond. Nevertheless, deviations from the anharmonicity correlation, when observed (as in prehnite), may provide insights into anomalous effects on the hydroxyl potential well induced by bifurcated hydrogen bonds, pressure-dependent Davydov splitting, the influence of neighboring cations, or decreased barrier heights associated with symmetrization of the hydrogen bond.

An additional shortcoming could, in concept, arise if the form of the potential shifts markedly for (say) intermediate or strongly hydrogen-bonded hydroxyl environments in minerals (loosely defined by Novak (1974) as those with stretching frequencies below ~ 3100 cm−1) due to the effects of a double-welled potential shape, or the ultimate symmetrization of the hydrogen bond. In these instances, there is a substantial likelihood of a different slope to the trend of Fig. 6A (this effect might be presaged by the large negative Grüneisen parameter of zoisite, the furthermost left point on Fig. 6A). Furthermore, intermediate and strongly hydrogen-bonded systems may encounter anomalies in their anharmonicity when vibrational levels approach the barrier tops in double-welled systems. Such complexities associated with barrier top effects, including those induced by tunneling, have long been documented both theoretically and experimentally (e.g., Somorjai and Hornig 1962; Matsushita and Matsubara 1982; Goncharov et al. 1996; Larsen and Williams 1998).

Conclusions

The anharmonicity of the hydroxyl stretching vibrations of glaucophane has been examined under pressure from data on the pressure shift of both its fundamental infrared hydroxyl stretching vibrations and combination bands that closely approximate its first overtone. The anharmonicity factor of glaucophane varies only slightly with compression to 15 GPa, with its absolute magnitude decreasing slightly at high pressures. This near-constancy of the anharmonicity factor under compression is in accord with prior results on several materials, and indicates that the overall curvature of the potential well associated with the hydroxyl unit in amphiboles is often nearly constant under compression.

Based on this constancy, a simple scaling relation between the Grüneisen parameters of hydroxyl vibrations and their anharmonicity factors is proposed. The relation appears to provide a more consistent trend for more strongly hydrogen-bound minerals than classic mode frequency-pressure shift proportionalities, but works less well for weakly hydrogen bound, similarly structured hydroxyl environments (layer silicates and amphiboles). Assessing the generality of this trend will hinge on increases in the data set of minerals with intermediate hydrogen-bonding strength, assignable combination bands and pressure-induced mode shifts (as one example, no combination band data appear to be available for synthetic dense hydrous magnesium silicate phases: a notable absence). This scaling relation may also provide a tool with which to detect phases with complex hydrogen bonding geometries (prehnite, with its bifurcated hydrogen bond, provides a possible illustration of this utility). Finally, the tandem utilization of hydroxyl mode Grüneisen parameters and their anharmonicity factors holds the prospect of providing strong constraints on the shapes of the hydroxyl potentials of dense hydrous phases, with relevance for the retention and mobility of hydrogen at extreme conditions.