Mathematics Subject Classification 92D25, 92D30, 92D40

Introduction

Mathematical models are important tools for analyzing ecological models. The dynamic relationship between predator and its prey is one of the dominant themes in mathematical ecology due to its universality (cf. Anderson and May (1981), Beretta and Kuang (1998), Freedman (1990), Hadeler and Freedman (1989), Hethcote et al. (2004), Ma and Takeuchi (1998), Venturino (1995), ** on functional response of predators. Theor Popul Biol 56:65–75" href="/article/10.1007/s40808-016-0143-5#ref-CR8" id="ref-link-section-d225711904e354">1999), Cui and Takeuchi (2006), Huo et al. (2007) and Hwang (2003)), but these studies are questioned by several biologists. The most crucial element in these models is the “functional response”—the expression that describes the rate at which the prey are consumed by a predator. Models were limited to use the Malthusian growth function, the predator per capita consumption of prey following Holling types II and III functional responses or density dependent mortality rates. These functional responses depend only on the prey volume x, but soon it became clear that the predator volume y can influence this function by direct interference while searching or by pseudo interference (cf. Curds and Cockburn (1968), Hassell and Varley (1969) and Salt (1974)). A simple way of incorporating predator dependence in the functional response was proposed by Arditi and Ginzburg Arditi and Ginzburg (1989), who considered this response as a function of the ratio x/y. The ratio-dependent response function produces richer dynamics than that of all the Holling types responses, but it is often criticized for the paradox that occurs at low densities of both populations. Normally one would expect that the population growth rate decrease when both the populations fall bellow some critical size, because food-searching effort becomes very high. For some ecological interactions ratio-dependent model give negative feed back. The Lotka–Volterra type predator–prey model with the Beddington–DeAngelis functional response has been proposed and well studied. This proposed model can be expressed as follows:

$$\begin{aligned} \left\{ \begin{array}{ll} \frac{dx'_1}{dt}& = rx'_1\bigl (1- \frac{x'_1}{k}\bigr )-\frac{c_{1}x'_1 x'_2}{a_{1}+x'_1+b_{1}x'_2}\\ \frac{dx'_2}{dt}& = -\delta _{1}x'_2+\frac{c_{1}e_{1}x'_1x'_2}{a_{1}+x'_1+b_{1}x'_2}\end{array}\right. \end{aligned}$$
(1.1)

with the initial conditions \({x'_1}(0) = {x'_{1}}^{0} > 0\) and \({x'_{2}}(0) ={x'_{2}}^{0} >0\). The functions \({x'_1}(t), ~{x'_2}(t)\) are the sizes of prey and predator at any time t. All the system parameters are assumed to be positive and have their usual biological meanings. The functional response \(\frac{c_{1}x'_1 x'_2}{a_{1}+x'_1+b_{1}x'_2}\) in system (1.1) was introduced by Beddington (1975) and DeAngelis et al. (1975). It is similar to the well-known Holling type-II functional response but has an extra term \(b_1 x_2\) in the denominator which models mutual interference between predators. It represents the most qualitative features of the ratio-dependent models, but avoids the “low-densities problem”, which usually is the source of controversy. It can be derived mechanistically from considerations of time utilization (cf. Beddington (1975)) or spatial limits on predation.

The present study is organized as follows: The basic assumptions and the model formation are proposed in Sect. 2. Section 3 deals with some preliminary results. The equilibria and their feasibility are given in Sect. 4. The local analyses of the system around the boundary as well as interior equilibria are discussed in Sect. 5. The global analysis of the system around the interior equilibrium is studied at length in Sect. 6. Simulation results are reported in Sect. 7 while a final discussion and interpretation of the results of the present study in ecological terms appear in the concluding Sect. 8.

Model formulation

Firstly we replaced the logistic growth function \(r x_1(1-\frac{x_1}{k})\) of the prey species by the modified quasi-linear growth function \(rx_1(1-\frac{x_1}{x_1+k}) = r (\frac{k}{k+x_1}) x_1 = r' x_1\) \((r'<r)\) in order to make the model free from any axial equilibrium. This fits better some special type of ecosystems, where the environmental carrying capacity varies w.r.t. its prey size, i.e., the carrying capacity is always greater than its present prey size. In the present model we introduce one more predator species in the model (1.1) to make it closer to reality. Thus, our final model is

$$\begin{aligned} \left\{ \begin{array}{l} \frac{dx_1}{dt} = rx_1(1-\frac{x_1}{x_1+k})-\frac{c_{1}x_1 x_2}{a_{1}+x_1+b_{1}x_2} -\frac{c_{2}x_1x_3}{a_{2}+x_1+b_{2}x_3} \\ \frac{dx_2}{dt} = -\delta _{1}x_2+\frac{c_{1}e_{1}x_1x_2}{a_{1}+x_1+b_{1}x_2},\\ \frac{dx_3}{dt} = -\delta _{2}x_3+\frac{c_{2}e_{2}x_1x_3}{a_{2}+x_1+b_{2}x_3} \end{array}\right. \end{aligned}$$
(2.1)

where \(x_1\) is the population size of the prey and \(x_2,\) \(x_3\) are the population sizes of the predator species at any time t. It is assumed that all the system parameters are positive constants. Here r and k are the growth rate and the half-saturation constant for the prey species, \(\delta _1,\) \(\delta _2\) are the first and second predators death rates respectively. \(c_{1}\), \(c_{2}\) are the respective search rates of the first and second predator on the prey species,  \(\frac{c_1}{a_1}\), \(\frac{c_2}{a_2}\) are the maximum number of prey that can be eaten by the first and second predator per unit time respectively; \(\frac{1}{a_1}\), \(\frac{1}{a_2}\) are their respective half saturation rates while \(e_1\), \(e_2\) are the conversion factors, denoting the number of newly born of the first and second predator for each captured prey species respectively \((0<e_1,~e_2<1)\). The parameters \(b_1\) and \(b_2\) measure the coefficients of mutual interference among the first and second predator respectively. The terms \(\frac{c_{1}x_1 x_2}{a_{1}+x_1+b_{1}x_2}\) and \(\frac{c_{2}x_1x_3}{a_{2}+x_1+b_{2}x_3}\) denote the respective predator responses.

Some preliminary results

Existence and positive invariance

Letting, \(x = (x_1,x_2,x_3)^t,\) \(f : \mathbf {R}^{3} \rightarrow \mathbf {R}^3\), \(f = (f_1,f_2,f_3)^t,\) the system (2.1) can be rewritten as \(\dot{x} = f(x)\). Here \(f_i \in C^{\infty }(\mathbf {R})\) for \(i=1,2,3,\)  where \(f_1=rx_1(1-\frac{x_1}{x_1+k})-\frac{c_{1}x_1 x_2}{a_{1}+x_1+b_{1}x_2} -\frac{c_{2}x_1x_3}{a_{2}+x_1+b_{2}x_3},\) \(f_2=-\delta _{1}x_2+\frac{c_{1}e_{1}x_1x_2}{a_{1}+x_1+b_{1}x_2}\) and \(f_3=-\delta _{2}x_3+\frac{c_{2}e_{2}x_1x_3}{a_{2}+x_1+b_{2}x_3}.\) Since the vector function f is a smooth function of the variables \((x_1,x_2,x_3)\) in the positive octant \(\Omega ^0=\{(x_1,x_2,x_3):~x_1>0,x_2>0,x_3>0\},\) the local existence and uniqueness of the solution of the system (2.1) hold.

Persistence

If a compact set \(D\subset \Omega ^0=\{(x_1,x_2,x_3):~ x_{i}> 0, ~ i =1, 2, 3\}\) exists such that all solutions of (2.1) eventually enter and remain in D, the system is called persistent.

Proposition 3.1

The system (2.1) is persistent if the conditions: \((i)\, r> \delta _1 + \delta _{2},~ (ii) ~ x_{1_{1}}>\frac{a_{2}\delta _{2}}{c_{2} e_{2} -\delta _{2}}, \, (iii) \, x_{1_{2}} >\frac{a_{1}\delta _{1}}{c_{1} e_{1} -\delta _{1}}\) are satisfied.

Proof

We use the method of average Lyapunov function (cf. Gard and Hallam (1979)), considering a function of the form

$$\begin{aligned} V(x_1,x_2,x_3) = x_1^{\gamma _{1}} x_2^{\gamma _{2}} x_3^{\gamma _{3}}, \end{aligned}$$

where \(\gamma _{1}, \gamma _{2}\) and \(\gamma _{3}\) are positive constants to be determined. We define

$$\begin{aligned} \Pi (x_1,x_2,x_3)&= {} \frac{\dot{V}}{V}\\&= \gamma _{1}\Bigl ( r-\frac{r x_1}{x_1+k}-\frac{c_{1} x_2}{a_{1}+x_1+b_{1}x_2} -\frac{c_{2}x_3}{a_{2}+x_1+b_{2}x_3}\Bigr ) \\& \quad+ \gamma _{2}\Bigl (-\delta _{1}+\frac{c_{1}e_{1}x_1}{a_{1}+x_1+b_{1}x_2}\Bigr ) \\& \quad+ \gamma _{3}\Bigl (-\delta _{2}+\frac{c_{2}e_{2}x_1}{a_{2}+x_1+b_{2}x_3}\Bigr ). \end{aligned}$$

We now prove that this function is positive at each of the boundary equilibria. Let \(\gamma _{i} = \gamma ,\) for \(i= 1, ~ 2, ~3.\) In fact at \(E_{0},\) we have \(\Pi (0, 0, 0) =\gamma (r - \delta _1 - \delta _{2}) > 0\) from the condition (i). Moreover, from condition (ii) and (iii), we find the values of \(\Pi\) at \(E_{1}\) and \(E_{2}\) respectively,

$$\begin{aligned} \Pi (x_{{1}_1},x_{{2}_1},0) = \gamma \Bigl (-\delta _{2}+\frac{e_{2}c_{2}x_{1_{1}}}{a_{2}+ x_{{1}_1}}\Bigr )> 0,\\ \Pi (x_{{1}_2},0,x_{{3}_2}) = \gamma \Bigl (-\delta _{1}+\frac{e_{1}c_{1}x_{1_{2}}}{a_{1}+ x_{{1}_2}}\Bigr ) > 0 . \end{aligned}$$

Hence, there always exists a positive number \(\gamma\) such that \(\Pi > 0\) at the boundary equilibria. Hence V is an average Lyapunov function and thus, the system (2.1) is persistent. \(\square\)

Since the system is uniformly persistent, there exists \(\sigma>\)0 and \(\tau>\)0 such that \(x_{i}(t) > \sigma ,\) for all  \(t > \tau ,\) \(i = 1,~ 2,~ 3.\)

Boundedness

Boundedness implies that the system is biologically consistent. The following propositions ensure the boundedness of the system (2.1).

Proposition 3.2

The prey population is always bounded from above.

Proof

Before proving that the prey population is bounded above, we need to prove that the predator populations \(x_{2}\) and \(x_3\) are bounded above. To prove this result, considering the second sub equation of the system (2.1) and one can obtain the following differential inequality:

$$\begin{aligned} \frac{dx_2}{dt}\le - (\delta _1-c_1 e_1)x_{2}. \end{aligned}$$

Integrating the above differential inequality between the limits 0 and t,  we have \(x_{2}(t)\le x_{2}(0) e^{-(\delta _1-c_1 e_1)t}.\) Thus, if \((\delta _1-c_1 e_1)>0,\) then a positive number \(\tau _{1}\) is found and there exist a positive constant \(m_1\) such that \(x_{2}(t) \le m_1,\) for all \(t\ge \tau _{1}.\) By using a similar argument, one can obtain that, if \((\delta _2-c_2 e_2)>0,\) then corresponding to a positive number \(\tau _{2}\) there exists a positive constant \(m_2\) such that \(x_{3}(t) \le m_2,\) for all \(t\ge \tau _{2}.\) Both results can be written as \(x_{i}> m = \min {(m_{1}, m_{2})}\) for all \(t> \tau _3= \max {(\tau _1, \tau _2)},\) \(i =2,3,\) with the additional condition \(\min {(\delta _1-c_1 e_1,~\delta _2-c_2 e_2)} >0.\)

Now from the first sub-equation of (2.1), the following inequality is found

$$\begin{aligned} \frac{dx_1}{dt}\le \frac{\bigl ((e_1+e_2)\sigma -rk\bigr )x_1}{km}\Biggl (\frac{k \bigl (r m-(e_1+e_2)\sigma \bigr )}{(e_1+e_2)\sigma -rk}-x_1\Biggr ). \end{aligned}$$

Hence, by using simple standard arguments, we have

$$\begin{aligned} \limsup _{t\rightarrow +\infty }x_1(t)\le \frac{k r m -(e_1+e_2) k\sigma }{(e_1+e_2)\sigma -rk}= w, \, \text{ where }\,\, \frac{rm}{e_1+e_2}<\sigma <\frac{rk}{e_1+e_2}. \end{aligned}$$

\(\square\)

Proposition 3.3

The solutions of (2.1) starting in \(\Omega ^0\) are uniformly bounded with an ultimate bound.

Proof

Considering the total environment population \(\chi =x_1+\frac{x_2}{e_1}+\frac{x_3}{e_2},\) using the theorem on differential inequality (cf. Birkhoff and Rota (1982)) and following the steps of Haque and Venturino (2006), Sarwardi et al. (2013), boundedness of the solution trajectories of this model is established. In particular,

$$\begin{aligned} \limsup _{t\rightarrow +\infty }{\Bigl (x_1+\frac{x_2}{e_1}+\frac{x_3}{e_2}\Bigr )} \le \frac{(r+1)k + w}{\rho }= M, \, \text{ where }~ \rho =\min {(1, \delta _1, \delta _2)}, \end{aligned}$$
(3.1)

with the last bound independent of the initial condition.

Hence, all the solutions of (2.1) starting in \(\mathbf {R}_{+}^3\) for any \(\theta>\)0 evolve with respect to time in the compact region

$$\begin{aligned} \bar{\Omega } =\left\{ (x_1,x_2,x_3)\in \mathbf {R}_{+}^3 : x_1+\frac{x_2}{e_1}+\frac{x_3}{e_2}\le M + \theta \right\} . \end{aligned}$$
(3.2)

Equilibria and their feasibility

The equilibria of the dynamical system (2.1) are:

  1. 1.
    1. (a)

      The trivial equilibrium point \(E_{0}(0,0,0)\) is always feasible.

  2. 2.
    1. (a)

      The first boundary equilibrium point is \(E_{1}(x_{1_1},x_{2_1},0).\) The component \(x_{1_1}\) is a root of the quadratic equation \(l_1 x^2_{1_1}+(l_2+l_1 k+r k b_1 e_1) x_{1_1}+l_2 k=0,\) where \(l_1=(\delta _1-c_1e_1)\), \(l_2=a_1\delta _1.\) If \(l_1<\)0, then the quadratic equation in \(x_{1_1}\) possesses a unique positive root and consequently \(x_{2_1}=\frac{(c_{1}e_{1}-\delta _{1})x_{1_1}-a_{1}\delta _{1}}{b_{1}\delta _{1}}.\) The feasibility of the equilibrium \(E_1\) is maintained if the condition \(x_{1_1}> \frac{b_1 \delta _1}{c_{1}e_{1}-\delta _{1}}\) is satisfied.

    2. (b)

      The second boundary equilibrium point is \(E_{2}(x_{1_2},0,x_{3_2}).\) The component \(x_{1_2}\) is the root of the quadratic equation \(m_1 x^2_{1_2}+(m_2+m_1 k+r kb_2 e_2) x_{1_2}+m_2 k=0,\) where \(m_1=(\delta _2-c_2e_2)\), \(l_2=a_2\delta _2.\) If \(m_1<\)0, the quadratic equation in \(x_{1_2}\) possesses a unique positive root and consequently \(x_{3_2}=\frac{(c_{2}e_{2}-\delta _{2})x_{1_2}-a_{2}\delta _{2}}{b_{2}\delta _{2}}.\) The feasibility of the equilibrium \(E_2\) holds if the condition \(x_{1_2}> \frac{b_2 \delta _2}{c_{2}e_{2}-\delta _{2}}\) holds.

  3. 3.
    1. (a)

      The interior equilibrium point is \(E_*(x_{1*}, x_{2*}, x_{3*}),\) where the first component \(x_{1*}\) is the root of the following quadratic equation:

      $$\begin{aligned} n_1 x^2_{1*}+(n_2+ n_1 k+ rkb_{{1}}b_{{2}}e_{{1}}e_{{2}})x_{1*}+n_2 k=0, \end{aligned}$$
      (4.1)

    where \(n_1 = b_{{1}}e_{{1}}(\delta _{{2}}-c_2 e_2) +b_{{2}}e_2(\delta _{{1}}-c_{{1}}e_{{1}})\) and \(n_2 =b_{{2}}e_{{2}}\delta _{{1}}a_{{1}}+b_{{1}}e_{{ 1}}\delta _{{2}}a_{{2}}.\)

  1. Case I:

    Let \(n_1<\)0. In this case there exists exactly one positive root of the quadratic equation (4.1) irrespective of the sign of \((n_2+ n_1 k+ rkb_{{1}}b_{{2}}e_{{1}}e_{{2}}).\)

  2. Case II:

    Let \(n_1>\)0. In this case there are two possibilities: (i) if \(n_2+ n_1 k+ rkb_{{1}}b_{{2}}e_{{1}}e_{{2}}>0\), then there is no positive solution and (ii) if \(n_2+ n_1 k+ rkb_{{1}}b_{{2}}e_{{1}}e_{{2}}<0\), then there exists two positive roots or no positive root. Here we consider the Case I. Under this assumption the next two components of the interior equilibrium can be obtained as \(x_{2*}=\frac{(c_{1}e_{1}-\delta _{1})x_{1*}-a_{1}\delta _{1}}{b_{1}\delta _{1}},\)  \(x_{3*} =\frac{(c_{2}e_{2}-\delta _{2})x_{1*}-a_{2}\delta _{2}}{b_{2}\delta _{2}}.\) The feasibility of this equilibrium point \(E_{*}\) holds under the condition \(x_{1*}>\max \left\{ \frac{a_1\delta _1}{c_1e_1-\delta _1}, \frac{a_2\delta _2}{c_2e_2-\delta _2} \right\} .\) Moreover, the positivity condition of second and third components of the interior equilibrium ensures the impossibility of the Case II.

Remark

The feasibility and existences conditions of both the planar equilibria \(E_{1}\) and \(E_{2}\) immediately implies the existence of the unique feasible interior equilibrium point \(E_{*}.\) But the existence of the unique feasible interior equilibrium point \(E_{*}\) implies three possibilities: (i) \(E_1\) exists and \(E_2\) does not exist, (ii) \(E_2\) exists and \(E_1\) does not exist, (iii) existence of both.

Local stability and bifurcation

The Jacobian matrix J(x) of the system (2.1) at any point \(x=(x_1, x_2,x_3)\) is given by

$$\begin{aligned} J(x)_{3\times 3}=\left( \begin{array}{lll} \frac{r k^2}{(x_1+k)^{2}}-\frac{c_{1} x_2(a_{1}+b_{1}x_2)}{(a_1+x_1+b_{1} x_2)^2}-\frac{c_{2}x_3(a_2+b_{2}x_3)}{(a_{2}+x_1+b_{2}x_3)^{2}} &{} -\frac{c_{1} x_1 (a_{1}+x_1)}{(a_{1}+x_1+b_{1} x_2)^2} &{} -\frac{c_{2} x_1 (a_{2}+x_1)}{(a_2+x_1+b_{2} x_3)^2} \\ \frac{c_{1}e_{1}x_2(a_{1}+b_{1} x_2)}{(a_{1}+x_1+b_{1} x_2)^2} &{} -\delta _1 + \frac{c_{1}e_{1}x_1(a_1+x_1)}{(a_{1}+x_1+b_{1} x_2)^2} &{} 0 \\ \frac{c_{2}e_{2} x_3(a_2+b_{2} x_3)}{(a_{2}+x_1+b_{2} x_3)^2} &{} 0 &{} -\delta _2 + \frac{c_{2}e_{2} x_1(a_2+ x_1)}{(a_{2}+x_1+b_{2} x_3)^2} \end{array} \right) . \end{aligned}$$
(5.1)

Its characteristic equation is \(\Delta (\lambda ) = \lambda ^3+k_{1}\lambda ^2+k_{2}\lambda +k_{3}=0\), where \(k_{1} = -\text {tr}(J)\), \(k_{2} = M\) and \(k_{3} = -\det (J)\); where M is the sum of the principal minors of order two of J.

Note that a Hopf bifurcation occurs if there exist a certain bifurcation parameter \(r =r _{c}\) such that \(C_{2}(r _{c})=k _{1}(r _{c})k_{2}(r _{c})-k_{3}(r _{c})=0\) with \(k_{2}(r_{c})> 0\) and \(\frac{d}{dr}{(\text{ Re }(\lambda (r)))}|_{r =r_{c}} \ne 0,\) where \(\lambda\) is root of the characteristic equation \(\Delta (\lambda )=0\).

Local analysis of the system around \(E_0,~ E_{1},~ E_2\)

Stability The eigenvalues of the Jacobian matrix \(J(E_0)\) are \(r, -\delta _1\) and \(-\delta _2\). Hence \(E_{0}\) is unstable in nature (saddle point). Let \(J(E_1) =(\xi _{ij})_{3\times 3}\) and \(J(E_2) =(\eta _{ij})_{3\times 3}.\) Using the Routh-Hurwitz criterion, it can be easily shown that the eigenvalues of the matrices \(J(E_1)\) and \(J(E_2)\) have negative real parts iff the conditions \(e_1 x_{1_1} + x_{2_1}>\frac{k(1-b_1 e_1)-a_1}{b_1}\) and \(e_2 x_{1_2} + x_{3_2}>\frac{k(1-b_2 e_2)-a_2}{b_2}\) are satisfied. Hence the equilibria \(E_{1}\) and \(E_2\) are locally asymptotically stable under the above conditions (cf. Sect. 4 of Sarwardi et al. (2012)).

Bifurcation Since the equilibrium point \(E_0\) is a saddle, there is no Hopf bifurcation around it. In order to have Hopf bifurcation around the equilibria \(E_1\), \(E_2\), it is sufficient to show that the coefficient of \(\lambda\) in the quadratic factor of the characteristic polynomial of \(J(E_k)\) \((k= 1, 2)\) is zero and the constant term is positive. The conditions for which annihilation of the linear terms in the quadratic factors of the characteristic polynomials of \(J(E_1)\) and \(J(E_2)\) can be made possible are  \(\xi _{11}+\xi _{22}=0\) and \(\eta _{11}+\eta _{33}=0.\) For a detailed analysis, interested readers are referred to appendix A of Haque and Venturino (2006). The parametric regions where Hopf bifurcations occur around \(E_1\) and \(E_2\) are respectively established by the equality constraints \(e_1 x_{1_1} + x_{2_1} = \frac{k(1-b_1 e_1)-a_1}{b_1}\) and \(e_2 x_{1_2} + x_{3_2}=\frac{k(1-b_2 e_2)-a_2}{b_2}\).

Local analysis of the system around the interior equilibrium

Proposition 5.1

The system (2.1) around \(E_{*}\) is locally asymptotically stable if the condition (i) \(k< \min {\{a_1+b_1 x_{2*},~ a_2+b_2 x_{3*}\}}\) is satisfied.

Proof

Let \(J(x_*)\) = \({(J_{ij})}_{3\times 3}\) be the Jacobian matrix at the interior equilibrium point \(E_* =x_*\) of the system (2.1). The components of \(J(x_*)\) are \(J_{11}=\frac{c_1 x_{1*} x_{2*}\bigl (k-(a_1+b_1 x_2)\bigr )}{(x_{1*}+k)(a_1+x_{1*} +b_1 x_{2*})} +\frac{c_2 x_{1*} x_{3*}\bigl (k-(a_2+b_2 x_3)\bigr )}{(x_{1*}+k)(a_2+x_{1*} +b_2 x_{3*})},\) \(J_{12}=-\frac{c_1 x_{1*}(a_1+x_{1*})}{(a_1 + x_{1*} + b_1 x_{2*})^2} < 0\), \(J_{13}=-\frac{c_2 x_{1*}(a_2+x_{1*})}{(a_2 + x_{1*} + b_2 x_{3*})^2} < 0\), \(J_{21}=\frac{c_1e_1 x_{2*}(a_1+b_1 x_{2*})}{(a_1 + x_{1*} + b_1 x_{2*})^2} > 0\), \(J_{22}= -\frac{b_1c_1e_1 x_{1*} x_{2*}}{(a_1 + x_{1*} + b_1 x_{2*})^2} < 0\), \(J_{23}=0\), \(J_{31}=\frac{c_2e_2 x_{3*}(a_2+b_2 x_{3*})}{(a_2 + x_{1*} + b_2 x_{3*})^2} > 0\), \(J_{32}=0\), \(J_{33}= -\frac{b_2 c_2 e_2 x_{1*} x_{3*}}{(a_2 + x_{1*} + b_2 x_{3*})^2} < 0.\)

Then the characteristic equation of the Jacobian matrix \(J(x_*)\) can be written as

$$\begin{aligned} \lambda ^3+k_1\lambda ^2+k_2\lambda +k_3=0, \end{aligned}$$
(5.2)

where \(k_1=-\text{ tr }(J)=-(J_{11}+J_{22}+J_{33})\), \(k_2=M_{11}+M_{22}+M_{33}=(J_{11}J_{22}-J_{21}J_{12})+J_{22}J_{33}+(J_{11}J_{33}-J_{31}J_{13})\), \(k_3=-\det {(J)} = -\bigl (J_{11}J_{22}J_{33}-J_{12}J_{21}J_{33}-J_{31}J_{13}J_{22}\bigr )\), and  \(C_{2} = k_1 k_2 -k_3 = -(J_{11} +J_{22})\bigl (J_{33}(J_{11}+J_{22}+J_{33})+(J_{11}J_{22}-J_{21}J_{12})\bigr ) +J_{13}J_{31}(J_{11} +J_{33}).\)

It is clear that \(k_{1}>\)0 if \(J_{11}<\)0, i.e., \(k< \min {\{a_1+b_1 x_{2*},~ a_2+b_2 x_{3*}\}}\) and consequently \(C_{2}>\)0. Hence the Routh–Hurwitz condition is satisfied for the matrix \(J_{*}\), i.e., all the characteristic roots of \(J_{*}\) have negative real parts. So the system is locally asymptotically stable around \(E_{*}\).

Theorem 5.2

The dynamical system (2.1) undergoes a Hopf bifurcation around the interior equilibrium point \(E_{*}\) whenever the critical parameter r attains the value \(r = r_{c}\) in the domain

$$\begin{aligned} D_{HB} = \Bigl \{r_{c}\in {\mathbf {R}}^{+} : C_{2}(r_c)=k_{1}(r_c)k_{2}(r_c)-k_{3}(r_c)=0 ~\text{ with }~k_{2}(r_c) >0 ~\text{ and }~ \frac{d C_{2}}{dr }|_{r =r_{c}}\ne 0\Bigr \}. \end{aligned}$$

Proof

The equation (5.2) will have a pair of purely imaginary roots if \(k_1k_2-k_3=0\) for some set of values of the system parameters. Let us now suppose that \(r=r_c\) is the value of r satisfying the condition \(k_1k_2-k_3=0\). Here only \(J_{11}\) contains r explicitly. So, we write the equation \(k_1k_2-k_3=0\) as an equation in \(J_{11}\) to find \(r_c\) as follows:

$$\begin{aligned} h_1J_{11}^2+h_2J_{11}+h_3=0, \end{aligned}$$
(5.3)

where \(h_1=J_{22}+J_{33}\),  \(h_2=-J^2_{22}+J^2_{33}-J_{13}J_{31}-J_{12}J_{21}\),  \(h_3=(J_{22}+J_{33})J_{22}J_{33}-J_{13}J_{31}J_{33}-J_{12}J_{21}J_{22}\).

Thus, \(J_{11}=\frac{1}{2h_1} (-h_2\pm \sqrt{h^2_2-4h_1h_3})=J^*_{11}.\)

Or,

$$\begin{aligned} r=\frac{(x_{1*}+k)^{2}}{ k^2}\left[ J^*_{11}+\frac{c_{1} x_{2*}(a_{1}+b_{1}x_{2*})}{(a_1+x_{1*}+b_{1} x_{2*})^2}-\frac{c_{2}x_{3*}(a_2+b_{2}x_{3*})}{(a_{2}+x_{1*}+b_{2}x_{3*})^{2}}\right] =r_c. \end{aligned}$$
(5.4)

Using the condition \(k_1k_2-k_3=0,\) from equation (5.2) one can obtain

$$\begin{aligned} (\lambda +k_{1})(\lambda ^2+k_{2})=0, \end{aligned}$$
(5.5)

which has three roots \(\lambda _{1}=+i\sqrt{k}_{2},\)   \(\lambda _{2}=-i\sqrt{k}_{2},\)  \(\lambda _{3}=-k_{1}.\) Thus, there is a pair of purely imaginary eigenvalues \(\pm i\sqrt{k}_{2}\). For all values of \(\lambda\), the roots are, in general, of the form \(\lambda _{1}(r)=\xi _{1}(r)+i\xi _{2}(r ), ~ \lambda _{2}(r)=\xi _{1}(r )-i\xi _{2} (r),~ \lambda _{3}(r )=-k_{1}(r).\)

Differentiating the characteristic equation (5.2) w.r.t. r, we have

$$\begin{aligned} \frac{d \lambda }{d r}= & {} -\frac{\lambda ^2 \dot{k}_{1} + \lambda \dot{k}_{2}+\dot{k}_{3}}{3\lambda ^2 + 2k_{1}\lambda +k_{2}}{\mid }_{\lambda = i \sqrt{k_2}}\nonumber \\= & {} \frac{\dot{k}_{3}-k_2 \dot{k}_{1} + i\dot{k}_{2}\sqrt{k_2}}{2(k_2 - ik_{1} \sqrt{k_2})}\nonumber \\= & {} \frac{\dot{k}_{3}-(\dot{k}_{1} k_2 +k_1 \dot{k}_{2})}{2(k_{1}^{2} +k_{2})}+i\frac{\sqrt{k_2}(k_1\dot{k}_{3}+k_2\dot{k}_{2} -k_1 \dot{k}_{1}k_2)}{2k_2(k_{1}^{2} +k_{2})}\nonumber \\ {}= & {} -\frac{\frac{dC_2}{dr}}{2(k_{1}^{2} +k_{2})}+i\Bigg [\frac{\sqrt{k_2}\dot{k}_{2}}{2k_2} -\frac{k_1\sqrt{k_2}\frac{dC_2}{d r}}{2k_2(k_{1}^{2} +k_{2})}\Bigg ].\hbox {~~~~~~~~~~~~~~~~~~~~~~~~~~} \end{aligned}$$
(5.6)

Hence,

$$\begin{aligned} \frac{d}{dr}{\bigl (\text{ Re }(\lambda (r))\bigr )}{\mid }_{r = r_{c}}= & {} -\frac{\frac{dC_2}{dr}}{2(k_{1}^{2} +k_{2})}{\mid }_{r = r_{c}} \ne 0. \end{aligned}$$
(5.7)

Using the monotonicity condition of the real part of the complex root \(\frac{\text{ d }{(\text{ Re }(\lambda (r)))}}{\text{ d }r }{\mid }_{r =r_{c}} \ne 0\) (cf. Wiggins (2003), pp. 380), one can easily establish the transversality condition \(\frac{dC_2}{dr}|_{r =r_{c}}\ne 0,\) to ensure the existence of Hopf bifurcation around \(E_{*}.\)

Global analysis of the system around the interior equilibrium

Direction of Hopf bifucation of the system (2.1) around \(E_{*}\)

In this Section we study on the direction of Hopf bifucation around the interior equilibrium. From the model equations (2.1), we have

$$\begin{aligned} \dot{x}={f}(x), \end{aligned}$$
(6.1)

where \({x}=(x_1,x_2,x_3)^t\), \({f} =(f^1,f^2,f^3)^t= \left( \begin{array}{l} rx_1(1-\frac{x_1}{x_1+k})-\frac{c_{1}x_1 x_2}{a_{1}+x_1+b_{1}x_2} -\frac{c_{2}x_1x_3}{a_{2}+x_1+b_{2}x_3} \nonumber \\ -\delta _{1}x_2+\frac{c_{1}e_{1}x_1x_2}{a_{1}+x_1+b_{1}x_2}\nonumber \\ -\delta _{2}x_3+\frac{c_{2}e_{2}x_1x_3}{a_{2}+x_1+b_{2}x_3} \\ \end{array}\right).\) Here, at \(x=x_*\), \(f=0\). Let \({y}= (y_1, y_2, y_3)={(x_1-x_1*,~x_2-x_2*,~x_3-x_3*)}\). Putting in equation (6.1), we have

$$\begin{aligned} \dot{y}=J(x_{1*}, x_{2*},x_{3*}){y}+ \phi , \end{aligned}$$
(6.2)

where the components of nonlinear vector function \(\phi =(\phi _1,\phi _2, \phi _3)^t\) are given by

$$\begin{aligned} \phi _{i}=f^i_{x_1x_1}y^2_1+f^i_{x_2x_2}y^2_2+f^i_{x_3x_3}y^2_3+2f^i_{x_2x_3}y_2y_3+2f^i_{x_3x_1}y_3y_1+2f^i_{x_1x_2}y_1y_2+\text{ h.o.t. },~ i=1,2,3. \end{aligned}$$
(6.3)

The coefficients of nonlinear terms in \(y_{i},\) \(i = 1,2,3\) are given by

$$\begin{aligned}&f^{1}_{x_1x_1}=-\frac{2rk^2}{(x_1+k)^3}+\frac{2c_1x_2(a_1+b_1x_2)}{(a_1+x_1+b_{1} x_2)^3} +\frac{2c_2x_3(a_2+b_2x_3)}{(a_{2}+x_1+b_{2}x_3)^3},~ f^{1}_{x_2x_2}=\frac{2b_1c_1x_1(a_1+x_1)}{(a_1+x_1+b_{1} x_2)^3},~f^{1}_{x_3x_3}=\frac{2b_2c_2x_1(a_2+x_1)}{(a_2+x_1+b_{2} x_3)^3},\\&f^{1}_{x_2 x_3}=0,\,\, f^{1}_{x_1 x_2}=\, -\frac{c_1 a_1(a_1 + x_1+b_1x_2)+ 2b_1c_1 x_1 x_2}{(a_1+x_1+b_{1} x_2)^3},\,~ f^{1}_{x_3x_1}=-\frac{c_2 a_2(a_2 + x_1+b_2x_3)+ 2b_2c_2 x_3 x_1}{(a_2+x_1+b_{2} x_3)^3};\, ~f^{2}_{x_1x_1}= \\&-\frac{2c_{1}e_{1}x_2(a_{1}+b_{1} x_2)}{(a_{1}+x_1+b_{1} x_2)^3},~f^{2}_{x_2x_2}=-\frac{2b_1c_1e_1x_1(a_1+x_1)}{(a_1+x_1+b_{1}x_2)^3},~f^{2}_{x_3x_3}=0, ~ f^{2}_{x_1x_2}=\frac{a_1 c_1e_1(a_1+x_1+b_1x_2)+2b_1 c_1 e_1x_1 x_2}{(a_1+x_1+b_1x_2)^3}, \end{aligned}$$
$$\begin{aligned}&f^{2}_{x_2x_3}=0,~f^{2}_{x_3x_1}=0;~ f^{3}_{x_1x_1}=-\frac{2c_2e_2x_3(a_2+b_2x_3)}{(a_{2}+x_1+b_{2} x_3)^3},~ f^{3}_{x_2x_2}=0,~ f^{3}_{x_3x_3}=-\frac{2b_2c_2e_2x_1(a_2+x_1)}{(a_2+x_1+b_2x_3)^3},\\&f^{3}_{x_2x_3}=0,~ f^{3}_{x_3x_1}=\frac{a_2c_2e_2(a_2+x_1+b_2x_3)+2b_2c_2e_2 x_1 x_3}{(a_2+x_1+b_2x_3)^3},~ f^{3}_{x_1x_2}=0. \end{aligned}$$

Let P be the matrix formed by the column vectors \((\mathbf{u_2, u_1,u_3}),\) which are the eigenvectors corresponding to the eigenvalues \(\lambda _{1,2}=\pm i\sqrt{k_2}\) and \(\lambda _3=-k_1\) of \(J(x_{1*}, x_{2*},x_{3*}).\) Then \(J(x_{1*}, x_{2*},x_{3*})\mathbf{u_2}=i\sqrt{k_2}{} \mathbf{u_2},\)  \(J(x_{1*},x_{2*},x_{3*})\mathbf{u_1}=-i\sqrt{k_2}{} \mathbf{u_1},\) and \(J(x_{1*}, x_{2*},x_{3*})\mathbf{u_3}=-k_1\mathbf{u_3}.\)

Thus,

$$P=\left( \begin{aligned} 0 &\quad{} 1 &\quad{} 1\\ \frac{-J_{21}\sqrt{k_2}}{J^{2}_{22}+k_2} &\quad{} \frac{-J_{21}J_{22}}{J^{2}_{22}+k_2} &\quad{} \frac{-J_{21}}{J_{22}+k_1}\\ \frac{-J_{31}\sqrt{k_2}}{J^{2}_{33}+k_2} &\quad{} \frac{-J_{31}J_{33}}{J^{2}_{33}+k_2} &\quad{} \frac{-J_{31}}{J_{33}+k_1}\\ \end{aligned}\right) =(p_{ij})_{3\times 3}.$$

Let us make use of the transformation \(\mathbf{y}=P\mathbf{z},\) so that the system (6.2) is reduced to the following one

$$\begin{aligned} \dot{\mathbf{z}}=P^{-1}J(x_{1*}, x_{2*},x_{3*})P\mathbf{z} +P^{-1}\phi =\left( \begin{array}{lll} 0 &{} -i\sqrt{k_2} &{} 0\\ i\sqrt{k_2} &{} 0 &{} 0\\ 0 &{} 0 &{} -k_1 \end{array}\right) \mathbf{z}+P^{-1}\phi . \end{aligned}$$
(6.4)

Here \(P^{-1}=\frac{\text{ Adj }P}{\det P}=(q_{ij})_{3\times 3},\) where

$$\begin{aligned} q_{11}&=\frac{1}{\det P}\Bigg(\frac{J_{21}J_{22}J_{31}}{(J^{2}_{22}+k_2)(J_{33}+k_1)}- \frac{J_{21}J_{33}J_{31}}{(J^{2}_{22}+k_2)(J_{22}+k_1)}\Bigg),~ q_{12}=\frac{1}{\det P}\Bigg( \frac{J_{31}}{J^{2}_{33}+k_1}- \frac{J_{31}J_{33}}{J^{2}_{33}+k_2}),\\ q_{13}&=\frac{1}{\det P}\Bigg(\frac{-J_{21}}{J_{21}+k_1}+\frac{J_{21}J_{22}}{J^{2}_{22}+k_2}\Bigg),~q_{21}=\frac{1}{\det P}\Bigg(\frac{J_{21}\sqrt{k_2}J_{31}}{(J^{2}_{22}+k_2)(J_{22}+k_1)}- \frac{J_{21}\sqrt{k_2}J_{31}}{(J^{2}_{33}+k_2)(J_{22}+k_1)}\Bigg),\\ q_{22}&=\frac{1}{\det P}\frac{\sqrt{k_2}J_{31}}{(J^{2}_{33}+k_2)}, \, ~ q_{23}=\frac{1}{\det P}\frac{-\sqrt{k_2}J_{31}}{(J^{2}_{33}+k_2)},~ q_{31}=\frac{1}{\det P}\Bigg(\frac{J_{21}\sqrt{k_2}J_{31}J_{33}}{(J^{2}_{22}+k_2)(J^{2}_{33}+k_2)}- \frac{J_{21}\sqrt{k_2}J_{31}J_{22}}{(J^{2}_{33}+k_2)(J^{2}_{22}+k_2)}\Bigg),\\ q_{32}&=\frac{1}{\det P}\frac{-\sqrt{k_2}J_{21}}{(J^{2}_{22}+k_2 )},\, q_{33}=\frac{1}{\det P}\frac{\sqrt{k_2}J_{21}}{(J^{2}_{22}+k_2)}. \end{aligned}$$

The system (6.4) can be written as

$$\begin{aligned} \frac{d}{dt}\left( \begin{array}{l} z_1 \\ z_2 \\ \end{array}\right)= & {} \left( \begin{array}{ll} 0 &{} -\sqrt{k_2} \\ \sqrt{k_2} &{} 0 \end{array}\right) \left( \begin{array}{l} z_1 \\ z_2 \\ \end{array}\right) +F(z_1,z_2,z_3),\end{aligned}$$
(6.5)
$$\begin{aligned} \frac{dz_3}{dt}= & {} -k_1z_3+G(z_1,z_2,z_3). \end{aligned}$$
(6.6)

On the center-manifold (cf. Carr (1981), Kar et al. (2012))

$$\begin{aligned} z_3=\frac{1}{2}\left( b_{11}z^2_1+2b_{12}z_1z_2+b_{22}z^2_2\right) \end{aligned}$$
(6.7)

Therefore,

$$\begin{aligned}&\dot{z}_3=\left( \begin{array}{ll} b_{11} z_1+b_{12}z_2 &{} b_{12}z_1+b_{22}z_2 \nonumber \\ \end{array}\right) \left( \begin{array}{ll} 0 &{} -\sqrt{k_2} \\ \sqrt{k_2} &{} 0 \end{array}\right) \left( \begin{matrix} z_1 \\ z_2 \end{matrix} \right) \\&=\sqrt{k_2} b_{12} z^2_1 +\sqrt{k_2}(b_{22}-b_{11})z_1z_2-\sqrt{k_2} b_{12}z^2_2 \end{aligned}$$
(6.8)

Using (6.4) and (6.6), we have

$$\begin{aligned} \dot{z}_3=-k_1z_3+q_{31}\phi _1+q_{32}\phi _2+q_{33}\phi _3 \end{aligned}$$
(6.9)

From the Eqs. (6.8) and (6.9), we have

$$\begin{aligned} &\sqrt{k_2} b_{12} z^2_1+\sqrt{k_2}(b_{22}-b_{11})z_1z_2-\sqrt{k_2} b_{12}z^2_2 \\ &\quad = -\frac{1}{2}k_1(b_{11}z^2_1+2b_{12}z_1z_2+b_{22}z^2_2) +q_{31} \bigl [f^1_{x_1x_1}\{p_{11}z_1+p_{12}z_2+p_{13}\frac{1}{2}(b_{11}z^2_1+2b_{12}z_1z_2+b_{22}z^2_2)\}^2\\ &\quad +f^1_{x_2x_2}\{p_{21}z_1+p_{22}z_2+p_{23}\frac{1}{2}(b_{11}z^2_1+2b_{12}z_1z_2+b_{22}z^2_2)\}^2 +f^1_{x_3x_3}\{p_{31}z_1+p_{32}z_2+p_{33}\frac{1}{2}(b_{11}z^2_1 +2b_{12}z_1z_2+b_{22}z^2_2)\}^2 \\ &\quad +2f^1_{x_3x_1}\{p_{31}z_1+p_{32}z_2+p_{33}\frac{1}{2}(b_{11}z^2_1+2b_{12}z_1z_2+b_{22}z^2_2)\}\{p_{11}z_1+p_{12}z_2+p_{13}\frac{1}{2}(b_{11}z^2_1+2b_{12}z_1z_2+b_{22}z^2_2)\} \\ &\quad+2f^1_{x_1x_2}\{p_{11}z_1+p_{12}z_2+p_{13}\frac{1}{2}(b_{11}z^2_1+2b_{12}z_1z_2+b_{22}z^2_2)\} \\ &\quad \times \{p_{21}z_1 +p_{22}z_2+p_{23}\frac{1}{2}(b_{11}z^2_1+2b_{12}z_1z_2+b_{22}z^2_2)\}\bigr ] \\&\quad+q_{32}[f^2_{x_1x_1}\{p_{11}z_1+p_{12}z_2+p_{13}\frac{1}{2}(b_{11}z^2_1+2b_{12}z_1z_2+b_{22}z^2_2)\}^2 \\& \quad +f^2_{x_2x_2}\{p_{21}z_1+p_{22}z_2 \\ &\quad+p_{23}\frac{1}{2}(b_{11}z^2_1+2b_{12}z_1z_2+b_{22}z^2_2)\}^2 +f^2_{x_3x_3}\{p_{31}z_1+p_{32}z_2+p_{33}\frac{1}{2}(b_{11}z^2_1+2b_{12}z_1z_2+b_{22}z^2_2)\}^2 \\ &\quad +2f^2_{x_2x_3}\{p_{21}z_1+p_{22}z_2 +p_{23}\frac{1}{2}(b_{11}z^2_1+2b_{12}z_1z_2+b_{22}z^2_2)\}\{p_{31}z_1+p_{32}z_2+p_{33}\frac{1}{2}(b_{11}z^2_1 +2b_{12}z_1z_2+b_{22}z^2_2)\} \\ &\quad +2f^2_{x_3x_1}\{p_{31}z_1+p_{32}z_2+p_{33}\frac{1}{2}(b_{11}z^2_1+2b_{12}z_1z_2+b_{22}z^2_2)\}\{p_{11}z_1+p_{12}z_2 + p_{13}\frac{1}{2}(b_{11}z^2_1 +2b_{12}z_1z_2+b_{22}z^2_2)\}\\ &\quad+2f^2_{x_1x_2}\{p_{11}z_1+p_{12}z_2 +p_{13}\frac{1}{2}(b_{11}z^2_1+2b_{12}z_1z_2+b_{22}z^2_2)\} \times \{p_{21}z_1+p_{22}z_2 +p_{23}\frac{1}{2}(b_{11}z^2_1+2b_{12}z_1z_2+b_{22}z^2_2)\}\bigr ]\\ &\quad +q_{33}\bigl [f^3_{x_1x_1}\{p_{11}z_1+p_{12}z_2 +p_{13}\frac{1}{2}(b_{11}z^2_1+2b_{12}z_1z_2+b_{22}z^2_2)\}^2+f^3_{x_2x_2}\{p_{21}z_1+p_{22}z_2 +p_{23} \frac{1}{2}(b_{11}z^2_1+2b_{12}z_1z_2+b_{22}z^2_2)\}^2 \\ &\quad +f^3_{x_3x_3}\{p_{31}z_1+p_{32}z_2 +p_{33}\frac{1}{2}(b_{11}z^2_1+2b_{12}z_1z_2+b_{22}z^2_2)\}^2 +2f^3_{x_2x_3}\{p_{21}z_1+p_{22}z_2 \\ &\quad +p_{23}\frac{1}{2} (b_{11}z^2_1+2b_{12}z_1z_2+b_{22}z^2_2)\}\{p_{31}z_1+p_{32}z_2 +p_{33}\frac{1}{2}(b_{11}z^2_1 +2b_{12}z_1z_2+b_{22}z^2_2)\} +2f^3_{x_3x_1}\{p_{31}z_1 +p_{32}z_2\\ &\quad+p_{33}\frac{1}{2}(b_{11}z^2_1+2b_{12}z_1z_2+b_{22}z^2_2)\} \{p_{11}z_1 +p_{12}z_2 +p_{13}\frac{1}{2}(b_{11}z^2_1+2b_{12}z_1z_2+b_{22}z^2_2)\}+2f^3_{x_1x_2}\{p_{11}z_1+p_{12}z_2\\ &\quad +p_{13}\frac{1}{2} (b_{11}z^2_1 +2b_{12}z_1z_2+b_{22}z^2_2)\}\{p_{21}z_1+p_{22}z_2 +p_{23}\frac{1}{2}(b_{11}z^2_1+2b_{12}z_1z_2+b_{22}z^2_2)\}\bigr ]. \end{aligned}$$

Comparing the coefficients of \(z^2_1\), \(z_1z_2\) and \(z^2_2\) from both sides, we have

$$\begin{aligned}&\sqrt{k_2} b_{12} +\frac{k_1}{2}b_{11}\nonumber \\&=q_{31}\left[ f^1_{x_1x_1} p^2_{11}+f^1_{x_2x_2} p^2_{21}+f^1_{x_3x_3} p^2_{31}+2f^1_{x_2x_3} p_{21}p_{31}+2f^1_{x_3x_1} p_{31}p_{11}+2f^1_{x_1x_2} p_{11}p_{21}\right] \nonumber \\&+q_{32}\left[ f^2_{x_1x_1} p^2_{11}+f^2_{x_2x_2} p^2_{21}+f^2_{x_3x_3} p^2_{31}+2f^2_{x_2x_3} p_{21}p_{31}+2f^2_{x_3x_1} p_{31}p_{11}+2f^2_{x_1x_2} p_{11}p_{21}\right] \nonumber \\&+q_{33}\left[ f^3_{x_1x_1} p^2_{11}+f^3_{x_2x_2} p^2_{21}+f^3_{x_3x_3} p^2_{31}+2f^3_{x_2x_3} p_{21}p_{31}+2f^3_{x_3x_1} p_{31}p_{11}+2f^3_{x_1x_2} p_{11}p_{21}\right] \nonumber \\&=\Omega _1, \end{aligned}$$
(6.10)
$$\begin{aligned}&-\sqrt{k_2} (b_{11}-b_{22})+k_1 b_{12}\nonumber \\&= 2q_{31}[ f^1_{x_1x_1} p_{11}p_{12}+f^1_{x_2x_2} p_{21}p_{22}+f^1_{x_3x_3} p_{31}p_{32}+f^1_{x_2x_3} (p_{21}p_{32}+p_{22}p_{31}) + f^1_{x_3x_1} (p_{11}p_{32}\nonumber \\&+p_{12}p_{31})+f^1_{x_1x_2}(p_{11}p_{22}+p_{12}p_{21})]+q_{32}[f^2_{x_1x_1} p_{11}p_{12}+f^2_{x_2x_2} p_{21}p_{22}+f^2_{x_3x_3}p_{31}p_{32} +f^2_{x_2x_3}\nonumber \\&\times (p_{21}p_{32}+p_{22}p_{31}) + f^2_{x_3x_1} (p_{11}p_{32}+p_{12}p_{31})+f^2_{x_1x_2}(p_{11}p_{22}+p_{12}p_{21})]+q_{33}\left[ f^3_{x_1x_1} p_{11}p_{12}\right. \nonumber \\&\left. + f^3_{x_2x_2} p_{21}p_{22}+f^3_{x_3x_3} p_{31}p_{32}+f^3_{x_2x_3} (p_{21}p_{32}+p_{22}p_{31}) + f^3_{x_3x_1} (p_{11}p_{32}+p_{12}p_{31})\right. \nonumber \\&\left. + f^3_{x_1x_2}(p_{11}p_{22}+p_{12}p_{21})\right] =\Omega _2, \end{aligned}$$
(6.11)

and

$$\begin{aligned}&-\sqrt{k_2} b_{12}+\frac{k_1}{2}b_{22}\nonumber \\&=q_{31}\left[ f^1_{x_1x_1} p^2_{12}+f^1_{x_2x_2} p^2_{22}+f^1_{x_3x_3} p^2_{32}+2f^1_{x_2x_3} p_{22}p_{32}+2f^1_{x_3x_1} p_{31}p_{12}+2f^1_{x_1x_2} p_{12}p_{22}\right] \nonumber \\&+q_{32}\left[ f^2_{x_1x_1} p^2_{12}+f^2_{x_2x_2} p^2_{22}+f^2_{x_3x_3} p^2_{32}+2f^2_{x_2x_3} p_{22}p_{32}+2f^2_{x_3x_1} p_{31}p_{12}+2f^2_{x_1x_2} p_{12}p_{22}\right] \nonumber \\&+q_{33}\left[ f^3_{x_1x_1} p^2_{12}+f^3_{x_2x_2} p^2_{22}+f^3_{x_3x_3} p^2_{32}+2f^3_{x_2x_3} p_{22}p_{32}+2f^3_{x_3x_1} p_{31}p_{12}+2f^3_{x_1x_2} p_{12}p_{22}\right] \nonumber \\&=\Omega _3. \end{aligned}$$
(6.12)

From equations (6.10), (6.11) and (6.12), we have

$$\begin{aligned} \left( \begin{array}{lll} \frac{1}{2}k_1 &{} \sqrt{k_2} &{} 0 \\ -\sqrt{k_2} &{} k_1 &{} \sqrt{k_2}\\ 0 &{} -\sqrt{k_2} &{} \frac{1}{2}k_1 \\ \end{array} \right) \left( \begin{array}{l} b_{11} \\ b_{12} \\ b_{22} \end{array} \right) =\left( \begin{array}{l} \Omega _1 \\ \Omega _2 \\ \Omega _3 \end{array} \right) . \end{aligned}$$
(6.13)

The equation (6.13) gives the coefficients \(b_{11}\), \(b_{12}\) and \(b_{22}\) as follows:

$$\begin{aligned} b_{11}= & {} \frac{k_2(\Omega _1+\Omega _3) -\frac{k_1}{2}(\sqrt{k_2}\Omega _2 -k_1\Omega _1)}{(\frac{k_1^3}{4} +k_1 k_2)},\\ b_{12}= & {} \frac{\frac{k_1^2 \Omega _2}{4} -\frac{k_1 \sqrt{k_2}}{2}(\Omega _3 -\Omega _1)}{(\frac{k_1^3}{4} +k_1 k_2)},\\ b_{22}= & {} \frac{k_2(\Omega _1+\Omega _3) +\frac{k_1^2 \Omega _3}{2} + \frac{k_1\sqrt{k_2}}{2}\Omega _2}{(\frac{k_1^3}{4} +k_1 k_2)}. \end{aligned}$$

The flow of the central manifold is characterized by the reduced system as

$$\begin{aligned} \frac{d}{dt}\left( \begin{array}{l} z_1 \\ z_2 \end{array}\right) =\left( \begin{array}{ll} 0 &{} -\sqrt{k_2} \\ \sqrt{k_2} &{} 0 \end{array}\right) \left( \begin{array}{l} z_1 \\ z_2 \end{array}\right) +\left( \begin{array}{l} F^1 \\ F^2 \end{array}\right) , \end{aligned}$$
(6.14)

where \(F^1=q_{11}\phi _1+q_{12}\phi _2+q_{13}\phi _3+h.o.t\), \(F^2=q_{21}\phi _1+q_{22}\phi _2+q_{23}\phi _3+h.o.t\). The stability of the bifurcating limit cycle can be determined by the sign of the parametric expression

$$\begin{aligned} \Pi = F^1_{111}+F^2_{112}+F^1_{122}+F^2_{222}+\frac{F^1_{12}(F^1_{11}+F^1_{22})-F^2_{12}(F^2_{11}+F^2_{22})-F^1_{11}F^2_{11}+F^1_{22}F^2_{22}}{\sqrt{k_2}}, \end{aligned}$$
(6.15)

where \(F_{ijk}=\frac{\partial ^3 F}{\partial z_i\partial z_j \partial z_k}\) at the origin. If the value of the above expression is negative, then the Hopf bifurcating limit cycle is stable and we have a supercritical Hopf bifurcation. If the value is positive, then the Hopf bifurcating limit cycle is unstable and the bifurcation is subcritical.

Here

$$\begin{aligned} F^1_{11} =& {} 2q_{11}[f^1_{x_1x_1}p^2_{11} + f^1_{x_2x_2}p^2_{21}+ f^1_{x_3x_3}p^2_{31}+2f^1_{x_3x_1}p_{11}p_{31} +2f^1_{x_1x_2}p_{11}p_{21}]+2q_{12}[f^2_{x_1x_1}p^2_{11} + f^2_{x_2x_2}\\ & \times p^2_{21}+2f^2_{x_1x_2}p_{11}p_{21}]+2q_{13}[f^3_{x_1x_1}p^2_{11} + f^3_{x_3x_3}p^2_{31}+2f^3_{x_3x_1}p_{11}p_{31}], \\ F^1_{12}& ={} 2q_{11}[f^1_{x_1x_1}p_{11}p_{12} + f^1_{x_2x_2}p_{21}p_{22}+ f^1_{x_3x_3}p_{31}p_{32}+f^1_{x_3x_1}(p_{11}p_{32}+p_{12}p_{31}) +f^1_{x_1x_2}(p_{12}p_{21}\\&+p_{22}p_{11})]+2q_{12}[f^2_{x_1x_1}p_{11}p_{12} + f^2_{x_2x_2}p_{21}p_{22}+ f^2_{x_1x_2}(p_{12}p_{21}+p_{22}p_{11})] +2q_{13}[f^3_{x_1x_1}p_{11}p_{12} \\&+ f^3_{x_3x_3}p_{31}p_{32}+f^3_{x_3x_1}(p_{11}p_{32}+p_{12}p_{31})],\\ F^1_{22}= & {} 2q_{11}[f^1_{x_1x_1}p_{12}^2 + f^1_{x_2x_2}p_{22}^2+ f^1_{x_3x_3}p_{32}^2+ 2f^1_{x_3x_1}p_{12}p_{32} +2f^1_{x_1x_2}p_{12}p_{22}] +2q_{12}[f^2_{x_1x_1}p_{12}^2 \\&+ f^2_{x_2x_2}p_{22}^2+ 2f^2_{x_1x_2}p_{12}p_{22}] +2q_{13}[f^3_{x_1x_1}p_{12}^2 + f^3_{x_3x_3}p_{32}^2+f^3_{x_3x_1}p_{12}p_{32})], \\ F^1_{111} =& {} 6q_{11}b_{11}[f^1_{x_1x_1}p_{11}p_{13}+f^1_{x_2x_2}p_{21}p_{23}+f^1_{x_3x_3}p_{31}p_{33} +f^1_{x_3x_1}(p_{11}p_{33}+p_{13}p_{31})+f^1_{x_1x_2}(p_{11}p_{23} \\ &+p_{21}p_{13})] +6q_{12}b_{11}[f^2_{x_1x_1}p_{11}p_{13}+f^2_{x_2x_2}p_{21}p_{23}+f^2_{x_3x_3}p_{31}p_{33} +f^2_{x_1x_2}(p_{11}p_{23}+p_{13}p_{21})] \\ & +6q_{13}b_{11}[f^3_{x_1x_1}p_{11}p_{13}+f^3_{x_3x_3}p_{31}p_{33} +f^3_{x_3x_1}(p_{11}p_{33}+p_{13}p_{31})], \\ F^1_{122} =& {} 2q_{11}[f^1_{x_1x_1}(2p_{12}p_{13}b_{12}+p_{11}p_{13}b_{22})+f^1_{x_2x_2}(2p_{22}p_{33}b_{12}+p_{21}p_{23}b_{22}) +f^1_{x_3x_3}(2p_{32}p_{33}b_{12} \\ & +p_{31}p_{33}b_{22}) + f^1_{x_3x_1}(2p_{13}p_{32}b_{12}+p_{11}p_{33}b_{22}+p_{13}p_{31}b_{22}+2p_{12}p_{33}b_{12}) + f^1_{x_1x_2}(2p_{12}p_{23} \\ & \times b_{12} +p_{13}p_{21}b_{22}+p_{11}p_{23}b_{22}+2p_{22}p_{13}b_{12})] +2q_{12}[f^2_{x_1x_1}(2p_{12}p_{13}b_{12}+p_{11}p_{13}b_{22}) +f^2_{x_2x_2} \\ & \times (2p_{22}p_{23}b_{12}+p_{21}p_{23}b_{22}) +f^2_{x_1x_2}(2p_{12}p_{23}b_{12}+p_{11}p_{23}b_{22}+2p_{13}p_{22}b_{12}+p_{13}p_{21}b_{22})] \\ & + 2q_{13}[f^3_{x_1x_1}(2p_{13}p_{12}b_{12}+p_{11}p_{13}b_{22})+f^3_{x_3x_3}(2p_{32}p_{33}b_{12}+p_{31}p_{33}b_{22}) +f^3_{x_3x_1}(2p_{32}p_{13}b_{12} \\ & +p_{31}p_{13}b_{22}+2p_{12}p_{13}b_{12}+p_{33}p_{11}b_{22})], \end{aligned}$$
$$\begin{aligned} F^2_{11} = 2q_{21}[f^1_{x_1x_1}p^2_{11} + f^1_{x_2x_2}p^2_{21}+ f^1_{x_3x_3}p^2_{31}+2f^1_{x_3x_1}p_{11}p_{31} +2f^1_{x_1x_2}p_{11}p_{21}]+2q_{22}[f^2_{x_1x_1}p^2_{11} + f^2_{x_2x_2} \times p^2_{21}+2f^2_{x_1x_2}p_{11}p_{21}]+2q_{23}[f^3_{x_1x_1}p^2_{11} + f^3_{x_3x_3}p^2_{31}+2f^3_{x_3x_1}p_{11}p_{31}],\\ F^2_{12}= 2q_{21}[f^1_{x_1x_1}p_{11}p_{12} + f^1_{x_2x_2}p_{21}p_{22}+ f^1_{x_3x_3}p_{31}p_{32}+f^1_{x_3x_1}(p_{11}p_{32}+p_{12}p_{31}) +f^1_{x_1x_2}(p_{12}p_{21}+p_{22}p_{11})]+2q_{22}[f^2_{x_1x_1}p_{11}p_{12} + f^2_{x_2x_2}p_{21}p_{22}+ f^2_{x_1x_2}(p_{12}p_{21}+p_{22}p_{11})] +2q_{23}[f^3_{x_1x_1}p_{11}p_{12} + f^3_{x_3x_3}p_{31}p_{32}+f^3_{x_3x_1}(p_{11}p_{32}+p_{12}p_{31})],\\ F^2_{22}= 2q_{21}[f^1_{x_1x_1}p_{12}^2 + f^1_{x_2x_2}p_{22}^2+ f^1_{x_3x_3}p_{32}^2+ 2f^1_{x_3x_1}p_{12}p_{32} +2f^1_{x_1x_2}p_{12}p_{22}] +2q_{22}[f^2_{x_1x_1}p_{12}^2 + f^2_{x_2x_2}p_{22}^2+ 2f^2_{x_1x_2}p_{12}p_{22}] +2q_{23}[f^3_{x_1x_1}p_{12}^2 + f^3_{x_3x_3}p_{32}^2+f^3_{x_3x_1}p_{12}p_{32})], \\F^2_{112} = 2q_{21}[f^1_{x_1x_1}(2p_{11}p_{13}b_{12}+p_{12}p_{13}b_{11})+f^1_{x_2x_2}(2p_{21}p_{23}b_{12}+p_{22}p_{23}b_{11}) +f^1_{x_3x_3}(2p_{31}p_{33}b_{12} +p_{32}p_{33}b_{11}) + f^1_{x_3x_1}(2p_{11}p_{33}b_{12}+p_{13}p_{32}b_{11}+p_{12}p_{33}b_{11}+2p_{13}p_{31}b_{12}) + f^1_{x_1x_2}(2p_{13}p_{21} \times b_{12} +p_{12}p_{23}b_{11}+ 2p_{11}p_{23}b_{12}+p_{22}p_{13}b_{11})] +2q_{22}[f^2_{x_1x_1}(2p_{11}p_{13}b_{12}+p_{12}p_{13}b_{11}) +f^2_{x_2x_2} \times (2p_{21}p_{23}b_{12}+p_{22}p_{23}b_{11}) +f^2_{x_1x_2}(2p_{11}p_{23}b_{12}+p_{12}p_{23}b_{11}+2p_{13}p_{21}b_{12}+p_{13}p_{22}b_{11})] + 2q_{23}[f^3_{x_1x_1}(2p_{11}p_{13}b_{12}+p_{12}p_{13}b_{11})+f^3_{x_3x_3}(2p_{31}p_{33}b_{12}+p_{32}p_{33}b_{11}) +f^3_{x_3x_1}(2p_{31}p_{13}b_{12} +p_{33}p_{12}b_{11}+2p_{11}p_{33}b_{12}+p_{32}p_{13}b_{11})],\\ F^2_{222}= 6q_{21}b_{22}[f^1_{x_1x_1}p_{12}p_{13}+f^1_{x_2x_2}p_{22}p_{23}+f^1_{x_3x_3}p_{32}p_{33} +f^1_{x_3x_1}(p_{12}p_{33}+p_{13}p_{32})+f^1_{x_1x_2}(p_{12}p_{23} + p_{13}p_{22})] +6q_{22}b_{22}[f^2_{x_1x_1}p_{12}p_{13}+f^2_{x_2x_2}p_{22}p_{23}+f^2_{x_1x_2}(p_{12}p_{23}+p_{13}p_{22})] +6q_{23}b_{22}[f^3_{x_1x_1}p_{12}p_{13}+f^3_{x_3x_3}p_{32}p_{33} +f^3_{x_3x_1}(p_{12}p_{33}+p_{13}p_{32})].\end{aligned}$$

Global stability of the system (2.1) around \(E_{*}\)

Theorem 6.1

The interior equilibrium \(E_{*}\) is globally asymptotically stable if the condition

$$\begin{aligned} (\text{i})\,~ a_1 a_2 b_1 b_2 r k> (x_{1*} +k)(w +k)(a_1 b_1 c_2 + a_2 b_2 c_1) ~\hbox {\,is satisfied}. \end{aligned}$$

Proof

Let

$$\begin{aligned} L(x_1,x_2,x_3)=L_{1}(x_1,x_2,x_3)+L_{2}(x_1,x_2,x_3)+L_{3}(x_1,x_2,x_3) \end{aligned}$$
(6.16)

be a positive Lyapunov function, where

$$\begin{aligned} ~L_{1}=s_{1}\bigl (x_1-x_{1*}-x_{1*}\ln (\frac{x_1}{x_{1*}}) \bigr ),~ L_{2} =s_{2}\bigl (x_2-x_{2*}-x_{2*}\ln (\frac{x_2}{x_{2*}}) \bigr ),\\ ~L_{3}=s_{3}\bigl (x_3-x_{3*}-x_{3*}\ln (\frac{x_3}{x_{3*}})\bigr ); \end{aligned}$$

\(s_{1},~s_{2}\) and \(s_{3}\) being positive real constants.

This function is well-defined and continuous in Int(\({R_{+}}^3\)). It can be easily verified that the function \(L(x_1,x_2,x_3)\) is zero at the equilibrium point \(E_{*}\) and is positive for all other positive values of \((x_1,x_2,x_3),\) and thus \(E_{*}\) is the global minimum of \(L(x_1,x_2,x_3)\).

Since the solutions of the system are bounded and ultimately enter the set \({\Omega }=\{(x_1,x_2,x_3);x_1>0, x_2>0, x_3>0: x_1+\frac{x_2}{e_1} + \frac{x_3}{e_2}\le M+\epsilon ,~\forall ~\epsilon > 0 \}\), we restrict our study in \({\Omega }\). The time derivative of L along with the solutions of the system (2.1) gives (cf. Sarwardi et al. (2010), Sarwardi et al. (2012))

$$\begin{aligned} \frac{dL}{dt}= & {} -s_{1}\Bigl [\frac{rk}{(x_{1*}+k)(x_{1}+k)}-\frac{c_1 x_{2*}}{(a_1 + x_1 +b_1 x_2)(a_1 + x_{1*} +b_1 x_{2*})}\nonumber \\&- {} \frac{c_2 x_{3*}}{(a_2 + x_1 +b_2 x_3)(a_2 + x_{1*} +b_2 x_{3*})}\Bigr ](x_1-x_{1*})^2- s_{2}\Bigl [\frac{c_1e_1(a_1+b_1)}{(a_1 + x_1 +b_1 x_2)(a_1 + x_{1*} +b_1 x_{2*})}\Bigr ]\nonumber \\&\times {} (x_2-x_{2*})^2 -s_{3}\Bigl [\frac{c_2e_2(a_2+b_2)}{(a_2 + x_1 +b_2 x_3)(a_2 + x_{1*} +b_2 x_{3*})}\Bigr ](x_3-x_{3*})^2\nonumber \\&+ {} \frac{c_1\bigl (s_2 b_1e_1 x_{2*} - s_1(a_1+x_{1*})\bigr )(x_1-x_{1*})(x_2-x_{2*})}{(a_1 + x_1 +b_1 x_2)(a_1 + x_{1*} +b_1 x_{2*})} +\frac{c_2\bigl (s_3 b_2e_2 x_{3*} - s_1(a_2+x_{1*})\bigr )}{(a_2 + x_1 +b_2 x_2)(a_2 + x_{1*} +b_2 x_{2*})}\nonumber \\&\times {} (x_1-x_{1*})(x_3-x_{3*}). \end{aligned}$$
(6.17)

Letting \(s_{1} = 1\),  \(s_{2} = \frac{a_1+x_{1*}}{b_1 e_1 x_{2*})}\) and \(s_{3} =\frac{a_2+x_{1*}}{b_2 e_2 x_{3*})},\) we have

$$\begin{aligned} \frac{dL}{dt}\le & {} -\Bigl [\frac{rk}{(x_{1*}+k)(x_{1}+k)}-\frac{c_1 x_{2*}}{(a_1 + x_1 +b_1 x_2)(a_1 + x_{1*} +b_1 x_{2*})}\nonumber \\& - {} \frac{c_2 x_{3*}}{(a_2 + x_1 +b_2 x_3)(a_2 + x_{1*} +b_2 x_{3*})}\Bigr ](x_1-x_{1*})^2\nonumber \\&<-\Bigl [\frac{rk}{(x_{1*}+k)(w+k)} -\frac{c_1}{a_1b_1}-\frac{c_2}{a_2b_2}\Bigr ](x-x_{*})^2 \nonumber \\&< {} 0, \hbox { by condition (i)}, \end{aligned}$$
(6.18)

along all the trajectories in the positive octant except \((x_{1*}, x_{2*}, x_{3*})\). Also \(\frac{dL}{dt} = 0\) when \((x_1,x_2,x_3) = (x_{1*}, x_{2*}, x_{3*})\). The proof follows from (6.16) and Lyapunov-Lasalle’s invariance principle (cf. Hale (1989)).

Table 1 Schematic representation of our analytical findings
Full size table
Table 2 The set of system parameter (including the critical parameter \(r_{c}\)) values and their corresponding Figures with description
Full size table

Numerical simulations

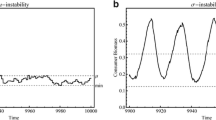
Numerical simulations have been carried out by making use of MATLAB-R2010a and Maple-12. The analytical findings of the present study are summarized and represented schematically in Tables 1 and 2. These results are all verified by means of numerical illustrations of which some chosen ones are shown in the figures. We took a set of admissible parameter values: \(r=1.7, k=200, a_1=a_2=100, b_1=b_2=0.5, c_1=c_2 = 1.8, \delta _1 =0.82, \delta _2=0.62, e_1=0.8143, e_2=0.6250.\) For this set of parameter values, the system possessed an unique interior equilibrium point \(E_{*} = (169.1663564,55.36073780, 62.98120968).\) The system parameter r is the growth rate of the prey population. It plays a crucial role in regulating the dynamical behaviour of the proposed system. For this reason, we try to determine the system’s possible outcomes by varying this parameter within its feasible range. The interior equilibrium \(E_*\) is stable for \(r>r_c=1.320961640\) (cf. Figs. 4, 5 for local stability and Fig. 6 for global stability). The system (2.1) experiences a Hopf bifurcation when the parameter r crosses the critical value \(r_c\) from left to right, i.e., when \(r = r_c\), all the species coexist oscillating. Following the steps discussed in Subsect. 6.1, we have found the value of \(\Pi =1.042431405>0,\) which indicates that the obtained Hopf bifurcation is a subcritical bifurcation (cf. Fig. 7).

It is observed that, if the interference coefficient \(b_1\) (interference effect on the first predator due to the presence of the second predator) increases it stabilizes the system for \(b_1=0.7,\) while it is unstable at \(b_1=0.6.\) When the parameter \(b_1\) exceeds its value 20, the first predator population disappears from the system. Similarly, the interference on the second predator due to the presence of first predator, parameterized by \(b_2\) also plays an important role to stabilize the system. If the interference coefficient \(b_2\) increases it stabilizes the system for \(b_2=0.6,\) while it is unstable at \(b_2=0.5.\) It also regulates the existence of second predator in the system. As the parameter \(b_2\) exceeds 20.9, the second predator population gets extinguished.

Analogously, if the parameter \(\delta _1,\) denoting the death rate of the first predator increases then the size of the first predator decreases as well as the second predator population increases. If \(\delta _1\) decreases, the first predator population increases and second predator population decreases. If the death rate \(\delta _1\) is gradually increased to a certain level the first predator population goes to extinction. A similar result is observed for the case of the second predator’s death rate. The above observations ensure that the model under consideration is consistent with biological  observations (Figures are not reported here).

Fig. 1
figure 1

2D view of Hopf bifurcation around the interior equilibrium \(E_{*}\) of the system (2.1) with parameter values: \(r= 1.37 > r_{c} = 1.320961640, k = 200, a_1 = 100, a_2= 100, b_1 = 0.5, b_2 = 0.5; c_1 = 1.8, c_2 = 1.8, \delta _1 = 0.82, \delta _2 = 0.62, e_1 = 0.8143, e_2 = 0.6250\)

Full size image
Fig. 2
figure 2

Limit cycle behaviour of the dynamical system at \(E_{*}\) with the same parameter values used for Fig. 1

Full size image
Fig. 3
figure 3

Bifurcation diagram for all the populations with r as the bifurcating parameter around the interior equilibrium \(E_{*}\) of the system (2.1)

Full size image
Fig. 4
figure 4

2D view of Local asymptotic stability of the system (2.1) around the interior equilibrium \(E_{*}\) of the system (2.1) with parameter values: \(r= 1.47 > r_{c} = 1.320961640, k = 200, a_1 = 100, a_2= 100, b_1 = 0.5, b_2 = 0.5; c_1 = 1.8, c_2 = 1.8, \delta _1 = 0.82, \delta _2 = 0.62, e_1 = 0.8143, e_2 = 0.6250\)

Full size image
Fig. 5
figure 5

3D view of local asymptotic stability of the dynamical system at \(E_{*}\) with the same parameter values used for Fig. 4

Full size image
Fig. 6
figure 6

Solution plots with different starting points converge to the interior equilibrium point \(E_{*}=(169.1663564,55.36073780, 62.98120968),\) showing that the system (2.1) is global asymptotic stable. Here the same set of parameter values is used for Fig. 4 except \(r=1.29\)

Full size image
Fig. 7
figure 7

Solution plots showing that the system (2.1) experiences subcritical Hopf bifurcation for \(r>r_{\text {sub}}.\) Here the set of parameter values used is mention in the last row of Table 2

Full size image

Concluding remarks

The problem described by the system (2.1) is well posed. The \(x_1,\) \(x_{2}\) and \(x_{3}\) axes are invariant under the flow of the system. To our knowledge this is the first attempt to study an ecological system with quasi-linear/bilinear growth of the prey population. Generally, researchers only studied biological model systems with logistic/linear growth of prey population. One of the important results is that the prey population becomes unbounded in absence of its admissible predator in the long run. But in the presence of predator the prey population can be bounded under suitable combinations of system parameters. As a consequence the total environmental population is bounded above (cf. Subsect. 3.3). Therefore, any solution starting in the interior of the first octant never leaves it. This mathematical fact is consistent with the biological interpretation of the system. Due to the inclusion of quasi-linear/bilinear growth of the prey population, the axial equilibrium point is driven away by the system, a fact which is rarely found in the modern research work on mathematical biology. Thus, the prey population alone cannot survive in stable condition without the predator populations. Only the mutual interference between the predators, which are parameterized by \(b_{1}\) and \(b_{2}\) can alone stabilize the prey–predator interactions even when a quasi-linear/bilinear intrinsic growth rate of prey population is considered in the proposed mathematical model. These parameters contribute in stabilizing prey–predator interactions when only linear intrinsic growth rate is considered in some mathematical models (cf. Dimitrov and Kojouharov (2005)). There exist a balance between the predator’s need for food and its saturation level. In this case a periodic behaviour is expected. This behaviour is neutrally stable but relatively unstable. A small change in the parameters (caused by environmental changes for instances) forces the system to stabilize around the interior equilibrium or to oscillate indefinitely around it (by going away from it, which causes collapse of the system or breaks the coexistence of the population). Representative numerical simulations of this case are shown in Figs. 1, 2 and 3, which support our analytical findings (cf. Theorems 5.2 and 6.1). We have also established the sufficient conditions for the global stability of the coexistence equilibrium (cf. Figs. 5, 6).