SpringerLink
Log in

Lump and lump-soliton solutions to the \((2+1)\)-dimensional Ito equation

  • Published:
Analysis and Mathematical Physics Aims and scope Submit manuscript

Abstract

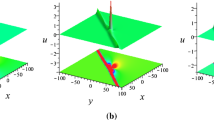
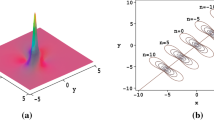
Based on the Hirota bilinear form of the \((2+1)\)-dimensional Ito equation, one class of lump solutions and two classes of interaction solutions between lumps and line solitons are generated through analysis and symbolic computations with Maple. Analyticity is naturally guaranteed for the presented lump and interaction solutions, and the interaction solutions reduce to lumps (or line solitons) while the hyperbolic-cosine (or the quadratic function) disappears. Three-dimensional plots and contour plots are made for two specific examples of the resulting interaction solutions.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
EUR 32.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or Ebook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price includes VAT (Germany)

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2

Similar content being viewed by others

References

  1. Hirota, R.: The Direct Method in Soliton Theory. Cambridge University Press, New York (2004)

    Book  MATH  Google Scholar 

  2. Freeman, N.C., Nimmo, J.J.C.: Soliton solutions of the Korteweg–de Vries and Kadomtsev–Petviashvili equations: the Wronskian technique. Phys. Lett. A 95(1), 1–3 (1983)

    Article  MathSciNet  MATH  Google Scholar 

  3. Ma, W.X., You, Y.: Solving the Korteweg–de Vries equation by its bilinear form: Wronskian solutions. Trans. Am. Math. Soc. 357(5), 1753–1778 (2005)

    Article  MathSciNet  MATH  Google Scholar 

  4. Ma, W.X.: Wronskian solutions to integrable equations. Discrete Contin. Dyn. Syst. Suppl, 506–515 (2009)

    MathSciNet  MATH  Google Scholar 

  5. Wazwaz, A.-M., El-Tantawy, S.A.: New (3 + 1)-dimensional equations of Burgers type and Sharma–Tasso–Olver type: multiple-soliton solutions. Nonlinear Dyn. 87(4), 2457–2461 (2017)

    Article  MathSciNet  MATH  Google Scholar 

  6. Satsuma, J., Ablowitz, M.J.: Two-dimensional lumps in nonlinear dispersive systems. J. Math. Phys. 20(7), 1496–1503 (1979)

    Article  MathSciNet  MATH  Google Scholar 

  7. Ablowitz, M.J., Clarkson, P.A.: Solitons, Nonlinear Evolution Equations and Inverse Scattering. Cambridge University Press, Cambridge (1991)

    Book  MATH  Google Scholar 

  8. Caudrey, P.J.: Memories of Hirota’s method: application to the reduced Maxwell–Bloch system in the early 1970s. Philos. Trans. R. Soc. A 369(1939), 1215–1227 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  9. Ma, W.X.: Lump solutions to the Kadomtsev–Petviashvili equation. Phys. Lett. A 379(36), 1975–1978 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  10. Manakov, S.V., Zakharov, V.E., Bordag, L.A., Matveev, V.B.: Two-dimensional solitons of the Kadomtsev–Petviashvili equation and their interaction. Phys. Lett. A 63(3), 205–206 (1977)

    Article  Google Scholar 

  11. Kaup, D.J.: The lump solutions and the Bäcklund transformation for the three-dimensional three-wave resonant interaction. J. Math. Phys. 22(6), 1176–1181 (1981)

    Article  MathSciNet  MATH  Google Scholar 

  12. Gilson, C.R., Nimmo, J.J.C.: Lump solutions of the BKP equation. Phys. Lett. A 147(8–9), 472–476 (1990)

    Article  MathSciNet  Google Scholar 

  13. Yang, J.Y., Ma, W.X.: Lump solutions of the BKP equation by symbolic computation. Int. J. Mod. Phys. B 30(28–29), 1640028 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  14. Imai, K.: Dromion and lump solutions of the Ishimori-I equation. Prog. Theor. Phys. 98(5), 1013–1023 (1997)

    Article  Google Scholar 

  15. Ma, W.X., You, Y.: Rational solutions of the Toda lattice equation in Casoratian form. Chaos Solitons Fract. 22(2), 395–406 (2004)

    Article  MathSciNet  MATH  Google Scholar 

  16. Ankiewicz, A., Kedziora, D.J., Akhmediev, N.: Rogue wave triplets. Phys. Lett. A 375(28–29), 2782–2785 (2011)

    Article  MATH  Google Scholar 

  17. Gaillard, P.: Rational solutions to the KPI equation and multi rogue waves. Ann. Phys. 367, 1–5 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  18. Chakravarty, S., Kodama, Y.: Line-soliton solutions of the KP equation. In: Nonlinear and Modern Mathematical Physics, AIP Conference Proceedings, 1212, pp. 312–341. American Institute of Physics, Melville, NY (2010)

  19. Aslan, İ.: Rational and multi-wave solutions to some nonlinear physical models. Rom. J. Phys. 58(7–8), 893–903 (2013)

    MathSciNet  Google Scholar 

  20. Zhang, Y., Ma, W.X.: Rational solutions to a KdV-like equation. Appl. Math. Comput. 256, 252–256 (2015)

    MathSciNet  MATH  Google Scholar 

  21. Zhang, Y.F., Ma, W.X.: A study on rational solutions to a KP-like equation. Z. Naturforsch. A 70(4), 263–268 (2015)

    Article  Google Scholar 

  22. Zhang, Y., Dong, H.H., Zhang, X.E., Yang, H.W.: Rational solutions and lump solutions to the generalized (3 + 1)-dimensional shallow water-like equation. Comput. Math. Appl. 73(2), 246–252 (2017)

    Article  MathSciNet  MATH  Google Scholar 

  23. Ma, W.X., Qin, Z.Y., Lü, X.: Lump solutions to dimensionally reduced p-gKP and p-gBKP equations. Nonlinear Dyn. 84(2), 923–931 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  24. Yu, J.P., Sun, Y.L.: Lump solutions to dimensionally reduced Kadomtsev–Petviashvili-like equations. Nonlinear Dyn. 87(2), 1405–1412 (2017)

    Article  MathSciNet  Google Scholar 

  25. Ito, M.: An extension of nonlinear evolution equations of the K-dV (mK-dV) type to higher orders. J. Phys. Soc. Jpn. 49(2), 771–778 (1980)

    Article  MathSciNet  MATH  Google Scholar 

  26. Wazwaz, A.-M.: Multiple-soliton solutions for the generalized (1 + 1)-dimensional and the generalized (2 + 1)-dimensional Ito equations. Appl. Math. Comput. 202, 840–849 (2008)

    MathSciNet  MATH  Google Scholar 

  27. Tang, Y.N., Tao, S.Q., Qing, G.: Lump solitons and the interaction phenomena of them for two classes of nonlinear evolution equations. Comput. Math. Appl. 72(9), 2334–2342 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  28. Gilson, C., Lambert, F., Nimmo, J., Willox, R.: On the combinatorics of the Hirota D-operators. Proc. R. Soc. Lond. Ser. A 452(1945), 223–234 (1996)

    Article  MathSciNet  MATH  Google Scholar 

  29. Ma, W.X.: Bilinear equations, Bell polynomials and linear superposition principle. J. Phys. Conf. Ser. 411, 012021 (2013)

    Article  Google Scholar 

  30. Dorizzi, B., Grammaticos, B., Ramani, A., Winternitz, P.: Are all the equations of the Kadomtsev–Petviashvili hierarchy integrable? J. Math. Phys. 27(12), 2848–2852 (1986)

    Article  MathSciNet  MATH  Google Scholar 

  31. Konopelchenko, B., Strampp, W.: The AKNS hierarchy as symmetry constraint of the KP hierarchy. Inverse Probl. 7(2), L17–L24 (1991)

    Article  MathSciNet  MATH  Google Scholar 

  32. Li, X.Y., Zhao, Q.L., Li, Y.X., Dong, H.H.: Binary Bargmann symmetry constraint associated with 3 \(\times \) 3 discrete matrix spectral problem. J. Nonlinear Sci. Appl. 8(5), 496–506 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  33. Dong, H.H., Zhang, Y., Zhang, X.E.: The new integrable symplectic map and the symmetry of integrable nonlinear lattice equation. Commun. Nonlinear Sci. Numer. Simul. 36, 354–365 (2016)

    Article  MathSciNet  Google Scholar 

  34. Ma, W.X.: Generalized bilinear differential equations. Stud. Nonlinear Sci. 2(4), 140–144 (2011)

    Google Scholar 

  35. Ma, W.X.: Bilinear equations and resonant solutions characterized by Bell polynomials. Rep. Math. Phys. 72(1), 41–56 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  36. Ma, W.X.: Trilinear equations, Bell polynomials, and resonant solutions. Front. Math. China 8(5), 1139–1156 (2013)

    Article  MathSciNet  MATH  Google Scholar 

Download references

Acknowledgements

The work was supported in part by a university grant XKY2016112 from Xuzhou Institute of Technology, NSFC under the Grants 11371326, 11301331, and 11371086, NSF under the Grant DMS-1664561, and the Distinguished Professorships by Shanghai University of Electric Power and Shanghai Second Polytechnic University.

Author information

Authors and Affiliations

  1. School of Mathematical and Physical Sciences, Xuzhou Institute of Technology, Xuzhou, 221111, Jiangsu, People’s Republic of China

    **-Yun Yang

  2. Department of Mathematics and Statistics, University of South Florida, Tampa, FL, 33620, USA

    Wen-**u Ma

  3. College of Mathematics and Systems Science, Shandong University of Science and Technology, Qingdao, 266590, Shandong, People’s Republic of China

    Wen-**u Ma

  4. International Institute for Symmetry Analysis and Mathematical Modelling, Department of Mathematical Sciences, North-West University Mafikeng Campus, Private Bag X2046, Mmabatho, 2735, South Africa

    Wen-**u Ma

  5. School of Mathematics and Key Lab for Nonlinear Mathematical Models and Methods, Fudan University, Shanghai, 200433, People’s Republic of China

    Zhenyun Qin

  6. Department of Mathematics, Zhejiang Normal University, **hua, 321004, Zhejiang, People’s Republic of China

    Wen-**u Ma

  7. College of Mathematics and Physics, Shanghai University of Electric Power, Shanghai, 200090, People’s Republic of China

    Wen-**u Ma

Authors
  1. **-Yun Yang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Wen-**u Ma
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Zhenyun Qin
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Wen-**u Ma.

Ethics declarations

Conflict of interest

The authors declare that they have no conflict of interest.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Yang, JY., Ma, WX. & Qin, Z. Lump and lump-soliton solutions to the \((2+1)\)-dimensional Ito equation. Anal.Math.Phys. 8, 427–436 (2018). https://doi.org/10.1007/s13324-017-0181-9

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s13324-017-0181-9

Keywords

Mathematics Subject Classification

Search

Navigation