SpringerLink
Log in

Vortex-induced vibration of a linearly sprung cylinder with an internal rotational nonlinear energy sink in turbulent flow

  • Original Paper
  • Published:
Nonlinear Dynamics Aims and scope Submit manuscript

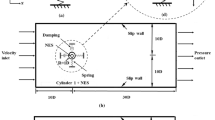
Abstract

We computationally investigate flow past a three-dimensional linearly sprung cylinder undergoing vortex-induced vibration (VIV) transverse to the free stream and equipped with an internal dissipative rotational nonlinear energy sink (NES). The rotational NES consists of a line mass allowed to rotate at constant radius about the cylinder axis, with linearly damped rotational motion. We consider a value of the Reynolds number (\(\textit{Re}=10{,}000\), based on the cylinder diameter and free-stream velocity) at which flow past a linearly sprung cylinder with no NES is three-dimensional and fully turbulent. For this \(\textit{Re}\) value, we show that the rotational NES is capable of passively harnessing a substantial amount of kinetic energy from the rectilinear motion of the cylinder, leading to a significant suppression of cylinder oscillation and a nearly twofold reduction in drag. The results presented herein are of practical significance since they demonstrate a novel passive mechanism for VIV suppression and drag reduction in a high-\(\textit{Re}\) bluff body flow, and lay down the groundwork for designing nonlinear energy sinks with a view to enhancing the performance of VIV-induced power generation in marine currents.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9

Similar content being viewed by others

References

  1. Williamson, C.H.K., Govardhan, R.: Vortex-induced vibrations. Annu. Rev. Fluid Mech. 36, 413–455 (2004)

    MathSciNet  MATH  Google Scholar 

  2. Païdoussis, M.P., Price, S.J., De Langre, E.: Fluid–Structure Interactions: Cross-Flow-Induced Instabilities. Cambridge University Press, Cambridge (2010)

    MATH  Google Scholar 

  3. Owen, J.C., Bearman, P.W., Szewczyk, A.A.: Passive control of VIV with drag reduction. J. Fluids Struct. 15, 597–605 (2001)

    Google Scholar 

  4. Bernitsas, M.M., Raghavan, K.: Reduction/suppression of VIV of circular cylinders through roughness distribution at \(8\times 10^3 < Re < 1.5 \times 10^5\). In: ASME 2008 27th International Conference on Offshore Mechanics and Arctic Engineering, pp. 1001–1005 (2008)

  5. Assi, G.R.S., Bearman, P.W., Kitney, N., Tognarelli, M.A.: Suppression of wake-induced vibration of tandem cylinders with free-to-rotate control plates. J. Fluids Struct. 26, 1045–1057 (2010)

    Google Scholar 

  6. Bernitsas, M.M., Raghavan, K., Ben-Simon, Y., Garcia, E.M.: VIVACE (Vortex Induced Vibration Aquatic Clean Energy): a new concept in generation of clean and renewable energy from fluid flow. J. Offshore Mech. Arct. Eng. 130, 041101 (2008)

    Google Scholar 

  7. Bernitsas, M.M., Ben-Simon, Y., Raghavan, K., Garcia, E.M.: The VIVACE converter: model tests at high dam** and Reynolds number around \(10^5\). J. Offshore Mech. Arct. Eng. 131, 011102 (2009)

    Google Scholar 

  8. Barrero-Gil, A., Pindado, S., Avila, S.: Extracting energy from vortex-induced vibrations: a parametric study. Appl. Math. Modell. 36, 3153–3160 (2012)

    Google Scholar 

  9. Grouthier, C., Michelin, S., Bourguet, R., Modarres-Sadeghi, Y., De Langre, E.: On the efficiency of energy harvesting using vortex-induced vibrations of cables. J. Fluids Struct. 49, 427–440 (2014)

    Google Scholar 

  10. Ng, K.W., Lam, W.H., Ng, K.C.: 2002–2012: 10 years of research progress in horizontal-axis marine current turbines. Energies 6, 1497–1526 (2013)

    Google Scholar 

  11. Vakakis, A.F., Gendelman, O.V., Bergman, L.A., McFarland, D.M., Kerschen, G., Lee, Y.S.: Nonlinear Targeted Energy Transfer in Mechanical and Structural Systems. Springer, New York (2008)

    MATH  Google Scholar 

  12. Gendelman, O.V., Vakakis, A.F., Bergman, L.A., McFarland, D.M.: Asymptotic analysis of passive nonlinear suppression of aeroelastic instabilities of a rigid wing in subsonic flow. SIAM J. Appl. Math. 70, 1655–1677 (2010)

    MathSciNet  MATH  Google Scholar 

  13. Nucera, F., Iacono, F.L., McFarland, D.M., Bergman, L.A., Vakakis, A.F.: Application of broadband nonlinear targeted energy transfers for seismic mitigation of a shear frame: experimental results. J. Sound Vib. 313, 57–76 (2008)

    Google Scholar 

  14. Wierschem, N.E., Luo, J., Hubbard, S., Fahnestock, L.A., Spencer, B.F., Vakakis, A.F., Bergman, L.A.: Experimental testing of a large 9-story structure equipped with multiple nonlinear energy sinks subjected to an impulsive loading. In: Structures Congress 2013: Bridging Your Passion with Your Profession, pp. 2241–2252 (2013)

  15. Bellet, R., Cochelin, B., Herzog, P., Mattei, P.O.: Experimental study of targeted energy transfer from an acoustic system to a nonlinear membrane absorber. J. Sound Vib. 329, 2768–2791 (2010)

    Google Scholar 

  16. Quinn, D.D., Triplett, A.L., Vakakis, A.F., Bergman, L.A.: Energy harvesting from impulsive loads using intentional essential nonlinearities. J. Vib. Acoust. 133, 011004 (2011)

    Google Scholar 

  17. Ahmadabadi, Z.N., Khadem, S.E.: Nonlinear vibration control and energy harvesting of a beam using a nonlinear energy sink and a piezoelectric device. J. Sound Vib. 333, 4444–4457 (2014)

    Google Scholar 

  18. Zhang, Y., Tang, L., Liu, K.: Piezoelectric energy harvesting with a nonlinear energy sink. J. Intell. Mater. Syst. Struct. 28, 307–322 (2017)

    Google Scholar 

  19. Fang, Z.W., Zhang, Y.W., Li, X., Ding, H., Chen, L.Q.: Integration of a nonlinear energy sink and a giant magnetostrictive energy harvester. J. Sound Vib. 391, 35–49 (2017)

    Google Scholar 

  20. Remick, K., Quinn, D.D., McFarland, D.M., Bergman, L., Vakakis, A.: High-frequency vibration energy harvesting from impulsive excitation utilizing intentional dynamic instability caused by strong nonlinearity. J. Sound Vib. 370, 259–279 (2016)

    Google Scholar 

  21. Mann, B.P., Sims, N.D.: Energy harvesting from the nonlinear oscillations of magnetic levitation. J. Sound Vib. 319, 515–530 (2009)

    Google Scholar 

  22. Kremer, D., Liu, K.: A nonlinear energy sink with an energy harvester: transient responses. J. Sound Vib. 333, 4859–4880 (2014)

    Google Scholar 

  23. Quinn, D.D., Triplett, A.L., Bergman, L.A., Vakakis, A.F.: Comparing linear and essentially nonlinear vibration-based energy harvesting. J. Vib. Acoust. 133, 011001 (2011)

    Google Scholar 

  24. Tumkur, R.K.R., Calderer, R., Masud, A., Pearlstein, A.J., Bergman, L.A., Vakakis, A.F.: Computational study of vortex-induced vibration of a sprung rigid circular cylinder with a strongly nonlinear internal attachment. J. Fluids Struct. 40, 214–232 (2013)

    Google Scholar 

  25. Tumkur, R.K.R., Domany, E., Gendelman, O.V., Masud, A., Bergman, L.A., Vakakis, A.F.: Reduced-order model for laminar vortex-induced vibration of a rigid circular cylinder with an internal nonlinear absorber. Commun. Nonlinear Sci. Numer. Simul. 18, 1916–1930 (2013)

    MathSciNet  MATH  Google Scholar 

  26. Tumkur, R.K.R., Pearlstein, A.J., Masud, A., Gendelman, O.V., Blanchard, A.B., Bergman, L.A., Vakakis, A.F.: Effect of an internal nonlinear rotational dissipative element on vortex shedding and vortex-induced vibration of a sprung circular cylinder. J. Fluid Mech. 828, 196–235 (2017)

    MathSciNet  MATH  Google Scholar 

  27. Blanchard, A.B., Gendelman, O.V., Bergman, L.A., Vakakis, A.F.: Capture into slow-invariant-manifold in the fluid–structure dynamics of a sprung cylinder with a nonlinear rotator. J. Fluids Struct. 63, 155–173 (2016)

    Google Scholar 

  28. Blanchard, A.B., Bergman, L.A., Vakakis, A.F., Pearlstein, A.J.: Coexistence of multiple long-time solutions for two-dimensional laminar flow past a linearly-sprung circular cylinder with a rotational nonlinear energy sink. Phys. Rev. Fluids (2018, submitted)

  29. Mehmood, A., Nayfeh, A.H., Hajj, M.R.: Effects of a non-linear energy sink (NES) on vortex-induced vibrations of a circular cylinder. Nonlinear Dyn. 77, 667–680 (2014)

    Google Scholar 

  30. Dai, H.L., Abdelkefi, A., Wang, L.: Vortex-induced vibrations mitigation through a nonlinear energy sink. Commun. Nonlinear Sci. Numer. Simul. 42, 22–36 (2017)

    Google Scholar 

  31. Dongyang, C., Abbas, L.K., Guo**, W., **%2CW&author=**aoting%2CE&author=Marzocca%2CP"> Google Scholar 

  32. Sigalov, G., Gendelman, O.V., Al-Shudeifat, M.A., Manevitch, L.I., Vakakis, A.F., Bergman, L.A.: Resonance captures and targeted energy transfers in an inertially-coupled rotational nonlinear energy sink. Nonlinear Dyn. 69, 1693–1704 (2012)

    MathSciNet  Google Scholar 

  33. Roshko, A.: On the development of turbulent wakes from vortex streets. NACA TN 2913 (1954)

  34. Blanchard, A., Bergman, L.A., Vakakis, A.F.: Targeted energy transfer in laminar vortex-induced vibration of a sprung cylinder with a nonlinear dissipative rotator. Phys. D Nonlinear Phenom. 350, 26–44 (2017)

    MathSciNet  Google Scholar 

  35. Fischer, P.F., Lottes, J.W., Kerkemeier, S.G.: nek5000 Web page (2008). http://nek5000.mcs.anl.gov

  36. Prasanth, T.K., Mittal, S.: Effect of blockage on free vibration of a circular cylinder at low \(Re\). Int. J. Numer. Methods in Fluids 58, 1063–1080 (2008)

    MATH  Google Scholar 

  37. Braza, M., Faghani, D., Persillon, H.: Successive stages and the role of natural vortex dislocations in three-dimensional wake transition. J. Fluid Mech. 439, 1–41 (2001)

    MATH  Google Scholar 

  38. Dong, S., Karniadakis, G.E.: DNS of flow past a stationary and oscillating cylinder at \(Re=10000\). J. Fluids Struct. 20, 519–531 (2005)

    Google Scholar 

  39. Pontaza, J.P., Chen, H.C.: Three-dimensional numerical simulations of circular cylinders undergoing two degree-of-freedom vortex-induced vibrations. J. Offshore Mech. Arct. Eng. 129, 158–164 (2007)

    Google Scholar 

  40. Fischer, P., Mullen, J.: Filter-based stabilization of spectral element methods. C. R. l’Acad. Sci. Ser. I Math. 332, 265–270 (2001)

    MathSciNet  MATH  Google Scholar 

  41. Boyd, J.P.: Two comments on filtering (artificial viscosity) for Chebyshev and Legendre spectral and spectral element methods. J. Comput. Phys. 143, 283–288 (1998)

    MathSciNet  MATH  Google Scholar 

  42. Tumkur, R.K.R.: Modal interactions and targeted energy transfers in laminar vortex-induced vibrations of a rigid cylinder with strongly nonlinear internal attachments. Ph.D. thesis, University of Illinois at Urbana–Champaign (2014)

  43. Barton, D.A.W., Burrow, S.G., Clare, L.R.: Energy harvesting from vibrations with a nonlinear oscillator. J. Vib. Acoust. 132, 021009 (2010)

    Google Scholar 

  44. Leontini, J.S., Stewart, B.E., Thompson, M.C., Hourigan, K.: Wake state and energy transitions of an oscillating cylinder at low Reynolds number. Phys. Fluids 18, 067101 (2006)

    MathSciNet  MATH  Google Scholar 

  45. Nguyen, L.T.T., Temarel, P.: Numerical simulation of an oscillating cylinder in cross-flow at a Reynolds number of 10,000: forced and free oscillations. In: ASME 2014 33rd International Conference on Ocean, Offshore and Arctic Engineering, p. V002T08A022. American Society of Mechanical Engineers (2014)

  46. Jeong, J., Hussain, F.: On the identification of a vortex. J. Fluid Mech. 285, 69–94 (1995)

    MathSciNet  MATH  Google Scholar 

  47. Stansby, P.K., Slaouti, A.: Simulation of vortex shedding including blockage by the random-vortex and other methods. Int. J. Numer. Methods Fluids 17, 1003–1013 (1993)

    MATH  Google Scholar 

  48. Anagnostopoulos, P.: Numerical investigation of response and wake characteristics of a vortex-excited cylinder in a uniform stream. J. Fluids Struct. 8, 367–390 (1994)

    Google Scholar 

  49. Henderson, R.D.: Details of the drag curve near the onset of vortex shedding. Phys. Fluids 7, 2102–2104 (1995)

    Google Scholar 

  50. Shiels, D., Leonard, A., Roshko, A.: Flow-induced vibration of a circular cylinder at limiting structural parameters. J. Fluids Struct. 15, 3–21 (2001)

    Google Scholar 

  51. Fischer, P., Schmitt, M., Tomboulides, A.: Recent developments in spectral element simulations of moving-domain problems. In: Melnik, R., Makarov, R., Belair, J. (eds.) Recent Progress and Modern Challenges in Applied Mathematics. Modeling and Computational Science, pp. 213–244. Springer, New York (2017)

    MATH  Google Scholar 

  52. Bishop, R.E.D., Hassan, A.Y.: The lift and drag forces on a circular cylinder in a flowing fluid. Proc. R. Soc. Lond. A Math. Phys. Eng. Sci. 277, 32–50 (1964)

    Google Scholar 

  53. Gopalkrishnan, R.: Vortex-induced forces on oscillating bluff cylinders. Technical report, Woods Hole Oceanographic Institution, MA (1993)

  54. Norberg, C.: Fluctuating lift on a circular cylinder: review and new measurements. J. Fluids Struct. 17, 57–96 (2003)

    Google Scholar 

  55. Dong, S., Karniadakis, G.E., Ekmekci, A., Rockwell, D.: A combined direct numerical simulation-particle image velocimetry study of the turbulent near wake. J. Fluid Mech. 569, 185–207 (2006)

    MATH  Google Scholar 

Download references

Acknowledgements

The authors gratefully acknowledge use of the facilities at the Argonne National Laboratory. The first author acknowledges the Computational Science and Engineering Fellowship program at the University of Illinois at Urbana–Champaign. This work was supported in part by National Science Foundation Grant CMMI-1363231. Any opinion, findings, and conclusions or recommendations expressed in this work are those of the authors and do not necessarily reflect the views of the National Science Foundation.

Funding

This study was partially funded by National Science Foundation Grant CMMI-1363231. A. B. was partially supported by the Computational Science and Engineering Fellowship program at the University of Illinois at Urbana–Champaign.

Author information

Author notes

  1. Antoine Blanchard

    Present address: Massachusetts Institute of Technology, Cambridge, MA, 02139, USA

Authors and Affiliations

  1. Department of Aerospace Engineering, University of Illinois at Urbana–Champaign, Urbana, IL, 61801, USA

    Antoine Blanchard & Lawrence A. Bergman

  2. Department of Mechanical Science and Engineering, University of Illinois at Urbana–Champaign, Urbana, IL, 61801, USA

    Alexander F. Vakakis

Authors
  1. Antoine Blanchard
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Lawrence A. Bergman
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Alexander F. Vakakis
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Antoine Blanchard.

Ethics declarations

Conflict of interest

The authors declare that they have no conflict of interest.

Additional information

This work is dedicated to the memory of Prof. Ali H. Nayfeh, outstanding educator, respected teacher, admired scholar.

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Appendix: Validation of the computational approach

Appendix: Validation of the computational approach

The computational approach is validated in two steps. We first compute flow past a fixed cylinder and a linearly sprung cylinder with no NES at \(\textit{Re}=100\). At this Reynolds number, the flow is expected to be two-dimensional, laminar, and time periodic. For the linearly sprung case, we use parameters \(f_\mathrm {n}^*=0.167\) and \(m^*=10\) in order to facilitate comparison with previous results. Table 2 shows statistics computed with the 3-D mesh (with dimensions and number of elements given in Sect. 2.2) for the fixed and linearly sprung configurations. The statistics computed on the 3-D mesh are compared with values computed on the 2-D baseline mesh, as well as values reported in the literature for 2-D computations. The results in Table 2 validate the 3-D computational approach for nominally 2-D flows with and without mesh motion.

The next step is to validate the computational approach in a situation where the flow is 3-D and fully turbulent. Because our production runs are at \(\textit{Re}=10{,}000\), we choose that value for the convergence study as well. The amount of computational results available in the literature for transverse VIV at \(\textit{Re}=10{,}000\) is vanishingly small, so we decide to benchmark our code against results for flow past a fixed cylinder at that Reynolds number. The statistics reported in Table 3 show that the spectral element framework guarantees adequate robustness of the results with respect to the computational parameters.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Blanchard, A., Bergman, L.A. & Vakakis, A.F. Vortex-induced vibration of a linearly sprung cylinder with an internal rotational nonlinear energy sink in turbulent flow. Nonlinear Dyn 99, 593–609 (2020). https://doi.org/10.1007/s11071-019-04775-3

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11071-019-04775-3

Keywords

Search

Navigation