Effect of Reduced Mass on Two-Dimensional Compressible Flow Past Circular Cylinder

Abstract

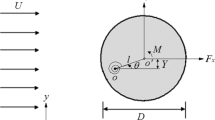
There are numerous experimental and numerical studies available on the Vortex-Induced Vibration (VIV) for 2D and 3D incompressible flow past bluff bodies (Sen et al in J Fluid Mech 620:89–119, 2009 [1]; Sharma et al in Phys Fluids, 2022 [2]). However, similar analysis is lacking for the case of high-speed compressible flows past bluff bodies. Here, we assess the effect of reduced mass on the unsteady two-dimensional (2D) VIV of the undamped elastically suspended circular cylinder constrained to move in the vertical y-direction only. We perform Direct Numerical Simulation (DNS) by solving the governing Navier–Stokes equation (NSE) by using high-accurate schemes for spatial discretization and time integration. The computational study has been performed for Reynolds number (based on the diameter of the circular cylinder) of $150$ and free-stream Mach number of $0.5$ for three cases of reduced mass $m_{*} = 2m/\rho_{\infty } D^{2} = 1.0, 5.0, {\text{and}} 10,$ where $m$ and $\rho_{\infty }$ are the mass of cylinder per unit length and free-stream density of the fluid, respectively. We analyze time-dependent variations in coefficient of lift ($C_{l}$), coefficient of drag ($C_{d}$), displacement $y_{CM}$ of the cylinder, and variation of ($C_{l}$) with ($C_{d}$) for a wide range of the reduced velocity ($U_{*} = U_{\infty } / f_{N} D$), to determine its response. Here, $k_{y}$ and $f_{N} = 1/2\pi \sqrt {k_{y} /m}$ are the spring constant and the natural frequency of the vibration of the cylinder, respectively. Based on the results plotted, we have noted interesting patterns in the time history of $C_{l}$, $C_{d} ,$ and $y_{CM}$. . For lesser values of the reduced velocity ($U_{*}$), presence of multiple modes in the response is noted, while at a higher value of $U_{*}$, presence of super-harmonics are noted. The maximum amplitude of the response is noted for some intermediate value of the reduced velocity $U_{*}$. We also plot pressure and vorticity contours for the computed cases for visualization of the vorticity patterns and propagation of resulting acoustic waves due to the influence of compressibility whose details will be explained in the presented article.