Abstract
Our main goal is to investigate whether the infinitary rules for the quantifiers endorsed by Elia Zardini in a recent paper are plausible. First, we will argue that they are problematic in several ways, especially due to their infinitary features. Secondly, we will show that even if these worries are somehow dealt with, there is another serious issue with them. They produce a truth-theoretic paradox that does not involve the structural rules of contraction.




Similar content being viewed by others
Notes
A similar distinction is available if the rule of structural weakening is rejected (or if both rules are rejected).
The terminology varies, though. On occasions, the labels ‘extensional/intensional’ or ‘lattice-/group-theoretic’ are used.
Multisets are basically sets with repetitions. That is, a multiset is just like a set except for the fact that it is sensitive to the different occurrences of a member. For example, the multiset with members a, a, and b is not the same as the multiset with members a and b. Obviously, we need to use collections that are sensitive to the occurrences of formulas because we do not want to take for granted that contraction holds. Also, since multisets are insensitive to the order in which its members occur, the structural rules of exchange are assumed to hold.
The name M A L L and the notation for the logical vocabulary is taken from [5].
The idea that quantifiers obeying these rules should be identified as the additive quantifiers (or, at least, that there is an additive—rather than a multiplicative—flavor to them) has been endorsed on several occasions (e.g., in [5, p. 509], in [15, p. 316], in [16, p. 304], and even in [21, p. 509-512]). The identification is likely grounded in the algebraic treatment of these quantifiers, where the universal quantifier is characterized as the infimum in a lattice of values and the existential quantifier as the supremum, thus mimicking additive conjunction and additive disjunction, respectively. While this can be regarded as a compelling reason to support the identification, the matter is not entirely obvious. In fact, below (see footnote 13) we will point to one way in which someone might reject the identification that strikes us at least as worth mentioning.
This, we reckon, is particularly troubling for those concerned with the concept of truth. If truth is to serve as a device that (perhaps among other things) allows us to express restricted universal and existential quantifications, then we should have the appropriate resources in our theory for truth to fulfill this requirement.
For example, [11] introduces multiplicative quantifiers for many-valued logic. And [15] and [23] provide philosophical arguments to show how interesting non-extensional quantifiers can be. In particular, [23] argues that in the case of the universal quantifier the additive/multiplicative distinction can be more or less equated with the natural language distinction between ‘anything’ and ‘everything’.
In these weakening rules, Γ(Δ)is properly included in Γ′(Δ′),where inclusion between multisets is understood in the following way: Γis a sub-multiset of Γ′if and only if every member of Γis a member of Γ′and occurs at least as many times in Γ′.In particular, there is nothing preventing an application of the rules where, say, Γis a finite multiset and Γ′is an infinite multiset.
We are using ‘ Γ ⇔ Δ’ as an abbreviation of ‘ Γ ⇒ Δ and Δ ⇒ Γ’.
It is worth noticing that, in virtue of the compactness property, these contraction rules, as well as the weakening rules introduced above, are equivalent over classical logic to the standard rules of contraction and weakening, which only allow us to contract or weaken on a single formula per application.
The reader might be skeptical of the use of infinitary structural rules in the proof of the equivalence between ∃Z and ∃A. But if we are already on board with the idea of infinitary rules for the quantifiers, it seems unproblematic to endorse structural rules like these. In any case, we will see below that there are independent reasons to reject Zardini’s quantifiers, so we need not worry at this point about other infinitary rules.
See [16] for a criticism along these lines.
To further elaborate on the idea hinted at in footnote 5, we should note that it is not entirely out of the question for someone like Zardini to endorse the claim that both the additive and the multiplicative quantifiers should obey infinitary rules. In fact, if infinitary rules are taken to be unproblematic, L ∃? seems to be a generalization of L ⊔ in exactly the same way as L ∃Z is a generalization of L ⊕. However, neither Zardini nor, as far as we know, anyone else has taken this route, so there is no need to discuss it here.
We are very grateful to an anonymous referee for suggesting this way of presenting the argument.
In case the reader is wondering about the interaction of this quantifier with the other ones, this will ultimately depend on the right-hand side rule for ∃? (which, presumably, should be the same as that for ∃A). But even if we leave this unspecified, it can be shown that, assuming weakening, ∃? x ϕ ⇒∃Z x ϕ is derivable, and even without weakening, ∃? x ϕ ⇒∃A x ϕ is derivable.
A transparent truth theory is, roughly, a theory where for any formula ϕ, ϕ and ϕ is true are everywhere intersubstitutable. In the contextof a sequent calculus this amounts to the idea that if Γ ⇒ Δis derivable and Γ′⇒ Δ′is obtained from Γ ⇒ Δby replacing (possibly within a formula) ϕ for ϕ is true (or vice versa), then Γ′⇒ Δ′is derivable too.
Recall that a theory is ω-inconsistent if it proves ⇒∃x ϕ and it also proves \(\phi (\overline {n})\Rightarrow \)for each n.In this context, we could equivalently say—using infinitary sequents—that a theory is ω-inconsistentif it proves ∃x ϕ ⇒and also \(\Rightarrow \phi (\overline {0}), \phi (\overline {1}), \phi (\overline {2}),...\). Bacon makes a distinction between strongly ω-inconsistenttheories and weakly ω-inconsistenttheories. However, for our purposes this distinction will be unnecessary.From a semantic point of view, the models of a consistent but ω-inconsistentarithmetical theory cannot be standard: each model of the theory contains in itsdomain non-standard numbers. In other words, among other undesirable consequences, ω-inconsistenttheories disrupt the intended ontology of the basearithmetical theory (see [2] and [8]). The issue of ω-inconsistencyhas not received much attention in the literature on substructuralapproaches to the truth-theoretic paradoxes. One exceptionis [4], where Andreas Fjellstad shows how to prove the ω-inconsistencyof certain theories without assuming the transitivity of the corresponding consequencerelations. At certain points in the proof of Theorem 1 below we rely on some of Fjellstad’sinsights.
We assume familiarity with the dot notation and with the overlining notation. The reader can look at [7] for the details.
Despite appearances, this is not too demanding. There are extremely weak arithmetical theories satisfying this requirement, such as Baby Arithmetic (see e.g. [19]).
Typically, the identity predicate also requires the following additional rule:
$$=-\text{pop}\frac{\Gamma, t=t\Rightarrow\Delta}{\Gamma\Rightarrow\Delta} $$However, as an anonymous referee rightly pointed out, this rule is admissible through the application of the T e r m s rule (see below) and C u t.
Another rule that comes to mind for ⊥ is this:
$$\bot-\text{drop} \frac{\Gamma\Rightarrow\bot, \Delta}{\Gamma\Rightarrow\Delta} $$In \(IKT^{\omega }_{+}\) ⊥-drop and L ⊥ are interderivable, so we can use either one. For definiteness, we will stick to L ⊥.
And similarly for R ∀Z. If \(\Gamma \Rightarrow \phi (\overline {n}), \Delta \) is derivable for each n, using C u t and R = , it follows that for each closed term t, Γ ⇒ ϕ(t), Δ is also derivable.
In what follows, for the sake of simplicity, we will be sloppy with the substitution of identicals. Observe that what the rules L = and R = allow us to do—with the help of the rules for f, T e r m s, and C u t—is to substitute identical terms. So, instead of explicitly applying these rules, we will directly substitute identical terms in the derivations and we will mark the steps at which we do this with the label “Subs of id”.
In this respect, R ∃Z is similar to the more well-known (see [20], p. 77):
$$\text{R}\exists^{*}\frac{\Gamma \Rightarrow\exists^{*} x A(x), A(t), \Delta} {\Gamma \Rightarrow \exists^{*} x A(x), \Delta } $$in that they both can be used to provide a sequent calculus where contraction is absorbed (pending the appropriate choice of the other rule for the existential quantifier and the rest of the logical rules). Moreover, in the proof of ω-inconsistency developed by Fjellstad in [4], it is precisely this kind rule that is used (actually, because Fjellstad’s proof is given in terms of the universal quantifier, what is needed is a dual rule for introducing the universal quantifier on the left-hand side of the sequent arrow, but this is not important).
Moreover, the referee also points out that a quick inspection of Fjellstad’s proof will reveal that for it to go through it is only required that the right-hand side rule of the quantifier employed admits contraction.
Another interesting question that might be posed is if the proof holds for the purely additive fragment of the language (i.e., the fragment with the additive quantifier and the additive conditional). The rules for the additive conditional (\(\sqsupset \)) are as follows:
$$\begin{array}{llll} \text{L}\sqsupset\frac{\Gamma\Rightarrow\phi, \Delta \qquad \Gamma, \psi\Rightarrow\Delta}{\Gamma, \phi\sqsupset\psi\Rightarrow\Delta} &\qquad \qquad \text{R}\sqsupset \frac{\Gamma, \phi\Rightarrow \Delta}{\Gamma\Rightarrow\phi\sqsupset\psi, \Delta}&\text{R}\sqsupset \frac{\Gamma\Rightarrow\psi, \Delta}{\Gamma\Rightarrow\phi\sqsupset\psi, \Delta} \end{array}$$With these rules, it is easy to check that the step from \(\Rightarrow \phi \sqsupset \exists ^{A}x\psi \) to \(\Rightarrow \exists ^{A}x(\phi \sqsupset \psi )\) is indeed valid (because L\(\sqsupset \) contracts the context). However, the interest of this is moot. As far as we know, no one has advocated a truth theory based on the additive conditional in the literature. Therefore, we will not explore this alternative.
As expected, for the additive quantifier the notion of ω-inconsistency is indeed different from the notion of plain inconsistency or triviality.
The situation is the same as that for non-classical theories of truth that include a non-standard negation. When studying paradoxes in a logic that is, say, paracomplete or paraconsistent, we assume that there is a sentence λ which is equivalent to (in the sense that it has the same value as) \(\neg Tr\ulcorner \lambda \urcorner \), where ¬ is the non-classical negation of the logic. In doing so, we are assuming a background syntax theory which proves that equivalence.
References
Bacon, A. (2013). Curry’s Paradox and ω-Inconsistency. Studia Logica, 101(1), 1–9.
Barrio, E. (2010). Theories of truth without standard models and Yablo’s sequences. Studia Logica, 96(3), 375–391.
Cobreros, P., Egré, P., Ripley, D., & van Rooij, R. (2013). Reaching transparent truth. Mind, 122(488), 841–866.
Fjellstad, A. (2016). Omega-inconsistency without cuts and nonstandard models. Australasian Journal of Logic, 13(5), 96–122.
French, R., & Ripley, D. (2015). Contractions of noncontractive consequence relations. The Review of Symbolic Logic, 8(3), 506–528.
Girard, J.Y. (1987). Linear logic. Theoretical Computer Science, 50(1), 1–101.
Halbach, V. (2011). Axiomatic theories of truth. Cambridge: Cambridge University Press.
Leitgeb, H. (2007). What theories of truth should be like (but cannot be). Philosophy Compass, 2(2), 276–290.
Mares, E., & Paoli, F. (2014). Logical consequence and the paradoxes. Journal of Philosophical Logic, 43(2-3), 439–469.
McGee, V. (1985). How truthlike can a predicate be? A negative result. Journal of Philosophical Logic, 14, 399–410.
Montagna, F. (2004). Storage operators and multiplicative quantifiers in many-valued logics. Journal of Logic and Computation, 14, 299–322.
Negri, S., & von Plato, J. (1998). Cut elimination in the presence of axioms. Bulletin of Symbolic Logic, 4, 418–435.
Negri, S. (2003). Contraction-free sequent calculi for geometric theories with an application to Barr’ theorem. Archive for Mathematical Logic, 42, 389–401.
Paoli, F. (2002). Substructural logics: a primer. Dordrecht: Kluwer.
Paoli, F. (2005). The ambiguity of quantifiers. Philosophical Studies, 124(3), 313–330.
Ripley, D. (2015). Comparing substructural theories of truth. Ergo, 13(2), 299–328.
Shapiro, L. (2015). Naive structure, contraction and paradox. Topoi, 34(1), 75–87.
Shaw-Kwei, M. (1954). Logical paradoxes for many-valued systems. Journal of Symbolic Logic, 19(1), 37–40.
Smith, P. (2007). An introduction to Gödel’s theorems. Cambridge: Cambridge University Press.
Troelstra, A.S., & Schwichtenberg, H. (2000). Basic proof theory. Cambridge: Cambridge University Press.
Zardini, E. (2011). Truth without contra(dic)ction. The Review of Symbolic Logic, 4(4), 498–535.
Zardini, E. (2014). Naive truth and naive logical properties. The Review of Symbolic Logic, 7(2), 351–384.
Zardini, E. (2015). ∀ & ω. In Torza, A. (Ed.), Quantifiers, quantifiers and quantifiers: Springer.
Zardini, E. (2016). Restriction by non-contraction. Notre Dame Journal of Formal Logic, 57(2), 287–327.
Acknowledgements
Earlier versions of the material in this paper have been presented in 2016 at the 3rd CLE-Buenos Aires Logic Group Workshop in Buenos Aires and in 2017 at the Munich Center for Mathematical Philosophy (MCMP) in Munich. We are very grateful to the members of those audiences. We also owe thanks to two reviewers of this journal (and one of another) for their insightful comments and suggestions. Special thanks go to Elia Zardini for patiently discussing some of the ideas in this paper with us. We are also grateful to Eduardo Barrio, Natalia Buacar, Marcelo Coniglio, Carlo Nicolai, Lavinia Picollo, Damián Szmuc, and Paula Teijeiro for their contributions. This paper could not have been written without the financial aid of the National Scientific and Technical Research Council (CONICET).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Da Ré, B., Rosenblatt, L. Contraction, Infinitary Quantifiers, and Omega Paradoxes. J Philos Logic 47, 611–629 (2018). https://doi.org/10.1007/s10992-017-9441-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10992-017-9441-2



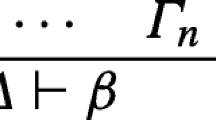

 , omitting the dot notation for the function.
, omitting the dot notation for the function.