Explaining the description-experience gap in risky decision-making: learning and memory retention during experience as causal mechanisms

Abstract

When making decisions based on probabilistic outcomes, people guide their behavior using knowledge gathered through both indirect descriptions and direct experience. Paradoxically, how people obtain information significantly impacts apparent preferences. A ubiquitous example is the description-experience gap: individuals seemingly overweight low probability events when probabilities are described yet underweight them when probabilities must be experienced firsthand. A leading explanation for this fundamental gap in decision-making is that probabilities are weighted differently when learned through description relative to experience, yet a formal theoretical account of the mechanism responsible for such weighting differences remains elusive. We demonstrate how various learning and memory retention models incorporating neuroscientifically motivated learning mechanisms can explain why probability weighting and valuation parameters often are found to vary across description and experience. In a simulation study, we show how learning through experience can lead to systematically biased estimates of probability weighting when using a traditional cumulative prospect theory model. We then use hierarchical Bayesian modeling and Bayesian model comparison to show how various learning and memory retention models capture participants’ behavior over and above changes in outcome valuation and probability weighting, accounting for description and experience-based decisions in a within-subject experiment. We conclude with a discussion of how substantive models of psychological processes can lead to insights that heuristic statistical models fail to capture.

In modern life, we make numerous decisions between competing options despite probabilistic outcomes and incomplete knowledge surrounding their potential outcomes. Indeed, whether we are deciding between movies, car insurance plans, or even serious medical procedures, we frequently seek out statistics to help evaluate the probability of various good or bad outcomes. In these situations, in the absence of prior experience and where probabilities are explicitly described (description-based decisions or DBDs), people appear to act as if they overestimate or overweight low probability events. This has led to the idea that people assign weights to explicitly described likelihoods, resulting in risk-seeking choices for low-probability gains due to overweighting of rare events and risk-averse behavior for high-probability gains due to underweighting of common events (Kahneman & Tversky, 1979; Scholten & Read, 2014). Notably, this probability weighting bias has long been thought to play a primary role in how people evaluate real-world phenomena, including the prevalence rates for rare causes of death (Lichtenstein et al., 1978), the value of insurance policies for rare events (Friedman & Savage, 1948), and changes in preferences for political and economic policies (Quattrone & Tversky, 1988).

Recently, however, it has become clear that the format in which probabilities are presented to us can dramatically affect our apparent preferences. Specifically, people act as if they underweight low probabilities when they are learned through experience (experience-based decision or EBD), a paradoxical reversal of traditional probability weighting bias now termed the description-experience gap (Barron & Erev, 2003; Hertwig et al., 2004; Ungemach et al., 2009; Weber et al., 2004; Wulff et al., 2018). Drawing from the examples above, we would expect more people to purchase rare event insurance or opt out of a medical procedure with rare harmful side effects if they are making a decision based purely on described probabilities rather than based on their previous experiences of these events.

As inference on parameters derived from computational models of both DBD and EBD tasks becomes increasingly common to assess clinical (Ahn & Busemeyer, 2016; Montague et al., 2012), social (Chung et al., 2015), affective (Eldar et al., 2016; Etkin et al., 2015), developmental (Steingroever et al., 2019), and medical decision-making (Lejarraga et al., 2016), it is becoming increasingly important that we identify the potential mechanism(s) that gives rise to the description-experience gap to ensure that variation in key model parameters is driven by individual characteristics (e.g., cognitive development, clinical status, personality traits) rather than task-specific design choices. Therefore, given the importance of the description-experience gap for understanding real-world, human decision-making, we aimed to develop an explanatory cognitive mechanism linking preferences in DBDs to those of EBDs.

Mechanisms of the description-experience gap

Although many explanations of the gap have been proposed, three mechanisms in particular have been the focus of much prior research: (1) reliance on small samples and sampling bias when learning probabilities (i.e., sampling error), (2) reliance on more recently experienced samples, and (3) changes in the psychological representation of probability (Figure 1; Fox & Hadar, 2006; Hertwig & Erev, 2009). Regarding (1), the format of the tasks used to assess EBDs (i.e., sampling paradigms with optional stop**) is such that some participants either never or less frequently encounter the “rare event” when drawing samples from a choice option, which naturally leads to apparent underweighting of low probability events once making a choice (Hau et al., 2010; Hertwig et al., 2004). Such biased sampling occurs because rare event frequency follows a binomial distribution, which is heavily skewed when few samples are drawn (i.e., n is low), meaning that the actual experienced proportion of encounters with a given outcome will often be biased relative to the true outcome probability (Hertwig et al., 2004). For similar reasons, (2) can lead to an apparent underweighting because higher probability outcomes are more likely to be recently observed relative to lower probability outcomes in small sample settings, and people tend to place higher weight on more recent outcomes or simply ignore or forget less recent outcomes when making EBDs (Hertwig et al., 2004). Finally, although less parsimonious than (1) or (2), (3) suggests that people evaluate probabilities differently between tasks, assigning less weight to low-probability outcomes in EBDs relative to DBDs (see Fig. 1 for a graphic example). Ungemach et al. (2009) showed that when using an experimental design to eliminate sampling bias (by matching the experienced proportion of each outcome to its respective objective probability of occurring), cumulative prospect theory modeling still revealed underweighting of rare events in EBDs. Many studies have since followed suit, and a recent meta-analysis of more than 6,000 individual participants draws similar conclusions (Wulff et al., 2018).

Fig. 1

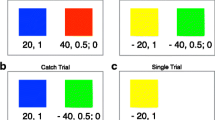
Description- versus experience-based decisions. Note. Examples of description- versus experience-based decisions for a gamble between winning $4 with probability 0.8 ($0 with probability 0.2) versus $3 for certain. As depicted, people tend to choose the safe option when the probability is given. Conversely, when people must sample both options to learn the probabilities of each outcome (i.e., sampling paradigm), they tend to choose the risky option. Such preference differences often are interpreted as differences in evaluating the probability of rare events. Multiple mechanisms have been proposed to explain this difference, including sampling error and recency, which will lead to experienced probabilities that are different from the true probabilities when people draw low numbers of samples (e.g., ~20) before making a contingent choice (i.e., preference judgement). Alternatively, people may actually weight probabilities differently between task presentations, which can be captured by the $\gamma$ parameter from cumulative prospect theory. Specifically, $\gamma <1$ indicates overweighting of rare events, whereas $\gamma >1$ indicates underweighting of rare events

Altogether, available evidence suggests that sampling biases and recency contribute to the description-experience gap but also that probabilities or rewards are fundamentally different when evaluated based on description compared to experience (Hertwig & Erev, 2009; Kellen et al., 2016; Wulff et al., 2018). This begs the question—how does context affect something as fundamental to preferential decision-making as the value of rewards and probabilities?

Modeling the gap

In one of the first studies of its kind, Glöckner et al. (2016) examined differences in CPT valuation parameters between description and experience tasks from multiple previous studies and found that rare events carried more weight for EBDs relative to DBDs—a reversal of the typical description-experience gap. Follow-up analyses revealed that the type of gamble was a significant moderator of the size and direction of the gap, such that analyses of “reduced” gambles, including at least one certain option produced a traditional gap, and “nonreduced” gambles containing no certain options predicted a reversal of the gap (Glöckner et al., 2016).¹ Using a within-subject design, Kellen et al. (2016) replicated and expanded Glöckner et al.’s (2016) findings of a reversed description-experience gap by using hierarchical Bayesian modeling of CPT parameters across more than 100 participants who underwent the same set of 114 gambles for both description and experience presentations, concluding that “Our results suggest that outcome and probability information translate into systematically different subjective representations in description- versus experience-based choice.” (Kellen et al., 2016, p. 126). These foundational applications of CPT to model the description-experience gap—which moved away from heuristic methods of testing hypotheses in favor of more formalized, substantive models of psychological processes—led to novel and counterintuitive insights into a previously well-replicated behavioral phenomenon.

Learning and memory as causal mechanisms

Similar to Regenwetter and Robinson (2017), we argue that the most commonly used method of modeling EBDs with CPT relies on a set of strong assumptions that introduce bias into the estimation of probability weighting due to model mis-specification. Specifically, to control for participants’ unique learning history in EBDs, the probability of each outcome is assumed to be equal to the experienced proportion of outcomes observed for each participant-gamble pair (Camilleri & Newell, 2011; Glöckner et al., 2016; Kellen et al., 2016). For example, if a person draws samples $\in \{\$4, \$4, \$4, \$0\}$ for gamble $g$, the probability for each outcome $j$ is heuristically set to the empirical proportion of samples that it was observed before CPT modeling (if $j=1$ indicates $4, and $j=2$ indicates $0, then ${p}_{g,1}=0.75$ and ${p}_{g,2}=0.25$). However, this heuristic method implicitly makes three strong assumptions, all of which are difficult to reconcile with learning and memory research:

• (1) Learning and memory for all past samples is perfect;

• (2) There are no individual differences in trial-by-trial learning across participants; and

• (3) Learning occurs through a single, static mechanism.

These assumptions are easier to scrutinize if we formalize the implicit learning and memory models underlying them. Note that readers can refer to Table 1 for an overview of the model terms and interpretations while reading through the next section.

Table 1. Competing models and assumptions

If we assume learning progresses through a strength-based learning mechanism, the following delta learning rule is implied as samples are experienced (a.k.a., simplified Rescorla-Wagner updating rule; Rescorla & Wagner, 1972):

$${p}_{g,j}:={p}_{g,j}+A\times ({I}_{g,j,s}-{p}_{g,j})$$

(1)

which can be rewritten as follows to better correspond to memory models that we discuss later on:

$${p}_{g,j}:=(1-A)\times {p}_{g,j}+A\times {I}_{g,j,s}$$

(2)

$A$ is a learning rate, $j$ indicates the outcome within a given gamble $g$, $s$ indicates the sample number, and is an indicator that equals 1 or 0 if outcome $j$ is observed or unobserved on the given sample, respectively (Ahn et al., 2012; Haines et al., 2019). In this formulation, irrespective to the initial value for ${p}_{g,j}$, if the learning rate is set such that $A=\frac{1}{s}$, then ${p}_{g,j}$ will always be equivalent to the proportion of times that outcome $j$ is observed up to sample $s$, resulting in the same behavioral predictions (perfect knowledge and memory of all previous outcomes) as the heuristic CPT implementation.

We could equivalently formalize the heuristic CPT analyses with an instance-based memory model (Gonzalez et al., 2011). For example, if we assume that each encounter with an outcome leaves a memory trace of that outcome, that each trace decays exponentially in time (indexed by sample number) and that the salience of each outcome is determined by the relative strength of its memory traces compared to traces for alternative outcomes within the given choice option, then we can use the following simplified decay memory rule to generate outcome probabilities:

$$\begin{array}{l}{n}_{g,j}:=\left(1-A\right)\cdot {n}_{g,j}+{I}_{g,j},s\\ {p}_{g,j}:=\frac{{n}_{g,j}}{\sum_{k=1}^{J}{n}_{g,k}}\end{array}$$

(3)

Here, ${n}_{g,j}$ indicates the number of times that outcome $j$ has been observed for gamble $g$ up to the current sample $s$, $(1-A)$ is a memory trace decay rate, $J$ is the number of different outcomes that can be observed within the given gamble, and ${I}_{g,j,s}$ is the same indicator as described above. If $(1-A)=1$, then ${n}_{g,j}$ will always equal the objective number of times that outcome $j$ has been observed up to sample $s$, and the summation (i.e. “blending”) will subsequently return the proportion of times that outcome $j$ is observed across trials, akin to the delta learning rule above. Note that in this specific setting, the delta learning and decay memory rules are equivalent except that in the decay memory rule, the experienced outcome is given a weight of 1 as opposed to being weighted in proportion to the learning rate. There are more general relationships between the delta and decay rule, but they are not relevant for the current analyses (Turner, 2019).

Given these formal definitions, we now turn back to assumptions 1-3 listed above. Assumptions (1) and (2) imply that either $A=\frac{1}{s}$ or $A=0$ for all participants in the case of the delta learning or decay memory rules, respectively, thus giving equivalent weight to all experienced outcomes irrespective to the time at which they were experienced. However, it is well known that people place higher weight on more recent samples when making EBDs and that there are substantial individual differences in learning rate or memory decay between people. In fact, individual differences in learning rate or memory decay during EBDs are associated with neurodegenerative disease status (Busemeyer & Stout, 2002), delinquent behavior (Yechiam et al., 2005), and age-related changes in impulsive decision-making (Wood et al., 2005). More generally, there is an extensive and longstanding literature on the basic psychological mechanisms underlying frequency or probability learning that reveals biases (e.g., toward recently experienced outcomes, attention to wins versus losses, etc.) in how people estimate probabilities or assign salience to outcomes (Estes, 1976; Gonzalez, 2013; Zacks & Hasher, 2002).

Regarding assumption (3), there is growing evidence that people learn at different rates for positive versus negative surprises (i.e., prediction errors) or outcomes, which can lead to risk-seeking or risk-averse behavior (Christakou et al., 2013; Daw et al., 2002; Doll et al., 2009; Gershman, 2015; Haines et al., 2018; Niv et al., 2012; Turner, 2019). In fact, the magnitude of such individual differences in learning rates is genetically linked to striatal dopamine functioning (Cox et al., 2015; Frank et al., 2004, 2007). Moreover, learning from positive outcomes is associated with Striatal D1 receptor density, whereas learning from negative outcomes is associated with D2 receptor binding. Although both are modulated by dopamine, this dissociation implies that the two components of learning—positive and negative—correspond to physiologically (Cox et al., 2015) and genetically (Frank et al., 2007) distinct processes. Converging evidence from fMRI BOLD analyses showed that manipulations of reward variance led to distinct prediction error signals in nucleus accumbens corresponding to rates of positive and negative prediction errors, favoring a model with distinct positive and negative learning rates (Niv et al., 2012).

Current study

Altogether, most approaches to studying the description-experience gap assume that people have optimal learning rates, decay-free memory representations of experienced outcome frequencies (which we term “imperfect learning and memory”), and no individual differences in learning or decay rates. These tenuous assumptions can both lead to biased inferences on performance differences between DBDs and EBDs when using the heuristic CPT method. Furthermore, there is growing neural and behavioral evidence that people learn asymmetrically from positive versus negative predictions errors. As demonstrated in Fig. 2, such biased learning can partially explain changes in behavior consistent with the description-experience gap, yet typical approaches to modeling the gap fail to account for asymmetric learning.

Fig. 2

Effect of asymmetric learning on probability estimation. Note. Model-predicted probability of the high outcome [Pr(H)] occurring for both the “reduced” gamble (i.e., one option is certain and the other risky/probabilistic) exemplified in Fig. 1 and another “nonreduced” gamble (i.e., both options are probabilistic/risky). To generate sample-to-sample probabilities, we used a simple strength-based reinforcement learning model with separate learning rates for positive (${A}_{+}$) and negative (${A}_{-}$) prediction errors (see Eq. 8 in the Method section), where option A and B were sampled with equal probability. All outcome probabilities are updated after each sample in proportion to both the difference between the expected and actual outcome (prediction error) and the learning rate—we show only Pr(H) for visual purposes. Panels denote each combination of ${A}_{+}$ and ${A}_{-}$ with values of 0.1, 0.3, and 0.5, and shaded intervals around predicted values indicate ±2 standard errors of the mean across repeated iterations. The shaded region highlights the first 20 samples. Probability estimates converge to true values for certain options (irrespective to the learning rates), but converge to biased estimates when outcomes are probabilistic and learning rates are not equivalent. Additionally, effects of sampling error and recency are apparent even when learning rates are equivalent, where the random nature of the sampling process has not yet allowed for learning to converge to the true outcome probability and estimates are subsequently biased toward 0.5. The Supplement details how we generated the above predictions

We examined the consequences of removing these assumptions by integrating learning and memory models with decision-making theories. Our core argument is that, rather than estimating additional parameters in the CPT utility function to describe the description-experience gap, it is more fruitful to explain the gap by identifying and modeling psychological learning or memory mechanism(s) that lead to preference differences across description and experience. To do so, we first conduct a simulation study to determine how individual differences in learning during the sampling phase of EBDs (and asymmetric learning in particular) can bias CPT parameters when using the heuristic method that assumes no learning or memory effects. Next, we develop a variety of computational models that instantiate different learning or memory mechanisms and determine which model provides the best joint statistical account of behavior in DBDs and EBDs. This latter model comparison approach allowed us to test specific hypotheses regarding differences between DBD and EBD tasks, including whether the proposed learning mechanism described true behavior better than CPT models assuming differences in probability weighting, risk aversion, or loss aversion in addition to other mechanism we describe below.

Inspired by the results of our simulation study, we next fit a series of competing models to empirical within-subject data collected from 104 participants across 114 unique description- and experience-based gambles to determine the degree to which people engage in behavior consistent with the integrated learning and decision-making models we propose.

Finally, we conclude with a discussion of how formalizing and quantitatively comparing competing hypotheses can enhance our understanding of complex psychological phenomena in a way not afforded by experimental design alone. We begin below with a mathematical overview of the models used throughout both our simulation and empirical study.

Mathematical models

Cumulative prospect theory

The core of CPT contains three main parameters, namely: (1) probability weighting $\gamma (0<\gamma <5)$, risk sensitivity $\alpha (0<\alpha <5)$, and loss sensitivity $\lambda (0<\lambda <10)$. Note that full CPT model typically includes separate probability weighting and risk sensitivity parameters for losses versus gains, but we use a single parameter across gain and loss domains (i.e., restricted CPT) due to known parameter estimation problems (Nilsson et al., 2011). Also, there are no theoretical upper bounds on CPT parameters ($\gamma ,\alpha ,\lambda$). Practically, however, values greater than the upper bounds above are rarely or never encountered (as parameter values further exceed these bounds, model predictions remain the same), so we set the bounds to make for more efficient estimation (see Nilsson et al., 2011). We show in Figure S4 that this choice did not bias our results. Each parameter captures systematic deviations of an individual’s choices from the objective expected value of each gamble—which we refer to as the subjective value (${V}_{g}$)—given as²:

$${V}_{g}=\sum_{j=1}^{J}W\left({p}_{g,j}\right)U({x}_{g,j})$$

(4)

${p}_{g,j}$ and ${x}_{g,j}$ are the probability (e.g., 0.8) and objective payoff value (e.g., $4) for each possible outcome $j$ within a given gamble $g$. CPT assumes that people subjectively weight the probability of each outcome such that:

$$W\left({p}_{g,j}\right)=\frac{{p}_{g,j}^{\gamma }}{{p}_{g,j}^{\gamma }+{(1-{p}_{g,j})}^{\gamma }}$$

(5)

Here, values for $\gamma <1$ indicate overweighting of low-probability events and values for $\gamma >1$ indicate underweighting of low probability events (Fig. 1). $\gamma$ has the opposite interpretation for high probability events (Fig. 1). Note also that Eq. 5 is a single-parameter version of Goldstein and Einhorn’s (1987) probability weighting function (Karmarkar, 1978; Gonzalez & Wu, 1999), which is different from the original CPT probability weighting in that it is symmetric around the objective probability (i.e., omitting the $1/\gamma$ exponent on the denominator). We used this single-parameter version, because we were most interested in changes in probability weighting rather than probability elevation. The symmetry allows for easier interpretation compared with CPT’s original instantiation.³ Importantly, Eq. 5 is a key component of CPT, which is necessary to capture the well-known fourfold pattern of risk attitudes (Tversky & Kahneman, 1992).

Additionally, CPT assumes that payoff values are evaluated nonlinearly such that the subjective utility of ${x}_{g,j}$ is given by

$$U\left({x}_{g,j}\right)=\left\{\begin{array}{ll}{x}_{g,j}^{\alpha } & \mathrm{if }\;{x}_{g,j}\ge 0\\ -\uplambda {\left|{x}_{g,j}\right|}^{\alpha },& \mathrm{otherwise}\end{array}\right.$$

(6)

where values for $\alpha <1$ indicate risk-aversion (i.e., insensitivity to differences between large-magnitude values), and values for $\alpha >1$ indicate risk-seeking behavior. Loss-aversion is captured by $\lambda >1$ (i.e., losses are weighted more heavily than gains), whereas loss-seeking is captured by $\lambda <1$. Hence, the subjective value ${V}_{g}$ in Eq. 4 is computed as a weighted sum of probability weights and subjective utilities for each gamble.

Although the original CPT model is deterministic, we employ a commonly used probabilistic choice rule to convert the subjective values for each option (from Eq. 4) to expected choice probabilities that sum to one (Stott, 2006). Specifically, we use a multinomial logistic function—also known as the softmax function—which is closely related to the Luce choice rule:

$$\mathrm{Pr}\left[Choice=g\right]=\frac{\mathrm{exp}(\phi \times {V}_{g})}{\sum_{k=1}^{2}\mathrm{exp}(\phi \times {V}_{k})}$$

(7)

Here, the probability ($\mathrm{Pr}$) of choosing gamble $g$ is determined as a function of its subjective value ${V}_{g}$ relative to all $K$ gambles available within the current problem. Note that we focus only on choices where two competing gambles are considered. The choice sensitivity parameter $\phi (0<\phi <\infty )$ controls how deterministically (larger $\phi$) versus randomly (smaller $\phi$) an individual makes choices according to the subjective value ${V}_{g}$ of each gamble. For the simulation study, we set $\phi =1$ for convenience and did not estimate it as a free parameter. For the empirical study, we estimated $\phi$ as a free parameter. Our use of the logistic choice rule as opposed to the original Luce choice rule allows for the model to capture individual differences in maximization behavior through the use of the choice sensitivity parameter ($\phi$). The Luce choice rule of the form $\mathrm{Pr}\left[Choice=g\right]= \frac{{V}_{g}}{{\sum }_{k=1}^{2}{V}_{k}}$ is scale invariant, such that multiplying each $V$ term by a constant factor (i.e. a choice sensitivity or inverse temperature parameter) has no effect on the resulting probabilities. Additionally, the logistic rule has many practical benefits—namely, it (1) is a key component of many models of EBDs that generalize well to novel data (Erev et al., 2010); (2) captures variation in choice across multiple decision domains (Friedman & Massaro, 1998); and (3) is a well-studied probabilistic extension of traditional CPT (Nilsson et al., 2011).

Reinforcement learning CPT hybrid model

The RL-CPT model extends CPT from pure description-based tasks into experience-based tasks by assuming that the probability (${p}_{g,j}$) for each choice outcome is learned through experience during sampling for EBDs. Therefore, RL-CPT assumes that traditional CPT parameters ($\gamma ,\alpha , \lambda$) are equivalent across DBDs and EBDs. Any differences in preferences between tasks are captured by the effects of a dynamic learning mechanism. When ${p}_{g,j}$ is given (i.e., DBDs), the RL-CPT model simply reduces to traditional CPT, with a single set of valuation parameters estimated for each participant. Conversely, when ${p}_{g,j}$ is not given, the RL-CPT learns ${p}_{g,j}$ through repeated sampling using the strength-based learning rule described in the introduction (Eqs. 1-2). Specifically, we assume that ${p}_{g,j}$ = 0.5 once the given outcome is observed—indicating maximum uncertainty—and is then updated after each sample $s$ with a different learning rate depending on whether the observed outcome is better or worse than expected. If outcome $j$ is not observed while sampling option $g$, then ${p}_{g,j}$ remains at 0 and the outcome subsequently plays no role in the final preference judgement. Additionally, we assumed that, if one outcome has already been observed such that ${p}_{g,1}$ has already taken on some value different from 0 or 0.5, then upon observing outcome ${p}_{g,2}$ for the first time, updating begins from $1-{p}_{g,1}$ rather than from $0.5$. Setting the initial values for ${p}_{g,j}$ in this way assumes that people keep track of how likely various outcomes within a given option are relative to one another, such that if one outcome is very common, the other must be rare and vice versa. Furthermore, this scheme ensures that if people observe more than one outcome for a given option, that the outcome probabilities sum to 1 (i.e., ${p}_{g,1}+{p}_{g,2}=1$). The learning rule is then:

$$\forall j\in J,{p}_{g,j}:={p}_{g,j}+\left\{\begin{array}{cc}{A}_{+}\times & \left({I}_{g,j,s}-{p}_{g,j}\right),\; \mathrm{if }\;PE\ge 0\\ {A}_{-}\times & \left({I}_{g,j,s}-{p}_{g,j}\right),\; \mathrm{Otherwise}\end{array}\right.$$

(8)

${A}_{+} (0<{A}_{+}<1)$ and ${A}_{-} (0<{A}_{-}<1)$ are learning rates for positive and negative prediction errors, respectively, and $PE=U\left(outcom{e}_{s}\right)-{V}_{g}$ is the prediction error generated after observing the outcome of sample $s$. The first term, $U(outcom{e}_{s})$, is the utility (Eq. 6) of the experienced outcome upon drawing sample $s$. Then, ${V}_{g}$ is the expected value (Eq. 4) for gamble $g$ that was sampled. Intuitively, the learning rule described by Eq. 8 assumes that people update their expectations for how likely each outcome is to occur differently based on whether the observed outcome was better ($PE\ge 0$) or worse ($PE<0$) than expected. If ${A}_{+}={A}_{-}$, then Eq. 8 is identical to the single learning rate learning rule described in the introduction (Eq. 1). However, when ${A}_{+}<{A}_{-}$, higher negative relative to positive learning rates leads to an underestimation of the high outcome probability and therefore produces risk-averse behavior.

After iterating through each sample a participant draws before making a choice, the resulting ${p}_{g,j}$ estimates from Eq. 8 are entered into Eq. 5. This explicit learning mechanism contrasts the traditional heuristic analyses of EBDs, where ${p}_{g,j}$ is simply set to the experienced proportion of each outcome (Glöckner et al., 2016; Kellen et al., 2016). As we described in detail in the introduction, the heuristic method of setting ${p}_{g,j}$ to the experienced proportion of each outcome is analytically equivalent to a special case of the RL-CPT model wherein ${A}_{+}={A}_{-}=\frac{1}{s}$. This mathematical correspondence allows us to find evidence for traditional probability weighting and mean-tracking models (described below) as special/nested cases of the RL-CPT model. All other aspects of RL-CPT are equivalent to standard CPT.

The RL-CPT differs from other learning and memory models of EBDs in two important ways. First, learning and memory models including the scanning model (Estes, 1976), Value-updating Model (Hau et al., 2008), Decay-reinforcement model (Erev & Roth, 1998), delta-rule learning model (Busemeyer & Myung, 1992), prospect valence learning model (Ahn et al, 2008), and the ACT-R inspired Instance-Based Learning model (Gonzalez et al., 2011) do not directly estimate probabilities. Instead, they assume that people either learn the expected average return of an option (in the case of learning models) or sample memory traces of previously encountered stimuli to evaluate the relative frequency of potential outcomes (in the case of memory models). By contrast, the RL-CPT model assumes that people directly learn the probability of each outcome occurring before integrating probabilities with their respective outcome values (see also Haines et al., 2018). Despite making different mechanistic assumptions, models that update toward the average value of an option (e.g., the delta-rule learning model) produce the same behavioral predictions as a special case of the RL-CPT, where learning rates are equivalent (${A}_{+}={A}_{-}$) and all CPT valuation parameters ($\gamma ,\alpha ,\lambda$) are set to 1. In this reduced case, the RL-CPT model will update toward the objective expected value of an option. More generally, the explicit tracking of probabilities in the RL-CPT is necessary to both: (1) model DBDs, which ask people to integrate potential outcomes with their explicitly given probabilities; and (2) compare probability weighting across DBDs and EBDs. Therefore, the RL-CPT can only be compared with the above learning and memory models in the context of EBDs, because other learning and memory models do not make clear predictions for DBDs. However, because memory decay is a reasonable competing explanation for differences between DBDs and EBDs, we also tested an instance-based model that estimates outcome probabilities using a memory decay mechanism as a competing mechanism to the RL-CPT model. We describe this model in the next section.

Second, the RL-CPT includes a pair of learning rates to account for asymmetric learning of positive versus negative predictions errors (Gershman, 2015; Mihatsch & Neuneier, 2002; Niv et al., 2012), whereas the abovementioned models contain only a single learning or memory decay mechanism. The asymmetric learning mechanism in the RL-CPT is qualitatively different from attention mechanisms in other models, which assume that people differentially attend to gains versus losses (Busemeyer & Stout, 2002; Estes, 1976). Specifically, because the learning rate is dependent on the sign of the sample-to-sample prediction error rather than the outcome domain (Eq. 8), a learning asymmetry can lead to biased probability expectations within any domain (e.g., for gains, losses, or mixed gambles). Conversely, asymmetric attention to gains versus losses is necessarily a between-domain effect.

In summary, the RL-CPT can produce biased expectations of outcome probabilities (Fig. 2), which allows it to account for preference differences between DBDs and EBDs in a way that alternative models are unable to capture. Furthermore, because traditional CPT characterizes risk sensitivity through valuation parameters alone, it follows that any changes in risky behavior resulting from an asymmetric learning mechanism may lead to biased inferences in CPT valuation parameters.

Instance-based memory CPT hybrid model

As a competing mechanism to strength-based updating rule in the RL-CPT, we also developed an instance-based memory and CPT hybrid model (IB-CPT) that estimates the probability (${p}_{g,j}$) for each choice outcome in EBDs using the memory decay plus normalization step described in the introduction (Eq. 3). From the instance-based perspective, ${p}_{g,j}$ is thought of as the memory salience of a given outcome relative to other possible outcomes. All other aspects of the IB-CPT model are equivalent to the RL-CPT model described above—traditional CPT parameters ($\gamma ,\alpha , \lambda$) are assumed to be equivalent across DBDs and EBDs, and differences in preferences between contexts are captured by the effects of the dynamic memory decay mechanism. As described in the introduction, the memory decay rule in the IB-CPT reduces to the heuristic CPT implementation when the memory decay rate $A$ is set to 0.

Despite sharing core features with other instance-based models, the IB-CPT differs from other instance-based models in one important way. For example, the Instance-Based Learning model is one extant model that assumes that people multiply (i.e. “blend”) probabilities and their respective outcomes to determine the subjective value for each gamble (Gonzalez et al., 2011). The probabilities are determined by sampling memory traces of experienced outcomes, which allows the model to capture deviations of individuals’ choices from the objective expected value of each gamble—the use of memory decay and “blending” to arrive at outcome probabilities and expected values is equivalent to our formulation of the IB-CPT. For DBDs, however, the memory trace sampling process in the Instance-Based Learning model drops out of the equation (there are no prior experiences to sample), reducing to a simple expected value model which assumes that people make choices to maximize the objective expected value of each pair of gambles. Because this assumption is: (1) inconsistent with research on DBDs, (2) is contained as a special case of the CPT model that we tested (when $\gamma =\alpha =\lambda =1$), and (3) extends to all instance-based models described above, we did not test Gonzalez et al.’s (2011) specific implementation of an instance-based learning model in the current study, opting instead for the formulation of the IB-CPT described above.

In summary, the traditional CPT, RL-CPT, and IB-CPT models are all equivalent in the context of DBDs, but they differ in how they assume people learn to integrate experienced outcomes into their decision process in the context of EBDs. Therefore, comparing the models allows us to determine how well each of the proposed learning and memory mechanisms can account for the description-experience gap. Before fitting the models to empirical data, however, we conducted a simulation study to determine what the heuristic CPT analyses will reveal if data are actually generated by the learning model instantiated by the RL-CPT.

Simulation study

We focus our simulations on the RL-CPT due to the relationships between asymmetric learning and risk aversion, which could drive differences in probability weighting (and outcome valuation more generally) between DBDs and EBDs. However, we emphasize that memory decay in the IB-CPT could give rise to similarly biased estimates.

For our simulation study, we first simulated both description- and experience-based choices from the RL-CPT model by using a single set of CPT parameters with separate positive and negative learning rates. Next, we fit the simulated data with a traditional CPT model by using the heuristic method of setting ${p}_{g,j}$ to the experienced proportion of rare events. The traditional CPT model assumed differences in probability weighting ($\gamma$), risk sensitivity ($\alpha$), and loss sensitivity ($\lambda$) between DBDs and EBDs, which is consistent with previous computational analyses of the description-experience gap (Glöckner et al., 2016; Kellen et al., 2016). With this design, any preference differences inferred across DBDs and EBDs are wholly attributable to the proposed learning mechanism as opposed to true differences in CPT valuation parameters. Furthermore, by kee** the valuation parameters constant while varying the learning rates, we were able to determine exactly how much (and in what direction) learning during EBDs could bias traditional CPT valuation parameters in the context of EBDs.

Simulation experiment design

The problem set used for the simulation study was taken directly from Kellen et al. (2016), and we refer the reader to the original study for details (see Table S1 for all gamble pairs). We used this specific problem set, because it encompasses gambles used in many studies on both DBDs and EBDs, many of which were selected for estimating important parameters in CPT. Briefly, there are 114 different gambles, where each gamble was used for description (i.e., a one-shot preference judgement) and experience (i.e., repeated sampling before preference judgement). Individual gambles include those that were:

• (1) used in original studies on the description-experience gap,

• (2) randomly generated across gain, loss, and mixed gains and loss domains,

• (3) selected to measure loss and risk aversion,

• (4) used in previous EBD studies,

• (5) a mix between those with safe versus risky options (reduced gambles), and

• (6) those composed of two risky options (nonreduced gambles).

Because previous studies suggest that the description-experience gap may vary across reduced and nonreduced gambles (Glöckner et al., 2016), we ran separate simulations for the reduced and nonreduced sets of gambles from Kellen et al. (2016) to determine whether asymmetric learning could account for such differences.

Simulation model specification

We generated pseudo-participants’ person-level RL-CPT valuation parameters by using random draws from group-level normal distributions with means of ${\alpha }_{\mu }=0.88$, ${\lambda }_{\mu }=2.25$, and ${\gamma }_{\mu }=0.65$, and with SDs of ${\alpha }_{\sigma }\approx {\lambda }_{\sigma }\approx 0.10$ and ${\gamma }_{\sigma }\approx 0.3$ (see Supplementary Text for full details). Note that these specific group-level means were chosen to match those estimated in the original CPT study (Tversky & Kahneman, 1992), and SDs were chosen to ensure a realistic amount of variability across individuals. For learning rates, we generated a grid of all possible combinations of group-level learning rates for ${A}_{+}\in \{0.25, 0.5, 0.75\}$ and ${A}_{-}\in \{0.05, 0.15, \dots , 0.95\}$, totaling 30 unique group-level combinations. Additionally, we simulated choices (i.e., preference judgements in Fig. 1) after pseudo-subjects drew either 19 or 99 total random samples from either choice option, where Eq. 8 was used to update ${p}_{g,j}$ after each sample. We chose these specific sample sizes based on both meta-analytic estimates of the number of samples typically drawn during free sampling (Wulff et al., 2018) and to determine whether effects change when a larger number of samples are drawn. Finally, we simulated data separately for reduced (n_reduced = 19) and nonreduced (n_nonreduced = 95) sets of gambles. Altogether, the simulations amounted to a 30 $\times$ 2 $\times$ 2 design (i.e., learning rates by sample size by gamble type), where each cell is a full set of simulated choices across 100 pseudo-participants. We refer the reader to the Supplement for more specific details on simulation model parameters.

Simulation results

Probability weighting

Figure 3 shows that asymmetric learning leads to biased estimates of CPT probability weighting ($\gamma$) when using the traditional heuristic method of setting ${p}_{g,j}$ to the experienced proportion of outcomes observed within participant-gamble pairs.⁴ For reduced gambles, probability weighting for EBDs—but not DBDs—is significantly biased by asymmetric learning in small sample settings, such that it is overestimated when learning occurs more rapidly for positive prediction errors and underestimated when learning occurs more rapidly for negative prediction errors. Furthermore, as participants draw more samples, the effect reverses such that more rapid learning from negative prediction errors leads to overestimation of probability weighting in EBDs. We did not observe this differential bias when both learning rates were closer to 1, in which case EBD probability weighting ($\gamma$) was more consistently overestimated. Because the overestimate was close to $\gamma =1$, these results may reflect uncertainty in estimates caused by rapid updating (i.e., high variation) of the outcome probability that, on average, will tend to drive estimates toward 0.5.

Fig. 3

Biases in experience-based CPT probability weighting ($\gamma$) estimates. Note. Estimates for group-level CPT probability weighting in DBDs and EBDs when setting ${p}_{g,j}$ to the experienced proportion of rare events. Because $\gamma$ was left unchanged across all simulations of the RL-CPT, all deviance between EBD probability estimates and the true values reflect biases induced by the asymmetric learning mechanism (Eq. 8). For reduced gambles, when learning rates are generally lower (i.e. <0.5) and participants draw fewer samples, $\gamma$ is overestimated (underestimated) when learning occurs more rapidly for positive (negative) prediction errors. Importantly, this effect reverses in larger sample settings, revealing an interaction between learning asymmetry and sample size. For nonreduced gambles, probability weighting is more consistently overestimated across all levels of learning rates relative to reduced gambles only (particularly in small sample settings), leading to apparent underweighting of rare events for EBDs relative to DBDs in the absence of a true difference in probability weighting. Therefore, the same pair of learning rates can lead to different biases in probability weighting across reduced and nonreduced gambles for EBDs, particularly in small sample settings (cf. ${A}_{+}$ = 0.25 and ${A}_{+}$ = 0.5 across reduced and nonreduced gambles). Shading indicates the 95% HDI of the posterior estimate

The results are different for nonreduced gambles, which lead to more consistent overestimation of probability weighting for EBDs in small sample settings (except when learning rates are lower and equal, or ${A}_{+}={A}_{-}\approx 0.25$). In larger samples, however, nonreduced gambles tend to produce accurate recovery of probability weighting estimates when learning rates are equivalent, but biased estimates when learning is asymmetric (where the direction of bias depends on the strength of both learning rates).

Figure 3 suggests that if people do learn asymmetrically from positive versus negative prediction errors, then (1) a single pair of learning rates can lead to biased probability weighting estimates for EBDs using traditional CPT modeling, and (2) the same pair of learning rates has different effects on probability weighting estimates across reduced and nonreduced sets of gambles (i.e., “contextual” effects), where the direction of the bias is dependent on the number of samples that participants draw. For example, in small sample settings when both learning rates are approximately 0.5, traditional CPT modeling leads to linear probability weighting ($\gamma \approx 1$) for reduced gambles, but apparent overweighting of rare events ($\gamma <1$) for nonreduced gambles.

Risk aversion

Figures S1 and S2 show traditional CPT estimates of risk- and loss-aversion between description and experience generated by participants who learn at different rates for positive and negative prediction errors. For risk-aversion, two general trends are worth noting. First, $\alpha$ is consistently underestimated for experience-based decisions (EBDs), whereas it is accurately estimated for description-based decisions (DBDs). A small exception is that for nonreduced gambles, there is a tendency for $\alpha$ to be slightly underestimated even for DBDs. Second, across both reduced and nonreduced sets of gambles, biased estimates of $\alpha$ are most extreme when both learning rates are low (i.e., <0.25), become less pronounced as learning rates become more rapid (i.e. >0.25), and sometimes become more biased as learning again becomes more rapid (i.e. both learning rates >0.75). However, this latter trend is minor.

Loss aversion

Results were different for loss-aversion. For reduced gambles, $\lambda$ is consistently underestimated when both learning rates are low (i.e., <0.25) but becomes better estimated as the negative prediction error learning rate (${A}_{-}$) becomes increasingly large. Furthermore, as the positive prediction error learning rate (${A}_{+}$) increases, $\lambda$ becomes increasingly underestimated irrespective to ${A}_{-}$. Conversely, for nonreduced gambles, $\lambda$ estimates showed the opposite pattern, where $\lambda$ is increasingly underestimated as ${A}_{-}$ becomes increasingly large. Overall, like for $\alpha$, $\lambda$ is generally underestimated for EBDs, particularly for nonreduced gambles where $\lambda$ often is estimated to be less than 1. In fact, such apparent reversals of loss aversion (i.e., $\lambda <1$) in nonreduced EBDs may explain the apparent loss-seeking behavior found in studies that use prospect theory valuation functions to model EBDs (Ahn et al., 2014).

Interim summary of simulation study

Our simulation study confirmed that if people do learn in a way consistent with the RL-CPT while sampling gambles (i.e., they are most sensitive to recent outcomes and update expectations differently based on whether outcomes were better or worse than expected), then heuristic applications of CPT are bound to reveal differences in valuation parameters across DBDs and EBDs even when there are no true differences in valuation. Furthermore, the direction and magnitude of this bias is not initially intuitive—it is dependent on both the average value of learning rates, the magnitude of the difference in learning from positive versus negative predictions errors, the number of samples that a person draws, and features of the specific gambles that people are given (i.e., reduced vs. nonreduced). However, as opposed to designing an experimental manipulation to control these various factors to explore the description-experience gap, we can explicitly model the learning and memory mechanisms underlying EBDs to identify potential invariances in valuation between DBDs and EBDs. Without an explicit model of learning, we risk misinterpreting CPT valuation parameters estimated in the context of EBDs due to our inability to experimentally control for complex learning and memory effects. Following this rationale, we next conducted a model comparison study using empirical data to determine the extent to which asymmetric learning captures observed within-person preference differences between DBDs and EBDs. For empirical model comparisons, we include the IB-CPT model as a competing learning/memory mechanism to the RL-CPT.

Empirical study

Participants and experiment

For the empirical study, we used actual participant data from Kellen et al. (2016). A total of 104 participants underwent all 114 description- and experience-based gambles as described above (see Simulation Experiment). We refer readers to the original study for more details on participants’ characteristics, and provide summary statistics for the choice proportions within description and experience for each pair of gambles in Table S1. For description-based gambles, participants were presented with gamble pairs one at a time, and they were instructed to choose the option that they preferred. For experience-based gambles, participants were allowed to sample from each option in whatever order and for how ever many trials they preferred before making a final preference judgement. Importantly, the order of description and experience was counterbalanced across participants, and the description and experience sessions were separated by at least one full week within each participant to minimize potential order effects. For EBDs, participants drew an average of 21.04 (SD = 9.4) samples before making a contingent choice (i.e., preference judgement). Previous CPT modeling of these data revealed an overweighting of rare events in EBDs relative to DBDs (i.e., ${\gamma }_{E}<{\gamma }_{D}<1$; Kellen et al., 2016). Our simulations above indicated that an asymmetric learning mechanism could produce this overweighting result if: (1) learning rates are both below 0.75; (2) people learn more rapidly from negative relative to positive prediction errors; and (3) people draw around 20 samples on average (see the top row in Fig. 3). Conversely, the traditional description-experience gap arising from apparent underweighting of rare events in EBDs can occur if: (1) learning rates are both >0.75, (2) people learn more rapidly from positive relative to negative prediction errors and draw around 20 samples (see the bottom panel in Fig. 3), or (3) people learning more rapidly from negative prediction errors and draw a large number (~100) of samples.

Although Kellen et al. (2016) found a reversal of the traditional description-experience gap in their aggregate data using CPT modeling, noncomputational analyses (i.e., those relying on the heuristic prediction-focused method critiqued by Regenwetter and Robinson 2017) of their data reveal the traditional description-experience gap as reported by Hertwig et al. (2004). As we described in our simulation study, Kellen et al.’s dataset contains four distinct sets of gambles. Wulff et al. (2018) showed in their meta-analysis that two of these gamble sets show a traditional description-experience gap when analyzed separately: (a) Set 1, which is comprised of the gambles used in the original work by Hertwig et al. (2004) on the description-experience gap, and (b) Set 3, which is comprised of gambles that were chosen to optimize estimation of risk and loss aversion.

This finding that the same exact participants show variation in both the magnitude and direction of the description-experience gap across different sets of gambles is consistent with our simulation study—the contextual nature of learning during EBDs gives rise to apparent differences in valuation across different sets of gambles despite the underlying cognitive mechanisms being invariant. Although experimental designs such as the matched sampling paradigm can partially control for these factors, they still succumb to the unrealistic assumptions described in the introduction (i.e., perfect learning and memory). Therefore, we compared various models that make explicit assumptions about learning and memory during sampling on the dataset as a whole and individually to each of the four sets. We compared models both across and within sets to determine whether the same model (or class of model) could best capture performance across gambles that do versus do not show the traditional description-experience gap.

Competing model specifications

We developed three classes of competing models to determine which cognitive mechanisms provided the best statistical account of within-person preference differences between DBDs and EBDs. Table 1 describes each of the models considered in the current study, which we describe in more detail below.

CPT models

First, we fit an array of traditional CPT models using the heuristic method of setting ${p}_{g,j}$ to the proportion of samples that it was experienced for the given participant. To determine which particular valuation mechanism best accounted for preference differences between DBDs and EBDs according to traditional CPT, we developed models for each combination of differences in probability weighting, risk sensitivity, loss sensitivity, choice sensitivity, or probability elevation for positive and negative outcomes (described in more detail below). We also developed a base model that assumed CPT valuation parameters were identical within-participants across tasks. Of the CPT models, we were particularly interested in the variant with different valuation parameters across DBDs and EBDs (model ${\alpha }_{\Delta }, {\lambda }_{\Delta },{\gamma }_{\Delta }$ in Table 1). This model is theoretically important because, as outlined in the introduction, prior research has suggested that differences in risk sensitivity, loss sensitivity, or probability weighting could explain the description-experience gap.

RL-CPT models

Second, we tested three different variants of the RL-CPT model, including a version with a single learning rate for positive and negative prediction errors, a version with a different learning rate for each positive and negative prediction errors, and a version that includes probability elevation parameters (see section below titled The Role of Probability Elevation). Throughout our results, we focus our attention on the RL-CPT variant used in our simulation study (model ${A}_{\pm }$ in Table 1) due to its theoretical relevance.

IB-CPT models

Third, we tested two variants of the IB-CPT model, including the version described in the introduction (i.e., a memory decay rate with a single set of valuation parameters across description and experience; model ${A}_{IB}$ in Table 1) in addition to one with probability elevation parameters. As with the RL-CPT model, we focus attention on the ${A}_{IB}$ variant due to its theoretical relevance.

The role of probability elevation

Although we did not consider it in our simulation study, we tested variants of Kellen et al.’s (2016) CPT formulation in our empirical model comparisons, which included a probability elevation parameter in the CPT probability weighting function. In particular, Eq. 5 can be expanded as follows:

$$W\left({p}_{g,j}\right)=\frac{{\delta p}_{g,j}^{\gamma }}{({\delta p}_{g,j}^{\gamma }+{\left(1-{p}_{g,j}\right)}^{\gamma })}$$

(9)

ws:where $\delta (0<\delta <+\infty )$ is an added probability elevation parameter that often is interpreted as optimism ($\delta >1$) versus pessimism ($\delta <1$) toward probabilistic outcomes. Mathematically, when $\delta >1$, the probability weighting function is shifted upward, indicating a general overestimation of the strength of probabilities (i.e., optimism); when $\delta <1$, the function is shifted downward, indicating a general underestimation (i.e., pessimism). Oftentimes, a separate $\delta$ parameter is estimated for gains and losses to capture differential optimism or pessimism towards gains versus losses. Kellen et al. (2016) included probability elevation for gains ${\delta }_{+} (0<{\delta }_{+}<+\infty )$ and for losses ${\delta }_{-} (0<{\delta }_{-}<+\infty )$, according to the following rule:

$$\delta=\left\{\begin{array}{lc}\delta+&\mathrm{if}\;x_{g,j}\geq0\\\delta-&\mathrm{otherwise}\end{array}\right.$$

(10)

which sets $\delta$ from Eq. 10 to ${\delta }_{+}$ when the potential outcome ${x}_{g,j}$ for the respective probability ${p}_{g,j}$ is positive, and to ${\delta }_{-}$ otherwise. We tested variants of the CPT, RL-CPT, and IB-CPT models that included differential probability elevation for gains versus losses that either varied or were set to be the same across description and experience.

In addition to including probability elevation parameters, Kellen et al.’s (2016) CPT formulation assumed differences in all parameters across DBDs and EBDs, including all CPT valuation parameters and the choice sensitivity parameter. We term this model the Saturated CPT model, given that it includes both probability elevation parameters described above and assumes that all within-person valuation and choice mechanisms vary across DBDs and EBDs. Saturated CPT contains 12 parameters per person (${\gamma }_{D}, {\gamma }_{E}, {\alpha }_{D},{\alpha }_{E},{\lambda }_{D},{\lambda }_{E}, {{\delta }_{+}}_{D}, {{\delta }_{+}}_{E},{{\delta }_{-}}_{D}, {{\delta }_{-}}_{E},{\varphi }_{D},{\varphi }_{E}$).

Empirical model fitting

As with the simulated model fitting, we used hierarchical Bayesian modeling of all models listed in Table 1. We assumed the same hierarchical structure, with person-level parameters drawn from group-level normal distributions. Likewise, we assumed that group-level means and standard deviations also followed normal distributions centered around 1 for valuation parameters ($\gamma ,\alpha , \lambda$; Eq. 10), and learning rates normally distributed around 0.5. We parameterized learning rates using the same scheme as described by Eq. 10, but with group-level means distributed as ${{\mu }_{A}}_{+}\sim \mathrm{Normal}(0, 0.2)$ and ${{\sigma }_{A}}_{+}\sim \text{half} - \mathrm{Normal}(0, 0.2)$. Unlike in the simulation study, we estimated the choice sensitivity parameter ($\varphi$) for all empirical models, with priors ${\mu }_{\varphi }\sim \mathrm{Normal}(-0.87, 0.2)$ and ${\sigma }_{\varphi }\sim \text{half} - \mathrm{Normal}(0, 0.2)$, where person-level parameters followed the noncentered parameterization described in Eq. 10 (but replacing the inverse probit transform and scaling factor with the exponential transform to ensure $0<\varphi <+\infty$). We used the same prior distribution for a given parameter across all models in order to minimize the potential effects of our choice of prior distribution on model performance (e.g., the prior for $\varphi$ was the same for all models, etc.).

We fit each model using three sampling chains for 3,000 total iterations each, 1,000 of which were discarded from each chain as warm-up samples, resulting in 6,000 total samples for each estimated posterior. To assess model convergence, we visually checked traceplots, and ensured that all $\widehat{R}$ values were under 1.1 (Gelman & Rubin, 1992).

Empirical model comparison

We used the leave-one-out information criterion (LOOIC) to determine which model provided the best fit to the data while penalizing for model complexity (Vehtari et al., 2017). LOOIC is a fully Bayesian information criterion that estimates true leave-one-out cross validation; LOOIC is therefore an estimate of how well a model will perform relative to competing models on out-of-sample data. To compute LOOIC, we first computed the log-likelihood of each participant’s choices given their estimated parameters for each posterior sample (i.e., log pointwise predictive density or LPPD) and gamble (Ahn et al., 2017; Haines et al., 2018). This procedure results in separate posterior samples by participant by gamble ($S\times N\times G)$ LPPD arrays for description- and experience-based gambles. We then combined both arrays on the gamble dimension and input the resulting array in the loo R package (Vehtari et al., 2017) to estimate LOOIC across DBDs and EBDs. Lower relative LOOIC values indicate better than expected out-of-sample predictions for the given model. Alongside LOOIC, we calculated Bayesian model averaging weights (pseudo-BMA+ weights per Yao, Vehtari, Simpson, and Gelman, 2018). Pseudo-BMA weights asymptotically select the single model among a set of models that best minimizes Kullback-Leibler divergence, thus behaving similarly to Bayes Factors for model selection.

We caution that a lower LOOIC (or higher pseudo-BMA+ weights) does not indicate that a model is “true” or a better representation of the cognitive processes of interest in an absolute sense. Instead, we believe that such model comparison metrics are useful to compare the relative predictive performance of various models, and that the theoretical value of each model includes both predictive performance and other more qualitative considerations (e.g., assumptions they make about learning and memory, connections with the broader literature; Navarro, 2019).

Empirical results

Model comparison

Figure 4 shows the estimated differences in model fit between the best fitting model and all competing models, both across all 114 gambles and within each of the 4 gamble sets. Within each gamble set, LOOIC results showed that learning and memory models (RL-CPT and IB-CPT models) performed equal to or better than those assuming perfect learning with changes in valuation parameters across DBDs and EBDs (traditional CPT models). Across all sets, the RL-CPT with asymmetric learning and a single set of valuation and choice parameters across DBDs and EBDs (model ${A}_{\pm }$ in Table 1) performed better than all variants of CPT, including the most complex CPT model (i.e., the Saturated CPT model with 12 free parameters per person). Similarly, the IB-CPT model with probability elevation parameters showed better performance than all CPT models, although it performed worse than the RL-CPT model with asymmetric learning rates. This latter finding demonstrates the importance of asymmetric learning for predicting behavior in EBDs.

Fig. 4

Comparison of competing models. Note. Relative difference in leave-one-out information criterion (LOOIC) between the best fitting model and all other models within each gamble set, where lower LOOIC values indicate better model fit while penalizing for model complexity (see Table 1 for model notation and descriptions). Numbers in each row indicate the pseudo-BMA+ weights for each model within the given set. Sets 1 and 3 show the traditional description-experience gap, and Sets 2 and 4 show a reversed gap (see Participants and Experiment section; Wulff et al., 2018). Error bars reflect ±1 standard errors of the difference between the best fitting model within each gamble set and the respective competing model

Overall, our model comparison results offer strong evidence that people do have imperfect learning and memory while sampling during EBDs—asymmetric learning alone (model ${A}_{\pm }$ in Table 1) can better capture within-person changes in behavior across DBDs and EBDs than a model assuming perfect learning/memory and changes in all valuation and choice mechanisms (the Saturated CPT model).

Posterior Predictions

To better understand the absolute performance of the models, we focus attention on posterior predictions derived from the model in each class that we deemed most theoretically relevant given prior research on the description-experience gap: (1) the ${\alpha }_{\Delta }$, ${\lambda }_{\Delta }$, ${\gamma }_{\Delta }$ variant of CPT; (2) the ${A}_{\pm }$ variant of RL-CPT; and (3) the ${A}_{IB}$ variant of IB-CPT. Despite these models not showing the best fit to empirical data within a given gamble set, we believe they best instantiate competing theories of the description-experience gap as detailed in the introduction. Figure 5 shows the group-level predictive performance for each of the three models. Notably, the models are almost indistinguishable in the description condition, yet the RL-CPT shows generally better predictive performance in the experience condition. For a more fine-grained view of Fig. 5, Table S1 includes the group-level observed and predicted choice proportions for each individual gamble and for each model.

Fig. 5

Posterior predictive distributions derived from CPT and RL-CPT across description and experience. Note. Posterior predictive distributions for both CPT (the ${\alpha }_{\Delta }$, ${\lambda }_{\Delta }$, ${\gamma }_{\Delta }$ variant from Table 1), RL-CPT (${A}_{\pm }$ from Table 1), and IB-CPT (${A}_{IB}$ from Table 1) for each of the 114 choice problems/gambles across description and experience. Pr(Choose B) indicates the proportion of participants choosing option B for each gamble. The dark red points indicate the in-sample (i.e., observed) Pr(Choose B). Note that gambles were reordered by the observed Pr(Choose B) within each condition for interpretability. Light red points and intervals indicate the model-predicted means and 95% highest density intervals of Pr(Choose B), and the annotated text in each panel is the posterior mean and 95% HDI (in square brackets) for the correlation between observed and posterior-predicted Pr(Choose B). The models are practically indistinguishable in the description condition, yet the RL-CPT exhibits generally more accurate predictions in the experience condition relative to both other models.

Interpreting Model Parameters

The posterior distributions for group- and person-level parameters from the ${A}_{\pm }$ variant of RL-CPT model are shown in Fig. 6. The group-level negative prediction error learning rate is larger than the group-level positive prediction error learning rate (95% highest density interval [HDI] of ${A}_{-}-{A}_{+}$= [0.13, 0.24]), which is consistent with previous literature and indicates risk-averse learning (Cox et al., 2015; Doll et al., 2009; Frank et al., 2004, 2007; Gershman, 2015; Mihatsch & Neuneier, 2002; Niv et al., 2012). Furthermore, the magnitudes of the learning rates for positive (95% HDI of ${A}_{+}$ = [0.19, 0.25]) and negative (95% HDI of ${A}_{-}$ = [0.35, 0.45]) prediction errors were consistent with what our simulations predicted based on previous studies. Specifically, traditional CPT modeling would indicate more overweighting of rare events in EBDs relative to DBDs given the absolute magnitude and the differences between learning rates (Fig. 3, top panels), a finding that is consistent with previous applications of CPT to these data (Kellen et al., 2016). Lastly, the valuation parameters from the RL-CPT resemble those classically found for DBDs—we found evidence for risk aversion (95% HDI of $\alpha$ = [0.61, 0.65]), loss aversion (95% HDI of $\lambda$ = [1.14, 1.35]), and overweighting of rare events (95% HDI of $\gamma$ = [0.62, 0.72]). This indicates that the “traditional” overweighting of rare events from CPT may still be present in EBDs but that it is masked by the presence of asymmetric learning in the sampling process. The person-level posterior distributions demonstrate that there are strong individual differences in learning rates and valuation parameters alike, which provides further evidence against the assumption that people have perfect learning and memory during EBDs.

Fig. 6

Posterior distributions of group- and person-level RL-CPT parameters. Note. Posterior distributions for each group- and person-level parameter from the ${A}_{\pm }$ variant of the RL-CPT. The group-level panels show the posterior density of the group-level mean for each parameter. The annotation on each panel represents that posterior mean and 95% HDI of the corresponding group-level mean parameter. Points and intervals for the bottom panel indicate the means and 95% HDI for each of the person-level parameters. The dashed gray line is simply included as a visual reference, indicating 0.5 for the learning rates and 1 for the valuation/choice parameters. Note that the group-level valuation parameters are in the same direction as those found in Tversky and Kahneman’s (1992) original analyses of DBDs, indicating risk aversion ($\alpha <1$), loss aversion ($\lambda >1$), and overweighting of rare/low probability events ($\gamma <1$) across both DBDs and EBDs.

Discussion

In the current study, we used a combination of computational model simulations and empirical model fitting to show that preference differences between description- and experience-based gambles can be attributed to an asymmetric learning mechanism rather than context-dependent changes in psychological valuation across tasks. We developed a hybrid reinforcement learning and cumulative prospect theory (RL-CPT) model that used separate learning rates for positive and negative prediction errors and assumed that probabilities and outcomes are valued equivalently across DBDs and EBDs. Through Bayesian model comparison, we found that the ${A}_{\pm }$ variant of the RL-CPT model (Table 1) provided a better account of within-subject differences in DBDs versus EBDs compared with traditional CPT models that assume perfect learning and memory with differences in risk aversion, loss aversion, probability weighting, choice sensitivity, and probability elevation for gains and losses (i.e., saturated CPT).

Put together, the RL-CPT offers improved performance for EBDs without compromising performance on DBDs relative to traditional CPT models (Fig. 5). The RL-CPT with asymmetric learning also performed better than a competing instance-based memory model (${A}_{IB}$ from Table 1). While other studies have shown that learning and memory models can account for EBDs (Busemeyer & Myung, 1992; Erev & Roth, 1998; Estes, 1976; Gonzalez et al., 2011; Hau et al., 2008), they did not demonstrate any ability to capture the description-experience gap. To our knowledge, this is the first study to directly and quantitatively compare a variety of computational models that make explicit assumptions regarding how learning and memory can give rise to preference differences between DBDs and EBDs. This was only possible because the learning and memory models that we developed directly estimate the payoff probabilities associated with each outcome, which allows for them to simultaneously capture decisions from both description- and experience-based tasks in a straightforward manner.

The RL-CPT (${A}_{\pm }$ variant) suggests that foundational cognitive biases, including risk aversion, loss aversion, and overweighting of rare events, hold true across both DBDs and EBDs when asymmetric learning during sampling in EBDs is accounted for (Fig. 6). Furthermore, our finding that people learn more rapidly from negative as opposed to positive predictions errors extends previous findings (Cox et al., 2015; Doll et al., 2009; Frank et al., 2004, 2007; Gershman, 2015). A higher learning rate for negative as opposed to positive prediction errors produces “risk sensitive” decision-making (Mihatsch & Neuneier, 2002). Conceptually, it follows that typical CPT valuation parameters—which also capture risk sensitivity—could be poorly estimated in EBDs if asymmetric learning occurs. Indeed, our simulations confirmed this quantitatively, predicting that more rapid learning of negative relative to positive prediction errors will lead to an underestimation of probability weighting in EBDs relative to DBDs when using traditional CPT modeling (Fig. 3), which can explain contextual effects of more overweighting of rare events in EBDs compared with DBDs (Glöckner et al., 2016; Kellen et al., 2016). To the extent that these learning rates vary across the lifespan, we might observe apparent differences between older and younger adults that are specific to experience-based decisions and physiological measures (Rosenbaum et al., 2021). Responses to positive and negative surprises will impact not only probability weighting and value sensitivity but also measures like pupil dilation that are known to reflect the magnitude prediction errors during learning on these types of tasks (Braem et al., 2015; Lavín et al., 2014).

Given previous findings that people learn more rapidly when experiencing intense negative rather than positive affect (Haines et al., 2019), future research may explore the relationships between physiological states and learning throughout EBDs. Such studies may reveal insights into the known differences in risky decision-making between healthy and clinical populations (Ahn et al., 2014; Maner et al., 2007; Yechiam et al., 2005). Lastly, because both valuation and learning mechanisms interact to produce behavior, the competing effects of overweighting rare events and risk-averse learning may produce the expected-value maximizing behavior that often is observed in EBDs (Wulff et al., 2018). Indeed, it is an open question why people make more choices that maximize expected value in EBDs relative to DBDs, and risk-averse learning mechanisms may provide a partial explanation.

An important limitation of the current study is that the RL-CPT model does not predict participant’s sampling behavior, which means that it is not a full generative model of how people behave during EBDs. Part of the reason for this is that sampling behavior is intensely idiosyncratic, with information search varying according to momentary fluctuations in experienced sample variance, participants working memory capacity, and sampling heuristics that vary widely across participants or even within a session (Kopsacheilis, 2018). Despite this, models, including search or optional stop** rules, show promising results (Busemeyer, 1985; Markant et al., 2015; Wulff et al., 2019) and may be well-suited to integrate with models, such as the RL-CPT. Nevertheless, RL-CPT does account for variation in behavior across participants by leveraging the information that they gain across samples to estimate the learning rates (Eq. 8). Furthermore, the learning mechanism of the RL-CPT is generalizable in the sense that it can be applied to both sampling EBDs, repeated choice EBDs, and EBDs with more than two choices. Specifically, if each sample that participants draw is treated as a choice (i.e., preference judgement in Fig. 1), the probability estimates and resulting expected values on each sample (or trial in repeated choice tasks) can be used to estimate the likelihood of repeated, trial-by-trial choices for each choice option (Gershman, 2015; Haines et al., 2019; Niv et al., 2012). Therefore, we view the addition of an optional stop** rule as a task-specific extension, and not a competing mechanism, of the RL-CPT.

In summary, our findings suggest that future research on the description-experience gap should focus on learning, memory, search (i.e., during sampling), and optional stop** mechanisms, all of which could lead to deeper insights into human decision-making under risk. Additionally, future studies could use experimental manipulations that are known to influence learning rates to determine if the RL-CPT can capture subsequent changes in risk preferences. More broadly, our findings demonstrate the benefits of using formal computational cognitive models of behavior to understand how individual differences at one level-of-analysis (e.g., psychological mechanisms) can affect inferences made at another level (e.g., behavioral differences). Computational modeling allowed us to merge different areas of research (i.e., reinforcement learning and risky decision-making) in a formalized, straightforward way, which led to circumscribed predictions regarding the relationship between psychological mechanisms (i.e., probability and outcome valuation), neural mechanisms (i.e., differential dopamine response to positive versus negative prediction errors), and an observed behavioral phenomenon (i.e., the description-experience gap). We then leveraged Bayesian model comparison of multiple competing theoretical models to determine which theory was most consistent with the data. This work therefore extends the past modeling work on the essential learning component of EBDs (Busemeyer & Myung, 1992; Erev & Roth, 1998; Gonzalez et al., 2011; Haines et al., 2018; Hau et al., 2008) in a theoretically motivated way to solve an empirical paradox.

Conclusions

Asymmetric learning offers causal mechanisms to explain the apparent changes in probability weighting—and valuation more generally—across both description- and experience-based decisions and different forms of experience-based decisions. Classic findings of risk-aversion, loss-aversion, and overweighting of rare events can apply for both description- and experience-based decisions, but only when asymmetric learning is appropriately incorporated. More work needs to be done to refine joint models of description and experience that are both predictively powerful and psychologically realistic with regard to mechanisms underlying learning and memory in addition to valuation and action selection. More broadly, computational models offer a formalized way to combine substantive theories from different areas of research, which can reveal simple rules underlying otherwise complex, context-dependent psychological effects inferred using theoretically inconsistent statistical procedures.