Introduction

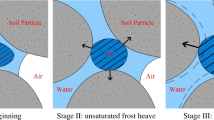
Frost heave in the soil leads to various engineering problems, such as cracks in road pavements, slope failures, damage to structures, and destruction of pipelines. This phenomenon is complex, involving coupling of thermal, hydraulic, and mechanical behaviors. To conduct reliable analyses and research on frost heave, a fundamental understanding of its mechanisms is essential. Frost heave can be distinguished by volume expansion caused by phase changes in pore water (in-situ freezing) and volume expansion resulting from ice lens formation. Generally, the volume expansion due to in-situ freezing is approximately 9% [1]. However, frost heave caused by ice lens formation can expand up to several tens of centimeters, leading to a severe damage to ground structures (Fig. 1).

Fig. 1
figure 1

Damage caused by frost heave (image sources: left [14], right [17])

Full size image

In recent times, as abnormal climate patterns have been increasing, many countries, including Europe, United States, China, and Russia, are experiencing a higher likelihood of frost heave occurrences. Consequently, the research on prediction of frost heave damage has become crucial. Furthermore, considering the ongoing development of urban infrastructure in permafrost regions of these countries, the prevention of damages caused by frost heave is expected to become an important task.

Extensive studies have been carried out on frost heave. Taber [24] proved that frost heave caused by ice lens formation is the primary factor for volume expansion of frozen soil through experiments using benzene. In the 1960s and 1970s, mainly studies using the capillary theory based on the Laplace surface tension equation were conducted [5, 18]. Later, the segregation potential (SP0) model was proposed for frost heave prediction [9]. Furthermore, an analysis model that indirectly simulates frost heave using a porosity rate function was proposed [12], and subsequent studies related to this model have been conducted [13, 29]. Laboratory experiments and numerical analysis were actively conducted for soil freezing characteristic analyses. Song et al. [21] and Kim et al. [8] investigated the thermal conductivity characteristics of frozen soil. Shin and Park [19] investigated the frost heave pressure characteristics according to the unfrozen water content within a frozen soil. Subsequently, Shin et al. [20] developed a thermo-hydro-mechanical (THM) constitutive model for porous materials through a numerical analysis. Other THM modeling studies using the Clausius–Clapeyron equation to simulate cryogenic suction of freezing soils has also been conducted [7, 10, 11, 15, 16, 22, 23, 25, 32]. For example, Nishimura et al. [16] developed a fully coupled THM model including a new mechanical model, and verified the model’s performance by referring to the in-situ pipeline frost heave test. Suh and Sun [22] conducted THM analysis based on a multiphase-field microporchanics theory. Go et al. [7] conducted a sensitivity analysis on influencing factors related to frost heave by a THM analysis on a frost-susceptible soil.

Despite the considerable number of THM studies on frost heave, most of them have focused on laboratory experiments and the analysis of frozen soil characteristics and behaviors at the specimen scale. This is because the fully coupled THM model using the Clausius–Clapeyron equation tends to exhibit significant convergence issues when simulating frost heave behavior at the in-situ scale. For this reason, there are only a few cases where the response behavior of retaining wall structures interacting with frost heave in the soil has been evaluated. Particularly, there is a significant lack of research that considers the initial ground water level conditions, and retaining wall design guidelines. Therefore, in this study, we conducted a porosity rate function-based numerical analysis to assess the mechanical behavior of concrete retaining wall structures susceptible to frost heave damages. Additionally, the mechanical responses of the retaining wall structures subjected to frost heave was evaluated, considering realistic initial ground water level conditions and design guidelines.

Numerical analysis

Mechanism of frost heave in soil

When freezing occurs near the surface of a frost-susceptible soil, the unfrozen moisture in the unfrozen zone moves toward the freezing front due to cryogenic suction. This process is driven by the thermal gradient in the ground. As a result, ice lenses are formed continuously. The expansion displacement of soil that occurs during this process is referred to as frost heave. There are three prerequisites for frost heave occurrence [13]: (1) the soil should be frost-susceptible, such as silty soil; (2) there should be a continuous water supply; and (3) the thermal conditions that induce frost heave should be met. The freezing front movement should be sufficiently slow to allow the unfrozen pore water to migrate toward the freezing front.

Energy conservation equation

In this analysis, the following assumptions were applied to effectively simulate the frost behavior of frost-susceptible soil.

  1. I.

    The soil’s material properties are considered to be isotropic.

  2. II.

    The soil is a fully saturated medium, and is considered to have a three-phase structure consisting of soil particles, water, and ice.

  3. III.

    Three-phase soil materials satisfy the local thermal equilibrium.

Then, the study employed the Abaqus UMATHT user subroutine to define the thermal property change according to the volumetric fractions of constituent components (soil particles, pore water, ice) in a saturated frost-susceptible soil material. The aim of this code is to characterize the thermal property variations and latent heat effects associated with variations in unfrozen water content. Assuming local thermal equilibrium, the temperature variation in the freezing soil can be simulated through the following energy conservation equation [4, 13]:

$$\left(\rho C - L\frac{{\partial \theta_{i} }}{\partial T}\rho_{i} \right)\frac{\partial T}{{\partial t}} + \nabla ( - \lambda_{eff} \nabla T) = 0$$
(1)

where T is the soil temperature (℃), L is the latent heat of fusion per unit mass of water (kJ/kg), ρi is the density of ice (kg/m3), and t is time. Equation (1) includes a term representing the energy release due to the phase change of pore water during freezing. The volumetric heat capacity (ρC) and effective thermal conductivity (λeff) of the soil are expressed as functions of the volume fraction of each constituent in the soil.

$$\rho C = \sum\limits_{j} {\rho_{j} C_{j} \theta_{j} } ,\quad j = s,w,i$$
(2)
$$\lambda_{eff} = \prod\limits_{j} {\lambda_{j}^{{\theta_{j} }} ,\quad } with\;\sum\limits_{j} {\theta_{j} = 1} ,\quad j = s,w,i$$
(3)

where θj is the volume fraction of each constituent in the soil, where the subscripts s, w, and i refer to soil particles, pore water, and ice, respectively. Each volume fraction can be defined as

$$\theta_{s} = 1 - n, \, \quad \theta_{w} = nS_{u} = \frac{{\rho_{s} }}{{\rho_{w} }}(1 - n)\omega , \, \quad \theta_{i} = n(1 - S_{u} ) = n - \frac{{\rho_{s} }}{{\rho_{w} }}(1 - n)\omega$$
(4)

where n is the porosity of soil and Su is the unfrozen water saturation, ρw is the density of water (kg/m3), ρs is the density of soil particle (kg/m3), ω is the gravimetric unfrozen water content.

Soil freezing characteristic curve (SFCC)

In the freezing process of the soil, some amount of moisture in the pores exists in an unfrozen state, which is referred to as unfrozen water [26, 28]. The unfrozen water is determined by the type of soil and characteristics of the soil particle size distribution. The relationship between the unfrozen water content and subzero temperatures in a freezing soil is referred to as soil freezing characteristic curve (SFCC), a concept similar to the soil water characteristic curve (SWCC) for an unsaturated soil [3, 27]. The SFCC is an important input parameter used in numerical analyses related to geotechnical engineering, such as frost heave and artificial ground freezing simulations. Various models related to the estimation of the SFCC have been proposed (Table 1). As an example, Michalowski [12] proposed the following empirical model for the unfrozen water content curve, which is based on unfrozen water measurements carried out by Anderson and Tice [2].

$$\omega_{u} = \left\{ \begin{aligned} &\omega_{o} \, \quad \, \quad \, \quad \, \quad \, \quad \, \quad \, \quad \, \quad \, \quad \, \quad \quad \quad T \ge T_{0} \hfill \\ & \omega_{r} + (\omega_{o} - \omega_{r} )\exp [\mu (T - T_{0} )] \, \quad T < T_{0}^{{}} ,^{{}} {\raise0.7ex\hbox{${\partial T}$} \!\mathord{\left/ {\vphantom {{\partial T} {\partial t}}}\right.\kern-0pt} \!\lower0.7ex\hbox{${\partial t}$}} < 0 \hfill \\ \end{aligned} \right.$$
(5)

where ω0 is the initial gravimetric water content under nonfreezing conditions, ωr is the residual gravimetric water content at low temperatures, T0 is the freezing point of the soil, and μ is a curve-fitting coefficient that varies depending on the material properties of the soil. Michalowski and Zhu [13] determined the curve-fitting parameters of the empirical model based on unfrozen water data measured by Fukuda et al. [6] for a clay specimen (ω0 = 0.285, ω0 = 0.285, μ = 0.16 ℃−1). In this study, the same curve-fitting coefficients were applied to the simulation model (Fig. 2).

Table 1 Empirical model for the estimation of the SFCC
Full size table
Fig. 2
figure 2

SFCC proposed by Michalowski and Zhu [13]

Full size image

Porosity rate model

In this study, to predict the frost heave behavior in frost-susceptible soils, the porosity rate model proposed by Michalowski [12] was applied to the simulation model. The porosity rate model in Eq. (6) is a function that simulates the variation in porosity rate of the soil due to freezing. This model has the advantage of prediction of the frost heave process without the need for a separate fluid flow analysis.

$$\dot{n} = \dot{n}_{m} \left( {\frac{{T - T_{0} }}{{T_{m} }}} \right)^{2} \cdot e^{{1 - \left( {\frac{{T - T_{0} }}{{T_{m} }}} \right)^{2} }} \cdot \frac{{\left| {\frac{\partial T}{{\partial l}}} \right|}}{{g_{T} }} \cdot e^{{ - \frac{{\left| {\overline{\sigma }_{kk} } \right|}}{\zeta }}}$$
(6)

where nm is the maximum rate of change in porosity (s−1), Tm is the temperature at the occurrence of nm, T is the temperature of the soil, T0 is the freezing point of the soil, \(\left| {{\raise0.7ex\hbox{${\partial T}$} \!\mathord{\left/ {\vphantom {{\partial T} {\partial l}}}\right.\kern-0pt} \!\lower0.7ex\hbox{${\partial l}$}}} \right|\) is the temperature gradient in the soil (℃/m), and gT is the temperature gradient at Tm. \(e^{{ - \left| {\overline{{\sigma_{kk} }} } \right|/\varsigma }}\) considers the frost heave suppression due to the overburden pressure on the soil, σkk is the first invariant of stress in the soil, and ζ is a parameter determined by the type of soil. The incremental change (dn) in the porosity is then determined (i.e.,\(dn=\dot{n}dt\)). Assuming the old porosity at time t is nt, the updated porosity at time t + dt can be expressed as follow.

$$n_{t + dt} = \frac{{n_{t} + dn}}{1 + dn}$$
(7)

Thus, the volume fractions of Eq. (4) are recalculated after updating the porosity at the end of each time step using the following relationships [33].

$$(\theta_{s} )_{t + dt} = 1 - n_{t + dt}$$
(8)
$$(\theta_{w} )_{t + dt} = \frac{{\rho_{s} }}{{\rho_{w} }}\omega_{t + dt} (1 - n_{t + dt} )$$
(9)
$$(\theta_{w} )_{t + dt} = n_{t + dt} - \frac{{\rho_{s} }}{{\rho_{w} }}\omega_{t + dt} (1 - n_{t + dt} )$$
(10)

Equilibrium equation

In this modeling study, it is assumed that the frozen soil reacts to applied loads in an elastic manner; however, the elastic properties depend on the temperature. Thus, the equilibrium equation is as follow.

$$\nabla \sigma_{ij} + F_{i} = 0$$
(11)

where σij is the total stress (Pa), Fi is the body force (N).

Meanwhile, the total strain increment consists of both elastic strain increment (\(d\varepsilon_{ij}^{e}\)) and strain increment due to the change in porosity (\(d\varepsilon_{ij}^{p}\)) [33].

$$d\varepsilon_{ij} = d\varepsilon_{ij}^{e} + d\varepsilon_{ij}^{p}$$
(12)

The elastic increment can be defined by the elastic constitutive law as follow.

$$d\varepsilon_{ij}^{e} = B_{ijkl} d\sigma_{kl}$$
(13)

where Bijkl is the elastic compliance tensor, which is dependent on the soil temperature. dσkl is the Cauchy total stress tensor increment.

ABAQUS subroutine for a TM analysis

In this study, the frost heave was simulated using a user subroutine of the commercial numerical software ABAQUS. As illustrated in Fig. 3, the temperature and displacement fields are successively updated using an isothermal operator splitting solution scheme, instead of employing a monolithic solver. The two user subroutines used in this study (UMATHT and UEXPAN) interact with each other at each time increment and contribute to the analysis. UMATHT is a user subroutine that defines the thermal properties and volumetric changes of soil particles, water, and ice at each integration point, while UEXPAN is involved in the expansion of the soil due to the frost heave. The strain increment matrix regarding the frost heave under two-dimensional (2D) plane strain conditions is expressed as follow [13, 33].

$$\left\{ {\begin{array}{*{20}c} {d\varepsilon_{x}^{p} } \\ {d\varepsilon_{y}^{p} } \\ {d\varepsilon_{xy}^{p} } \\ \end{array} } \right\} = \left[ {\begin{array}{*{20}c} {m^{2} } & {n^{2} } & { - mn} \\ {n^{2} } & {m^{2} } & {mn} \\ {2mn} & { - 2mn} & {m^{2} - n^{2} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {d\varepsilon_{11}^{p} } \\ {d\varepsilon_{22}^{p} } \\ {d\varepsilon_{12}^{p} } \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} {m^{2} [\xi + \frac{1}{2}\mu (1 - \xi )] + n^{2} \frac{1}{2}(1 + \mu )(1 - \xi )} \\ {n^{2} [\xi + \frac{1}{2}\mu (1 - \xi )] + m^{2} \frac{1}{2}(1 + \mu )(1 - \xi )} \\ {mn(3\xi - 1)} \\ \end{array} } \right\}\dot{n}dt$$
(14)

where ζ is a value ranging from 0.33 to 1. If ζ equals 0.33, it signifies isotropic volume expansion, whereas ζ equal to 1 indicates one-dimensional volume expansion. μ is the Poisson’s ratio. m and n are denoted as cos(θ) and sin(θ), respectively, where θ is the angle between the x-axis and direction of heat flow direction. θ is calculated by following equation [33].

$$\theta = \tan^{ - 1} \left[ {\left( {\frac{\partial T}{{\partial y}}} \right)/\left( {\frac{\partial T}{{\partial x}}} \right)} \right]$$
(15)
Fig. 3
figure 3

Flow chart for determination of strain increment caused by frost heave [33]

Full size image

The strain increment matrix calculated by Eq. (14) is defined at the end of each time step within the UEXPAN subroutine. The numerical analysis model used the implicit finite-element solver, ABAQUS Standard, and was discretized using the CPE4T element, a four-node quadrilateral plane strain element for a thermal stress analysis. The frost heave analysis was applied only to the frost-susceptible soil in the entire analysis domain. The mechanical response behavior of the concrete retaining wall structure due to frost heave was evaluated based on the linear elastic model. The material properties used in the numerical analysis are listed in Table 2. The material properties used in the model were obtained from a previous study [13].

Table 2 Material properties used in the numerical simulation model
Full size table

Initial and boundary conditions

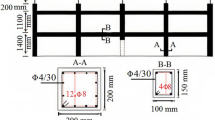
In recent retaining wall designs, a highly permeable backfill material such as sand or gravel is used behind the retaining wall to prevent deformation or failure caused by pore water pressure or frost heave pressure acting on the back of the wall. Additionally, drainage systems are commonly installed at the bottom of the wall [14]. In this study, to consider the design conditions of such retaining wall structures, initial groundwater levels were set considering the effects of the drainage material installed on the back of the retaining wall. The soil below the groundwater level was considered to be a fully saturated frost-susceptible soil, while the other soil was assumed to be an unsaturated and significantly less frost susceptible soil (Fig. 4). Herein, the initial water content of the saturated ground in unfrozen state was assumed to be approximately 0.285. Furthermore, a preprocessing was performed to examine the realistic initial groundwater level and temperature distribution in the winter season. Subsequently, a constant-temperature condition (-20 °C) was imposed at the ground surface boundary for 90 days to gradually initiate freezing from the ground surface. The shape and dimensions of the retaining wall structure were set according to Zhu [33] for reference.

Fig. 4
figure 4

Boundary conditions and analysis domain specifications (unit: m)

Full size image

Results and discussion

Validation of the frost heave model

Before the evaluation of the mechanical response behavior of the retaining wall due to frost heave from the soil, the prediction reliability of the simulation model used in this study was analyzed. This technique has been validated through comparisons to frost heave experimental results by Fukuda et al. [6] in previous studies [13, 29]. In Fukuda’s 1D freezing experiment, the step-freezing method involves applying constant temperatures to the top and bottom of the specimen, gradually freezing it from the bottom to the top. This method considers ice lens growth in one direction. As a result of the experiment, final frost heave amount for a specimen with a height of 7 cm was approximately 15 mm, while the frost depth was approximately 5 cm [6]. Figure 5 compares the frost heave experimental results of Fukuda et al. [6], predictions of Michalowski and Zhu [13], and simulation results obtained by the model used in this study. Under the same experimental conditions, the simulation results of this study closely match the experimental results of Fukuda et al. [6] and prediction results of Michalowski and Zhu [13].

Fig. 5
figure 5

Comparison results for the one-dimensional frost heave test with step freezing conditions

Full size image

After model validation, we performed numerical analyses for three cases, as shown in Fig. 6, to evaluate the response behavior of the retaining wall interacting with a frost-susceptible soil. The results of these analyses were compared. Case 1 represents conditions where the groundwater level has risen to the ground surface in the backfilled subgrade (conditions where the entire backfilled subgrade is considered as a frost-susceptible soil). In Case 2, the groundwater level has lowered to some extent in a portion of the backfilled subgrade considering the actual initial groundwater level during the winter season. Case 3 represents the initial groundwater level conditions considering the influence of drainage materials installed on the backside of the retaining wall.

Fig. 6
figure 6

Simulation domain according to the location of the initial groundwater level and presence of the drainage material

Full size image

Comparison of analysis results for different initial groundwater levels

Figures 7 and 8 present simulation results of frost heave and response behavior of the retaining wall based on different initial groundwater levels under conditions without drainage material (comparison of Cases 1 and 2). The legend indicates the state variables used in the ABAQUS user subroutine, where SDV13 represents the porosity of the soil and NT11 represents the soil temperature. Figure 7a shows the simulation results when the entire backfill is a frost-susceptible soil, while Fig. 7b presents results of a simulation considering realistic initial groundwater levels that could form during the winter season obtained through a preprocessing analysis. According to the contour results in Figs 7c and d, the advancement of the freezing front observed within the frost-susceptible soil determines the region where frost heave occurs. The total frost heave amount was larger in Case 1 than in Case 2. However, the maximum von Mises stress acting on the retaining wall due to frost heave was higher in Case 2, as shown in Fig. 8. This occurred because the unsaturated soil in the upper part of the groundwater level, which does not exhibit frost heave, acts as an overburden pressure on the frost-susceptible soil, restraining vertical displacements and resulting in a larger horizontal frost heave pressure acting toward the retaining wall.

Fig. 7
figure 7

Comparisons of porosity and temperature for Case 1 and 2. Case 1: unrealistic initial GWL condition. i.e., initial GWL is located at ground surface, Case 2: realistic initial GWL condition in winter season

Full size image
Fig. 8
figure 8

Comparisons of von Mises stress and deformation change for Cases 1 and 2

Full size image

Comparison of analysis results with drainage

Figures 9 and 10 show analysis results according to the presence of drainage material at the back of the retaining wall (comparison between Cases 2 and 3). In cases where the drainage material is present, there was a significant reduction in the von Mises stress exerted on the retaining wall due to frost heave. As shown in Fig. 10, under the condition where the drainage material is present at the back of the retaining wall, the von Mises stresses acting on the retaining wall were approximately 1/7 of the stresses observed in the absence of the drainage material. This is possibly due to changes in groundwater levels after the installation of drainage. With the installation of drainage material in the backfill soil, fully saturated area subjected to frost heaving has been reduced. Consequently, even though similar temperature contours are identified for both Cases (Fig. 9c and d), Case 3 generated relatively lesser amounts of frost heave (Fig. 9a and b). It appears that the drainage material has acted as a buffer, preventing frost heave pressure from acting on the retaining wall. This implies that the presence of drainage material behind the retaining wall can significantly influence its response to frost heave. Therefore, it is necessary to consider the influence of the drainage material when assessing the mechanical response of the retaining wall.

Fig. 9
figure 9

Comparisons of porosity and temperature for Case 2 and 3. Case 2: realistic initial GWL condition, Case 3: realistic initial GWL condition with drainage installed

Full size image
Fig. 10
figure 10

Comparisons of von Mises stress and deformation change for Case 2 and 3

Full size image

Limitations

In this study, the concrete retaining wall was considered as an elasto-plastic material to evaluate the mechanical behavior of the retaining wall under frost heave pressures. Although it is possible to identify sections where the structural vulnerability is expected to be high based on the distribution of von Mises stress exerted on the retaining wall, the assessment technique limitations hinder the evaluation of internal damages and failure zones within the wall. Furthermore, a highly advanced thermo-hydro-mechanically coupled model still needs to be developed, which can be combined with a proper set of constitutive laws depending on the effective stress, suction, and temperature. This is essential even in the geotechnical problem with in-situ scale. Therefore, for assessing the vulnerability and damage of the retaining wall due to frost heaving of the backfill soil, a highly improved modeling schemes for both the soil and concrete retaining wall need to be developed in future studies.

Conclusions

In this study, a porosity rate function-based TM model was used to numerically evaluate the mechanical behavior of the retaining wall caused by frost heave in a frost-susceptible soil. A comparative analysis was conducted to evaluate the variations in the response and interpretation results of the interaction between the frost-heave soil and retaining wall structure according to the initial groundwater level in the retaining wall backfill and presence or absence of a drainage material. Based on the findings, the following conclusions can be summarized.

The modeling technique used in this study is based on the TM model with the porosity rate function proposed by Michalowski and Zhu [13], which provided a good agreement with the results of one-dimensional frost heave experiments conducted by Fukuda et al. [6] and simulation results reported by Michalowski and Zhu [13]. Subsequently, the numerical analysis model was scaled up from the specimen size scale to the ground-wall structure size scale, which enabled to evaluate the response behavior of the retaining wall structure interacting with the frost-heaved soil.

The response behavior of the retaining wall due to frost heave varies depending on the initial groundwater level of the backfill ground. As the initial groundwater level on the retaining wall's backfill lowers, the absolute amount of frost heave decreases. On the other hand, the von Mises stress exerted on the retaining wall due to frost heave was even larger. This phenomenon can be attributed to the unsaturated soil above the groundwater level exerting a downward pressure on the frost-heave soil, restraining vertical displacements and causing a concentration of frost heaving pressure in the horizontal direction toward the wall.

Under the conditions where the drainage material was present on the retaining wall's back face, the stress exerted on the wall due to frost heaving was significantly lower, approximately 1/7 of the level with the conditions without drainage material. The frost heave response behavior of the retaining wall structure varied significantly with the presence of the drainage material on the back of the retaining wall. These findings underscore the necessity of consideration of the influence of the drainage material for the assessment of the mechanical response behavior against frost heaving.