Introduction

With the significant advances of Internet of Things (IoT), large amounts of data are generated through terminal IoT devices at the edge of the network [1]. Edge computing [2], that extends the capabilities of cloud centre to locations close to terminal IoT devices, has been widely recognized as a potential big data analysis framework. To further mine the potential value of IoT big data, there is an increasing need to bring machine learning (ML) to edge computing, namely edge learning [3, 4]. However, if all data analysis and processing tasks are placed on the edge nodes, the quality of data analysis services is difficult to guarantee due to the limited capabilities of edge nodes [5]. Moreover, in some scenarios, single edge node holds incomplete training data and wants to cooperate with the cloud center to accomplish the model training.

Unfortunately, the data collected by edge nodes from terminal IoT devices is generally valuable and sensitive, and is not able to be directly exchanged in real-world applications due to regulatory regulations and commercial competition [6]. That is, data is commonly stored locally and isolated among different data nodes, which is also called the “data isolation” problem [7]. Blockchain, as a decentralized, distributed, and immutable ledger structure, is considered an adaptable alternative for tackling trust-absence issue in a distributed environment. Consequently, the distributed structure of blockchain is suitable for building cloud-edge collaborative computing [8]. Blockchain technology has been used ensure the security and fairness of data processing. Recently, there is a growing focus on training machine learning models across distributed blockchain nodes without compromising privacy or violating regulations. The concept of collaborative learning (CL) has been introduced [9] to meet such requirements, which refers to the process where all parties keep training data locally and can collaboratively train a joint model without exchanging their raw data [10]. Recently, CL for logistic regression (CLLR) [11] has received considerable attention for its efficiency, simplicity and interpretability, which offloads the logistic regression (LR) training tasks of edge nodes to the cloud center. Based on privacy protection methods like homomorphic encryption (HE) [12], secure multi-party computation (MPC) [13], and differential privacy (DP) [14], several privacy-preserving CLLR schemes have been proposed. According to the distribution characteristics of training data, the existing works [15,16,17,18,19,20,21,22,23,24,25,26,27,28] are divided into two categories: horizontal CLLR (HCLLR) [15,16,17,18,19] and vertical CLLR (VCLLR) [20,21,22,23,24,25,26,27,28]. HCLLR is suitable for datasets held by different entities with the same feature dimensions but different sample spaces [15]. By contrast, VCLLR is applicable to the scenario where different features of the same set of objects are owned by different entities [20]. For the VCLLR, the features owned by a single entity are incomplete, the model training requires all entities to complete together, and thus the training process is more complicated [27].

However, for HE-based methods, the update of model parameters has the potential risk of additional private information leakage even in the semi-honest security setting [29]. For MPC-based methods, after performing secret sharing (SS) [30] on sparse samples, the sparse samples will become dense, and thus could not be handled efficiently. For DP-based methods, due to the model training process adds the noise, the speed of model convergence will be affected, and model accuracy degrades. To address these problems, we present a privacy-preserving cloud-edge CLLR (CECLLR) in this paper.

Our contributions

This work has the following main contributions:

  • Firstly, using an approximate HE algorithm [31], we present a secure CECLLR on vertically partitioned data without the coordination of the third-party, which can train a shared model by combining the data from edge node and cloud centre without disclosing raw data and model information, and reduces the complexity of collaborative learning.

  • Secondly, using the batching technique [31] and SIMD operation, the proposed CECLLR scheme enables the parallel computing, which greatly improves the computational efficiency and considerably reduces the communication complexity. Besides, the proposed scheme uses least squares to solve the problem that HE cannot efficiently compute sigmoid function.

  • Finally, on three available datasets [32], the performance comparisons demonstrate that, for the proposed CECLLR scheme, compared with related schemes [20, 26], the training time is reduced by nearly \(3.6\% - 83.0\%\); the accuracy, F1-score, and AUC improves almost \(0.3\% - 2.9\%\), \(0.1\% - 5.9\%\), and \(0 - 0.02\), respectively. Moreover, the security analysis indicates that our scheme can guarantee the security.

Organization

The remainder of this work is arranged as follows. Section Related works reviews the previous literature. In Section Preliminaries, the preliminaries are discussed. Section Proposed scheme explains our scheme in detail. Section Performance evaluation describes the evaluation results. In Section Security analysis, the security of our scheme is proved. Finally, Section Conclusion summarizes the work.

Related works

There have been several studies [15,16,17,18,19,20,21,22,23,24,25,26,27,28] training LR model while preserving the privacy of sensitive data. In general, existing works implement CLLR by using techniques such as HE [12], MPC [13], and DP [14]. According to the distribution characteristics of training data, existing works [15,16,17,18,19,20,21,22,23,24,25,26,27,28] are able to be divided into two categories: HCLLR [15,16,17,18,19] and VCLLR [20,21,22,23,24,25,26,27,28]. A review and summary of the existing works [15,16,17,18,19,20,21,22,23,24,25,26,27,28] are introduced below.

For the HCLLR schemes [15,16,17,18,19], using an additive HE algorithm [33] and a dada aggregation protocol [34], Mandal et al. [15] proposed a secure horizontal federated LR, where each party is able to train its own model on local dataset and upload its updated model weights to a third-party coordinator that generates a global model weights by aggregating the received model weights. Adopting an additive SS [35, 36], Cock et al. [16] designed a privacy-preserving high-performance CLR training scheme with a TTP initializer. Wang et al. [17] proposed a CECLLR analysis method between cloud centre and edge nodes through multi-key fully HE [37]. By an additive HE [38], Zhu et al. [18] described a value-blind model update method for privacy-preserving LR analysis in a collaborative setting, which protects model privacy by sharing encrypted model parameters among the training parties. Ghavamipour et al. [19] introduced two distributed training methods for secure collaborative LR analysis, but each party needs to transmit multiple shares of its data to other parties separately, which results in a high communication burden. However, in the existing HCLLR schemes [15,16,17,18,19], data communication among data owners and third-party coordinator increases the training complexity and the risk of privacy leakage. Moreover, it’s hard to find a third-party that is trusted by any parties.

For the VCLLR schemes [20,21,22,23,24,25,26,27,28], based on an additive HE scheme [38], Hardy et al. [20] designed an approximation of Sigmoid to achieve federated LR, but their scheme degrades the model accuracy and requires third-party coordinator. Yang et al. [21] presented a vertical federated LR using quasi-Newton method and additive HE [38]. By an additive SS [39], Zhang et al. [22] introduced a secure CL framework for distributed features. Yang et al. [23] presented a parallel distributed vertical federated LR architecture based on an additive HE scheme [38], which does not require a third-party entity. Li et al. [24] described a vertical CL system for two-party LR based on an approximate HE scheme [31]. Using an additive HE algorithm [38], Wei et al. [25] designed a secure two-parties CLLR on vertically partitioned data. Combining an additive HE algorithm [38] and an secret sharing technique [40], on vertically distributed large-scale sparse training data, Chen et al. [26] presented a secure CLLR scheme by sharing model parameters between two parties. Based on an additive HE [38], He et al. [27] introduced a parallel solution for implementing secure vertical federated LR, which ensures the model accuracy by utilizing a piecewise function, but degrades the efficiency. By adopting an DP algorithm [41] and an HE scheme [38], Sun et al. [28] presented a federated learning algorithm for privacy-preserving vertical CLR, which removes the third-party entity. However, existing VCLLR schemes [20,21,22,23,24,25,26,27,28] have a low training efficiency and model accuracy.

Preliminaries

System model

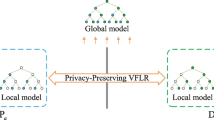
As is shown in Fig. 1, the system model consists of two semi-trusted parties: cloud centre \(\textrm{P}_a\) and edge node \(\textrm{P}_b\). The datasets \(\textrm{D}_a\) and \(\textrm{D}_b\) of \(\textrm{P}_a\) and \(\textrm{P}_b\) are vertically partitioned, namely, \(\textrm{P}_a\) has the labels and part of the features, \(\textrm{P}_b\) has another part of the features. \(\textrm{D}_a\) and \(\textrm{D}_b\) are isolated due to regulations and privacy concerns. \(\textrm{P}_a\) and \(\textrm{P}_b\) collaboratively obtain a joint LR model over their data without revealing the privacy of their sensitive data. The blockchain collects the iterative model parameters as audit records. The description of symbols in this paper are introduced in Table 1.

Fig. 1
figure 1

System model

Full size image
Table 1 The description of symbol
Full size table

Homomorphic encryption

HE allows direct calculation on ciphertext without decryption, and can ensure that the calculation on ciphertext is consistent with that on plaintext. Cheon et al. [31] described an approximate HE based on ring learning with errors [42], which includes the operations as follows:

  • \(\{\textrm{sk}_i, \textrm{pk}_i, \textrm{gk}_i, \textrm{rk}_i\} \leftarrow\) KeyGen(N, Q): On input the parameters \(\{N, Q\}\), it outputs secret key \(\textrm{sk}_i\), public key \(\textrm{pk}_i\), galois key \(\textrm{gk}_i\), and relinearization key \(\textrm{rk}_i\) for party \(\textrm{P}_i\).

  • \([\![ \boldsymbol{m}_1 ]\!] \leftarrow\) Enc\((\boldsymbol{m}_1, \textrm{pk}_i)\): On input the message vector \(\boldsymbol{m}_1\) and \(\textrm{pk}_i\), it outputs the ciphertext \([\![ \boldsymbol{m}_1 ]\!]\).

  • \(\boldsymbol{m}_1 \leftarrow\) Dec\(([\![ \boldsymbol{m}_1 ]\!], \textrm{sk}_i)\): On input the ciphertext \([\![ \boldsymbol{m}_1 ]\!]\) and \(\textrm{sk}_i\), it outputs the message vector \(\boldsymbol{m}_1\).

  • \([\![ \boldsymbol{m}_1 + \boldsymbol{m}_2 ]\!] \leftarrow\) Add\(([\![ \boldsymbol{m}_1 ]\!], [\![ \boldsymbol{m}_2 ]\!])\): On input two ciphertexts \([\![ \boldsymbol{m}_1 ]\!]\) and \([\![ \boldsymbol{m}_2 ]\!]\), it outputs the ciphertext \([\![ \boldsymbol{m}_1 + \boldsymbol{m}_2 ]\!]\) = \([\![ \boldsymbol{m}_1 ]\!] + [\![ \boldsymbol{m}_2 ]\!]\).

  • \([\![ \boldsymbol{m}_1 + \boldsymbol{m}_2 ]\!] \leftarrow\) Add_Plain\(([\![ \boldsymbol{m}_1 ]\!], \boldsymbol{m}_2)\): On input the ciphertext \([\![ \boldsymbol{m}_1 ]\!]\) and message vector \(\boldsymbol{m}_2\), it outputs the ciphertext \([\![ \boldsymbol{m}_1 + \boldsymbol{m}_2 ]\!]\) = \([\![ \boldsymbol{m}_1 ]\!] + \boldsymbol{m}_2\).

  • \([\![ \boldsymbol{m}_1 + \cdots + \boldsymbol{m}_{n} ]\!] \leftarrow\) Add_Many\(([\![ \textrm{M} ]\!])\): On input the ciphertext list \([\![ \textrm{M} ]\!]\) = \(\{[\![ \boldsymbol{m}_1 ]\!], \cdots , [\![ \boldsymbol{m}_{n} ]\!] \}\), it outputs the ciphertext \([\![ \boldsymbol{m}_1 + \cdots + \boldsymbol{m}_{n} ]\!]\) = \([\![ \boldsymbol{m}_1 ]\!] + \cdots + [\![ \boldsymbol{m}_{n} ]\!]\).

  • \([\![ \boldsymbol{m}_1 - \boldsymbol{m}_2 ]\!] \leftarrow\) Sub(\([\![ \boldsymbol{m}_1 ]\!], [\![ \boldsymbol{m}_2 ]\!]\)): On input two ciphertexts \([\![ \boldsymbol{m}_1 ]\!]\) and \([\![ \boldsymbol{m}_2 ]\!]\), it outputs the ciphertext \([\![ \boldsymbol{m}_1 - \boldsymbol{m}_2 ]\!]\) = \([\![ \boldsymbol{m}_1 ]\!] - [\![ \boldsymbol{m}_2 ]\!]\).

  • \([\![ \boldsymbol{m}_1 - \boldsymbol{m}_2 ]\!] \leftarrow\) Sub_Plain\(([\![ \boldsymbol{m}_1 ]\!], \boldsymbol{m}_2)\): On input the ciphertext \([\![ \boldsymbol{m}_1 ]\!]\) and message vector \(\boldsymbol{m}_2\), it outputs the ciphertext \([\![ \boldsymbol{m}_1 - \boldsymbol{m}_2 ]\!]\) = \([\![ \boldsymbol{m}_1 ]\!] - \boldsymbol{m}_2\).

  • \([\![ \boldsymbol{m}_1 * \boldsymbol{m}_2 ]\!] \leftarrow\) Mul(\([\![ \boldsymbol{m}_1 ]\!], [\![ \boldsymbol{m}_2 ]\!], \textrm{rk}_i\)): On input two ciphertexts \([\![ \boldsymbol{m}_1 ]\!]\), \([\![ \boldsymbol{m}_2 ]\!]\) and relinearization key \(\textrm{rk}_i\), it outputs the ciphertext \([\![ \boldsymbol{m}_1 * \boldsymbol{m}_2 ]\!]\) = \([\![ \boldsymbol{m}_1 ]\!] * [\![ \boldsymbol{m}_2 ]\!]\).

  • \([\![ \boldsymbol{m}_1 * \boldsymbol{m}_2 ]\!] \leftarrow\) Mul_Plain(\([\![ \boldsymbol{m}_1 ]\!], \boldsymbol{m}_2, rk_i\)): On input the ciphertext \([\![ \boldsymbol{m}_1 ]\!]\), message vector \(\boldsymbol{m}_2\), and relinearization key \(\textrm{rk}_i\), it outputs the ciphertext \([\![ \boldsymbol{m}_1 * \boldsymbol{m}_2 ]\!]\) = \([\![ \boldsymbol{m}_1 ]\!] * \boldsymbol{m}_2\).

  • \([\![ \boldsymbol{m}_2 ]\!] \leftarrow\) Rotate_Vector(\([\![ \boldsymbol{m}_1 ]\!], k, \textrm{gk}_i\)): On input the ciphertext \([\![ \boldsymbol{m}_1 ]\!]\) = \([\![ [m_{1,0}, m_{1,1}, \cdots , m_{1,\frac{N}{2}-1}] ]\!]\), k, and \(\textrm{gk}_i\), it rotates \([\![ \boldsymbol{m}_1 ]\!]\) left by k, and outputs the ciphertext \([\![ \boldsymbol{m}_2 ]\!]\) = \([\![ [m_{1,k}, \cdots , m_{1,\frac{N}{2}-1}, m_{1,0}, \cdots , m_{1,k-1} ] ]\!]\).

Sigmoid approximation

The main idea of binary LR is to output weights \(\boldsymbol{w} = \{ {w_0}, \cdots ,{w_{n}}\}\) that minimizes the loss function

$$\begin{aligned} J(\boldsymbol{w}) = -\frac{1}{m}\sum \nolimits _{i = 1}^{m} {( (1-y_i) \cdot (1-\log (\sigma ({\boldsymbol{x}_i} \cdot \boldsymbol{w}))) + y_i \cdot \log (\sigma ({\boldsymbol{x}_i} \cdot \boldsymbol{w})) )}, \end{aligned}$$

where \(\boldsymbol{x}_i = \{ 1, x_{i,1}, \cdots , x_{i,n} \}\) and \(y_i \in \{0, 1\}\). The following gradient descent (GD)

$$\begin{aligned} {\boldsymbol{w}^{(k + 1)}} = {\boldsymbol{w}^{(k)}} - \frac{\alpha ^{(k)}}{m}\sum \nolimits _{i = 1}^{m} {( (\sigma ( \boldsymbol{x}_i \cdot {\boldsymbol{w}^{(k)}} ) -y_i) \cdot {\boldsymbol{x}_i} )}, \end{aligned}$$

can be employed to obtain the extremum of \(J(\boldsymbol{w})\), where \(\alpha ^{(k)}\) and \(\boldsymbol{w}^{(k)}\) are the learning rate and the weights at the k-th iteration. Since approximate HE algorithm [31] is unable to perform sigmoid operations \(\sigma (x)= \frac{1}{{1 + {e^{ - x}}}}\) effectively, the evaluation of \(\sigma (x)\) is a barrier to the implementation of CECLLR. By the method of least squares, we obtain a polynomial function \(f(x) = w_0 + w_1 x - w_3 x^3 + w_5 x^5 - w_7 x^7\) of 7-degree to approximate sigmoid function \(\sigma (x)\), where \(w_0 = \frac{1}{2} ,w_1 = \frac{1.73496}{8},w_3 = {\frac{4.19407}{8^3}}, w_5 = {\frac{5.43402}{8^5}}, w_7 = {\frac{2.50739}{8^7}}\). The maximum error value between g(x) and \(\sigma (x)\) is about 0.032 over the domain \([-8, 8]\).

Proposed scheme

We present a privacy-preserving CECLLR on vertically partitioned datasets \(\textrm{D}_a\) and \(\textrm{D}_b\), where \(\textrm{D}_a\) contains m samples \(\{y_i, x_{i,1}, \cdots , x_{i,n_1} \}\) with \(y_i \in \{0, 1\}\), \(\textrm{D}_b\) contains m samples \(\{ x_{i,n_1+1}, \cdots , x_{i,n_1+n_2}\}\), and \(i \in [m]\). The first column and other columns of \(\textrm{D}_a\) represent the label and features, respectively. Each column of \(\textrm{D}_b\) represents a feature. For ease of description, we assume \(m = l \cdot \frac{N}{2}\) for \(l \in \mathbb {Z}^ *\), if the constraint do not meet, the parties pad 0. Moreover, we define the Algorithm 1, 2, which are able to be found in Appendix A. Using the batching techniques from RLWE-based approximate HE [31], our scheme is able to pack and encrypt a message vector containing \(\frac{N}{2}\) messages into one ciphertext, and thus reduces the time of model training by parallel processing based on SIMD. We describe our CECLLR scheme as follows.

Preprocessing

 

  • \(\textrm{P}_b\) computes \(l=\left\lceil { \frac{2m}{N} }\right\rceil\), produces \(\{ \textrm{sk}_b, \textrm{pk}_b, \textrm{rk}_b, \textrm{gk}_b \} \leftarrow \textrm{KeyGen}(N,Q)\), encrypts \(\textrm{D}_b\) into \((l \times n_2)\) ciphertexts

    $$\begin{aligned}{}[\![ {\boldsymbol{x}_{i,n_1+j}} ]\!] = \textrm{Enc} ( [ {x_{i \cdot \frac{N}{2},n_1+j}}, \cdots ,{x_{(i+1) \cdot \frac{N}{2} -1,n_1+j}} ], \textrm{pk}_a ), \end{aligned}$$
    (1)

    where \(i = 0,1,\cdots ,l-1, j = 1,2,\cdots ,n_2\), encrypts the initial weights \(\{ {w^{(0)}_{n_1+1}}, \cdots ,{w^{(0)}_{n_1+n_2}}\}\) into \(n_2\) ciphertexts

    $$\begin{aligned}{}[\![ {\boldsymbol{w}^{(0)}_{n_1+j}} ]\!] = \textrm{Enc}( [ w^{(0)}_{n_1+j},\cdots ,w^{(0)}_{n_1+j} ]_{1\times \frac{N}{2}}, \textrm{pk}_a) , \end{aligned}$$
    (2)

    where \(j = 1,2,\cdots ,n_2\), and sends \(\{N, Q\}\), \(\textrm{pk}_b\), \(\textrm{rk}_b\), \(\textrm{gk}_b\), e, \(\{ [\![ {\boldsymbol{x}_{i,n_1+j}} ]\!]: i = 0,1,\cdots ,l-1, j = 1,2,\cdots ,n_2 \}\), \(\{ [\![ {\boldsymbol{w}^{(0)}_{n_1+j}} ]\!]: j = 1,2,\cdots ,n_2 \}\) to \(\textrm{P}_a\).

  • \(\textrm{P}_a\) computes \(l=\left\lceil { \frac{2m}{N} }\right\rceil\), sets \(\textrm{D}_a\) into \((l \times (n_1+1))\) message vectors

    $$\begin{aligned} {\boldsymbol{x}_{i,j}} = [ {x_{i \cdot \frac{N}{2},j}}, \cdots ,{x_{(i+1) \cdot \frac{N}{2}-1,j}} ], \end{aligned}$$
    (3)
    $$\begin{aligned} {\boldsymbol{y}_{i}} = [ {y_{i \cdot \frac{N}{2}}}, \cdots ,{y_{(i+1) \cdot \frac{N}{2}-1}} ], \end{aligned}$$
    (4)

    where \(i = 0,1,\cdots ,l-1\), \(j = 1,2,\cdots ,n_1\), sets the message vectors

    $$\begin{aligned} {\boldsymbol{x}_{i,0}} = [ 1, \cdots ,1 ]_{1\times \frac{N}{2}}, \end{aligned}$$
    (5)

    where \(i = 0,1,\cdots ,l-1\), encrypts the initial weights \(\{ {w^{(0)}_{0}}, \cdots ,{w^{(0)}_{n_1}}\}\) into \((n_1+1)\) ciphertexts

    $$\begin{aligned}{}[\![ {\boldsymbol{w}^{(0)}_{j}} ]\!] = \textrm{Enc}( [ w^{(0)}_{j}, \cdots ,w^{(0)}_{j} ]_{1\times \frac{N}{2}}, \textrm{pk}_b ), \end{aligned}$$
    (6)

    where \(j = 1,2,\cdots ,n_1\), sets the message vectors

    $$\begin{aligned} {\boldsymbol{\frac{\alpha }{m}}}=[ \frac{\alpha }{m}, 0, \cdots , 0 ]_{1\times \frac{N}{2}}, \end{aligned}$$
    (7)
    $$\begin{aligned} \boldsymbol{a}_i = [ a_i, \cdots , a_i ]_{1\times \frac{N}{2}}, \end{aligned}$$
    (8)

    where \(i=0,1,3,5,7\), and sets the lists

    $$\begin{aligned} \boldsymbol{\textrm{X}}'{[i]} = \{ {\boldsymbol{x}_{i,0}}, \cdots , {\boldsymbol{x}_{i,n_1}} \}, \end{aligned}$$
    (9)
    $$\begin{aligned}{}[\![ \boldsymbol{\textrm{X}}^{\prime \prime }]\!]{[i]} = \{ [\![ {\boldsymbol{x}_{i,n_1+1}} ]\!], \cdots , [\![ {\boldsymbol{x}_{i,n_1+n_2}} ]\!] \}, \end{aligned}$$
    (10)

    where \(i = 0,1,\cdots ,l-1\),

    $$\begin{aligned}{}[\![ \textrm{Y} ]\!] = \{ [\![ {\boldsymbol{y}_{0}} ]\!], \cdots , [\![ {\boldsymbol{y}_{l-1}} ]\!] \}, \end{aligned}$$
    (11)
    $$\begin{aligned}{}[\![ \textrm{W}^{(0)} ]\!] = \{ [\![ {\boldsymbol{w}^{(0)}_{0}} ]\!], \cdots , [\![ {\boldsymbol{w}^{(0)}_{n_1+n_2}} ]\!] \}. \end{aligned}$$
    (12)

Training

\(\textrm{P}_a\) and \(\textrm{P}_b\) jointly perform the Algorithm 3.

figure a

Algorithm 1Training

Reconstructing

 

  • \(\textrm{P}_a\) sends \(\{ \textrm{O}^{(e)}{[n_1+1][0]},\cdots ,\textrm{O}^{(e)}{[n_1+n_2][0]} \}\) to \(\textrm{P}_b\), \(\textrm{P}_b\) computes

    $$\begin{aligned} & \{ w^{(e)}_{n_1+1}, \cdots , w^{(e)}_{n_1+n_2} \} \nonumber\\ =&\{ \textrm{P}^{(e)}{[n_1+1][0]}+\textrm{O}^{(e)}{[n_1+1][0]}, \cdots , \textrm{P}^{(e)}{[n_1+n_2][0]}+\textrm{O}^{(e)}{[n_1+n_2][0]} \} \end{aligned}$$
    (13)

  • \(\textrm{P}_b\) sends \(\{ \textrm{P}^{(e)}{[0][0]},\textrm{P}^{(e)}{[1][0]}, \cdots ,\textrm{P}^{(e)}{[n_1][0]} \}\) to \(\textrm{P}_a\), \(\textrm{P}_a\) computes

    $$\begin{aligned} \{ w^{(e)}_{0}, \cdots , w^{(e)}_{n_1} \} = \{ \textrm{P}^{(e)}{[0][0]}+\textrm{O}^{(e)}{[0][0]},\cdots ,\textrm{P}^{(e)}{[n_1][0]}+\textrm{O}^{(e)}{[n_1][0]} \} \end{aligned}$$
    (14)

Performance evaluation

We compare our CECLLR and related schemes [20, 26]. All evaluations are performed on a 64-bits desktop with Linux system, 16 GB memory and i7 CPU. We choose initial weights \(\{ {w^{(0)}_{0}}, \cdots ,{w^{(0)}_{n_1}}\}\) = \(\{ 0, \cdots ,0 \}\), \(\{ {w^{(0)}_{n_1+1}}, \cdots ,{w^{(0)}_{n_1+n_2}}\}\) = \(\{ 0, \cdots ,0 \}\), learning rate \(\varphi =0.15\), and maximum number of iterations \(e =20\). For the schemes [20, 26], Paillier cryptosystem [38] is chosen to support HE computations. For our scheme, we utilize the SEAL library [43] to instantiate HE computations [31]. To ensure the security with \(\kappa = 80\) bits, we select prime number \(p, q=512\) bits and \(n=1024\) bits in schemes [20, 26]. In our scheme, the rescaling operation in Mul and Mul_Plain needs the modulus reduction of \(6q_0\) and \(4q_1\) bits, the ciphertext modulus of the output in each iteration \(q_2\) needs to be larger than \(q_0\) to achieve the correctness and accuracy. Let \(q_0 = 50\), \(q_1 = 40\) and \(q_2 = 60\), we obtain \(Q = 6q_0 + 4q_1 + q_2 = 520\) bits, \(N =2^{15} \ge \frac{{\kappa + 110}}{{7.2}} \cdot \log Q\). On three datasets [32]: \(\Phi _1\) - uis, \(\Phi _2\) - Edinburgh, and \(\Phi _3\) - nhanes3, we compare our CECLLR with related schemes [20, 26] in terms of training time, accuracy, F1-score, AUC. \(\Phi _1\) has 8 features and 575 samples; \(\Phi _2\) has 9 features and 1253 samples; \(\Phi _3\) has 15 features and 15649 samples. \(\textrm{P}_a\) has the labels and the first 4 features \(\{\mathfrak {l}, \mathfrak {f}_1-\mathfrak {f}_4\}\) of \(\Phi _1\), \(\textrm{P}_b\) has the last 4 features \(\{\mathfrak {f}_5-\mathfrak {f}_8\}\) of \(\Phi _1\); \(\textrm{P}_a\) has the labels and the first 5 features \(\{\mathfrak {l}, \mathfrak {f}_1-\mathfrak {f}_5\}\) of \(\Phi _2\), \(\textrm{P}_b\) has the last 4 features \(\{\mathfrak {f}_6-\mathfrak {f}_9\}\) of \(\Phi _2\); \(\textrm{P}_a\) has the labels and the first 8 features \(\{\mathfrak {l}, \mathfrak {f}_1-\mathfrak {f}_8\}\) of \(\Phi _3\), \(\textrm{P}_b\) has the last 7 features \(\{\mathfrak {f}_9-\mathfrak {f}_{15}\}\) of \(\Phi _3\). All presented results are the average of 10 tests, the validity of results is obtained by 5-fold cross-validation. The performance comparisons among our CECLLR scheme and the schemes [20, 26] are shown in Table 2, where “\(\surd\)” means “Satisfied”, “\(\times\)” denotes “Not satisfied”. From Table 2, we obtain that our CECLLR is able to train a model in less time without degrading the model performance than the schemes [20, 26], and does not need a third-party coordinator.

Table 2 Performance comparisons
Full size table

From Fig. 2, we see that, compared with [20, 26], the training time in our method (1.23 min) reduces nearly 3.9% and 46.8% over \(\Phi _1\); the training time in our method (2.15 min) reduces almost 3.6% and 35.4% over \(\Phi _2\); the training time in our method (2.45 min) reduces about 73.0% and 83.0% over \(\Phi _3\).

Fig. 2
figure 2

Training time

Full size image

From Fig. 3, we see that, compared with [20, 26], the accuracy in our method (74.4%) is nearly 0.3% and 0.3% increase over \(\Phi _1\); the accuracy in our method (91.7%) is almost 0.4% and 0.8% increase over \(\Phi _2\); the accuracy in our method (85.6%) is about 1.0% and 2.9% increase over \(\Phi _3\).

Fig. 3
figure 3

Accuracy

Full size image

From Fig. 4, we see that, compared with [20, 26], the F1-score in our method (85.2%) has nearly 0.1% and 0.1% increase over \(\Phi _1\); the F1-score in our method (77.9%) has almost 0.4% and 2.6% increase over \(\Phi _2\); the F1-score in our method (61.5%) has about 5.9% and 1.4% increase over \(\Phi _3\).

Fig. 4
figure 4

F1-score

Full size image

From Fig. 5, we see that, compared with [20, 26], the AUC in our method (0.58) is nearly 0.01 and 0.02 increase over \(\Phi _1\); the AUC in our method (0.96) is the same over \(\Phi _2\); the AUC in our method (0.90) is about 0.01 and 0.01 increase over \(\Phi _3\).

Fig. 5
figure 5

AUC

Full size image

Security Analysis

Let \(\textrm{P}_a\) and \(\textrm{P}_b\) learn \({pk}_b\), \({rk}_b\), \({gk}_b\), and only \(\textrm{P}_b\) gets \({sk}_b\), our CECLLR is to compute an objective functionality \(f =\{f_a, f_b\}\) in semi-honest model [44]. For inputs \(\{m_a, m_b\}\) of \(\{ \textrm{P}_a, \textrm{P}_b \}\), the outputs \(\{f_a(m_a,m_b), f_b(m_a,m_b)\}\) for \(\{ \textrm{P}_a, \textrm{P}_b \}\) are random, and neither party can infer private data beyond its output. Next, we demonstrate the security of our CECLLR by means of simulation-based security [45].

Definition 1

Let \(\Pi\) represent a protocol to calculate deterministic functionality \(f =\{f_a, f_b\}\). Given inputs \(\{m_a, m_b\}\) of \(\{ \textrm{P}_a, \textrm{P}_b \}\), and security parameter \(\kappa\), the views for \(\textrm{P}_a\) and \(\textrm{P}_b\) in \(\Pi\) are represented as \(\mathcal {V}_{a} (\kappa , m_a, m_b) = \{ {pk}_b, {rk}_b, {gk}_b, m_a, o_a \}\) and \(\mathcal {V}_{b} (\kappa , m_a, m_b) = \{ {sk}_b, {pk}_b, {rk}_b, {gk}_b, m_b, o_b \}\), where \(m_a\) denotes \(\textrm{P}_a\)’s input, \(m_b\) denotes \(\textrm{P}_b\)’s input, \(o_a\) represents the output for \(\textrm{P}_a\), and \(o_b\) represents the output for \(\textrm{P}_b\). \(\Pi\) has the ability to calculate f securely in the semi-honest model if there are two simulators \(\mathcal {S}_a\) and \(\mathcal {S}_b\) with probabilistic polynomial-time, such that

$$\begin{aligned} \{ \mathcal {S}_{a} (1^{\kappa }, m_a,f_a(m_a,m_b)) \}_{\kappa ,m_a,m_b} \cong \{ \mathcal {V}_{a} (\kappa , m_a,m_b) \}_{\kappa ,m_a,m_b}, \end{aligned}$$
$$\begin{aligned} \{ \mathcal {S}_{b} (1^{\kappa }, m_b,f_b(m_a,m_b)) \}_{\kappa ,m_a,m_b} \cong \{ \mathcal {V}_{b} (\kappa , m_a,m_b) \}_{\kappa ,m_a,m_b}. \end{aligned}$$

Theorem 1

Suppose that \({P}_a\) and \({P}_b\) do not collude, and approximate HE algorithm [31] meets the semantic security, the proposed CECLLR could achieve the security under semi-honest model.

Proof

Following simulation-based security [45], we demonstrate that we could construct \(\mathcal {S}_{\mathcal {A}_a}\) and \(\mathcal {S}_{\mathcal {A}_b}\), such that

$$\begin{aligned} \{ \mathcal {S}_{\mathcal {A}_a} (1^{\kappa }, [\![ \boldsymbol{c} ]\!], \boldsymbol{o}_a)) \}_{\kappa ,[\![ \boldsymbol{c} ]\!],sk_b} \cong \{ \mathcal {V}_{\mathcal {A}_a} (\kappa , [\![ \boldsymbol{c} ]\!], sk_b) \}_{\kappa ,[\![ \boldsymbol{c} ]\!],sk_b}, \end{aligned}$$
$$\begin{aligned} \{ \mathcal {S}_{\mathcal {A}_b} (1^{\kappa },\boldsymbol{o}_b, sk_b) \}_{\kappa ,[\![ \boldsymbol{c} ]\!], sk_b} \cong \{ \mathcal {V}_{\mathcal {A}_b} (\kappa ,[\![ \boldsymbol{c} ]\!], sk_b) \}_{\kappa ,[\![ \boldsymbol{c} ]\!], sk_b}, \end{aligned}$$

where \(\mathcal {V}_{\mathcal {A}_a}\) and \(\mathcal {V}_{\mathcal {A}_b}\) represent the views of corrupted parties \(\mathcal {A}_a\) and \(\mathcal {A}_b\), respectively. We prove that \(\mathcal {A}_a\) and \(\mathcal {A}_b\) cannot distinguish the above two equations.

Against corrupted \(\mathcal {A}_a\): Given \(\kappa\), input \([\![ \boldsymbol{c} ]\!]\) and output \(\boldsymbol{o}_a\) of \(\mathcal {A}_a\), we build a \(\mathcal {S}_{\mathcal {A}_a}\) to simulate the view of \(\mathcal {A}_a\). To do this, we analyze \(\mathcal {V}_{\mathcal {A}_a} (\kappa , [\![ \boldsymbol{C} ]\!], sk_b)\). Since \(\mathcal {A}_a\) does not get other message from \(\mathcal {A}_b\), \(\mathcal {V}_{\mathcal {A}_a} (\kappa , [\![ \boldsymbol{c} ]\!], sk_b)\) consists of \([\![ \boldsymbol{c} ]\!]\) and random message \(\boldsymbol{r}_a\). Given \(\kappa\), \([\![ \boldsymbol{c} ]\!]\), and \(\boldsymbol{o}_a\), \(\mathcal {S}_{\mathcal {A}_a}\) produces the simulation \(([\![ \boldsymbol{c} ]\!], \boldsymbol{r}_a)\) of \(\mathcal {V}_{\mathcal {A}_a} (\kappa , [\![ \boldsymbol{c} ]\!], sk_b)\). Therefore, we obtain:

$$\begin{aligned} \mathcal {V}_{\mathcal {A}_a} (\kappa , [\![ \boldsymbol{c} ]], sk_b) = ([\![ \boldsymbol{c} ]\!], \boldsymbol{r}_a), \mathcal {S}_{\mathcal {A}_a} (1^{\kappa }, [\![ \boldsymbol{c} ]\!], \boldsymbol{o}_a)) = ([\![ \boldsymbol{c} ]\!], \boldsymbol{r}_a). \end{aligned}$$

According to the above analysis, we could obtain that \(\mathcal {S}_{\mathcal {A}_a}\)’s output and \(\mathcal {A}_a\)’s view is indistinguishable. Therefore, our CECLLR is secure against semi-honest \(\mathcal {A}_a\).

Against corrupted \(\mathcal {A}_b\): Given \(\kappa\), input \(sk_b\) and output \(\boldsymbol{o}_b\) of \(\mathcal {A}_b\), we build a \(\mathcal {S}_{\mathcal {A}_b}\) to simulate the view of \(\mathcal {A}_b\). With regards to this, we analyze \(\mathcal {V}_{\mathcal {A}_b} (\kappa , [\![ \boldsymbol{c} ]\!], sk_b)\). Since the only data received by \(\mathcal {A}_b\) is \([\![ \boldsymbol{c} ]\!]\), \(\mathcal {V}_{\mathcal {A}_b} (\kappa , [\![ \boldsymbol{c} ]\!], sk_b)\) consists of \(sk_b\) of \(\mathcal {A}_b\), random messager \(\boldsymbol{r}_b\) and ciphertext \([\![ \boldsymbol{o}_b ]\!]\). Given \(\kappa\), \(sk_b\), and \(\boldsymbol{o}_b\), \(\mathcal {S}_{\mathcal {A}_b}\) produces the simulation of \(\mathcal {V}_{\mathcal {A}_b} (\kappa , [\![ \boldsymbol{c} ]\!], sk_b)\). \(\mathcal {S}_{\mathcal {A}_b}\) encrypts \(\boldsymbol{o}_b\) with \(pk_b\) into \([\![ \boldsymbol{o}^{\prime }_b ]\!]\), and produces the output \((sk_b, \boldsymbol{r}_b, [\![ \boldsymbol{o}^{\prime }_b ]\!])\). Therefore, we obtain:

$$\begin{aligned} \mathcal {V}_{\mathcal {A}_b} (\kappa , [\![ \boldsymbol{c} ]\!], sk_b) = (sk_b, \boldsymbol{r}_b, [\![ \boldsymbol{o}_b ]\!]), \mathcal {S}_{\mathcal {A}_b} (1^{\kappa }, sk_b, \boldsymbol{o}_b)) = (sk_b, \boldsymbol{r}_b, [\![ \boldsymbol{o}^{\prime }_b ]\!]). \end{aligned}$$

From the above analysis, we could obtain that \(\mathcal {S}_{\mathcal {A}_b}\)’s output and \(\mathcal {A}_b\)’s view is indistinguishable. Therefore, our CECLLR is secure against semi-honest \(\mathcal {A}_b\).

Conclusion

In this paper, using an approximate HE algorithm, we present a CECLLR without third-party coordinator while achieving the security of the raw data and model information for all parties. The proposed scheme adopts the batching and SIMD achieves a parallel processing. The performance evaluations based on the experiments show that, compared with existing methods, our scheme has lower training time and higher model performance. In future work, we will improve our scheme to support complex model training and datasets, and optimize our scheme to resist attacks by malicious parties.