Abstract
In this paper, we propose two new contractions via simulation function that involves rational expression in the setting of partial b-metric space. The obtained results not only extend, but also generalize and unify the existing results in two senses: in the sense of contraction terms and in the sense of the abstract setting. We present an example to indicate the validity of the main theorem.
Similar content being viewed by others
1 Introduction and preliminaries
The origin of the fixed point theory goes back a century, to the pioneer work of Banach. Since the first study of Banach, researchers have been extended, improved, and generalized this very simple stated but at the same time very powerful theorem. For this purpose, the terms of the contraction inequality and the abstract structure of Banach’s theorem have been investigated. In this paper, we shall combine these two trends and introduce two new type contraction via simulation functions involving rational terms in the more general setting, partial-b-metric space.
For the sake of the completeness of the manuscript, we shall recall some basic results and concepts here.
Theorem 1
([1])
Let \((\mathcal {A},\delta )\) be a complete metric space and  be a map**. If there exist
be a map**. If there exist  , with \(\kappa _{1}+ \kappa _{2}<1\) such that
, with \(\kappa _{1}+ \kappa _{2}<1\) such that

for all  , then
, then  has a unique fixed point \(\mathsf {u}\in \mathcal {A}\) and the sequence
has a unique fixed point \(\mathsf {u}\in \mathcal {A}\) and the sequence  converges to the fixed point u for all \(x\in \mathcal {A}\).
converges to the fixed point u for all \(x\in \mathcal {A}\).
Theorem 2
([2])
Let \((\mathcal {A}, \delta )\) be a complete metric space and  be a continuous map**. If there exist \(\kappa _{1}, \kappa _{2}\in [0,1 )\), with \(\kappa _{1}+ \kappa _{2}<1\) such that
be a continuous map**. If there exist \(\kappa _{1}, \kappa _{2}\in [0,1 )\), with \(\kappa _{1}+ \kappa _{2}<1\) such that

for all distinct  , then
, then  possesses a unique fixed point in \(\mathcal {A}\).
possesses a unique fixed point in \(\mathcal {A}\).
We mention that over the last few years many interesting and different generalizations for rational contractions have been provided; see, for example [3–8].
Let Γ be the set of all non-decreasing and continuous functions \(\psi :[0,+\infty )\rightarrow [0,+\infty )\). such that \(\psi (0)=0\).
Definition 1
([9])
A function \(\eta :\mathbb{R}^{+}_{0}\times \mathbb{R}^{+}_{0}\rightarrow \mathbb{R}\) is a ψ-simulation function if there exists \(\psi \in \Gamma \) such that the following conditions hold:
- \((\eta _{1})\):
-
\(\eta (\mathsf {r},\mathsf {t})<\psi (\mathsf {t})-\psi (\mathsf {r})\) for all \(\mathsf {r},\mathsf {t}\in \mathbb{R}^{+}\);
- \((\eta _{2})\):
-
if \(\{\mathsf {r}_{n}\},\{\mathsf {t}_{n}\}\) are two sequences in \([0,+\infty )\) such that \(\lim_{n\rightarrow +\infty }\mathsf {r}_{n}= \lim_{n\rightarrow +\infty }\mathsf {t}_{n}>0\), then
$$\begin{aligned} \limsup_{n\rightarrow +\infty }\eta (\mathsf {r}_{n},\mathsf {t}_{n})< 0. \end{aligned}$$(1.3)
We will denote by \(\mathcal{Z}_{\psi }\) the family of all ψ-simulation functions; see e.g. [10–22]. It is clear, due to the axiom \((\eta _{1})\), that
Definition 2
([23])
On a non-empty set \(\mathcal {A}\), a function \(\rho :\mathcal {A}\times \mathcal {A}\rightarrow \mathbb{R}^{+}_{0}\) is a partial metric if the following conditions:
- \((\rho _{1})\):
-
 ;
; - \((\rho _{2})\):
-
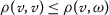 ;
; - \((\rho _{3})\):
-
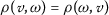 ;
; - \((\rho _{4})\):
-
 ;
;
hold for all  .
.
The pair \((\mathcal {A}, \rho )\) is called a partial-metric space.
Every partial metric ρ on \(\mathcal {A}\) generates a \(\mathsf{T}_{0}\) topology on \(\mathcal {A}\), that has a base of the set of all open balls  , where an open ball for a partial metric ρ on \(\mathcal {A}\) is defined [23] as
, where an open ball for a partial metric ρ on \(\mathcal {A}\) is defined [23] as

for each  and \(\mathsf{e}>0\).
and \(\mathsf{e}>0\).
If \((\mathcal {A}, \rho )\) is a partial-metric space and  a sequence in \(\mathcal {A}\), then:
a sequence in \(\mathcal {A}\), then:
-
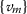 is convergent to a limit \(\mathsf {u}\in \mathcal {A}\), if
is convergent to a limit \(\mathsf {u}\in \mathcal {A}\), if 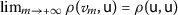 ;
; -
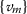 is a Cauchy sequence if
is a Cauchy sequence if 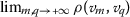 exists and is finite.
exists and is finite.
Moreover, we say that the partial-metric space \((\mathcal {A},\rho )\) is complete if every Cauchy sequence  in \(\mathcal {A}\) converges to a point \(\mathsf {u}\in \mathcal {A}\), that is,
in \(\mathcal {A}\) converges to a point \(\mathsf {u}\in \mathcal {A}\), that is,

Remark 1
The limit in a partial metric space may not be unique. For a sequence  on \((\mathcal {A},\rho )\), we denote by
on \((\mathcal {A},\rho )\), we denote by  the set of limit points (if there exist any),
the set of limit points (if there exist any),

We recall some results in the context of partial-metric spaces, necessary in our following considerations.
Lemma 1
Let \((\mathcal {A}, \rho )\) be a partial-metric space and  be a sequence in \(\mathcal {A}\) such that
be a sequence in \(\mathcal {A}\) such that  . If
. If  , then there exist \(\mathsf{e}>0\) and subsequences
, then there exist \(\mathsf{e}>0\) and subsequences  ,
,  of
of  such that
such that

Lemma 2
([24])
Let  be a Cauchy sequence on a complete partial-metric space \((\mathcal {A}, \rho )\). If there exists
be a Cauchy sequence on a complete partial-metric space \((\mathcal {A}, \rho )\). If there exists  with
with  , then
, then  , for every subsequence
, for every subsequence  of
of  .
.
Lemma 3
([25])
If  , \(\{ \omega _{m} \} \) are two sequences in a partial-metric space \((\mathcal {A}, \rho )\) such that
, \(\{ \omega _{m} \} \) are two sequences in a partial-metric space \((\mathcal {A}, \rho )\) such that

then  . Moreover,
. Moreover,  , for each \(\mathsf {u}\in \mathcal {A}\).
, for each \(\mathsf {u}\in \mathcal {A}\).
On a partial-metric space \((\mathcal {A}, \rho )\), a map**  is continuous at
is continuous at  if and only if for every \(\mathsf{e}>0\), there exists \(\delta >0\) such that
if and only if for every \(\mathsf{e}>0\), there exists \(\delta >0\) such that

( is continuous if it is continuous at every point
is continuous if it is continuous at every point  .)
.)
Lemma 4
([24])
On a complete partial-metric space \((\mathcal {A}, \rho )\), let  be a continuous map** and
be a continuous map** and  be a Cauchy sequence in \(\mathcal {A}\). If there exists
be a Cauchy sequence in \(\mathcal {A}\). If there exists  with
with  , then
, then  .
.
Definition 3
([26])
Let \(\mathcal {A}\) be a non-empty set and \(\mathsf {s}\geq 1\). A function \(\rho _{\mathsf{b}}:\mathcal {A}\times \mathcal {A}\rightarrow \mathbb{R}^{+}_{0}\) is a partial b-metric with a coefficient s if the following conditions hold for all 
- \((\rho _{b}1)\):
-
 ;
; - \((\rho _{b}2)\):
-
 ;
; - \((\rho _{b}3)\):
-
 ;
; - \((\rho _{b}4)\):
-
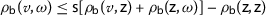 .
.
In this case, we say that \((\mathcal {A},\rho _{\mathsf{b}},\mathsf {s})\) is a partial b-metric space.
Example 1
([26])
Let \(\mathcal {A}\) be a non-empty set and  .
.
-
if ρ is a partial metric on \(\mathcal {A}\), then the function \(\rho _{\mathsf{b}}\) defined as
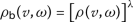 (1.6)
(1.6)is a partial b-metric on \(\mathcal {A}\), with \(\mathsf {s}=2^{\lambda -1}\), for \(\lambda >1\).
-
if b is a b-metric and ρ is a partial metric on \(\mathcal {A}\), then the function
 (1.7)
(1.7)is a partial b-metric on \(\mathcal {A}\).
A sequence  in a partial b-metric space \((\mathcal {A}, \rho _{\mathsf{b}}, \mathsf {s})\) is said to be \(\rho _{\mathsf{b}}\)-convergent to a point \(\mathsf {u}\in \mathcal {A}\) if
in a partial b-metric space \((\mathcal {A}, \rho _{\mathsf{b}}, \mathsf {s})\) is said to be \(\rho _{\mathsf{b}}\)-convergent to a point \(\mathsf {u}\in \mathcal {A}\) if

If the limit  exists and it is finite, the sequence
exists and it is finite, the sequence  is said to be \(\rho _{\mathsf{b}}\)-Cauchy. Moreover, if every \(\rho _{\mathsf{b}}\)-Cauchy sequence in \(\mathcal {A}\) is \(\rho _{\mathsf{b}}\)-convergent to \(\mathsf {u}\in \mathcal {A}\), that is
is said to be \(\rho _{\mathsf{b}}\)-Cauchy. Moreover, if every \(\rho _{\mathsf{b}}\)-Cauchy sequence in \(\mathcal {A}\) is \(\rho _{\mathsf{b}}\)-convergent to \(\mathsf {u}\in \mathcal {A}\), that is

we say that the partial b-metric space \((\mathcal {A}, \rho _{\mathsf{b}}, \mathsf {s})\) is \(\rho _{\mathsf{b}}\)-complete.
Remark 2
In [27] it is proved that a partial b-metric induces a b-metric, say \(\delta _{\mathsf {b}}\), with

for all  .
.
On the other hand, in [28], the notion of 0-\(\rho _{\mathsf{b}}\)-completeness was introduced and the relation between 0-\(\rho _{\mathsf{b}}\)-completeness and \(\rho _{\mathsf{b}}\)-completeness of a partial b-metric was established.
Definition 4
([28])
A sequence  on a partial b-metric space \((\mathcal {A}, \rho _{\mathsf{b}}, \mathsf {s})\) is 0-\(\rho _{\mathsf{b}}\)-Cauchy if
on a partial b-metric space \((\mathcal {A}, \rho _{\mathsf{b}}, \mathsf {s})\) is 0-\(\rho _{\mathsf{b}}\)-Cauchy if  . Moreover, the space \((\mathcal {A}, \rho _{\mathsf{b}}, \mathsf {s})\) is said to be 0-\(\rho _{\mathsf{b}}\)-complete if for each 0-\(\rho _{\mathsf{b}}\)-Cauchy sequence in \(\mathcal {A}\), there is \(\mathsf {u}\in \mathcal {A}\), such that
. Moreover, the space \((\mathcal {A}, \rho _{\mathsf{b}}, \mathsf {s})\) is said to be 0-\(\rho _{\mathsf{b}}\)-complete if for each 0-\(\rho _{\mathsf{b}}\)-Cauchy sequence in \(\mathcal {A}\), there is \(\mathsf {u}\in \mathcal {A}\), such that

Lemma 5
([28])
If the partial b-metric space \((\mathcal {A}, \rho _{\mathsf{b}}, \mathsf {s})\) is \(\rho _{\mathsf{b}}\)-complete, then it is 0-\(\rho _{\mathsf{b}}\)-complete.
Lemma 6
([29])
Let \((\mathcal {A}, \rho _{\mathsf{b}}, \mathsf {s})\) be a partial b-metric space. If  then
then  and
and  for all
for all  .
.
The next result is important in our future considerations.
Lemma 7
([30])
Let \((\mathcal {A}, \rho _{\mathsf{b}}, \mathsf {s}\geq 1)\) be a partial b-metric space,  a map** and a number \(\kappa \in [0,1)\). If
a map** and a number \(\kappa \in [0,1)\). If  is a sequence in \(\mathcal {A}\), where
is a sequence in \(\mathcal {A}\), where  and
and

for each \(m\in \mathbb{N}\), then the sequence  is 0-\(\rho _{\mathsf{b}}\)-Cauchy.
is 0-\(\rho _{\mathsf{b}}\)-Cauchy.
2 Main results
We start with the definition of simulation function for partial b-metric spaces.
Definition 5
Let \((\mathcal {A},\rho _{\mathsf{b}}, \mathsf {s}\geq 1)\) be a partial b-metric space. A b-ψ-simulation function is a function \(\eta _{\mathsf {b}}:[0,+\infty )\times [0,+\infty )\rightarrow \mathbb{R}\) satisfying:
- \((\eta _{b1})\):
-
\(\eta _{\mathsf {b}}(\mathsf {r},\mathsf {t})<\psi (\mathsf {t})-\psi (\mathsf {r})\) for all \(\mathsf {r},\mathsf {t}\in \mathbb{R}^{+}\);
- \((\eta _{b2})\):
-
if \(\{\mathsf {r}_{n}\},\{\mathsf {t}_{n}\}\) are two sequences in \([0,+\infty )\), such that for \(p>0\)
$$\begin{aligned} \limsup_{n\rightarrow +\infty }\mathsf {t}_{n}= \mathsf {s}^{p} \lim_{n\rightarrow +\infty }\mathsf {r}_{n}>0, \end{aligned}$$(2.1)then
$$\begin{aligned} \limsup_{n\rightarrow +\infty }\eta _{\mathsf {b}}\bigl(\mathsf {s}^{p} \mathsf {r}_{n}, \mathsf {t}_{n}\bigr)< 0. \end{aligned}$$(2.2)
We shall denote by \(\mathcal{Z}_{\psi _{b}}\) the family of all b-ψ-simulation functions.
Example 2
Let \(\psi \in \Gamma \) and \(\gamma :[0,+\infty )\rightarrow [0,+\infty )\) be a function such that \(\limsup_{\mathsf {t}\rightarrow \mathsf {t}_{0}}\gamma ( \mathsf {t})<1\) for every \(\mathsf {t}_{0}>0\) and \(\phi (\mathsf {t})=0\) if and only if \(\mathsf {t}=0\). Then \({\eta _{\mathsf {b}}}(\mathsf {r}, \mathsf {t})=\gamma (\mathsf {t})\psi ( \mathsf {t})-\psi (\mathsf {r})\), for \(\mathsf {r},\mathsf {t}\geq 0\) is a b-ψ-simulation function.
Example 3
Let \(\psi \in \Gamma \) and \(\phi :[0,+\infty )\rightarrow [0,+\infty )\) be a function such that \(\lim_{\mathsf {t}\rightarrow \mathsf {t}_{0}}\phi (\mathsf {t})>0\) for every \(\mathsf {t}_{0}>0\) and \(\phi (\mathsf {t})=0\) if and only if \(\mathsf {t}=0\). Then \({\eta _{\mathsf {b}}}(\mathsf {r}, \mathsf {t})=\psi (\mathsf {t})-\phi (\mathsf {t})- \psi (\mathsf {r})\), for \(\mathsf {r},\mathsf {t}\geq 0\) is a b-ψ-simulation function.
Obviously, \((\eta _{b1})\) holds. Now, considering two sequences \(\{ \mathsf {r}_{n} \} \) and \(\{ \mathsf {t}_{n} \} \) in \((0,+\infty )\) such that (2.1) holds, we have
Thus, also \((\eta _{b2})\) holds, that is \({\eta _{\mathsf {b}}}\in \mathcal{Z}_{\psi _{b}}\).
Definition 6
Let \((\mathcal {A},\rho _{\mathsf{b}}, \mathsf {s}\geq 1)\) be a partial b-metric space. A map**  is called \((\eta _{\mathsf {b}})\)-rational contraction of type A if there exists a function \(\eta _{\mathsf {b}}\in \mathcal{Z}_{\psi _{b}}\) such that
is called \((\eta _{\mathsf {b}})\)-rational contraction of type A if there exists a function \(\eta _{\mathsf {b}}\in \mathcal{Z}_{\psi _{b}}\) such that

for every  , where \(\mathcal{D}_{A}\) is defined as
, where \(\mathcal{D}_{A}\) is defined as

With the purpose to simplify the demonstrations, we prefer in the sequel, to discuss separately, the cases
Theorem 3
Let \((\mathcal {A},\rho _{\mathsf{b}}, \mathsf {s}>1)\) be a \(\rho _{\mathsf{b}}\)-complete partial b-metric space and  be a \((\eta _{\mathsf {b}})\)-rational contraction of type A. Then
be a \((\eta _{\mathsf {b}})\)-rational contraction of type A. Then  admits exactly one fixed point.
admits exactly one fixed point.
Proof
Let  be an arbitrary but fixed point and
be an arbitrary but fixed point and  be the sequence in \(\mathcal {A}\) defined as follows:
be the sequence in \(\mathcal {A}\) defined as follows:

Thus, we can assume that  for every \(m\in \mathbb{N}\). Indeed, if we suppose that there exists \(m_{0}\in \mathbb{N}\) such that
for every \(m\in \mathbb{N}\). Indeed, if we suppose that there exists \(m_{0}\in \mathbb{N}\) such that  . Taking into account (2.5) we get
. Taking into account (2.5) we get  , that is,
, that is,  is a fixed point of
is a fixed point of  . Therefore, substituting
. Therefore, substituting  and
and  in (2.4), we have
in (2.4), we have

Moreover, by (2.3) we get

which implies

Now, taking into account \((\eta _{b1})\), the above inequality yields

or, equivalently,

Consequently, due to the monotony of the function ψ, we obtain

If there exists \(m_{1}\in \mathbb{N}\) such that  , (2.6) becomes
, (2.6) becomes  , which is a contradiction (because \(\mathsf {s}>1\)). Therefore, for any \(m\in \mathbb{N}\) we have
, which is a contradiction (because \(\mathsf {s}>1\)). Therefore, for any \(m\in \mathbb{N}\) we have

or

Denoting \(\frac{1}{\mathsf {s}^{p}}\) by κ, we have  , with \(0\leq \kappa <1\). Thus, by Lemma 7 we see that the sequence
, with \(0\leq \kappa <1\). Thus, by Lemma 7 we see that the sequence is a 0-\(\rho _{\mathsf{b}}\)-Cauchy sequence on the \(\rho _{\mathsf{b}}\)-complete partial b-metric space. Since by Lemma 5, the space is also 0-\(\rho _{\mathsf{b}}\)-complete, it follows that there exists \(\mathsf {u}\in \mathcal {A}\) such that
is a 0-\(\rho _{\mathsf{b}}\)-Cauchy sequence on the \(\rho _{\mathsf{b}}\)-complete partial b-metric space. Since by Lemma 5, the space is also 0-\(\rho _{\mathsf{b}}\)-complete, it follows that there exists \(\mathsf {u}\in \mathcal {A}\) such that

Now, we claim that

Assuming the contrary, we can find \(m_{0}\in \mathbb{N}\) such that

which is a contradiction. Thus, there exists a subsequence  of
of  such that
such that

which implies

where

Therefore, letting \(l\rightarrow +\infty \) and kee** (2.8) in mind we get

On one hand, without loss of generality, we assume that  , for infinitely many \(m\in \mathbb{N}\). Thus,
, for infinitely many \(m\in \mathbb{N}\). Thus,

which by \((\eta _{b1})\) leads us to

Taking into account the non-decreasing property of ψ

On the other hand,

Letting \(m\rightarrow +\infty \) in the above inequality and kee** in mind (2.8) and (2.9) we get

Therefore,  . Thus, letting
. Thus, letting  and
and  , by \((\eta _{b2})\) it follows \(\limsup_{m\rightarrow +\infty }\eta _{\mathsf {b}}(\mathsf {s}^{p} \mathsf {r}_{m}, \mathsf {t}_{m})<0\), which is a contradiction. Then
, by \((\eta _{b2})\) it follows \(\limsup_{m\rightarrow +\infty }\eta _{\mathsf {b}}(\mathsf {s}^{p} \mathsf {r}_{m}, \mathsf {t}_{m})<0\), which is a contradiction. Then  , that is, u is a fixed point of
, that is, u is a fixed point of  .
.
As a last step, we establish uniqueness of the fixed point. Indeed, if we can find another point, \(\mathsf {z}\in \mathcal {A}\), \(\mathsf {z}\neq \mathsf {u}\) such that  ,
,

which implies

which is a contradiction. Thus, \(\mathsf {u}=\mathsf {z}\). □
Example 4
Let the set \(\mathcal {A}= \{ 10,11,12,13 \} \) and \(\rho _{\mathsf{b}}\) be the partial b-metric on \(\mathcal {A}\) (\(\mathsf {s}=2\)), where  We define the map**
We define the map**  ,
,  and we choose \(\phi \in \Gamma \), \(\phi (\mathsf {t})=\frac{\mathsf {t}}{2}\) and \(\eta _{\mathsf {b}}(\mathsf {r},\mathsf {t})= \frac{\frac{15}{16}\mathsf {t}-\mathsf {r}}{2}\). It is easy to see that \(\eta _{\mathsf {b}}\in \mathcal{Z}_{\psi _{b}}\) (by taking \(\gamma (\mathsf {t})=\frac{15}{16}\) in Example 2). We have
and we choose \(\phi \in \Gamma \), \(\phi (\mathsf {t})=\frac{\mathsf {t}}{2}\) and \(\eta _{\mathsf {b}}(\mathsf {r},\mathsf {t})= \frac{\frac{15}{16}\mathsf {t}-\mathsf {r}}{2}\). It is easy to see that \(\eta _{\mathsf {b}}\in \mathcal{Z}_{\psi _{b}}\) (by taking \(\gamma (\mathsf {t})=\frac{15}{16}\) in Example 2). We have
|
|
|
|---|---|---|
10 | 10 | 0 |
11 | 10 | 1 |
12 | 10 | 4 |
13 | 11 | 4 |
and shall consider the following cases:
-
1.
For
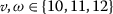 , we have
, we have  , and then
, and then

which implies

-
2.
For
 we have
we have 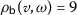 ,
,  ,
,  ,
, 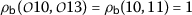 and then
and then
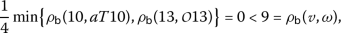
which implies
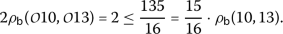
-
3.
For
 we have
we have  ,
,  ,
,  ,
,  and then
and then
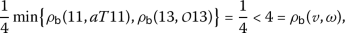
which implies

-
4.
For
 we have
we have  ,
,  ,
,  ,
,  and then
and then
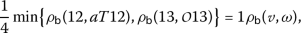
which implies
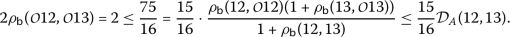
Thus, the hypothesis of Theorem 3 are satisfied and
 is the fixed point of the map**
is the fixed point of the map** 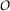 .
.
Definition 7
Let \((\mathcal {A},\rho _{\mathsf{b}}, \mathsf {s}>1)\) be a partial b-metric space. The map**  is said to be a \((\eta _{\mathsf {b}})\)-rational contraction of type B if there exists \(\eta _{\mathsf {b}}\in \mathcal{Z}_{\psi _{b}}\) such that
is said to be a \((\eta _{\mathsf {b}})\)-rational contraction of type B if there exists \(\eta _{\mathsf {b}}\in \mathcal{Z}_{\psi _{b}}\) such that

for all  ,
,  , where
, where

Theorem 4
On a \(\rho _{\mathsf{b}}\)-complete partial b-metric space \((\mathcal {A},\rho _{\mathsf{b}}, \mathsf {s}>1)\) any continuous \((\eta _{\mathsf {b}})\)-rational contraction of type B,  admits exactly one fixed point.
admits exactly one fixed point.
Proof
Let the sequence  be defined by (2.5). Since
be defined by (2.5). Since  , for each \(m\in \mathbb{N}\) (by similar reasoning as in the proof of Theorem 3), we have
, for each \(m\in \mathbb{N}\) (by similar reasoning as in the proof of Theorem 3), we have

which implies

where

Therefore

and since the function ψ is non-decreasing, we get, for any \(m\in \mathbb{N}\),

Moreover, if  we get a contradiction, and then it follows that
we get a contradiction, and then it follows that

and by Lemma (7), we conclude that  is a 0-\(\rho _{\mathsf{b}}\)-Cauchy on a \(\rho _{\mathsf{b}}\)-complete b-partial-metric space, and there exists \(\mathsf {u}\in \mathcal {A}\) such that
is a 0-\(\rho _{\mathsf{b}}\)-Cauchy on a \(\rho _{\mathsf{b}}\)-complete b-partial-metric space, and there exists \(\mathsf {u}\in \mathcal {A}\) such that  .
.
Taking into account the continuity of the map**  , we have
, we have

that is, u is a fixed point of the map**  .
.
We claim that the fixed point of  is unique. Let \(\mathsf {u},\mathsf {z}\in \mathcal {A}\) be two different fixed point of
is unique. Let \(\mathsf {u},\mathsf {z}\in \mathcal {A}\) be two different fixed point of  . Then
. Then

which implies

which is a contradiction. Therefore, \(\rho _{\mathsf{b}}(\mathsf {u}, \mathsf {z})=0\), that is (by Lemma 6), \(\mathsf {u}=\mathsf {z}\). □
Example 5
Let the set \(\mathcal {A}=[0,1]\), and \(\rho _{\mathsf{b}}:\mathcal {A}\times \mathcal {A}\rightarrow [0,+\infty )\),  be a partial b-metric on \(\mathcal {A}\). Let the continuous map**
be a partial b-metric on \(\mathcal {A}\). Let the continuous map**  be defined by
be defined by  and the functions \(\psi \in \Gamma \), \(\eta _{\mathsf {b}}\in \mathcal{Z}_{\psi _{b}}\), where \(\psi (\mathsf {t})=\frac{\mathsf {t}}{2}\) and \(\eta _{\mathsf {b}}(\mathsf {r},\mathsf {t})=\frac{8}{9}(\frac{\mathsf {t}}{2})- \frac{\mathsf {r}}{2}\).
and the functions \(\psi \in \Gamma \), \(\eta _{\mathsf {b}}\in \mathcal{Z}_{\psi _{b}}\), where \(\psi (\mathsf {t})=\frac{\mathsf {t}}{2}\) and \(\eta _{\mathsf {b}}(\mathsf {r},\mathsf {t})=\frac{8}{9}(\frac{\mathsf {t}}{2})- \frac{\mathsf {r}}{2}\).
We verify that  is a \((\eta _{\mathsf {b}})\)-ψ-rational contraction of type B.
is a \((\eta _{\mathsf {b}})\)-ψ-rational contraction of type B.
-
1.
For
 , if
, if 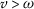 , (the case
, (the case  is similar), we have
is similar), we have

Therefore,
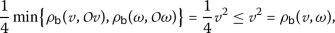
which implies

-
2.
For
 , if
, if 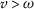 , (the case
, (the case 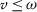 is similar), we have
is similar), we have

Therefore,
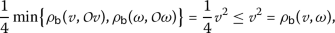
which implies
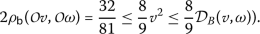
-
3.
For
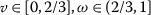 , we have
, we have
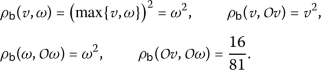
Therefore,
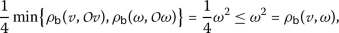
which implies
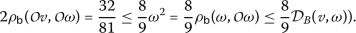
Therefore, all the hypotheses of Theorem 2.10 are satisfied and
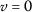 is the unique fixed point of
is the unique fixed point of  .
.
Removing the condition  in Theorem 3, respectively, Theorem 4, we immediately obtain the next results.
in Theorem 3, respectively, Theorem 4, we immediately obtain the next results.
Corollary 1
Let \((\mathcal {A},\rho _{\mathsf{b}}, \mathsf {s}>1)\) be a \(\rho _{\mathsf{b}}\)-complete partial b-metric space and  be a map** such that there exists \(\eta _{\mathsf {b}}\in \mathcal{Z}_{\psi _{b}}\) such that
be a map** such that there exists \(\eta _{\mathsf {b}}\in \mathcal{Z}_{\psi _{b}}\) such that

for all  , where \(\mathcal{D_{A}}\) is defined by (2.4). Then
, where \(\mathcal{D_{A}}\) is defined by (2.4). Then  has a unique fixed point.
has a unique fixed point.
Corollary 2
Let \((\mathcal {A},\rho _{\mathsf{b}}, \mathsf {s}>1)\) be a \(\rho _{\mathsf{b}}\)-complete partial b-metric space and  be a continuous map** such that there exists \(\eta _{\mathsf {b}}\in \mathcal{Z}_{\psi _{b}}\) such that
be a continuous map** such that there exists \(\eta _{\mathsf {b}}\in \mathcal{Z}_{\psi _{b}}\) such that

for all distinct  , where \(\mathcal{D}_{B}\) is defined by (2.11). Then
, where \(\mathcal{D}_{B}\) is defined by (2.11). Then  has a unique fixed point.
has a unique fixed point.
Corollary 3
Let  be a map** on a \(\rho _{\mathsf{b}}\)-complete partial b-metric space \((\mathcal {A},\rho _{\mathsf{b}}, \mathsf {s}>1)\). Suppose that \(\psi \in \Gamma \) and \(\phi :[0,+\infty )\rightarrow [0,+\infty )\) is a function such that \(\liminf_{\mathsf {t}\rightarrow \mathsf {t}_{0}}\phi ( \mathsf {t})>0\), for \(\mathsf {t}_{0}>0\) and \(\phi (\mathsf {t})=0 \Leftrightarrow \mathsf {t}=0\). If for every \(\mathsf {r}, \mathsf {t}\in \mathcal {A}\)
be a map** on a \(\rho _{\mathsf{b}}\)-complete partial b-metric space \((\mathcal {A},\rho _{\mathsf{b}}, \mathsf {s}>1)\). Suppose that \(\psi \in \Gamma \) and \(\phi :[0,+\infty )\rightarrow [0,+\infty )\) is a function such that \(\liminf_{\mathsf {t}\rightarrow \mathsf {t}_{0}}\phi ( \mathsf {t})>0\), for \(\mathsf {t}_{0}>0\) and \(\phi (\mathsf {t})=0 \Leftrightarrow \mathsf {t}=0\). If for every \(\mathsf {r}, \mathsf {t}\in \mathcal {A}\)

which implies

then  admits a unique fixed point.
admits a unique fixed point.
Proof
Let \(\eta _{\mathsf {b}}(\mathsf {r}, \mathsf {t})=\psi (\mathsf {t})-\phi (\mathsf {t})- \psi (\mathsf {r})\) in Theorem 3 and take into account Example 2. □
Corollary 4
Let  be a continuous map** on a \(\rho _{\mathsf{b}}\)-complete partial b-metric space \((\mathcal {A},\rho _{\mathsf{b}}, \mathsf {s}>1)\). Suppose that \(\psi \in \Gamma \) and \(\phi :[0,+\infty )\rightarrow [0,+\infty )\) is a function such that \(\liminf_{\mathsf {t}\rightarrow \mathsf {t}_{0}}\phi ( \mathsf {t})>0\), for \(\mathsf {t}_{0}>0\) and \(\phi (\mathsf {t})=0 \Leftrightarrow \mathsf {t}=0\). If for every distinct \(\mathsf {r}, \mathsf {t}\in \mathcal {A}\)
be a continuous map** on a \(\rho _{\mathsf{b}}\)-complete partial b-metric space \((\mathcal {A},\rho _{\mathsf{b}}, \mathsf {s}>1)\). Suppose that \(\psi \in \Gamma \) and \(\phi :[0,+\infty )\rightarrow [0,+\infty )\) is a function such that \(\liminf_{\mathsf {t}\rightarrow \mathsf {t}_{0}}\phi ( \mathsf {t})>0\), for \(\mathsf {t}_{0}>0\) and \(\phi (\mathsf {t})=0 \Leftrightarrow \mathsf {t}=0\). If for every distinct \(\mathsf {r}, \mathsf {t}\in \mathcal {A}\)

which implies

then  admits a unique fixed point.
admits a unique fixed point.
Proof
Let \(\eta _{\mathsf {b}}(\mathsf {r}, \mathsf {t})=\psi (\mathsf {t})-\phi (\mathsf {t})- \psi (\mathsf {r})\) in Theorem 4 and take into account Example 3. □
Corollary 5
Let  be a map** on a \(\rho _{\mathsf{b}}\)-complete partial b-metric space \((\mathcal {A},\rho _{\mathsf{b}}, \mathsf {s}>1)\). Suppose that \(\psi \in \Gamma \) and \(\gamma :[0,+\infty )\rightarrow [0,1)\) is a function such that \(\limsup_{\mathsf {t}\rightarrow \mathsf {t}_{0}}\gamma ( \mathsf {t})<1\), for \(\mathsf {t}_{0}>0\) and \(\gamma (\mathsf {t})=0 \Leftrightarrow \mathsf {t}=0\). If for every \(\mathsf {r}, \mathsf {t}\in \mathcal {A}\)
be a map** on a \(\rho _{\mathsf{b}}\)-complete partial b-metric space \((\mathcal {A},\rho _{\mathsf{b}}, \mathsf {s}>1)\). Suppose that \(\psi \in \Gamma \) and \(\gamma :[0,+\infty )\rightarrow [0,1)\) is a function such that \(\limsup_{\mathsf {t}\rightarrow \mathsf {t}_{0}}\gamma ( \mathsf {t})<1\), for \(\mathsf {t}_{0}>0\) and \(\gamma (\mathsf {t})=0 \Leftrightarrow \mathsf {t}=0\). If for every \(\mathsf {r}, \mathsf {t}\in \mathcal {A}\)

which implies

then  admits a unique fixed point.
admits a unique fixed point.
Proof
Let \(\eta _{\mathsf {b}}(\mathsf {r},\mathsf {t})=\gamma (\mathsf {t})\psi (\mathsf {t})- \psi (\mathsf {r})\) in Theorem 3 and take into account Example 2. □
Corollary 6
Let  be a continuous map** on a \(\rho _{\mathsf{b}}\)-complete partial b-metric space \((\mathcal {A},\rho _{\mathsf{b}}, \mathsf {s}>1)\). Suppose that \(\psi \in \Gamma \) and \(\gamma :[0,+\infty )\rightarrow [0,1)\) is a function such that \(\limsup_{\mathsf {t}\rightarrow \mathsf {t}_{0}}\gamma ( \mathsf {t})<1\), for \(\mathsf {t}_{0}>0\) and \(\gamma (\mathsf {t})=0 \Leftrightarrow \mathsf {t}=0\). If for every \(\mathsf {r}, \mathsf {t}\in \mathcal {A}\), with
be a continuous map** on a \(\rho _{\mathsf{b}}\)-complete partial b-metric space \((\mathcal {A},\rho _{\mathsf{b}}, \mathsf {s}>1)\). Suppose that \(\psi \in \Gamma \) and \(\gamma :[0,+\infty )\rightarrow [0,1)\) is a function such that \(\limsup_{\mathsf {t}\rightarrow \mathsf {t}_{0}}\gamma ( \mathsf {t})<1\), for \(\mathsf {t}_{0}>0\) and \(\gamma (\mathsf {t})=0 \Leftrightarrow \mathsf {t}=0\). If for every \(\mathsf {r}, \mathsf {t}\in \mathcal {A}\), with  ,
,

which implies

then  admits a unique fixed point.
admits a unique fixed point.
Proof
Let \(\eta _{\mathsf {b}}(\mathsf {r}, \mathsf {t})=\gamma (\mathsf {t})\psi (\mathsf {t})- \psi (\mathsf {r})\) in Theorem 4 and take into account Example 2. □
We will prove below results similar to those stated in Theorems 3, 4 that can be formulated for the case \(\mathsf {s}=1\).
Theorem 5
Let \((\mathcal {A},\rho )\) be a \(\rho _{\mathsf{b}}\)-complete partial-metric space and  be a map**. If there exists a function \(\eta \in \mathcal{Z}_{\psi }\) such that
be a map**. If there exists a function \(\eta \in \mathcal{Z}_{\psi }\) such that

for every distinct  , where \(\mathcal{D}^{1}_{A}\) is defined as
, where \(\mathcal{D}^{1}_{A}\) is defined as

then  admits exactly one fixed point.
admits exactly one fixed point.
Proof
For  , let
, let  be the sequence defined by (2.5),
be the sequence defined by (2.5),  , for any \(m\in \mathbb{N}\).
, for any \(m\in \mathbb{N}\).
First of all, we claim that  . From (2.13), we have
. From (2.13), we have

which implies

Consequently, we get

which, since ψ is non-decreasing, implies

Therefore, the sequence  is decreasing, so, we can find \(\theta \geq 0\) such that
is decreasing, so, we can find \(\theta \geq 0\) such that  . On the other hand, it is easy to see that
. On the other hand, it is easy to see that  , as well. Assuming that \(\theta >0\), from (\(\eta _{2}\)) and (2.13) it follows that
, as well. Assuming that \(\theta >0\), from (\(\eta _{2}\)) and (2.13) it follows that

which is a contradiction. So, we found that

We claim that  is a Cauchy sequence. If we suppose that
is a Cauchy sequence. If we suppose that  , there exist two subsequences
, there exist two subsequences  ,
,  of the sequence
of the sequence  and a number \(\mathsf{e}>0\) such that
and a number \(\mathsf{e}>0\) such that  .
.
Moreover, by Lemma 1, we have

Looking on the definition of the function \(\mathcal{D}_{A}^{1}\), we have

and kee** in mind (2.15) and (2.16) we get

Now, letting  and
and  , by \((\eta _{2})\) we get
, by \((\eta _{2})\) we get

On the other hand, by (2.15), we have

Thus, by the triangle inequality and taking into account (2.20), we get

and then  . Therefore,
. Therefore,

which implies

which contradicts (2.19). Thus,

and  is a Cauchy sequence in the complete partial-metric space \((\mathcal {A},\rho )\). This implies that there exists \(\mathsf {u}\in \mathcal {A}\) such that
is a Cauchy sequence in the complete partial-metric space \((\mathcal {A},\rho )\). This implies that there exists \(\mathsf {u}\in \mathcal {A}\) such that

We shall prove that  . By \((\rho _{b2})\), we get
. By \((\rho _{b2})\), we get

which implies

Thus, by the non-decreasing property of ψ, we obtain

and using (2.21) we get  . Thus,
. Thus,  and u is a fixed point of
and u is a fixed point of  .
.
In order to show the uniqueness of the fixed point, let \(\mathsf {u}, \mathsf {z}\in \mathcal {A}\) such that  and
and  . We have
. We have

which implies

which is a contradiction. Thus, we conclude that u is the unique fixed point of  . □
. □
Theorem 6
Let \((\mathcal {A},\rho )\) be a \(\rho _{\mathsf{b}}\)-complete partial-metric space and  be a continuous map**. If there exists a function \(\eta \in \mathcal{Z}_{\psi }\) such that
be a continuous map**. If there exists a function \(\eta \in \mathcal{Z}_{\psi }\) such that

holds for every  ,
,  where \(\mathcal{D}^{1}_{A}\) is defined as
where \(\mathcal{D}^{1}_{A}\) is defined as

then  admits exactly one fixed point.
admits exactly one fixed point.
Proof
Let  and consider the sequence
and consider the sequence  , with
, with  . We assume that
. We assume that  for each \(m\in \mathbb{N}\) because we remark that, on the contrary, if there exits \(l_{0}\) such that
for each \(m\in \mathbb{N}\) because we remark that, on the contrary, if there exits \(l_{0}\) such that  , that is
, that is  is a fixed point for the map**
is a fixed point for the map**  , then by (2.23), for any terms
, then by (2.23), for any terms  and
and  we have
we have

On the other hand, by (2.22),

which implies

But \(\psi \in \Gamma \) and then

If for some m,  then (2.24) becomes
then (2.24) becomes  , which is a contradiction. Then, for each \(m\geq 0\),
, which is a contradiction. Then, for each \(m\geq 0\),  , the inequality (2.24) yields
, the inequality (2.24) yields

Thus, the sequence  is decreasing, so it is convergent (being bounded from below). In this case, we can find a real number
is decreasing, so it is convergent (being bounded from below). In this case, we can find a real number  such that
such that  . Assume that
. Assume that  , let
, let  and
and  . Since
. Since

from \((\eta _{2})\) we have
This is a contradiction, so that

As a next step, we claim that  is a Cauchy sequence in \((\mathcal {A}, \rho )\). Reasoning by contradiction, we suppose that
is a Cauchy sequence in \((\mathcal {A}, \rho )\). Reasoning by contradiction, we suppose that  . Then, by Lemma 1, there exist the subsequences
. Then, by Lemma 1, there exist the subsequences  ,
,  of the sequence
of the sequence  , with \(q_{l}>m_{l}>l\), and a number \(\mathsf{e}>0\) such that
, with \(q_{l}>m_{l}>l\), and a number \(\mathsf{e}>0\) such that  and
and

Now, according to (2.25), there exists \(n_{1}\in \mathbb{N}\), such that

and \(n_{2}\in \mathbb{N}\), such that

Therefore, for \(l>\max \{ n_{1},n_{2} \} \) we have

and we can conclude  . Thus,
. Thus,

which implies

On the other hand,

and \((\eta _{2})\) implies

which contradicts (2.26). Therefore,  is a Cauchy sequence in a ρ-complete partial-metric space \((\mathcal {A}, \rho )\) and there exists \(\mathsf {u}\in \mathcal {A}\) such that
is a Cauchy sequence in a ρ-complete partial-metric space \((\mathcal {A}, \rho )\) and there exists \(\mathsf {u}\in \mathcal {A}\) such that

On the other hand, due to the continuity of the map**  , we get
, we get

Consequently, from (2.27), (2.28), on account of Lemma 3, we see that u is a fixed point of  . The uniqueness of the fixed point follows immediately as in the previous theorem. □
. The uniqueness of the fixed point follows immediately as in the previous theorem. □
Availability of data and materials
Not applicable.
References
Dass, B.K., Gupta, S.: An extension of Banach contraction principle through rational expressions. Indian J. Pure Appl. Math. 6, 1455–1458 (1975)
Jaggi, D.S.: Some unique fixed point theorems. Indian J. Pure Appl. Math. 8, 223–230 (1977)
Karapınar, E., Dehici, A., Redjel, N.: On some fixed points of \((\alpha -\psi )\)-contractive map**s with rational expressions. J. Nonlinear Sci. Appl. 10, 1569–1581 (2017)
Karapınar, E., Roldan, A., Sadarangani, K.: Existence and uniqueness of best proximity points under rational contractivity conditions. Math. Slovaca 66(6), 1427–1442 (2016)
Karapınar, E., Marudai, M., Pragadeeswarar, V.: Fixed point theorems for generalized weak contractions satisfying rational expression on a ordered partial metric space. Lobachevskii J. Math. 34(1), 116–123 (2013)
Karapınar, E., Shatanawi, W., Tas, K.: Fixed point theorem on partial metric spaces involving rational expressions. Miskolc Math. Notes 14(1), 135–142 (2013)
Chandok, S., Karapınar, E.: Common fixed point of generalized rational type contraction map**s in partially ordered metric spaces. Thai J. Math. 11(2), 251–260 (2013)
Mustafa, Z., Karapınar, E., Aydi, H.: A discussion on generalized almost contractions via rational expressions in partially ordered metric spaces. J. Inequal. Appl. 2014, 219 (2014)
Joonaghany, G.H., Farajzadeh, A., Azhini, M., Khojasteh, F.: New common fixed point theorem for Suzuki type contractions via generalized ψ-simulation functions. Sahand Commun. Math. Anal. 16, 129–148 (2019)
Khojasteh, F., et al.: A new approach to the study of fixed point theory for simulation functions. Filomat 29(6), 1189–1194 (2015)
Chandok, S., et al.: Simulation functions andd graghty type results. Bol. Soc. Parana. Mat. 39(1), 35–50 (2021)
Aleksić, S., et al.: Simulation functions and Boyd–Wong type results. Tbil. Math. J. 12(1), 105–115 (2019)
Radenović, S., Chandok, S.: Simulation type functions and coincidence point results. Filomat 32(1), 141–147 (2018)
Alsubaie, R., Alqahtani, B., Karapınar, E., Hierro, A.F.R.L.: Extended simulation function via rational expressions. Mathematics 8, 710 (2020)
Alqahtani, O., Karapınar, E.: A bilateral contraction via simulation function. Filomat 33(15), 4837–4843 (2019)
Alghamdi, M.A., Gulyaz-Ozyurt, S., Karapınar, E.: A note on extended Z-contraction. Mathematics 8, 195 (2020)
Agarwal, R.P., Karapınar, E.: Interpolative Rus–Reich–Ciric type contractions via simulation functions. An. Ştiinţ. Univ. ‘Ovidius’ Constanţa, Ser. Mat. 27(3), 137–152 (2019)
Aydi, H., Karapınar, E., Rakocevic, V.: Nonunique fixed point theorems on b-metric spaces via simulation functions. Jordan J. Math. Stat. 12(3), 265–288 (2019)
Monfared, H., Asadi, M., Farajzadeh, A.: New generalization of Darbo’s fixed point theorem via α-admissible simulation functions with application. Sahand Commun. Math. Anal. 17(2), 161–171 (2020)
Asadi, M., Azhini, M., Karapınar, E., Monfared, H.: Simulation functions over M-metric spaces. East Asian Math. J. 33(5), 559–570 (2017)
Asadi, M., Gabeleh, M., Vetro, C.: A new approach to the generalization of Darbo’s fixed point problem by using simulation functions with application to integral equations. Results Math. 74, Article ID 86 (2019)
Asadi, M.: Discontinuity of control function in the (F, Φ, θ)-contraction in metric spaces. Filomat 31(17), 5427–5433 (2017)
Matthews, S.G.: Partial metric topology. In: Proc. 8th Summer Conference on General Topology and Application. Ann. New York Acad. Sci., vol. 728, pp. 183–197 (1994)
Karapınar, E.: On Jaggi type contraction map**s. U.P.B. Sci. Bull., Ser. A 80(4), (2018)
Abdeljawad, T., Karapınar, E., Tas, K.: Existence and uniqueness of a common fixed point on partial metric spaces. Appl. Math. Lett. 24(11), 1894–1899 (2011)
Shukla, S.: Partial b metric spaces and fixed point theorems. Mediterr. J. Math. 11, 703–711 (2014)
Mustafa, Z., Roshan, J.R., Parvaneh, V., Kadelburg, Z.: Some common fixed point results in ordered partial b-metric spaces. J. Inequal. Appl. 2013, 562 (2013)
Dung, N.V., Hang, V.T.L.: Remarks on partial b-metric spaces and fixed point theorems. Mat. Vesn. 69(4), 231–240 (2017)
Karapınar, E.: Fixed point theory for cyclic weak Φ-contraction. Appl. Math. Lett. 24, 822–825 (2011)
Vujaković, J., Aydi, H., Radenović, S., Mukheimer, A.: Some remarks and new results in ordered partial b-metric spaces. Mathematics 7, 334 (2019). https://doi.org/10.3390/math7040334
Funding
This research received no external funding.
Author information
Authors and Affiliations
Contributions
All authors contributed equally and significantly in writing this article. All authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare that they have no competing interests.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Karapınar, E., Chen, CM., Alghamdi, M.A. et al. Advances on the fixed point results via simulation function involving rational terms. Adv Differ Equ 2021, 409 (2021). https://doi.org/10.1186/s13662-021-03564-w
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13662-021-03564-w




 ;
;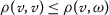 ;
;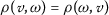 ;
; ;
;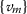 is convergent to a limit
is convergent to a limit 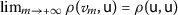 ;
;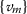 is a Cauchy sequence if
is a Cauchy sequence if 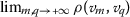 exists and is finite.
exists and is finite. ;
; ;
; ;
;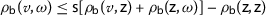 .
.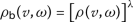




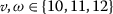 , we have
, we have  , and then
, and then


 we have
we have 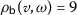 ,
,  ,
,  ,
, 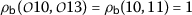 and then
and then
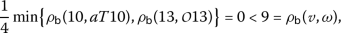
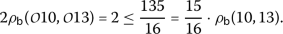
 we have
we have  ,
,  ,
,  ,
,  and then
and then
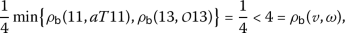

 we have
we have  ,
,  ,
,  ,
,  and then
and then
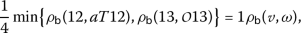
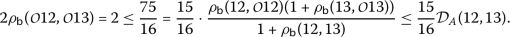
 is the fixed point of the map**
is the fixed point of the map** 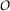 .
. , if
, if 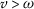 , (the case
, (the case  is similar), we have
is similar), we have

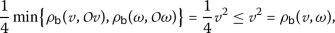

 , if
, if 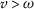 , (the case
, (the case 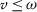 is similar), we have
is similar), we have

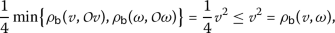
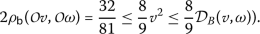
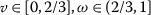 , we have
, we have
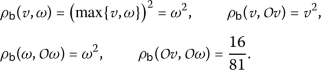
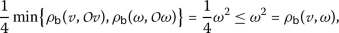
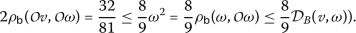
 is the unique fixed point of
is the unique fixed point of  .
.