1 Introduction

The real-world problem shows the distinct effect of environmental noise on the biological phenomenon. The variations of environment have an ultimate impact on the epidemic development [1, 2]. Due to these ranges of perturbation and the unpredictable individual to individual contacts and population, the form of an epidemic outbreak for disease in humans is naturally random [3, 4]. So the nature of the epidemic is inevitably determined by variation and randomness of the surroundings. Modeling with a deterministic approach has a limitation, and it is very difficult to accurately predict the dynamics of a system. This occurs because deterministic models do not incorporate the effect of a fluctuating environment.

Hepatitis B virus is considered as one of the fatal infections due to which millions of people have died. Hepatitis B virus infects the liver of the human body and is the main cause of liver cancer. The transmission of hepatitis B virus from infected to susceptible people is vertical as well horizontal. Hepatitis B is divided into two stages i.e. acute and chronic. The acute stage consists of the first few months normally considered as six months after exposure to the virus, during which the immune system of the human body is capable of controlling the infection. Feeling sick and high temperature are the two main symptoms of the acute stage, which fade away after some weeks due to the immune system. The chronic stage is the worst stage in which the liver fails to function properly and cancer cells develop. The treatment of a person in the chronic stage takes several years. Many deterministic epidemic models have been developed for the description of viral dynamics of hepatitis B (see for details [5–10])

Mathematical modeling is considered to be an effective tool for describing the dynamic behavior of infections. For realizing and controlling the outbreak of transmissible diseases in a group, many researchers have formulated models. The application of mathematical modeling has been in vogue for the study of transmissible infectious diseases (see e.g. [11–16]). Epidemic models are mostly studied by two approaches i.e. deterministic and stochastic. The most effective approach for studying an epidemic model is the stochastic one [17], because it results in a larger degree of realism between evaluation in imitation. The stochastic one gives us a more valuable output with the comparison to the deterministic model. By executing the stochastic model various times, we can make a distribution of outcomes [18–22]. To study the dynamics of various infectious diseases, mathematical modeling is considered as one of the best techniques to formulate the phenomenon in the system of equations. Several researchers have worked on different infectious diseases. They have developed different mathematical models for epidemic diseases that help in the prevention of diseases in daily life. Modeling of epidemic models is helpful to academia as well as to daily life. Epidemic models are broadly classified into two categories i.e. deterministic and stochastic. The stochastic models have an advantage over the deterministic models as these models are very close to nature and depict exact biological phenomena. In explicating many fields of natural and engineering sciences, the role of stochastic models is pivotal. In medical and biological processes, the inherent variability can be studied using stochastic models. They can be used to counter (i) the risk effects in managerial economics (ii) psychological complexities, and (iii) fluctuation in rates. Many researchers have worked on stochastic epidemic models to analyze and control different diseases for example hepatitis B, avian influenza, leishmaniasis, tuberculosis, etc. Therefore, motivated by the aforementioned work, very few attempts have been established by the researchers using stochastic hepatitis epidemic model with random perturbation.

Here, our objective is to improve a deterministic model [23] by considering environmental interactions in terms of fluctuating environment. We formulate the model for the dynamics of infectious disease. We subdivide the entire population into the susceptible, the infected (acute), the chronic, and the recovered. In all these, we distribute the transmission rate by white noise. We study the disease extinction and persistence to find out sufficient conditions. We also verify our theoretical findings using numerical simulation.

The organization of the manuscript is performed as follows: We present model formulation in Sect. 2. The existence and uniqueness are discussed in Sect. 3. We discuss the disease extinction and the disease persistence with sufficient conditions in Sect. 4. Finally, in Sect. 5, we present numerical simulation of the proposed model.

2 Model formulation

To develop a mathematical model for the description of the dynamics of the proposed model with fluctuating environment population, we assume the following:

\((A_{1})\):

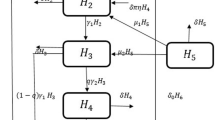
The entire population \(N(t)\) at time t is divided into four compartments: the susceptible individuals \(S(t)\), the acutely infected with hepatitis individuals \(I_{1}(t)\), the chronically infected with hepatitis individuals \(I_{2}(t)\), and the recovered individuals \(R(t)\) i.e. \(N(t)=S(t)+I_{1}(t)+I_{2}(t)+R(t)\) varies with time t.

\((A_{2})\):

All parameters and state variables of the proposed model are nonnegative.

\((A_{3})\):

The vaccine of the disease provides life-time protection. Therefore, successfully vaccinated population goes to the removed class.

\((A_{4})\):

For the effect of randomly fluctuating environment, take \(\alpha \rightarrow \alpha +\sigma \dot{B}(t)\), where \(\sigma ^{2}>0\) denotes the intensity of white noise and \(B(t)\) represents the standard Brownian motion satisfying the condition \(B(0)=0\).

Assumptions \((A_{1})\)–\((A_{4})\) lead to the stochastic epidemic model, which is represented by the following system of four stochastic differential equations:

$$ \begin{aligned} &dS(t)= \bigl(b-\alpha I_{1}(t) S(t)-\alpha S(t)I_{2}(t)-(v+ \mu _{0})S(t) \bigr)\,dt-\xi \alpha S(t)I_{1}(t)\,dB(t) \\ &\hphantom{dS(t)=}{}-\xi \alpha S(t)I_{2}(t)\,dB(t), \\ & dI_{1}(t)= \bigl(\alpha I_{1}(t)S(t)+\alpha S(t)I_{2}(t)-( \beta +\mu _{0}+\gamma _{1})I_{1}(t) \bigr)\,dt+\xi \alpha S(t)I_{1}(t)\,dB(t) \\ &\hphantom{dI_{1}(t)=}{}-\xi \alpha S(t)I_{2}(t)\,dB(t), \\ &dI_{2}(t)= \bigl(-(\gamma _{2}+\mu _{0}+\mu _{1})I_{2}(t)+ \beta I_{1}(t) \bigr)\,dt , \\ &dR(t)= \bigl(-\mu _{0} R(t)+vS(t)+\gamma _{2}I_{2}(t)+ \gamma _{1}I_{1}(t) \bigr)\,dt. \end{aligned} $$
(1)

The description of parameters with their units is presented in Table 1.

Table 1 Parameters used in the model (1)
Full size table

If the white noise intensities \(\xi _{i}=0\) for \(i =1,2,3,4\) in system (1), then the deterministic epidemic model becomes as follows:

$$ \begin{aligned} &\frac{dS}{dt}=b-\alpha I_{1}(t) S(t)- \alpha S(t)I_{2}(t)-(v+\mu _{0})S(t), \\ &\frac{dI_{1}}{dt}=\alpha I_{1}(t)S(t)+\alpha S(t)I_{2}(t)-( \beta +\mu _{0}+\gamma _{1})I_{1}(t), \\ &\frac{dI_{2}}{dt}=-(\gamma _{2}+\mu _{0}+\mu _{1})I_{2}(t)+ \beta I_{1}(t), \\ & \frac{dR}{dt}=-\mu _{0} R(t)+vS(t)+\gamma _{2}I_{2}(t)+ \gamma _{1}I_{1}(t). \end{aligned} $$
(2)

Moreover, the above model i.e. system (2) has multiple equilibria: \(E_{0} = (S_{0}, 0, 0, R^{0})\), where \(S_{0} = \frac{b}{(\mu _{0}+v)}\) and \(R^{0} = \frac{vb}{\mu _{0}(\mu _{0}+v)}\). In addition, \(E^{*} = (S^{*}, I_{1}^{*}, I_{2}^{*}, R^{*})\), where

$$\begin{aligned}& S^{*}=\frac{1}{\alpha \beta }(\beta +\mu _{0}+\gamma _{1}) ( \gamma _{2}+\mu _{0}+\mu _{1}), \\& I_{1}^{*}=\frac{1}{\alpha \beta }(\mu _{0}+v) (\gamma _{2}+\mu _{0}+ \mu _{1})[R_{0}-1], \\& I^{*}=\frac{1}{\alpha }(\mu _{0}+v)[R_{0}-1], \\& R^{*}=\frac{1}{\mu _{0}} \biggl[ \biggl( \frac{\gamma _{1}}{\alpha \beta }( \mu _{0}+v) (\gamma _{2}+\mu _{0}+ \mu _{1})+\frac{\gamma _{2}}{\alpha }(\mu _{0}+v)[R_{0}-1] \biggr) \\& \hphantom{R^{*}=}{}+ \frac{v}{\alpha \beta }(\beta +\mu _{0}+\gamma _{1}) (\gamma _{2}+\mu _{0}+ \mu _{1}) ) \biggr], \end{aligned}$$

with

$$ R_{0}= \frac{\alpha \beta b}{(\mu _{0}+v)(\beta +\mu _{0}+\gamma _{1})(\gamma _{2}+\mu _{0}+\mu _{1})}. $$

3 Uniqueness and existence

We prove the uniqueness and existence.

Theorem 1

For the initial data, the solution of (3) is unique for \(t\geq 0\). Moreover,

$$ N(t)\rightarrow \frac{b}{\mu _{0}} \quad \textit{as } t \rightarrow \infty , $$
(3)

where \(N(t)\) symbolizes the total population.

Proof

For the initial population, system (3) coefficients are locally Lipschitz continuous. It gives that a local unique solution on \(t\in [0,\tau _{e})\) exists, in which the temporal explosion is symbolized by \(\tau _{e}\) [17]. To verify that the solution is global, we only need to show that \(\tau _{e}=\infty \) a.s. Let \(k_{0}\geq 0\) be sufficiently large. We choose \(k_{0}\) in a way that \(S(0)\), \(I_{1}(0)\), \(I_{2}(0)\), and \(R(0)\) lie in \([\frac{1}{k_{0}},k_{0}]\). For each \(k_{0}\leq k\), we define

$$ \tau _{k}= \bigl\{ t\in [0,\tau _{e}): \max \bigl\{ S(t),I_{1}(t),I_{2}(t),R(t) \text{ or } k \min \bigl\{ S(t),I_{1}(t),I_{2}(t),R(t) \bigr\} \leq t \bigr\} \bigr\} . $$

We use the notion \(\inf \phi =\infty \), where ϕ is an empty set, throughout this study. \(\tau _{k}\) increases as k approaches to ∞. The setting of \(\tau _{\infty }=\lim_{k\rightarrow \infty }\) along with the use of \(\tau _{\infty }\leq \tau _{e}\) a.s. proves that \(\tau _{\infty }\) is =∞ a.s., and the solution of (3) lies in \(R^{4}_{+}\) a.s. \(\forall t\geq 0\). Also, for the completion of conclusion, we will prove \(\tau _{e}=\infty \) a.s. If this is not true, then a pair of constants exists for \(T>0\) and \(\epsilon \in (0,1)\),

$$ P\{\tau _{\infty }\leq T\}>\epsilon . $$
(4)

Therefore, \(k_{1}\geq k_{0}\), where \(k_{1}\) and \(k_{2}\) are integers such that

$$ P\{T\geq \tau _{k}\}\geq \epsilon \quad \text{for all } k_{1}\leq k . $$

Since \(N(t)\) is the total population, then \(\tau _{k}\leq t\), we have

$$ dN(t)= \bigl(-\mu _{1}C(t)-\mu _{0}N(t)+b \bigr)\,dt\leq \bigl(-\mu _{0}N(t)+b \bigr) \,dt. $$
(5)

Solving Eq. (5), we obtain

$$ N(t)\leq \textstyle\begin{cases} \frac{b}{\mu _{0}}, & \text{if } N(0)\leq \frac{b}{\mu _{0}}, \\ N(0), & \text{if } N(0)>\frac{b}{\mu _{0}}, \end{cases}\displaystyle \quad :=M. $$
(6)

Define a \(C^{2}\)-function \(V:R^{4}_{+}\rightarrow R_{+}\) such that

$$ V(t)=\ln \bigl(S(t)I_{1}(t)I_{2}(t) \bigr). $$

Clearly V is nonnegative. Let \(k\geq k_{0}\) and \(T>0\) be arbitrary. By Itô’s formula, we have

$$ \begin{aligned} dV(t)&=LV(t)+\xi \biggl( \frac{S(t)}{I_{1}(t)}-1 \biggr) \bigl(I_{2}(t)+{I_{1}(t)} \bigr)\,dB(t), \end{aligned} $$

where

$$ \begin{aligned} LV(t)=&- \bigl(\alpha I_{2}(t)+\alpha I_{1}(t)+v+\mu _{0} \bigr)- \frac{1}{2}\xi ^{2} \bigl(I_{2}(t)+I_{1}(t) \bigr)^{2}-(\gamma _{1}+\mu _{0}+ \beta ) \\ &{}-\frac{1}{2}\frac{S^{2}(t)}{I^{2}(t)}\xi ^{2} \bigl(I_{2}(t)+I_{1}(t) \bigr)^{2}-( \gamma _{2}+\mu _{0}+\mu _{1}). \end{aligned} $$

By definition

$$ \begin{aligned} &V(t)\geq V(0)+ \int _{0}^{t}LV(s)\,ds+ \int _{0}^{t}\xi \biggl(\frac{S(t)}{I(t)}-1 \biggr) \bigl(I_{2}(t)+I_{1}(t) \bigr)\,dB(s), \\ &-\infty \geq V(t)\geq V(0)+ \int _{0}^{t}LV(s)\,ds+ \int _{0}^{t}\xi \biggl(\frac{S(t)}{I(t)}-1 \biggr) \bigl(I_{2}(t)+I_{1}(t) \bigr)\,dB(s)>-\infty , \end{aligned} $$
(7)

which is in contradiction with the assumptions. We observe from system (2) that

$$ d \bigl(N(t) \bigr)= \bigl(b-\mu _{0} \bigl(N(t) \bigr)-\mu _{1}I_{2}(t) \bigr)\,dt. $$

The solution of the last equation takes the following form:

$$ N(t)=e^{-\mu _{0}t} \biggl(N(0)+ \int _{0}^{t} \bigl(b-\mu _{1}I_{2}(s) \bigr)e^{ \mu _{0}s}\,ds \biggr). $$

The application of the L’Hospital rule yields

$$ \begin{aligned} \lim_{t\rightarrow \infty } \bigl(N(t) \bigr)=\frac{b}{\mu _{0}} \quad \text{a.s}. \end{aligned} $$

 □

4 Extinction and persistence

To study the extinction as well as persistence, first we introduce the following definitions.

$$ \bigl\langle z(t) \bigr\rangle =\frac{1}{t} \int _{0}^{t}z(r)\,dr. $$

Definition 1

([24])

The proposed system (3) is persistent if

$$ \lim_{t\rightarrow \infty } \inf \int _{0}^{t}I(r)\,dr>0\quad \text{a.s.} $$

Theorem 2

In the solution of (3) with \((S(0),I_{1}(0),I_{2}(0),R(0))\in \Omega ^{*}\), if \(\xi ^{2}>\frac{\alpha ^{2}}{2(\gamma _{1}+\mu _{0}+\beta )}\), then

$$ I_{1}(t),I_{2}(t),R(t)\rightarrow 0\quad \textit{a.s and} \quad S(t)\rightarrow \frac{b}{\mu _{0}}\quad \textit{a.s as } t \rightarrow \infty . $$

Proof

The application of Ito’s formula to the second equation of (1) gives

$$ \begin{aligned} d \bigl(\log I_{1}(t) \bigr)={}&{-\frac{\xi ^{2}}{2} \biggl[ \frac{S(t)}{I_{1}} \bigl(I_{2}(t)+I_{1}(t) \bigr)-\frac{\alpha }{\xi ^{2}} \biggr]^{2}-( \gamma _{1}+ \mu _{0}+\beta )+ \frac{\alpha ^{2}}{2\xi ^{2}}}\,dt \\ &{}+\xi \frac{S(t)}{I_{1}(t)} \bigl(I_{2}(t)+I_{1}(t) \bigr)\,dB(t). \end{aligned} $$
(8)

Integrating the last equation and then dividing it by t gives

$$ \begin{aligned} \frac{\log I_{1}(t)}{t}&\leq \frac{\alpha ^{2}}{2\xi ^{2}}-(\gamma _{1}+\mu _{0}+\beta )+ \frac{M(t)}{t}+\frac{\log I_{1}(0)}{t}, \end{aligned} $$
(9)

where

$$\begin{aligned}& M(t)= \int _{0}^{t}\xi \frac{S(t)}{I_{1}(t)} \bigl(I_{2}(t)+I_{1}(t) \bigr)\,dB(t), \\& \lim_{t\rightarrow \infty }\sup \frac{ \langle M,M \rangle _{t}}{t}\leq \frac{\xi ^{2} b^{2}}{\mu _{0}^{2}}< \infty . \end{aligned}$$

Applying the large number theorem for martingales, we have

$$\begin{aligned}& \lim_{t\rightarrow \infty } \frac{M(t)}{t}=0, \\& \lim_{t\rightarrow \infty }\sup \frac{\log I_{1}(t)}{t}\leq \frac{\alpha ^{2}}{2\xi ^{2}}-( \gamma _{1}+\mu _{0}+\beta )< 0, \end{aligned}$$
(10)

which implies that

$$ \lim_{t\rightarrow \infty }I_{1}(t)=0 \quad \text{a.s.} $$

Now solving system (3) for \(I_{2}(t)\) gives

$$\begin{aligned} I_{2}(t) =&e^{-(\gamma _{2}+\mu _{0}+\mu _{1}) t} \biggl[I_{2}(0)+ \int _{0}^{t} \bigl(\beta I_{1}(s) \bigr)e^{(\gamma _{2}+\mu _{0}+\mu _{1})s}\,ds \biggr] \\ \leq& I_{2}(0)e^{-( \gamma _{2}+\mu _{0}+\mu _{1})} + \beta \int _{0}^{t} \bigl( I_{1}(s) \bigr) \,ds. \end{aligned}$$

This also implies that

$$ \lim_{t\rightarrow \infty }I_{2}(t)=0 \quad \text{a.s.} $$

In a similar fashion \(\lim_{t\rightarrow \infty }R(t)=0\) a.s. Since \(N(t)=S(t)+I_{1}(t)+I_{2}(t)+R(t)\) and we know that \(N(t)\rightarrow \frac{b}{\mu _{0}}\) as \(t\rightarrow \infty \), replacing \(I_{1}(t),I_{2}(t),R(t)\rightarrow 0\) a.s. \(t\rightarrow \infty \), we obtain \(S(t)\rightarrow \frac{b}{\mu _{0}}\) a.s. \(t\rightarrow \infty \). □

Theorem 3

Suppose

$$ \begin{aligned} K_{1}=(\gamma _{1}+\mu _{0}+\beta ) \biggl( \frac{\mu _{0}}{2b}- \frac{\alpha }{v+\mu _{0}} \biggr) \end{aligned} $$

for any initial data in \(\in \Omega ^{*}\) such that

$$ \begin{aligned} N(t)\rightarrow \frac{b}{\mu _{0}} \quad \textit{as } t\rightarrow \infty . \end{aligned} $$

If \(K_{1}\neq 0\), \(\frac{1}{K_{1}} (\frac{b}{v+\mu _{0}}-\frac{1}{2}\xi ^{2} \frac{b^{2}}{\mu _{0}^{2}} )>0\), then the solution \((S(t),I_{1}(t),I_{2}(t),R(t))\) satisfies

$$ \begin{aligned} \lim_{t\rightarrow \infty }\inf \bigl\langle I_{1}(t) \bigr\rangle \geq \frac{1}{K_{1}} \biggl( \frac{b}{v+\mu _{0}}- \frac{1}{2}\xi ^{2} \frac{b^{2}}{\mu _{0}^{2}} \biggr). \end{aligned} $$

Proof

The integration of (3) leads to

$$ \begin{aligned} \frac{-S(0)+S(t)}{t}={}&b-\alpha \bigl\langle S(t)I_{1}(t) \bigr\rangle - \alpha \bigl\langle S(t)I_{2}(t) \bigr\rangle -(v+\mu _{0}) \bigl\langle S(t) \bigr\rangle \\ &{}-\frac{\xi }{t} \int _{0}^{t} \bigl(I_{1}(t)-I_{2}(t) \bigr)SdB(r), \\ \frac{I_{1}(t)-I_{1}(0)}{t}={}&\alpha \bigl\langle S(t)I_{1}(t) \bigr\rangle +\alpha \bigl\langle S(t)I_{2}(t) \bigr\rangle -(\gamma _{1}+\beta +\mu _{0}) \bigl\langle I_{1}(t) \bigr\rangle \\ &{}+\frac{\xi }{t} \int _{0}^{t} \bigl(I_{1}(t)+I_{2}(t) \bigr)SdB(r), \\ \frac{I_{2}(t)-I_{2}(0)}{t}={}&\beta \bigl\langle I_{1}(t) \bigr\rangle -( \gamma _{2}+ \mu _{1}+\mu _{0}) \bigl\langle I_{2}(t) \bigr\rangle , \\ \frac{R(t)-R(0)}{t}={}&\gamma _{1} \bigl\langle I_{1}(t) \bigr\rangle +\gamma _{2} \bigl\langle I_{2}(t) \bigr\rangle +v \bigl\langle S(t) \bigr\rangle -\mu _{0} \bigl\langle R(t) \bigr\rangle . \end{aligned} $$
(11)

Adding the first two equations of system (10), we have

$$ \frac{-S(0)+S(t)}{t}+\frac{I_{1}(t)-I_{1}(0)}{t}=b-(v+\mu _{0}) \bigl\langle S(t) \bigr\rangle -(\gamma _{1}+\mu _{0}+\beta ) \bigl\langle I_{1}(t) \bigr\rangle . $$

From here, we have

$$ \bigl\langle S(t) \bigr\rangle =\frac{b}{v+\mu _{0}}- \frac{\gamma _{1}+\beta +\mu _{0}}{v+\mu _{0}} \bigl\langle I_{1}(t) \bigr\rangle - \frac{K(t)}{v+\mu _{0}}, $$
(12)

where \(K(t)\) is defined by

$$ K(t)= \biggl[\frac{S(t)-S(0)}{t}+\frac{I_{1}(t)-I_{1}(0)}{t} \biggr]. $$

Choosing a function

$$ V=\log \bigl(I_{1}(t)+I_{2}(t) \bigr). $$

Applying the Itô’s, we get

$$ d\log \bigl(I_{1}(t)+I_{2}(t) \bigr)= \biggl[\alpha S(t)- \frac{(\gamma _{1}+\mu _{0}+\beta )I_{1}(t)}{I_{1}(t)+I_{2}(t)}- \frac{1}{2}\xi ^{2}S^{2}(t) \biggr]\,dt+\xi S(t)\,dB(t). $$

Integration of the above inequality and then division by t leads to

$$\begin{aligned} & \frac{\log (I_{1}(t)+I_{2}(t))-\log (I_{1}(0)+I_{2}(0))}{t} \\ &\quad \geq \alpha \bigl\langle S(t) \bigr\rangle +\frac{\mu _{0}}{2b}(\gamma _{1}+ \beta + \mu _{0}) \bigl\langle I_{1}(t) \bigr\rangle - \frac{1}{2}\xi ^{2}\frac{b^{2}}{\mu ^{2}}+ \frac{\xi }{t} \int _{0}^{t} S(r)\,dB(r) \\ &\quad \geq \alpha \biggl[\frac{b}{v+\mu _{0}}- \frac{\gamma _{1}+\beta +\mu _{0}}{v+\mu _{0}} \bigl\langle I_{1}(t) \bigr\rangle - \frac{K(t)}{v+\mu _{0}} \biggr] \\ &\qquad {}+\frac{\mu _{0}}{2b}(\gamma _{1}+\beta +\mu _{0}) \bigl\langle I_{1}(t) \bigr\rangle - \frac{1}{2}\xi ^{2} \frac{b^{2}}{\mu _{0}^{2}}+\frac{M(t)}{t} \\ &\quad \geq \frac{\alpha b}{v+\mu _{0}}+ \biggl[(\gamma _{1}+\beta +\mu _{0}) \biggl( \frac{\mu _{0}}{2b}-\frac{\alpha }{v+\mu _{0}} \biggr) \biggr] \bigl\langle I_{1}(t) \bigr\rangle -\frac{1}{2}\xi ^{2} \frac{b^{2}}{\mu _{0}^{2}} \\ &\qquad {}+\frac{M(t)}{t}-\frac{\alpha K(t)}{v+\mu _{0}}. \end{aligned}$$

It follows

$$\begin{aligned} \bigl\langle I_{1}(t) \bigr\rangle \geq{}& \frac{1}{K_{1}} \biggl[ \frac{\alpha b}{v+\mu _{0}}- \frac{1}{2} \frac{\xi ^{2} b}{\mu _{0}^{2}}+\frac{M(t)}{t}- \frac{\alpha K(t)}{v+\mu _{0}} \\ &{}- \frac{\log (I_{1}(t)+I_{2}(t))-\log (I_{1}(0)-I_{2}(0))}{t} \biggr], \end{aligned}$$
(13)

where \(K_{1}=(\mu _{0}+\beta +\gamma _{1}) (\frac{\mu _{0}}{2b}- \frac{\alpha }{\mu _{0}+v} )\) and \(M(t)=\xi \int _{0}^{t} S(t)\,dB(t)\). \(M(t)\) is a continuous local martingale, which satisfies the condition \(\lim_{t\rightarrow \infty }\sup \frac{ \langle M,M \rangle _{t}}{t}\leq \frac{\xi ^{2} b^{2}}{\mu _{0}^{2}}<\infty \) a.s. By the application of the large number theorem [25], we get \(\lim_{t\rightarrow \infty }\frac{M(t)}{t}=0\) a.s. \(N(t)\leq \frac{b}{\mu _{0}}\),

$$ -\infty < \log \bigl(I_{2}(t)+I_{1}(t) \bigr)< \log \frac{2b}{\mu _{0}}. $$

Furthermore, \(\lim_{t\rightarrow \infty }K(t)=0\). Taking limit inferior to Eq. (11), we get

$$ \lim_{t\rightarrow \infty }\inf \bigl\langle I_{1}(t) \bigr\rangle \geq \frac{1}{K_{1}} \biggl( \frac{b}{v+\mu _{0}}- \frac{1}{2}\xi ^{2} \frac{b^{2}}{\mu _{0}^{2}} \biggr), $$

which completes the proof. □

5 Numerical simulation

We present simulations of system (1) to illustrate our theoretical results using the Runge–Kutta method of stochastic type. To perform the stochastic process influence, we compare the stochastic and deterministic cases with each other, see Fig. 1–Fig. 2. To show the feasibility of the extinction i.e. Theorem 2, the parameter values are assumed and given in Table 1 with vaccination rate \(v=0.4\). Most of parameter values i.e. the experimental values are borrowed from [24], while the values of some one are assumed with much more biological feasibility. The inequality \(\xi ^{2}>\frac{\alpha ^{2}}{2(\gamma _{1}+\mu _{0}+\beta )}\) from Theorem 2 is satisfied: \(\xi ^{2}-\frac{\alpha ^{2}}{2(\gamma _{1}+\mu _{0}+\beta )}=0.425>0\), see Fig. 1(a). Likewise, in the case of persistence, the same parameter values with \(v=0.6\) are used and this ensures the persistence i.e. Theorem 3 holds; \(\frac{1}{K_{1}} (\frac{b}{v+\mu _{0}}-\frac{1}{2}\xi ^{2} \frac{b^{2}}{\mu _{0}^{2}} )=0.0965>0\), see Fig. 2(a).

Figure 1
figure 1

Simulation of system (3) with time step and initial size of the population \(\Delta t=0.01\) and \((S(0),I_{1}(0),I_{2}(0),R(0) )= (0.4,0.3,0.2,0.1 )\) respectively

Full size image
Figure 2
figure 2

Simulation of system (3) with time step and initial size of the population \(\Delta t=0.01\) and \((S(0),I_{1}(0),I_{2}(0),R(0) )= (0.7,0.6,0.4,0.2 )\) respectively

Full size image

6 Conclusion

Most of the real-world problems include stochastic influence. In the current paper, we investigated the transmission dynamics of the hepatitis stochastic epidemic model. By using a proper stochastic Lyapunov function, we showed the existence of positive solutions. We obtained sufficient conditions for the extinction and persistence of hepatitis in terms of the parameters involved in the model. We also proved that the intensity of the noise has a significant influence on the transmission of the disease. We showed that the extinction of the disease increases with the increase in the noise parameter. Similarly, the disease decreases with the increased noise term. All these theoretical findings are verified using large scale numerical simulations.