1 Introduction

Over the last two decades, the interest in fractional derivatives and their implementations has been intensified. Various physical phenomena in technological developments have been determined in terms of fractional derivatives or differential equations. Moreover, the modeling of many engineering problems relies on fractional operators. There are many reasons for the need for fractional calculus, but the most important ones can be stated as the singular kernel with locality and also the nonsingular kernel with nonlocality. In order to overcome these problems, Baleanu and Atangana came up with new fractional operators, namely Atangana–Baleanu (AB) derivative operators, with fractional order based upon the recognized Mittag-Leffler function [1]. Those noninteger derivatives have all the usefulness of those of past provisions. These trend ideas on operators have got the attention of many mathematicians and scientists. AB derivatives have been used for analyzing engine oil based generalized Brinkman-type nano-liquid with molybdenum disulfide nanoparticles of spherical shape [2]. Modeling and analysis of the fractional HBV model with the Atangana–Baleanu derivative have been studied in [3]. These operators have been also applied to nanofluids to enhance the performance of solar collectors, and the same researchers have also compared Atangana–Baleanu and Caputo–Fabrizio fractional models [4]. The logarithmic-KdV equation involving Mittag-Leffler type kernel with AB derivative has been investigated in [5]. AB derivatives have been used for numerical patterns in the reaction-diffusion system [6]. Adams–Bashforth scheme has been formulated with Atangana–Baleanu–Caputo fractional derivative to model chaotic problems [7]. Three different fractional derivatives including ABC have been considered to solve the Korteweg–de Vries and Korteweg–de Vries–Burger equations [8]. ABC-fractional masks have been designed in image processing [9]. In addition to ABC derivatives, Caputo–Fabrizio fractional operators have been also used by many authors. Transient response of the parallel RCL circuit by using the Caputo–Fabrizio fractional derivative has been analyzed by Rezapour et al. in [10]. Other works can also be counted as in [11–15]. In addition to all these articles, readers are advised to read the works in [16–35].

Most of the dynamical systems have long-range temporal memory. Modeling of these systems with fractional-order derivatives has more advantages than classical models such as in [36–38]. The main reason for using fractional derivatives in these models is the memory concept. Generally, when the output of a system at each time t depends only on the input at time t, such systems are called memoryless systems. On the other hand, when the system has to remember previous values of the input in order to determine the current value of the output, such systems are said to be non-memoryless systems or memory systems. One of the well-known memoryless systems is the Markov chain phenomena. Human decision making or shape memory alloy are non-memoryless systems [39]. For instance, in [36], a biological model a fractional-order model for Ebola virus infection with delayed immune response on heterogeneous complex networks has been investigated. It has been demonstrated that Chua’s model with fractional derivative with a lower order 2.7 has been able to replicate a chaotic attractor [37]. The model of the Wien bridge oscillator has been also analyzed within the scope of fractional calculus, and the results obtained therein showed that a limit cycle can be replicated for any fractional order, with an adequate value of the amplifier gain [38]. The jerk model has been investigated using the concept of fractional derivative, and a chaotic attractor has been obtained with the system order as low as 2.1 [40].

One of the basic mathematical systems is Chua’s circuit system as shown in Fig. 1. This typical nonlinear electronic circuit and modified models have been investigated by many authors. Hartley et al. analyzed chaos in fractional-order Chua’s system [37]. Controlling spiral waves in a model of two-dimensional arrays of Chua’s circuits have been investigated in [41]. Some analytical and numerical methods for hidden attractors’ localization have been proposed in [42]. This system has been solved also for comparison purposes of the Atangana–Baleanu and Caputo–Fabrizio derivatives [40]. Analyzing the circuit using Kirchhoff’s circuit laws, the dynamics of Chua’s circuit can be accurately modeled by means of a system of three nonlinear ordinary differential equations in the variables \(x(t)\), \(y(t)\), and \(z(t)\), which represent the voltages across the capacitors \(C_{1}\) and \(C_{2}\) and the electric current in the inductor L respectively. As in the papers [37, 40, 41], a mathematical model of Chua’s circuit model can be displayed as follows:

$$ \begin{gathered} \frac{x(\tau )}{d\tau }=\theta \bigl[y(\tau )-x(\tau )-f \bigl(x(\tau ) \bigr) \bigr], \\ \mathit{RC}_{2}\frac{y(\tau )}{d\tau }= x(\tau )-y(\tau )+ Rz(\tau ), \\ \frac{z(\tau )}{d\tau }=-\phi y(\tau ), \end{gathered} $$
(1.1)

where \(f(x(\tau ))=mx(\tau )+\frac{1}{2}(n-m)( \vert x(\tau )+1 \vert - \vert x(\tau )-1 \vert )\) demonstrates the electrical response of the nonlinear resistor. θ and ϕ are parameters determined by the particular values of the circuit components. The shape of \(f(x(\tau ))\) relies on the rigorous model on its components.

Figure 1
figure 1

Classical Chua’s system

Full size image

In this paper we try to solve the above system by using the optimal perturbation iteration algorithms (OPIAs) and different fractional operators. This technique has been applied to many types of ODEs and PDEs such as Bratu-type [43], Riccati differential equation [44], heat transfer equations [45], nonlinear systems [46], Lane–Emden types [47], generalized regularized long wave equations [48]. More studies can also be found in [49–57]. The rest of the current paper is planned as follows. In Sect. 2, we give some basic concepts of the optimal perturbation iteration algorithms, and we apply this technique to systems of ordinary differential equations. In Sect. 3, we propose some modifications to the classical Chua circuit by using trend fractional derivatives. In Sect. 4, two illustrations of some well-known problems are carried out to validate the proposed method. Finally, a conclusion part is given in the last section.

2 Formulation of OPIAs for systems of ordinary differential equations

Deniz and Bildik presented the optimal perturbation iteration algorithms (OPIA) in 2016 [43]. It has been proven that these algorithms can be safely applied to many types of differential equations [44–52]. In this section, we give a short description of OPIA for systems of ordinary differential equation. Then we will be able to generate OPIA for the modified fractional Chua’s circuit model (MFCCM) in the next section. The modified fractional Chua’s circuit model can be converted into a standard model by replacing the fractional numbers with integer ones.

Let us consider the following system of ODEs:

$$ A_{k}(\dot{x}_{k},x_{j},\epsilon ,\tau )=0;\quad k=1,2,\ldots,K; j=1,2,\ldots,K. $$
(2.1)

Here, k represents the number of ODEs in Eq. (2.1). Clearly, this system can be rewritten as

$$ \begin{gathered} A_{1}=A_{1}( \dot{x}_{1},x_{1},x_{2},x_{3}, \ldots,x_{K},\epsilon ,\tau )=0, \\ A_{2}=A_{2}(\dot{x}_{2},x_{1},x_{2},x_{3}, \ldots,x_{K},\epsilon ,\tau )=0, \\ \vdots \\ A_{k}=A_{k}(\dot{x}_{k},x_{1},x_{2},x_{3}, \ldots,x_{K},\epsilon ,\tau )=0. \end{gathered} $$
(2.2)

By taking first correction term in the classical perturbation series, an approximate solution of the system will be considered as

$$ x_{k,n+1}=x_{k,n}+\varepsilon x^{c}_{k,n}, $$
(2.3)

where n denotes the nth-order approximate solution to be obtained and \(x^{c}_{k,n}\)s are the correction terms. By using Taylor series expansions in the neighborhood of \(\varepsilon =0\), we can approximate this system as follows:

$$ A_{k}=\sum_{m=0}^{M} \frac{1}{m!} \biggl[ \biggl(\frac{d}{d\varepsilon } \biggr)^{m} A_{k} \biggr]_{\varepsilon =0}\varepsilon ^{m}; \quad k=1,2, \ldots,K, $$
(2.4)

where

$$ \frac{d}{d\varepsilon }= \frac{\partial \dot{x}_{k,n+1}}{\partial \varepsilon } \frac{\partial }{\partial \dot{x}_{k,n+1}}+ \sum _{j=1}^{K} \biggl( \frac{\partial \dot{x}_{k,n+1}}{\partial \varepsilon } \frac{\partial }{\partial \dot{x}_{k,n+1}} \biggr)+ \frac{\partial }{\partial \varepsilon } $$
(2.5)

is given for the \((n+1)\)th iteration

$$ A_{k}(\dot{x}_{k,n+1} , x_{j,n+1},\epsilon ,\tau )=0. $$
(2.6)

Furnishing Eq. (2.5) into (2.4), an iteration algorithm will be established as follows:

$$ A_{k}= \sum_{m=0}^{M} \frac{1}{m!} \Biggl[ \Biggl(\dot{x}^{c}_{k,n} \frac{\partial }{\partial \dot{x}_{k,n+1}} + \sum_{j=1}^{K} \biggl( \dot{x}^{c}_{j,n} \frac{\partial }{\partial \dot{x}_{j,n+1}} \biggr)+ \frac{\partial }{\partial \varepsilon } \Biggr)^{m} H_{k} \Biggr]_{ \varepsilon =0} \varepsilon ^{m} = 0. $$
(2.7)

Equation (2.7) is a first-order ordinary differential equation. Therefore, the solution can be found for the correction terms \(x^{c}_{k,n}\). After that, by using Eq. (2.3), the \((n+1)\)th approximation can be reached. Iterations can be stopped when an adequate approximation is achieved.

In this work, we give a novel technique for PIAs to ameliorate the approximations. First of all, we insert convergence-control parameters \(p_{i}\), (\(i=0,1,\ldots\)) into Eq. (2.3) to get the following functions:

$$ \begin{gathered} x_{k,1}(t;p)=x_{k,0} + p_{0} x^{c}_{k,0}, \\ x_{k,2}(t;p)=x_{k,1} + p_{1} x^{c}_{k,1}, \\ \vdots \\ x_{k,m+1}(t;p)=x_{k,n} + p_{m} x^{c}_{k,m}. \end{gathered} $$
(2.8)

It is obvious that Eq. (2.8) will reduce to ordinary PIM when all of the parameters \(p_{m}\) are one. In order to find an optimal value of p, we substitute the approximate solution \(x_{m}\) into Eq. (2.1). Thus, the following residual will be obtained:

$$ \begin{gathered} {\mathit{Res}}_{A_{1}}=A_{1}( \dot{x}_{1,m},x_{1,m},x_{2,m},\ldots,x_{K,m},p_{0}, \epsilon ,t)=0, \\ {\mathit{Res}}_{A_{2}}=A_{2}(\dot{x}_{2},x_{1,m},x_{2,m}, \ldots,x_{K,m},p_{1}, \epsilon ,t)=0, \\ \vdots \\ {\mathit{Res}}_{A_{k}}=A_{k}(\dot{x}_{k},x_{1,m},x_{2,m}, \ldots,x_{K,m},p_{m}, \epsilon ,t)=0. \end{gathered} $$
(2.9)

One can easily say that when \({\mathit{Res}}(t;p_{m})=0\), \(x_{m}(t;p)\) is the wanted solution of the given problem. Otherwise, we can compute the following functional:

$$ \begin{gathered} J{\mathit{Res}}_{A_{1}}(p_{1})= \int _{\Theta }({{{{\mathit{Res}}_{A_{1}}})^{2}}}(t;p_{0}) \,dt, \\ J{\mathit{Res}}_{A_{2}}(p_{2})= \int _{\Theta }({{{{\mathit{Res}}_{A_{2}}})^{2}}}(t;p_{1}) \,dt, \\ \vdots \\ J{\mathit{Res}}_{A_{k}}(p_{K})= \int _{\Theta }({{{{\mathit{Res}}_{A_{k}}})^{2}}}(t;p_{K-1}) \,dt, \end{gathered} $$
(2.10)

where Θ is the physical domain of the considered equations. By doing so, the optimal values for parameters p can be reached by solving

$$ \frac{dJ{\mathit{Res}}_{A_{1}}}{dp_{1}}=0, \quad\quad \frac{dJ{\mathit{Res}}_{A_{2}}}{dp_{2}}=0 ,\quad\quad \ldots,\quad \quad \frac{dJ{\mathit{Res}}_{A_{K}}}{dp_{K}}=0. $$
(2.11)

3 OPIA for MCCM with different fractional derivatives

In this part, we give a brief formulation of OPIA for modified Chua’s circuit model (MCCM). For this reason, we use Caputo (C), Caputo–Fabrizio (CF), and Atangana–Baleanu (ABC) fractional operators, respectively.

3.1 Algorithm with Caputo fractional operator

The standard systems can be turned into the fractional differential forms. Equivalent systems for classical form of Chua’s circuit model by Caputo derivatives can be reached by changing the derivatives \(D_{\tau }^{\beta }x\), \(D_{\tau }^{\beta }y\), \(D_{\tau }^{\beta }z\) by \({}_{0}^{C}D_{\tau }^{\beta }x\), \({}_{0}^{C}D_{\tau }^{\beta }y\), and \({}_{0}^{C}D_{\tau }^{\beta }z\), respectively. Note here that \(0<\beta \leq 1\). With these changes, we have the following new forms:

$$\begin{aligned}& {}_{0}^{C}D_{\tau }^{\beta }x( \tau ) - \theta \bigl[y(\tau )-x(\tau )-f \bigl(x( \tau ) \bigr) \bigr]=0, \end{aligned}$$
(3.1)
$$\begin{aligned}& \mathit{RC}_{2} {}_{0}^{C}D_{\tau }^{\beta }y( \tau ) - x(t)+y(t)- Rz(t) =0, \end{aligned}$$
(3.2)
$$\begin{aligned}& {}_{0}^{C}D_{\tau }^{\beta }z( \tau ) + \phi y(\tau )=0, \end{aligned}$$
(3.3)

where

$$\begin{aligned}& {}_{0}^{C}D_{\tau }^{\beta }x=\frac{1}{\Gamma (1-\beta )} \int _{0}^{\tau } (\tau -t)^{-\beta } x'(t) \,dt, \\& {}_{0}^{C}D_{\tau }^{\beta }y=\frac{1}{\Gamma (1-\beta )} \int _{0}^{\tau } (\tau -t)^{-\beta } y'(t) \,dt, \\& {}_{0}^{C}D_{\tau }^{\beta }z=\frac{1}{\Gamma (1-\beta )} \int _{0}^{\tau } (\tau -t)^{-\beta } z'(t) \,dt. \end{aligned}$$

We can represent the above equations in a closed form as follows:

$$ \begin{gathered} F_{1} \bigl({}_{0}^{C}D_{\tau }^{\beta }x,x,y,z, \varepsilon \bigr)=0, \\ F_{2} \bigl({}_{0}^{C}D_{\tau }^{\beta }y,x,y,z, \varepsilon \bigr)=0, \\ F_{3} \bigl({}_{0}^{C}D_{\tau }^{\beta }z,y, \varepsilon \bigr)=0, \end{gathered} $$
(3.4)

where \(\varepsilon =1\) is the artificial perturbation parameter which can be inserted into Eqs. (3.1)–(3.3) as follows:

$$ \begin{gathered} {}_{0}^{C}D_{\tau }^{\beta }x( \tau ) - \theta \bigl[y(\tau )-x(\tau )- \varepsilon f \bigl(x(\tau ) \bigr) \bigr]=0, \\ \mathit{RC}_{2} {}_{0}^{C}D_{\tau }^{\beta }y( \tau ) - x(t)+y(t)- \varepsilon Rz(t) =0, \\ {}_{0}^{C}D_{\tau }^{\beta }z(\tau ) + \phi \varepsilon y(\tau )=0. \end{gathered} $$
(3.5)

Processing as in Sect. 2, the first approximate solution in the perturbation series can be taken as

$$ \begin{gathered} x_{n+1}=x_{n}+ \varepsilon { ( {x_{c}} )}_{n}, \\ y_{n+1}=y_{n}+\varepsilon { ( {y_{c}} )}_{n}, \\ z_{n+1}=z_{n}+\varepsilon { ( {z_{c}} )}_{n} \end{gathered} $$
(3.6)

with only one correction term. Here, \(n\in {\mathrm{N}}\cup \{ 0 \} \) and \({ ( {x_{c}} )}_{n}\), \({ ( {y_{c}} )}_{n}\), \({ ( {z_{c}} )}_{n}\) are nth correction terms. Then, by replacing Eq. (3.6) into (3.4) and using the Taylor series, we get

$$ \begin{gathered} {F_{1}}+{F_{1}}_{{}_{0}^{C}D_{\tau }^{\beta }x } \bigl( (x_{c} )_{n} \bigr) \varepsilon +{F_{1}}_{x } \bigl( (x_{c} )_{n} \bigr) \varepsilon +{F_{1}}_{y} (y_{c} )_{n} \varepsilon +{F_{1}}_{z} (z_{c} )_{n} \varepsilon +{F_{1}}_{ \varepsilon } \varepsilon =0, \\ {F_{2}}+{F_{2}}_{{}_{0}^{C}D_{\tau }^{\beta }y } \bigl( (y_{c} )_{n} \bigr) \varepsilon +{F_{2}}_{x } \bigl( (x_{c} )_{n} \bigr) \varepsilon +{F_{2}}_{y} (y_{c} )_{n} \varepsilon +{F_{2}}_{z} (z_{c} )_{n} \varepsilon +{F_{2}}_{ \varepsilon } \varepsilon =0, \\ {F_{3}}+{F_{3}}_{{}_{0}^{C}D_{\tau }^{\beta }z } \bigl( (z_{c} )_{n} \bigr) \varepsilon + {F_{3}}_{y} (y_{c} )_{n} \varepsilon +{F_{3}}_{\varepsilon } \varepsilon =0, \end{gathered} $$
(3.7)

where

$$ {F_{1}}_{x} =\frac{\partial {F_{1}}}{\partial x} ,\quad\quad {F_{1}}_{y} = \frac{\partial {F_{1}}}{\partial y} ,\quad\quad {F_{2}}_{z} = \frac{\partial {F_{2}}}{\partial z} ,\quad\quad {F_{1}}_{\varepsilon } = \frac{\partial {F_{1}}}{\partial \varepsilon },\quad\quad \ldots. $$

3.2 Algorithm with Caputo–Fabrizio fractional operator

By performing the same changes as in the previous subsection, we obtain the new fractional case for the new modified system via changing \(D_{\tau }^{\beta }x\), \(D_{\tau }^{\beta }y\), \(D_{\tau }^{\beta }z\) by \({}_{0}^{\mathrm{CF}}D_{\tau }^{\beta }x\), \({}_{0}^{\mathrm{CF}}D_{\tau }^{\beta }y\), and \({}_{0}^{\mathrm{CF}}D_{\tau }^{\beta }z\), respectively. Therefore, new Caputo–Fabrizio (C–F) fractional forms will be

$$\begin{aligned}& {}_{0}^{\mathrm{CF}}D_{\tau }^{\beta }x(\tau ) - \theta \bigl[y(\tau )-x(\tau )-f \bigl(x( \tau ) \bigr) \bigr]=0, \end{aligned}$$
(3.8)
$$\begin{aligned}& \mathit{RC}_{2} {} _{0}^{\mathrm{CF}}D_{\tau }^{\beta }y( \tau ) - x(t)+y(t)- Rz(t) =0, \\ \end{aligned}$$
(3.9)
$$\begin{aligned}& {}_{0}^{\mathrm{CF}}D_{\tau }^{\beta }z(\tau ) + \phi y( \tau )=0. \end{aligned}$$
(3.10)

\({}_{0}^{\mathrm{CF}}D_{\rho }^{\beta }\) represents C–F fractional derivatives of order β, and it is given by

$$\begin{aligned}& {}_{0}^{\mathrm{CF}}D_{\tau }^{\beta }x(t)= \frac{M(\beta )}{1-\beta } \int _{0}^{ \tau } \exp \biggl(\frac{-\beta (\tau -t)}{1-\beta } \biggr) D x(t) \,dt, \\& {}_{0}^{\mathrm{CF}}D_{\tau }^{\beta }y(\tau )= \frac{M(\beta )}{1-\beta } \int _{0}^{ \tau } \exp \biggl(\frac{-\beta (\tau -t)}{1-\beta } \biggr) D y(t) \,dt, \\& {}_{0}^{\mathrm{CF}}D_{\tau }^{\beta }z(\tau )= \frac{M(\beta )}{1-\beta } \int _{0}^{ \tau } \exp \biggl(\frac{-\beta (\tau -t)}{1-\beta } \biggr) D z(t) \,dt, \end{aligned}$$

where \(M (\beta )\) is a normalization function such that \(M(0) = M(1) = 1\).

Applying similar procedures, one can get the following:

$$ \begin{gathered} {F_{1}}+{F_{1}}_{{}_{0}^{\mathrm{CF}}D_{\tau }^{\beta }x } \bigl( (x_{c} )_{n} \bigr) \varepsilon +{F_{1}}_{x } \bigl( (x_{c} )_{n} \bigr) \varepsilon +{F_{1}}_{y} (y_{c} )_{n} \varepsilon +{F_{1}}_{z} (z_{c} )_{n} \varepsilon +{F_{1}}_{ \varepsilon } \varepsilon =0, \\ {F_{2}}+{F_{2}}_{{}_{0}^{\mathrm{CF}}D_{\tau }^{\beta }y } \bigl( (y_{c} )_{n} \bigr) \varepsilon +{F_{2}}_{x } \bigl( (x_{c} )_{n} \bigr) \varepsilon +{F_{2}}_{y} (y_{c} )_{n} \varepsilon +{F_{2}}_{z} (z_{c} )_{n} \varepsilon +{F_{2}}_{ \varepsilon } \varepsilon =0, \\ {F_{3}}+{F_{3}}_{{}_{0}^{\mathrm{CF}}D_{\tau }^{\beta }z } \bigl( (z_{c} )_{n} \bigr) \varepsilon + {F_{3}}_{y} (y_{c} )_{n} \varepsilon +{F_{3}}_{\varepsilon } \varepsilon =0. \end{gathered} $$
(3.11)

3.3 Algorithm with Atangana–Baleanu fractional operator

As a final work, we consider the ABC derivatives [1] form of the MCCM with the similar changes \(D_{\tau }^{\beta }x\), \(D_{\tau }^{\beta }y\), \(D_{\tau }^{\beta }z\) by \({}_{0}^{\mathrm{ABC}}D_{\tau }^{\beta }x\), \({}_{0}^{\mathrm{ABC}}D_{\tau }^{\beta }y\), and \({}_{0}^{\mathrm{ABC}}D_{\tau }^{\beta }z\). Thus, the new modified system can be obtained as follows:

$$\begin{aligned}& {}_{0}^{\mathrm{ABC}}D_{\tau }^{\beta }x(\tau ) - \theta \bigl[y(\tau )-x(\tau )-f \bigl(x( \tau ) \bigr) \bigr]=0, \end{aligned}$$
(3.12)
$$\begin{aligned}& \mathit{RC}_{2} {}_{0}^{\mathrm{ABC}}D_{\tau }^{\beta }y( \tau ) - x(t)+y(t)- Rz(t) =0, \end{aligned}$$
(3.13)
$$\begin{aligned}& {}_{0}^{\mathrm{ABC}}D_{\tau }^{\beta }z(\tau ) + \phi y( \tau )=0. \end{aligned}$$
(3.14)

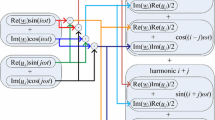
Here, \({}_{0}^{\mathrm{ABC}}D_{\tau }^{\beta }(\cdot )\) stands for an ABC fractional derivative in the Liouville–Caputo sense of order β and can be given as

$$\begin{aligned}& {}_{0}^{\mathrm{ABC}}D_{\tau }^{\beta }x(t)= \frac{M(\beta )}{1-\beta } \int _{0}^{ \tau } E_{\beta } \biggl( \frac{-\beta (\tau -t)}{1-\beta } \biggr) D x( \tau ) \,dt, \\& {}_{0}^{\mathrm{ABC}}D_{\tau }^{\beta }y(t)= \frac{M(\beta )}{1-\beta } \int _{0}^{ \tau } E_{\beta } \biggl( \frac{-\beta (\tau -t)}{1-\beta } \biggr) D y( \tau ) \,dt, \\& {}_{0}^{\mathrm{ABC}}D_{\tau }^{\beta }z(t)= \frac{M(\beta )}{1-\beta } \int _{0}^{ \tau } E_{\beta } \biggl( \frac{-\beta (\tau -t)}{1-\beta } \biggr) D z( \tau ) \,dt, \end{aligned}$$

where

$$ E_{\beta }(z)=\sum_{k=0}^{\infty } \frac{z^{k}}{\Gamma (\beta k+1)} $$
(3.15)

is the famous Mittag-Leffler function. Likewise, using the Taylor series with perturbation theorem, one can get

$$ \begin{gathered} {F_{1}}+{F_{1}}_{{}_{0}^{\mathrm{ABC}}D_{\tau }^{\beta }x } \bigl( (x_{c} )_{n} \bigr) \varepsilon +{F_{1}}_{x } \bigl( (x_{c} )_{n} \bigr) \varepsilon +{F_{1}}_{y} (y_{c} )_{n} \varepsilon +{F_{1}}_{z} (z_{c} )_{n} \varepsilon +{F_{1}}_{ \varepsilon } \varepsilon =0, \\ {F_{2}}+{F_{2}}_{{}_{0}^{\mathrm{ABC}}D_{\tau }^{\beta }y } \bigl( (y_{c} )_{n} \bigr) \varepsilon +{F_{2}}_{x } \bigl( (x_{c} )_{n} \bigr) \varepsilon +{F_{2}}_{y} (y_{c} )_{n} \varepsilon +{F_{2}}_{z} (z_{c} )_{n} \varepsilon +{F_{2}}_{ \varepsilon } \varepsilon =0, \\ {F_{3}}+{F_{3}}_{{}_{0}^{\mathrm{ABC}}D_{\tau }^{\beta }z } \bigl( (z_{c} )_{n} \bigr) \varepsilon + {F_{3}}_{y} (y_{c} )_{n} \varepsilon +{F_{3}}_{\varepsilon } \varepsilon =0. \end{gathered} $$
(3.16)

We will call all of Eqs. (3.7), (3.11), and (3.16) OPIAs for the corresponding systems with interested derivatives. By making the necessary computations at \(\varepsilon =0\) for Eqs. (3.1)–(3.3), we can reach any order of OPIAs. Guess functions \(u_{0}\), \(v_{0}\) should be chosen fittingly according to the given conditions to begin the iteration procedures. Accordingly, first correction functions \((u_{c})_{0}\), \((v_{c})_{0}\) are evaluated using the OPIAs with \(x_{0}\), \(y_{0}\), \(z_{0}\) and the initial conditions. After that, the first approximations \(u_{1}\), \(v_{1}\) can be established by knowing \(x_{0}\), \(y_{0}\), \(z_{0}\) with \((x_{c})_{0}\), \((y_{c})_{0}\), \((z_{c})_{0}\) and so on. To advance the correctness of the solutions and capability of the proposed method, the concept of optimal parameters may be used. Subsequently, using the optimal parameters, we can evaluate the errors with the aid of residuals (2.10).

4 Illustration

In this section, we deal with MCCM (3.1)–(3.3) based on the aforementioned fractional operators.

Example 4.1

Consider the following modified nonlinear Chua’s circuit system [37]:

$$\begin{aligned}& {}_{0}^{\Lambda }D_{\tau }^{\beta }x(\tau ) = \theta \biggl[y+ \frac{x-2x^{3}}{7} \biggr], \\& {}_{0}^{\Lambda }D_{\tau }^{\beta }y(\tau )= x- y + z, \\& {}_{0}^{\Lambda }D_{\tau }^{\beta }z(\tau ) = \phi y, \end{aligned}$$
(4.1)

where Λ is the corresponding fractional operator.

Closed and perturbed form of the above system can be written as follows:

$$\begin{aligned}& {}_{0}^{\Lambda }D_{\tau }^{\beta }x(\tau ) - \theta \biggl[y+ \varepsilon \frac{x-2x^{3}}{7} \biggr]=0, \\& {}_{0}^{\Lambda }D_{\tau }^{\beta }y(\tau ) - x + y - z=0, \\& {}_{0}^{\Lambda }D_{\tau }^{\beta }z(\tau ) - \phi y=0. \end{aligned}$$
(4.2)

By taking the one correction term from the classical perturbation expansion, the approximate solution can be taken as follows:

$$ \begin{gathered} x_{n+1}=x_{n}+ \varepsilon { ( {x_{c}} )}_{n}, \\ y_{n+1}=y_{n}+\varepsilon { ( {y_{c}} )}_{n}, \\ z_{n+1}=z_{n}+\varepsilon { ( {z_{c}} )}_{n}. \end{gathered} $$
(4.3)

By inserting (4.3) into the closed form of the system and by using algorithms (3.7), (3.11), and (3.16), one can construct the related functional equations for the system with the aid of residual (2.9), optimal parameters \(p_{1}\), \(p_{2}\), \(p_{3}\) can be computed as mentioned in Sect. 2.

One can see the results of third-order OPIA solutions from Figs. 2–4. Figure 2 displays the semi-analytical solutions and attractors for \(x(0)=9.95\), \(y(0)=9.88\), \(z(0)=9.79\), \(\beta = 0.95\), \(\theta =14\), \(\phi =10\) for derivatives in the Caputo sense.

Figure 2
figure 2

OPIM – C solutions of the modified Chua’s circuit in Example 4.1

Full size image

By using algorithm (3.11) with \(x(0)=9.81\), \(y(0)=9.84\), \(z(0)=9.99\), \(\beta = 0.95\), \(\theta =11\), \(\phi =20\), OPIA solutions in the Caputo–Fabrizio (C–F) sense can be sketched as in Fig. 3.

Figure 3
figure 3

OPIM – CF solutions of the modified Chua’s circuit in Example 4.1

Full size image

From Fig. 4, one can see the semi-analytical solutions and attractors for \(x(0)=9.93\), \(y(0)=10.012\), \(z(0)=9.94\), \(\beta = 0.95\), \(\theta =13\), \(\phi =21\) for derivatives in the ABC sense.

Figure 4
figure 4

OPIM – ABC solutions of the modified Chua’s circuit in Example 4.1

Full size image

Example 4.2

As a second example, we consider the modified Chua’s circuit in [40]. In order to compare our results, we will benefit from the solution of numerical techniques such as the Adams–Bashforth rule as in [7].

To start the iterations, we can use the same initial conditions as \(x(0)=0.6\), \(y(0)=0.3\), \(z(0)=-0.5\) as in [40].

Absolute residual errors, or briefly ARE, of \(x(\tau )\) for all of three fractional forms are given in Table 1 at \(\beta =0.9\) and for some specific values of τ. Tables 2 and 3 show the AREs obtained by using the fractional operators for \(y(\tau )\) and \(z(\tau )\), respectively.

Table 1 AREs of \(x(\tau )\) obtained by fourth-order OPIA solutions using different fractional operators at \(\beta =0.9\)
Full size table
Table 2 AREs of \(y(\tau )\) obtained by fourth-order OPIA solutions using different fractional operators at \(\beta =0.9\)
Full size table
Table 3 AREs of \(x(\tau )\) obtained by fourth-order OPIA solutions using different fractional operators at \(\beta =0.9\)
Full size table

From Figs. 5–7, we can detect all of the AREs obtained by sixth-order approximation and various operators plotted by (•), (▲), and (–) for Caputo, Caputo–Fabrizio and Atangana–Baleanu derivatives at \(\beta =0.7\). Figures 8–10 show the same draws for \(\beta =0.8\).

Figure 5
figure 5

ARES by sixth-order approximations at \(\beta =0.7\), C (•), CF (▲), and ABC (–) for \(x(\tau )\)

Full size image
Figure 6
figure 6

ARES by sixth-order approximations at \(\beta =0.7\), C (•), CF (▲), and ABC (–) for \(y(\tau )\)

Full size image
Figure 7
figure 7

ARES by sixth-order approximations at \(\beta =0.7\), C (•), CF (▲), and ABC (–) for \(z(\tau )\)

Full size image
Figure 8
figure 8

ARES by tenth-order approximations at \(\beta =0.8\), C (•), CF (▲), and ABC (–) for \(x(\tau )\)

Full size image
Figure 9
figure 9

ARES by tenth-order approximations at \(\beta =0.8\), C (•), CF (▲), and ABC (–) for \(y(\tau )\)

Full size image
Figure 10
figure 10

ARES by tenth-order approximations at \(\beta =0.8\), C (•), CF (▲), and ABC (–) for \(z(\tau )\)

Full size image

5 Conclusion

In this research paper, we have applied the optimal perturbation iteration method to analyze the modified fractional Chua’s circuit model (MFCCM) semi-analytically. We change the classical forms of MFCCM with fractional ones with the help of three different fractional operators. Two specific examples of modified fractional Chua’s circuit model are solved by the presented technique. Figure 2 shows the OPIM solutions and attractors for \(x(0)=9.95\), \(y(0)=9.88\), \(z(0)=9.79\) and different values of parameters. Figures 3 and 4 display the semi-analytical solutions when the same algorithm is applied with \(x(0)=9.81\), \(y(0)=9.84\), \(z(0)=9.99\) in the (C–F) sense and \(x(0)=9.93\), \(y(0)=10.012\), \(z(0)=9.94\) in the ABC sense, respectively. Also, absolute residual errors are sketched in Figs. 5–7 by using three operators and various values of parameters. One can say that there is no big difference in using different operators for solving this system. The results are nearly the same for all three derivatives, and they are indistinguishable on graphics. In addition, illustrations show the availability and usefulness of the OPIAs for the system of differential equations.