Application of new quintic polynomial B-spline approximation for numerical investigation of Kuramoto–Sivashinsky equation

Abstract

A spline is a piecewise defined special function that is usually comprised of polynomials of a certain degree. These polynomials are supposed to generate a smooth curve by connecting at given data points. In this work, an application of fifth degree basis spline functions is presented for a numerical investigation of the Kuramoto–Sivashinsky equation. The finite forward difference formula is used for temporal integration, whereas the basis splines, together with a new approximation for fourth order spatial derivative, are brought into play for discretization in space direction. In order to corroborate the presented numerical algorithm, some test problems are considered and the computational results are compared with existing methods.

1 Introduction

The Kuramoto–Sivashinsky (KS) equation, a canonical nonlinear evolution equation, crops up in mathematical modeling of several physical phenomena indicating reaction–diffusion systems, unstable drift waves in plasmas, pattern formation on thin hydrodynamic films, flame front instability, long waves on the interface between two viscous fluids, fluid flow on a vertical plate and spatially uniform oscillating chemical reaction in some homogeneous medium [1, 2]. The KS equation has chaotic behavior and exhibits a traveling wave like solution that moves without changing its shape in a finite spatial domain [3–5]. The generalized KS equation is given by

$$ \begin{aligned}[b] &\frac{\partial y(x,t)}{\partial t}+y(x,t) \frac{\partial y(x,t)}{\partial x}+ \alpha \frac{\partial ^{2} y(x,t)}{\partial x^{2}} +\beta \frac{\partial ^{3} y(x,t)}{\partial x^{3}}+\gamma \frac{\partial ^{4} y(x,t)}{\partial x^{4}}=0, \\ &x \in [a,b], \quad t \in [0,T], \end{aligned} $$

(1)

subject to the following conditions:

$$\begin{aligned}& y(x,0)=\phi (x), \end{aligned}$$

(2)

$$\begin{aligned}& \textstyle\begin{cases} y(a,t)=\phi _{1}(t), \qquad y(b,t)=\phi _{2}(t), \\ y_{x}(a,t)=\psi _{1}(t), \qquad y_{x}(b,t)=\psi _{2}(t), \end{cases}\displaystyle \end{aligned}$$

(3)

where $y(x,t)$ gives the wave displacement at position x and time t, α, β, γ are constants and $\phi (x)$, $\phi _{i}(t)$, $\psi _{i}(t)$ are known functions. The term $y_{xx}$ is responsible for instability at broad scales and the dissipative term $y_{xxxx}$ controls the dam** effect at small scales. The nonlinear term $yy_{x}$ serves as an energy stabilizer by transmitting it between small and large scales [6]. The nonlinear evolution equations have attracted a considerable amount of research work in recent years [7–15]. Several numerical and analytical techniques have been proposed for solving these equations [16–23]. Khater and Temsah [24] employed the Chebyshev spectral collocation approach for an approximate solution of the generalized fourth order KS equation. Lai and Ma [25] proposed a lattice Boltzmann model for solving the nonlinear KS equation, A mesh free approach based on radial basis functions was used in [26] for an approximate solution of the generalized KS equation. Mittal and Arora [27] explored the numerical solution to KS equation by means of the Crank–Nicolson scheme and quintic B-spline (QnBS) functions. Porshokouhi and Ghanbari [28] implemented a variational iteration method for series solution of KS equation. The authors in [29] presented a numerical approach based on basis spline functions for an approximate solution of the KS equation. Rageh et al. [30] implemented a restrictive Taylor approximation method to find a numerical solution for the KS equation. Ersoy and Dag [31] proposed an exponential cubic B-spline method for numerical solution of KS equation. Mittal and Dahiya [6] proposed a differential quadrature method based on QnBS functions for solving the generalized KS equation. Gomes et al. [32] used linear feedback controls and techniques to stabilize the non-uniform unstable steady states of the generalized KS equation. The authors in [33] used polynomial scaling functions for solving the generalized KS equation. Akgul and Bonyah [34] proposed a reproducing kernel Hilbert space method for the solving generalized KS equation.

In this article, the numerical investigation of the nonlinear KS equation has been presented. The finite forward difference formulation and quintic polynomial basis spline functions are used to discretize the problem in time and spatial domains, respectively. The spatial order of convergence of a typical QnBS approximation scheme has been improved by involving a new approximation for the fourth order derivative. The stability of proposed algorithm has been studied by means of Von-Neumann stability analysis.

This study is organized as: In the first section, we discuss some basic ideas related to QnBS functions. The development of new approximation for $y^{4}(x)$ is explained in Sect. 3. The numerical method is discussed in Sect. 4. Section 5–6 consists of a stability and error analysis and finally the computational results are reported in Sect. 7.

2 Quintic polynomial B-spline functions

Let us partition the domain $[a,b]$ into n intervals, $[x_{i},x_{i+1}]$, of equal length such that $x_{i}=a+(i\times h)$, $i=0,1,\ldots ,n$, $a=x_{0}$, $b=x_{n}$ and $h=\frac{1}{n}(b-a)$. The rth polynomial B-spline of degree q, order $q+1$, is defined as [35]

$$ B_{q,r}(x)=L_{q,r}B_{q-1,r}(x)+ (1-L_{q,r+1} )B_{q-1,r+1}(x), \quad x \in [x_{r},x_{r+1+q}], $$

(4)

where $q>0$, $L_{q,r}=\frac{(x-x_{r})}{(x_{r+q}-x_{r})}$ and

$$ B_{0,r}(x)= \textstyle\begin{cases} 1, & \text{if } x\in [x_{r},x_{r+1}], \\ 0, & \text{otherwise}. \end{cases} $$

(5)

Using (5)–(4) with $q=5$, we get fifth degree basis spline functions [36]:

$$ \begin{aligned}[b] &B_{5,r}(x)\\ &\quad =\frac{1}{120h^{5}}\\ &\qquad {}\times \textstyle\begin{cases} (x-x_{r-3})^{5}, & x\in [x_{r-3},x_{r-2}], \\ h^{5}+5h^{4}(x-x_{r-2})+10h^{3}(x-x_{r-2})^{2}+10h^{2}(x-x_{r-2})^{3}\\ \quad {}+5h(x-x_{r-2})^{4}-5(x-x_{r-2})^{5}, & x\in [x_{r-2},x_{r-1}], \\ 26h^{5}+50h^{4}(x-x_{r-1})+20h^{3}(x-x_{r-1})^{2}-20h^{2}(x-x_{r-1})^{3}\\ \quad {}-20h(x-x_{r-1})^{4}+10(x-x_{r-1})^{5}, & x\in [x_{r-1},x_{r}], \\ 26h^{5}+50h^{4}(x_{r+1}-x)+20h^{3}(x_{r+1}-x)^{2}-20h^{2}(x_{r+1}-x)^{3}\\ \quad {}-20h(x_{r+1}-x)^{4}+10(x_{r+1}-x)^{5}, & x\in [x_{r},x_{r+1}], \\ h^{5}+5h^{4}(x_{r+2}-x)+10h^{3}(x_{r+2}-x)^{2}+10h^{2}(x_{r+2}-x)^{3}\\ \quad {}+5h(x_{r+2}-x)^{4}-5(x_{r+2}-x)^{5}, & x\in [x_{r+1},x_{r+2}], \\ (x_{r+3}-x)^{5}, & x\in [x_{r+2},x_{r+3}], \\ 0 & \text{otherwise,} \end{cases}\displaystyle \end{aligned} $$

(6)

where $r=-2,-1,0,\ldots ,n+2$. The QnBS approximation $Y(x)$ for a sufficiently smooth function $y(x)$ is given by

$$ Y(x)=\sum_{r=-2}^{n+2}\sigma _{r}B_{5,r}(x), $$

(7)

where the $\sigma _{r}$ are to be calculated. Let $Y_{i}$, $m_{i}$, $M_{i}$, $T_{i}$ and $F_{i}$ represent the QnBS approximations for $y(x_{i})$, $y^{\prime }(x_{i})$, $y^{(2)}(x_{i})$, $y^{(3)}(x_{i})$ and $y^{(4)}(x_{i})$, respectively.

Using (6) and (7), we have

$$\begin{aligned}& Y_{i} = \frac{1}{120} (\sigma _{i-2}+26\sigma _{i-1}+66\sigma _{i}+26 \sigma _{i+1}+\sigma _{i+2} ), \end{aligned}$$

(8)

$$\begin{aligned}& m_{i} = \frac{1}{24h} (-\sigma _{i-2}-10\sigma _{i-1}+10\sigma _{i+1}+ \sigma _{i+2} ), \end{aligned}$$

(9)

$$\begin{aligned}& M_{i} = \frac{1}{6h^{2}} (\sigma _{i-2}+2\sigma _{i-1}-6\sigma _{i}+2 \sigma _{i+1}+\sigma _{i+2} ), \end{aligned}$$

(10)

$$\begin{aligned}& T_{i} = \frac{1}{2h^{3}} (-\sigma _{i-2}+2\sigma _{i-1}-2\sigma _{i+1}+ \sigma _{i+2} ), \end{aligned}$$

(11)

$$\begin{aligned}& F_{i} = \frac{1}{h^{4}} (\sigma _{i-2}-4\sigma _{i-1}+6\sigma _{i}-4 \sigma _{i+1}+\sigma _{i+2} ). \end{aligned}$$

(12)

Moreover, from (8)–(12), we establish the following relations [37–39]:

$$\begin{aligned}& m_{i} = y^{\prime }(x_{i})+\frac{h^{6}}{5040}y^{(7)}(x_{i})- \frac{h^{8}}{21\mbox{,}600}y^{(9)}(x_{i})+\cdots , \end{aligned}$$

(13)

$$\begin{aligned}& M_{i} = y^{\prime \prime }(x_{i})+\frac{h^{4}}{720}y^{(6)}(x_{i})- \frac{h^{6}}{3360}y^{(8)}(x_{i})+\cdots , \end{aligned}$$

(14)

$$\begin{aligned}& T_{i} = y^{(3)}(x_{i})-\frac{h^{4}}{240}y^{(7)}(x_{i})+ \frac{11h^{6}}{30\mbox{,}240}y^{(9)}(x_{i})+\cdots , \end{aligned}$$

(15)

$$\begin{aligned}& F_{i} = y^{(4)}(x_{i})-\frac{h^{2}}{12}y^{(6)}(x_{i})+ \frac{h^{4}}{240}y^{(8)}(x_{i})+\cdots . \end{aligned}$$

(16)

We see that the truncation error in $F_{i}$ is $O(h^{2})$. Instead of using (12), the authors in [36, 40] proposed a new $O(h^{3})$ accurate approximation for the fourth order derivative. For the sake of completeness, we reproduce those results in the following section.

3 Derivation of new approximation for $y^{(4)}(x)$

From (16), we establish the following relation for $F_{i-2}$ at the knot $x_{i}$, ($i=2,3,4,\ldots ,n-2$):

$$\begin{aligned} F_{i-2} =& y^{(4)}(x_{i-2})-\frac{h^{2}}{12}y^{(6)}(x_{i-2})+ \frac{h^{4}}{240}y^{(8)}(x_{i-2})+\cdots \\ =& y^{(4)}(x_{i})-2hy^{(5)}(x_{i})+ \frac{23h^{2}}{12}y^{(6)}(x_{i})- \frac{7h^{3}}{6}y^{(7)}(x_{i})+ \cdots . \end{aligned}$$

(17)

Similar expressions for $F_{i-1}$, $F_{i+1}$ and $F_{i+2}$ at $x_{i}$ are derived as follows:

$$\begin{aligned}& F_{i-1} = y^{(4)}(x_{i})-hy^{(5)}(x_{i})+ \frac{5h^{2}}{12}y^{(6)}(x_{i})- \frac{h^{3}}{12}y^{(7)}(x_{i})+ \cdots , \end{aligned}$$

(18)

$$\begin{aligned}& F_{i+1} = y^{(4)}(x_{i})+hy^{(5)}(x_{i})+ \frac{5h^{2}}{12}y^{(6)}(x_{i})+ \frac{h^{3}}{12}y^{(7)}(x_{i})+ \cdots , \end{aligned}$$

(19)

$$\begin{aligned}& F_{i+2} = y^{(4)}(x_{i})+2hy^{(5)}(x_{i})+ \frac{23h^{2}}{12}y^{(6)}(x_{i})+ \frac{7h^{3}}{6}y^{(7)}(x_{i})+ \cdots . \end{aligned}$$

(20)

Suppose $\overset{\sim }{F}_{i}$ denotes the new approximation for $y^{(4)}(x_{i})$ s.t.

$$ \overset{\sim }{F}_{i}=a_{1}F_{i-2}+a_{2}F_{i-1}+a_{3}F_{i}+a_{4}F_{i+1}+a_{5}F_{i+2}. $$

(21)

Using (17)–(20) in (21), we obtain $a_{1}=-\frac{1}{240}$, $a_{2}=\frac{1}{10}$, $a_{3}=\frac{97}{120}$, $a_{4}=\frac{1}{10}$ and $a_{5}=-\frac{1}{240}$.

Hence

$$ \begin{aligned}[b] \overset{\sim }{F}_{i}&= \frac{1}{240h^{4}} (-\sigma _{i-4}+28\sigma _{i-3}+92 \sigma _{i-2}-604\sigma _{i-1}+970\sigma _{i}-604\sigma _{i+1} \\ &\quad {}+92\sigma _{i+2}+28\sigma _{i+3}-\sigma _{i+4} ),\quad i=2,3,\ldots ,n-2. \end{aligned} $$

(22)

For $x=x_{0}$, we consider

$$ \overset{\sim }{F}_{0}=a_{1}F_{0}+a_{2}F_{1}+a_{3}F_{2}+a_{4}F_{3}, $$

(23)

where

$$\begin{aligned}& F_{0} = y^{(4)}(x_{0})-\frac{h^{2}}{12}y^{(6)}(x_{0})+ \frac{h^{4}}{240}y^{(8)}(x_{0})+\cdots , \end{aligned}$$

(24)

$$\begin{aligned}& F_{1} = y^{(4)}(x_{0})+hy^{(5)}+ \frac{5h^{2}}{12}y^{(6)}(x_{0})+ \frac{h^{3}}{12}y^{(7)}(x_{0})+ \cdots , \end{aligned}$$

(25)

$$\begin{aligned}& F_{2} = y^{(4)}(x_{0})+2hy^{(5)}+ \frac{23h^{2}}{12}y^{(6)}(x_{0})+ \frac{7h^{3}}{6}y^{(7)}(x_{0})+ \cdots , \end{aligned}$$

(26)

$$\begin{aligned}& F_{3} = y^{(4)}(x_{0})+3hy^{(5)}+ \frac{53h^{2}}{12}y^{(6)}(x_{0})+ \frac{17h^{3}}{4}y^{(7)}(x_{0})+ \cdots . \end{aligned}$$

(27)

From (23)–(27), we get $a_{1}=\frac{7}{6}$, $a_{2}=-\frac{5}{12}$, $a_{3}=\frac{1}{3}$ and $a_{4}=-\frac{1}{12}$ to obtain the following relation:

$$ \overset{\sim }{F}_{0}=\frac{1}{12h^{4}} (14\sigma _{-2}-61\sigma _{-1}+108 \sigma _{0}-103\sigma _{1}+62\sigma _{2}-27\sigma _{3}+8\sigma _{4}- \sigma _{5} ). $$

(28)

Working in similar way, the following relations can be derived at $x_{1}$, $x_{n-1}$ and $x_{n}$:

$$\begin{aligned}& \overset{\sim }{F}_{1}=\frac{1}{12h^{4}} (\sigma _{-2}+6\sigma _{-1}-33 \sigma _{0}+52\sigma _{1}-33\sigma _{2}+6\sigma _{3}+\sigma _{4} ), \end{aligned}$$

(29)

$$\begin{aligned}& \overset{\sim }{F}_{n-1}=\frac{1}{12h^{4}} (\sigma _{n-4}+6\sigma _{n-3}-33 \sigma _{n-2}+52\sigma _{n-1}-33\sigma _{n}+6\sigma _{n+1}+\sigma _{n+2} ), \end{aligned}$$

(30)

$$\begin{aligned}& \begin{aligned}[b] \overset{\sim }{F}_{n}&=\frac{1}{12h^{4}} (-\sigma _{n-5}+8\sigma _{n-4}-27 \sigma _{n-3}+62\sigma _{n-2}\\ &\quad {}-103\sigma _{n-1}+108\sigma _{n}-61 \sigma _{n+1}+14\sigma _{n+2} ). \end{aligned} \end{aligned}$$

(31)

4 Description of the numerical method

Applying a finite forward difference formula and θ weighted scheme in the time direction, the semi-discretized form of problem (1) is obtained as follows:

$$ \begin{aligned}[b] &\frac{y^{j+1}-y^{j}}{\Delta t}+\theta \bigl[(yy_{x})^{j+1}+\alpha y_{xx}^{j+1}+ \beta y_{xxx}^{j+1}+\gamma y_{xxxx}^{j+1} \bigr] \\ &\quad {}+(1-\theta ) \bigl[y^{j}y_{x}^{j}+ \alpha y_{xx}^{j}+\beta y_{xxx}^{j+1}+ \gamma y_{xxxx}^{j} \bigr]=0, \end{aligned} $$

(32)

where Δt is the mesh size in the time direction, $0\leq \theta \leq 1$ and $y^{j+1}$ is used to denote $y(x,t_{j}+\Delta t)$. The nonlinear term $(yy_{x})^{j+1}$ is treated as [33]

$$ (yy_{x})^{j+1}=y^{j+1}y_{x}^{j}+y^{j}y_{x}^{j+1}-y^{j}y_{x}^{j}. $$

(33)

Substituting (33) into (32), we get

$$ \begin{aligned}[b] &\frac{y^{j+1}-y^{j}}{\Delta t}+\theta \bigl[y^{j+1}y_{x}^{j}+y^{j}y_{x}^{j+1}-y^{j}y_{x}^{j}+ \alpha y_{xx}^{j+1} +\beta y_{xxx}^{j+1}+ \gamma y_{xxxx}^{j+1} \bigr] \\ &\quad {}+(1-\theta ) \bigl[y^{j}y_{x}^{j}+ \alpha y_{xx}^{j}+\beta y_{xxx}^{j}+ \gamma y_{xxxx}^{j} \bigr]=0. \end{aligned} $$

(34)

For $\theta =\frac{1}{2}$, Eq. (34) can be rearranged as

$$ \begin{aligned}[b] & \biggl[\frac{2}{\Delta t}+y_{x}^{j} \biggr]y^{j+1}+y^{j}y_{x}^{j+1}+ \alpha y_{xx}^{j+1}+\beta y_{xxx}^{j+1}+\gamma y_{xxxx}^{j+1} \\ &\quad =\frac{2}{\Delta t} y^{j}-\alpha y_{xx}^{j}- \beta y_{xxx}^{j}-\gamma y_{xxxx}^{j}. \end{aligned} $$

(35)

Now, let us divide the spatial domain $[a,b]$ in n equal parts $[x_{i},x_{i+1}]$ s.t. $x_{i}=x_{0}+i\times h$, $i=0,1,\ldots ,n$, $a=x_{0}$, $b=x_{n}$ and $h=\frac{1}{n}(b-a)$.

Let $Y(x,t_{j})$ be the QnBS solution for (1) at $t=t_{j}$ s.t.

$$ Y(x,t_{j})=\sum_{r=-2}^{n+2} \sigma _{r}^{j}B_{5,r}(x), $$

(36)

where the $\sigma _{r}^{j}$ are unknown control points. Substituting (36) into (35), at $x=x_{i}$, we obtain

$$ w_{i}^{j}Y_{i}^{j+1}+Y_{i}^{j}m_{i}^{j+1}+ \alpha M_{i}^{j+1}+\beta T_{i}^{j+1}+ \gamma F_{i}^{j+1}=z_{i}^{j}, $$

(37)

where $w_{i}^{j}=\frac{2}{\Delta t}+m_{i}^{j}$ and $z_{i}^{j}=\frac{2}{\Delta t} Y_{i}^{j}-\alpha M_{i}^{j}-\beta T_{i}^{j}- \gamma F_{i}^{j}$.

Using (8)–(11), (22), (28) and (29)–(31) in (37), for $i=0,1,2,3,\ldots ,n$, we get $n+1$ linear equations involving $n+5$ control points:

$$\begin{aligned}& \begin{aligned}[b] &\frac{w_{0}^{j}}{120} \bigl(\sigma _{-2}^{j+1}+26\sigma _{-1}^{j+1}+66 \sigma _{0}^{j+1}+26\sigma _{1}^{j+1}+\sigma _{2}^{j+1} \bigr) - \frac{Y_{0}^{j}}{24h} \bigl(\sigma _{-2}^{j+1}+10\sigma _{-1}^{j+1}-10 \sigma _{1}^{j+1}-\sigma _{2}^{j+1} \bigr) \\ &\qquad {}+\frac{\alpha }{6h^{2}} \bigl(\sigma _{-2}^{j+1}+2\sigma _{-1}^{j+1}-6 \sigma _{0}^{j+1}+2\sigma _{1}^{j+1}+\sigma _{2}^{j+1} \bigr) - \frac{\beta }{3h^{3}} \bigl(\sigma _{-2}^{j+1}-2\sigma _{-1}^{j+1}+2 \sigma _{1}^{j+1}-\sigma _{2}^{j+1} \bigr) \\ &\qquad {}+\frac{\gamma }{12h^{4}} \bigl(14\sigma _{-2}^{j+1} -61 \sigma _{-1}^{j+1}+108 \sigma _{0}^{j+1}-103 \sigma _{1}^{j+1}+62\sigma _{2}^{j+1}-27 \sigma _{3}^{j+1}+8 \sigma _{4}^{j+1}-\sigma _{5}^{j+1} \bigr)\\ &\quad =z_{0}^{j}, \end{aligned} \end{aligned}$$

(38)

$$\begin{aligned}& \begin{aligned}[b] &\frac{w_{1}^{j}}{120} \bigl(\sigma _{-1}^{j+1}+26\sigma _{0}^{j+1}+66 \sigma _{1}^{j+1}+26\sigma _{2}^{j+1}+ \sigma _{3}^{j+1} \bigr) - \frac{Y_{1}^{j}}{24h} \bigl(\sigma _{-1}^{j+1}+10\sigma _{0}^{j+1}-10 \sigma _{2}^{j+1}-\sigma _{3}^{j+1} \bigr) \\ &\quad {}+\frac{\alpha }{6h^{2}} \bigl(\sigma _{-1}^{j+1}+2\sigma _{0}^{j+1}-6 \sigma _{1}^{j+1}+2\sigma _{2}^{j+1}+\sigma _{3}^{j+1} \bigr) - \frac{\beta }{3h^{3}} \bigl(\sigma _{-1}^{j+1}-2\sigma _{0}^{j+1}+2 \sigma _{2}^{j+1}-\sigma _{3}^{j+1} \bigr) \\ &\quad {}+\frac{\gamma }{12h^{4}} \bigl(\sigma _{-2}^{j+1}+6\sigma _{-1}^{j+1}-33 \sigma _{0}^{j+1}+52\sigma _{1}^{j+1} -33\sigma _{2}^{j+1}+6\sigma _{3}^{j+1}+ \sigma _{4}^{j+1} \bigr)=z_{1}^{j}, \end{aligned} \end{aligned}$$

(39)

$$\begin{aligned}& \begin{aligned}[b] &\frac{w_{i}^{j}}{120} \bigl(\sigma _{i-2}^{j+1}+26\sigma _{i-1}^{j+1}+66 \sigma _{i}^{j+1}+26\sigma _{i+1}^{j+1}+ \sigma _{i+2}^{j+1} \bigr) - \frac{Y_{i}^{j}}{24h} \bigl(\sigma _{i-2}^{j+1}+10\sigma _{i-1}^{j+1}-10 \sigma _{i+1}^{j+1}-\sigma _{i+2}^{j+1} \bigr) \\ &\qquad {}+\frac{\alpha }{6h^{2}} \bigl(\sigma _{i-2}^{j+1}+2 \sigma _{i-1}^{j+1}-6 \sigma _{i}^{j+1}+2 \sigma _{i+1}^{j+1}+\sigma _{i+2}^{j+1} \bigr) - \frac{\beta }{3h^{3}} \bigl(\sigma _{i-2}^{j+1}-2\sigma _{i-1}^{j+1}+2 \sigma _{i+1}^{j+1}-\sigma _{i+2}^{j+1} \bigr) \\ &\qquad {}-\frac{\gamma }{240h^{4}} \bigl(\sigma _{i-4}^{j+1}-28 \sigma _{i-3}^{j+1}-92 \sigma _{i-2}^{j+1}+604 \sigma _{i-1}^{j+1}-970\sigma _{i}^{j+1}\\ &\qquad {}+604 \sigma _{i+1}^{j+1}-92\sigma _{i+2}^{j+1}-28 \sigma _{i+3}^{j+1}+ \sigma _{i+4}^{j+1} \bigr) \\ &\quad =z_{i}^{j}, \quad i=2,3,4,\ldots ,n-2, \end{aligned} \end{aligned}$$

(40)

$$\begin{aligned}& \begin{aligned}[b] &\frac{w_{n-1}^{j}}{120} \bigl(\sigma _{n-3}^{j+1}+26\sigma _{n-2}^{j+1}+66 \sigma _{n-1}^{j+1}+26\sigma _{n}^{j+1}+ \sigma _{n+1}^{j+1} \bigr) - \frac{Y_{n-1}^{j}}{24h} \bigl(\sigma _{n-3}^{j+1}+10\sigma _{n-2}^{j+1}-10 \sigma _{n}^{j+1}-\sigma _{n+1}^{j+1} \bigr) \\ &\quad {}+\frac{\alpha }{6h^{2}} \bigl(\sigma _{n-3}^{j+1}+2\sigma _{n-2}^{j+1}-6 \sigma _{n-1}^{j+1}+2\sigma _{n}^{j+1}+\sigma _{n+1}^{j+1} \bigr) - \frac{\beta }{3h^{3}} \bigl(\sigma _{n-3}^{j+1}-2\sigma _{n-2}^{j+1}+2 \sigma _{n}^{j+1}-\sigma _{n+1}^{j+1} \bigr) \\ &\quad {}+\frac{\gamma }{12h^{4}} \bigl(\sigma _{n-4}^{j+1}+6\sigma _{n-3}^{j+1}-33 \sigma _{n-2}^{j+1}+52\sigma _{n-1}^{j+1} -33\sigma _{n}^{j+1}+6 \sigma _{n+1}^{j+1}+\sigma _{n+2}^{j+1} \bigr) =z_{n-1}^{j}, \end{aligned} \end{aligned}$$

(41)

$$\begin{aligned}& \begin{aligned}[b] &\frac{w_{n}^{j}}{120} \bigl(\sigma _{n-2}^{j+1}+26\sigma _{n-1}^{j+1}+66 \sigma _{n}^{j+1}+26\sigma _{n+1}^{j+1}+ \sigma _{n+2}^{j+1} \bigr) - \frac{Y_{n}^{j}}{24h} \bigl(\sigma _{n-2}^{j+1}+10\sigma _{n-1}^{j+1}-10 \sigma _{n+1}^{j+1}-\sigma _{n+2}^{j+1} \bigr) \\ &\qquad {}+\frac{\alpha }{6h^{2}} \bigl(\sigma _{n-2}^{j+1}+2\sigma _{n-1}^{j+1}-6 \sigma _{n}^{j+1}+2\sigma _{n+1}^{j+1}+\sigma _{n+2}^{j+1} \bigr) - \frac{\beta }{3h^{3}} \bigl(\sigma _{n-2}^{j+1}-2\sigma _{n-1}^{j+1}+2 \sigma _{n+1}^{j+1}-\sigma _{n+2}^{j+1} \bigr) \\ &\qquad {}-\frac{\gamma }{12h^{4}} (\sigma _{n-5}-8\sigma _{n-4}+27 \sigma _{n-3}-62 \sigma _{n-2} +103\sigma _{n-1}-108 \sigma _{n}+61\sigma _{n+1}+14 \sigma _{n+2} )\\ &\quad =z_{n}^{j}. \end{aligned} \end{aligned}$$

(42)

From the given end conditions (3), we get

$$\begin{aligned}& \bigl(\sigma _{-2}^{j+1}+26\sigma _{-1}^{j+1}+66 \sigma _{0}^{j+1}+26 \sigma _{1}^{j+1}+ \sigma _{2}^{j+1} \bigr)/120 = \phi _{1}(t_{j+1}), \end{aligned}$$

(43)

$$\begin{aligned}& \bigl(-\sigma _{-2}^{j+1}-10\sigma _{-1}^{j+1}+10 \sigma _{1}^{j+1}+ \sigma _{2}^{j+1} \bigr)/24h = \psi _{1}(t_{j+1}), \end{aligned}$$

(44)

$$\begin{aligned}& \bigl(-\sigma _{n-2}^{j+1}-10\sigma _{n-1}^{j+1}+10 \sigma _{n+1}^{j+1}+ \sigma _{n+2}^{j+1} \bigr)/24h = \psi _{2}(t_{j+1}), \end{aligned}$$

(45)

$$\begin{aligned}& \bigl(\sigma _{n-2}^{j+1}+26\sigma _{n-1}^{j+1}+66 \sigma _{n}^{j+1}+26 \sigma _{n+1}^{j+1}+ \sigma _{n+2}^{j+1} \bigr)/120 = \phi _{2}(t_{j+1}). \end{aligned}$$

(46)

The set of equations (38)–(46) can be written in matrix form as

$$ L\sigma ^{j+1}=R, $$

(47)

where L is the $(n+5) \times (n+5)$ coefficient matrix, R is $(n+5) \times 1$ matrix and $\sigma ^{j+1}= [\sigma _{-2}^{j+1}\ \sigma _{-1}^{j+1}\ \sigma _{0}^{j+1}\ \cdots \ \sigma _{n+2}^{j+1} ]^{T}$. Solving (47), we get $\sigma ^{j+1}$ and put these control points into (36) to get the approximate solution at $(j+1)$th time level. However, first we need to find $\sigma ^{0}$, using the given initial condition, as follows (2):

$$\begin{aligned}& \bigl(-\sigma _{-2}^{0}-10\sigma _{-1}^{0}+10 \sigma _{1}^{0}+\sigma _{2}^{0} \bigr)/24h = \phi ^{\prime }(x_{0}), \\& \bigl(\sigma _{-2}^{0}+2\sigma _{-1}^{0}-6 \sigma _{0}^{0}+2\sigma _{1}^{0}+ \sigma _{2}^{0} \bigr)/6h^{2} = \phi ^{\prime \prime }(x_{0}), \\& \bigl(\sigma _{i-2}^{0}+26\sigma _{i-1}^{0}+66 \sigma _{i}^{0}+26 \sigma _{i+1}^{0}+ \sigma _{i+2}^{0} \bigr)/120 = \phi (x_{i}), \quad i=0,1, \ldots ,n, \\& \bigl(\sigma _{n-2}^{0}+2\sigma _{n-1}^{0}-6 \sigma _{n}^{0}+2\sigma _{n+1}^{0}+ \sigma _{n+2}^{0} \bigr)/6h^{2} = \phi ^{\prime \prime }(x_{n}), \\& \bigl(-\sigma _{n-2}^{0}-10\sigma _{n-1}^{0}+10 \sigma _{n+1}^{0}+ \sigma _{n+2}^{0} \bigr)/24h = \phi ^{\prime }(x_{n}). \end{aligned}$$

In matrix form, we have

$$ L\sigma ^{0}=R. $$

(48)

The matrix system (48) can easily be solved using for $\sigma ^{0}$ using a modified form of Thomas algorithm. The numerical simulation is run in Mathematica 10.

5 Stability analysis

Setting $y=\eta$ in the nonlinear term $yy_{x}$, Eq. (32) takes the following form:

$$ \begin{aligned}[b] &\frac{y^{j+1}-y^{j}}{\Delta t}+\theta \bigl[\eta (y_{x})^{j+1}+ \alpha y_{xx}^{j+1}+\beta y_{xxx}^{j+1}+\gamma y_{xxxx}^{j+1} \bigr] \\ &\quad {}+(1-\theta ) \bigl[\eta y_{x}^{j}+\alpha y_{xx}^{j}+\beta y_{xxx}^{j+1}+ \gamma y_{xxxx}^{j} \bigr]=0. \end{aligned} $$

(49)

Setting $\theta =0.5$, the fully discretized form of (49) is as follows:

$$ \begin{aligned}[b] & Y_{i}^{j+1}+ \frac{\Delta t}{2} \bigl[\eta m_{i}^{j+1}+\alpha M_{i}^{j+1}+ \beta T_{i}^{j+1}+\gamma F_{i}^{j+1} \bigr]\\ &\quad =Y_{i}^{j}- \frac{\Delta t}{2} \bigl[\eta m_{i}^{j}+\alpha M_{i}^{j}+\beta T_{i}^{j+1}+ \gamma F_{i}^{j} \bigr]. \end{aligned} $$

(50)

Using (8)–(11) and (22) in (50), we have

$$ \begin{aligned}[b] &{-}d_{3}\sigma _{i-4}^{j+1}+28d_{3} \sigma _{i-3}^{j+1}+2\bigl(46d_{3}-60hd_{2}+20h^{2}d_{1}-5h^{3}d_{4}+2h^{4} \bigr) \sigma _{i-2}^{j+1} \\ &\qquad {}+4\bigl(-151d_{3}+60hd_{2}+20h^{2}d_{1}-25h^{3}d_{4}+26h^{4} \bigr)\sigma _{i-1}^{j+1}\\ &\qquad {}+2\bigl(485d_{3}-120hd_{1} +132h^{4}\bigr)\sigma _{i}^{j+1}\\ &\qquad {}+4 \bigl(-151d_{3}-60hd_{2}-20h^{2}d_{1}+25h^{3}d_{4}+26h^{4}\bigr)\sigma _{i+1}^{j+1} \\ &\qquad {} +2\bigl(46d_{3}+60hd_{2}+20h^{2}d_{1}+5h^{3}d_{4}+2h^{4} \bigr) \sigma _{i+2}^{j+1} +28d_{3}\sigma _{i+3}^{j+1}-d_{3}\sigma _{i+4}^{j+1} \\ &\quad =d_{3}\sigma _{i-4}^{j}-28d_{3} \sigma _{i-3}^{j}+2\bigl(-46d_{3}+60hd_{2}-20h^{2}d_{1}+5h^{3}d_{4}+2h^{4} \bigr) \sigma _{i-2}^{j} \\ &\qquad {} +4\bigl(151d_{3}-60hd_{2}-20h^{2}d_{1}+25h^{3}d_{4}+26h^{4} \bigr)\sigma _{i-1}^{j}\\ &\qquad {}+2\bigl(-485d_{3}+120hd_{1}+132h^{4} \bigr) \sigma _{i}^{j}\\ &\qquad {} +4\bigl(151d_{3}+60hd_{2}-20h^{2}d_{1}-25h^{3}d_{4}+26h^{4}\bigr)\sigma _{i+1}^{j} \\ &\qquad {} +2\bigl(-46d_{3}-60hd_{2}-20h^{2}d_{1}-5h^{3}d_{4}+2h^{4} \bigr) \sigma _{i+2}^{j} -28d_{3}\sigma _{i+3}^{j}+d_{3}\sigma _{i+4}^{j}, \end{aligned} $$

(51)

where $d_{1}=\alpha \Delta t$, $d_{2}=\beta \Delta t$, $d_{3}=\gamma \Delta t$, $d_{4}=\eta \Delta t$.

Now, following [27, 41], we substitute $\sigma _{i}^{j}=\xi ^{j}\mathrm{e}^{i m\varphi }$ into (51):

$$\begin{aligned} &\xi ^{j+1} \bigl[-d_{3} \mathrm{e}^{\iota (m-4)\varphi }+28d_{3} \mathrm{e}^{\iota (m-3)\varphi }+2 \bigl(46d_{3}-60hd_{2}+20h^{2}d_{1}-5h^{3}d_{4}+2h^{4} \bigr) \mathrm{e}^{\iota (m-2)\varphi } \\ &\qquad {}+4\bigl(-151d_{3}+60hd_{2}+20h^{2}d_{1}-25h^{3}d_{4}+26h^{4} \bigr)\mathrm{e}^{ \iota (m-1)\varphi } \\ &\qquad {}+2\bigl(485d_{3}-120hd_{1}+132h^{4} \bigr)\mathrm{e}^{\iota m \varphi } \\ &\qquad {}+4\bigl(-151d_{3}-60hd_{2}-20h^{2}d_{1}+25h^{3}d_{4}+26h^{4} \bigr)\mathrm{e}^{ \iota (m+1)\varphi } \\ &\qquad {}+2\bigl(46d_{3}+60hd_{2}+20h^{2}d_{1}+5h^{3}d_{4}+2h^{4}\bigr)\mathrm{e}^{\iota (m+2)\varphi } \\ &\qquad {} +28d_{3} \mathrm{e}^{\iota (m+3) \varphi }-d_{3}\mathrm{e}^{\iota (m+4)\varphi } \bigr] \\ &\quad =\xi ^{j} \bigl[d_{3} \mathrm{e}^{\iota (m-4)\varphi }-28d_{3} \mathrm{e}^{\iota (m-3)\varphi } \\ &\qquad {}+2\bigl(-46d_{3}+60hd_{2}-20h^{2}d_{1}+5h^{3}d_{4}+2h^{4} \bigr)\mathrm{e}^{\iota (m-2) \varphi } \\ &\qquad {} +4\bigl(151d_{3}-60hd_{2}-20h^{2}d_{1}+25h^{3}d_{4}+26h^{4} \bigr) \mathrm{e}^{\iota (m-1)\varphi } \\ &\qquad {}+2\bigl(-485d_{3}+120hd_{1}+132h^{4} \bigr)\mathrm{e}^{\iota m\varphi } \\ &\qquad {}+4\bigl(151d_{3}+60hd_{2}-20h^{2}d_{1}-25h^{3}d_{4}+26h^{4} \bigr) \mathrm{e}^{\iota (m+1)\varphi } \\ &\qquad {}+2\bigl(-46d_{3}-60hd_{2}-20h^{2}d_{1}-5h^{3}d_{4}+2h^{4} \bigr)\mathrm{e}^{ \iota (m+2)\varphi } \\ &\qquad {} -28d_{3}\mathrm{e}^{\iota (m+3)\varphi }+d_{3} \mathrm{e}^{\iota (m+4)\varphi } \bigr], \end{aligned}$$

(52)

where $\iota =\sqrt{-1}$, $\varphi =\zeta h$ and ζ is the mode number.

After some simplification, (52) takes the following form:

$$ \begin{aligned}[b] &\xi \bigl[-d_{3}\cos 4\varphi +28d_{3}\cos 3\varphi +2\bigl(46d_{3}+20h^{2}d_{1}+2h^{4} \bigr) \cos 2\varphi \\ &\qquad {}+2\iota \bigl(60hd_{2}+5h^{3}d_{4}\bigr) \sin 2\varphi +4\bigl(-151d_{3}+20h^{2}d_{1}+26h^{4} \bigr) \cos \varphi \\ &\qquad {}+4\iota \bigl(-60hd_{2}+25h^{3}d_{4} \bigr)\sin \varphi+485d_{3}-120hd_{1}+132h^{4} \bigr]\\ &\quad = \bigl[d_{3}\cos 4\varphi -28d_{3} \cos 3\varphi +2 \bigl(-46d_{3}-20h^{2}d_{1}+2h^{4}\bigr) \cos 2\varphi \\ &\qquad {}+2\iota \bigl(-60hd_{2}-5h^{3}d_{4}\bigr) \sin 2\varphi +4\bigl(151d_{3}-20h^{2}d_{1}+26h^{4} \bigr) \cos \varphi \\ &\qquad {}+4\iota \bigl(60hd_{2}-25h^{3}d_{4} \bigr)\sin \varphi-485d_{3}+120hd_{1}+132h^{4} \bigr]. \end{aligned} $$

(53)

Equation (53) can be written as $\xi =\frac{\nu _{1}-i\omega }{\nu _{2}+i\omega }$, where

$$\begin{aligned}& \begin{aligned} \nu _{1} &= d_{3}\cos 4\varphi -28d_{3}\cos 3\varphi +2\bigl(-46d_{3}-20h^{2}d_{1}+2h^{4} \bigr) \cos 2\varphi \\ &\quad {}+4\bigl(151d_{3}-20h^{2}d_{1}+26h^{4} \bigr)\cos \varphi -485d_{3}+120hd_{1}+132h^{4}, \end{aligned} \\& \begin{aligned} \nu _{2} &= -d_{3}\cos 4\varphi +28d_{3}\cos 3\varphi +2\bigl(46d_{3}+20h^{2}d_{1}+2h^{4} \bigr) \cos 2\varphi \\ &\quad {}+4\bigl(-151d_{3}+20h^{2}d_{1}+26h^{4} \bigr)\cos \varphi +485d_{3}-120hd_{1}+132h^{4}, \end{aligned} \\& \omega = 2\bigl(-60hd_{2}-5h^{3}d_{4}\bigr)\sin 2 \varphi +4\bigl(60hd_{2}-25h^{3}d_{4}\bigr) \sin \varphi . \end{aligned}$$

Now

$$ \begin{aligned} \nu _{2}^{2}-\nu _{1}^{2}&=64h^{4}(33+26 \cos \varphi +\cos 2\varphi ) \sin ^{2}\frac{\varphi }{2} \bigl[170d_{3}-80d_{1}h^{2} \\ &\quad {}-5\bigl(29d_{3}+8d_{1}h^{2}\bigr)\cos \varphi -26d_{3}\cos 2\varphi +d_{3}\cos 3 \varphi \bigr]. \end{aligned} $$

We plug in the values of $d_{1}$ and $d_{3}$ with $\alpha =-1$, $\gamma =1$ in the last expression to get

$$ \begin{aligned} \nu _{2}^{2}-\nu _{1}^{2}&=64h^{4}(33+26 \cos \varphi +\cos 2\varphi ) \sin ^{2}\frac{\varphi }{2}\Delta t \biggl[(97+24\cos \varphi -\cos 2 \varphi ) \sin ^{2}\frac{\varphi }{2} \\ &\quad {}+40h^{2}(2+\cos \varphi ) \biggr]. \end{aligned} $$

Since

$$\begin{aligned}& 64h^{4}(33+26\cos \varphi +\cos 2\varphi )\sin ^{2} \frac{\varphi }{2} \Delta t \geq 0, \\& (97+24\cos \varphi -\cos 2\varphi )\sin ^{2}\frac{\varphi }{2} \geq 0, \\& 40h^{2}(2+\cos \varphi ) ] \geq 0, \end{aligned}$$

we have $\nu _{2}^{2}-\nu _{1}^{2} \geq 0$.

Consequently $|\xi | \leq 1$, the proposed algorithm is proved to be stable.

6 Error analysis

From (8)–(11), we can obtain the following expressions [38, 39]:

$$\begin{aligned}& \begin{aligned}[b] &h \bigl[Y^{\prime }(x_{i-2})+26Y^{\prime }(x_{i-1})+66Y^{\prime }(x_{i})+26Y^{ \prime }(x_{i+1})+Y^{\prime }(x_{i+2}) \bigr] \\ &\quad {}=5 \bigl[-Y(x_{i-2})-10Y(x_{i-1})+10Y(x_{i+1})+Y(x_{i+2}) \bigr], \end{aligned} \end{aligned}$$

(54)

$$\begin{aligned}& \begin{aligned}[b] &h^{2} \bigl[Y^{\prime \prime }(x_{i-2})+26Y^{\prime \prime }(x_{i-1})+66Y^{ \prime \prime }(x_{i})+26Y^{\prime \prime }(x_{i+1})+Y^{\prime \prime }(x_{i+2}) \bigr] \\ &\quad {}=20 \bigl[Y(x_{i-2})+2Y(x_{i-1})-6Y(x_{i})+2Y(x_{i+1})+Y(x_{i+2}) \bigr], \end{aligned} \end{aligned}$$

(55)

$$\begin{aligned}& \begin{aligned}[b] &h^{3} \bigl[Y^{\prime \prime \prime }(x_{i-2})+26Y^{\prime \prime \prime }(x_{i-1})+66Y^{ \prime \prime \prime }(x_{i}) +26Y^{\prime \prime \prime }(x_{i+1})+Y^{ \prime \prime \prime }(x_{i+2}) \bigr] \\ &\quad {}=60 \bigl[-Y(x_{i-2})+2Y(x_{i-1})-2Y(x_{i+1})+Y(x_{i+2}) \bigr]. \end{aligned} \end{aligned}$$

(56)

Similarly, using (10), (11) and (22), we have

$$ \begin{aligned}[b] h^{4}Y^{(4)}(x_{i})&= \frac{h^{2}}{40}\bigl[-Y^{\prime \prime }(x_{i-2})+114Y^{ \prime \prime }(x_{i-1}) -142Y^{\prime \prime }(x_{i})+30Y^{\prime \prime }(x_{i+1})-Y^{\prime \prime }(x_{i+2}) \bigr] \\ &\quad {}+\frac{7h^{3}}{10}\bigl[Y^{\prime \prime \prime }(x_{i-1})+2Y^{\prime \prime \prime }(x_{i}) \bigr]. \end{aligned} $$

(57)

Employing the operator notation, $E^{\lambda }(Y^{\prime }(x_{i}))=Y^{\prime }(x_{i+\lambda })$, $\lambda \in \mathbb{Z}$, Eqs. (54)–(56) are written as [37]

$$\begin{aligned}& h \bigl[E^{-2}+26E^{-1}+66+26E^{1}+E^{2} \bigr]Y^{\prime }(x_{i})=5 \bigl[-E^{-2}-10E^{-1}+10E^{1}+E^{2} \bigr]y(x_{i}), \end{aligned}$$

(58)

$$\begin{aligned}& h^{2} \bigl[E^{-2}+26E^{-1}+66+26E^{1}+E^{2} \bigr]Y^{\prime \prime }(x_{i})=20 \bigl[E^{-2}-2E^{-1}+-6+2E^{1}+E^{2} \bigr]y(x_{i}), \end{aligned}$$

(59)

$$\begin{aligned}& h^{3} \bigl[E^{-2}+26E^{-1}+66+26E^{1}+E^{2} \bigr]Y^{\prime \prime \prime }(x_{i})=60 \bigl[-E^{-2}+2E^{-1}-2E^{1}+E^{2} \bigr]y(x_{i}). \end{aligned}$$

(60)

Using $E=\mathrm{e}^{hD}$, $D\equiv d/dx$, Eqs. (58)–(60) give the following expressions, respectively [38, 39]:

$$\begin{aligned}& Y^{\prime }(x_{i}) = y^{\prime }(x_{i})+ \frac{h^{6}}{5040}y^{(7)}(x_{i})- \frac{h^{8}}{21\mbox{,}600}y^{(9)}(x_{i}) +\frac{h^{10}}{1\mbox{,}036\mbox{,}800}y^{(11)}(x_{i})+ \cdots , \end{aligned}$$

(61)

$$\begin{aligned}& Y^{\prime \prime }(x_{i}) = y^{\prime \prime }(x_{i})+ \frac{h^{4}}{720}y^{(6)}(x_{i})- \frac{h^{6}}{3360}y^{(8)}(x_{i}) +\frac{h^{8}}{86\mbox{,}400}y^{(10)}(x_{i})+ \cdots , \end{aligned}$$

(62)

$$\begin{aligned}& Y^{\prime \prime \prime }(x_{i}) = y^{(3)}(x_{i})- \frac{h^{4}}{240}y^{(7)}(x_{i})+ \frac{11h^{6}}{30\mbox{,}240}y^{(9)}(x_{i}) -\frac{h^{8}}{288\mbox{,}00}y^{(11)}(x_{i})+ \cdots . \end{aligned}$$

(63)

Similarly, writing (57) in operator notation, we get

$$ h^{4}Y^{(4)}(x_{i})= \frac{h^{2}}{40}\bigl[-E^{-2}+114E^{-1}-142+30E^{1}-E^{2} \bigr]y^{ \prime \prime }(x_{i}) +\frac{7h^{3}}{10}\bigl[E^{-1}+2 \bigr]y^{(3)}(x_{i}). $$

(64)

The above relation can be expanded as

$$ \begin{aligned}[b] h^{4}Y^{(4)}(x_{i})&= \frac{h^{2}}{40} \biggl[-84hD+68h^{2}D^{2}-14h^{3}D^{3}+ \frac{14}{3}h^{4}D^{4}+\cdots \biggr]y^{\prime \prime }(x_{i}) \\ &\quad {}+\frac{7h^{3}}{10} \biggl[3-hD+\frac{1}{2}h^{2}D^{2}- \frac{1}{6}h^{3}D^{3}+ \frac{1}{24}h^{4}D^{4} \biggr]y^{(3)}(x_{i}). \end{aligned} $$

(65)

After some simplification, we obtain

$$ Y^{(4)}(x_{i})=y^{(4)}(x_{i})+ \frac{7h^{3}}{600}y^{(7)}(x_{i})- \frac{19h^{4}}{3600}y^{(8)}(x_{i})+ \cdots . $$

(66)

Now, the generalized KS equation (1) can be written as

$$ y_{t}=G(x,t,y), $$

(67)

where $G=-yy_{x}-\alpha y_{xx}-\beta y_{xxx}-\gamma y_{xxxx}$, with $y_{i}^{j+1}-y_{i}^{j}=\Delta t [\theta G_{i}^{j+1}+(1-\theta )G_{i}^{j} ]$.

Applying a Taylor series about $(j+\theta )\Delta t$, we obtain

$$ \begin{aligned}[b] &(y_{t})_{i}- \frac{2\theta -1}{2}\Delta t (y_{tt})_{i}+ \frac{1+3\theta (\theta -1)}{6} \Delta t^{2} (y_{ttt})_{i}+\cdots \\ &\quad =G_{i}-\frac{\theta (\theta -1)}{2}\Delta t^{2}(G_{tt})_{i}+ \frac{\theta (\theta -1)(2\theta -1)}{2}\Delta t^{3}(G_{ttt})_{i}+ \cdots . \end{aligned} $$

(68)

Setting $y=\eta$ in the nonlinear term $yy_{x}$ and using (67) in (68), we get

$$ (y_{t})_{i}=G_{i}+ \frac{2\theta -1}{2}\Delta t (G_{t})_{i}- \frac{1+6\theta (\theta -1)}{6} \Delta t^{2}(G_{tt})_{i}+\cdots . $$

(69)

From (67), the truncation error is defined as

$$\begin{aligned}& e_{i}=(y_{t})_{i}- \bigl[-\eta (Y_{x})_{i}-\alpha (Y_{xx})_{i}-\beta (Y_{xxx})_{i}- \gamma (Y_{xxxx})_{i} \bigr], \\& e_{i}=\frac{2\theta -1}{2}\Delta t (y_{tt})_{i}+ \frac{ 7\gamma h^{3}}{600}(y_{xxxxxxx})_{i}+\cdots . \end{aligned}$$

(70)

Hence, theoretically, the proposed numerical algorithm for KS equation is $O(\Delta t+h^{3})$ convergent.

7 Numerical results

To show the versatility of numerical algorithm, we have presented four numerical experiments. The accuracy and efficiency of the method is tested by the maximum, Euclidian and the global relative error (GRE) norms, which are calculated as [27, 42]

$$ L_{\infty }=\max_{0\leq i \leq n} \vert y_{i}-Y_{i} \vert , \qquad L_{2}= \sqrt{h \sum _{i=0}^{n}(y_{i}-Y_{i})^{2}}, \qquad \text{GRE}= \frac{\sum_{i=0}^{n} \vert y_{i}-Y_{i} \vert }{\sum_{i=0}^{n} \vert y_{i} \vert }, $$

where $Y_{i}$ and $y_{i}$ are the approximate and exact solutions at the ith spatial knot, respectively. The numerical outcomes are compared with the Lattice Boltzmann model (LBM) [25], the Quintic B-spline collocation method (QnBSM) [27], B-spline functions (BSF) [29], the Exponential cubic B-spline collocation method (ExCBSM) [31], the QnBS differential quadrature method (QnBS–DQM) [6] and Polynomial scaling functions (PSF) [33].

Problem 1

Consider the following KS equation [6, 25, 27, 31]:

$$ y_{t}+yy_{x}+y_{xx}+y_{xxxx}=0, \quad x \in [-30,30], t \in [0,4]. $$

The piecewise defined spline solution at $t=1$ using the proposed method for Example 1, when $n=100$, $\Delta t=0.01$, $\lambda =5$ and $\nu =-12$, is given by

$$ Y(x,1)= \textstyle\begin{cases} 3.89237+x(0.0153636+x(0.00100909+x(0.0000332031\\ \quad {}+(5.47221E-7+3.61331E-9 x)x))), \quad \mbox{if } x\in [-30,-\frac{147}{5}],\\ 3.87164+x(0.0118388+x(0.000769305+x(0.0000250471\\ \quad {}+(4.08512E-7+2.66971E-9 x)x))), \quad \mbox{if } x\in [-\frac{147}{5},-\frac{144}{5}],\\ 3.92466+x(0.0210431+x(0.0014085+x(0.0000472413\\ \quad {}+(7.93828E-7+5.34552E-9 x)x))), \quad \mbox{if } x\in [-\frac{144}{5},-\frac{141}{5}],\\ 3.97167+x(0.0293783+x(0.00199965+x(0.000068204\\ \quad {}+(1.16551E-6+7.98154E-9 x)x))), \quad \mbox{if } x\in [-\frac{141}{5},-\frac{138}{5}],\\ \vdots , \quad \vdots \\ 6.06349+x(0.103044+x(-0.037693+x(0.00881429\\ \quad {}+(-0.00141027+0.000132128 x)x))), \quad \mbox{if } x\in [-\frac{3}{5},0],\\ 6.06349+x(0.103044+x(-0.037693+x(0.00881429\\ \quad {}+(-0.00141027+0.000135264 x)x))), \quad \mbox{if } x\in [0,\frac{3}{5}],\\ \vdots , \quad \vdots \\ 6.20139+x(6.48201E-7+x(-4.4005E-8+x(1.5134E-9\\ \quad {}+(-2.56932E-11+ 1.74971E-13 x)x))), \quad \mbox{if } x\in [\frac{138}{5},\frac{141}{5}],\\ 6.2014 + x (4.54485E-7 +x (-3.11993E-8 +x (1.03319E-9 \\ \quad {}+ (-1.72804E-11 + 1.16351E-13 x) x))), \quad \mbox{if } x\in [\frac{141}{5},\frac{144}{5}],\\ 6.2014 + x (3.27826E-7 + x (-2.16532E-8 + x (6.98492E-10 \\ \quad {}+ (-1.15961E-11 + 7.63833E-14 x) x))), \quad \mbox{if } x\in [\frac{144}{5},\frac{147}{5}],\\ 6.2014 + x (1.22935E-7 +x (-7.45058E-9 +x (2.32831E-10\\ \quad {}+ (-3.63798E-12 + 2.22045E-14 x) x))), \quad \mbox{if } x\in [\frac{147}{5},30]. \end{cases} $$

The exact solution is

$$y(x,t)=\lambda +\frac{30}{19}\mu \bigl[-9\tanh (\mu (x-\lambda t-\nu )+11 \tanh ^{3}\bigl(\mu (x-\lambda t-\nu )\bigr) \bigr], $$

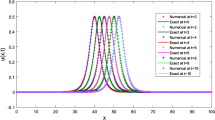
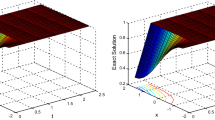
where $\mu =\frac{1}{2}\sqrt{\frac{11}{19}}$ and the initial and end conditions can be derived from the given exact solution. The GRE corresponding to $\lambda =5$, $\nu =-12$, $n=100$ and $\Delta t=0.01$ is listed in Table 1 at $t=1,2,3,4$. It can be observed that our approximate results are better than LBM [25], QnBSM [27], ExCBSM [31] and QnBS–DQM [6]. Table 2 shows a comparison of computational error norms with QnBS-DQM [6] corresponding to $\lambda =0.1$, $\nu =-10$, $n=100$ and $\Delta t=0.01$ at $t=0.1,0.3,0.5,0.5,0.7,1.0$. The 2D plots of approximate and exact solutions at different time stages are displayed in Fig. 1 and the 3D graphics of the exact and numerical solutions are portrayed in Fig. 2.

Figure 1

Numerical and exact solution for Problem 1 using $n=100$, $\Delta t=0.01$, $\lambda =5$ and $\nu =-12$

Figure 2

Exact and approximate solution for Problem 1 when $0\leq t \leq 4$, $-30\leq x \leq 30$, $n=100$, $\Delta t=0.01$, $\lambda =5$ and $\nu =-12$

Table 1 Global relative error for Problem 1 when $\lambda =5$ and $\nu =-12$

Table 2 $L_{2}$ and $L_{\infty }$ norms for Problem 1 when $\lambda =0.1$ and $\nu =-10$

Problem 2

Consider the following KS equation [6, 25, 27, 31]:

$$ y_{t}+yy_{x}-y_{xx}+y_{xxxx}=0, \quad x \in [-50,50], t \in [0,4]. $$

The piecewise defined spline solution at $t=1$ using the proposed method for Example 2, when $n=100$, $\Delta t=0.01$, $\lambda =5$ and $\nu =-25$, is given by

$$ Y(x,1)= \textstyle\begin{cases} 5.33339 + x (-0.00293376 + x (-0.000119332 + x (-2.42684E-6 \\ \quad {}+ (-2.4676E-8 - 1.00357E-10 x) x))), \quad \mbox{if } x\in [-50,-49],\\ 5.36867 +x (0.00066654 + x (0.0000276187 + x (5.72159E-7\\ \quad {}+ (5.92601E-9 + 2.4549E-11 x) x))), \quad \mbox{if } x\in [-49,-48],\\ 5.35992 +x (-0.000244348 + x (-0.000010335 +x (-2.18545E-7 \\ \quad {}+ (-2.31046E-9 - 9.76963E-12 x) x))), \quad \mbox{if } x\in [-48,-47],\\ 5.36312 +x (0.0000959346 + x (4.14508E-6 + x (8.95434E-8 \\ \quad {}+ (9.67049E-10 + 4.17727E-12 x) x))), \quad \mbox{if } x\in [-47,-46],\\ \vdots , \quad \vdots \\ 5.36221 +x (-0.000010259 +x (-2.33857E-6 + x (-3.5414E-7 \\ \quad {}+ (-3.93807E-8 - 2.85432E-9 x) x))), \quad \mbox{if } x\in [-1,0],\\ 5.36221 +x (-0.000010259 +x (-2.33857E-6 +x (-3.5414E-7\\ \quad {}+ (-3.93807E-8 - 4.44859E-9 x) x))), \quad \mbox{if } x\in [0,1],\\ \vdots , \quad \vdots \\ 9.30952 +x (-0.474015 +x (0.01929 +x (-0.000393476 \\ \quad {}+ (4.02218E-6 - 1.64808E-8 x) x))), \quad \mbox{if } x\in [46,47],\\ 7.96662 +x (-0.331153 +x (0.0132108 + x (-0.000264131 \\ \quad {}+ (2.64617E-6 - 1.06255E-8 x) x))), \quad \mbox{if } x\in [47,48],\\ 6.74426 +x (-0.203824 +x (0.00790544 + x (-0.000153602 \\ \quad {}+ (1.49483E-6 - 5.82822E-9 x) x))), \quad \mbox{if } x\in [48,49],\\ 6.32486 + x (-0.161028 +x (0.00615866 +x (-0.000117953 \\ \quad {}+ (1.13107E-6 - 4.34348E-9 x) x))), \quad \mbox{if } x\in [49,50]. \end{cases} $$

The exact solution is

$$y(x,t)=\lambda +\frac{30}{19}\mu \bigl[-3\tanh \bigl(\mu (x-\lambda t-\nu )\bigr)+ \tanh ^{3}\bigl(\mu (x-\lambda t-\nu )\bigr) \bigr], $$

where $\mu =\frac{1}{2\sqrt{19}}$ and the initial and boundary constraints can be derived from given exact solution. In Table 3, the GRE corresponding to $\lambda =5$, $\nu =-25$, $n=100$ and $\Delta t=0.01$ is compared with LBM [25], QnBSM [27], ExCBSM [31] and QnBS–DQM [6] at $t=6,8,10,12$. Figure 3 exhibits 2D plots of the exact and numerical solution at different time stages. The 3D graphs of the exact and numerical solutions are shown in Fig. 4.

Figure 3

Numerical and analytical exact solutions for Problem 2 with $\Delta t=0.01$, $n=100$, $\lambda =5$ and $\nu =-25$

Figure 4

Exact and numerical solutions for Problem 2 when $0\leq t \leq 10$, $-50\leq x \leq 50$, $n=100$, $\Delta t=0.01$, $\lambda =5$ and $\nu =-25$

Table 3 Global relative error for Problem 2 when $\lambda =5$ and $\nu =-25$

Problem 3

Consider the following KS equation [29, 33]:

$$ y_{t}+yy_{x}+y_{xx}+0.5y_{xxxx}=0, \quad x \in [-10,10], t \in [0,10]. $$

The piecewise defined spline solution at $t=1$ using proposed method for Example 3, when $n=100$, $\Delta t=0.01$ and $\lambda =0.1$, is given by

$$ Y(x,1)= \textstyle\begin{cases} -968493. + x (-492419. + x (-100141. \\ \quad {}+ x (-10182.2 + (-517.634 - 10.5255 x) x))), & \mbox{if } x\in [-10,-\frac{49}{5}],\\ 221758. + x (114852. + x (23791.4 \\ \quad {}+ x (2463.98 + x (127.581 + 2.64218 x)))), & \mbox{if } x\in [-\frac{49}{5},-\frac{48}{5}],\\ -83398.6 + x (-44083.7 + x (-9320.23 \\ \quad {}+ x (-985.155 + (-52.0609 - 1.10037 x) x))), & \mbox{if } x\in [-\frac{48}{5},-\frac{47}{5}],\\ 34542.2 + x (18650.8 + x (4027.53 \\ \quad {}+ x (434.82 + (23.4696 + 0.506665 x) x))), & \mbox{if } x\in [-\frac{47}{5},-\frac{46}{5}],\\ \vdots , &\vdots \\ -0.938649 + x (-3.92441 + x (1.00339\\ \quad {} + x (1.6944 + (-0.425134 - 0.459114 x) x))), & \mbox{if } x\in [-\frac{1}{5},0],\\ -0.938649 + x (-3.92441 + x (1.00339 \\ \quad {}+ x (1.6944 + (-0.425134 - 0.321792 x) x))), & \mbox{if } x\in [0,\frac{1}{5}],\\ \vdots , &\vdots \\ -34545.3 + x (18652.3 + x (-4027.88 \\ \quad {}+ x (434.858 + (-23.4718 + 0.506711 x) x))), & \mbox{if } x\in [\frac{46}{5},\frac{47}{5}],\\ 83405.8 + x (-44087.6 + x (9321.05 \\ \quad {}+ x (-985.241 + (52.0654 - 1.10046 x) x))), & \mbox{if } x\in [\frac{47}{5},\frac{48}{5}],\\ -221773. + x (114859. + x (-23792.9 \\ \quad {}+ x (2464.13 + x (-127.589 + 2.64235 x)))), & \mbox{if } x\in [\frac{48}{5},\frac{49}{5}],\\ 968551. + x (-492448. + x (100147.\\ \quad {} + x (-10182.8 + (517.664 - 10.5261 x) x))), & \mbox{if } x\in [\frac{49}{5},10]. \end{cases} $$

The exact solution is

$$ y(x,t)=-\frac{\lambda }{\mu }+\frac{60}{19}\mu \bigl(-38\gamma \mu ^{2}+ \alpha \bigr)\tanh (\mu x+\lambda t)+120\gamma \mu ^{3} \tanh ^{3}(\mu x+ \lambda t), $$

where $\mu =\frac{1}{2}\sqrt{11\alpha /19\gamma }$ and the initial and boundary constraints are obtained from the given exact solution. The error norms, $L_{2}$ and $L_{\infty }$, with $\lambda =0.1$ and $\Delta t=0.1,0.01,0.001$ are reported in Table 4. It is clear that our numerical algorithm provides a better approximation to the exact solution than BSF [29] and PSF [33]. The 2D graphs of numerical and true solutions at different time levels are shown in Fig. 5, and Fig. 6 depicts the 3D plots of the exact and numerical solutions in the temporal domain $0 \leq t \leq 10$ using $\Delta t=0.01$.

Figure 5

Numerical and exact solutions for Problem 3 at $t=1,5,10$ using $n=100$ and $\Delta t=0.01$

Figure 6

Exact and approximate solutions for Problem 3 when $0\leq t \leq 1$, $\Delta t=0.001$ and $\lambda =0.1$

Table 4 Error norms for Problem 3 when $\lambda =0.1$

Problem 4

Consider the KS equation [6, 25]

$$ y_{t}+yy_{x}+y_{xx}+4y_{xxx}+y_{xxxx}=0, \quad x \in [-30,30], t \in [0,4]. $$

The piecewise defined spline solution at $t=1$ using the proposed method for Example 4, when $n=100$, $\Delta t=0.01$, $\lambda =6$, $\mu =0.5$ and $\nu =-10$, is given by

$$ Y(x,1)= \textstyle\begin{cases} -50671. + x (-8613.05 +x (-585.635 + x (-19.9104 \\ \quad {}+ (-0.338466 - 0.00230157 x) x))), \quad \mbox{if } x\in [-30,-\frac{147}{5}],\\ 3735.51 + x (639.763 +x (43.808 + x (1.49923 \\ \quad {}+ (0.0256427 + 0.000175363 x) x))), \quad \mbox{if } x\in [-\frac{147}{5},-\frac{144}{5}],\\ -2485.85 +x (-440.333 +x (-31.1986 + x (-1.10517 \\ \quad {}+ (-0.0195726 - 0.000138632 x) x))), \quad \mbox{if } x\in [-\frac{144}{5},-\frac{141}{5}],\\ 968.556 +x (172.149 +x (12.2398 + x (0.435199\\ \quad {}+ (0.00773898 + 0.0000550672 x) x))), \quad \mbox{if } x\in [-\frac{141}{5},-\frac{138}{5}],\\ \vdots , \quad \vdots \\ 0.0379155 + x (-0.0741793 +x (0.0714278 + x (-0.0447254\\ \quad {}+ (0.0190591 - 0.00966862 x) x))), \quad \mbox{if } x\in [-\frac{3}{5},0],\\ 0.0379155 +x (-0.0741793 +x (0.0714278 + x (-0.0447254 \\ \quad {}+ (0.0190591 - 0.00431186 x) x))), \quad \mbox{if } x\in [0,\frac{3}{5}],\\ \vdots , \quad \vdots \\ -1.40981E-9 + x (2.61336E-10 +x (-1.93724E-11 +x (7.1782E-13 \\ \quad {}+ (-1.3295E-14 + 9.84664E-17 x) x))), \quad \mbox{if } x\in [\frac{138}{5},\frac{141}{5}],\\ 2.24784E-8 + x (-3.97417E-9 + x (2.81018E-10 +x (-9.93432E-12 \\ \quad {}+ (1.75573E-13 - 1.24102E-15 x) x))), \quad \mbox{if } x\in [\frac{141}{5},\frac{144}{5}],\\ -5.50318E-8 + x (9.48247E-9 +x (-6.53471E-10 + x (2.25132E-11 \\ \quad {}+ (-3.87752E-13 + 2.67096E-15 x) x))), \quad \mbox{if } x\in [\frac{144}{5},\frac{147}{5}],\\ 1.16927E-8 +x (-1.86523E-9 +x (1.18482E-10 +x (-3.74368E-12 \\ \quad {}+ (5.87933E-14 - 3.66767E-16 x) x))), \quad \mbox{if } x\in [\frac{147}{5},30]. \end{cases} $$

The exact solution is

$$ y(x,t)=9+\lambda -15 \bigl[\tanh (\mu (x-\lambda t-\nu )+\tanh ^{2}( \mu (x-\lambda t-\nu )+\tanh ^{3}(\mu (x-\lambda t-\nu ) \bigr]. $$

The initial and end conditions are established from given exact solution. Table 5 portrays the comparison of GRE with LBM [25] and QnBS-DQM [6] corresponding to $\lambda =6$, $\mu =0.5$, $\nu =-10$, $n=150$ and $\Delta t=0.001$ at $t=1,2,3,4$. Figure 7 shows the comparison of approximate and exact solution at different time stages. The 3D graphics of the exact and numerical solutions are given in Fig. 8 when $-30 \leq x \leq 30$, $0 \leq t \leq 1$ using $n=100$ and $\Delta t=0.01$.

Figure 7

Numerical and analytical exact solutions for Problem 4 with $\Delta t=0.01$, $n=100$, $\lambda =6$, $\mu =0.5$ and $\nu =-10$

Figure 8

Exact and approximate solutions for Problem 4 when $-30\leq x \leq 30$, $0\leq t \leq 4$, $n=100$, $\Delta t=0.01$, $\lambda =6$, $\mu =0.5$ and $\nu =-10$

Table 5 Global relative error for Problem 4 when $\lambda =6$, $\mu =0.5$ and $\nu =-10$

8 Conclusion

In this work, an application of a new quintic polynomial B-spline approximation approach has been presented for a numerical investigation of the Kuramoto–Sivashinsky equation. The numerical scheme employs typical fifth degree polynomial basis spline functions in association with a new approximation and a Crank–Nicolson scheme to discretize the problem in the space and time directions, respectively. The error and stability analysis of the proposed scheme is carried out. Four test problems are considered from the available literature and the simulation results are compared with LBM [25], QnBSM [27], BSF [29], ExCBSM [31], QnBS-DQM [6] and PSF [33]. It is concluded that the presented algorithm outperforms the other variants on the topic with superior accuracy and straightforward implementation.