1 Introduction

The study on the hepatitis B virus has gained great attention among the researchers for several decades [1]. This is because of the necessity to know in detail about a life threatening virus and, moreover, to know how it spreads. This disease spreads through physical contact, blood transfusion, and gets transmitted from the affected mother to child during the pregnancy [2, 3]. The hepatitis B virus possibly leads to acute liver diseases. It has been noticed that most of the patients get affected with chronic HBV during birth or after the birth. A solution can be offered by mathematical models by understanding the virulence of Hepatitis B. Min et al. [4] proposed HBV infection model of ordinary differential equations of the population of uninfected target cells, infected cells and the density of virus, which will be written as

$$ \textstyle\begin{cases} \frac{dX}{dt} = \alpha - \varphi VX - d_{T}X, \\ \frac{dY}{dt} = \varphi VX - bY, \\ \frac{dV}{dt} = rY - cZ, \end{cases} $$
(1.1)

where X, Y and V represent the concentration of uninfected target cells, infected cells, and virus particles at time t, respectively. The parameters α, \(d_{T}\), φ, b, r, c are positive constants, where α is the production constant of the hepatocyte, \(d_{T}\) is the death rate of the hepatocyte, φ is the rate of infectivity, b is the infected hepatocyte killing rate, r is the virus production, c is the virus clearance rate from the system.

In this model, a strong antitherapy is given to patients who have average immune response to clear the infected cells. Zou et al. [5] assumed that this therapy would be fit for the patients, but it is understood that it would not be suitable for the virus data. Therefore, Thornle et al. [6] introduced a better model that also does not have an effective productiveness. Though the earlier introduced methods fail to possess efficacy, a new parameter ε is introduced to prohibit the growth of new virus and \(\varepsilon =1\) means that therapy completely prohibits virus growth [7]. So the model is written as

$$ \textstyle\begin{cases} \frac{dX}{dt} = \alpha - \varphi ZX - d_{T}X, \\ \frac{dY}{dt} = \varphi ZX - bY, \\ \frac{dV}{dt} = (1 - \varepsilon )rY - cZ. \end{cases} $$
(1.2)

Zou et al. [8] introduced some changes in the model. Unlike HIV infected cells, infected hepatocytes have the ability to recover because the virus does not integrate. Thus, it can be eliminated. Equation (1.2) can be modified to

$$ \textstyle\begin{cases} \frac{dX}{dt} = \alpha - \varphi ZX - d_{T}X + bY,\\ \frac{dY}{dt} = \varphi VX - \delta Y - bY, \\ \frac{dV}{dt} = (1 - \varepsilon )rY - cZ. \end{cases} $$
(1.3)

Zhang et al. [9] applied this model for prohibiting the virion production and then they investigated the drug efficacy to see whether the virion production is blocked or not. The model is written as

$$ \textstyle\begin{cases} \frac{dX}{dt} = \alpha + r_{X}X ( 1 - \frac{X + Y}{K} ) - (1 - \eta )\varphi VX - d_{T}X + bY, \\ \frac{dY}{dt} = r_{Y}Y ( 1 - \frac{X + Y}{K} ) + (1 - \eta )\varphi VX - \delta Y - bY, \\ \frac{dV}{dt} = (1 - \varepsilon )vY - cZ. \end{cases} $$
(1.4)

Mann et al. [10] included to increase target cells and infected cells, \(r_{X}\) and \(r_{Y}\), respectively, and the carrying capacity. This was included in [4] together with another parameter η which explains the effectiveness of the drug in blocking infection. Analogously to ε, the range for η is \([0, 1]\).

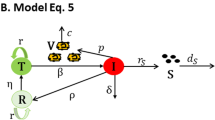
In this model, we extend the work of Khalid Hattaf et al. [11] in which the immune response of CTL cells is added in the fourth compartment. It is an action occurring in a in-host model among liver cells (uninfected and infected) and the virus, and the immune response of CTL cells is obtained by the mathematical model. Here, X means the target uninfected cells (uninfected hepatocytes), Y means the infected cells (infected hepatocytes), V means the HBV virus and Z represents the immune response of the CTL cells. This model stands for the target cells infected at the rate φ and infection happens because of the association with target cells and virus. Initially, this target cell produces the hepatocytes at the rate α and the natural death rate is \(d_{T}\). The infected cells die at a rate of δ and they are returned to uninfected hepatocytes at the rate a for which they get infected. These infected cells are killed by the immune response of the CTL cell at a rate of b and production of new virus at a rate of r. The rate of decay is c, CTL cells can expand the immune response to viral antigen which is derived from Y at a rate \(sYZ / ( \varepsilon + Y )\), here the CTL stimulation rate is s and the viral load is ε. The rate of antigenic stimulation without decay is σ. The export rate of precursor CTL cells from the thymus is ρ. The immune response of CTL cells has the potentiality to kill the infected cells. These assumptions lead to the model shown in Fig. 1.

Figure 1
figure 1

Compartmental diagram for HBV virus dynamics model

Full size image

We have taken four cells: uninfected target cells, the infected cells, hepatitis B virus and the CTL cells [12]. This model expresses the relation to the target liver cells and the HBV [13]. Due to the strong immune response, the HBV infection is completely cured. The compartmental diagram for HBV virus dynamics model is shown in Fig. 1 and the entire value of parameters are shown in Table 1. When our model is compared to the Min, Su, and Kuang [4] model, the rate of recovery is not given in the target uninfected cells compartment and they did not discuss the effect of therapy in blocking infection and the effect of a drug in blocking new virus production. Similarly, Zhang, Wang, and Zhang, and Zou, Zhang, and Ruan [7, 8] did not discuss the effect of therapy in blocking infection in the compartmental target uninfected cells and infected cells. However, we elaborately discussed in our model whatever they did not discuss in their models. Already we have analyzed the nonlinear problem which matches with Mojtaba Hajipour et al.’s work [14, 15] who studied the accurate discretization of highly nonlinear boundary value problems. This work proposes a sixth-order approximation [16]; however, our work not only proposes a sixth-order approximation but also possibly a higher-order approximation for the same problem. Baleanu. et al. [17, 18] discussed a new mathematical model for HIV and the human liver using a homotopy analysis method. One also used in this work the Caputo-Fabrizio function applied to a higher-order differential equation under different conditions [19–22]. We have to use the parametric estimation for the numerical simulation [23]. This model becomes

$$ \begin{gathered} \frac{dX}{dt} = \alpha - d_{T}X - \varphi VX + bYZ, \\ \frac{dY}{dt} = \varphi VX - \delta Y - ( a + b )YZ, \\ \frac{dV}{dt} = rY - cV, \\ \frac{dZ}{dt} = \rho + \frac{sYZ}{\varepsilon + Y} - \sigma Z. \end{gathered} $$
(1.5)

The initial and boundary conditions of finding the solution of Eq. (1.5) are

$$\begin{aligned}& X(0) = 0; \qquad Y(0) = 0; \qquad Y(0) = 0; \qquad Z(0) =0; \\& X(0) = 10^{8};\qquad Y(0) = 10^{-2};\qquad V(0) = 10; \qquad Z(0) = 100. \end{aligned}$$
Table 1 The parameter values of the proposed model
Full size table

This forms the basis of this paper. The parameters show that some patients very quickly are cured due to the immunity response when the treatment is given but it works relatively slow for other patients [24]. So, the treatment is stopped and it is observed how the virus is degenerated in patients [25]. In this paper, we tried to have the highest understanding of the transition of the viral infection by having antiviral therapy for HBV infection. Such knowledge of understanding helps to know what treatment is to be given, when to start and how long this treatment is to be continued [26–29]. The prime objective of this paper is to obtain greater knowledge and understanding on HBV antiviral therapy for young researchers in the field of science and medicine. Generally, it is quite complex to find the analytical solution for this model. But we found the analytical solution with the use of the LHAM method in this model. Our model can be very useful for finding the analytical solution and numerical simulation in the easiest way for the similar equations using MATLAB.

This article has six parts. The initial part is an introduction dealing with existing literature and proposed work. The second and third parts are for the LHAM method and applications which are used to find the solutions. The fourth part is for the numerical experiments, and an error analysis forms the fifth part of the paper. The final part of the paper is for our conclusion.

2 Liao’s Homotopy Analysis Method (LHAM)

We consider the equation

$$\mathrm{K}\bigl[a(t)\bigr] = 0. $$

Then

$$ ( 1 - p )\Re \bigl[ \psi ( t;p ) - a_{0} ( t ) \bigr] = hp\mathrm{A} ( t )\mathrm{K} \bigl[ \psi ( t;p ) \bigr],\quad p \in [0,1],h \ne 0. $$
(2.1)

The above zeroth-order deformation equation stems from [30–34].

Here ℜ is an auxiliary linear operator such that \(\Re [x_{i}] = 0\) for integral constants

$$x_{i}\quad ( i = 1, 2, 3 ). $$

When \(p = 0\) and \(p = 1\), (2.1) can be written as

$$\begin{aligned}& \chi (t;0) = a_{0}(t). \\& \chi (t;1) = a(t). \end{aligned}$$

Using a Taylor series expansion of \(\chi (t;p)\) with respect to p we get

$$ \chi (t,p) = a_{0}(t) + \sum_{i = 0}^{\infty } a_{i}(t) p^{i}. $$
(2.2)

Here \(a_{i} = \frac{1}{i!}\frac{\partial ^{i}\chi (t;p)}{\partial p^{i}} |_{p = 0}\).

Differentiating the equation i times with respect to p, then setting \(p = 0\), and finally dividing them by i!, we get the ith order deformation equations,

$$ \Re \bigl[a_{i}(t) - \xi _{i}a_{i - 1}(t)\bigr] = hA(t)\beta _{i}\Bigl[\vec{a}_{i - 1}(t) \Bigr]. $$
(2.3)

Here,

$$\beta _{i}\Bigl[\vec{a}_{i - 1}(t)\Bigr] = \frac{1}{(i - 1)!}\frac{\partial ^{i - 1}\mathbb{R}[\psi (t;p)]}{\partial p^{n - 1}} \biggm|_{p = 0} $$

and also

$$\xi _{i} = \left \{ \textstyle\begin{array}{c@{\quad }c} 0 & i \le 1 \\ 1 & i > 1 \end{array}\displaystyle \right \} . $$

3 Applications

The solution of Eq. (1.5) is defined by using LHAM method as follows:

$$\begin{aligned}& \frac{dX}{dt} - \alpha + d_{T}X + \varphi VX - bYZ = 0, \end{aligned}$$
(3.1)
$$\begin{aligned}& \frac{dY}{dt} - \varphi VX + \delta Y + ( a + b )YZ = 0, \end{aligned}$$
(3.2)
$$\begin{aligned}& \frac{dV}{dt} - rY + cV = 0, \end{aligned}$$
(3.3)
$$\begin{aligned}& \frac{dZ}{dt} - \rho - \frac{sYZ}{\varepsilon + Y} + \sigma Z = 0. \end{aligned}$$
(3.4)

To obtain the analytical solution, the homotopy is

$$\begin{aligned}& ( 1 - p ) \biggl( \frac{dX}{dt} - \alpha + d_{T}X \biggr) = hp \biggl( \frac{dX}{dt} - \alpha + d_{T}X + \varphi VX - bYZ \biggr), \end{aligned}$$
(3.5)
$$\begin{aligned}& ( 1 - p ) \biggl( \frac{dY}{dt} + \delta Y \biggr) = hp \biggl( \frac{dY}{dt} - \varphi VX + \delta Y + ( a + b )YZ \biggr), \end{aligned}$$
(3.6)
$$\begin{aligned}& ( 1 - p ) \biggl( \frac{dV}{dt} - rY + cV \biggr) = hp \biggl( \frac{dV}{dt} - rY + cV \biggr), \end{aligned}$$
(3.7)
$$\begin{aligned}& ( 1 - p ) \biggl( \frac{dZ}{dt} - \rho + \sigma Z \biggr) = hp \biggl( \frac{dZ}{dt} - \rho - \frac{sYZ}{\varepsilon + Y} + \sigma Z \biggr). \end{aligned}$$
(3.8)

Equating \(p^{0}\) terms we get

$$\begin{aligned}& p^{0}: \biggl( \frac{dX_{0}}{dt} - \alpha + d_{T}X_{0} \biggr) = 0, \end{aligned}$$
(3.9)
$$\begin{aligned}& p^{0}: \biggl( \frac{dY_{0}}{dt} + \delta Y_{0} \biggr) = 0, \end{aligned}$$
(3.10)
$$\begin{aligned}& p^{0}: \biggl( \frac{dV_{0}}{dt} - rY_{0} + cV_{0} \biggr) = 0, \end{aligned}$$
(3.11)
$$\begin{aligned}& p^{0}: \biggl( \frac{dZ_{0}}{dt} - \rho + \sigma Z_{0} \biggr) = 0. \end{aligned}$$
(3.12)

From Eq. (3.9) ⇒ \(X_{0} = ( 10^{8} - \frac{\alpha }{d_{T}} )e^{ - d_{T}t} + \frac{\alpha }{d_{T}}\).

From Eq. (3.10) ⇒ \(Y_{0} = 10^{ - 2}e^{ - \delta t}\).

From Eq. (3.11) ⇒ \(V_{0} = ( 10 - \frac{r10^{ - 2}}{c} )e^{ - ct} + \frac{r10^{ - 2}}{c}\).

From Eq. (3.12) ⇒ \(Z_{0} = ( 100 - \frac{\rho }{\sigma } )e^{ - \sigma t} + \frac{\rho }{\sigma } \).

Again equating \(p^{1}\) terms we get

$$\begin{aligned}& p^{1}:\frac{dX_{1}}{dt} + d_{T}X_{1} - \frac{dX_{0}}{dt} - d_{T}X_{0} = h \biggl( \frac{dX_{0}}{dt} - \alpha + d_{T}X_{0} + \varphi V_{0}X_{0} - ( a + b )Y_{0}Z_{0} \biggr) , \end{aligned}$$
(3.13)
$$\begin{aligned}& p^{1}:\frac{dY_{1}}{dt} + \delta Y_{1} - \frac{dY_{0}}{dt} - \delta Y_{0} = h \biggl( \frac{dY_{0}}{dt} - \varphi V_{0}X_{0} + \delta Y_{0} + ( a + b )Y_{0}Z_{0} \biggr) , \end{aligned}$$
(3.14)
$$\begin{aligned}& p^{1}:\frac{dV_{1}}{dt} - rY_{1} + cV_{1} - \frac{dV_{0}}{dt} + rY_{0} - cV_{0} = h \biggl( \frac{dV_{0}}{dt} - rY + cV_{0} \biggr) , \end{aligned}$$
(3.15)
$$\begin{aligned}& p^{1}:\frac{dZ_{1}}{dt} + \sigma Z_{1} - \frac{dZ_{0}}{dt} - \sigma Z_{0} = h \biggl( \frac{dZ_{0}}{dt} - \rho - \frac{sY_{0}Z_{0}}{\varepsilon + Y_{0}} + \sigma Z_{0} \biggr) . \end{aligned}$$
(3.16)

From Eq. (3.13) ⇒ \(X_{1} = ( 10^{8} - \frac{\lambda _{1}}{\delta + \sigma - d_{T}} - \frac{\lambda _{2}}{\delta - d_{T}} - \frac{\lambda _{3}}{c + d_{T}} - \frac{\lambda _{4}}{d_{T}} )e^{ - d_{T}t} + \frac{\lambda _{1}e^{ - ( \delta + \sigma )t}}{\delta + \sigma - d_{T}} + \frac{\lambda _{2}e^{ - \delta t}}{\delta - d_{T}} + \frac{\lambda _{3}e^{ - ct}}{c + d_{T}} + \frac{\lambda _{4}}{d_{T}}\). Here

$$\begin{aligned}& \lambda _{1} = b10^{ - 2} \biggl( 100 - \frac{\rho }{\sigma } \biggr);\qquad \lambda _{2} = \frac{b\rho }{\sigma }; \qquad \lambda _{3} = h\varphi \biggl( 10 - \frac{r10^{ - 2}}{c} \biggr) + \frac{hr10^{ - 2}}{c}; \\& \lambda _{4} = \frac{\alpha }{d_{T}} ( 1 + h ) - h\alpha . \end{aligned}$$

From Eq. (3.14) ⇒ \(Y_{1} = ( 10^{ - 2} + \frac{\lambda _{6}}{c - \delta + d_{T}} + \frac{\lambda _{7}}{d_{T} - \delta } + \frac{\lambda _{8}}{c} + \frac{\lambda _{9}}{\delta } )e^{ - \delta t} + t\lambda _{5}e^{ - \delta t} - \frac{\lambda _{6}e^{ - ( c + d_{T} )t}}{c - \delta + d_{T}} - \frac{\lambda _{7}e^{ - d_{T}t}}{d_{T} - \delta } - \frac{\lambda _{8}e^{ - ( \delta + c )t}}{c} + \frac{\lambda _{9}}{\delta } \). Here

$$\begin{aligned}& \lambda _{5} = \frac{h\rho ( a + b )}{\sigma };\qquad \lambda _{6} = h\varphi \biggl( 10 - \frac{r10^{ - 2}}{c} \biggr) \biggl( 10^{8} - \frac{\alpha }{d_{T}} \biggr);\\& \lambda _{7} = \biggl( \frac{h\varphi r10^{ - 2}}{c} \biggr) \biggl( 10^{8} - \frac{\alpha }{d_{T}} \biggr);\qquad \lambda _{8} = 10^{ - 2}h ( a + b ) \biggl( 100 - \frac{\rho }{\sigma } \biggr);\\& \lambda _{9} = \frac{10^{ - 2}h\varphi r\alpha }{cd_{T}}. \end{aligned}$$

From Eq. (3.15) ⇒ \(V_{1} = [ 10 - \frac{\psi _{1}}{c - \delta } + \frac{\psi _{3}}{d_{T}} + \frac{\psi _{4}}{c - d_{T}} + \frac{\psi _{5}}{\delta } + \frac{\psi _{6}}{c} ]e^{ - ct} + \frac{e^{ - \delta t}}{c - \delta } ( \psi _{1} - t\psi _{2} ) + \frac{\psi _{3}e^{ - ( c + d_{T} )t}}{d_{T}} + \frac{\psi _{4}e^{ - d_{T}t}}{c - d_{T}} + \frac{\psi _{5}e^{ - ( \delta + c )t}}{\delta } + \frac{\psi _{6}}{c}\), where

$$\begin{aligned}& \psi _{1} = r \biggl[ \frac{\lambda _{6}}{c + d_{T} - \delta } + \frac{\lambda _{7}}{d_{T} - \delta } + \frac{\lambda _{8}}{c} - \frac{\lambda _{9}}{\delta } - 10^{ - 2}h \biggr]; \qquad \psi _{2} = rt\lambda _{5};\qquad \psi _{3} = \frac{r\lambda _{6}}{c + d_{T} - \delta }; \\& \psi _{4} = \frac{r\lambda _{7}}{d_{T} - \delta };\qquad \psi _{5} = \frac{r\lambda _{8}}{c};\qquad \psi _{6} = r \biggl( 10^{ - 2} + h + \frac{\lambda _{9}}{\delta } \biggr). \end{aligned}$$

From Eq. (3.16) ⇒ \(Z_{1} = ( 100 - \frac{\xi _{1}}{\delta - \sigma } + \frac{\xi _{2}}{\delta } )e^{ - \sigma t} + 2t ( - 100\sigma + \rho )e^{ - \sigma t} + \frac{\xi _{1}e^{ - \delta t}}{\delta - \sigma } - \frac{\xi _{2}e^{ - ( \delta + \sigma )t}}{\delta } \).

Here

$$\xi _{1} = \frac{h\sigma s}{\varepsilon + 10^{ - 2}}; \qquad \xi _{2} = \frac{10^{ - 2}hs\rho }{\varepsilon + 10^{ - 2}}. $$

The analytical solution of this model using the LHAM is

$$X ( t ) = \lambda e^{ - d_{T}t} + \frac{\lambda _{1}e^{ - ( \delta + \sigma )t}}{\delta + \sigma - d_{T}} + \frac{\lambda _{2}e^{ - \delta t}}{\delta - d_{T}} + \frac{\lambda _{3}e^{ - ct}}{c + d_{T}} + \frac{\lambda _{4}}{d_{T}}. $$

Here \(\lambda = 99980099.99\), \(\lambda _{1} = 58.89999852\), \(\lambda _{2} = 0.000147978\), \(\lambda _{3} = 0.003196348\), \(\lambda _{4} = 199\).

$$\begin{aligned}& \begin{gathered} \therefore X(t) = 99980099.99e^{ - 0.01t} + 3.76 \times 10^{ - 7}e^{ - 170000000.1t} \\ \hphantom{\therefore X(t) =}{}+ 2.9596 \times 10^{ - 3}e^{ - 0.06t} + 7.796 \times 10^{ - 3}e^{0.7t} + 19900. \\ Y ( t ) = \varpi e^{ - \delta t} + t\lambda _{5}e^{ - \delta t} - \frac{\lambda _{6}e^{ - ( c + d_{T} )t}}{c - \delta + d_{T}} - \frac{\lambda _{7}e^{ - d_{T}t}}{d_{T} - \delta } - \frac{\lambda _{8}e^{ - ( \delta + c )t}}{c} + \frac{\lambda _{9}}{\delta }. \end{gathered} \end{aligned}$$
(3.17)

Here \(\varpi = 7.362624103\), \(\lambda _{5} = 1.484046882 \times 10^{12}\), \(\lambda _{6} = 2.0999979\), \(\lambda _{7} = - 2 \times 10^{ - 4}\), \(\lambda _{8} = 59.06999852\), \(\lambda _{9} = 3.196347032 \times 10^{ - 12}\).

$$ \begin{gathered} \therefore Y ( t ) = 7.362624103e^{ - 0.06t} + t1.484046882 \times 10^{12}e^{ - 0.06t} - 5.999994e^{0.71t} \\ \hphantom{\therefore Y ( t ) =}{} - 4 \times 10^{ - 3}e^{ - 0.01t}- 1.348630103e^{0.64t} + 5.327245053 \times 10^{ - 11}, \\ V ( t ) = \varsigma e^{ - ct} + \frac{\psi _{1}e^{ - \delta t}}{c - \delta } - \frac{\psi _{2}te^{ - \delta t}}{c - \delta } + \frac{\psi _{3}e^{ - ( c + d_{T} )t}}{d_{T}} + \frac{\psi _{4}e^{ - d_{T}t}}{c - d_{T}} + \frac{\psi _{5}e^{ - ( \delta + c )t}}{\delta } + \frac{\psi _{6}}{c}. \end{gathered} $$
(3.18)

Here \(\varsigma = - 861.7346244\), \(\psi _{1} = 10.27967374\), \(\psi _{2} = 2.077665635 \times 10^{12}\), \(\psi _{3} = 8.3999916\), \(\psi _{4} = 0.0056\), \(\psi _{5} = 1.888082144\), \(\psi _{6} = 1.414\).

$$\begin{aligned}& \begin{aligned}[b] \therefore V ( t ) ={}& {-} 861.7346244e^{0.7t} + 0.23501769e^{ - 0.06t} - 4.750035745e^{ - 0.06t} \\ &{} + 839.99916e^{0.69t}+ 1.27883 \times 10^{ - 4}e^{ - 0.01t} + 31.46803573e^{0.64t}\\ &{} + 3.2283105 \times 10^{ - 2}, \end{aligned} \\& Z ( t ) = \vartheta e^{ - \sigma t} + 2t ( - 100\sigma + \rho )e^{ - \sigma t} + \frac{\xi _{1}e^{ - \delta t}}{\delta - \sigma } - \frac{\xi _{2}e^{ - ( \delta + \sigma )t}}{\delta }. \end{aligned}$$
(3.19)

Here \(\vartheta = 2903.236246\), \(\xi _{1} = 6601941748\), \(\xi _{2} = 165.8640777\).

$$ \begin{aligned}[b] \therefore Z ( t ) ={}& 2903.236246e^{ - 1.7 \times 10^{8}t} - 3.399999915 \times 10^{10}te^{ - 1.7 \times 10^{8}t} \\ &{} - 38.83495148e^{ - 0.06t}- 2764.401295e^{ - 170000000.1t}. \end{aligned} $$
(3.20)

4 Numerical experiment

Let us consider the values for numerical results are

$$X_{0} = 10^{8},\qquad Y_{0} = 10^{ - 2},\qquad V_{0} = 10,\qquad Z_{0} = 100. $$

Let us use Matlab software to obtain the sixth-order expansions for \(X ( t )\), \(Y ( t )\), \(V ( t )\) and \(Z ( t )\):

$$\begin{aligned}& \begin{aligned}[b] X ( t ) ={}& 10\mbox{,}00\mbox{,}00\mbox{,}000 + 9\mbox{,}99 \mbox{,}80\mbox{,}234.978ht + 8\mbox{,}87\mbox{,}34\mbox{,}454.347h^{2}t \\ &{}+ 47\mbox{,}58\mbox{,}843.56h^{3}t + 7\mbox{,}54\mbox{,}53\mbox{,}444.757h^{4}t + 4\mbox{,}66 \mbox{,}76\mbox{,}678.34h^{5}t \\ &{}+ 92\mbox{,}392.342h^{6}t+ 46\mbox{,}347.647h^{2}t^{2} + 6\mbox{,}37 \mbox{,}299.23h^{3}t^{2}+ 2\mbox{,}326.8293h^{4}t^{2} \\ &{} + 789.737h^{5}t^{2} + 6.67889h^{6}t^{2}+ 0.63467343h^{3}t^{3} \\ &{}+ 2.6646h^{4}t^{3}+ 10.2980376h^{5}t^{3} + 0.9864763638h^{6}t^{3} + \cdots \end{aligned} \end{aligned}$$
(4.1)
$$\begin{aligned}& \begin{aligned}[b] Y ( t ) ={}& 0.01 + 0.03889431ht + 0.04545347h^{2}t + 0.0845956h^{3}t \\ &{} + 0.75743507h^{4}t+ 0.043455634h^{5}t+ 0.420346045h^{6}t \\ &{} + 0.63242347h^{2}t^{2} + 0.22478453h^{3}t^{2}+ 0.18200093h^{4}t^{2}\\ &{} + 0.700037h^{5}t^{2}+ 0.6734889h^{6}t^{2} + 0.00634343h^{3}t^{3}\\ &{}+ 0.05464646h^{4}t^{3} + 0.1046667465h^{5}t^{3} + 0.9354378h^{6}t^{3} + \cdots \end{aligned} \end{aligned}$$
(4.2)
$$\begin{aligned}& \begin{aligned}[b] V ( t ) ={}& 10 + 620.5464546761ht + 4.4746545h^{2}t + 30.3465436576h^{3}t \\ &{}+ 2.7346566h^{4}t + 0.05575634h^{5}t + 1.444567045h^{6}t+ 5.45656347h^{2}t^{2}\\ &{} + 0.22765803h^{3}t^{2} + 140.74687649h^{4}t^{2} + 45.4455657h^{5}t^{2} \\ &{}+ 99.645465698h^{6}t^{2} + 80.00698765h^{3}t^{3} + 00.976534646h^{4}t^{3} \\ &{}+ 6.196465465h^{5}t^{3} + 750.32126378h^{6}t^{3} + \cdots \end{aligned} \end{aligned}$$
(4.3)
$$\begin{aligned}& \begin{aligned}[b] Z ( t ) ={}& 100 + 464.85565555ht + 46.654222h^{2}t + 355.255015h^{3}t \\ &{}+ 587.466621336h^{4}t + 54.22233021h^{5}t+ 41.555501h^{6}t \\ &{} + 23.517347h^{2}t^{2} + 78.15553697h^{3}t^{2} + 102.6879412h^{4}t^{2} \\ &{}+ 478.66987132h^{5}t^{2} + 785.6694125h^{6}t^{2} + 74.68841269h^{3}t^{3} \\ &{}+ 2.3698455h^{4}t^{3} + 40.368715h^{5}t^{3} + 72.3684156h^{6}t^{3} + \cdots \end{aligned} \end{aligned}$$
(4.4)

We have plotted the target uninfected cell rate, the infected cell rate, the virus rate and the CTL cell response rate observing the values of parameters using Wolfram Mathematica 12 software. For doing the mathematical modeling, we used 12 parameters at different values that explain the differences seen in the data among patients undergoing combination therapy. When the antiviral therapy is given, the target rate of uninfected cell is completely increased [35]. In particular, if the death rate of hepatocytes gets decreased during the antiviral therapy then the target uninfected cell rate would also increase [36]. After that, the killing rate of the infected hepatocytes will be increased as we give the treatment.

Since a prompt treatment is given, the death rate of both hepatocytes and the HBV infection decreases significantly [7–10, 35]. When the rate of virus clearance increases through the application of the treatment, the rate of infected cell decreases. At first, we give the treatment for killing the infected hepatocytes and then the treatment is given for HBV infection. As the rate of virus clearance increases through the proper treatment, the infected cell rate gets reduced. Consequently, the virus clearance rate of infected cells decreased.

When the regular treatment is given, the death rate of hepatocytes as well as virus rate will be decreased [37]. When the treatment is continued, the production of new virus and the virus infectivity rate get massively reduced [38]. The killing rate of infected hepatocytes increases as the treatment is regularly given and the virus production is completely reduced to the percentage zero. The new virus production will be completely blocked since the treatment is continued for a period of time; therefore the virus production will be completely decreased to the level zero. Consequently, the patient becomes disease free as the liver cells get cured completely. He or she can be stable and lead a normal life. This is possible only due to the therapy; otherwise the death of the patient is inevitable.

5 Error analysis

For getting the convergence solution, we substitute Eqs. (4.1) to (4.4) in (1.5) which is recommended by Liao [31–34]. Figures 2–9 show the plots of third- and fourth-order approximations of \(X ( t )\), \(Y ( t )\), \(V(t)\) and \(Z ( t )\). It is clear from these curves that the valid region of ‘h’ is parallel to the horizontal axis. The valid region of h value ranges are given in Table 2. Figures 10–13 show the residual error function of Eqs. (5.1) to (5.4) using the third-order approximate solution for the different values of \(h = - 1.1\), \(h = - 1.2\), \(h = - 0.62\) and \(h = - 1.4\). Figures 14–17 show the optimum and minimum values of h, the minimum values are shown in Table 3 and the residual errors are calculated in Table 4. We have

$$\begin{aligned}& \begin{aligned}[b] ER_{1}(X,Y,V,Z;h_{1}) ={}& \frac{d\phi _{X}(t;h_{1})}{dt} - \alpha + d_{T X}(t;h_{1}) + \varphi _{V}(t;h_{1})_{X}(t;h_{1})\\ &{} - b_{Y}(t;h_{1})_{Z}(t;h_{1}), \end{aligned} \end{aligned}$$
(5.1)
$$\begin{aligned}& \begin{aligned}[b] ER_{2}(X,Y,V,Z;h_{2}) ={}& \frac{d\phi _{Y}(t;h_{2})}{dt} - \varphi _{V}(t;h_{2})_{X}(t;h_{2}) + \delta _{Y}(t;h_{2})\\ &{} + ( a + b )_{Y}(t;h_{2})_{Z}(t;h_{2}), \end{aligned} \end{aligned}$$
(5.2)
$$\begin{aligned}& ER_{3}(X,Y,V,Z;h_{3}) = \frac{d\phi _{V}(t;h_{3})}{dt} - r_{Y}(t;h_{3}) + c_{V}(t;h_{3}), \end{aligned}$$
(5.3)
$$\begin{aligned}& ER_{4}(X,Y,V,Z;h_{4}) = \frac{d\phi _{Z}(t;h_{4})}{dt} - \rho - \frac{s_{Y}(t;h_{4})_{Z}(t;h_{4})}{\varepsilon +_{Y}(t;h_{4})} + \sigma _{Z}(t;h_{4}). \end{aligned}$$
(5.4)
Figure 2
figure 2

The h-curves of the third-order approximations for \(X(t)\)

Full size image
Figure 3
figure 3

The h-curves of the third-order approximations for \(Y(t)\)

Full size image
Figure 4
figure 4

The h-curves of the third-order approximations for \(V(t)\)

Full size image
Figure 5
figure 5

The h-curves of the third-order approximations for \(Z(t)\)

Full size image
Figure 6
figure 6

The h-curves of the fourth-order approximations for \(X(t)\)

Full size image
Figure 7
figure 7

The h-curves of the fourth-order approximations for \(Y(t)\)

Full size image
Figure 8
figure 8

The h-curves of the fourth-order approximations for \(V(t)\)

Full size image
Figure 9
figure 9

The h-curves of the fourth-order approximations for \(Z(t)\)

Full size image
Figure 10
figure 10

The residual error function of Eq. (5.1)

Full size image
Figure 11
figure 11

The residual error function of Eq. (5.2)

Full size image
Figure 12
figure 12

The residual error function Eq. (5.3)

Full size image
Figure 13
figure 13

The residual error function Eq. (5.4)

Full size image
Figure 14
figure 14

The optimum and minimum values of \(X(t)\)

Full size image
Figure 15
figure 15

The optimum and minimum values of \(Y(t)\)

Full size image
Figure 16
figure 16

The optimum and minimum values of \(V(t)\)

Full size image
Figure 17
figure 17

The optimum and minimum values of \(Z(t)\)

Full size image
Table 2 The h value is
Full size table
Table 3 The minimum values of \(RX ( h_{1}* )\), \(RY (h_{2}* )\), \(RV ( h_{3}* )\), \(RZ ( h_{4}* )\)
Full size table
Table 4 The residual errors for \(ER_{1}\), \(ER_{2}\), \(ER_{3}\) and \(ER_{4}\) for \(t \in ( 0,1 )\)
Full size table

Let us consider the square residual error for sixth order approximation:

$$\begin{aligned}& RX(h_{1}) = \int _{0}^{1} \bigl( ER_{1} ( X,Y,V,Z;h_{1} ) \bigr)^{2}\,dt, \end{aligned}$$
(5.5)
$$\begin{aligned}& RY(h_{2}) = \int _{0}^{1} \bigl( ER_{2} ( X,Y,V,Z;h_{2} ) \bigr)^{2}\,dt, \end{aligned}$$
(5.6)
$$\begin{aligned}& RV(h_{3}) = \int _{0}^{1} \bigl( ER_{3} ( X,Y,V,Z;h_{3} ) \bigr)^{2}\,dt, \end{aligned}$$
(5.7)
$$\begin{aligned}& RZ(h_{4}) = \int _{0}^{1} \bigl( ER_{4} ( X,Y,V,Z;h_{4} ) \bigr)^{2}\,dt. \end{aligned}$$
(5.8)

The minimal values of \(RX ( h_{1} )\), \(RY ( h_{2} )\), \(RV ( h_{3} )\) and \(RZ ( h_{4} )\) are

$$\frac{dRX(h_{1}*)}{dh_{1}} = 0,\qquad \frac{dRY(h_{2}*)}{dh_{2}} = 0,\qquad \frac{dRV(h_{3}*)}{dh_{3}} = 0,\qquad \frac{dRZ(h_{4}*)}{dh_{4}} = 0. $$

We consider the optimal values of \(h_{1}*\), \(h_{2}*\), \(h_{3}*\) and \(h_{4}*\) for all of the cases to be

$$h_{1}* = - 0.573541,\qquad h_{2}* = - 0.245765,\qquad h_{3}* = - 0.765459,\qquad h_{4}*= - 0.347556. $$

It is of prime importance for any patient infected with the hepatitis B virus, to be given an antiviral therapy which is being considered as one of the very efficient methods of treatment [39]. The hepatics B virus, which leads to acute liver disease, affects most of the patients during birth or after the birth. The W.H.O. report says that the 90 % of the HBV infected persons get cured naturally by the biological process in one year [40]. However, in the rest of the 10% sometimes fail to show any kind of symptom of the disease.

When the patients are severely infected, it concerns around 90% of their liver cells, and hepatocytes get damaged [41, 42]. It is due to the immune response to the infected hepatocytes. There has been no specific treatment for patients with acute infection [43]. In most of the situations, it does not show any symptoms but in rare situations it shows indications like extreme fatigue nausea, vomiting and abdominal pain [38, 44–48]. It is assumed that the acute infection can be easily overcome but the problem is still there as there is evidence of many deaths. While there are enormous treatment options for the chronic patients, none of the treatment methods is found to be useful and efficient [49–51]. Clinical data shows that most of the virus gets decayed when the HBV patients undergo the therapy. Applying the mathematical models to such data shows the result that, if the patients have an immune response, they get cured very quickly when the treatment is given, and in other cases the treatment works comparatively slow [52].

Vaccine has been used for HBV infected patients from 1982. However, eradication of this disease is not possible. Today, the vaccination focused on the highest risk of develo** chronic infection in children who are below 6 years old [53]. The best vaccination strategy for newborns is that the first dose has to be given within the first 24 h of birth [54]. Therefore, the children will be protected at the maximum rate from infection at least for 20 years. It is recommended to vaccinate for reducing the HBV infected patients. It needs to be extended to groups in high danger, such as patients requiring transplantation or dialysis, health-care workers, travelers before visiting an endemic area, people in prisons, or people with multiple sexual partners. When the vaccine is given to patients, it gives positive results for the eradication of the disease [37]. Therefore, we need a good therapy to cure patients who got infected earlier.

Mathematical models have been one of the very useful methods for the understanding of virus and drug dynamics under drug therapy in infections such as HIV, hepatitis C (HCV), and HBV. To have a deeper understanding of virus-host dynamics, spectacular studies have been done combining with the clinical data and mathematical models. However, Ciupe et al. [55] in their studies showed that a strong immune response can be the key to overcoming the disease. Similar studies have been continued to find the efficacy of drugs in curing hepatitis B. For instance, Anna et al. [56] have estimated 95% lamivudine efficacy in blocking new virus production which can be elevated to 99% when combined with famcilovir. Thus, we have studied the comparisons of existing work [4, 5, 57, 58] will be a great resource to extend this for further research. If two of their works are understood, we could extend our work effectively with some other parameter estimation.