1 Introduction

In 1893, Picard [1] introduced the theory of lower and upper solutions to demonstrate the existence of solutions for scalar ordinary differential equations. In 1937, Nagumo [2] proposed a classical upper and lower solutions theory for general differential equation

$$ {y}''(t)=\varphi \bigl( t,y(t),{y}'(t) \bigr). $$

The methodology of upper and lower solutions has found extensive applications in the analysis of boundary value problems associated with nonlinear differential equations [3–9]. In addition, some scholars have also focused on how to apply upper and lower solution methods to solve coupled differential systems [10–13], but currently, there are few achievements in this type of research.

In 2016, by applying the upper and lower solutions method combined with Schauder’s fixed point theorem, Talib, Asif, and Tunc [11] studied the coupled second-order system

$$ \textstyle\begin{cases} -{{{y}_{1}}}''(t)=\psi (t,{{y}_{2}}(t)), \\ -{{{y}_{2}}}''(t)=\varphi (t,{{y}_{1}}(t)), \\ f({{y}_{1}}(0),{{y}_{2}}(0),{{{y}_{1}}}'(0),{{{y}_{2}}}'(0),{{{y}_{1}}}'(1),{{{y}_{2}}}'(1))=(0,0), \\ g ({{y}_{1}}(0),{{y}_{2}}(0))+({{y}_{1}}(1),{{y}_{2}}(1))=(0,0), \end{cases} $$
(1)

where \(\psi,\varphi \in C([0,1]\times \mathbb{R},\mathbb{R})\), \(f \in C({{\mathbb{R}}^{6}},{{\mathbb{R}}^{2}})\), and \(g \in C({{\mathbb{R}}^{2}},{{\mathbb{R}}^{2}})\). The equations in system (1) are explicit functions of \({{y}_{1}}\) and \({{y}_{2}}\), respectively.

Recently, Fonda et al. extended the method of upper and lower solutions to the planar system

$$ \textstyle\begin{cases} {{{y}_{1}}}'(t)=\psi (t,{{y}_{1}},{{y}_{2}}), \\ {{{y}_{2}}}'(t)=\varphi (t,{{y}_{1}},{{y}_{2}}). \end{cases} $$
(2)

In [12], they studied the existence of a solution to the periodic problem for system (2). And in [13], system (2) with separated boundary conditions was studied for the existence of a solution. However, their works are only studied in the first-order planar differential systems.

As is well known, the elastic beam equation can be described by the following fourth-order differential equation:

$$ {{\bigl(\phi \bigl({y}''(t)\bigr) \bigr)}^{\prime \prime }}=\varphi \bigl(t,y,{y}''\bigr), $$
(3)

where \(\phi (0)=0\), \(\phi:{{K}_{1}}\to {{K}_{2}}\) is an increasing homeomorphism between two intervals \({{K}_{1}}\) and \({{K}_{2}}\) containing 0. The upper solution Ā and the lower solution \(\underline{B}\) of (3) satisfy

$$ \bigl(\phi \bigl({\bar{A}}''(t)\bigr){ \bigr)}''\ge \varphi \bigl(t,\bar{A}(t),{ \bar{A}}''(t)\bigr),\quad \text{and} \quad\bigl(\phi \bigl({ \underline{B}}''(t)\bigr){\bigr)}'' \ge \varphi \bigl(t, \underline{B}(t),{\underline{B}}''(t) \bigr). $$

We observed that (3) is equivalent to the following differential system:

$$ \textstyle\begin{cases} {{{y}_{1}}}''(t)={{\phi }^{-1}}({{y}_{2}}(t)), \\ {{{y}_{2}}}''(t)=\tilde{\varphi }(t,{{y}_{1}},{{y}_{2}}), \end{cases} $$

which is a special case of a second-order coupled differential system, where \(\tilde{\varphi }(t,{{y}_{1}},{{y}_{2}})=\varphi (t,{{y}_{1}},{{\phi }^{-1}}({{y}_{2}}))\). Consider the upper solution Ā and the lower solution \(\underline{B}\) whose second derivatives take their values in the domain of ϕ. By defining functions \({{y}_{2}}_{{\bar{A}}}(t)=\phi ({\bar{A}}''(t))\) and \({{y}_{2}}_{{\underline{B}}}(t)=\phi ({\underline{B}}''(t))\), the inequalities regarding upper and lower solutions can be transformed into

$$ {{{{y}_{2}}}_{\bar{A} }}^{\prime \prime }(t)\ge \tilde{\varphi } \bigl(t, \bar{A} (t),{{{{y}_{2}}}_{\bar{A} }}(t)\bigr) \quad\text{and}\quad {{{{y}_{2}}}_{ \underline{B} }}^{\prime \prime }(t)\le \tilde{\varphi } \bigl(t, \underline{B} (t),{{{{y}_{2}}}_{\underline{B} }}(t)\bigr). $$

Therefore, inspired by the work above, in this article we propose a method of upper and lower solutions to study the existence of solutions for second-order coupled system

$$ (P)\quad \textstyle\begin{cases} {{{y}_{1}}}''(t)=\psi (t,{{y}_{1}},{{y}_{2}}), \\ {{{y}_{2}}}''(t)=\varphi (t,{{y}_{1}},{{y}_{2}}), \\ {{y}_{1}}(a)={{y}_{1}}(b)={{y}_{2}}(a)={{y}_{2}}(b)=0, \end{cases} $$

where \(\psi, \varphi \in C([a,b]\times {{\mathbb{R}}^{2}},\mathbb{R})\). Here, using the conversion of (3) as a guide, we give two crucial definitions for problem \((P)\).

Definition 1

If there exist a function \(\underline{B} \in {{C}^{2}} [ a,b ]\) and a function \({{v}_{\underline{B} }}\in {{C}^{2}} [ a,b ]\) such that

$$ \textstyle\begin{cases} \psi (t,\underline{B} (t),{{y}_{2}}(t))\le {\underline{B} }''(t) \quad \text{for all } {{y}_{2}}\le {{{{y}_{2}}}_{ \underline{B} }}(t), t\in [a,b], \\ \psi (t,\underline{B} (t),{{y}_{2}}(t))\ge {\underline{B} }''(t) \quad\text{for all } {{y}_{2}}\ge {{{{y}_{2}}}_{ \underline{B} }}(t), t\in [a,b], \\ {{{{y}_{2}}}_{\underline{B} }}^{\prime \prime }(t)\le \varphi (t, \underline{B} (t),{{{{y}_{2}}}_{\underline{B} }}(t)) \quad\text{for all } t\in [a,b] \end{cases} $$
(4)

and

$$ \underline{B} (a)\le 0,\qquad \underline{B} (b)\le 0,\qquad {{{{y}_{2}}}_{ \underline{B} }}(a)\ge 0,\qquad {{{{y}_{2}}}_{\underline{B} }}(b) \ge 0, $$
(5)

then we say \(\underline{B}\) is a lower solution for problem \((P)\).

Definition 2

If there exist a function \(\bar{A} \in {{C}^{2}} [ a,b ]\) and a function \({{v}_{\bar{A} }}\in {{C}^{2}} [ a,b ]\) such that

$$ \textstyle\begin{cases} \psi (t,\bar{A} (t),{{y}_{2}}(t))\le {\bar{A} }''(t), \quad \text{for all } {{y}_{2}}\le {{{{y}_{2}}}_{\bar{A} }}(t), t\in [a,b], \\ \psi (t,\bar{A} (t),{{y}_{2}}(t))\ge {\bar{A} }''(t), \quad\text{for all } {{y}_{2}}\ge {{{{y}_{2}}}_{\bar{A} }}(t), \enspace t\in [a,b], \\ {{{{y}_{2}}}_{\bar{A} }}^{\prime \prime }(t)\ge \varphi (t,\bar{A} (t),{{{{y}_{2}}}_{ \bar{A} }}(t)), \quad\text{for all } t\in [a,b], \end{cases} $$
(6)

and

$$ \bar{A} (a)\ge 0,\qquad \bar{A} (b)\ge 0, \qquad{{{{y}_{2}}}_{\bar{A} }}(a) \le 0,\qquad {{{{y}_{2}}}_{\bar{A} }}(b)\le 0, $$
(7)

then we say Ā is an upper solution for problem \((P)\).

If \({{y}_{1}}\) is both the upper and lower solution of problem \((P)\), then \(({{y}_{1}},{{y}_{2}})\) satisfies \((P)\).

The structure of this paper is as follows. In Sect. 2, by constructing a homotopy parameter and using the maximum principle, we apply the upper and lower solutions method to obtain the existence of a solution for problem \((P)\). In Sect. 3, we provide two examples.

2 Existence result

We are committed to establishing the existence of a solution for the coupled second-order problem \((P)\) in this section.

Theorem 1

Suppose that there are \(\bar{A} \in {{C}^{2}} [ a,b ]\) and \(\underline{B} \in {{C}^{2}} [ a,b ]\), which are the upper and lower solutions of problem \((P)\), respectively, with \(\underline{B} \le \bar{A} \), \({{{{y}_{2}}}_{\bar{A} }}\le {{{{y}_{2}}}_{\underline{B} }}\) if \(g, f\in C([a,b]\times {{\mathbb{R}}^{2}},\mathbb{R})\) satisfy the following assumptions:

then problem \((P)\) admits a solution \(({{y}_{1}},{{y}_{2}})\) that satisfies

$$ \underline{B} (t)\le {{y}_{1}}(t)\le \bar{A} (t) \quad\textit{and}\quad {{v}_{ \bar{A} }}(t)\le {{y}_{2}}(t)\le {{v}_{\underline{B} }}(t). $$
(8)

Proof

First, we construct a truncation function as follows:

$$ \phi ( y;u,v )=\textstyle\begin{cases} v & \text{for } y>v, \\ y & \text{for } u\le y\le v, \\ u & \text{for } y< u. \end{cases} $$

Define

$$ \bar{\psi}(t,{{y}_{1}},{{y}_{2}})=\psi \bigl(t,\phi ({{y}_{1}}, \underline{B},\bar{A} ),\phi ({{y}_{2}},{{{{y}_{2}}}_{\bar{A} }},{{{{y}_{2}}}_{ \underline{B} }}) \bigr) $$

and

$$ \bar{\varphi} (t,{{y}_{1}},{{y}_{2}})=\varphi \bigl(t,\phi ({{y}_{1}}, \underline{B},\bar{A} ),\phi ({{y}_{2}},{{{{y}_{2}}}_{\bar{A} }},{{{{y}_{2}}}_{ \underline{B} }}) \bigr), $$

then we consider the problem as

$$ (\bar{P})\quad \textstyle\begin{cases} {{{y}_{1}}}''(t)=\bar{\psi} ( t,{{y}_{1}},{{y}_{2}} ), \\ {{{y}_{2}}}''(t)=\bar{\varphi} ( t,{{y}_{1}},{{y}_{2}} ), \\ {{y}_{1}}(a)={{y}_{1}}(b)={{y}_{2}}(a)={{y}_{2}}(b)=0. \end{cases} $$

If \((\bar{P})\) has a solution that satisfies (8), then the solution of \((\bar{P})\) is also the solution of \((P)\). Next we deduce the existence of a solution for \((\bar{P})\) and prove that this solution satisfies (8). The following proof is divided into two steps.

Step 1: Prove that there is a solution to problem \((\bar{P})\).

Using \(\lambda \in [ 0,1 ]\) as the homotopy parameter, we construct the problem

$$ ({{P}_{\lambda }})\quad \textstyle\begin{cases} {{y}_{1}}''(t)=\lambda {y}_{2}+(1-\lambda )\bar{\psi}(t,{y}_{1},{y}_{2}), \\ {{y}_{2}}''(t)=\lambda {y}_{1}+(1-\lambda )\bar{\varphi}(t,{y}_{1},{y}_{2}), \\ {y}_{1}(a)={y}_{1}(b)={y}_{2}(a)={y}_{2}(b)=0. \end{cases} $$

Notice that problem \(({{P}_{1}})\) is a linear problem with only one trivial solution for \(\lambda =1\), and \(({{P}_{0}})\) is \(({\bar{P}})\) for \(\lambda =0\).

We claim that there exists \(R>0\) such that for any \(\lambda \in [0,1]\), \({{ \Vert w \Vert }_{\infty }}< R\), where \(w=({y}_{1},{y}_{2})\) is the solution of problem \(( {{{P}}_{\lambda }} )\) and \({{ \Vert w \Vert }_{\infty }}=\max \sqrt{{{{y}_{1}}^{2}}(t)+{{{y}_{2}}^{2}}(t)}\), \(t\in [a,b]\).

Rewrite problem \(( {{P}_{\lambda}} )\) as

$$ \textstyle\begin{cases} {{y}_{1}}''(t)=(1-\lambda )(\bar{\psi}(t,{y}_{1},{y}_{2})-{y}_{2})+{y}_{2}, \\ {{y}_{2}}''(t)=(1-\lambda )(\bar{\varphi}(t,{y}_{1},{y}_{2})-{y}_{1})+{y}_{1}, \\ {y}_{1}(a)={y}_{1}(b)={y}_{2}(a)={y}_{2}(b)=0. \end{cases} $$

By contradiction, we suppose \(\mathop{\lim }_{n\to \infty } {{ \Vert {{w}_{n}} \Vert }_{\infty }}=+\infty \), where \({{w}_{n}}= ( {{{y}_{1}}_{n}},{{{y}_{2}}_{n}} )\) is the solution of problem \(({{P}_{{{\lambda }_{n}}}})\). Let \({{z}_{n}}= \frac{{{w}_{n}}}{{{ \Vert {{w}_{n}} \Vert }_{\infty }}}\), then \({{z}_{n}}= ( {{p}_{n}},{{q}_{n}} )\) solves the following problem:

$$ \textstyle\begin{cases} {p}''(t)=\frac{1}{{{ \Vert {{w}_{n}} \Vert }_{\infty }}}(1-{{ \lambda }_{n}})(\bar{\psi}(t,{{ \Vert {{w}_{n}} \Vert }_{\infty }}p,{{ \Vert {{w}_{n}} \Vert }_{\infty }}q)-{{ \Vert {{w}_{n}} \Vert }_{\infty }}q)+q(t), \\ {q}''(t)=\frac{1}{{{ \Vert {{w}_{n}} \Vert }_{\infty }}}(1-{{ \lambda }_{n}})(\bar{\varphi}(t,{{ \Vert {{w}_{n}} \Vert }_{ \infty }}p,{{ \Vert {{w}_{n}} \Vert }_{\infty }}q)-{{ \Vert {{w}_{n}} \Vert }_{\infty }}p)+p(t), \\ p(a)=p(b)=q(a)=q(b)=0. \end{cases} $$

Since \({{z}_{n}} \in {{C}^{2}} ( [ a,b ],{{\mathbb{R}}^{2}} )\), we deduce \({{ \Vert {{z}_{n}} \Vert }_{\infty }}=1\) and \({{ \Vert {{{{z}'}}_{n}} \Vert }_{\infty }}\) is bounded. We have that \(\tilde{z}= ( \tilde{p},\tilde{q} )\) with \({{ \Vert {\tilde{z}} \Vert }_{\infty }}=1\) and \(\tilde{\lambda }\in [ 0,1 ]\) by a compactness argument, such that the following subsequence converges:

$$ \mathop{\lim }_{n\to \infty } {{ \Vert {{z}_{n}}- \tilde{z} \Vert }_{\infty }}=0,\qquad \mathop{\lim }_{n\to \infty } {{\lambda }_{n}}= \tilde{\lambda }, $$

where \(\tilde{z}\in {{C}^{2}} ( [ a,b ],{{\mathbb{R}}^{2}} )\).

By the limit as \(n\to \infty \), we get that \(\tilde{z}= ( \tilde{p},\tilde{q} )\) is a solution of the system

$$ \textstyle\begin{cases} {\tilde{p}}''(t)=\tilde{q}(t), \\ {\bar{q}}''(t)=\tilde{p}(t), \\ \tilde{p}(a)=\tilde{p}(b)=\tilde{q}(a)=\tilde{q}(b)=0. \end{cases} $$

Since this problem only has a trivial solution, which contradicts \({{ \Vert {\tilde{z}} \Vert }_{\infty }}=1\), there is an \(R>0\) such that for every w of problem \(( {{{P}}_{\lambda }} )\) it satisfies \({{ \Vert w \Vert }_{\infty }}< R\).

Define the linear operator \(L:{{C}^{2}} ( [ a,b ],{{\mathbb{R}}^{2}} ) \to {C} ( [ a,b ],{{\mathbb{R}}^{2}} )\),

$$ L\begin{pmatrix} {y}_{1} ( t ) \\ {y}_{2} ( t ) \end{pmatrix}=\begin{pmatrix} {{y}_{1}}'' ( t ) \\ {{y}_{2}}'' ( t ) \end{pmatrix}, $$

and the nonlinear operator \({{N}_{\lambda }}:{{C}^{2}} ( [ a,b ],{{\mathbb{R}}^{2}} )\to {{C}^{2}} ( [ a,b ],{{\mathbb{R}}^{2}} )\),

$$ {{N}_{\lambda }}\begin{pmatrix} {y}_{1}(t) \\ {y}_{2}(t) \end{pmatrix}=\begin{pmatrix} \lambda {y}_{2}+(1-\lambda )\bar{\psi}(t,{y}_{1},{y}_{2}) \\ \lambda {y}_{1}+(1-\lambda )\bar{\varphi}(t,{y}_{1},{y}_{2}) \end{pmatrix}. $$

Therefore, problem \(( {{P}_{\lambda }} )\) is rewritten as

$$ Lw={{N}_{\lambda }}w, $$

where \(w=({y}_{1},{y}_{2})\). The operator \({{N}_{\lambda }}\) is L-completely continuous by coincidence degree theory [14], and the degree \({{D}_{L}} ( L-{{N}_{\lambda }},{{B}_{R}} )\) is well defined and its value is independent of \(\lambda \in [ 0,1 ]\).

Since \(( {{P}_{1}} )\) is a linear problem with only one trivial solution,

$$ {{D}_{L}} ( L-{{N}_{0}},{{B}_{R}} )={{D}_{L}} ( L-{{N}_{1}},{{B}_{R}} )=\pm 1. $$

Therefore problem \((\bar{P})\) has a solution.

Step 2: Prove that the solution of problem \((\bar{P})\) satisfies (8).

To argue with contradictions, for \(a\le {{a}_{1}}\le {{b}_{1}}\le b\), we assume that \({y}_{2}(t)>{{{y}_{2}}_{\underline{B} }}(t)\) for every \(t\in ({{a}_{1}},{{b}_{1}})\) and \({y}_{2}(t)\le {{{y}_{2}}_{\underline{B} }}(t)\) for every \(t\in { [ a,b ]}/{ ( {{a}_{1}},{{b}_{1}} )} \).

For every \(t\in [ a,b ]\), define \(H(t)={y}_{2}(t)-{{{y}_{2}}_{\underline{B} }}(t)\). It follows that

$$ {H}''(t)={{y}_{2}}''(t)-{{{y}_{2}}_{\underline{B} }''}(t)= \bar{\varphi}\bigl(t,{y}_{1}(t),{y}_{2}(t) \bigr)-{{{y}_{2}}_{\underline{B} }''}(t). $$

Furthermore, by \(({{A}_{2}})\) and \(({{A}_{3}})\), one has

Hence, for every \(t\in [ a,b ]\), \({H}''(t)\ge 0\). It follows from the convexity of \(H(t)\) and (5) that \({y}_{2}(t)\le {{{y}_{2}}_{\underline{B} }}(t)\) for every \(t\in [ a,b ]\), which contradicts our assumption. Similarly, for every \(t\in [ a,b ]\), we obtain that \({y}_{2}(t)\ge {{{y}_{2}}_{\bar{A} }}(t)\).

To argue with contradictions, for \(a\le {{a}_{2}}\le {{b}_{2}}\le b\), we assume that \({y}_{1}(t)<\underline{B} (t)\) for every \(t\in ( {{a}_{2}},{{b}_{2}} )\) and \({y}_{1}(t)\ge \underline{B} (t)\) for every \(t\in { [ a,b ]}/{ ( {{a}_{1}},{{b}_{1}} )} \).

For every \(t\in [ a,b ]\), defining \(K(t)={y}_{1}(t)-\underline{B} (t)\). It follows that

$$ {K}''(t)={{y}_{1}}''(t)-{ \underline{B} }''(t)=\bar{\psi}(t,{y}_{1},{y}_{2})-{ \underline{B} }''(t). $$

Furthermore, by \(({{A}_{1}})\), one has

Hence, for every \(t\in [ a,b ]\), \({K}''(t)\le 0\). It follows from the concavity of \(K(t)\) and (5) that \({y}_{1}(t)\ge \underline{B} (t)\) for every \(t\in [ a,b ]\), which contradicts our assumption. Similarly, for every \(t\in [ a,b ]\), we obtain that \({y}_{1}(t)\le \bar{A} (t)\).

Therefore, the solution of problem \((\bar{P})\) satisfies (8). By combining Step 1 and Step 2, we can obtain problem \((P)\) has a solution that satisfies (8). □

3 Some examples

Example 1

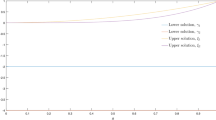
Consider the second-order coupled system

$$ \textstyle\begin{cases} {{y}_{1}}''=\frac{1}{1+{{e}^{-{y}_{2}}}}+{{e}^{-\frac{{y}_{1}}{10}}}+t, \\ {{y}_{2}}''=\frac{1}{1+{{e}^{-{y}_{1}}}}+{{e}^{-\frac{{y}_{2}}{10}}}+t, \\ {y}_{1}(0)={y}_{1}(1)={y}_{2}(0)={y}_{2}(1)=0, \end{cases} $$
(9)

where \(t\in [0,1]\). We find \(\bar{A} (t)=-4{{t}^{2}}+6\) and \(\underline{B} (t)=4{{t}^{2}}-6\) are the upper and lower solutions of (9) respectively, and that \({{v}_{\underline{B} }}(t)=-4{{t}^{2}}+6\) and \({{v}_{\bar{A} }}(t)=4{{t}^{2}}-6\) satisfy Theorem 1.

Since (9) satisfies all the assumptions in Theorem 1, we can get that problem (9) has a solution that satisfies

$$ 4{{t}^{2}}-6\le {y}_{1}(t)\le -4{{t}^{2}}+6,\qquad 4{{t}^{2}}-6\le {y}_{2}(t) \le -4{{t}^{2}}+6. $$

Example 2

Consider the second-order coupled system

$$ \textstyle\begin{cases} {{y}_{1}}''=\frac{1}{1+{{e}^{-{y}_{2}}}}-\frac{{{{y}_{1}}^{3}}}{26}+{{t}^{2}}, \\ {{y}_{2}}''=\frac{1}{1+{{e}^{-{y}_{1}}}}-\frac{{{{y}_{2}}^{3}}}{26}+{{t}^{2}}, \\ {y}_{1}(0)={y}_{1}(1)={y}_{2}(0)={y}_{2}(1)=0, \end{cases} $$
(10)

where \(t\in [0,1]\). We find \(\bar{A} (t)=-4{{t}^{2}}+\sin \frac{\pi }{2}t+5\) and \(\underline{B} (t)=4{{t}^{2}}-\sin \frac{\pi }{2}t-5\) are the upper and lower solutions of (10) respectively, and that \({{v}_{\underline{B} }}(t)=-3{{t}^{2}}+t+4\) and \({{v}_{\bar{A} }}(t)=3{{t}^{2}}-t-4\) satisfy Theorem 1.

Since (10) satisfies all the assumptions in Theorem 1, we can get that problem (10) has a solution that satisfies

$$ 4{{t}^{2}}-\sin \frac{\pi }{2}t-5\le {y}_{1}(t)\le -4{{t}^{2}}+\sin \frac{\pi }{2}t+5,\qquad 3{{t}^{2}}-t-4\le {y}_{2}(t)\le -3{{t}^{2}}+t+4. $$