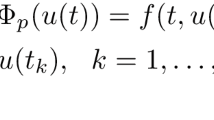Positive solutions for nonlinear double impulsive differential equations with p-Laplacian on infinite intervals

Abstract

In this paper, we investigate nonlinear second-order double impulsive differential equations integral boundary value problem with p-Laplacian on an infinite interval with the infinite number of impulsive times. Based on the cone theory and monotone iterative technique, we establish the existence of minimal nonnegative solution and iteration of positive solutions for such a boundary value problem. The main results are new and extend the existing results. At last, some examples are worked out to demonstrate the use of the main results.

1 Introduction

Boundary value problems on infinite intervals appear often in applied mathematics and physics, for example, in the study of the unsteady flow of a gas through semi-infinite porous medium, in analyzing the heat transfer in radial flow between circular disks, in the study of plasma physics, and in an analysis of the mass transfer on a rotating disk in non-Newtonian fluid, see [1, 2] and the references therein. For extensive applications, this kind of BVPs attract lots of scholars to devote themselves to develo** them. Scholars do some work and apply many techniques to deal with such problems, see [3–10] and the references therein. While boundary value problems with integral boundary conditions for ordinary differential equations on an infinite interval also arise in different fields such as heat conduction, chemical engineering, underground water flow, thermoelasticity, and plasma physics. In the past few years, many people have started to be active in studying the existence of the solutions to nonlinear integral boundary value problems (IBVPs) on infinite intervals. Some conclusions appeared in the meantime, see [11–18] and the references therein.

Considering the theory of impulsive differential equations, it has been emerging as an important area of investigation in recent years and has been extensively applied in chemical technology, population dynamics, and so on. It is much wider because all the structure of its emergence has deep physical background and realistic mathematical model and coincides with many phenomena in nature. For an introduction of the basic theory of impulsive differential equations in $R^{n}$, see [19–21] and the references therein.

We notice that there has been increasing interest in studying nonlinear differential equation and impulsive integro differential equation on an infinite interval with an infinite number of impulsive times to identify a few, see [22–26] and the references therein. There are relatively few papers available for integral boundary value problems for impulsive differential equations on an infinite interval with an infinite number of impulsive times up to now, see [27–31] and the references therein.

Recently, in [32], Zhang et al. investigated the existence of minimal nonnegative solution for the following second-order impulsive differential equation IBVP:

$$\begin{aligned} \left \{ \textstyle\begin{array}{@{}l} -x''(t)=f(t,x(t),x'(t)),\quad t\in J, t\neq t_{k}, \\ \Delta x|_{t=t_{k}}=I_{k}(x(t_{k})), \quad k=1,2,\ldots, \\ \Delta x'|_{t=t_{k}}=\overline{I}_{k}(x(t_{k})), \quad k=1,2,\ldots, \\ x(0)= \int_{0}^{+\infty}g(t)x(t)\,dt,\qquad x'(\infty )=0, \end{array}\displaystyle \right . \end{aligned}$$

where $f\in C(J\times J\times J,J)$, $I_{k}, \overline{I}_{k} \in C(R,R)$, $J=[0,+\infty)$, $0=t_{0}< t_{1}<\cdots<t_{k}<\cdots$, $t_{k}\rightarrow\infty$ for $k=1,2,\ldots$ , and $g(t)\in L[J,J]$ with $0< \int_{0}^{+\infty}g(t)\,dt<1$. $\Delta x|_{t_{k}}$ denotes the jump of $x(t)$ at $t=t_{k}$, that is,

$$\Delta x|_{t=t_{k}}=x\bigl(t_{k}^{+}\bigr)-x\bigl(t_{k}^{-}\bigr), $$

where $x(t_{k}^{+})$ and $x(t_{k}^{-})$ represent the right-hand limit and left-hand limit of $x(t)$ at $t=t_{k}$, respectively, $\Delta x'|_{t_{k}}$ has a similar meaning to $x'(t)$.

More recently, in [33], Zhang studied the existence and iteration of positive solutions for nonlinear second-order impulsive IBVP with p-Laplacian on infinite intervals

$$\begin{aligned} \left \{ \textstyle\begin{array}{@{}l} (\phi_{p}(x'(t)))'+q(t)f(t,x(t),x'(t)),\quad t\in J'_{+}, \\ \Delta x|_{t=t_{k}}=I_{k}(x(t_{k})), \quad k=1,2,\ldots, \\ x(0)= \int_{0}^{+\infty}g(t)x(t)\,dt, \qquad x'(\infty)=x_{\infty}, \end{array}\displaystyle \right . \end{aligned}$$

where $\phi_{p}(s)=|s|^{p-2}s$, $p>1$, $J=[0,+\infty)$, $J_{+}=(0,+\infty)$, $J'_{+}=J_{+}\backslash\{t_{1},t_{2},\ldots,t_{k},\ldots \}$, $0< t_{1}< t_{2}<\cdots<t_{k}<\cdots$, $t_{k}\rightarrow\infty$ for $k=1,2,\ldots$ , and $g(t)\in L[J,J]$ with $\int_{0}^{+\infty}g(t)\,dt<1$, $\int_{0}^{+\infty}tg(t)\,dt<\infty$, and $0 \leq x'(\infty)=\lim_{t\rightarrow+\infty}x'(t)$.

However, to the authors’ knowledge, the corresponding theory for double impulsive integral boundary value problems with p-Laplacian operator and infinite impulsive times on infinite intervals has not been considered till now. Motivated by the above mentioned works, in this paper, we study the existence of solutions for nonlinear double impulsive IBVPs of second-order differential equations with p-Laplacian on an infinite interval

$$\begin{aligned} \left \{ \textstyle\begin{array}{@{}l} (\phi_{p}(x'(t)))'+a(t)f(t,x(t),x'(t))=0,\quad t\in J, t\neq t_{k}, \\ \Delta x|_{t=t_{k}}=I_{k}(x(t_{k})), \quad k=1,2,\ldots, \\ \Delta\phi_{p}(x')|_{t=t_{k}}=\overline {I}_{k}(x(t_{k})), \quad k=1,2,\ldots, \\ x(0)= \int_{\eta}^{+\infty}g(t)x(t)\,dt,\qquad x'(\infty )=0, \end{array}\displaystyle \right . \end{aligned}$$

(1.1)

where $\phi_{p}(s)=|s|^{p-2}s$, $p>1$, $\eta\geq0$ is a constant, $f\in C(J^{3},J)$, $J=[0,+\infty)$, $0=t_{0}< t_{1}<\cdots<t_{k}<\cdots$, $t_{k}\rightarrow\infty$ for $k=1,2,\ldots$ and note $J_{0}=[0,t_{1}]$ and $J_{i}=(t_{i},t_{i+1}]$ ($i=1,2,\ldots$), $g(t)\in L^{1}[J,J]$ with $\int_{\eta}^{+\infty}g(t)\,dt<1$, $\int_{\eta }^{+\infty}tg(t)\,dt<+\infty$, $I_{k}, \overline{I}_{k} \in C(R,R)$, and

$$\begin{aligned} \Delta x|_{t=t_{k}}=x\bigl(t_{k}^{+}\bigr)-x \bigl(t_{k}^{-}\bigr), \qquad \Delta \phi_{p} \bigl(x'\bigr)|_{t=t_{k}}= \phi_{p} \bigl(x'\bigl(t_{k}^{+}\bigr)\bigr)- \phi_{p}\bigl(x'\bigl(t_{k}^{-}\bigr) \bigr). \end{aligned}$$

It is clear that

$$\begin{aligned}& \phi_{p}(s+t)\leq \left \{ \textstyle\begin{array}{@{}l@{\quad}l} 2^{p-1}(\phi_{p}(s)+\phi_{p}(t)), & p\geq2, s,t>0, \\ \phi_{p}(s)+\phi_{p}(t), & 1< p< 2, s,t>0, \end{array}\displaystyle \displaystyle \displaystyle \right . \end{aligned}$$

(1.2)

$$\begin{aligned}& \phi_{p}^{-1}(s+t)\leq \left \{ \textstyle\begin{array}{@{}l@{\quad}l} 2^{\frac{1}{p-1}}(\phi_{p}^{-1}(s)+\phi_{p}^{-1}(t)), & p\geq 2, s,t>0, \\ \phi_{p}^{-1}(s)+\phi_{p}^{-1}(t), & 1< p< 2, s,t>0. \end{array}\displaystyle \displaystyle \displaystyle \right . \end{aligned}$$

(1.3)

Throughout this paper, we adopt the following assumptions:

(H₁):

Suppose that $f\in C[J\times J\times J,J]$, and there exist $p,q,r\in C(J,J)$ such that

$$f(t,u,v)\leq p(t)\phi_{p}(u)+q(t)\phi_{p}(v)+r(t), \quad \forall t\in J\mbox{ and } \forall u,v\in J, $$

and note

$$\begin{aligned}& p^{*}= \int_{0}^{+\infty }a(t)p(t) (1+t)^{p-1}\,dt< +\infty,\qquad q^{*}= \int _{0}^{+\infty}a(t)q(t)\,dt< +\infty, \\& r^{*}= \int_{0}^{+\infty}a(t)r(t)\,dt< + \infty. \end{aligned}$$

(H₂):

$I_{k},\overline{I}_{k}\in C(J,J)$ and there exist nonnegative constants $a_{k}\geq0$, $b_{k}\geq0$, $c_{k}\geq0$, $d_{k}\geq0$ such that

$$\begin{aligned}& 0\leq I_{k}(u)\leq a_{k}u+b_{k}, \quad\forall u \in J\ (k=1,2,3,\ldots), \\& 0\leq\overline{I}_{k}(u)\leq c_{k}\phi _{p}(u)+d_{k}, \quad \forall u\in J\ (k=1,2,3,\ldots) \end{aligned}$$

and note

$$\begin{aligned}& a^{*}=\sum_{k=1}^{\infty}(t_{k}+1)a_{k}< + \infty,\qquad b^{*}=\sum_{k=1}^{\infty}b_{k}< + \infty, \\& c^{*}=\sum_{k=1}^{\infty }(t_{k}+1)^{p-1}c_{k}< + \infty,\qquad d^{*}=\sum_{k=1}^{\infty}d_{k}< + \infty, \end{aligned}$$

with $a^{*}<(1/3)(1-\int_{\eta}^{\infty}g(t)\,dt)$ and $c^{*}<\phi_{p}(1/(3n))$, where n is a constant and it firstly appears in (3.12).

(H₃):

$f(t,u_{1},v_{1})\leq f(t,u_{2},v_{2})$, $I_{k}(u_{1})\leq I_{k}(u_{2})$, $\overline{I}_{k}(u_{1})\leq \overline{I}_{k}(u_{2})$ for $t\in J$, $u_{1}\leq u_{2}$, $v_{1}\leq v_{2}$ ($k=1,2,3,\ldots$).

(H₄):

Suppose that $f\in C[J\times J\times J,J]$, $f(t,0,0)\neq0$ on any subinterval of J, and u, v are bounded, $f(t,(1+t)u,v)$ is bounded on J.

(H₅):

$a(t)$ is a nonnegative measurable function defined in $J\backslash\{0\}$, and $a(t)$ does not identically vanish on any subinterval of $J\backslash\{0\}$, and

$$\begin{aligned}& 0< \int_{0}^{+\infty}a(t)\,dt< +\infty,\qquad 0< \int _{0}^{+\infty}\phi_{p}^{-1}\biggl( \int_{t}^{+\infty}a(s)\,ds\biggr)\,dt< +\infty. \end{aligned}$$

2 Preliminary results

In this section, we firstly present some definitions and lemmas, which will be needed in the proof of the main results.

Definition 2.1

Let E be a real Banach space. A nonempty closed set $P\subset E$ is said to be a cone provided that

• (1) $au+bv\in P$ for all $u,v\in P$ and all $a\geq0$, $b\geq0$,

• (2) $u,-u\in P$ implies that $u=0$.

Definition 2.2

A map $\alpha:P\rightarrow[0,+\infty)$ is said to be concave on P if

$$\alpha\bigl(tu+(1-t)v\bigr)\geq\alpha(u)+(1-t)\alpha(v)\quad \mbox{for all }u,v \in P\mbox{ and }t\in[0,1]. $$

Definition 2.3

(see [8])

Let $V=\{x\in X:\|x\|< l\}$ ($l>0$), $V_{1}:=\{\frac{x(t)}{1+t},x\in V\}\cup\{x'(t),x\in V\}$ is called equiconvergent at infinity if and only if for all $\varepsilon>0$, there exists $T=T(\varepsilon)>0$ such that for all $x\in V_{1}$, the following holds:

$$\begin{aligned} \biggl|\frac{x(t_{1})}{1+t_{1}}-\frac{x(t_{2})}{1+t_{2}} \biggr|< \varepsilon, \qquad\bigl|x'(t_{1})-x'(t_{2})\bigr|< \varepsilon, \quad \mbox{for all }t_{1}, t_{2}\geq T. \end{aligned}$$

Lemma 2.4

(see [34, 35])

If $\{\frac{x(t)}{1+t},x\in V\}$ and $\{x'(t),x\in V\}$ are both equicontinuous on any compact intervals of $[0,+\infty)$ and equiconvergent at infinity, then V is relatively compact on X.

Definition 2.5

Let $J'=J\setminus\{t_{1},t_{2},\ldots t_{k},\ldots\}$, $x\in E\cap C^{2}[J',R]$ is called a nonnegative solution of IBVP (1.1) if $x(t)\geq0$, $x'(t)\geq0$ and $x(t)$ satisfies IBVP (1.1). Moreover, $\overline{x}(t)$ is called a minimal nonnegative solution if x is an arbitrary nonnegative solution of (1.1), then $x(t)\geq \overline{x}(t)$, $x'(t)\geq\overline{x}'(t)$ for all $t\in J'$.

Let

$$\begin{aligned}& \begin{aligned}[b] PC[J,R]={}&\bigl\{ x:x\mbox{ is a map from }J\mbox{ into }R \mbox{ such that }x(t) \mbox{ is continuous at }t\neq t_{k}, \\ &{}\mbox{left continuous at }t=t_{k}\mbox{ and } x \bigl(t_{k}^{+}\bigr)\mbox{ exist for }k=1,2,\ldots\bigr\} , \end{aligned} \\& \begin{aligned}[b] PC^{1}[J,R]={}&\bigl\{ x\in PC[J,R]:x'(t) \mbox{ exists and is continuous at } t\neq t_{k}, \\ &{}\mbox{left continuous at }t=t_{k}\mbox{ and } x' \bigl(t_{k}^{+}\bigr)\mbox{ exist for }k=1,2,\ldots\bigr\} , \end{aligned} \\& E=\Bigl\{ x\in PC^{1}[J,R]:\sup_{t\in J} \bigl(\bigl|x(t)\bigr|/(1+t)\bigr)< \infty,\sup_{t\in J}\bigl|x'(t)\bigr|< \infty\Bigr\} \end{aligned}$$

with the norm $\|x\|=\max\{\|x\|_{1},\|x'\|_{\infty}\}$, where $\|x\|_{1}=\sup_{t\in J}\frac{|x(t)|}{1+t}$, $\|x'\|_{\infty}=\sup_{t\in J}|x'(t)|$. At the same time, define a cone $P\subset E$ by

$$P=\bigl\{ x\in E:x(t)\geq0,x'(t)\geq0\bigr\} . $$

Lemma 2.6

Suppose that (H₁), (H₂) hold. Then, for all $x\in P$, $\int_{0}^{+\infty}a(t)f(t,x(t),x'(t))\,dt$, $\sum_{k=1}^{\infty}I_{k}(x(t_{x}))$ and $\sum_{k=1}^{\infty}\overline{I}_{k}(x(t_{x}))$ are convergent.

Proof

By (H₁) and (H₂), we have

$$\begin{aligned}& f\bigl(t,x(t),x'(t)\bigr)\leq p(t) (1+t)^{p-1} \phi_{p}\biggl(\frac{x(t)}{1+t}\biggr)+q(t)\phi _{p} \bigl(x'(t)\bigr)+r(t), \\& I_{k}\bigl(x(t_{k})\bigr)\leq a_{k}(1+t_{k}) \frac {x(t_{k})}{1+t_{k}}+b_{k}, \\& \overline{I}_{k}\bigl(x(t_{k})\bigr)\leq c_{k}(1+t_{k})^{p-1}\phi_{p}\biggl( \frac {x(t_{k})}{1+t_{k}}\biggr)+d_{k}. \end{aligned}$$

Thus

$$\begin{aligned}& \int_{0}^{+\infty}a(t)f\bigl(t,x(t),x'(t) \bigr)\leq p^{*}\phi_{p}\bigl(\bigl\| x(t)\bigr\| _{1} \bigr)+q^{*}\phi_{p}\bigl(\bigl\| x(t)\bigr\| _{\infty} \bigr)+r^{*}< \infty, \\& \sum_{k=1}^{\infty}I_{k} \bigl(x(t_{k})\bigr)\leq a^{*}\bigl\| x(t)\bigr\| _{1}+b^{*}< \infty, \\& \sum_{k=1}^{\infty}\overline{I}_{k} \bigl(x(t_{k})\bigr)\leq c^{*}\phi_{p}\bigl( \bigl\| x(t)\bigr\| _{1}\bigr)+d^{*}< \infty. \end{aligned}$$

The proof is complete. □

Lemma 2.7

Let $y(t)\in L^{1}[0,+\infty)$ and $\int_{\eta}^{+\infty}g(t)\,dt<1$, then the IBVP

$$\begin{aligned} \left \{ \textstyle\begin{array}{@{}l} (\phi_{p}(x'(t)))'=-y(t),\quad t\in J, t\neq t_{k}, \\ \Delta x|_{t=t_{k}}=I_{k}(x(t_{k})), \quad k=1,2,\ldots,\\ \Delta\phi_{p}(x')|_{t=t_{k}}=\overline {I}_{k}(x(t_{k})), \quad k=1,2,\ldots, \\ x(0)= \int_{\eta}^{+\infty}g(t)x(t)\,dt,\qquad x'(\infty )=0, \end{array}\displaystyle \right . \end{aligned}$$

(2.1)

has a unique solution

$$\begin{aligned} x(t) =&\frac{1}{1-\int_{\eta}^{+\infty}g(t)\,dt} \biggl[\sum _{t_{i}< t}\int_{t_{i-1}}^{t_{i}} \phi_{p}^{-1} \biggl(\int_{s}^{+\infty}y( \tau)\,d\tau-\sum_{t_{k}\geq s}\overline{I}_{k} \bigl(x(t_{k})\bigr) \biggr)\,ds \\ &{}+\int_{\eta}^{+\infty}g(t)\int_{t_{i}}^{t} \phi_{p}^{-1} \biggl(\int_{s}^{+\infty}y( \tau)\,d\tau-\sum_{t_{k}\geq s}\overline{I}_{k} \bigl(x(t_{k})\bigr) \biggr)\,ds\,dt +\sum_{t_{i}< t}I_{i}\bigl(x(t_{i}) \bigr) \biggr] \\ &{}+\int_{t_{i}}^{t}\phi_{p}^{-1} \biggl(\int_{s}^{+\infty}y(\tau)\,d\tau-\sum _{t_{k}\geq s}\overline{I}_{k}\bigl(x(t_{k}) \bigr) \biggr)\,ds. \end{aligned}$$

(2.2)

Proof

For $t\in[0,t_{1}]$, integrating (2.1) from 0 to t, we have

$$\begin{aligned} \int_{0}^{t}\bigl(\phi_{p} \bigl(x'(\tau)\bigr)\bigr)'\,d\tau=-\int _{0}^{t}y(\tau)\,d\tau. \end{aligned}$$

That is,

$$\begin{aligned} \phi_{p}\bigl(x'(t)\bigr)= \phi_{p}\bigl(x'(0)\bigr)-\int_{0}^{t}y( \tau)\,d\tau, \end{aligned}$$

(2.3)

which implies that

$$\begin{aligned} \phi_{p}\bigl(x'\bigl(t_{1}^{-} \bigr)\bigr)=\phi_{p}\bigl(x'(0)\bigr)-\int _{0}^{t_{1}}y(\tau)\,d\tau. \end{aligned}$$

(2.4)

For $t\in[t_{1},t_{2}]$, integrating (2.1) from $t_{1}$ to t, we have

$$\begin{aligned} \int_{t_{1}}^{t}\bigl(\phi_{p} \bigl(x'(\tau)\bigr)\bigr)'\,d\tau=-\int _{t_{1}}^{t}y(\tau)\,d\tau. \end{aligned}$$

That is,

$$\begin{aligned} \phi_{p}\bigl(x'(t)\bigr)= \phi_{p}\bigl(x'\bigl(t_{1}^{+}\bigr) \bigr)-\int_{t_{1}}^{t}y(\tau)\,d\tau. \end{aligned}$$

(2.5)

Adding (2.4) and (2.5) together, we have

$$\begin{aligned} \phi_{p}\bigl(x'(t)\bigr)= \phi_{p}\bigl(x'(0)\bigr)-\int_{0}^{t}y( \tau)\,d\tau+\overline {I}_{1}\bigl(x(t_{1})\bigr). \end{aligned}$$

(2.6)

Repeating the previous process, for any $t\in[0,+\infty)$, we get that

$$\begin{aligned} \phi_{p}\bigl(x'(t)\bigr)= \phi_{p}\bigl(x'(0)\bigr)-\int_{0}^{t}y( \tau)\,d\tau+\sum_{t_{k}< t}\overline{I}_{k} \bigl(x(t_{k})\bigr). \end{aligned}$$

(2.7)

Taking limit for $t\rightarrow+\infty$, by the boundary condition, we have

$$\begin{aligned} x'(t)=\phi_{p}^{-1} \biggl(\int _{t}^{+\infty}y(\tau)\,d\tau-\sum _{t_{k}\geq t}\overline{I}_{k}\bigl(x(t_{k}) \bigr) \biggr). \end{aligned}$$

(2.8)

For $t\in[0,t_{1}]$, integrating (2.8) from 0 to t, we have

$$\begin{aligned} x(t)=x(0)+\int_{0}^{t} \phi_{p}^{-1} \biggl(\int_{s}^{+\infty}y( \tau)\,d\tau -\sum_{t_{k}\geq s}\overline{I}_{k} \bigl(x(t_{k})\bigr) \biggr)\,ds, \end{aligned}$$

(2.9)

which implies that

$$\begin{aligned} x\bigl(t_{1}^{-}\bigr)=x(0)+\int _{0}^{t_{1}}\phi_{p}^{-1} \biggl( \int_{s}^{+\infty }y(\tau)\,d\tau-\sum _{t_{k}\geq s}\overline{I}_{k}\bigl(x(t_{k}) \bigr) \biggr)\,ds. \end{aligned}$$

(2.10)

For $t\in[t_{1},t_{2}]$, integrating (2.8) from $t_{1}$ to t, we have

$$\begin{aligned} x(t)=x\bigl(t_{1}^{+}\bigr)+\int _{t_{1}}^{t}\phi_{p}^{-1} \biggl( \int_{s}^{+\infty }y(\tau)\,d\tau-\sum _{t_{k}\geq s}\overline{I}_{k}\bigl(x(t_{k}) \bigr) \biggr)\,ds. \end{aligned}$$

(2.11)

Adding (2.10) and (2.11) together, we have

$$ \begin{aligned}[b] x(t)={}&x(0)+\int_{0}^{t_{1}} \phi_{p}^{-1} \biggl(\int_{s}^{+\infty}y( \tau )\,d\tau-\sum_{t_{k}\geq s}\overline{I}_{k} \bigl(x(t_{k})\bigr) \biggr)\,ds\\ &{} +\int_{t_{1}}^{t}\phi_{p}^{-1} \biggl(\int_{s}^{+\infty}y(\tau )\,d\tau-\sum _{t_{k}\geq s}\overline{I}_{k}\bigl(x(t_{k}) \bigr) \biggr)\,ds+I_{1}\bigl(x(t_{1})\bigr). \end{aligned} $$

(2.12)

Repeating the previous process, for any $t\in[0,+\infty)$, we get that

$$\begin{aligned} x(t) =&x(0)+ \sum_{t_{i}< t}\int _{t_{i-1}}^{t_{i}}\phi_{p}^{-1} \biggl( \int_{s}^{+\infty}y(\tau)\,d\tau-\sum _{t_{k}\geq s}\overline{I}_{k}\bigl(x(t_{k}) \bigr) \biggr)\,ds \\ &{}+\int_{t_{i}}^{t}\phi_{p}^{-1} \biggl(\int_{s}^{+\infty}y(\tau)\,d\tau-\sum _{t_{k}\geq s}\overline{I}_{k}\bigl(x(t_{k}) \bigr) \biggr)\,ds+\sum_{t_{i}< t}I_{i} \bigl(x(t_{i})\bigr). \end{aligned}$$

(2.13)

By (2.13) and the boundary condition, for any $t\in[0,+\infty)$, we have

$$\begin{aligned} x(t) =&\frac{1}{1-\int_{\eta}^{+\infty}g(t)\,dt} \biggl[\sum_{t_{i}< t}\int _{t_{i-1}}^{t_{i}}\phi_{p}^{-1} \biggl( \int_{s}^{+\infty}y(\tau)\,d\tau-\sum _{t_{k}\geq s}\overline{I}_{k}\bigl(x(t_{k}) \bigr) \biggr)\,ds \\ &{}+\int_{\eta}^{+\infty}g(t)\int_{t_{i}}^{t} \phi_{p}^{-1} \biggl(\int_{s}^{+\infty}y( \tau)\,d\tau-\sum_{t_{k}\geq s}\overline{I}_{k} \bigl(x(t_{k})\bigr) \biggr)\,ds\,dt +\sum_{t_{i}< t}I_{i}\bigl(x(t_{i}) \bigr) \biggr] \\ &{}+\int_{t_{i}}^{t}\phi_{p}^{-1} \biggl(\int_{s}^{+\infty}y(\tau)\,d\tau-\sum _{t_{k}\geq s}\overline{I}_{k}\bigl(x(t_{k}) \bigr) \biggr)\,ds. \end{aligned}$$

This completes the proof. □

Define an integral operator $T:P\rightarrow E$ by

$$\begin{aligned} (Tx) (t) =&\frac{1}{1-\int_{\eta}^{+\infty }g(t)\,dt} \\ &{}\times \biggl[\sum_{t_{i}< t}\int _{t_{i-1}}^{t_{i}}\phi_{p}^{-1} \biggl( \int_{s} ^{+\infty}a(\tau)f\bigl(\tau,x( \tau),x'(\tau)\bigr)\,d\tau-\sum_{t_{k}\geq s} \overline{I}_{k}\bigl(x(t_{k})\bigr) \biggr)\,ds \\ &{}+\int_{\eta}^{+\infty}g(t)\int_{t_{i}}^{t} \phi_{p}^{-1} \biggl(\int_{s}^{+\infty} a(\tau)f\bigl(\tau,x(\tau),x'(\tau)\bigr)\,d\tau-\sum _{t_{k}\geq s}\overline{I}_{k}\bigl(x(t_{k}) \bigr) \biggr)\,ds\,dt \\ &{}+\sum_{t_{i}< t}I_{i}\bigl(x(t_{i}) \bigr) \biggr] \\ &{}+\int_{t_{i}}^{t}\phi_{p}^{-1} \biggl(\int_{s}^{+\infty}a(\tau)f\bigl(\tau ,x( \tau),x'(\tau)\bigr)\,d\tau-\sum_{t_{k}\geq s} \overline{I}_{k}\bigl(x(t_{k})\bigr) \biggr)\,ds. \end{aligned}$$

(2.14)

Obviously, T is well defined and $x\in PC(J,R)$ is a solution of BVP (1.1) if and only if x is a fixed point of T.

Lemma 2.8

Assume that (H₁)-(H₃) hold. Then the operator T maps P into P, and

$$\begin{aligned} \|Tx\|\leq A\|x\|+B,\quad \forall x\in P. \end{aligned}$$

(2.15)

Moreover, for $x,y\in P$ with $x(t)\leq y(t)$, $x'(t)\leq y'(t)$, for all $t\in J$, and one has

$$\begin{aligned} (Tx) (t)\leq(Ty) (t), \qquad (Tx)'(t) \leq(Ty)'(t),\quad \forall t\in J, \end{aligned}$$

(2.16)

where

$$ \begin{aligned} &A=\frac{1}{1-\int_{\eta}^{\infty}g(t)\,dt} \biggl[a^{*}+\biggl(2+\int_{\eta }^{\infty}(t-1)g(t) \,dt\biggr)\Lambda_{1} \biggr], \\ &B=\frac{1}{1-\int_{\eta}^{\infty}g(t)\,dt} \biggl[b^{*}+\biggl(2+\int_{\eta }^{\infty}(t-1)g(t) \,dt\biggr)\Lambda_{2} \biggr],\\ &\Lambda_{1}=\left \{ \textstyle\begin{array}{@{}l@{\quad}l} \phi _{p}^{-1}(p^{*}+q^{*}+c^{*}), & 1< p< 2, \\ 2^{\frac{1}{p-1}}\phi_{p}^{-1}(p^{*}+q^{*}+c^{*}), & p\geq 2, \end{array}\displaystyle \displaystyle \displaystyle \right . \\ &\Lambda_{2}=\left \{ \textstyle\begin{array}{@{}l@{\quad}l} \phi_{p}^{-1}(r^{*}+d^{*}), & 1< p< 2, \\ 2^{\frac{1}{p-1}}(\phi_{p}^{-1}(r^{*}+d^{*})), & p\geq 2. \end{array}\displaystyle \displaystyle \displaystyle \displaystyle \displaystyle \displaystyle \displaystyle \displaystyle \displaystyle \displaystyle \displaystyle \right . \end{aligned} $$

(2.17)

Proof

Let $x\in P$. From the definition of T, (H₁)-(H₃) and (2.15), we can obtain that T is an operator from P to P, and

$$\begin{aligned} \frac{|(Tx)(t)|}{1+t} =&\frac{1}{1+t}\frac{1}{1-\int_{\eta}^{+\infty }g(t)\,dt} \\ &{}\times \biggl|\sum_{t_{i}< t}\int_{t_{i-1}}^{t_{i}} \phi_{p}^{-1} \biggl(\int_{s}^{+\infty}a( \tau)f\bigl(\tau,x(\tau),x'(\tau)\bigr)\,d\tau -\sum _{t_{k}\geq s}\overline{I}_{k}\bigl(x(t_{k}) \bigr) \biggr)\,ds \\ &{}+\int_{\eta}^{+\infty}g(t)\int_{t_{i}}^{t} \phi_{p}^{-1} \biggl(\int_{s}^{+\infty}a( \tau)f\bigl(\tau,x(\tau),x'(\tau)\bigr)\,d\tau -\sum _{t_{k}\geq s}\overline{I}_{k}\bigl(x(t_{k}) \bigr) \biggr)\,ds\,dt \\ &{}+\sum_{t_{i}< t}I_{i}\bigl(x(t_{i}) \bigr) \biggr| \\ &{}+\frac{1}{1+t} \biggl|\int_{t_{i}}^{t} \phi_{p}^{-1} \biggl(\int_{s}^{+\infty }a( \tau)f\bigl(\tau,x(\tau),x'(\tau)\bigr)\,d\tau-\sum _{t_{k}\geq s}\overline{I}_{k}\bigl(x(t_{k}) \bigr) \biggr)\,ds \biggr| \\ \leq& \frac{1}{1-\int_{\eta}^{+\infty }g(t)\,dt} \\ &{}\times \Biggl|\frac{1}{1+t}\int_{0}^{t} \phi_{p}^{-1} \Biggl(\int_{0}^{+\infty }a( \tau)f\bigl(\tau,x(\tau),x'(\tau)\bigr)\,d\tau +\sum _{k=1}^{\infty}\overline{I}_{k} \bigl(x(t_{k})\bigr) \Biggr)\,ds \\ &{}+\int_{\eta}^{+\infty}g(t)\int_{0}^{t} \phi_{p}^{-1} \Biggl(\int_{0}^{+\infty}a( \tau)f\bigl(\tau,x(\tau),x'(\tau)\bigr)\,d\tau +\sum _{k=1}^{\infty}\overline{I}_{k} \bigl(x(t_{k})\bigr) \Biggr)\,ds\,dt \\ &{}+\sum_{i=1}^{\infty}I_{i} \bigl(x(t_{i})\bigr) \Biggr| \\ &{}+\frac{1}{1+t} \biggl|\int_{t_{i}}^{t} \phi_{p}^{-1} \biggl(\int_{s}^{+\infty }a( \tau)f\bigl(\tau,x(\tau),x'(\tau)\bigr)\,d\tau-\sum _{t_{k}\geq s}\overline{I}_{k}\bigl(x(t_{k}) \bigr) \biggr)\,ds \biggr| \\ \leq&\frac{1}{1-\int_{\eta}^{+\infty}g(t)\,dt} \Biggl[\biggl(2+\int_{\eta}^{+\infty }(t-1)g(t) \,dt\biggr) \\ &{}\times\phi_{p}^{-1} \Biggl(\int_{0}^{+\infty}a( \tau)f\bigl(\tau ,x(\tau),x'(\tau)\bigr)\,d\tau +\sum _{k=1}^{\infty}\overline{I}_{k} \bigl(x(t_{k})\bigr) \Biggr) +\sum_{i=1}^{\infty}I_{i} \bigl(x(t_{i})\bigr) \Biggr]. \end{aligned}$$

(2.18)

Therefore,

$$\begin{aligned} \frac{|(Tx)(t)|}{1+t} \leq& \frac{1}{1-\int_{\eta}^{+\infty}g(t)\,dt} \biggl[\biggl(2+\int _{\eta}^{+\infty }(t-1)g(t)\,dt\biggr) \\ &{}\times\phi_{p}^{-1} \bigl(p^{*} \phi_{p}\bigl(\|x\|_{1}\bigr)+q^{*}\phi_{p}\bigl( \bigl\| x'\bigr\| _{\infty }\bigr)+r^{*}+c^{*} \phi_{p}\bigl(\|x\|_{1}\bigr)+d^{*} \bigr)\\ &{}+a^{*}\bigl( \|x\| _{1}\bigr)+b^{*} \biggr] \\ \leq& A\|x\|+B, \quad\forall t\in J. \end{aligned}$$

Direct differentiation of T implies, for $t\neq t_{k}$,

$$\begin{aligned} (Tx)'(t)=\phi_{p}^{-1}\biggl(\int _{t}^{+\infty}a(\tau)f\bigl(\tau,x(\tau),x'( \tau )\bigr)\,d\tau -\sum_{t_{k}\geq t}\overline{I}_{k} \bigl(x(t_{k})\bigr)\biggr). \end{aligned}$$

Thus, we have

$$\begin{aligned} \bigl|(Tx)'(t)\bigr|\leq\phi_{p}^{-1}\Biggl(\int _{0}^{+\infty}a(\tau)f\bigl(\tau ,x(\tau),x'( \tau)\bigr)\,d\tau +\sum_{i=1}^{\infty} \overline{I}_{k}\bigl(x(t_{k})\bigr)\Biggr)\leq A\|x\|+B, \quad\forall t\in J. \end{aligned}$$

It follows that (2.15) is satisfied and equation (2.16) is easily obtained by (H₃). □

Lemma 2.9

Let (H₂), (H₄), and (H₅) hold. Then $T:P\rightarrow P$ is completely continuous.

Proof

For any $x\in P$, by (2.14), we have

$$\begin{aligned}& \phi_{p}\bigl((Tx)'(t)\bigr)=\int_{t}^{+\infty}a( \tau)f\bigl(\tau,x(\tau),x'(\tau )\bigr)\,d\tau -\sum _{t_{k}\geq t}\overline{I}_{k}\bigl(x(t_{k}) \bigr), \end{aligned}$$

(2.19)

$$\begin{aligned}& \bigl(\phi _{p}\bigl((Tx)'(t)\bigr)\bigr)'=-a(t)f \bigl(t,x(t),x'(t)\bigr). \end{aligned}$$

(2.20)

It follows from (2.14), (2.19) and (H₄) that

$$\begin{aligned} (Tx) (t)\geq0,\qquad (Tx)'(t)\geq0, \qquad (Tx)''(t) \leq 0, \end{aligned}$$

that is, $T(P)\subset P$. Next, we divide the proof into two steps.

Step 1. We prove that T is continuous.

Let $x_{n}\rightarrow x$ as $n\rightarrow\infty$ in P, then there exists $r_{0}$ such that $\sup_{n\in N\setminus\{0\}}\|x\|< r_{0}$. Set $B_{r_{0}}=\sup\{f(t,(1+t)u,v), (t,u,v)\in J\times [0,r_{0}]^{2}\}$, and we have

$$\begin{aligned} \int_{0}^{+\infty}a(\tau)\bigl|f\bigl( \tau,x_{n}(\tau),x'_{n}(\tau)\bigr)-f\bigl(\tau ,x(\tau),x'(\tau)\bigr)\bigr|\,d\tau \leq2B_{r_{0}}\int _{0}^{+\infty}a(\tau)\,d\tau< +\infty. \end{aligned}$$

(2.21)

Therefore, by the Lebesgue dominated convergence theorem, we have

$$\begin{aligned} &\bigl|\phi_{p}\bigl((Tx_{n})'(t) \bigr)-\phi_{p}\bigl((Tx)'(t)\bigr)\bigr| \\ &\quad= \biggl|\int _{t}^{+\infty }a(\tau)f\bigl(\tau,x_{n}( \tau),x'_{n}(\tau)\bigr)\,d\tau -\sum _{t_{k}\geq t}\overline{I}_{k}(x_{n}(t_{k}) \\ &\qquad{}-\int_{t}^{+\infty}a(\tau)f\bigl(\tau,x( \tau),x'(\tau)\bigr)\,d\tau +\sum_{t_{k}\geq t} \overline{I}_{k}\bigl(x(t_{k})\bigr) \biggr| \\ &\quad\leq \int_{t}^{+\infty}a(\tau)\bigl|f\bigl( \tau,x_{n}(\tau),x'_{n}(\tau)\bigr)-f\bigl( \tau,x(\tau ),x'(\tau)\bigr)\bigr|\,d\tau +\sum _{t_{k}\geq t}\bigl|\overline{I}_{k}(x_{n}(t_{k})- \overline{I}_{k}(x(t_{k})\bigr| \\ &\quad\rightarrow 0 \quad (n\rightarrow\infty ). \end{aligned}$$

(2.22)

From above and (H₄), (H₅), we get

$$\begin{aligned} & \biggl|\frac{(Tx_{n})(t)}{1+t}-\frac{(Tx_{n})(t)}{1+t} \biggr| \\ &\quad=\frac{1}{1+t} \biggl|\frac{1}{1-\int_{\eta}^{+\infty }g(t)\,dt} \\ &\qquad{}\times \biggl[\sum_{t_{i}< t}\int _{t_{i-1}}^{t_{i}}\phi_{p}^{-1} \biggl( \int_{s}^{+\infty}a(\tau)f\bigl(\tau,x_{n}( \tau),x'_{n}(\tau)\bigr)\,d\tau -\sum _{t_{k}\geq s}\overline{I}_{k}\bigl(x_{n}(t_{k}) \bigr) \biggr)\,ds \\ &\qquad{}-\sum_{t_{i}< t}\int_{t_{i-1}}^{t_{i}} \phi_{p}^{-1} \biggl( \int_{s}^{+\infty}a( \tau)f\bigl(\tau,x(\tau),x'(\tau)\bigr)\,d\tau -\sum _{t_{k}\geq s}\overline{I}_{k}\bigl(x(t_{k}) \bigr)\biggr) \,ds \\ &\qquad{}+\int_{\eta}^{+\infty}g(t)\int _{t_{i}}^{t}\phi_{p}^{-1} \biggl( \int_{s}^{+\infty}a(\tau)f\bigl(\tau,x_{n}( \tau),x'_{n}(\tau)\bigr)\,d\tau-\sum _{t_{k}\geq s}\overline{I}_{k}\bigl(x_{n}(t_{k}) \bigr) \biggr)\,ds\,dt \\ &\qquad{}-\int_{\eta}^{+\infty}g(t)\int _{t_{i}}^{t}\phi_{p}^{-1} \biggl( \int_{s}^{+\infty}a(\tau)f\bigl(\tau,x( \tau),x'(\tau)\bigr)\,d\tau-\sum_{t_{k}\geq s} \overline{I}_{k}\bigl(x(t_{k})\bigr) \biggr)\,ds\,dt \\ &\qquad{}+\sum_{t_{i}< t}I_{i} \bigl(x_{n}(t_{i})\bigr)-\sum_{t_{i}< t}I_{i} \bigl(x(t_{i})\bigr) \biggr] \\ &\qquad{}+\int_{t_{i}}^{t}\phi_{p}^{-1} \biggl( \int_{s}^{+\infty}a(\tau)f\bigl( \tau,x_{n}(\tau),x'_{n}(\tau)\bigr)\,d\tau-\sum _{t_{k}\geq s}\overline{I}_{k}\bigl(x_{n}(t_{k}) \bigr) \biggr)\,ds \\ &\qquad{}-\int_{t_{i}}^{t}\phi_{p}^{-1} \biggl( \int_{s}^{+\infty}a(\tau)f\bigl(\tau,x( \tau),x'(\tau)\bigr)\,d\tau-\sum_{t_{k}\geq s} \overline{I}_{k}\bigl(x(t_{k})\bigr) \biggr)\,ds \biggr| \\ &\quad\leq \frac{1}{1-\alpha\int_{\eta}^{+\infty }g(t)\,dt} \biggl[\sum_{t_{i}< t}\int _{t_{i-1}}^{t_{i}} \biggl| \phi_{p}^{-1} \biggl(\int_{s}^{+\infty}a(\tau)f\bigl( \tau,x_{n}(\tau ),x'_{n}(\tau)\bigr)\,d\tau -\sum _{t_{k}\geq s}\overline{I}_{k}\bigl(x_{n}(t_{k}) \bigr) \biggr) \\ &\qquad{}-\phi_{p}^{-1} \biggl(\int_{s}^{+\infty}a( \tau)f\bigl(\tau,x(\tau),x'(\tau )\bigr)\,d\tau -\sum _{t_{k}\geq s}\overline{I}_{k}\bigl(x(t_{k}) \bigr) \biggr) \biggr|\,ds \\ &\qquad{}+\int_{\eta}^{+\infty}g(t)\int _{t_{i}}^{t} \biggl| \phi_{p}^{-1} \biggl(\int_{s}^{+\infty}a(\tau)f\bigl( \tau,x_{n}(\tau ),x'_{n}(\tau)\bigr)\,d\tau -\sum _{t_{k}\geq s}\overline{I}_{k}\bigl(x_{n}(t_{k}) \bigr) \biggr) \\ &\qquad{}-\phi_{p}^{-1} \biggl(\int_{s}^{+\infty}a( \tau)f\bigl(\tau,x(\tau),x'(\tau )\bigr)\,d\tau -\sum _{t_{k}\geq s}\overline{I}_{k}\bigl(x(t_{k}) \bigr) \biggr) \biggr|\,ds\,dt \\ &\qquad{}+\sum_{t_{i}< t} \bigl|I_{i} \bigl(x_{n}(t_{i})\bigr)-I_{i} \bigl(x(t_{i})\bigr) \bigr| \biggr] \\ &\qquad{}+\int_{t_{i}}^{t} \biggl|\phi_{p}^{-1} \biggl(\int_{s}^{+\infty}a(\tau )f\bigl( \tau,x_{n}(\tau),x'_{n}(\tau)\bigr)\,d\tau-\sum _{t_{k}\geq s}\overline{I}_{k}\bigl(x_{n}(t_{k}) \bigr) \biggr) \\ &\qquad{}-\phi_{p}^{-1} \biggl(\int_{s}^{+\infty}a( \tau)f\bigl(\tau,x(\tau),x'(\tau )\bigr)\,d\tau-\sum _{t_{k}\geq s}\overline{I}_{k}\bigl(x(t_{k}) \bigr) \biggr) \biggr|\,ds \\ &\quad\rightarrow0 \quad (n\rightarrow\infty ), \end{aligned}$$

and

$$\begin{aligned} &\bigl|(Tx_{n})'(t)-(Tx)'(t)\bigr| \\ &\quad= \biggl|\phi_{p}^{-1} \biggl(\int_{t}^{+\infty}a( \tau)f\bigl(\tau,x_{n}(\tau ),x'_{n}(\tau)\bigr) \,d\tau -\sum_{t_{k}\geq t}\overline{I}_{k} \bigl(x_{n}(t_{k})\bigr) \biggr) \\ &\qquad{}-\phi_{p}^{-1} \biggl(\int_{t}^{+\infty}a( \tau)f\bigl(\tau,x(\tau),x'(\tau )\bigr)\,d\tau -\sum _{t_{k}\geq t}\overline{I}_{k}\bigl(x(t_{k}) \bigr) \biggr) \biggr| \\ &\quad\rightarrow0 \quad (n\rightarrow \infty ). \end{aligned}$$

We can easily get $\|Tx_{n}-Tx\|\rightarrow 0$ ($n\rightarrow\infty$). Hence, T is continuous.

Step 2. We prove that T is compact provided that it maps bounded sets into relatively compact sets.

First, let Ω be a bounded subset of P, then there exists $r>0$ such that $\|x\|< r$ for all $x\in\Omega$. By (2.18), we have

$$\begin{aligned} \frac{|(Tx)(t)|}{1+t} \leq&\frac{1}{1-\int_{\eta}^{+\infty }g(t)\,dt} \\ &{}\times\biggl[\biggl(2+\int_{\eta}^{+\infty}(t-1)g(t)\,dt\biggr) \phi_{p}^{-1} \biggl(B_{r}\int _{0}^{+\infty}a(\tau)\,d\tau+c^{*}\phi _{p}(r)+d^{*} \biggr)\\ &{}+a^{*}r+b^{*} \biggr] :=R_{1}, \end{aligned}$$

and

$$\begin{aligned} \bigl|(Tx)'(t)\bigr| =& \biggl|\phi_{p}^{-1} \biggl(\int _{s}^{+\infty}a(\tau)f\bigl(\tau ,x(\tau),x'( \tau)\bigr)\,d\tau -\sum_{t_{k}\geq s}\overline{I}_{k} \bigl(x(t_{k})\bigr) \biggr) \biggr| \\ \leq&\phi_{p}^{-1} \Biggl(\int_{0}^{+\infty}a( \tau)f\bigl(\tau,x(\tau),x'(\tau )\bigr)\,d\tau+\sum _{k=1}^{\infty}\overline{I}_{k} \bigl(x(t_{k})\bigr) \Biggr) \\ \leq&\phi_{p}^{-1} \biggl(B_{r}\int _{0}^{+\infty}a(\tau)\,d\tau+c^{*}\phi _{p}(r)+d^{*} \biggr):=R_{0}, \end{aligned}$$

where $R_{1}=\frac{1}{1-\int_{\eta}^{+\infty}g(t)\,dt} [(2+\alpha\int_{\eta}^{+\infty}g(t)\,dt)R_{0}+a^{*}r+b^{*} ]$. Hence, $\|Tx\|\leq\max\{R_{0},R_{1}\}$. So TΩ is bounded.

Second, for any $L\in(0,+\infty)$ and $t', t''\in J_{k}\cap[0,L]$ with $t'< t''$, we have

$$\begin{aligned} & \biggl|\frac{(Tx)(t')}{1+t'}-\frac{(Tx)(t'')}{1+t''} \biggr| \\ &\quad= \biggl|\frac{1}{1+t'}\frac{1}{1-\int_{\eta}^{+\infty }g(t)\,dt} \\ &\qquad{}\times \biggl[\sum_{t_{i}< t'}\int _{t_{i-1}}^{t_{i}}\phi_{p}^{-1} \biggl( \int_{s}^{+\infty}a(\tau)f\bigl(\tau,x( \tau),x'(\tau)\bigr)\,d\tau -\sum_{t_{k}\geq s} \overline{I}_{k}\bigl(x(t_{k})\bigr) \biggr)\,ds \\ &\qquad{}+\int_{\eta}^{+\infty}g(t)\int _{t_{i}}^{t'}\phi_{p}^{-1} \biggl( \int_{s}^{+\infty}a(\tau)f\bigl(\tau,x( \tau),x'(\tau)\bigr)\,d\tau -\sum_{t_{k}\geq s} \overline{I}_{k}\bigl(x(t_{k})\bigr) \biggr)\,ds\,dt \\ &\qquad{}+\sum_{t_{i}< t'}I_{i} \bigl(x(t_{i})\bigr) \biggr] \\ &\qquad{}-\frac{1}{1+t''}\frac{1}{1-\int_{\eta}^{+\infty}g(t)\,dt} \\ &\qquad{}\times\biggl[\sum_{t_{i}< t''}\int_{t_{i-1}}^{t_{i}} \phi_{p}^{-1} \biggl(\int_{s}^{+\infty}a( \tau)f\bigl(\tau,x(\tau),x'(\tau)\bigr)\,d\tau -\sum _{t_{k}\geq s}\overline{I}_{k}\bigl(x(t_{k}) \bigr) \biggr)\,ds \\ &\qquad{}+\int_{\eta}^{+\infty}g(t)\int _{t_{i}}^{t''}\phi_{p}^{-1} \biggl( \int_{s}^{+\infty}a(\tau)f\bigl(\tau,x( \tau),x'(\tau)\bigr)\,d\tau -\sum_{t_{k}\geq s} \overline{I}_{k}\bigl(x(t_{k})\bigr) \biggr)\,ds\,dt \\ &\qquad{}+\sum_{t_{i}< t''}I_{i} \bigl(x(t_{i})\bigr) \biggr] \\ &\qquad{}+\frac{1}{1+t'}\int_{t_{i}}^{t'} \phi_{p}^{-1} \biggl(\int_{s}^{+\infty }a( \tau)f\bigl(\tau,x(\tau),x'(\tau)\bigr)\,d\tau-\sum _{t_{k}\geq s}\overline{I}_{k}\bigl(x(t_{k}) \bigr) \biggr)\,ds \\ &\qquad{}-\frac{1}{1+t''}\int_{t_{i}}^{t''} \phi_{p}^{-1} \biggl(\int_{s}^{+\infty }a( \tau)f\bigl(\tau,x(\tau),x'(\tau)\bigr)\,d\tau-\sum _{t_{k}\geq s}\overline{I}_{k}\bigl(x(t_{k}) \bigr) \biggr)\,ds \biggr| \\ &\quad\leq\frac{1}{1-\int_{\eta}^{+\infty }g(t)\,dt} \\ &\qquad{}\times\biggl[\sum_{t_{i}< t''}\int_{t_{i-1}}^{t_{i}} \phi_{p}^{-1} \biggl(\int_{s}^{+\infty}a( \tau)f\bigl(\tau,x(\tau),x'(\tau)\bigr)\,d\tau -\sum _{t_{k}\geq s}\overline{I}_{k}\bigl(x(t_{k}) \bigr) \biggr)\,ds \\ &\qquad{}+\sum_{t_{i}< t''}I_{i} \bigl(x(t_{i})\bigr) \biggr] \biggl|\frac{1}{1+t'}-\frac {1}{1+t''} \biggr|\\ &\qquad{}+\frac{1}{(1+t')(1-\alpha\int_{\eta}^{+\infty }g(t)\,dt)} \\ &\qquad{}\times\int_{\eta}^{+\infty}g(t)\int _{t'}^{t''}\phi_{p}^{-1} \biggl( \int_{s}^{+\infty}a(\tau)f\bigl(\tau,x( \tau),x'(\tau)\bigr)\,d\tau-\sum_{t_{k}\geq s} \overline{I}_{k}\bigl(x(t_{k})\bigr) \biggr)\,ds\,dt \\ &\qquad{}+ \biggl|\frac{1}{1+t'}\int_{t_{i}}^{t'} \phi_{p}^{-1} \biggl(\int_{s}^{+\infty}a( \tau)f\bigl(\tau,x(\tau),x'(\tau)\bigr)\,d\tau-\sum _{t_{k}\geq s}\overline{I}_{k}\bigl(x(t_{k}) \bigr) \biggr)\,ds \\ &\qquad{}-\frac{1}{1+t''}\int_{t_{i}}^{t''} \phi_{p}^{-1} \biggl(\int_{s}^{+\infty }a( \tau)f\bigl(\tau,x(\tau),x'(\tau)\bigr)\,d\tau-\sum _{t_{k}\geq s}\overline{I}_{k}\bigl(x(t_{k}) \bigr) \biggr)\,ds \biggr| \\ &\quad\leq \frac{1}{1-\int_{\eta}^{+\infty }g(t)\,dt} \\ &\qquad{}\times \biggl[\sum_{t_{i}< t''}\int _{t_{i-1}}^{t_{i}}\phi_{p}^{-1} \biggl( \int_{s}^{+\infty}a(\tau)f\bigl(\tau,x( \tau),x'(\tau)\bigr)\,d\tau -\sum_{t_{k}\geq s} \overline{I}_{k}\bigl(x(t_{k})\bigr) \biggr)\,ds \\ &\qquad{}+\sum_{t_{i}< t''}I_{i} \bigl(x(t_{i})\bigr) \biggr] \biggl|\frac{1}{1+t'}-\frac {1}{1+t''} \biggr|+\frac{1}{1-\alpha\int_{\eta}^{+\infty }g(t)\,dt} \\ &\qquad{}\times\int_{\eta}^{+\infty}g(t)\int _{t'}^{t''}\phi_{p}^{-1} \biggl( \int_{s}^{+\infty}a(\tau)f\bigl(\tau,x( \tau),x'(\tau)\bigr)\,d\tau-\sum_{t_{k}\geq s} \overline{I}_{k}\bigl(x(t_{k})\bigr) \biggr)\,ds\,dt \\ &\qquad{}+\int_{0}^{t''}\phi_{p}^{-1} \biggl(\int_{s}^{+\infty}a(\tau)f\bigl(\tau,x(\tau ),x'(\tau)\bigr)\,d\tau-\sum_{t_{k}\geq s} \overline{I}_{k}\bigl(x(t_{k})\bigr) \biggr)\,ds \biggl| \frac{1}{1+t'}-\frac {1}{1+t''} \biggr| \\ &\quad\leq \biggl[\frac{1}{1-\int_{\eta}^{+\infty }g(t)\,dt}\bigl(t''R_{0}+a^{*}r+b^{*} \bigr)+t''R_{0} \biggr] \biggl|\frac{1}{1+t'}- \frac {1}{1+t''} \biggr| \\ &\qquad{}+\frac{R_{0}}{1-\int_{\eta}^{+\infty}g(t)\,dt} \int_{\eta}^{+\infty} \bigl(t'-t''\bigr)g(t)\,dt \rightarrow0, \quad \mbox{uniformly as } t'\rightarrow t'', \end{aligned}$$

and

$$\begin{aligned} & \bigl|\phi_{p}(Tx)'\bigl(t'\bigr)- \phi_{p}(Tx)'\bigl(t''\bigr) \bigr| \\ &\quad= \biggl|\int_{t'}^{+\infty}a(\tau)f\bigl(\tau,x( \tau),x'(\tau)\bigr)\,d\tau -\sum_{t_{k}\geq t'} \overline {I}_{k}\bigl(x(t_{k})\bigr) \\ &\qquad{}-\int_{t''}^{+\infty}a(\tau)f\bigl(\tau,x( \tau),x'(\tau)\bigr)\,d\tau +\sum_{t_{k}\geq t''} \overline{I}_{k}\bigl(x(t_{k})\bigr) \biggr| \\ &\quad\leq \int_{t'}^{t''}a(\tau)f\bigl(\tau,x( \tau),x'(\tau)\bigr)\,d\tau+\sum_{t'\leq t_{k}\leq t''} \overline {I}_{k}\bigl(x(t_{k})\bigr) \\ &\quad\leq B_{r}\int_{t'}^{t''}a(\tau) \,d\tau+\sum_{t'\leq t_{k}\leq t''}\bigl(c_{k} \phi_{p}(r)+d_{k}\bigr) \rightarrow0, \quad \mbox{uniformly as } t'\rightarrow t'', \end{aligned}$$

for all $x\in\Omega$. So TΩ is equicontinuous on any compact interval of $J_{k}$ ($k=1,2,\ldots$).

Third, we prove that for any $\varepsilon>0$, $x\in\Omega$, there exists sufficiently large $N>0$ such that

$$\begin{aligned}& \biggl|\frac{(Tx)(t')}{1+t'}-\frac{(Tx)(t'')}{1+t''} \biggr|< \varepsilon, \qquad \bigl|(Tx)'\bigl(t'\bigr)-(Tx)' \bigl(t'\bigr) \bigr|< \varepsilon, \quad\forall t',t''> N. \end{aligned}$$

For any $x\in\Omega$, we have

$$\begin{aligned} &\lim_{t\rightarrow+\infty} \frac{1}{1+t}\int_{t_{i}}^{t} \phi_{p}^{-1} \biggl(\int_{s}^{+\infty}a( \tau )f\bigl(\tau,x(\tau),x'(\tau)\bigr)\,d\tau-\sum _{t_{k}\geq s}\overline{I}_{k}\bigl(x(t_{k}) \bigr) \biggr)\,ds \\ &\quad=\lim_{t\rightarrow+\infty}\phi_{p}^{-1} \biggl( \int_{t}^{+\infty}a(\tau )f\bigl(\tau,x( \tau),x'(\tau)\bigr)\,d\tau-\sum_{t_{k}\geq t} \overline{I}_{k}\bigl(x(t_{k})\bigr) \biggr) \\ &\quad=0 \end{aligned}$$

and

$$\begin{aligned} &\lim_{t\rightarrow+\infty}\frac{1}{1+t}\frac{1}{1-\int_{\eta}^{+\infty }g(t)\,dt} \\ &\qquad{}\times \biggl[\sum_{t_{i}< t}\int _{t_{i-1}}^{t_{i}}\phi_{p}^{-1} \biggl( \int_{s}^{+\infty}a(\tau)f\bigl(\tau,x( \tau),x'(\tau)\bigr)\,d\tau -\sum_{t_{k}\geq s} \overline{I}_{k}\bigl(x(t_{k})\bigr) \biggr)\,ds \\ &\qquad{}+\int_{\eta}^{+\infty}g(t)\int _{t_{i}}^{t}\phi_{p}^{-1} \biggl( \int_{s}^{+\infty}a(\tau)f\bigl(\tau,x( \tau),x'(\tau)\bigr)\,d\tau -\sum_{t_{k}\geq s} \overline{I}_{k}\bigl(x(t_{k})\bigr) \biggr)\,ds\,dt \\ &\qquad{}+\sum_{t_{i}< t}I_{i} \bigl(x(t_{i})\bigr) \biggr] \\ &\quad\leq\lim_{t\rightarrow+\infty}\frac{1}{1+t}\frac{1}{1-\int_{\eta}^{+\infty }g(t)\,dt} \\ &\qquad{}\times \biggl[\int_{t_{i}}^{t} \phi_{p}^{-1} \biggl(\int_{s}^{+\infty}a( \tau)f\bigl(\tau ,x(\tau),x'(\tau)\bigr)\,d\tau-\sum _{t_{k}\geq s}\overline{I}_{k}\bigl(x(t_{k}) \bigr) \biggr)\,ds \\ &\qquad{}+R_{0}\int_{\eta}^{+\infty}tg(t) \,dt+a^{*}r+b^{*} \biggr] \\ &\quad=0. \end{aligned}$$

Hence, we obtain that

$$\begin{aligned} \lim_{t\rightarrow+\infty} \biggl|\frac{(Tx)(t)}{1+t} \biggr|=0, \end{aligned}$$

and

$$\begin{aligned} &\lim_{t\rightarrow+\infty} \bigl|(Tx)'(t) \bigr| \\ &\quad=\lim_{t\rightarrow+\infty}\phi_{p}^{-1} \biggl( \int_{t}^{+\infty}a(\tau )f\bigl(\tau,x( \tau),x'(\tau)\bigr)\,d\tau -\sum_{t_{k}\geq t} \overline{I}_{k}\bigl(x(t_{k})\bigr) \biggr)\,ds=0. \end{aligned}$$

So TΩ is equiconvergent at infinity. By Lemma 2.4, we obtain TΩ is relatively compact, that is, T is a compact operator.

Therefore, $T:P\rightarrow P$ is completely continuous. The proof is complete. □

Remark 2.10

Similarly, we may prove that when (H₁) and (H₂) hold, then $T:P\rightarrow P$ is completely continuous.

3 Main result

Theorem 3.1

Let conditions (H₁)-(H₃) be satisfied. Suppose further that $A<1$. Then IBVP (1.1) has the minimal nonnegative solution x̅ with $\|\overline{x}\|\leq\frac{B}{1-A}$, where A and B are defined as in Lemma  2.8. Moreover, if we let $x_{0}(t)=0$, $x_{n}(t)=(Tx_{n-1}(t))$ for all $t\in J$ ($n=1,2,\ldots$), then $x_{n}(t)\in P$ with

$$\begin{aligned}& 0=x_{0}(t)\leq x_{1}(t)\leq\cdots\leq x_{n}(t) \leq\overline{x}(t),\quad \forall t\in J, \end{aligned}$$

(3.1)

$$\begin{aligned}& 0=x_{0}'(t)\leq x_{1}'(t)\leq \cdots\leq x_{n}'(t)\leq\overline{x}'(t), \quad \forall t\in J, \end{aligned}$$

(3.2)

and $\{x_{n}(t)\}$ and $\{x_{n}'(t)\}$ converge uniformly to $\overline{x}(t)$ and $\overline{x}'(t)$ on $J_{i}$ ($i=1,2,\ldots$), respectively.

Proof

By Lemma 2.8 and the definition of operator T, we have $x_{n}(t)\in P$ and

$$\begin{aligned}& \|x_{n}\|\leq A\|x_{n-1}\|+B, \quad n=1,2, \ldots, \end{aligned}$$

(3.3)

$$\begin{aligned}& 0=x_{0}(t)\leq x_{1}(t)\leq\cdots\leq x_{n}(t) \leq\cdots, \quad \forall t\in J, \end{aligned}$$

(3.4)

$$\begin{aligned}& 0=x_{0}'(t)\leq x_{1}'(t)\leq \cdots\leq x_{n}'(t)\leq\cdots, \quad \forall t\in J. \end{aligned}$$

(3.5)

By (3.3), we can get

$$\begin{aligned} \|x_{n}\| \leq& A\|x_{n-1}\|+B\leq A\bigl(A \|x_{n-2}\|+B\bigr)+B=A^{2}\|x_{n-2}\|+AB+B \\ \leq& A^{2}\bigl(A\|x_{n-3}\|+B\bigr)+AB+B=A^{3} \|x_{n-3}\| +A^{2}B+AB+B\leq\cdots \\ \leq& A^{n}\|x_{0}\|+A^{n-1}B+A^{n-2}B+ \cdots+AB+B \\ =&\frac{B(1-A^{n})}{1-A}\leq \frac{B}{1-A} \quad (n=1,2,\ldots). \end{aligned}$$

(3.6)

From (3.4)-(3.6), we know that $\lim_{n\rightarrow+\infty}x_{n}(t)$ and $\lim_{n\rightarrow+\infty}x'_{n}(t)$ exist. Suppose that

$$\begin{aligned} \lim_{n\rightarrow+\infty}x_{n}(t)=\overline{x}(t), \qquad\lim_{n\rightarrow +\infty}x'_{n}(t)=h(t), \quad \forall t\in J. \end{aligned}$$

(3.7)

According to the definition of $x_{n}(t)$, we have

$$\begin{aligned}& x'_{n}(t)=\phi_{p}^{-1}\biggl( \phi_{p}(x_{\infty})+\int_{t}^{+\infty}f \bigl(\tau ,x_{n-1}(\tau),x'_{n-1}(\tau)\bigr)\,d \tau-\sum_{t_{k}\geq t}\overline{I}_{k} \bigl(x(t_{k})\bigr)\biggr), \\& \quad \forall t\in J, t\neq t_{k}\ (n=1,2,\ldots), \end{aligned}$$

(3.8)

$$\begin{aligned}& \bigl(\phi_{p}\bigl(x'_{n}(t)\bigr) \bigr)'=-a(t)f\bigl(t,x_{n-1}(t),x'_{n-1}(t) \bigr), \quad \forall t\in J, t\neq t_{k}\ (n=1,2,\ldots). \end{aligned}$$

(3.9)

From (3.6), we obtain

$$\begin{aligned} \frac{|x_{n}(t)|}{1+t}\leq\frac{B}{1-A},\qquad \bigl|x'_{n}(t)\bigr|\leq \frac{B}{1-A}, \quad \forall t\in J, t\neq t_{k}\ (n=1,2,\ldots). \end{aligned}$$

It follows that ${x_{n}(t)}$ is equicontinuous on every $J_{i}$ ($i=0,1,2,\ldots$). Combining this with the Ascoli-Arzela theorem and diagonal process, there exists a subsequence which converges uniformly to x̅ on $J_{i}$ ($i=0,1,2,\ldots$), which together with (3.4) imply that ${x_{n}(t)}$ converges uniformly to $\overline{x}(t)$ on $J_{i}$ ($i=0,1,2,\ldots$), and $\overline{x}(t)\in PC[J,R]$, $\|\overline{x}\|_{1}\leq \frac{B}{1-A}$. On the other hand, by (H₁), (3.6) and (3.9), we have

$$\begin{aligned} \bigl|x''_{n}(t)\bigr| \leq& a(\tau) \bigl(p(t) (t+1)^{p-1}\|\overline{x}_{n-1}\|_{1}+q(t)\bigl\| \overline {x}'_{n-1}\bigr\| _{\infty}+r(t)\bigr) \\ \leq&a(\tau) \biggl(p(t) (t+1)^{p-1}\frac{B}{1-A}+q(t) \frac {B}{1-A}+r(t)\biggr) \\ =&s(t)\in C(J,J_{+}), \quad \forall t\in J'\ (n=1,2, \ldots). \end{aligned}$$

Since $s(t)$ is bounded on $[0,M]$ (M is a finite positive number), ${x'_{n}(t)}$ is equicontinuous on every $J_{i}$ ($i=0,1,2,\ldots$). Combining this with the Ascoli-Arzela theorem and diagonal process, there exists a subsequence which converges uniformly to $h(t)$ on $J_{i}$ ($i=0,1,2,\ldots$), which together with (3.5) imply that ${x'_{n}(t)}$ converges uniformly to $h(t)$ on $J_{i}$ ($i=0,1,2,\ldots$), and $h(t)\in PC[J,R]$, $\|h\|_{\infty}\leq \frac{B}{1-A}$. From above, we know that $\overline{x}'(t)$ exists and $\overline{x}'(t)=h(t)$ for all $t\in J$. It follows that $\overline{x}\in P$ and $\|\overline{x}\|\leq\frac{B}{1-A}$. Now taking limits from two sides of $x_{n}(t)=(Tx_{n-1})(t)$, we have $\overline{x}(t)=(T\overline{x})(t)$, that is, T has a fixed point. By Lemma 2.7, $\overline{x}(t)$ is a nonnegative solution of IBVP (1.1).

Suppose that $x\in P\cap C^{2}[J, R]$ is an arbitrary nonnegative solution of IBVP (1.1). Then $x(t)=(Tx)(t)$. It is clear that $x(t)\geq0$, $x'(t)\geq0$, $\forall t\in J$. Suppose that $x(t)\geq x_{n-1}(t)$, $x'(t)\geq x'_{n-1}(t)$ for $t\in J$. By (2.14), we have $(Tx)(t)\geq(Tx_{n-1})(t)$, $(Tx)'(t)\geq(Tx_{n-1})'(t)$ for all $t\in J$. This means that $x(t)\geq x_{n}(t)$, $x'(t)\geq x'_{n}(t)$ for all $t\in J$ ($n=1,2,\ldots$). Taking limit, we have $x(t)\geq \overline{x}(t)$, $x'(t)\geq\overline{x}'(t)$ for all $t\in J$. The proof of Theorem 3.1 is complete. □

Next, for notational convenience, we denote that

$$\begin{aligned}& m=2^{\frac{2}{p-1}}\frac{1}{1-\int_{\eta}^{\infty}g(t)\,dt}\biggl(2+\int_{\eta }^{\infty}(t-1)g(t) \,dt\biggr)\phi_{p}^{-1}\biggl(\int_{0}^{\infty}a( \tau)\,d\tau\biggr), \end{aligned}$$

(3.10)

$$\begin{aligned}& m'=\frac{1}{1-\int_{\eta}^{\infty}g(t)\,dt}\biggl(2+\int_{\eta}^{\infty }(t-1)g(t) \,dt\biggr)\phi_{p}^{-1}\biggl(\int_{0}^{\infty}a( \tau)\,d\tau\biggr), \end{aligned}$$

(3.11)

$$\begin{aligned}& n=2^{\frac{2}{p-1}}\frac{1}{1-\int_{\eta}^{\infty}g(t)\,dt}\biggl(2+\int_{\eta }^{\infty}(t-1)g(t) \,dt\biggr), \end{aligned}$$

(3.12)

$$\begin{aligned}& n'=\frac{1}{1-\int_{\eta}^{\infty}g(t)\,dt}\biggl(2+\int_{\eta}^{\infty }(t-1)g(t) \,dt\biggr), \end{aligned}$$

(3.13)

$$\begin{aligned}& \Lambda=\max \biggl\{ \frac{b^{*}}{1-\int_{\eta}^{\infty }g(t)\,dt-3a^{*}},\frac{n\phi_{p}^{-1}(d^{*})}{1-3n\phi _{p}^{-1}(c^{*})} \biggr\} , \end{aligned}$$

(3.14)

$$\begin{aligned}& \Lambda'=\max \biggl\{ \frac{b^{*}}{1-\int_{\eta}^{\infty }g(t)\,dt-3a^{*}},\frac{n'\phi_{p}^{-1}(d^{*})}{1-3n'\phi _{p}^{-1}(c^{*})} \biggr\} . \end{aligned}$$

(3.15)

Theorem 3.2

Assume that (H₂)-(H₅) hold, and there exists

$$\begin{aligned} d\geq \left \{ \textstyle\begin{array}{@{}l@{\quad}l} 3\Lambda, & p\geq 2, \\ 3\Lambda', & 1< p< 2, \end{array}\displaystyle \displaystyle \displaystyle \right . \end{aligned}$$

such that

(A₁):

$$\begin{aligned} f\bigl(t,(1+t)u,v\bigr)\leq \left \{ \textstyle\begin{array}{@{}l@{\quad}l} \phi_{p}(\frac{d}{3m}), & p\geq2, \\ \phi_{p}(\frac{d}{3m'}),& 1< p< 2, \end{array}\displaystyle \displaystyle \displaystyle \right . \quad\textit{for }(t,u,v)\in[0,+\infty)\times[0,d]\times[0,d]. \end{aligned}$$

Then IBVP (1.1) admits positive, nondecreasing on $[0,+\infty)$ and concave solutions $w^{*}$ and $v^{*}$ such that $0<\|w^{*}\|\leq d$, and $\lim_{n\rightarrow+\infty}w_{n}=\lim_{n\rightarrow+\infty}A^{n}w_{0}=w^{*}$, where

$$\begin{aligned} w_{0}(t)=d+dt,\quad t\in J, \end{aligned}$$

(3.16)

and $0<\|v^{*}\|\leq d$, and $\lim_{n\rightarrow+\infty}v_{n}=\lim_{n\rightarrow+\infty}A^{n}v_{0}=v^{*}$, where $v_{0}(t)=0$, $t\in J$.

Proof

We only prove the case that $p\geq2$, another case can be proved in a similar way. By Lemma 2.9, we know that $T:P\rightarrow P$ is completely continuous. From the definition of T and (H₃), we can easily get that $Tx_{1}\leq Tx_{2}$ for any $x_{1},x_{2}\in P$ with $x_{1}\leq x_{2}$, $x'_{1}\leq x'_{2}$. Denote that

$$\begin{aligned} \overline{P}_{d}=\bigl\{ x\in P|\|x\|\leq d\bigr\} . \end{aligned}$$

(3.17)

In what follows, we first prove that $T:\overline{P}_{d}\rightarrow \overline{P}_{d}$. If $x\in\overline{P}_{d}$, then $\|x\|\leq d$. By (1.3), (2.18), (3.10), (3.12) and (3.14), we get that

$$\begin{aligned} \frac{|(Tx)(t)|}{1+t} \leq&\frac{1}{1-\int_{\eta}^{+\infty}g(t)\,dt} \biggl[2^{\frac {2}{p-1}}\biggl(2+\int _{\eta}^{+\infty }(t-1)g(t)\,dt\biggr) \\ &{}\times \biggl(\phi_{p}^{-1}\biggl(\phi_{p} \biggl(\frac{d}{3m}\biggr)\biggr) \phi_{p}^{-1}\biggl( \int_{0}^{+\infty}a(\tau)\,d\tau\biggr) + \phi_{p}^{-1}\bigl(c^{*}\bigr)d+ \phi_{p}^{-1}\bigl(d^{*}\bigr) \biggr)\\ &{}+\bigl(a^{*}d+b^{*}\bigr) \biggr] \\ \leq& \frac{d}{3}+\frac{d}{3}+\frac {d}{3}=d, \end{aligned}$$

and

$$\begin{aligned} \bigl|(Tx)'(t)\bigl| =& \biggl| \phi_{p}^{-1} \biggl(\int _{t}^{+\infty}a(\tau)f\bigl(\tau,x(\tau),x'( \tau )\bigr)\,d\tau-\sum_{t_{k}\geq t}\overline{I}_{k} \bigl(x(t_{k})\bigr) \biggr) \biggr| \\ \leq& 2^{\frac{2}{p-1}} \biggl(\phi_{p}^{-1}\biggl( \phi_{p}\biggl(\frac{d}{3m}\biggr)\biggr)+\phi _{p}^{-1}\bigl(c^{*}\bigr)d+\phi_{p}^{-1} \bigl(d^{*}\bigr) \biggr)< d. \end{aligned}$$

Thus, we get that $\|Tx\|\leq d$. Hence, we have proved that $T:\overline{P}_{d}\rightarrow\overline{P}_{d}$.

Let $w_{0}(t)=d+dt$, $0\leq t<+\infty$, then $w_{0}(t)\in \overline{P}_{d}$. Let $w_{1}(t)=Tw_{0}(t)$, $w_{2}(t)=T^{2}w_{0}(t)$, then by Lemma 2.9, we have $w_{1}(t)\in\overline{P}_{d}$ and $w_{2}(t)\in \overline{P}_{d}$. Denote that

$$\begin{aligned} w_{n+1}(t)=Tw_{n}(t)=T^{n+1}w_{0}(t), \quad n=0,1,2,\ldots. \end{aligned}$$

(3.18)

Since $T:\overline{P}_{d}\rightarrow\overline{P}_{d}$, we have that

$$\begin{aligned} w_{n}(t)\in T(\overline{P}_{d})\subset \overline{P}_{d},\quad n=1,2,\ldots. \end{aligned}$$

(3.19)

It follows from the complete continuity of T that $\{w_{n}\}_{n=1}^{\infty}$ has a convergent subsequence $\{w_{n_{k}}\}_{k=1}^{\infty}$, and there exists $w^{*}\in \overline{P}_{d}$ such that $w_{n_{k}}\rightarrow w^{*}$.

By (3.18), (H₃) and (A₁), we get that

$$\begin{aligned} w_{1}(t) =&\frac{1}{1-\int_{\eta}^{+\infty }g(t)\,dt} \\ &{}\times\biggl[\sum_{t_{i}< t}\int_{t_{i-1}}^{t_{i}} \phi_{p}^{-1} \biggl(\int_{s}^{+\infty}a( \tau)f\bigl(\tau,w_{0}(\tau),w'_{0}(\tau)\bigr) \,d\tau -\sum_{t_{k}\geq s}\overline{I}_{k} \bigl(w_{0}(t_{k})\bigr) \biggr)\,ds \\ &{}+\int_{\eta}^{+\infty}g(t)\int_{t_{i}}^{t} \phi_{p}^{-1} \biggl(\int_{s}^{+\infty}a( \tau)f\bigl(\tau,w_{0}(\tau),w'_{0}(\tau)\bigr) \,d\tau -\sum_{t_{k}\geq s}\overline{I}_{k} \bigl(w_{0}(t_{k})\bigr) \biggr)\,ds\,dt \\ &{}+\sum_{t_{i}< t}I_{i}\bigl(w_{0}(t_{i}) \bigr) \biggr] \\ &{}+\int_{t_{i}}^{t}\phi_{p}^{-1} \biggl(\int_{s}^{+\infty}a(\tau)f\bigl(\tau ,w_{0}(\tau),w'_{0}(\tau)\bigr)\,d\tau-\sum _{t_{k}\geq s}\overline{I}_{k}\bigl(w_{0}(t_{k}) \bigr) \biggr)\,ds \\ \leq& \frac{1}{1-\int_{\eta}^{+\infty}g(t)\,dt} \Biggl[\biggl(t+\int_{\eta}^{+\infty }tg(t) \,dt\biggr) \\ &{}\times\phi_{p}^{-1} \Biggl(\int_{0}^{+\infty}a( \tau)f\bigl(\tau,w_{0}(\tau ),w'_{0}(\tau) \bigr)\,d\tau +\sum_{k=1}^{\infty} \overline{I}_{k}\bigl(w_{0}(t_{k})\bigr) \Biggr) \Biggr] \\ &{}+t\phi_{p}^{-1} \Biggl(\int_{0}^{+\infty}a( \tau)f\bigl(\tau,w_{0}(\tau ),w'_{0}(\tau) \bigr)\,d\tau +\sum_{k=1}^{\infty} \overline{I}_{k}\bigl(w_{0}(t_{k})\bigr) \Biggr) \\ &{}+\frac{1}{1-\int_{\eta}^{+\infty }g(t)\,dt}\bigl(a^{*}d+b^{*}\bigr) \\ \leq&\frac{1}{1-\int_{\eta}^{+\infty}g(t)\,dt} \biggl[\biggl(2t+\int_{\eta}^{+\infty }(t-1)g(t) \,dt\biggr) \\ &{}\times\phi_{p}^{-1} \biggl(\int_{0}^{+\infty}a( \tau)\phi_{p}\biggl(\frac{d}{3m}\biggr)\,d\tau +c^{*} \phi_{p}(d)+d^{*} \biggr) \biggr] \\ &{}+\frac{1}{1-\alpha\int_{\eta}^{+\infty }g(t)\,dt}\bigl(a^{*}d+b^{*}\bigr) \\ \leq& \frac{1}{1-\int_{\eta}^{+\infty}g(t)\,dt} \biggl[2^{\frac{2}{p-1}}\biggl(2t+\int _{\eta}^{+\infty}(t-1)g(t)\,dt\biggr) \\ &{}\times \biggl(\phi_{p}^{-1}\biggl(\phi_{p} \biggl(\frac{d}{3m}\biggr)\biggr)\phi_{p}^{-1}\biggl( \int_{0}^{+\infty}a(\tau)\,d\tau\biggr)+ \phi_{p}^{-1}\bigl(c^{*}\bigr)d+\phi _{p}^{-1}\bigl(d^{*}\bigr) \biggr) \biggr] \\ &{}+\frac{1}{1-\int_{\eta}^{+\infty }g(t)\,dt}\bigl(a^{*}d+b^{*}\bigr) \\ \leq& d+dt=w_{0}(t), \end{aligned}$$

and

$$\begin{aligned} w'_{1}(t) =&(Tw_{0})'(t) \\ =&\phi_{p}^{-1} \biggl(\int_{t}^{+\infty}a( \tau)f\bigl(\tau,w_{0}(\tau ),w'_{0}(\tau) \bigr)\,d\tau-\sum_{t_{k}\geq t}\overline{I}_{k} \bigl(w_{0}(t_{k})\bigr) \biggr) \\ \leq& 2^{\frac{2}{p-1}} \biggl(\phi_{p}^{-1}\biggl( \phi_{p}\biggl(\frac{d}{3m}\biggr)\biggr)\phi _{p}^{-1}\biggl(\int_{0}^{+\infty}a( \tau)\,d\tau\biggr)\phi_{p}^{-1}\bigl(c^{*} \bigr)d+\phi _{p}^{-1}\bigl(d^{*}\bigr) \biggr) \\ \leq& d=w'_{0}(t),\quad 0\leq t< +\infty. \end{aligned}$$

So, by (3.18), (H₃) and (A₁), we have

$$\begin{aligned}& w_{2}(t)=(Tw_{1}) (t)\leq(Tw_{0}) (t)=w_{1}(t), \quad 0\leq t< +\infty, \end{aligned}$$

(3.20)

$$\begin{aligned}& w'_{2}(t)=(Tw_{1})'(t) \leq(Tw_{0})'(t)=(w_{1})'(t),\quad 0\leq t< +\infty. \end{aligned}$$

(3.21)

By induction, we see

$$\begin{aligned} w_{n+1}(t)\leq w_{n}(t), \qquad w'_{n+1}(t)\leq(w_{n})'(t),\quad 0 \leq t< +\infty, n=0,1,2,\ldots. \end{aligned}$$

(3.22)

Hence, we claim that $w_{n}\rightarrow w^{*}$ as $n\rightarrow \infty$. Applying the continuity of T and $w_{n+1}(t)=Tw_{n}(t)$, we know $Tw^{*}=w^{*}$. Let $v_{0}=0$, $0\leq t<+\infty$, then $v_{0}(t)\in\overline{P}_{d}$. Let $v_{1}=Tv_{0}$, $v_{2}=T^{2}v_{0}$. By Lemma 2.9, we get $v_{1}\in \overline{P}_{d}$ and $v_{2}\in\overline{P}_{d}$. Denote

$$\begin{aligned} v_{n+1}=Tv_{n}=T^{n+1}v_{0}, \quad n=0,1,2,\ldots. \end{aligned}$$

(3.23)

Since $T:\overline{P}_{d}\rightarrow\overline{P}_{d}$, we have $v_{n}\in T(\overline{P}_{d})\subset \overline{P}_{d}$, $n=1,2,\ldots$ . It follows from the complete continuity of T that $\{v_{n}\}_{n=1}^{\infty}$ is a sequentially compact set. Furthermore, we assert that $\{v_{n}\}_{n=1}^{\infty}$ has a convergent subsequence $\{v_{n_{k}}\}_{k=1}^{\infty}$, and there exists $v^{*}\in\overline{P}_{d}$ such that $v_{n_{k}}\rightarrow v^{*}$.

For $v_{1}=Tv_{0}\in\overline{P}_{d}$, we obtain

$$\begin{aligned}& v_{1}(t)=(Tv_{0}) (t)=(T_{0}) (t)\geq0, \quad 0 \leq t< +\infty, \end{aligned}$$

(3.24)

$$\begin{aligned}& v'_{1}(t)=(Tv_{0})'(t)=(T_{0})' \geq0, \quad 0\leq t< +\infty. \end{aligned}$$

(3.25)

By (H₃) and (A₁), we have

$$\begin{aligned}& v_{2}(t)=(Tv_{1}) (t)\geq(Tv_{0}) (t)=v_{1}(t), \quad 0\leq t< +\infty, \end{aligned}$$

(3.26)

$$\begin{aligned}& v'_{2}(t)=(Tv_{1})'(t) \geq(Tv_{0})'(t)=(v_{1})'(t),\quad 0\leq t< +\infty. \end{aligned}$$

(3.27)

By induction, we see

$$\begin{aligned} v_{n+1}(t)\geq v_{n}(t), \qquad v'_{n+1}(t)\geq(v_{n})'(t),\quad 0 \leq t< +\infty, n=0,1,2,\ldots. \end{aligned}$$

(3.28)

Hence, we claim that $v_{n}\rightarrow v^{*}$ as $n\rightarrow \infty$. Applying the continuity of T and $v_{n+1}(t)=Tv_{n}(t)$, we know $Tv^{*}=v^{*}$.

Since $f(t,0,0)\neq0$, $0\leq t<+\infty$, then the zero function is not the solution of IBVP (1.1). Thus, $v^{*}$ is a positive solution of IBVP (1.1). By Lemma 2.7, we know that $w^{*}$ and $v^{*}$ are positive, nondecreasing on $[0,\infty)$ and concave solutions of IBVP (1.1).

We can easily get that the theorem holds for $1< p<2$ in a similar way. □

Theorem 3.3

Assume that (H₂)-(H₅) hold, and there exists

$$\begin{aligned} d_{n}>d_{n-1}>\cdots>d_{1}\geq \left \{ \textstyle\begin{array}{@{}l@{\quad}l} 3\Lambda, & p\geq2, \\ 3\Lambda', & 1< p< 2, \end{array}\displaystyle \displaystyle \displaystyle \right . \end{aligned}$$

such that

(A₂):

$$\begin{aligned} &f\bigl(t,(1+t)u,v\bigr)\leq \left \{ \textstyle\begin{array}{@{}l@{\quad}l} \phi_{p}(\frac{d_{k}}{3m}), & p\geq2, \\ \phi_{p}(\frac{d_{k}}{3m'}), & 1< p< 2, \end{array}\displaystyle \displaystyle \displaystyle \right .\\ &\quad\textit{for }(t,u,v)\in[0,+\infty)\times[0,d_{k}]\times [0,d_{k}]. \end{aligned}$$

Then the boundary value problem (1.3) admits positive, nondecreasing on $[0,+\infty)$ and concave solutions $w_{k}^{*}$ and $v_{k}^{*}$ such that $0<\|w_{k}^{*}\|\leq d_{k}$, and $\lim_{n\rightarrow+\infty}w_{kn}=\lim_{n\rightarrow+\infty }A^{n}w_{k0}=w_{k}^{*}$, where

$$\begin{aligned} w_{0}(t)=d_{k}+d_{k}t, \quad t\in J, \end{aligned}$$

(3.29)

and $0<\|v_{k}^{*}\|\leq d$, and $\lim_{n\rightarrow+\infty}v_{kn}=\lim_{n\rightarrow+\infty }A^{n}v_{k0}=v_{k}^{*}$, where $v_{0}(t)=0$, $t\in J$.

Proof

It is similar to the proof of Theorem 3.2. □

4 Example

Example 4.1

Consider the following IBVP for double impulsive differential equation with p-Laplacian on an infinite interval:

$$\begin{aligned} \left \{ \textstyle\begin{array}{@{}l} (|x'|x')'+e^{-t}[\frac{\ln(1+\phi_{p}(x))}{100(1+t)^{2}}+\frac {e^{t}\arctan(\phi_{p}(x'))}{100(1+t^{2})}+1]=0, \quad t\in J,t\neq t_{k}, \\ \Delta x|_{t=t_{k}}=\frac{1}{4^{k}}(x(t_{k})+1)^{\frac {3}{16}},\quad t_{k}=2^{k},k=1,2,\ldots, \\ \Delta\phi_{p}(x')|_{t=t_{k}}=\frac{1}{5^{k}}(\frac{\ln(\phi _{p}(x(t_{k})))}{25(1+2^{k})^{2}}+1), \quad t_{k}=2^{k},k=1,2,\ldots, \\ x(0)=\int_{1}^{+\infty}\frac{1}{2}e^{-2t}x(t)\,dt, \qquad x'(+\infty )=0. \end{array}\displaystyle \right . \end{aligned}$$

(4.1)

Here, $p=3$, $a(t)=e^{-t}$, $f(t,x(t),x'(t))=\frac{\ln(1+\phi_{p}(x))}{100(1+t)^{2}}+\frac {e^{t}\arctan(\phi_{p}(x'))}{100(1+t^{2})}+1$, $I_{k}(x(t_{k}))=\frac{1}{4^{k}}(x(t_{k})+1)^{\frac{3}{16}}$, $\overline{I}_{k}(x(t_{k}))=\frac{1}{5^{k}}(\frac{\ln(\phi _{p}(x(t_{k})))}{25(1+2^{k})^{2}}+1)$, $g(t)=\frac{1}{2}e^{-2t}$, $\eta=1$. Evidently, $x(t)=0$ is not the solution of IBVP (4.1).

It is clear that $\int_{1}^{+\infty}\frac{1}{2}e^{-2t}\,dt<1$ and (H₃) is satisfied. Since

$$\begin{aligned}& f\bigl(t,x(t),x'(t)\bigr)\leq\frac{1}{100(1+t)^{2}} \phi_{p}(x)+\frac {e^{t}}{100(1+t^{2})}\phi_{p}\bigl(x' \bigr)+1, \\& I_{k}(x)\leq\frac{3}{16\cdot4^{k}}x+\frac{1}{4^{k}},\qquad \overline{I}_{k}(x)\leq\frac{1}{25(1+2^{k})^{2}5^{k}}\phi_{p}(x)+ \frac {1}{5^{k}},\quad k=1,2,\ldots. \end{aligned}$$

So we have

$$\begin{aligned}& p(t)=\frac{1}{100(1+t)^{2}}, \qquad q(t)=\frac {e^{t}}{100(1+t^{2})}, \qquad r(t)=1, \\& a_{k}=\frac{3}{16\cdot 4^{k}}, \qquad b_{k}=\frac{1}{4^{k}}, \qquad c_{k}=\frac {1}{25(1+2^{k})^{2}5^{k}}, \qquad d_{k}= \frac{1}{5^{k}}. \end{aligned}$$

Then we easily obtain that

$$\begin{aligned}& a^{*}=\sum_{k=1}^{\infty}(t_{k}+1)a_{k}= \frac{1}{4},\qquad b^{*}=\sum_{k=1}^{\infty}b_{k}= \frac{1}{3},\qquad c^{*}=\sum_{k=1}^{\infty}(t_{k}+1)^{2}c_{k}= \frac {1}{100}, \\& d^{*}=\sum_{k=1}^{\infty}d_{k}= \frac{1}{4},\qquad p^{*}=\int_{0}^{+\infty}a(t)p(t) (1+t)^{p-1}\,dt=\frac{1}{100},\\& q^{*}=\int _{0}^{+\infty}a(t)q(t)\,dt=\frac{\pi}{200}, \qquad r^{*}=\int_{0}^{+\infty}a(t)r(t)\,dt=1,\\& \int_{\eta}^{+\infty}g(t)\,dt=\frac {1}{4e^{2}}, \qquad \int_{\eta}^{+\infty}(t-1)g(t)\,dt= \frac{1}{8e^{2}}. \end{aligned}$$

Thus, (H₁) and (H₂) are satisfied. Clearly, $A\approx0.8166< 1$. By Theorem 3.1, we obtain that BVP (4.1) has a minimal positive solution x̅ and $\|\overline{x}\|\leq19.9189$.

Example 4.2

Consider the following IBVP for double impulsive differential equation with p-Laplacian on an infinite interval:

$$\begin{aligned} \left \{ \textstyle\begin{array}{@{}l} (|x'|x')'+e^{-4t}f(t,x(t),x'(t))=0, \quad t\in J,t\neq t_{k}, \\ \Delta x|_{t=t_{k}}=\frac{1}{2^{k}}(\frac{1}{2^{k}}x(t_{k})+1)^{\frac {1}{12}}, \quad t_{k}=2^{k},k=1,2,\ldots, \\ \Delta\phi_{p}(x')|_{t=t_{k}}=\frac{1}{52\cdot14^{k}}(\frac{\arctan (\phi_{p}(x(t_{k})))}{(1+2^{k})^{2}}+1), \quad t_{k}=2^{k},k=1,2,\ldots, \\ x(0)=\int_{1}^{+\infty}\frac {4}{(1+t)^{4}}x(t)\,dt, \qquad x'(+\infty)=0. \end{array}\displaystyle \right . \end{aligned}$$

(4.2)

Here,

$$\begin{aligned} f(t,u,v)=\left \{ \textstyle\begin{array}{@{}l@{\quad}l} \frac{1}{25}|\sin(t)|+\frac{1}{100}(\frac{u}{1+t})^{4}+\frac {v}{100}, & u\leq4, \\ \frac{1}{25}|\sin(t)|+\frac{1}{100}(\frac{1}{1+t})^{4}+\frac {v}{100}, & u\geq4. \end{array}\displaystyle \right . \end{aligned}$$

(4.3)

It is clear that (H₂) and (H₄) hold for $p=3$, $a(t)=e^{-4t}$, $g(t)=4/(1+t)^{4}$. By direct computation, we obtain that

$$\begin{aligned} \int_{0}^{+\infty}a(t)\,dt=\frac{1}{4}, \qquad \int_{0}^{+\infty}\phi_{p}\biggl(\int _{t}^{+\infty}a(s)\,ds\biggr)\,dt=\frac{1}{4}, \end{aligned}$$

which implies that (H₅) holds.

Obviously,

$$\begin{aligned} a_{k}=\frac{1}{12\cdot 4^{k}}, \qquad b_{k}=\frac{1}{2^{k}}, \qquad c_{k}=\frac {1}{52(1+2^{k})^{2}14^{k}}, \qquad d_{k}= \frac{1}{52\cdot14^{k}}. \end{aligned}$$

Hence, we can obtain that

$$\begin{aligned}& a^{*}=\sum_{k=1}^{\infty}(t_{k}+1)a_{k}= \frac{1}{9},\qquad b^{*}=\sum_{k=1}^{\infty}b_{k}=1, \qquad c^{*}=\sum_{k=1}^{\infty}(t_{k}+1)^{2}c_{k}= \frac {1}{676}, \\& d^{*}=\sum_{k=1}^{\infty}d_{k}= \frac{1}{676}, \qquad \int_{\eta }^{+\infty}g(t)\,dt= \frac{1}{6}, \qquad\int_{\eta}^{+\infty}(t-1)g(t) \,dt=\frac {1}{6}, \\& m=\frac{13}{5},\qquad n=\frac{26}{5}, \qquad \Lambda =2. \end{aligned}$$

Take $d=13$. In this case, we have

$$\begin{aligned} \phi_{p}\biggl(\frac{d}{3m}\biggr)=\phi_{p}\biggl( \frac{5}{3}\biggr)=\frac {25}{9}. \end{aligned}$$

On the other hand, nonlinear term f satisfies

$$\begin{aligned} f\bigl(t,(1+t)u,v\bigr)\leq\frac{1}{25}+\frac{256}{100}+ \frac{13}{100}=\frac {273}{100}< \phi_{p}\biggl(\frac{d}{3m} \biggr),\quad t\in J, u,v\in[0,13], \end{aligned}$$

which means that (A₂) holds. Thus, we have checked that all the conditions of Theorem 3.2 are satisfied. Therefore, we obtain that IBVP (4.2) has two iteration positive solutions.