1 Introduction

In order to determine the stationary point of optimization problems, the nonlinear conjugate gradient (CG) method does not necessitate the second derivative or its approximation. Here, the form we consider in the present investigation is as follows:

$$ \min f(x),\quad x \in R^{n}, $$
(1)

where \(f:R^{n} \to R\) as well as the gradient \(g(x) = \nabla f(x)\) is available. The following is how iterative approaches are usually applied to solve (1).

$$ x_{k + 1} = x_{k} + \alpha _{k}d_{k}, \quad k = 1, 2, \ldots, $$
(2)

where \(\alpha _{k}\) is obtained by an exact or inexact line search. Moreover, an inexact line search, for instance, a strong Wolfe–Powell (SWP) line [1, 2], is commonly used and may be expressed as the following:

$$ f(x_{k} + \alpha _{k}d_{k}) \le f(x_{k}) + \delta \alpha _{k}g_{k}^{T}d_{k}, $$
(3)

and

$$ \bigl\vert g(x_{k} + \alpha _{k}d_{k})^{T}d_{k} \bigr\vert \le \sigma \bigl\vert g_{k}^{T}d_{k} \bigr\vert . $$
(4)

A weak Wolfe-Powell (WWP) line search is as given by Equation (3) and

$$ g(x_{k} + \alpha _{k}d_{k})^{T}d_{k} \ge \sigma g_{k}^{T}d_{k} $$
(5)

with \(0 < \delta < \sigma < 1\).

The following expresses the search direction, \(d_{k}\) pertaining to two terms

$$ d_{k} = \textstyle\begin{cases} - g_{k},& k = 1,\\ - g_{k} + \beta _{k}d_{k - 1},&k \ge 2, \end{cases} $$
(6)

where \(g_{k} = g(x_{k})\), while \(\beta _{k}\) resembles the CG parameter. Here, the most well-known CG parameters are divided into two groups, the first of which is an efficient group defined as follows, which includes the Hestenses–Stiefel (HS) [3], Polak–Ribière–Polyak (PRP) [4], as well as Liu and Storey (LS) [5] methods.

$$ \beta _{k}^{\mathrm{HS}} = \frac{g_{k}^{T}y_{k - 1}}{d_{k - 1}^{T}y_{k - 1}}, \qquad \beta _{k}^{PRP} = \frac{g_{k}^{T}y_{k - 1}}{ \Vert g_{k - 1} \Vert ^{2}}, \qquad\beta _{k}^{LS} = - \frac{g_{k}^{T}y_{k - 1}}{d_{k - 1}^{T}g_{k - 1}}, $$

where \(y_{k - 1} = g_{k} - g_{k - 1}\). However, this group encounters a convergence problem if their values become negative [6]. In contrast, the second group is inefficient and exhibits strong global convergence. This category includes the Fletcher–Reeves (FR) [7], Fletcher (CD) [8], and Dai and Yuan (DY) [9] approaches, as defined by the following equations.

$$ \beta _{k}^{FR} = \frac{ \Vert g_{k} \Vert ^{2}}{ \Vert g_{k - 1} \Vert ^{2}}, \qquad\beta _{k}^{CD} = - \frac{ \Vert g_{k} \Vert ^{2}}{d_{k - 1}^{T}g_{k - 1}}, \qquad \beta _{k}^{DY} = \frac{ \Vert g_{k} \Vert ^{2}}{d_{k - 1}^{T}g_{k - 1}}. $$

The subsequent conjugacy condition was put forth by Dai and Liao [10].

$$ d_{k}^{T}y_{k - 1} = - tg_{k}^{T}s_{k - 1}, $$
(7)

where \(s_{k - 1} = x_{k} - x_{k - 1}\) and \(t \ge 0\). Pertaining to \(t = 0\), the classical conjugacy condition is then expressed as Equation (8) becomes the classical conjugacy condition. They also presented the CG formula below [10], utilizing (6) and (7).

$$ \beta _{k}^{DL} = \frac{g_{k}^{T}y_{k - 1}}{d_{k - 1}^{T}y_{k - 1}} - t\frac{g_{k}^{T}s_{k - 1}}{d_{k - 1}^{T}y_{k - 1}} = \beta _{k}^{\mathrm{HS}} - t\frac{g_{k}^{T}s_{k - 1}}{d_{k - 1}^{T}y_{k - 1}}. $$
(8)

Nonetheless, \(\beta _{k}^{DL}\) carries over the same issue as \(\beta _{k}^{PRP}\) and \(\beta _{k}^{\mathrm{HS}}\), e.g., \(\beta _{k}^{DL}\) is generally not nonnegative. Equation (8) was then replaced [10]:

$$ \beta _{k}^{DL +} = \max \bigl\{ \beta _{k}^{\mathrm{HS}},0 \bigr\} - t\frac{g_{k}^{T}s_{k - 1}}{d_{k - 1}^{T}y_{k - 1}}. $$

Hager and Zhang [11, 12] provided the CG formula below, predicated in Eq. (8).

$$ \beta _{k}^{\mathrm{HZ}} = \max \bigl\{ \beta _{k}^{N}, \eta _{k} \bigr\} , $$
(9)

where \(\beta _{k}^{N} = \frac{1}{d_{k}^{T}y_{k}} (y_{k} - 2d_{k}\frac{ \Vert y_{k} \Vert ^{2}}{d_{k}^{T}y_{k}} )^{T}g_{k}, \eta _{k} = - \frac{1}{ \Vert d_{k} \Vert \min \{ \eta , \Vert g_{k} \Vert \}}\), while \(\eta > 0\) is a constant. Note that \(t = 2\frac{ \Vert y_{k} \Vert ^{2}}{s_{k}^{T}y_{k}}\) when \(\beta _{k}^{N} = \beta _{k}^{DY}\).

Based on Equation (8), many researchers have suggested the three-term CG methods given below. Let the following equation represent the general form with regard to the three-term CG method:

$$ d_{k} = - g_{k} + \eta _{k}d_{k - 1} - \theta _{k}y_{k - 1}, $$
(10)

where \(\theta _{k} = \frac{g_{k}^{T}y_{k - 1} - tg_{k}^{T}s_{k - 1}}{y_{k - 1}^{T}d_{k - 1}}\) and \(\eta _{k} = \frac{g_{k}^{T}d_{k - 1}}{y_{k - 1}^{T}d_{k - 1}}\). We then obtain a wide variety of choices by replacing t in Eq. (10) with an appropriate term, as shown in Table 1.

Table 1 Some recent three-term CG methods
Full size table

By replacing \(y_{k - 1}\) with \(g_{k - 1}\), Liu et al. [17] proposed the following three-term CG method:

$$ d_{k} = - g_{k} + \biggl( \beta _{k}^{LS} - \frac{ \Vert g_{k - 1} \Vert ^{2}g_{k}^{T}d_{k - 1}}{(d_{k - 1}^{T}g_{k - 1})^{2}} \biggr)d_{k - 1} + \biggl( \frac{g_{k}^{T}d_{k - 1}}{d_{k - 1}^{T}y_{k - 1}} \biggr)g_{k - 1}, $$

with the following assumption

$$ \biggl( \frac{g_{k}^{T}d_{k - 1}}{d_{k - 1}^{T}g_{k - 1}} \biggr) > \nu \in (0,1). $$

Liu et al. [17] demonstrated how nonconvex functions may address nonlinear monotone equations if the sufficient descent condition is met. Meanwhile, Liu et al. [18] created the three-term CG methods given below and solved Equation (1) by utilizing it in order to avoid using the condition \(( \frac{g_{k}^{T}d_{k - 1}}{d_{k - 1}^{T}g_{k - 1}} ) > \nu \in (0,1)\).

$$ d_{k} = - g_{k} + \biggl( \beta _{k}^{LS} - \frac{ \Vert g_{k - 1} \Vert ^{2}g_{k}^{T}s_{k - 1}}{(d_{k - 1}^{T}g_{k - 1})^{2}} \biggr)d_{k - 1} - \biggl( \frac{g_{k}^{T}d_{k - 1}}{d_{k - 1}^{T}y_{k - 1}} \biggr)g_{k - 1}. $$

Yao et al. [19] suggested a three-term CG with the following new choice of t given by

$$ d_{k + 1} = - g_{k + 1} + \biggl( \frac{g_{k}^{T}y_{k} - t_{k}g_{k + 1}^{T}s_{k}}{y_{k}^{T}d_{k}} \biggr)d_{k} + \frac{g_{k + 1}^{T}d_{k}}{y_{k}^{T}d_{k}}y_{k}. $$

\(t_{k}\) was also chosen to meet the descent condition like the one below as per the SWP line search.

$$ t_{k} > \frac{ \Vert y_{k} \Vert ^{2}}{y_{k}^{T}s_{k}}. $$

Another theorem put forth by Yao et al. [19] states that if \(t_{k}\) is close to \(\frac{ \Vert y_{k} \Vert ^{2}}{y_{k}^{T}s_{k}}\), then the search direction produces a zigzag search path. Thus, they decided on the option \(t_{k}\) given below.

$$ t_{k} = 1 + 2\frac{ \Vert y_{k} \Vert ^{2}}{y_{k}^{T}s_{k}}. $$

At the beginning of the CG method, a nonnegative CG formula with a new restart property was presented by Alhawarat et al. [20].

$$ \beta _{k}^{AZPRP} = \textstyle\begin{cases} \frac{ \Vert g_{k} \Vert ^{2} - \mu _{k} \vert g_{k}^{T}g_{k - 1} \vert }{ \Vert g_{k - 1} \Vert ^{2}} &\mbox{if } \Vert g_{k} \Vert ^{2} > \mu _{k} \vert g_{k}^{T}g_{k - 1} \vert , \\ 0& \mbox{otherwise}, \end{cases} $$

where \(\Vert \cdot \Vert \) denotes the Euclidean norm, while \(\mu _{k}\) can be represented as

$$ \mu _{k} = \frac{ \Vert x_{k} - x_{k - 1} \Vert }{ \Vert y_{k - 1} \Vert }. $$

Similarly, Jiang et al. [21] suggested the CG method given by:

$$ \beta _{k}^{JJSL} = \frac{g_{k}^{T}y_{k - 1}}{g_{k - 1}^{T}y_{k - 1}}. $$

To improve the efficiency of prior methods, they constructed a restart criterion given as follows:

$$ d_{k} = \textstyle\begin{cases} - g_{k}, &k = 1, \\ - g_{k} + \beta _{k}^{JJSL}d_{k - 1} + \frac{g_{k}^{T}d_{k - 1}}{d_{{k - 1}}^{T}(g_{k} - g_{k - 1})}g_{k - 1}& \text{if }0 \le g_{k}^{T}g_{k - 1} \le \Vert g_{k} \Vert ^{2} \le \Vert g_{k - 1} \Vert ^{2}, k \ge 2, \\ - g_{k} + \xi \frac{g_{k}^{T}g_{k - 1}}{ \Vert g_{k - 1} \Vert ^{2}}g_{k - 1},& k \ge 2, \mbox{ otherwise}. \end{cases} $$

where \(0 < \xi < 1\).

Recently, a convex combination between two distinct search directions is presented by Alhawarat et al. [22] as follows:

$$ d_{k} = \lambda d_{k}^{(}(1)) + (1 - \lambda )d_{k}^{(}(2)) $$

where

$$\begin{aligned} &0 \le \lambda \le 1, \\ &d_{k}^{(}(1)) = \textstyle\begin{cases} - g_{k},& \text{if } k = 1,\\ - g_{k} + \beta _{k}^{(}(1))d_{k - 1}^{(}(1)),&\text{if } k \ge 2, \end{cases}\displaystyle \end{aligned}$$

and

$$ d_{k}^{(}(2)) = \textstyle\begin{cases} - g_{k}, &\text{if } k = 1,\\ - g_{k} + \beta _{k}^{(}(2)d_{k}^{(}(2),&\text{if } k \ge 2. \end{cases} $$

The authors selected \(\beta _{k}^{(}(1))\) and \(\beta _{k}^{(}(2))\) given below:

$$ \beta _{k}^{(}(1)) = \textstyle\begin{cases} \frac{ \Vert g_{k} \Vert ^{2} - \mu _{k} \vert g_{k}^{T}g_{k - 1} \vert }{d_{k - 1}^{(}(1)y_{k - 1}} &\mbox{if } \Vert g_{k} \Vert ^{2} > \mu _{k} \vert g_{k}^{T}g_{k - 1} \vert , \\ - t\frac{g_{k}^{T}s_{k - 1}}{d_{k - 1}^{(}(1)y_{k - 1}}& \mbox{otherwise}, \end{cases} $$

and

$$ \beta _{k}^{(}(2)) = \beta _{k}^{CG - DESCENT}. $$

The descent condition, also known as the downhill condition, given by

$$ g_{k}^{T}d_{k} < 0, \quad\forall k \ge 1, $$

helps research CG methods and is crucial to the validation of global convergence analysis. Al-Baali [23] also utilized the subsequent version of (13) to demonstrate the FR method.

$$ g_{k}^{T}d_{k} \le - c \Vert g_{k} \Vert ^{2},\quad \forall k \ge 1, $$
(11)

where \(c \in (0, 1)\). Next, the sufficient descent condition is given by Eq. (14) below. Moreover, it performs better than (13) because the quantity of \(g_{k}^{T}d_{k}\) can be controlled using \(\Vert g_{k} \Vert ^{2}\).

2 Proposed modified search direction (3TCGHS) and motivation

The main motivation for researchers in CG methods is to propose a positive CG method with an efficiency similar to that of PRP or HS, with a global convergence. In the following modification, we utilize the new search direction \(g_{k - 1}\) proposed by [17] with \(\beta _{k}^{\mathrm{HS}}\) restricted to be nonnegative, as given below:

$$ d_{k}^{\mathrm{Jiang}} = \textstyle\begin{cases} - g_{k},& k = 1, \\ - g_{k} + \beta _{k}^{\mathrm{HS}}d_{k - 1} + \frac{g_{k}^{T}d_{k - 1}}{d_{{k - 1}}^{T}(g_{k} - g_{k - 1})}g_{k - 1},& \text{if }\Vert g_{k} \Vert ^{2} > g_{k}^{T}g_{k - 1}, k \ge 2, \\ - \mu _{k}\frac{g_{k}^{T}s_{k - 1}}{d_{{k - 1}}^{T}(g_{k} - g_{k - 1})},& \mbox{otherwise}. \end{cases} $$
(12)

where \(\mu _{k} = \frac{ \Vert x_{k} - x_{k - 1} \Vert }{ \Vert g_{k} - g_{k - 1} \Vert }\).

The procedures acquired to determine the optimization function’s stationary point are outlined in the following Algorithm 1.

3 Global convergence properties

The assumption that follows is considered as a condition for the objective function.

Assumption 1

I. The level set \(\Psi = \{ x \in R^{n}:f(x) \le f(x_{1})\}\) is bounded. Here, a positive constant ρ exists; in this case

$$ \Vert x \Vert \le \rho , \quad \forall x \in \Psi . $$

II. f is a continuous and differentiable function in some neighborhood W of Ψ, and its gradient is Lipchitz continuous, meaning that, for every \(x,y \in W\), a constant \(L > 0\) exists, in which case

$$ \bigl\Vert g(x) - g(y) \bigr\Vert \le L \Vert x - y \Vert . $$

As per this assumption, there must be a positive constant η; in this case

$$ \bigl\Vert g(u) \bigr\Vert \le \eta , \quad \forall \eta \in W. $$

The CG method’s convergence properties are typically established using the following lemma proposed by Zoutendijk [24]. The method involves multiple line searches, including SWP and WWP line searches.

Lemma 3.1

Let Assumption 1hold. If \(\alpha _{k}\) satisfies the WWP line search with the descent condition (9), then take any form of (2) and (3). Then, the inequality that follows holds.

$$ \sum_{k = 1}^{\infty} \frac{(g_{k}^{T}d_{k})^{2}}{ \Vert d_{k} \Vert ^{2}} < \infty . $$
(13)

As can be seen from the following theorem, the new formula fulfills the descent condition (9).

Theorem 3.1

Let the sequences \(\{ x_{k}\}\) and \(\{ d_{k}^{\mathrm{Jiang}}\}\) be developed by Equations (2) and (12), and consider the line search method obtained using Equations (3) and (4). The sufficient descent condition (11) is then satisfied.

Proof

Multiply (12) by \(g_{k}^{T}\) to obtain

$$\begin{aligned} g_{k}^{T}d_{k}^{\mathrm{Jiang}}& = - \Vert g_{k} \Vert ^{2} + \frac{g_{k}^{T}(g_{k} - g_{k - 1})}{d_{{k - 1}}^{T}(g_{k} - g_{k - 1})}d_{k - 1} + \frac{g_{k}^{T}d_{k - 1}}{d_{{k - 1}}^{T}(g_{k} - g_{k - 1})}g_{k}^{T}g_{k - 1},\\ &= - \Vert g_{k} \Vert ^{2} + \frac{ \Vert g_{k} \Vert ^{2}}{d_{{k - 1}}^{T}(g_{k} - g_{k - 1})}g_{k}^{T}d_{k - 1}. \end{aligned}$$

Using a SWP line search, we obtain

$$ \le - \Vert g_{k} \Vert ^{2} + \frac{ \Vert g_{k} \Vert ^{2}}{(1 - \sigma )g_{k}^{T}d_{k - 1}}\sigma g_{k}^{T}d_{k - 1} = - \Vert g_{k} \Vert ^{2} + \frac{\sigma \Vert g_{k} \Vert ^{2}}{(1 - \sigma )}. $$

If \(\sigma \le \frac{1}{2}\),

$$ g_{k}^{T}d_{k}^{\mathrm{Jiang}} \le - c||g_{k}||^{2}. $$

The proof is now complete. □

Theorem 3.2

Let sequence \(\{ x_{k}\}\) be generated by Equation (2), where \(d_{k} = - \mu _{k}\frac{g_{k}^{T}s_{k - 1}}{d_{{k - 1}}^{T}(g_{k} - g_{k - 1})} \) is the step length obtained by SWP line search. Afterwards, condition (11) for a sufficient descent holds.

Proof

After multiplying (2) by \(g_{k}^{T}\) and substituting \(d_{k} = - \mu _{k}\frac{g_{k}^{T}s_{k - 1}}{d_{{k - 1}}^{T}(g_{k} - g_{k - 1})} \), we acquire

$$\begin{aligned} &g_{k}^{T}d_{k} = - \Vert g_{k} \Vert ^{2} - \mu _{k}\frac{\alpha _{k - 1}g_{k}^{T}d_{k - 1}}{d_{k - 1}^{T}y_{k - 1}} g_{k}^{T}d_{k - 1}, \\ &g_{k}^{T}d_{k} = - \Vert g_{k} \Vert ^{2} - \mu _{k}\frac{\alpha _{k - 1} \Vert g_{k}^{T}d_{k - 1} \Vert ^{2}}{d_{k - 1}^{T}y_{k - 1}} < 0. \end{aligned}$$

This completes the proof. □

Gilbert and Nocedal [25] outlined a property known as Property* to perform a specialized role in studies on CG formulas related to the PRP method. The property is described below.

Property*

Consider a method of the form (2) and (6), and let

$$ 0 < \gamma \le \Vert g_{k} \Vert \le \bar{\gamma}. $$
(14)

We claim that the method contains Property (*) provided that constants \(b > 1\) and \(\lambda > 0\) exist, where for every \(k \ge 1\), we acquire \(\vert \beta _{k} \vert \le b\). Meanwhile, if \(\Vert x_{k} - x_{k - 1} \Vert \le \lambda \), then

$$ \vert \beta _{k} \vert \le \frac{1}{2b}. $$

The lemma below illustrates that \(\beta _{k}^{\mathrm{HS}}\) inherits Property*. The proof is similar to that given by Gilbert and Nocedal [25].

Lemma 3.2

Let Assumption 1hold and consider any form of Equations (2) and (3). Consequently, \(\beta _{k}^{\mathrm{HS}}\) fulfills Property*.

Proof

Let \(b = \frac{2\bar{\gamma}}{(1 - \sigma )c\gamma ^{2}} > 1\), and \(\lambda = \frac{(1 - \sigma )c\gamma ^{4}}{2L\bar{\gamma} b}\). Then, using (14) and SWP line search, we obtain

$$ \bigl\vert \beta _{k}^{\mathrm{HS}} \bigr\vert \le \biggl\vert \frac{g_{k}^{T}(g_{k} - g_{k - 1})}{d_{k - 1}^{T}(g_{k} - g_{k - 1})} \biggr\vert \le \frac{ \Vert g_{k} \Vert ^{2} + \vert g_{k}^{T}g_{k - 1} \vert }{c(1 - \sigma ) \Vert g_{k - 1} \Vert ^{2}} = \frac{2\bar{\gamma}}{c(1 - \sigma )y^{2}} = b. $$

If \(\Vert x_{k + 1} - x_{k} \Vert \le \lambda \) holds with Assumption 1, then

$$\begin{aligned} \bigl\vert \beta _{k}^{\mathrm{HS}} \bigr\vert &\le \frac{g_{k}^{T}(g_{k} - g_{k - 1})}{d_{k - 1}^{T}(g_{k} - g_{k - 1})} \le \frac{ \Vert g_{k} \Vert \Vert g_{k} - g_{k - 1} \Vert }{c(1 - \sigma ) \Vert g_{k - 1} \Vert ^{2}} \le \frac{L \Vert g_{k} \Vert \Vert x_{k} - x_{k - 1} \Vert }{c(1 - \sigma ) \Vert g_{k - 1} \Vert ^{2}} \\ &\le \frac{L\bar{\gamma} \lambda}{ c(1 - \sigma )\gamma ^{2}} = \frac{1}{2b}. \end{aligned}$$

 □

Lemma 3.3

Via Algorithm 1, let Assumption 1hold while the sequences \(\{ g_{k} \}\) and \(\{ d_{k}^{\mathrm{Jiang}} \}\) are developed. The step size \(\alpha _{k}\) is determined by utilizing the SWP line search to ensure that the sufficient descent condition is met. Provided that \(\beta _{k} \ge 0\), then a constant \(\gamma > 0\) exists, where \(\Vert g_{k} \Vert > \gamma \) for every \(k \ge 1\). Afterwards, \(d_{k} \ne 0\) and

$$ \sum_{k = 0}^{\infty} \Vert u_{k + 1} - u_{k} \Vert ^{2} < \infty , $$
(15)

where \(u_{k} = \frac{d_{k}}{ \Vert d_{k} \Vert }\).

Proof

First, given that \(d_{k} = 0\), we can acquire \(g_{k} = 0\) from the sufficient descent condition. Hence, we can assume that \(d_{k} \ne 0\) and

$$ \bar{\gamma} \ge \Vert g_{k} \Vert \ge \gamma > 0, \quad\forall k \ge 1. $$
(16)

We provide definitions as below:

$$\begin{aligned} &u_{k} = w_{k} + \delta _{k}u_{k - 1},\\ &\eta _{k} = \frac{g_{k}^{T}(g_{k} - g_{k - 1})}{d_{{k - 1}}^{T}(g_{k} - g_{k - 1})}, \end{aligned}$$

where

$$ w_{k} = \frac{ - g_{k} + \frac{g_{k}^{T}d_{k - 1}}{d_{{k - 1}}^{T}(g_{k} - g_{k - 1})}g_{k - 1}}{ \Vert d_{k} \Vert }, \qquad \delta _{k} = \eta _{k}\frac{ \Vert d_{k - 1} \Vert }{ \Vert d_{k} \Vert }. $$

Since \(u_{k}\) denotes a unit vector, we have

$$ \Vert w_{k} \Vert = \Vert u_{k} - \delta _{k}u_{k - 1} \Vert = \Vert \delta _{k}u_{k} - u_{k - 1} \Vert . $$

By the triangular inequality and \(\delta _{k} \ge 0\), we obtain

$$\begin{aligned} \Vert u_{k} - u_{k - 1} \Vert &\le (1 + \delta _{k}) \Vert u_{k} - u_{k - 1} \Vert = \bigl\Vert u_{k} - \delta _{k}u_{k - 1} - (u_{k - 1} - \delta _{k}u_{k}) \bigr\Vert . \\ &\le \Vert u_{k} - \delta _{k}u_{k - 1} \Vert + \Vert u_{k - 1} - \delta _{k}u_{k} \Vert = 2 \Vert w_{k} \Vert . \end{aligned}$$
(17)

We now define

$$ \nu = - g_{k} + \frac{g_{k}^{T}d_{k - 1}}{d_{{k - 1}}^{T}(g_{k} - g_{k - 1})}g_{k - 1}. $$

Utilizing the triangular inequality, we establish

$$ \Vert \nu \Vert \le \Vert g_{k} \Vert + \biggl\vert \frac{g_{k}^{T}d_{k - 1}}{d_{{k - 1}}^{T}(g_{k} - g_{k - 1})} \biggr\vert \Vert g_{k - 1} \Vert . $$
(18)

Using the SWP Equations (4) and (5), we can obtain the following two inequalities.

$$\begin{aligned} &d_{k - 1}^{T}y_{k - 1} \ge (\sigma - 1)g_{k - 1}^{T}d_{k - 1},\\ & \biggl\vert \frac{g_{k}^{T}d_{k - 1}}{d_{k - 1}^{T}y_{k - 1}} \biggr\vert \le \biggl( \frac{\sigma}{1 - \sigma} \biggr). \end{aligned}$$

Hence, the inequality in Eq. (18) can be expressed in the following way:

$$ \Vert \nu \Vert \le B \biggl( 1 + \biggl( \frac{\sigma}{1 - \sigma} \biggr) \biggr). $$

Let

$$ T = B \biggl( 1 + \biggl( \frac{\sigma}{1 - \sigma} \biggr) \biggr). $$

Then, \(\Vert \nu \Vert \le T\). From Eq. (17), we have \(\Vert u_{k} - u_{k - 1} \Vert \le 2w\).

By Eqs. (16) and (15), we acquire what is presented below

$$ \sum_{k = 0}^{\infty} \Vert u_{k + 1} - u_{k} \Vert ^{2} \le 4 \sum_{k = 0}^{\infty} \Vert w \Vert ^{2} \le 4T^{2}\sum _{k = 0}^{\infty} \frac{1}{ \Vert d_{k} \Vert ^{2}} < \infty . $$

This completes the proof. □

By Lemmas 4.1 and 4.2 in [10], we are able to obtain the following outcome:

Theorem 3.3

Using the CG method in Eq. (12), let (2) and (3) generate the sequences \(\{ x_{k} \}\) and \(\{ d_{k}^{\mathrm{Jiang}} \}\), and let the step size satisfy (4) and (5). Utilizing Lemmas 3.2, 3.3, and Lemmas 4.1 and 4.2 in [10], we acquire such findings of \(\lim \ \inf_{ k \to \infty} \Vert g_{k} \Vert = 0\).

4 Numerical results and discussions

In this section, we provide some numerical findings to validate the efficiency for the proposed search direction. Details are provided in the Appendix. We used 166 test functions from the CUTEr library [26]. The functions can be downloaded in .SIF file format from the URL below.

https://www.cuter.rl.ac.uk/Problems/mastsif.shtml

We modified the code from CG-Descent 6.8 to implement the proposed search direction and DL+ method. The following website has the code available for download.

https://people.clas.ufl.edu/hager/software/

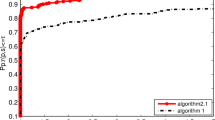
With an AMD A4-7210 CPU and 4 GB of RAM, the host computer was running Ubuntu 20.04 to carry out the necessary computations. We compared the modified search direction \(d_{k}^{\mathrm{Jiang}}\) with DL+ methods, and we used a SWP line search to acquire the step length with \(\sigma = 0.1\) and \(\delta = 0.01\) for 3TCGHS and DL+ and the previously mentioned approximate Wolfe-Powell line search for CG-Descent. Figures 1–4 present all outcomes via a performance measure first used by Dolan and More [27]. We utilize an SWP line search together with \(\sigma = 0.1\) and \(\delta = 0.01\) for \(d_{k}^{\mathrm{Jiang}}\) method and DL+. From Figs. 1–4, it may be observed that the new search direction strongly outperformed DL+ in terms of the number of iterations, function evaluation, CPU time, and a number of gradient evaluations. The subsequent big notations are used in the Appendix:

Figure 1
figure 1

Algorithm 1

Full size image
Figure 2
figure 2

Graph of the number of iterations

Full size image
Figure 3
figure 3

Graph of the number of function evaluations

Full size image
Figure 4
figure 4

Graph of CPU time

Full size image
Figure 5
figure 5

Graph of the number of number of gradient evaluations

Full size image

No. iter: Number of iterations.

No. function: Number of function evaluations

No. gradient: Number of gradient evaluations

4.1 Application to image restoration

To the original images, we applied Gaussian noise with a standard deviation of 25%. Next, we used 3TCGHS as well as the \(\beta _{k}^{DL +} \) (Dai–Liao) CG algorithm to restore these images. Take note that we made use of the (Dai–Liao) CG algorithm and 3TCGHS.

$$ \beta _{k}^{DL +} = \max \biggl( 0,\frac{g_{k}^{T}y_{k - 1}}{d_{k - 1}^{T}y_{k - 1}} \biggr) - t\frac{g_{k}^{T}s_{k - 1}}{d_{k - 1}^{T}y_{k - 1}}. $$

If the descent condition was met; if not, we employed the steepest-descent approach to restart the algorithm. We utilized the root-mean-square error (RMSE) between the restored image and the original true image to assess the quality of the restored image.

$$ RMSE = \frac{ \Vert \varsigma - \varsigma _{k} \Vert _{2}}{ \Vert \varsigma \Vert }. $$

The restored image is denoted by \(\varsigma _{k}\) and the true image by ς. The RMSE determines the quality of the restored image, in which lower values correspond to higher quality. The criteria for stop** is

$$ \frac{ \Vert x_{k + 1} - x_{k} \Vert _{2}}{ \Vert x_{k} \Vert _{2}} < \omega . $$

In this context, \(\omega = 10^{ - 3}\). Note that if \(\omega = 10^{ - 4}\) or \(\omega = 10^{ - 6}\), then RMSE remains constant, meaning that a fixed RMSE can vary in the number of iterations.

Table 2 compares 3TCGHS with the Dai-Liao CG algorithm through a series of numerical experiments. The RMSE, CPU time, and the number of iterations are all compared. It may be observed that the 3TCGHS method performed better than Dai–Liao with respect to CPU time, RMSE, and the number of iterations for most experimental tests.

Table 2 Numerical outcomes from images with Gaussian noise with a 25% standard deviation added to the original images using the Dai-Liao CG method as well as 3TCGHS
Full size table

Table 3 shows the outcomes of restoring destroyed images using Algorithm 1, indicating that it can be considered an efficient approach.

Table 3 Restoration of destroyed images of Coins, Cameraman,d Moon, an Baboon by reducing z via Algorithm 1
Full size table

4.2 Application to a regression problem

Table 4 shows data on the prices and demand for some commodities over several years. The data is similar to that used by [28].

Table 4 Data on demand and price
Full size table

The relation between x and y is parabolic; thus, the regression function can be defined as follows:

$$ r = w_{2}x^{2} + w_{1}x + w_{0}, $$
(19)

where \(w_{0}\), \(w_{1}\), and \(w_{2}\) are the regression parameters. We aim to solve the equation given below using the least square method.

$$ \min Q = \sum_{j = 1}^{n} \bigl(y_{j} - \bigl(w_{0} + w_{1} x_{j} + w_{2}x_{j}^{2} \bigr) \bigr)^{2}. $$

This equation is able to be modified to the following unconstrained optimization problem.

$$ \min \sum_{j = 1}^{n} f(w)_{w \in R^{3}} = \sum_{j = 1}^{n} \bigl(y_{j} - \psi \bigl(1 + x_{j} + x_{j}^{2} \bigr)^{T} \bigr)^{2}. $$

Next, we can use Algorithm 1 to get the subsequent outcomes. \(w_{2} = 0.1345,w_{1} = - 2.1925,w_{0} = 7.0762\).

4.3 Solving system of linear equations in electrical engineering

The main challenge is solving complex systems of linear equations generated from linear circuits with many components. The first CG formula was suggested by Hestenes and Steifel [3] in 1952 to solve the linear equation systems. The linear equation system is presented in the format

$$ Qx = b. $$

In the case where the matrix Q is symmetric and positive definite, it may be regarded as a method for resolving a corresponding quadratic function.

$$ \min f(x) = \frac{1}{2}x^{T}Qx - b^{T}x. $$

To see the similarities between the above equations, differentiate \(f(x)\) in relation to x and make the gradient zero. In other words,

$$ \nabla f(x) = Qx - b = 0. $$

The following example illustrates using the CG method to solve a linear equation system generated from the circuit.

Example 1

[29, 30]. Consider the circuit shown in Fig. 6. To create the loop equations, use loop analysis. Then, Algorithm 1 is applied to find the solution for the unknown currents.

Figure 6
figure 6

The circuit of Example 1

Full size image

Kirchhoff’s Current Law (often abbreviated as KCL) asserts that all currents entering and leaving a node must sum up to zero algebraically. This law describes the flow of charge into and out of a wire junction point or node. The circuit in Fig. 6 has four loops; thus, Kirchhoff’s Loop Equations can be written as follows:

$$\begin{aligned} &14 \mathrm{L}_{1} - 3 \mathrm{L}_{2} - 3 \mathrm{L}_{3} + 0 \mathrm{L}_{4} = 0, \\ &- 3 \mathrm{L}_{1} + 10 \mathrm{L}_{2} + 0 \mathrm{L}_{3} - 3 \mathrm{L}_{4} = 0, \\ &- 3 \mathrm{L}_{1} + 0 \mathrm{L}_{2} + 10 \mathrm{L}_{3} - 3 \mathrm{L}_{4} = 0, \\ &0 - 3 \mathrm{L}_{2} - 3 \mathrm{L}_{3} + 14 \mathrm{L}_{4} = 0, \end{aligned}$$

where the following is one way to write the system of equations:

$$ \begin{bmatrix} 14 & - 3 & - 3 & 0 \\ - 3 & 10 & 0 & - 3 \\ - 3 & 0 & 10 & - 3 \\ 0 & - 3 & - 3 & 14 \end{bmatrix} \begin{bmatrix} L1 \\ L2 \\ L3 \\ L4 \end{bmatrix} = \begin{bmatrix} 0 \\ - 5 \\ 5 \\ 0 \end{bmatrix}. $$

Thus, we can write the system \(Qx = b\) as follows:

$$ Q = \begin{bmatrix} 14 & - 3 & - 3 & 0 \\ - 3 & 10 & 0 & - 3 \\ - 3 & 0 & 10 & - 3 \\ 0 & - 3 & - 3 & 14 \end{bmatrix},\qquad x = \begin{bmatrix} L1 \\ L2 \\ L3 \\ L4 \end{bmatrix} = \begin{bmatrix} x_{1} \\ x_{2} \\ x_{3} \\ x_{4} \end{bmatrix},\qquad b = \begin{bmatrix} 0 \\ - 5 \\ 5 \\ 0 \end{bmatrix} $$

where Q denotes positive definite and symmetric matrix. Thus, we have the following form:

$$ f(x) = \frac{1}{2}x^{T}Qx - b^{T}x, $$

i.e.,

$$ f(x_{1},x_{2},x_{3},x_{4}) = \frac{1}{2} [ x_{1} x_{2} x_{3} x_{4} ] \begin{bmatrix} 14 & - 3 & - 3 & 0 \\ - 3 & 10 & 0 & - 3 \\ - 3 & 0 & 10 & - 3 \\ 0 & - 3 & - 3 & 14 \end{bmatrix} \begin{bmatrix} x_{1} \\ x_{2} \\ x_{3} \\ x_{4} \end{bmatrix} - [0\ 5\ -\ 5\ 0] \begin{bmatrix} x_{1} \\ x_{2} \\ x_{3} \\ x_{4} \end{bmatrix}. $$

After simple calculations, we compute the following function:

$$ f(x_{1},x_{2},x_{3},x_{4}) = 7x_{1}^{2} + 5x_{2}^{2} + 5x_{3}^{2} - 3x_{1}x_{2} - 3x_{3}x_{1} - 3x_{2}x_{4} - 3x_{3}x_{4} + 5x_{2} - 5x_{3}. $$
(20)

Using Algorithm 1, we can find the following solution for Eq. (20)

$$ ^{x_{1} = 0,x_{2} = - 0.5,x_{3} = 0.5,x_{4} = 0}, $$

and the function value is

$$ ^{f = - 2.5}. $$

5 Conclusion

We have outlined a three-term CG method in the present research that satisfies both the convergence analysis and the descent condition via an SWP line search. Moreover, we have presented numerical results with different values of sigma, showing that the new search direction strongly outperformed alternative approaches with regard to the number of iterations as well as was very competitive when it came to the number of functions, gradients, and CPU time evaluated. Additionally, we have offered an application of the new search direction of image restoration, regression analysis, and solving linear systems in electrical engineering. Algorithm 1 demonstrates its efficiency in restoring destroyed images from degraded pixel data. In addition, using Algorithm 1 to solve a system of linear equations is easier than other traditional methods. In regression analysis, we found Algorithm 1 useful for obtaining the value of regression parameters. In future research, we intend to utilize CG methods in machine learning, mathematical problems in engineering, and neural networks.