1 Introduction: what is hybrid modeling?

If we take a look at Gartner’s 2018 Hype Cycle of Emerging Technologies [43], Deep Learning has been at the top of inflated expectations and should now be moving towards the plateau of productivity. Indeed, machine learning and more general artificial intelligence technologies recently have spurred a lot of interest in the applied mathematics and industrial communities, see for instance [5, 10, 45], and [21] for an introduction.

The idea of combining physics with data has a long history. Following [10, p. 57], we call modeling based on first principles the Newtonian paradigm. Newton’s laws of motion provided (within their range of validity) “for the first time a unified quantitative explanation for a wide range of observations” [44]. Conversely, Johannes KeplerFootnote 1 started from astronomer Tycho Brahe’s and own measurement data, and worked towards a mathematical description to fit the measured data. Following again [10], we call this approach the Keplerian paradigm. Both paradigms complement each other. For a simple enough model system, Kepler’s laws can be derived from Newton’s theory. Conversely, starting from a two-body model system, actual trajectories of celestial bodies can be modeled by Newton’s laws plus data-driven terms that correct for perturbations due to effects that are not present in the model.

In modern terms, we call this complementary approach hybrid modeling.

Definition

Hybrid models combine first principle-based models with data-based models into a joint architecture, supporting enhanced model qualities, such as robustness and explainability.

First principles express formalized domain knowledge. For the purpose of this paper the domain knowledge results from physics. But there are other possibilities, such as statistics (e.g., probabilistic graphical models [3, Ch. 8]) or discourse (e.g., ontologies [16]). Data may be obtained from any source, in particular from observation or simulation. We find also the somewhat narrower terms scientific machine learning [29], physics-based machine learning [39] and predictive data science [45], respectively.

Consider a high-dimensional manifold that contains some big data. It might be that a submanifold can be identified, which is dictated to us by the laws of physics, e.g. regarding admissible system dynamics. Learning algorithms can then be used to project the data into this submanifold. In other words, the structure of submanifold embeds physical constraints. A classical example is Kálmán filtering [23]. Kálmán filtering was actually an enabling technology for the moon landing in 1969, where the goal was landing within ≈500 m after ≈400,000 km of travel. More preference is given to physics or data, depending on the level of uncertainty. Kálmán filtering can be recognized as recursive Bayesian estimation. A more sophisticated example is presented in Sect. 2. Ensemble Kálmán filtering is used in weather forecasting centers worldwide [37]. They have to deal with about 106 incoming data points per hour, and mathematical models with about 109 states. This use case is similar to digital twinning, since data from the field is acquired and used to update the models. Citing [45, p. 39]: “Learning from data through the lens of models is a way to exploit structure in an otherwise intractable problem.”

Looking closer into engineering, we notice that a large class of physics models can be decomposed into conservation laws and constitutive laws [40, Ch. 1.3], [41]. The conservation laws are of topological nature and can therefore be discretized easily, leaving little room for data-driven techniques. The situation is different for the constitutive relations, which are of metric nature, and encode phenomenological material properties. Except for simple media (local, linear) there are many potential complications (non-local, hysteretic, non-linear, multi-scale, multi-physics, etc.). Here, data-driven models can be useful, provided that the models fulfil certain admissibility criteria, which can often be expressed in terms of invariance with respect to symmetry groups (orthogonal group, Lorentz group, etc.). This is demonstrated in Sect. 3.

In physics-based modeling, one often aims at sparse models, by exploiting the principle of locality [18],Footnote 2 or at least at low-rank representations. Some popular hybrid approaches model physics by partial differential equations plus boundary conditions, represent the solution space by a deep neural network, and learn the solution in a data-driven fashion (Deep Ritz [11], Physics-Informed Neural Networks, PINNs [32]). In general, the notion of sparsity is then lost, though. Recently, Sparse, Physics-based, and partially Interpretable Neural Networks (SPINNs) were proposed, where sparsity is recovered by exploiting concepts from traditional mesh-free numerical methods [33].

To sum up, hybrid modeling has the potential to improve the Pareto tradeoff between simulation accuracy and simulation cost significantly, and therefore bring scientific computing in engineering to the next level. In the remainder of the paper we will showcase this by some recent achievements.

2 Blending data with physics [30]

This section deals with the characterization of normal and superconducting magnets of CERN’s accelerator complex. Due to the complex interplay of iron saturation, eddy currents and magnetic hysteresis, numerical field simulation alone fails to achieve the required accuracy for particle tracking applications. However, after a well-defined excitation current cycling, the physical state of the magnet is reproducible. The magnets are therefore precycled and the static magnetic field is characterized by measurements. It is beneficial to model the magnetostatic field by the Boundary Element Method (BEM). In this way, the reconstructed field is locally an exact magnetostatic solution, no domain discretization inside the air gap is required and high convergence rates are achieved for field evaluations [30].

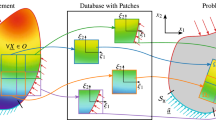
In the sequel, the field is represented by a double layer potential. The dipole layer is located on the boundary of the domain of interest, which follows the particle trajectory, such as the curved domain illustrated in Fig. 1. Following an isogeometric approach, the domain itself is described by NURBS (Non-Rational Uniform B-Splines) surfaces and the double layer density is discretized by higher oder basis splines [8]. This gives rise to a state vector \(\boldsymbol{\nu}\in\mathbb{R}^{N}\), with N degrees of freedom. The measurement data \(\boldsymbol{y}\in\mathbb{R}^{M}\) relates to the state vector ν, by means of the observation operator \(\boldsymbol{H} \in\mathbb{R}^{M\times N}: \boldsymbol{\nu}\to\boldsymbol{y}\).

Figure 1
figure 1

Magnetic field described by boundary elements on a curved geometry following the particle trajectory. Right: Sampled data obtained from Hall probe measurements. Middle: Boundary mesh described on a NURBS geometry. Left: Resulting double layer potential and B-field evaluation in the center of the domain

Full size image

Spatial field sampling is achieved by using alignment machines and magnetic field sensors, such as Hall probes or induction coils, which are supported on stages or beams with finite stiffness. To achieve a reasonable total measurement duration the data is almost always acquired on the fly. This means that the machine is performing moves along lines and a measurement is triggered whenever a certain distance is passed. As field gradients are large in the fringe field region of a magnet, most of the measurement uncertainty is due to positioning errors and vibrations. Such errors are perturbing the observation operator H. To quantify the impacts, the perturbations \(\boldsymbol{d}\in\mathbb{R}^{6 M}\) may be introduced, encoding the degrees of freedom of a rigid body motion of the sensor, six for each of the M measurements. As perturbations are small deviations from zero, the linearization \(\boldsymbol{y} = \boldsymbol{H}(\boldsymbol{\nu}) + \partial _{\boldsymbol{d}}\boldsymbol{H}(\boldsymbol{\nu}) \boldsymbol{d}\) is justified. The operator \(\partial_{\boldsymbol{d}}\boldsymbol{H}\) encodes the derivatives of H with respect to d. A hybrid model is established, by estimating the state vectors ν and d from measurement data. Considering both ν and d as unknown random variables, Bayesian inference provides the framework to utilize all the available knowledge. To this end, Bayes rule is applied to the joint probability density function \(p(\boldsymbol{\nu},\boldsymbol {d}|\boldsymbol{y}) \propto p(\boldsymbol{y}|\boldsymbol{\nu },\boldsymbol{d})p(\boldsymbol{\nu})p(\boldsymbol{d})\).

The distributions \(p(\boldsymbol{\nu})\) and \(p(\boldsymbol{d})\) are called prior distributions as they encode knowledge about ν and d, which has been available before the data y was collected. Due to the dependency of y on ν and d the explicit computation of the statistical moments of \(p(\boldsymbol{\nu },\boldsymbol{d}|\boldsymbol{y})\) is infeasible. However, under normal distribution assumptions, the conditionals \(p(\boldsymbol{\nu }|\boldsymbol{d},\boldsymbol{y})\) and \(p(\boldsymbol{d}|\boldsymbol{\nu },\boldsymbol{y})\) take on the least squares forms,

$$ \left . \begin{aligned} &p(\boldsymbol{\nu}|\boldsymbol{d}, \boldsymbol{y}) \\ &p(\boldsymbol{d}|\boldsymbol{\nu},\boldsymbol{y}) \end{aligned} \right \} \sim\exp \biggl( -\frac{1}{2} \bigl\Vert \boldsymbol{A}_{i}(\boldsymbol{\nu },\boldsymbol{d}) - \boldsymbol{b}_{i} \bigr\Vert ^{2} \biggr),\quad i \in\{ \boldsymbol{\nu},\boldsymbol{d}\} , $$
(1)

\(\boldsymbol{A}_{\boldsymbol{\nu}}\in\mathbb{R}^{(M+N)\times(M+N)}\), \(\boldsymbol{b}_{\boldsymbol{\nu}}\in\mathbb{R}^{M+N}\), \(\boldsymbol {A}_{\boldsymbol{d}}\in\mathbb{R}^{(M+6M) \times(M+6M)}\), \(\boldsymbol {b}_{\boldsymbol{d}}\in\mathbb{R}^{M+6M}\). With the conditionals at hand, samples from the joint distribution \(p(\boldsymbol{\nu},\boldsymbol{d}|\boldsymbol{y})\) can be computed by Gibbs sampling [35], according to Algorithm 1. As the mechanical degrees of freedom can be considered as uncorrelated between the moves, samples are drawn move-by-move in a blockwise fashion. In Fig. 2 the sampled mean as well as the maximum and minimum values for the vertical sensor position over a single move are drawn. For verification, an optical measurement was taken. Differences are within measurement precision.

Algorithm 1
figure a

Sampling from the posterior \(p(\boldsymbol{\nu},\boldsymbol {d}|\boldsymbol{y})\)

Full size image
Figure 2
figure 2

Recovered vertical sensor position \(w(t)\) determined by sampling from the posterior, for a single move. Solid red line: sampled mean. Dashed grey lines: maximum and minimum values, respectively. Dashed blue line: measured sensor position, by using a laser tracker with an effective precision of ∼10\(~\mu\)m as ground truth for verification. Typical parameter values: \(K\sim N\sim10^{3}\), \(M\sim 10^{5}\), \(J\sim50\ldots10^{3}\)

Full size image

In case of a linear observation operator H, sampling \(\boldsymbol{\nu}_{k}\) from the high dimensional \(p(\boldsymbol{\nu }|\boldsymbol{d},\boldsymbol{y})\) is efficient, when implemented as the solution of the stochastic linear equation system [31]

$$\begin{aligned} &\bigl(\widetilde{\boldsymbol{H}}_{k}^{T} \boldsymbol{R}^{-1} \widetilde {\boldsymbol{H}}_{k} + \boldsymbol{L}_{\boldsymbol{\nu}} \bigr) \boldsymbol{\nu}_{k} = \widetilde{\boldsymbol{H}}_{k}^{T}\boldsymbol {R}^{-1}\boldsymbol{y} + \boldsymbol{L}_{\boldsymbol{\nu}}\boldsymbol { \nu}_{0} + \bigl(\widetilde{\boldsymbol{H}}_{k}^{T} \boldsymbol {R}^{-1/2} , \boldsymbol{L}_{\boldsymbol{\nu}}^{1/2} \bigr) \boldsymbol {\epsilon} , \\ &\quad \boldsymbol{\epsilon} \sim\mathcal{N}(\boldsymbol{0},\boldsymbol {I}_{M+N}) , \end{aligned}$$
(2)

where a Gaussian prior \(p(\boldsymbol{\nu})\sim\mathcal{N}(\boldsymbol {\nu}_{0},\boldsymbol{L}^{-1}_{\boldsymbol{\nu}})\) was selected. The vector \(\boldsymbol{\nu}_{0}\in\mathbb{R}^{N}\) is the prior expected value of the BEM state vector and \(\boldsymbol{L}_{\boldsymbol{\nu }}\in\mathbb{R}^{N\times N}\) is the prior precision matrix. The matrix \(\boldsymbol{R}\in\mathbb{R}^{M\times M}\) is a sparse, symmetric and positive definite covariance matrix of the sensor noise and \(\widetilde {\boldsymbol{H}}_{k}\in\mathbb{R}^{M\times N}\) is the perturbed observation matrix, which is constructed by changing the sensor position and orientation in H according to the mechanical state vector \(\boldsymbol{d}_{k}\), by leveraging the linearization of the observation operator in d.

Equation (2) follows from the conditional \(p(\boldsymbol{\nu}|\boldsymbol{d},\boldsymbol{y})\) and the linearity of the expected value function [2, 1.17]. The structure of \(\widetilde{\boldsymbol{H}}_{k}\) depends on the underlying field representation. Boundary element formulations give rise to dense discrete operators. Fast multipole methods can be applied to compress the products \(\widetilde{\boldsymbol{H}}_{k}^{T}\boldsymbol {y}\) and \(\widetilde{\boldsymbol{H}}_{k}\boldsymbol{x}\) if required. A solution to (2) can then be obtained by conjugate gradient iterations.

The matrix \(\widetilde{\boldsymbol{H}}_{k}^{T} \boldsymbol{R}^{-1} \widetilde{\boldsymbol{H}}_{k} + \boldsymbol{L}_{\boldsymbol{\nu}}\) corresponds to the inverse of the posterior covariance matrix. It therefore needs to be symmetric and positive definite. This can generally be achieved with the selection of a symmetric and positive definite prior precision matrix \(\boldsymbol{L}_{\boldsymbol{\nu}}\), (see e.g. [2, 5.1.1]). In the results presented in Fig. 2, dense operators were used and the solution of (2) was computed by using the Cholesky solver of the Eigen C++ library [17].

3 Data-driven field simulation [7, 13, 14]

This section is about data-driven field simulation for magnetostatic problems. Here, data-driven simulation is meant in the context of simulations directly on the material data and was first introduced in [26]. Consider Maxwell’s equations for magnetostatics,

$$ \operatorname{curl} \boldsymbol{H}=\boldsymbol{j} ,\qquad \operatorname{div} \boldsymbol{B}=0\quad \text{in }\Omega , $$
(3)

where H denotes the magnetic field strength, j the imposed source current density, B the magnetic flux density, and Ω the considered domain. The problem formulation (3) is completed with appropriate boundary conditions.

The phase space of the system is denoted by \(\mathcal {Z}:= \{\boldsymbol{z}(\boldsymbol{x}):= (\boldsymbol {B}(\boldsymbol{x}),\boldsymbol{H}(\boldsymbol{x}) ) \}\), \(\boldsymbol{x}\in\Omega\). The set of all states that fulfill (3) and the boundary conditions is denoted by \(\mathcal {M}\subset\mathcal{Z}\), the set of Maxwell-conforming fields.Footnote 3 Yet, to uniquely solve equations (3), a relation between B and H is necessary. Following the conventional approach, first a material law is assumed. Secondly, various fitting techniques are employed to compute the coefficients of the considered material law such that it fits best to the available measurement data. However, this approach suffers from approximation errors and additionally introduces epistemic uncertainties, i.e. the uncertainty is in the actual choice of the material model. Note that in contrast Maxwell’s equations are derived from first principles and accepted to be known exactly.

The hybrid solver acts directly on material data and circumvents the demand for a fixed material model. The measurement data is collected in a set \(\mathcal{D}^{*}:= \{\boldsymbol {z}^{*}_{i}:= (\boldsymbol{B}^{*}_{i},\boldsymbol{H}^{*}_{i} ) ,i=1,\ldots,N \}\), where N is the number of measurement points. This gives rise to a set of discrete material states \(\mathcal {D}:= \{\boldsymbol{z}\in\mathcal{Z} | \boldsymbol {z}(\boldsymbol{x})\in\mathcal{D}^{*} \forall\boldsymbol{x}\in \Omega \}\). “The material response is not known exactly and, instead, it is imperfectly characterized” [26, p. 95] by the set \(\mathcal{D}\).

The solution is given by the states \(\mathcal{M}\cap\mathcal{D}\) that fulfill Maxwell’s equations, while being compatible with the material states. However, for a finite number of data points, this set is very likely to be empty, \(\mathcal{M}\cap\mathcal{D}=\emptyset\). Therefore, we define the solution \(\mathcal{S}\) by the relaxed condition

$$ \mathcal{S}:=\mathrm{argmin} \bigl\{ d(\boldsymbol{z}, \mathcal{D}) ,\boldsymbol{z}\in\mathcal{M} \bigr\} , $$
(4)

where the distance function

$$ d(\boldsymbol{z}\in\mathcal{M},\mathcal{D}):=\min_{\boldsymbol {z}^{*}\in\mathcal{D}} \biggl\{ \frac{1}{2} \bigl\Vert \boldsymbol{B}-\boldsymbol{B}^{*} \bigr\Vert ^{2}_{\tilde{\nu}}+\frac {1}{2} \bigl\Vert \boldsymbol{H}-\boldsymbol{H}^{*} \bigr\Vert ^{2}_{\tilde{\mu }} \biggr\} $$
(5)

is defined in terms of the auxiliary norms \(\|\cdot\|_{\tilde{\nu },\tilde{\mu}}\), which are defined as

$$ \left . \begin{aligned} &\bigl\Vert \boldsymbol{B}- \boldsymbol{B}^{*} \bigr\Vert ^{2}_{\tilde{\nu}} = \int_{\Omega} \bigl(\boldsymbol{B}-\boldsymbol{B}^{*} \bigr)\cdot \tilde{\boldsymbol{\nu}} \bigl(\boldsymbol{B}-\boldsymbol{B}^{*} \bigr) \, \mathrm{d}\Omega , \\ &\bigl\Vert \boldsymbol{H}-\boldsymbol{H}^{*} \bigr\Vert ^{2}_{\tilde{\mu}} = \int_{\Omega} \bigl(\boldsymbol{H}-\boldsymbol{H}^{*} \bigr)\cdot \tilde{\boldsymbol{\mu}} \bigl(\boldsymbol{H}-\boldsymbol{H}^{*} \bigr) \, \mathrm{d}\Omega , \end{aligned} \right \} $$
(6)

where \(\tilde{\boldsymbol{\nu}}\), \(\tilde{\boldsymbol{\mu}}\) are diagonal tensors carrying the so-called weighting factors \(\tilde{\nu },\tilde{\mu}\). Note that \(\tilde{\nu},\tilde{\mu}\) are of computational nature and do not represent physical material properties. Yet, their choice affects the convergence rate of the numerical scheme [13]. The optimization problem (4) is essentially a double minimization problem, where we accept a solution z that conforms to Maxwell’s equations, while at the same time being closest to available measurement data. The solution of (4) is organized as a fixed point iteration, see Fig. 3 right. Let \(\tilde{d}(\boldsymbol{z}_{1},\boldsymbol{z}_{2})\) denote the distance function between the two states \(\boldsymbol{z}_{1}\) and \(\boldsymbol {z}_{2}\) defined over the auxiliary norms (6). For any given state \(\boldsymbol{z}\in\mathcal{Z}\) a modified finite element solver is used to compute the state \(\boldsymbol{z}^{\odot}\in\mathcal {M}\) such that \(\tilde{d}(\boldsymbol{z},\boldsymbol{z}^{\odot })=\mathrm{min}\). The solver is based on a variational principle discussed in [34]. The idea is to solve Ampère’s and Faraday’s laws exactly and shift the discretization error entirely into the constitutive relation.Footnote 4 Given \(\boldsymbol{z}^{\odot}\in\mathcal{M}\), a discrete optimization selects the closest measurement data points, see Fig. 3 left. These so-called active measurement data are associated with a state \(\boldsymbol{z}^{\times}\in\mathcal {D}\) such that \(\tilde{d}(\boldsymbol{z}^{\times},\boldsymbol {z}^{\odot})=\mathrm{min}\). State \(\boldsymbol{z}=\boldsymbol {z}^{\times}\) is the starting point for the next iteration. Under convexity assumptions this algorithm converges to the solution of (4). Furthermore, it has been shown in [4] that for linear elasticity, the conventional solution is recovered with measurement data sets of increasing size.

Figure 3
figure 3

Iterative hybrid solver. Left: Measured \(B(H)\)-characteristic. Active measurement data (red crosses) are closest to given field points (blue circles). Right: The outer fixed point iteration combines solutions of a variational principle by a modified finite element solver (blue circles) with discrete optimizations that select states associated with active measurement data (red crosses)

Full size image

The hybrid solver was applied to the model of a two-dimensional quadrupole magnet in [7] and [13]. The first work [7] extended the hybrid solver to cope with problems that feature domains where only measurement data is at hand and domains where the material law is known, e.g. in the case of vacuum. Such known material laws can be naturally included into the data-driven iterations. To analyze the performance of the hybrid solver, a strongly nonlinear soft-magnetic material was considered in the iron part of the quadrupole magnet. As a baseline, a standard magnetostatic finite element solution was considered, by discretizing 1/8 of the geometry with 6k piecewise linear elements. For the novel method, data was created by an equidistant sampling of the given non-linear \(B(H)\) characteristic, without adding noise. Global weighting factors \(\tilde {\nu},\tilde{\mu}\) were employed throughout. The results show that the relative error to the reference solution, the so-called energy-mismatch, decreases as more measurement data is employed, see the dashed line in Fig. 4. However, depending on \(N = 10^{2}\dots10^{4}\) the proposed method required \(50\dots 1300\) outer iterations for convergence. In [13] local weighting factors \(\tilde{\nu}(\boldsymbol {x}),\tilde{\mu}(\boldsymbol{x})\) have been introduced and defined as to be the local tangent on the current operation point \(\boldsymbol {z}^{\times}\). Particularly in the case of unbalanced and/or data-starved sets \(\mathcal{D}\), local weighting factors yield significant improvement in accuracy, see the solid line in Fig. 4. Moreover, approximately 55 iterations are needed irrespective of the cardinality of \(\mathcal{D}\).

Figure 4
figure 4

Data-driven field simulation. Left: Relative error to reference solution for global and local weighting factors, respectively, in dependence of the number of data points. Right: Field solution \(|\boldsymbol{B}_{x}|,|\boldsymbol{H}_{x}|\) of conventional approach (extended Brauer) and data-driven solution at the quadrature points of the finite element model

Full size image

A computationally demanding 3D inductor model was considered in [14], where real-world measurement data [1] was employed for the iron part. For comparison, an extended Brauer model [22] was constructed on the measurement data and utilized in a standard Newton solver. Figure 4, right shows the absolute value of the x-component of the magnetic fields for the data-driven solution as well as the solution computed with the extended Brauer model. Furthermore, the available measurement data is depicted in red. The solution of the hybrid solver clusters around the measurement data, which is expected due to the sparse data set. Here, the data-driven solution is next to the available measurement data in all regimes of the BH-curve. That does not hold for the extended Brauer model which provides a good approximation in the linear part, but fails to properly model the Rayleigh part as well as the saturation part of the BH-curve. Both approaches lead to an acceptable solution, yet the employed material is well understood and significant effort has already been spent in the material model. If a more complex material is utilized, the hybrid solver should outperform the conventional approach.

In summary it can be said that so far hybrid solvers fail to be as computationally efficient as standard methods, albeit lots of effort is spent to improve the performance [24, 27]. Yet, hybrid solvers are advantageous if complex or novel materials are considered, since the effort for matching a material model to the measurement data is abolished. Furthermore, by circumventing the demand for a fixed material model, no epistemic uncertainties arise.

4 Bayesian free-shape optimization [36]

Bayesian optimization (BO) is an optimization method to optimize a given function which is expensive to evaluate [12]. It is built upon a hybrid architecture that blends intricate physical models with a Bayesian machine learning technique, such as Gaussian Process (GP) regression. The resulting surrogate models are cheap to evaluate, including derivatives, and keep track of their interpolation uncertainty. The core idea of BO is to successively refine those surrogates in regions of design space that are close to optimal, which are however not known beforehand. Regions with high surrogate uncertainty might be optimal even though the mean interpolation says otherwise. Thus, surrogate refinement requires balancing exploration against exploitation during sampling, the so-called bandit problem.Footnote 5 There are different strategies for achieving a good balance. One strategy considers the best value achieved so far and computes the Expected Improvement (EI). The next sample is taken at the point with the largest EI; this yields yet another optimization problem. The BO algorithm stops if the EI drops below some threshold. The BO approach can be generalized in various ways, such as BO with noise, BO in several dimensions, and BO for several objectives.

As an industrial example we consider BO of a differential trace pair on a printed circuit board. Differential signalling benefits from high immunity against electromagnetic interference and low crosstalk. However, bend discontinuities in transmission lines introduce (i) reflection and (ii) differential-to-common-mode conversion. An optimal design hence requires multi-objective optimization of the geometry. A parametric case was studied in [15], while we aim at free-shape optimization. Figure 5 shows a schematic for system simulation. The trace pair with ports 1,1’ and 2,2’, respectively, is described by an equivalent electrical circuit (EEC). Mode converters admit a separation of differential mode (D) and common mode (C) signal components. The optimization objectives can be stated in terms of S-parameters:Footnote 6

Figure 5
figure 5

Schematic for system simulation: extracted equivalent electrical circuit (EEC) of the trace pair, surrounded by mode converters

Full size image

(i) reflection \(|S_{\mathrm{DD11}}|\stackrel{!}{=}\mathrm {min}\); (ii) mixed mode conversion \(|S_{\mathrm{CD21}}|\stackrel {!}{=}\mathrm{min}\).

The geometric setting is depicted in Fig. 6 left. The outer trace is fixed, while the inner trace has a free interior surface. The geometry is described by a finite element mesh, and the free surface can be re-shaped by mesh morphing. This corresponds to a high-dimensional design space with ≈200 dimensions. This should be put in contrast to the six-dimensional design space that was considered in [15]. The optimization problem is: Find the Pareto front for the shape of the free surface that minimizes the objectives.

Figure 6
figure 6

Trace pair with bend. Left: The outer trace is fixed, the inner trace has a free interior surface. Right: Shape gradient vectors at the free surface for the two objectives (i) and (ii)

Full size image

The ingredients for solving the optimization problem are: finite element electromagnetic field solver, EEC extraction, and adjoint sensitivity analysis. Figure 6 right shows the shape gradient vectors at the free surface for the two objectives (i) and (ii). The two gradient vector fields point in opposite directions, so the objectives are conflicting. However, the gradient fields are not exactly negatives of each other, so there is still subtle room for improvement.

The BO is extended to the multi-objective case as follows. The Pareto front is approached via a sequence of auxiliary optimization problems, each with respect to a certain 2D affine subspace of the high-dimensional design space. This particular affine subspace is spanned by the adjoint-based gradients; it is the subspace of maximum objective variance. For each optimization problem of the sequence, BO learns and optimizes GP surrogate models for the objective functions, restricted to this subspace. Once the intermediate Pareto front is converged in this subspace, new subspaces may be chosen on the intermediate Pareto front. Figure 7 shows the result of this algorithm, after only ≈100 design evaluations. Note that even subtle improvement potentials will be exploited by the hybrid free-shape optimizer.

Figure 7
figure 7

Converged Pareto front for the trace pair with bend (green dots). The algorithm was started with a parametrically optimized design (black dot). An optimized design from the Pareto front was selected as an example (red dot)

Full size image

5 Summary and outlook

We highlighted three examples of hybrid modeling, cf. Table 1. Further examples stem from other applied mathematics and industrial domains, and involve artificial neural networks, such as Physics Informed Neural Networks (PINNs) [25], Deep Learning (DL) with embedded physics simulation [6], or Field Inversion and Machine Learning (FIML) [9]. They will soon find their way into scientific computing in electrical engineering, too.

Table 1 Three examples of hybrid modeling
Full size table