Background

Hepatocellular carcinoma (HCC) is the third leading cause of cancer-related death, with insignificant clinical manifestations and concealed symptoms at the initial stage of the disease [1, 2]. Conventional medical imaging techniques such as computed tomography (CT) and magnetic resonance imaging (MRI) are often used for the initial examination in clinical practice. However, they can only generate structural images and lack tumor metabolic information [3]. Positron emission tomography (PET)/CT has emerged as a noninvasive functional imaging method that allows assessment of metabolic function in tumors by injecting glucose analogs as radiotracers [4].

Although static 18F-FDG PET imaging obtains several parameters, such as standard uptake values (SUV), metabolic tumor volume and total lesion glycolysis, it is insufficient to describe the metabolic processes of 18F-FDG [5]. Dynamic PET/CT imaging can track the distribution of 18F-FDG in tissues and derive some kinetic parameters that accurately describe the cellular metabolic processes of 18F-FDG to enhance diagnosis and therapy in various diseases, and compartmental modeling is routinely applied to estimate kinetic parameters [6, 7]. Sarkar et al. [8] demonstrated that dynamic 18F-FDG PET with tracer kinetic modeling has the potential to diagnose nonalcoholic steatohepatitis. Wang et al. [9] found that dynamic 18F-FDG PET with optimization-derived blood input function kinetic modeling can effectively distinguish liver lesions. Considering 60-min or more dynamic PET/CT is not easily available in routine clinical settings. Samimi et al. [10] reported that 5-min dynamic PET / CT plus a static PET/CT enables accurate and robust estimation of kinetic parameters in patients with liver metastases. Our previous studies [11, 12] also demonstrated that 5-min dynamic 18F-FDG PET/CT can provide blood flow and metabolic information that enhances the detection of HCC lesions [11], and derived perfusion and early-uptake PET/CT are feasible for diagnosing HCC and provide added functional parameters to enhance diagnostic performance [12].

Nonlinear least squares (NLLS) is commonly used to estimate compartment model parameters [10, 12,13,14], and its essence is to minimize the sum of squared errors of the measured and estimated values; however, NLLS easily falls into the local optimum in the process of parameter estimation, and the set initial value has a great influence on the results [15]. The gravitational search algorithm (GSA) is a swarm intelligent optimization algorithm that is based on Newtonian gravity and has a strong searching ability [16]. It is more stochastic, does not require initial values, and can perform better parameter estimation compared to NLLS; however, whether GSA can function well to estimate compartment model parameters with dynamic 18F-FDG PET/CT is unclear. Additionally, a dynamic chaotic gravitational search algorithm (DCGSA) is proposed to improve the exploration ability and global search ability to enhance parameter estimation. Therefore, this study evaluated the role of the compartmental parameters of 5-min 18F-FDG PET/CT estimated by NLLS, GSA and DCGSA for distinguishing HCC from background liver tissue.

Methods

Patients

This study was approved by the Institutional Review Committee (IRB) of the First People’s Hospital of Yun-nan Province (No. 2017YYLH035), informed consent was obtained from all the patients, and all the methods were performed in accordance with the Declaration of Helsinki.

We recruited 28 patients with clinically suspected HCC, and a 5-min dynamic PET/CT scan was added before conventional PET/CT. Ten patients were excluded because they had a non-HCC pathological diagnosis (n = 5), lacked a pathological diagnosis (n = 3), and had suboptimal imaging quality (n = 2).

Eighteen patients (17 males and 1 female) who had pathologically confirmed HCC were finally included in this study. Sixteen patients had a single lesion, and two patients had two lesions. A total of 20 HCC tumors that were confirmed by surgery (n = 14) or biopsy (n = 6) were used in this study, and the long axis of these tumors was 1.9–15.0 cm (average 6.5 ± 3.6).

Dynamic PET/CT

All examinations were performed using a Philips Ingenuity TF PET/CT scanner (Cleveland, OH, USA), and a Philips IntelliSpace Portal v7.0.4.20175 was used for postprocessing. In summary, after the patients had fasted for at least 6 h, blood glucose was verified. A low-dose liver CT scan (120 kV, 100 mAs) was performed for attenuation correction and image fusion. A 5-min dynamic PET scan was performed over the liver region after intravenous administration of 5.5 MBq/kg 18F-FDG. Dynamic PET data were divided into 16 frames using the following sampling schedule: 12 frames of 5 s and 4 frames of 60 s each. Dynamic PET images were then reconstructed using the standard ordered subsets expectation maximization (OSEM) algorithm.

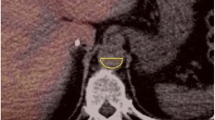
Regions of interest (ROIs) were drawn manually in the CT images of each patient, including the HCC, background liver tissue, aorta and portal vein (the extrahepatic portal vein rather than the intrahepatic portal vein), with manual slice-by-slice adjustment. An ROI was copied to the PET/CT images after image fusion, and time activity curves (TACs) consisting of the maximum SUV (SUVmax) extracted from each frame were generated. Figure 1 shows the ROIs drawn on a transaxial dynamic PET/CT image of a patient with HCC.

Fig. 1
figure 1

Region of interest drawn in dynamic PET/CT. a CT image, b PET/CT fusion image. The HCC is shown in the black circle, background liver tissue is shown in the green circle, the portal vein is shown in the red circle, and the aorta is shown in the yellow circle. Blood 18F-FDG enters the aorta, portal vein, spleen and HCC

Full size image

Kinetic modeling

A dual-input three-compartment model was used to assess the steady-state hepatic metabolism of 18F-FDG, as shown in Fig. 2 [17, 18].

Fig. 2
figure 2

A dual-input three-compartment model

Full size image

In Fig. 2, k1 (ml/min/ml) represents the rate constant of 18F-FDG from the blood to the liver tissue, and k2 represents the clearance rate back to the blood. k3 is the rate constant of further phosphorylation of 18F-FDG to 18F-FDG-6-phosphate and k4 is the dephosphorylation rate of phosphatase. CB(t) represents the 18F-FDG concentration in the blood:

$${C}_{B}\left(t\right)=HPI\times A\left(t\right)+\left(1-HPI\right)\times P\left(\mathrm{t}\right),$$
(1)

where A(t) represents the 18F-FDG concentration in the hepatic artery, and P(t) represents the 18F-FDG concentration in the portal vein. The HPI represents the hepatic artery perfusion index (the ratio of arterial blood volume to total blood volume). CM(t) represents the free-state 18F-FDG concentration and the metabolized 18F-FDG-6-phosphate concentration in the liver tissue compartment. CT(t) represents the curve of the tracer concentration in the tissue measured from the PET image over time and is the output function of the kinetic model:

$${C}_{T}\left(\mathrm{t}\right)=\frac{{K}_{1}}{{\alpha }_{2}-{\alpha }_{1}}\times \left[\left({k}_{3}+{k}_{4}-{\alpha }_{1}\right){e}^{-{\alpha }_{1}t}+\left({\alpha }_{2}-{k}_{3}-{k}_{4}\right){e}^{-{\alpha }_{2}t}\right]\otimes{C}_{B}\left(t\right)$$
(2)

where \({\alpha}_{2} \, {\text{and}} \, {\alpha}_{1}\) can be described as follows:

$${\alpha }_{1}=\frac{{k}_{2}+{k}_{3}+{k}_{4}-\sqrt{{({k}_{2}+{k}_{3}+{k}_{4})}^{2}-4{k}_{2}\times {k}_{4}}}{2}$$
(3)
$${\alpha }_{2}=\frac{{k}_{2}+{k}_{3}+{k}_{4}+\sqrt{{({k}_{2}+{k}_{3}+{k}_{4})}^{2}-4{k}_{2}\times {k}_{4}}}{2}$$
(4)

Estimation of the kinetic parameters

This study proposes an improved algorithm, the DCGSA, for the estimation of liver kinetic parameters. In the GSA, a solution space about the objective function is initialized randomly, with each individual in the space as one feasible solution in the objective function. With constant movement, individuals will move toward the most mass, which is the optimal solution of the search space [16]. The convergence speed of the GSA is faster, which makes it fall into a local optimum without global search [19].

In the DCGSA, the dynamic adjustment strategy is introduced for the gravitational constant of GSA to improve the algorithm exploration capacity and mining capacity. At the same time, inertia weights and chaotic sequences are added to the particle speed update process to avoid falling into a local optimum and to improve the global search ability. The overall flow of the DCGSA is shown in Fig. 3. The DCGSA can be simply divided into four parts: the initialization phase, the evaluation phase, the acceleration phase, and the update position phase.

Fig. 3
figure 3

Flowchart of the DCGSA

Full size image

Initialization phase

To start the search process for the DCGSA, the initial population of N individuals is randomly generated in the search space, which represents a set of model parameters (k1, k2, k3, k4 and the HPI). The position of each particle is represented by the following:

$${X}_{i} =\left({x}_{i}^{1}, {x}_{i}^{2},\cdots ,{x}_{i}^{d},\cdots ,{x}_{i}^{D}\right)\quad \text{for}\,\, i=1,\cdots ,N$$
(5)

where \({x}_{i}^{D}\) is the position of the ith individual in the D dimension.

Evaluation phase

The individual is evaluated according to the fitness function, defined as the sum of the squared errors squared errors of the experimental data and the fitted data:

$${fit}_{i}\left(t\right)= {\sum }_{i=1}^{N}{\left( {{C}_{T}}^{^{\prime}}\left(t\right)- {C}_{i}^{m}\left(t\right) \right)}^{2},$$
(6)

where N is the number of individuals, i is the index, \({{C}}{(}{{t}}{)}\) is the actual concentration of 18F-FDG in the obtained tissue, and \({{C}}_{{i}}^{{m}}{(}{{t}}{)}\) is the estimated concentration of 18F-FDG in the obtained tissue. After that, the individual continuously updates its inertial mass \({M}_{i}\left(t\right)\) during movement by the following equations, that is, to find the best model parameters in the search space:

$${{m}}_{{i}}\left({{t}}\right)= \frac{{{fi}}{{t}}_{{i}}\left({{t}}\right)- \text{worst}\left({{t}}\right)}{{\text{best}}\left({{t}}\right)-\text{worst}\left({{t}}\right)}$$
(7)
$${{M}}_{{i}}\left({{t}}\right)= \frac{{{m}}_{{i}}{(t)}}{{\sum }_{{j=1}}^{{N}}{{{m}}}_{{j}}{(t)}},$$
(8)

where best(t) and worst(t) are the best and worst fitness, respectively:

$$\mathrm{best}\left(t\right)= \underset{\mathrm{j}\in 1,\cdots ,\mathrm{N}}{\mathrm{min}}{\mathrm{fit}}_{\mathrm{j}}\left(\mathrm{t}\right)$$
(9)
$$\mathrm{worst}\left(t\right)= \underset{\mathrm{j}\in \{1,\cdots ,\mathrm{N}\}}{\mathrm{max}}{\mathrm{fit}}_{\mathrm{j}}(\mathrm{t})$$
(10)

Acceleration phase

The individual will be subjected to the force of other individuals in the search space. Based on the law of universal gravitation, the force \({\text{F}}_{\text{ij}}^{\text{d}}\left({\text{t}}\right)\) of individual i by individual j is:

$${F}_{ij}^{d}\left(t\right)=G\left(t\right)\frac{{M}_{i}\left(t\right)\times {M}_{j}\left(t\right)}{{R}_{ij}\left(t\right)+ \varepsilon }\left({x}_{i}^{d}\left(t\right) - {x}_{j}^{d}\left(t\right)\right)$$
(11)

where Mi(t) and Mj(t) are the inertial masses of individuals i and j at time t, respectively, that is, the TACs calculated by a set of kinetic parameters. \(\epsilon\) is a small value to prevent errors. Rij(t) is the Euclidean distance between individuals i and j. G(t) is a gravitational constant that decreases with time t and is described by Eq. (12); it can affect the force and acceleration of the individual:

$$G\left(t\right)={G}_{0} {e}^{-\alpha \frac{t}{T}}$$
(12)

where \({\text{G}}_{0}\) is an initial value, α is a constant, t is the current number of iterations, and T is the maximum number of iterations. The traditional gravitational constant was not fully explored in the early stage of iteration, and fell into a local optimum [20]. Lei et al. [21] introduced a self-adaptive gravitational constant, and Seyedali et al. [22] used chaotic map** to adjust the gravitational constant.

Therefore, this paper proposes a new gravitational constant expression, introducing an improved dynamic adjustment strategy, which contains a random variable as follows:

$${G}{{^{\prime}}\left(t\right)}={G}_{0} {e}^{-\alpha \frac{t}{{T}^{1.5}} \times \left({rand}_{t}+\frac{t}{T}\right)},$$
(13)

where \({\text{rand}}_{\text{t}}\) is a random number in (0,1). \(G{^{\prime}}\left(t\right)\) adopts a large step and long movement in the early stage of iteration to increase the particle exploration ability and enough time for optimization. Random variables can abruptly change the gravitational constant during iterations, improving the ability of particles to jump out of the local optimum. The process of moving in small steps is adopted in the later stage of iteration, which effectively avoids the premature convergence of particles and improves the mining capacity.

The resultant force of each particle is calculated as follows:

$${F}_{i}^{d}\left(t\right)=\sum_{j\in Kbest,j\ne i}{rand}_{j}{F}_{ij}^{d}\left(t\right)$$
(14)

where \({\text{Kbest}}\) decreases with the number of iterations, the initial value is N, and \({\text{rand}}_{\text{j}}\) is a random number between the interval (0, 1). The acceleration of particle i at time t is calculated as follows:

$${a}_{i}^{d}\left(t\right)= \frac{{F}_{i}^{d}(t)}{{M}_{i}(t)}$$
(15)

Update position phase

In each iteration, the particles update their velocity and position as follows:

$${v}_{i}^{d}\left(t+1\right)= {rand}_{i} \times {v}_{i}^{d}\left(t\right)+ {a}_{i}^{d}\left(t\right)$$
(16)
$${x}_{i}^{d}\left(t+1\right)= {x}_{i}^{d}\left(t\right)+{v}_{i}^{d}(t+1)$$
(17)

where \({\text{rand}}_{\text{i}}\) is a uniformly distributed random number between the interval (0, 1). However, some particles move too fast in the moving process, thus flying out of the solution space. Li et al. [23] introduced inertia weight instead of random variables to restrict the particle velocity. Gao et al. [24] replaced random variables with chaotic sequences. Therefore, this paper adds inertia weight and chaotic sequence to the particle speed updating process to further limit the particle speed:

$${v}_{i}^{d}\left(t+1\right)={W}^{d}(t)\times {v}_{i}^{d}\left(t\right)+ {a}_{i}^{d}\left(t\right)$$
(18)
$${x}_{i}^{d}\left(t+1\right)={x}_{i}^{d}\left(t\right)+{v}_{i}^{d}(t+1)\times c(i)$$
(19)
$${W}^{d}\left(t\right)={\omega }_{max}-\frac{{\omega }_{max}-{\omega }_{min}}{T}\times t,$$
(20)

where \({\omega}_{\text{max}}\) and \({\omega}_{\text{min}}\) are the inertia weights (\({\omega}_{\text{max}}\)=0.7, \({\omega}_{\text{min}}\)=0.1, which is mainly based on experience), and c(i) is a chaotic sequence. A larger inertia weight can improve the exploration ability, and a smaller inertia weight can improve the mining ability. Moreover, the ergodicity and dynamics of the chaotic sequence have the ability to jump out of the local optimum.

Statistical analysis

Statistical analysis was performed using MedCalc version 13.0.0.0 (MedCalc software, Ostend, Belgium). The derived parameters are expressed as the mean ‍ ± ‍ standard deviation. The Student’s t-test was used to compare the estimated parameters between HCCs and background liver tissues. The box plot was used to assess the consistency of the estimated k1 and k3 for the different methods. The diagnostic performance of k1 and k3 among the three methods was compared using receiver operating characteristic (ROC) curve analysis. P < 0.05 indicated significant differences. The fitting quality of the TACs among the three methods was compared using the Akaike information criterion (AIC) and the Bayesian information criterion (BIC), and a smaller value represents better curve fitting.

Results

Kinetic parameters

 The kinetic parameters (k1, k2, k3 and k4) and the HPI obtained by the three methods are shown in Table 1.

Table 1 Parameter estimation results of the three methods
Full size table

NLLS yielded a significant difference in HCCs due to its higher k1, k4 and the HPI than those in background liver tissue (P = 0.019, P < 0.001, and P < 0.001, respectively), and k2 and k3 did not show a significant difference between HCCs and background liver tissue (P = 0.067 and P = 0.411, respectively).

For the GSA, k1, k3, k4 and the HPI showed significant differences in distinguishing between HCCs and background liver tissue (P = 0.008, P < 0.001, P < 0.001, and P = 0.019, respectively), while k2 did not reach significance. (P = 0.688).

For the DCGSA, k1, k3 and the HPI were significantly higher in HCCs than in background liver tissue (P < 0.001, P < 0.001, and P < 0.001, respectively), and k2 and k4 were significantly lower in HCCs than in background liver tissue (P < 0.001 and P < 0.001, respectively).

The box plots of k1 and k3 estimated by the three methods are shown in Fig. 4. Compared with the GSA and NLLS, the DCGSA had a more compact data distribution and lower standard deviation of k1 and k3 in HCCs and in background liver tissues.

Fig. 4
figure 4

Box plots of k1 and k3 for the three methods

Full size image

Comparison of k 1 and k 3

Figure 5 shows the ROC curves of k1 and k3 estimated by the three methods. For k1, the diagnostic performance for differentiating HCCs from background liver tissue among the three methods was not significantly different (all P > 0.05). For k3, the DCGSA had higher diagnostic performance than the GSA and NLLS (P = 0.0024 and P = 0.0001, respectively); the diagnostic performance was not significantly different between the GSA and NLLS (P = 0.4420).

Fig. 5
figure 5

Comparison of the ROC curves of k1 and k3

Full size image

TAC fit quality

Figure 6 shows the mean and standard deviation of the AIC and BIC values for HCCs and background liver tissue using the DCGSA, GSA and NLLS. The DCGSA had the lowest AIC and BIC values among the three methods for HCCs, and the AIC and BIC values of the DCGSA were higher than those of the GSA and lower than those of NLLS for the background liver tissue.

Fig. 6
figure 6

AIC and BIC values of TAC fitting by the three methods

Full size image

Discussion

Conventional dynamic scans take 60 min or more, which is time-consuming, significantly limits the daily throughput of PET/CT scanners and the patients cannot remain immobile for a long period of time, thus it is not suitable for clinical settings. Based on previous study results, this paper used 5-min dynamic PET/CT for kinetic analysis to differentiate HCCs from background liver tissue [11, 10, 12]. The HPIs of HCC for NLLS, the GSA, and the DCGSA were 48.8 ± 32.8, 56.5 ± 13.8, and 66.7 ± 18.3, respectively, and the DCGSA was much closer to the expected clinical value. Most patients with HCC have a history of liver cirrhosis, which leads to an increase in the arterial blood supply of normal liver tissue [31]. When using the GSA and NLLS, the respective HPIs of normal liver tissue were 10.9 ± 15.7 and 21.8 ± 7.3 and were much lower than expected. However, the HPI of the DCGSA was 31.0 ± 9.2 and is closer to clinical practice.

Many glucose transporters (Gluts), which transport 18F-FDG from the blood into hepatocytes, are distributed on the plasma membrane of hepatocytes, and 18F-FDG is phosphorylated to 18F-FDG-6-phosphate by hexokinase (HK). The expression of Gluts is significantly higher in many cancer cells than in normal cells, and the uptake of glucose is increased. In addition, the expression of hexokinase and its affinity or functional activity of glucose phosphorylation is generally higher in cancer cells [32,33,34,35]. The transport rate k1 and phosphorylation rate k3, which are the parameters of major interest, are often used for quantitative analysis to achieve the diagnosis and assessment of HCC. Zuo et al. [36] reported the potential of using k1 to noninvasively evaluate human liver inflammation. Geist et al. [13] compared four different kinetic models for kinetic modeling of HCC and demonstrated significant differences in k3 between HCC and background liver tissue in all models.

In this study, k1 and k3 were greater in HCC than in background liver tissue by using the GSA and DCGSA, which is consistent with previous studies, implying increased Glut and HK activity in HCC [10, 37]. Meanwhile, the box plots showed higher consistency of k1 and k3 estimated with the DCGSA compared with NLLS and the GSA. Comparison of the ROC curves showed that the DCGSA had the highest diagnostic performance for k3 and was significantly higher than that of the GSA and NLLS.

G6P activity and the dephosphorylation rate k4 are higher in normal liver tissue than in HCC [6]. Our results showed that only k4 of the DCGSA conformed to the above clinical study, but that of the GSA and NLLS did not.

In summary, 18F-FDG kinetics can provide a comprehensive understanding of physiological systems and disease pathogenesis. The DCGSA can better estimate the kinetic parameters of the compartment model than the GSA and NLLS, which might play a significant role in clinical use for tumor characterization, monitoring the locoregional therapy and outcomes after resection.

This study has some limitations. First, the sample size of the experimental data is small. Second, there was a slight difference in ROI placement during TAC extraction, but we believe the influence was negligible. Third, this study did not explore lymph node involvement and other sites of metastasis, and we may explore other kinetic models in further studies. Fourth, the parameter estimation process is computationally expensive, and the proposed DCGSA might not be applicable to voxel level analysis for parametric images. It is necessary to improve the fitting algorithm to enhance the diagnostic performance and to develop more effective and efficient methods in our future research.

Conclusions

In this study, we demonstrated that the GSA can be used for parameter estimation of kinetic models on dynamic 18F-FDG PET/CT, and furthermore, the DCGSA was proposed to estimate the parameters more efficiently and reliably to distinguish HCC from background liver tissue.