1 Introduction

Water-lubricated bearing has been widely applied due to its low viscosity, low temperature rise, no pollution and etc. Spiral groove thrust bearing (SGTB) has advantages in hydrodynamic effect and stability. Nowadays, the water-lubricated spiral groove thrust bearing has been used in high-speed spindle. However, since inception cavitation number of water is larger than that of oil, cavitation phenomenon in water-lubricated bearings is more serious than the oil-lubricated bearing at high speed, and the water-lubricated bearing tends to fall into turbulent fluid condition when rotary speed exceeds a certain value.Hence,both cavitating effect and turbulent effect should be considered to model the high-speed water-lubricated bearing.

The cavitating and turbulent effects of water or oil bearings with different configurations have been investigated in previous studies. In the early studies on bearing cavitation, the different boundary conditions for lubrication equation including the Swift-Stiebe condition [1], the JFO condition [2], the Elrod condition [3] have been adopted to describe the cavitation effect of the lubricating film. With those conditions, solution of a two-phase flow in cavitated region can be avoided. However, the cavitating flow is not involved in those models. To overcome this problem,the cavitation lubricant is treated as two-phase mixed fluid. The two-phase mixed fluid models have been developed, those models can be divided into three types based on calculation approaches of gas phase volume fraction: (1) the model based on the R-P equation [4, 5] (2) the model based on gas solubility and surface tension of bubble [4, 6,7,8,‒9] (3) the model based on transport equation of the gas phase volume fraction [10,11,12,13,14,15]. In addition, with the rapid development of computational fluid dynamics (CFD) technology,some researchers have proposed performance analysis of bearings with the cavitation using the CFD software [7, 11, 16,17,18,‒19]. However, the interfacial effect (the momentum and energy transfer effect between phases at the interface of two phases) of the two-phase flow is not included in the above lubrication models of cavitating flow. Actually, the momentum and energy exchange between the two phases produces at the interface, so the interface effect is a very important feature for two-phase flow,which can not be ignored when modeling the high-speed water-lubricated bearing. In addition, the size distribution of the bubbles cannot be obtained using the present mixed fluid model or the CFD model. In our previous study, lubrication models considering the interface effect of two-phase flow have been proposed [20,21,22,23]. However, those models are established under heat isolation, and the bubble population equilibrium equation is solved directly. Since the bubble size probability density function is an unknown quantity, so it is difficult to determine the bubble size probability density function at the initial moment and at the interface. Furthermore, this kind of algorithm tends to unstable.

This study aims to establish a lubrication model for the water-lubricated spiral groove thrust bearings including both two-phase interfacial and fluid turbulent and bearing heat conduction effects. A generalized Reynolds equation considering the cavitation interface and turbulence, and an energy equation considering bearing heat conduction are derived. A population balance equation considering the breakage and coalescence of bubbles is introduced to describe the evolution of the size distribution of bubbles. A discrete interval method is employed to solve the bubble population balance equation. The influence of cavitation and turbulence on the dynamic characteristics of the SGTB is analyzed using the established model. The size distribution of cavitation bubbles and stiffness coefficient of water film are measured using a self-developed experimental device. A comparison of the simulating results with experimental ones is given to verify the proposed model.

2 Theoretical Model

2.1 Generalized Reynolds Equation Based on the Two-Phase Flow Theory

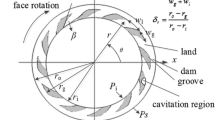
This paper studies the water-lubricated SGTB with the turbulent cavitating flow film (Figure 1). The classical Reynolds equation is not suitable for describing the bearing lubrication state, a Reynolds equation which contains turbulent and two-phase interfacial effects is needed, so the following basic assumptions are made for the modeling.

  1. (1)

    The bubbles in the cavitation flow be regarded as spheres.

  2. (2)

    The flow field is a small perturbation of the turbulent Couette flow [24].

  3. (3)

    The turbulent shear stress is defined by the law of wall, Reichardt [25] empirical formula is used to define the eddy viscosity coefficient.

  4. (4)

    The average viscosity along the film thickness is adopted in generalized turbulent Reynolds equation.

Figure 1
figure 1

Structure schematic of inward-pum** SGTB

Full size image

The spiral area is an irregular area in the polar coordinate system, a spiral coordinates system \((\eta ,\zeta )\) are adopted to improve numerical calculation accuracy. The polar coordinates \((\theta ,r)\) are converted into the spiral coordinates system \((\eta ,\zeta )\) as follows:

$$\begin{array}{ll}\zeta =r,\\ \eta =\theta -f\left(\zeta \right),\\ f\left(\zeta \right)=\frac{1}{\mathrm{cot}\beta }\mathrm{ln}\left(\frac{\zeta }{{\zeta }_{b}}\right).\end{array}$$
(1)

The spiral patterns before and after the coordinates conversion are shown in Figure 2.

Figure 2
figure 2

Coordinates transformation of spiral patterns

Full size image

A generalized turbulent Reynolds equation with cavitation interface effects and inertial effects in the \((\eta ,\zeta )\) coordinates is derived based on two-phase flow theory [26]:

$$\begin{array}{ll}\frac{\partial }{\partial \zeta }\left(\frac{{h}^{3}\zeta }{{\overline{\mu }}_{w}{k}_{r}}\frac{\partial {C}_{w}p}{\partial \zeta }\right)+\frac{\partial }{\partial \eta }\left(\left(\frac{{\zeta }^{2}{{f}^{^{\prime}}}^{2}\left(\zeta \right)}{{k}_{r}}+\frac{1}{{k}_{\theta }}\right)\frac{{h}^{3}}{{\overline{\mu }}_{w}\zeta }\frac{\partial {C}_{w}p}{\partial \eta }\right)\\ -\frac{\partial }{\partial \zeta }\left(\frac{{h}^{3}\zeta }{{\overline{\mu }}_{w}{k}_{r}}{f}^{^{\prime}}(\zeta )\frac{\partial {C}_{w}p}{\partial \eta }\right)-\frac{\partial }{\partial \eta }\left(\frac{{h}^{3}\zeta }{{\overline{\mu }}_{w}{k}_{r}}{f}^{^{\prime}}(\zeta )\frac{\partial {C}_{w}p}{\partial \zeta }\right)\\ =\frac{\partial }{\partial \eta }\left(\frac{hU{C}_{w}}{2}\right)+\frac{\partial }{\partial \eta }\left(\frac{{h}^{3}}{{\overline{\mu }}_{w}{k}_{\theta }}M(\eta )\right)\\ \quad+\, \frac{\partial }{\partial \zeta }\left(\frac{{h}^{3}{\rho }_{w}{\overline{u} }^{2}{C}_{w}}{{\overline{\mu }}_{w}{k}_{r}}\right)-\frac{\partial }{\partial \eta }\left({f}^{^{\prime}}(\zeta )\frac{{h}^{3}{\rho }_{w}{\overline{u} }^{2}{C}_{w}}{{\overline{\mu }}_{w}{k}_{r}}\right),\end{array}$$
(2)

where

$$\begin{array}{ll}{\overline{\mu }}_{w}=\frac{1}{h}\int\limits_{0}^{h}\,{\mu }_{w}\,\mathrm{d}z,\\ \overline{u }=\frac{1}{h}\int\limits_{0}^{h}\,u\mathrm{d}z,\end{array}$$
(3)
$$\begin{array}{ll}\frac{1}{{k}_{\theta }}=\int\limits_{0}^{1}\int\limits_{0}^{{z}^{*}}\frac{1}{{f}_{c}}\left(1-\frac{{g}_{c}}{{f}_{c}}\right)\left(\frac{1}{2}-{z}^{*\prime}\right)\mathrm{d}{z}^{*\prime}\mathrm{d}{z}^{*},\\ \frac{1}{{k}_{r}}=\int\limits_{0}^{1}\int\limits_{0}^{{z}^{*}}\frac{1}{{f}_{c}}\left(\frac{1}{2}-{z}^{*\prime}\right)\mathrm{d}{z}^{*\prime}\mathrm{d}{z}^{*},\\ {f}_{c}=0.4\left[{z}^{*}{h}_{c}^{*}-10.7th\left(\frac{{z}^{*}{h}_{c}^{*}}{10.7}\right)\right]+1,\\ {g}_{c}=0.2{z}^{*}{h}_{c}^{*}t{h}^{2}\left(\frac{{z}^{*}{h}_{c}^{*}}{10.7}\right),\\ {z}^{*}=\frac{z}{h},\end{array}$$
(4)
$${h}_{c}^{*}=\frac{h}{{\nu }_{w}}\sqrt{\frac{{\tau }_{c}}{{\rho }_{w}}}.$$
(5)

The following expression can be given for the logarithmic spirals:

$${f}^{\mathrm{^{\prime}}}\left(\zeta \right)=\frac{1}{\zeta \mathrm{cot}\beta }.$$
(6)

The circumferential velocity distribution of the water film is written as

$$u=\frac{U}{2}+\frac{{({h}_{c}^{*})}^{2}}{{R}_{c}}\frac{U}{{h}^{*}}{G}_{1}({z}^{*})-\frac{1}{{C}_{w}}\frac{{h}^{2}}{{\overline{\mu }}_{w}}(\frac{1}{\zeta }\frac{\partial ({C}_{w}p)}{\partial \eta }M(\eta )){G}_{2}({z}^{*}),$$
(7)

where

$$\begin{array}{ll}{G}_{1}\left({z}^{*}\right)=\int\limits_\frac{1}{2}^{{z}^{*}}\frac{1}{{f}_{c}}\mathrm{d}{z}^{*{{\prime}}},\\ {G}_{2}({z}^{*})=\int\limits_{0}^{{z}^{*}}\frac{1}{{f}_{c}}\left(1-\frac{{g}_{c}}{{f}_{c}}\right)\mathrm{d}{z}^{*{{\prime}}},\end{array}$$
(8)
$${C}_{w}=1-{C}_{g},$$
(9)
$${C}_{g}=\frac{\frac{\pi }{6}\int\limits_{0}^{\infty }{\varsigma }^{3}{f}_{eq}(\eta ,\varsigma )\mathrm{d}\varsigma }{1+\frac{\pi }{6}\int\limits_{0}^{\infty }{\varsigma }^{3}{f}_{eq}(\eta ,\varsigma )\mathrm{d}\varsigma },$$
(10)

where \({f}_{eq}(\eta ,\varsigma )\) is the equilibrium distribution function of the cavitation bubble diameter; \({f}_{eq}(\eta ,\varsigma )\mathrm{d}\varsigma\) represents the number of bubbles with diameter between \((\varsigma ,\varsigma +\mathrm{d}\varsigma )\) per unit volume of water at spatial coordinate η under the equilibrium state. The first term on the right-hand side of Eq. (2) is the hydrodynamic effect, the second term on the right side of Eq. (2) is the interface hydrodynamic effect, the third and fourth terms on the right side of Eq. (2) is the inertia hydrodynamic effect. The interface momentum transfer function includes the following three parts:

$$M\left(\eta \right)={M}_{1}\left(\eta \right)+{M}_{2}\left(\eta \right)+{M}_{3}(\eta ),$$
(11)

where \({M}_{1}(\eta )\) is the interface momentum transfer term due to mass transfer, \({M}_{2}(\eta )\) is the interface momentum transfer term due to viscous drag, \({M}_{3}(\eta )\) is the interface momentum transfer term due to surface tension. Because the film thickness is thin, the liquid velocity in \({M}_{1}\left(\eta \right),{M}_{2}(\eta )\) are approximated by the average velocity. \({M}_{1}(\eta ),{M}_{2}(\eta )\) and \({M}_{3}(\eta )\) are written as:

$$\begin{array}{ll}{M}_{1}=-\left[{\rho }_{w}\frac{\pi }{3}\int\limits_{0}^{\infty }{\varsigma }^{2}{f}_{eq}(\eta ,\varsigma )\mathrm{d}\varsigma \right]\overline{u }(\overline{u }-{u}_{b}),\\ {M}_{2}=\left[\frac{\pi }{3}{C}_{Ds}{\rho }_{w}\int\limits_{0}^{\infty }{\varsigma }^{2}{f}_{eq}(\eta ,\varsigma )\mathrm{d}\varsigma \right]{(\overline{u }-{u}_{b})}^{2},\\ {M}_{3}=2\pi \sigma \int\limits_{0}^{\infty }\varsigma {f}_{eq}(\eta ,\varsigma )d\varsigma ,\end{array}$$
(12)

where \({C}_{Ds}\text{=}\frac{24}{{R}_{e}}\).

Assume that the range of bubble diameter is divided into M smaller intervals, the diameter distribution of the bubbles is uniform in a smaller interval. So the equilibrium distribution function of bubble diameter in the kth smaller diameter interval \(({\varsigma }_{k},{\varsigma }_{k+1})\) can be expressed as:

$${f}_{eq}\left(\eta ,\varsigma \right)\approx {n}_{eq}^{k}\left(\eta \right)\delta \left(\varsigma -{x}_{k}\right),$$
(13)

where

$${n}_{eq}^{k}\left(\eta \right)=\int\limits_{{\varsigma }_{k}}^{{\varsigma }_{k+1}}{f}_{eq}(\eta ,\varsigma )\mathrm{d}\varsigma ,$$
(14)
$${x}_{k}=\frac{1}{2}\left({\varsigma }_{k}+{\varsigma }_{k+1}\right),$$
(15)

where \({n}_{eq}^{k}(\eta )\) is the number of bubbles in the kth diameter interval \(({\varsigma }_{k},{\varsigma }_{k+1})\). And the integral in Eq. (12) can be approximated as:

$$\begin{array}{ll}\int\limits_{0}^{\infty }{\varsigma }^{2}\,\,{f}_{eq}(\eta ,\varsigma )d\varsigma \approx \sum\limits_{k=1}^{M}{x}_{k}^{2}{n}_{eq}^{k}(\eta ),\\ \int\limits_{0}^{\infty }\varsigma\,\, {f}_{eq}(\eta ,\varsigma )d\varsigma \approx \sum\limits_{k=1}^{M}{x}_{k}{n}_{eq}^{k}(\eta ).\end{array}$$
(16)

The boundary conditions of Eq. (2) are as follows:

$$\begin{array}{c}{p|}_{\zeta ={\zeta }_{out}}=0,\\ {p|}_{\zeta ={\zeta }_{in}}={p}_{in},\\ p(\eta )=p(\eta +\frac{2\pi }{N}).\end{array}$$
(17)

The pressure at the groove-ridge boundary can be solved by using continuous condition of flow at the groove-ridge boundary. The finite volume at the groove-ridge boundary is shown in Figure 3.

Figure 3
figure 3

Finite volume separated by groove-ridge boundary

Full size image

In a finite volume at the groove-ridge boundary, the continuous condition of the flow can be written as

$${\sum }_{i}{Q}_{i}^{\eta }+{\sum }_{j}{Q}_{j}^{\zeta }=0,$$
(18)

where

$${Q}_{i}^{\eta }=\int\limits_{{\zeta }_{1}}^{{\zeta }_{2}}\left(\begin{array}{c}\zeta {f}^{^{\prime}}(\zeta )\left(\frac{{h}^{3}}{{C}_{w}{\bar {\mu }_{w}}}\left(\frac{\partial {C}_{w}p}{\partial \zeta }-\frac{1}{\zeta \mathrm{cot}\beta }\frac{\partial {C}_{w}p}{\partial \eta }\right)-\frac{{h}^{3}}{\bar {\mu }_{w}}\frac{\rho {\overline{u} }^{2}}{\zeta }\right)\frac{1}{{k}_{r}}\\ +\frac{Uh}{2}-\frac{{h}^{3}}{{\bar {\mu }_{w}}}\left(\frac{1}{\zeta {C}_{w}}\frac{\partial {C}_{w}p}{\partial \eta }-\frac{M(\eta )}{{C}_{w}}\right)\frac{1}{{k}_{\theta }}\end{array}\right)\mathrm{d}\zeta,\quad (i=BF,FC,DE,EA).$$
(19)
$${Q}_{j}^{\zeta }=\underset{{\eta }_{1}}{\overset{{\eta }_{2}}{\int }}\zeta \left(-\frac{{h}^{3}}{{C}_{w}{\bar {\mu }_{w}}}\left(\frac{\partial {C}_{w}p}{\partial \zeta }{f}^{^{\prime}}(\zeta )\frac{\partial {C}_{w}p}{\partial \eta }\right)\frac{1}{{k}_{\theta }}\frac{{h}^{3}}{{\bar {\mu }_{w}}}\frac{\rho {\overline{u} }^{2}}{\zeta }\frac{1}{{k}_{r}}\right)\mathrm{d}\eta.\,\, \left(j\text{=}AB,CD\right).$$
(20)

2.2 Turbulent Cavitating Flow Energy Equation

The temperature field of the cavitating flow water film can be obtained by solving the two-phase flow energy equation under high-speed conditions, and the following assumptions are adopted to simplify the energy equation.

  1. (1)

    The circumferential convection term is only considered in the energy equation, because the circumferential velocity is much larger than the radial velocity.

  2. (2)

    Turbulent pulsation heat conduction term is ignored.

  3. (3)

    The viscous dissipation term along the film thickness is only considered in the energy equation.

According to the above assumption, the energy equation in the \((\eta ,\zeta )\) coordinates in the spiral coordinate system can be simplified to

$${\rho }_{w}{c}_{v}\left(\frac{u}{\zeta }\frac{\partial \left({C}_{w}T\right)}{\partial \eta }\right)={C}_{w}{k}_{w}\frac{{\partial }^{2}T}{\partial {z}^{2}}+{C}_{w}\left({\tau }_{t}\left(z\right)\right)\left(\frac{\partial u}{\partial z}\right)+{E}_{int},$$
(21)

where

$$\left({\tau }_{t}\left(z\right)\right)=\frac{{({h}_{c}^{*})}^{2}{\overline{\mu }}_{w}U}{{R}_{c}h}+\frac{1}{{C}_{w}}\left(\frac{1}{\zeta }\frac{\partial ({C}_{w}p)}{\partial \eta }-M(\eta )\right)\left(z-\frac{h}{2}\right),$$
(22)
$$\frac{\partial u}{\partial z}=\frac{{({h}_{c}^{*})}^{2}}{{R}_{c}{h}^{*}}\frac{\partial {G}_{1}({z}^{*})}{\partial {z}^{*}}\frac{U}{h}-\frac{h}{{C}_{w}{\overline{\mu }}_{w}}\left(\frac{1}{\zeta }\frac{\partial \left({C}_{w}p\right)}{\partial \eta }M\left(\eta \right)\right)\frac{\partial {G}_{2}\left({z}^{*}\right)}{\partial {z}^{*}}.$$
(23)

The interface term \({E}_{\mathrm{int}}\) in the energy equation is expressed as

$$\begin{array}{c}{E}_{int}\approx {C}_{Ds}\pi {\left(\overline{u }-{u}_{b}\right)}^{2}\overline{u }\sum_{k=1}^{M}{x}_{k}^{2}{n}_{eq}^{k}\left(\eta \right)\\ -{\rho }_{w}{c}_{v}T(\overline{u }-{u}_{b})\pi \sum_{k=1}^{M}{x}_{k}^{2}{n}_{eq}^{k}(\eta )\\ +2\sigma \overline{u }\pi \sum_{k=1}^{M}{x}_{k}{n}_{eq}^{k}(\eta ).\end{array}$$
(24)

The following boundary conditions are adopted for the energy Eq. (21).

  1. (1)

    At the inlet of the spiral groove

    $$T\left(0,z\right)={T}_{0}.$$
    (25)
  2. (2)

    On the interface of the water film and the thrust disk

    $$T\left(\eta ,h\right)={T}_{d}(\eta ,0).$$
    (26)
  3. (3)

    On the interface of the water film and the stationary ring

    $$T\left(\eta ,0\right)={T}_{s}\left(\delta_{s} \right).$$
    (27)

The viscosity temperature relationship is written as

$${\mu }_{w}={\mu }_{w0}{e}^{(-b(T-{T}_{0}))}.$$
(28)

The water film temperature field can be obtained solved by simultaneously solving the energy Eq. (21), the heat conduction equation of the stationary ring and the heat conduction equation of the thrust disk.The surface temperature \({T}_{s}(\delta_{s} )\) of the stationary ring and surface temperature \({T}_{d}(\eta ,0)\) of the thrust plate are set as the boundary condition of the energy Eq. (21).

2.3 Heat Conduction Equation in Stationary Ring

The circumferential and radial heat conduction of the stationary ring are ignored, the heat conduction equation is simplified as follows:

$$\frac{{\partial }^{2}{T}_{\mathrm{s}}}{\partial {z}_{s}^{2}}=0 \left(0\le {z}_{s}\le {\delta }_{s}\right).$$
(29)

The boundary conditions of Eq. (29) are given as follows.

  1. (1)

    At the surface between the stationary ring and the fluid \(\left({z}_{s}={\delta }_{s}\right)\):

    $$\begin{array}{c}{-k}_{s}{\left.\frac{\partial {T}_{s}}{\partial {z}_{s}}\right|}_{{z}_{s}={\delta }_{s}}={\alpha }_{w}({\left.{T}_{s}\right|}_{{z}_{s}={\delta }_{s}}-{T}_{m}),\\ {T}_{m}=\frac{1}{h}\int\limits_{0}^{h}T\mathrm{d}z.\end{array}$$
    (30)
  2. (2)

    At the surface between the stationary ring and the ambient \(\left({z}_{s}={0}\right)\):

    $${k}_{s}{\left.\frac{\partial {T}_{s}}{\partial {z}_{s}}\right|}_{{z}_{s}=0}={\alpha }_{a}({{T}_{s}|}_{{z}_{s}=0}-{T}_{0}).$$
    (31)

The expression of the temperature at the surface of the stationary ring can be obtained from Eq. (29) and boundary conditions (30), (31). The temperature at the surface of the stationary ring is written as

$${{T}_{s}|}_{{z}_{s}={\delta }_{s}}=\frac{{T}_{m}-{T}_{0}}{\frac{{\alpha }_{w}}{{\alpha }_{a}}-\frac{{\alpha }_{w}}{{k}_{s}}{\delta }_{s}-1}+{T}_{m}.$$
(32)

2.4 Heat Conduction Equation in Thrust Disk

For the rotary thrust disk, the heat transfer effects in circumferential and radial directions are also ignored, the heat conduction equation is simplified as follows:

$$\frac{{k}_{d}}{{\rho }_{d}{c}_{d}}\frac{{\partial }^{2}{T}_{d}}{\partial {z}_{d}^{2}}=\omega \frac{\partial {T}_{d}}{\partial \eta }.\begin{array}{cc}& \left(0\le {z}_{d}\le {\delta }_{d}\right).\end{array}$$
(33)

The boundary conditions of Eq. (33) are given as follows:

  1. (1)

    At the surface between the thrust disk and the fluid \(({z}_{d}=0)\):

    $${k}_{d}{\left.\frac{\partial {T}_{d}}{\partial {z}_{d}}\right|}_{{z}_{d}=0}={\alpha }_{w}\left({{T}_{d}|}_{{z}_{d}=0}-{T}_{m}\right).$$
    (34)
  2. (2)

    At the surface between the thrust disk and the ambient \(({z}_{d}={\delta }_{d})\):

    $${k}_{d}{\left.\frac{\partial {T}_{d}}{\partial {z}_{d}}\right|}_{{z}_{d}={\delta }_{d}}=-{\alpha }_{a}\left({{T}_{d}|}_{{z}_{d}={\delta }_{d}}-{T}_{0}\right).$$
    (35)

2.5 Force Balance Equation of Bubble

The force balance equation of bubbles is expressed as

$${F}_{B}+{F}_{D}+{F}_{G}=0,$$
(36)

where

$${F}_{B}=\langle V\rangle ({\rho }_{w}-{\rho }_{g})g,$$
(37)
$${F}_{G}=({\rho }_{w}-{\rho }_{g})\langle V\rangle \frac{\mathrm{d}u}{\mathrm{d}t},$$
(38)
$$\frac{\mathrm{d}u}{\mathrm{d}t}=-\frac{1}{{\rho }_{w}}\frac{\partial p}{\zeta \partial \eta },$$
(39)
$$\langle V\rangle \approx \frac{\pi }{6}\sum_{k=1}^{M}{x}_{k}^{3}{n}_{eq}^{k}(\eta ),$$
(40)
$${F}_{D}=12\pi {\overline{\mu }}_{w}\langle {R}_{b}\rangle \left({u}_{b}-\overline{u }\right)\frac{1-{C}_{g}^\frac{5}{3}}{{\left(1-{C}_{g}\right)}^{2}},$$
(41)
$$\langle {R}_{b}\rangle \approx \frac{1}{2}\sum_{k=1}^{M}{x}_{k}{n}_{eq}^{k}\left(\eta \right).$$
(42)

The bubble velocity ub in the cavitating flow is calculated by the force balance Eq. (36). Substitute \({F}_{B}\), \({F}_{G}\), \({F}_{D}\) into Eq. (36), the bubble velocity ub can be expressed as [27]

$${u}_{b}=\overline{u }+\frac{{(1-{C}_{g})}^{2}({\rho }_{w}-{\rho }_{g})}{12\pi {\overline{\mu }}_{w}\langle {R}_{b}\rangle (1-{C}_{g}^\frac{5}{3})}\langle V\rangle \left(g+\frac{1}{{\rho }_{w}}\frac{\partial p}{\zeta \partial \eta }\right).$$
(43)

2.6 Population Balance Equation of Bubbles

Interface effect is an important phenomenon for cavitating flow, the momentum, mass and energy transfer occur through the interface between the gas-liquid. The interfacial area per unit volume liquid is positively correlated with the size distribution of the bubble, the bubble size distribution can be described by defining a probability density function \(f({\varvec{r}},\varsigma ,t)\), and the internal coordinates \(\varsigma\) are taken as bubble diameter in the model, and the \(f({\varvec{r}},\varsigma ,t)\mathrm{d}\varsigma\) represents the number of bubbles with between \((\varsigma ,\varsigma +\mathrm{d}\varsigma )\) at per volume liquid. Thus, integration of \(f\) over bubble diameter results in the total number of bubbles per volume liquid.The breakage, coalescence are two main factors affecting bubble size distribution in the cavitating flow, and bubble size distribution is predicted by the model of the breakage and coalescence processes of bubbles, this leads to the so-called population balance equation (PBE).

The PBE is a transport equation, the evolution of function \(f\) can be described by the PBE in the spiral coordinates \((\eta ,\zeta )\), the PBE is written as follows:

$$\begin{array}{ll}\frac{\partial f\left(\eta ,\varsigma ,t\right)}{\partial t}+{u}_{b}\frac{\partial }{\zeta \partial \eta }\left(f\left(\eta ,\varsigma ,t\right)\right)\\= -\,b(\varsigma )f(\eta ,\varsigma ,t)\\ \,\,+\int\limits_{\varsigma }^{{\varsigma }_{\mathrm{max}}}{h}_{b}\left(\xi ,\varsigma \right)b\left(\xi \right)f\left(\eta ,\xi ,t\right)\mathrm{d}\xi \\\,\, -\,f(\eta ,\varsigma )\int\limits_{0}^{{\varsigma }_{\mathrm{max}}}c(\varsigma ,\xi )f(\eta ,\xi ,t)\mathrm{d}\xi \\ \,\,+\,\frac{{\varsigma }^{2}}{2}\int\limits_{0}^{\varsigma }\frac{c\left({\left({\varsigma }^{3}-{\xi }^{3}\right)}^{1/3},\xi \right)}{{\left({\varsigma }^{3}-{\xi }^{3}\right)}^{2/3}}f\left(\eta ,{\left({\varsigma }^{3}-{\xi }^{3}\right)}^{1/3},t\right)f\left(\eta ,\xi ,t\right)\mathrm{d}\xi \\ \,\,+\,{S}_{c}(\varsigma ),\end{array}$$
(44)

where, the first term on the right-hand side of Eq. (44) represents breakup sink term of bubbles with diameter \(\varsigma\) per unit time, the second term on the right-hand side of Eq. (44) represents breakup source term of bubbles with diameter \(\varsigma\) per unit time, the third term on the right-hand side of Eq. (44) represents coalescence sink term of bubbles with diameter \(\varsigma\) per unit time,the fourth term on the right-hand side of Eq. (44) represents coalescence source term of bubbles with diameter \(\varsigma\) per unit time, the fifth term on the right-hand side of Eq. (44) represents bubbles with diameter \(\varsigma\) source term.

The initial condition for Eq. (44) is given

$$f(\eta ,\varsigma ,0)=0.$$
(45)

The breakage frequency \(b(\varsigma )\) is given as [28]:

$$b\left(\varsigma \right)=\frac{{\kappa }_{1}{\varepsilon }^{1/3}}{{\varsigma }^{2/3}}\mathrm{exp}\left(-\frac{\sigma {\kappa }_{2}}{{\rho }_{g}{\varepsilon }^{2/3}{\varsigma }^{5/3}}\right),$$
(46)
$$\varepsilon ={C}_{g}{u}_{b}g.$$
(47)

The daughter bubble size redistribution function \({h}_{b}(\xi ,\varsigma )\) is given as [28]

$${h}_{b}\left(\xi ,\varsigma \right)=\frac{4.8}{\xi }\mathrm{exp}\left(-4.5{\frac{(2\varsigma -\xi )}{{\xi }^{2}}}^{2}\right).$$
(48)

The coalescence closure is given as [28]:

$$\begin{array}{ll}c\left(\varsigma ,\xi \right)=0.05\frac{\pi }{4}{(\varsigma +\xi )}^{2}{\left[{\beta }_{c}{\left(\varepsilon \varsigma \right)}^{2/3}+{\beta }_{c}{(\varepsilon \xi )}^{2/3}\right]}^{1/2}\\ \mathrm{exp}\left(-\frac{{\left({r}_{c}^{3}{\rho }_{w}/16\sigma \right)}^{1/2}{\varepsilon }^{1/3}\mathrm{ln}\left({h}_{i}/{h}_{f}\right)}{{r}_{c}^{2/3}}\right),\end{array}$$
(49)
$${r}_{c}=\frac{1}{4}{\left(\frac{1}{\varsigma }+\frac{1}{\xi }\right)}^{-1}.$$
(50)

The value of parameter \({\beta }_{c}\) is taken as 2.48. The expression of source term \({S}_{c}(\varsigma )\) is

$${S}_{c}\left(\varsigma \right)={C}_{\rho }\sqrt{\left({p}_{v}-p\right)}\chi \left(\varsigma \right),$$
(51)

where

$$\chi \left(\varsigma \right)=\int\limits_{0}^{\varsigma }(\psi (\varsigma ,{\varsigma }_{c}){g}_{c}({\varsigma }_{c}))\mathrm{d}{\varsigma }_{c},$$
(52)
$${C}_{\rho }={\left(\frac{2}{3{\rho }_{w}}\right)}^{1/2}.$$
(53)

The redistribution function of bubble diameter \(\varsigma\) is given as

$$\psi \left({\varsigma }_{c},\varsigma \right)=\frac{{c}_{1}}{{\varsigma }_{c}}\mathrm{exp}\left(-\frac{{c}_{2}{(\varsigma -{\varsigma }_{c})}^{2}}{{\varsigma }_{\mathrm{max}}^{2}}\right).$$
(54)

The diameter distribution density function of the gas nucleus is given by experimental data [29]:

$${g}_{c}\left({\varsigma }_{c}\right)\approx \frac{\left(\alpha +1\right)}{{\varsigma }_{c\mathrm{max}}}{N}_{i}{\left(\frac{{\varsigma }_{c}}{{\varsigma }_{c\mathrm{max}}}\right)}^{\alpha },$$
(55)

where the value of parameter \(\mathrm{\alpha }\) is taken as − 10/3.

3 Calculation of Dynamic Characteristics of the SGTB

As shown in Figure 4, the origin of Cartesian coordinate is located at the center of the stationary ring. The possible independent motions of the thrust disk are axial movement along z axis and angular movements around x and y axes. The perturbed displacements and velocities of the thrust disk with respect to the steady equilibrium position are defined as \((\Delta z,\Delta {\varphi }_{x},\Delta {\varphi }_{y})\) and \((\Delta \dot{z},\Delta {\dot{\varphi }}_{x},\Delta {\dot{\varphi }}_{y})\). The assume initial position of the thrust disk is \(({h}_{0},{\varphi }_{x0},{\varphi }_{y0})\), the film thickness in quasi-equilibrium can be expressed as

Figure 4
figure 4

Motion of a SGTB

Full size image
$$h={h}_{0}+\Delta z+r\mathrm{cos}\theta\Delta {\varphi }_{y}-r\mathrm{sin}\theta\Delta {\varphi }_{x}.$$
(56)

The perturbations will have influence on the pressure distribution in the water film through Reynolds equation. The high order terms are ignored, the transient pressure of water film can be expressed as

$$p={p}_{0}+{p}_{z}\Delta z+{p}_{{\varphi }_{x}}\Delta {\varphi }_{x}+{p}_{{\varphi }_{y}}\Delta {\varphi }_{y}+ {p}_{\dot{z}}\Delta \dot{z}+{p}_{{\dot{\varphi }}_{x}}\Delta {\dot{\varphi }}_{x}+{p}_{{\dot{\varphi }}_{y}}\Delta {\dot{\varphi }}_{y}.$$
(57)

Substituting Eqs. (56) and (57) into Eq. (2), the zeroth and first-order perturbation generalized Reynolds equations in the \((\eta ,\zeta )\) coordinates system are obtained for the SGTB respectively,

$$Rey\left(\right)\left\{\begin{array}{c}{C}_{w}{p}_{z}\\ {{C}_{w}p}_{{\varphi }_{x}}\\ \begin{array}{c}{{C}_{w}p}_{{\varphi }_{y}}\\ {{C}_{w}p}_{\dot{z}}\\ \begin{array}{c}{{C}_{w}p}_{{\dot{\varphi }}_{x}}\\ {{C}_{w}p}_{{\dot{\varphi }}_{y}}\end{array}\end{array}\end{array}\right\}=\left\{\begin{array}{c}{q}_{z}\\ {q}_{{\varphi }_{x}}\\ \begin{array}{c}{q}_{{\varphi }_{y}}\\ {q}_{\dot{z}}\\ \begin{array}{c}{q}_{{\dot{\varphi }}_{x}}\\ {q}_{{\dot{\varphi }}_{y}}\end{array}\end{array}\end{array}\right\},$$
(58)

where the operator \(Rey()\) is defined as

$$\begin{array}{c}Rey()=\frac{\partial }{\partial \eta }\left(\frac{{h}_{0}^{3}}{{\overline{\mu }}_{w}\zeta }\left(\frac{{\zeta }^{2}{{f}^{^{\prime}}}^{2}(\zeta )}{{k}_{r}}\text{+}\frac{1}{{k}_{\theta }}\right)\frac{\partial }{\partial \eta }\right)\text{+}\frac{\partial }{\partial \zeta }\left(\frac{\zeta {h}_{0}^{3}}{{\overline{\mu }}_{w}{k}_{r}}\frac{\partial }{\partial \zeta }\right)\\ -\frac{\partial }{\partial \zeta }\left(\frac{{h}_{0}^{3}}{{\overline{\mu }}_{w}{k}_{r}}\zeta {f}^{^{\prime}}(\zeta )\frac{\partial }{\partial \eta }\right)-\frac{\partial }{\partial \eta }\left(\frac{{h}_{0}^{3}}{{\overline{\mu }}_{w}{k}_{r}}\zeta {f}^{^{\prime}}(\zeta )\frac{\partial }{\partial \zeta }\right),\end{array}$$

and \({q}_{j}\left(j=z,{\varphi }_{x},{\varphi }_{y},\dot{z},\dot{{\varphi }_{x}},\dot{{\varphi }_{y}}\right)\) can be found in Appendix.

The stiffness and dam** coefficients in the \((\eta ,\zeta )\) coordinates system can be found by the following integrals

$$\left[\begin{array}{ccc}{K}_{zz}& {K}_{z{\varphi }_{x}}& {K}_{z{\varphi }_{y}}\\ {K}_{{\varphi }_{x}z}& {K}_{{\varphi }_{x}{\varphi }_{x}}& {K}_{{\varphi }_{x}{\varphi }_{y}}\\ {K}_{{\varphi }_{y}z}& {K}_{{\varphi }_{y}{\varphi }_{x}}& {K}_{{\varphi }_{y}{\varphi }_{y}}\end{array}\right]=\underset{0}{\overset{2\pi }{\int }}\underset{{r}_{in}}{\overset{{r}_{out}}{\int }}\left[\begin{array}{c}-1\\ {G}_{1}(\eta ,\zeta )\\ -{G}_{2}(\eta ,\zeta )\end{array}\right]\{{p}_{z}{p}_{{\varphi }_{x}}{p}_{{\varphi }_{y}}\}\,\,\zeta \mathrm{d}\zeta \mathrm{d}\eta ,$$
(59)
$$\left[\begin{array}{ccc}{C}_{zz}& {C}_{z{\varphi }_{x}}& {C}_{z{\varphi }_{y}}\\ {C}_{{\varphi }_{x}z}& {C}_{{\varphi }_{x}{\varphi }_{x}}& {C}_{{\varphi }_{x}{\varphi }_{y}}\\ {C}_{{\varphi }_{y}z}& {C}_{{\varphi }_{y}{\varphi }_{x}}& {C}_{{\varphi }_{y}{\varphi }_{y}}\end{array}\right]=\underset{0}{\overset{2\pi }{\int }}\underset{{r}_{in}}{\overset{{r}_{out}}{\int }}\left[\begin{array}{c}-1\\ {G}_{1}(\eta ,\zeta )\\ -{G}_{2}(\eta ,\zeta )\end{array}\right]\{{p}_{\dot{z}}{p}_{{\dot{\varphi }}_{x}}{p}_{{\dot{\varphi }}_{y}}\}\,\,\zeta \mathrm{d}\zeta \mathrm{d}\eta ,$$
(60)

where

$$\begin{array}{c}{G}_{1}(\eta ,\zeta )=\zeta \mathrm{sin}(\eta +f(\zeta )),\\ {G}_{2}(\eta ,\zeta )=\zeta \mathrm{cos}(\eta +f(\zeta )).\end{array}$$
(61)

4 Numerical Calculation Method of Theoretical Model

The generalized Reynolds Eq. (2), energy Eq. (21), and PBE Eq. (44) are the main three governing equations for the bearing. The pressure field, temperature field, and bubble diameter distribution are obtained by solving these three equations respectively, and pressure field; temperature field and bubble diameter distribution are coupled to each other, and an iterative algorithm needs to be employed to solve these distributions. Eq. (2) and Eq. (21) are discretized using finite difference, the pressure field is obtained by solving discretization equations of Eq. (2) with the SOR iterative method, the temperature field is obtained by solving discretization equations of Eq. (21) with the step** method.

4.1 Calculation of Parameter \({{\varvec{h}}}_{{\varvec{c}}}^{\boldsymbol{*}}\)

The shear stress parameter \({h}_{c}^{*}\) of the Couette flow is included in turbulent velocity distribution Eq. (2), The governing equation for parameter \({h}_{c}^{*}\) is written as [24]

$${({h}_{c}^{*})}^{2}\int\limits_{0}^{1}\frac{\mathrm{d}{z}^{*}}{{f}_{c}({z}^{*},{h}_{c}^{*})}-{R}_{c}^{*}{h}^{*}=0.$$
(62)

Eq. (62) is a nonlinear equation with respect to \({h}_{c}^{*}\), the parameter \({h}_{c}^{*}\) can be solved using the Newton iteration method. The Newton iteration formula is expressed as \({h}_{c}^{*}\)

$${({h}_{c}^{*})}^{(k+1)}={({h}_{c}^{*})}^{(k)}-\frac{F\left({{h}_{c}^{*}}^{\left(k\right)}\right)}{{F}^{^{\prime}}\left({{h}_{c}^{*}}^{\left(k\right)}\right)},$$
(63)

where

$$F\left({h}_{c}^{*}\right)={\left({h}_{c}^{*}\right)}^{2}\int\limits_{0}^{1}\frac{\mathrm{d}{z}^{*}}{{f}_{c}\left({z}^{*},{h}_{c}^{*}\right)}-{R}_{c}^{*}{h}^{*}.$$
(64)

4.2 Numerical Solution of Bubble PBE

A discrete interval method [30] is employed to solve the bubble population balance Eq. (44). The procedure of the discrete interval method is as follows.

  1. (1)

    Assume that the entire bubble diameter range is divided into M smaller intervals. The bubble diameter is approximated uniform distribution at the kth representative diameter range \(({\varsigma }_{k},{\varsigma }_{k+1})\), then the \(f(\eta ,\varsigma )\) can be expressed by the bubble number density \({n}_{k}(\eta )\) at the kth representative diamete range \(({\varsigma }_{k},{\varsigma }_{k+1})\). Thus,

    $$f\left(\eta ,\varsigma ,t\right)\approx {n}_{k}\left(\eta ,t\right)\delta \left(\varsigma -{x}_{k}\right),$$
    (65)

    where

    $${n}_{k}\left(\eta ,t\right)=\int\limits_{{\varsigma }_{k}}^{{\varsigma }_{k+1}}f(\eta ,\varsigma ,t)\mathrm{d}\varsigma .$$
    (66)
  2. (2)

    The integrating the continuous Eq. (44) over a smaller range \(({\varsigma }_{k},{\varsigma }_{k+1})\). Thus,

    $$\begin{array}{ll}\frac{\partial }{\partial t}\int\limits_{{\varsigma }_{k}}^{{\varsigma }_{k+1}}f\left(\eta ,\varsigma ,t\right)\mathrm{d}\varsigma +{u}_{b}\frac{\partial }{\zeta \partial \eta }\left(\int\limits_{{\varsigma }_{k}}^{{\varsigma }_{k+1}}f\left(\eta ,\varsigma ,t\right)\mathrm{d}\varsigma \right)\\ = -\,\int\limits_{{\varsigma }_{k}}^{{\varsigma }_{k+1}}b(\eta ,\varsigma )f(\eta ,\varsigma ,t)\mathrm{d}\varsigma \\\,\, +\,\int\limits_{{\varsigma }_{k}}^{{\varsigma }_{k+1}}\mathrm{d}\varsigma \int\limits_{\varsigma }^{{\varsigma }_{max}}{h}_{b}(\xi ,\varsigma )b(\eta ,\xi )f(\eta ,\xi ,t)\mathrm{d}\xi \\ \,\,-\,\int\limits_{{\varsigma }_{k}}^{{\varsigma }_{k+1}}f(\eta ,\varsigma ,t)\mathrm{d}\varsigma \int\limits_{0}^{{\varsigma }_{max}}c(\varsigma ,\xi )f(\eta ,\xi ,t)\mathrm{d}\xi \\ \,\,+\,\frac{1}{2}\int\limits_{{\varsigma }_{k}}^{{\varsigma }_{k+1}}{\varsigma }^{2}\mathrm{d}\varsigma \int\limits_{0}^{\varsigma }\frac{c\left({\left({\varsigma }^{3}-{\xi }^{3}\right)}^{1/3},\xi \right)}{{\left({\varsigma }^{3}-{\xi }^{3}\right)}^{2/3}}f(\eta ,{\left({\varsigma }^{3}-{\xi }^{3}\right)}^{1/3},t)f(\eta ,\xi ,t)\mathrm{d}\xi \\\,\, +\,{C}_{\rho }\sqrt{\left({p}_{v}-p\right)}\int\limits_{{\varsigma }_{k}}^{{\varsigma }_{k+1}}\chi (\varsigma )\mathrm{d}\varsigma .\end{array}$$
    (67)
  3. (3)

    Since coalescence or breakage of bubbles of these diameters results in the formation of new bubbles whose diameters do not match with any of the node diameters, the new bubble diameter will be assigned to the adjoining node by introducing weight factor \(\gamma\), the weight factor \(\gamma\) can be determined by the total mass conservation of the bubble and the number of bubbles conservation. The expression is written as

    $$\begin{array}{c}{\gamma }_{k}{x}_{k}^{3}+{\gamma }_{k+1}{x}_{k+1}^{3}={\varsigma }^{3},\\ {\gamma }_{k}+{\gamma }_{k+1}=1.\end{array}$$
    (68)

Substituting Eq. (65) into Eq. (67), and the integral term at the right end of Eq. (67) is reconstructed using the mean value theorem on breakage frequency and coalescence frequency, so Eq. (67) can be closed, a closed set of equations with regard to \({n}_{k}\left(\eta ,t\right)\) can be written as

$$\begin{array}{ll}\frac{\partial {n}_{k}(\eta ,t)}{\partial t}+{u}_{b}\frac{\partial }{\zeta \partial \eta }({n}_{k}(\eta ,t))=-b(\eta ,{x}_{k}){n}_{k}(\eta ,t)\\ +\sum\limits_{i=k}^{M}{\alpha }_{k,i}b\left(\eta ,{x}_{i}\right){n}_{i}\left(\eta ,t\right)-{n}_{k}(\eta )\sum\limits_{i=1}^{M}c(\eta ,{x}_{k},{x}_{i}){n}_{i}(\eta ,t)\\ +\sum\limits^{j\ge i}_{j,i\, \, \, {x}_{k-1}\le {\left({x}_{j}^{3}+{x}_{i}^{3}\right)}^{1/3}\le {x}_{k+1}}\left(1-\frac{1}{2}{\delta }_{j,i}\right){\gamma }_{j,i}^{k}c\left(\eta ,{x}_{j},{x}_{i}\right){n}_{j}\left(\eta ,t\right){n}_{i}(\eta ,t)\\ +{C}_{\rho }\sqrt{\left({p}_{v}-p\right)}\int\limits_{{\varsigma }_{k}}^{{\varsigma }_{k+1}}\chi (\varsigma )\mathrm{d}\varsigma ,\end{array}$$
(69)

where

$${\gamma }_{j,i}^{k}=\left\{\begin{array}{ll}\frac{{x}_{k+1}^{3}-\left({{x}_{j}}^{3}+{x}_{i}^{3}\right)}{\left({x}_{k+1}^{3}-{x}_{k}^{3}\right)}, \quad {x}_{k}^{3}\le \left({{x}_{j}}^{3}+{x}_{i}^{3}\right)\le {x}_{k+1}^{3},\\ \frac{\left({{x}_{j}}^{3}+{x}_{i}^{3}\right)-{x}_{k}^{3}}{\left({x}_{k+1}^{3}-{x}_{k}^{3}\right)}, \quad\,\, {x}_{k-1}^{3}\le \left({{x}_{j}}^{3}+{x}_{i}^{3}\right)\le {x}_{k}^{3},\\ 0, \qquad \qquad\,\,\,\, \mathrm{else},\end{array}\right.$$
(70)
$$k=\mathrm{1,2},...,M-2 ,{\varsigma }^{3}={\varsigma }_{j}^{3}+{\varsigma }_{k}^{3},$$
$${\gamma }_{j,i}^{M-1}=\left\{\begin{array}{ll}\frac{\left({{x}_{j}}^{3}+{x}_{i}^{3}\right)}{{x}_{M-1}^{3}}, \quad\quad\quad {x}_{k-1}^{3}\le ({{x}_{j}}^{3}+{x}_{i}^{3})\le {\varsigma }_{M}^{3},\\ \frac{\left({{x}_{j}}^{3}{+x}_{i}^{3}\right)-{x}_{M-2}^{3}}{\left({x}_{M-1}^{3}-{x}_{M-2}^{3}\right)}, \quad \, {x}_{M-2}^{3}\le ({{x}_{j}}^{3}+{x}_{i}^{3})\le {x}_{M-1}^{3},\\ 0, \quad\quad\quad\quad\quad\,\, \mathrm{else},\end{array}\right.$$
(71)
$${\delta }_{j,i}=\left\{\begin{array}{ll}1,\quad j=i,\\ 0, \quad j\ne i.\end{array}\right.$$
(72)

Coefficient \({\alpha }_{k,i}\) is given as

$${\alpha }_{k,i}=\int\limits_{{x}_{k-1}}^{{x}_{k}}\frac{\left({\varsigma }^{3}-{x}_{k-1}^{3}\right)}{\left({x}_{k}^{3}-{x}_{k-1}^{3}\right)}{h}_{b}({x}_{i},\varsigma )\mathrm{d}\varsigma +\int\limits_{{x}_{k}}^{{x}_{k+1}}\frac{\left({x}_{k+1}^{3}-{\varsigma }^{3}\right)}{\left({x}_{k+1}^{3}-{x}_{k}^{3}\right)}{h}_{b}({x}_{i},\varsigma )\mathrm{d}\varsigma .$$
(73)

Eq. (69) is a set of first-order differential equations. Suppose that at a fixed time t, a set of nonlinear equations with regard to \({n}_{k,l}^{t}\) can be obtained by discretizing the second term on the left side of Eq. (69). The discrete equation at node \(l\) is written as follows:

$$\tilde{Q }({n}_{k,l}^{t})=0,$$
(74)

where the operator \(\tilde{Q }({n}_{k,l})\) are defined as

$$\begin{array}{ll}\tilde{Q }({n}_{k,l}^{t})=\frac{{u}_{b}}{{\zeta }_{m}}\frac{{n}_{k,l}^{t}-{n}_{k,l-1}^{t}}{\Delta \eta }+b({\eta }_{l},{x}_{k}){n}_{k,l}^{t}\\ -\sum_{i=k}^{M}{\alpha }_{k,i}b({\eta }_{l},{x}_{i}){n}_{i,l}^{t}+{n}_{k,l}^{t}\sum\limits_{i=1}^{M}c({\eta }_{l},{x}_{k},{x}_{i}){n}_{i,l}^{t}\\ -\sum\limits_{\begin{array}{c}j,i\\ {x}_{k-1}\le {x}_{j}+{x}_{i}\le {x}_{k+1}\end{array}}^{j\ge i}\left(1-\frac{1}{2}{\delta }_{j,i}\right){\gamma }_{j,i}^{k}c\left({\eta }_{l},{x}_{j},{x}_{i}\right){n}_{j,l}^{t}{n}_{i,l}^{t}\\ -\,{C}_{\rho }\sqrt{{p}_{v}-p}\int\limits_{{\varsigma }_{k}}^{{\varsigma }_{k+1}}\chi \left(\varsigma \right)\mathrm{d}\varsigma .\end{array}$$
(75)

Eq. (74) can be solved using the Newton-SOR iterative method.In addition, since \({h}_{b}({x}_{k},\varsigma )\) is a given function, the coefficient \({\alpha }_{k,i}\) can be calculated using the Gaussian integration method, and the value of the coefficient \({\alpha }_{k,i}\) is stored in a matrix, it will be called directly in the iterative calculation process, and the calculation time can be greatly saved by using the iterative process.

The term of the time derivativein the transient Eq. (69) is specially processed with finite difference,and a weighted averaging method is adopted for the time-differencing. It can be written as [31]

$$\frac{{n}_{k,l}^{t+1}-{n}_{k,l}^{t}}{\Delta t}+\left(\left(1-{\omega }_{t}\right)\tilde{Q }\left({n}_{k,l}^{t}\right)+\omega \tilde{Q }\left({n}_{k,l}^{t+1}\right)\right)=0,$$
(76)

where, \({n}_{k,l}^{t+1}={n}_{k,l}(t+\Delta t)\), weight factor \({0}\le {\omega }_{t}\le {1}\).

Aset of nonlinear equations with regard to \({n}_{k,l}^{t+1}\) can be rewritten as

$$\begin{array}{c}{F}_{q}\left({n}_{k,l}^{t+1}\right)={n}_{k,l}^{t+1}+\Delta t{\omega }_{t}\tilde{Q }\left({n}_{k,l}^{t+1}\right)\\ +\Delta t\left(1-{\omega }_{t}\right)\tilde{Q }\left({n}_{k,l}^{t}\right)-{n}_{k,l}^{t}=0.\\ \text{\hspace{0.17em}}(q=1,...,{N}_{q})\end{array}$$
(77)

The nonlinear Eq. (77) is also solved using the Newton-SOR iterative method. And downhill condition is adopted in numerical iterative procedure to improve convergence. The downhill condition is expressed as

$$\Vert {F}_{q}\left({n}_{k,l}^{t+1\left(m+1\right)}\right)\Vert \le \Vert {F}_{q}\left({n}_{k,l}^{t+1\left(m\right)}\right)\Vert ,$$
(78)

where \(m\) is iteration number. The overall algorithm flow diagram is given by Figure 5.

Figure 5
figure 5

Flow diagram of overall algorithm

Full size image

5 Results and Discussion

5.1 Experimental Verification of Theoretical Models

Table 1 list the related parameters of the water-lubricated SGTB for the numerical calculation.In order to verify this theoretical model, the simulating results of bubble distribution and axial stiffness coefficient are compared with experimental ones from our previous test study in Refs. [22, 23]. The experimental rotational speed are specified as 15000 r/min and 18000 r/min respectively, and the corresponding Reynolds numbers (1256 and 1507) are greater than the critical Reynolds number \({R}_{e}\left({R}_{e}=1000\right)\) [

Figure 8
figure 8

Comparison of the theoretical stiffness coefficients with the experimental ones at 15000 r/min

Full size image

5.2 Influence of Cavitation Effect on Dynamic Characteristics

5.2.1 Stiffness Coefficient

Figure 9 shows the influence of cavitation effect on the stiffness coefficients of the SGTB with different spiral angles. The results show the \({K}_{zz}^{*},{K}_{{\varphi }_{x}{\varphi }_{x}}^{*},{K}_{{\varphi }_{y}{\varphi }_{y}}^{*}\) predicted by the cavitation flow model are larger than that of the non-cavitation flow model when the spiral angle is less than 50°. This may be explained by the fact that the bubbles cause the interfacial hydrodynamic effect for the the cavitating flow. In addition, the relative deviation between the two models decreases with the increasing of spiral angle, so the interface hydrodynamic effect of the bubbles decreases with the spiral angle.It means that the influence of the cavitation effect on the water film stiffness is weakened with the increasing of spiral angle. The \({K}_{{\varphi }_{x}{\varphi }_{y}}^{*},{K}_{{\varphi }_{y}{\varphi }_{x}}^{*}\) are of opposite sign, and \({K}_{{\varphi }_{x}{\varphi }_{y}}^{*}\) and \({K}_{{\varphi }_{y}{\varphi }_{x}}^{*}\) of cavitating flow model with the angle generally coincide with those of non-cavitating flow model. It shows that the influence of cavitation effect on \({K}_{{\varphi }_{x}{\varphi }_{y}}^{*},{K}_{{\varphi }_{y}{\varphi }_{x}}^{*}\) are negligible. In addition, the \({K}_{{\varphi }_{x}z}^{*},{K}_{z{\varphi }_{x}}^{*},{K}_{{\varphi }_{y}z}^{*},{K}_{z{\varphi }_{y}}^{*}\) with different spiral angle sare approximately equal to zero for the cavitating flow or the non-cavitating flow.

Figure 9
figure 9

Influence of cavitation effect on the stiffness coefficient for different spiral angles (\(\omega =18000\, \mathrm{r}/\mathrm{min}\), \({h}_{s}=15 {\,}{\upmu}\mathrm{m}\), \({h}_{g}=40{\,}{\upmu}\mathrm{m}\))

Full size image

Figures 10 and 11 show the influence of cavitation effect on the water film stiffness coefficients for different groove depths and rotating speeds. The result also show the \({K}_{zz}^{*},\,{K}_{{\varphi }_{x}{\varphi }_{x}}^{*},{K}_{{\varphi }_{y}{\varphi }_{y}}^{*}\) predicted by the cavitation flow model are larger than that of the non-cavitation flow model at a specific groove depth and rotating speed. However, the deviation of \({K}_{zz}^{*},{K}_{{\varphi }_{x}{\varphi }_{x}}^{*},{K}_{{\varphi }_{y}{\varphi }_{y}}^{*}\) between the two models increase first and then decrease with the groove depth. Therefore, the interface hydrodynamic effect changes with the groove depth. A possible explanation is that the interface hydrodynamic effect is weakened and the cavitation effect is increased when the groove depth is increased in a certain range (20‒35 μm), and the interface hydrodynamic effect is increased and the cavitation effect is weakened when the groove depth exceeds a given value. And the deviation of \({K}_{zz}^{*},{K}_{{\varphi }_{x}{\varphi }_{x}}^{*},{K}_{{\varphi }_{y}{\varphi }_{y}}^{*}\) between the two models gradually increase as the rotating speed increases, This also can be explained by the fact that the interface hydrodynamic effect enhances and the cavitation effect is increased as the rotational speed increases.

Figure 10
figure 10

Influence of cavitation effect on stiffness coefficients for different groove depth (\(\omega =18000\, \mathrm{r}/\mathrm{min}\), \(\beta ={20}^{\circ }\), \({h}_{s}=15 {\,}{\upmu}\mathrm{m}\))

Full size image
Figure 11
figure 11

Influence of cavitationeffect on stiffness coefficients for different rotating speed (\(\beta ={20}^{\circ }\), \({h}_{s}=15 \,{\upmu}\mathrm{m}\), \({h}_{g}=40 \,{\upmu}\mathrm{m}\))

Full size image

In addition, the variation of the \({K}_{{\varphi }_{x}{\varphi }_{y}}^{*},{K}_{{\varphi }_{y}{\varphi }_{x}}^{*}\) with the groove depth is identical with that with the spiral angle. Similarly, it also shows that the influence of cavitation effect on \({K}_{{\varphi }_{x}{\varphi }_{y}}^{*},{K}_{{\varphi }_{y}{\varphi }_{x}}^{*}\) are negligible for different groove depths and rotating speeds. The \({K}_{{\varphi }_{x}z}^{*}\), \({K}_{z{\varphi }_{x}}^{*}\), \({K}_{{\varphi }_{y}z}^{*}\), \({K}_{z{\varphi }_{y}}^{*}\) predicted by the two models are approximately equal to zero for different groove depths and rotating speeds.

5.2.2 Dam** Coefficient

Figures 12 and 13 show the influence of cavitation effect on the water film dam** coefficients for different spiral angles and groove depths. It can be seen that the cavitation effect on dam** coefficients is very weak. Because the dam** coefficient is determined by the perturbed pressure, and the perturbed pressure with cavitating flow is only affected by the fraction \({C}_{g}\) of bubble volume, and the variation of bubble volume fraction is very small for the cavitating flow. In addition, the \({C}_{zz}^{*},{C}_{{\varphi }_{x}{\varphi }_{x}}^{*},{C}_{{\varphi }_{y}{\varphi }_{y}}^{*}\) decreases with the increasing of the spiral angle and groove depth, and the \({C}_{z{\varphi }_{x}}^{*},{C}_{{\varphi }_{x}z}^{*},{C}_{z{\varphi }_{y}}^{*},{C}_{{\varphi }_{y}z}^{*},{C}_{{\varphi }_{x}{\varphi }_{y}}^{*},{C}_{{\varphi }_{y}{\varphi }_{x}}^{*}\) predicted by the two models are also approximately equal to zero for different spiral angles and groove depth.

Figure 12
figure 12

Influence of cavitation effect on the dam** coefficients for different spiral angles (\(\omega =18000\,\mathrm{r}/\mathrm{min}\), \({h}_{s}=15 {\,}{\upmu}\mathrm{m}\), \({h}_{g}=40 {\,}{\upmu}\mathrm{m}\))

Full size image
Figure 13
figure 13

Influence of cavitation effect on dam** coefficients for different groove depth (\(\omega =18000\, \mathrm{r}/\mathrm{min}\), \(\beta \text{=}{20}^{\circ }\), \({h}_{s}=15 \,{\upmu}\mathrm{m}\))

Full size image

5.3 Influence of Turbulence Effect on Dynamic Characteristics

5.3.1 Stiffness Coefficient

Figure 14 shows the influence of turbulence effect on the water film stiffness coefficients for different spiral angles. It can be seen that the \({K}_{zz}^{*}\),\({K}_{{\varphi }_{x}{\varphi }_{x}}^{*}\), \({K}_{{\varphi }_{y}{\varphi }_{y}}^{*}\), \({K}_{{\varphi }_{x}{\varphi }_{y}}^{*}\), \({K}_{{\varphi }_{y}{\varphi }_{x}}^{*}\) calculated by the turbulent cavitating flow model are larger than those of the laminar cavitating flow model at a specified spiral angle. This may be explained by the fact that additional Reynolds shear stress generates due to pulsating velocity in the turbulent flow, and equivalent viscosity of the turbulent water film increases, and the force of the turbulent water film needed to produce unit displacement increases, so the stiffness of the water film increases. In addition, it can be seen that the deviation of stiffness coefficient between turbulence model and laminar model gradually decreases with the increase of the spiral angle. This is due to the fact that the outward pum** hydrodynamic effect increases first and then decreases with the increase of the spiral angle. Therefore, when the spiral angle exceeds a certain value, the outward pum** hydrodynamic effect becomes weak and the additional Reynolds shear stress of the turbulent flow reduces. This indicates that the influence of turbulence effect on the water film stiffness coefficients is weakened when the spiral angle exceeds a certain value. And the \({K}_{z{\varphi }_{x}}^{*},{K}_{{\varphi }_{x}z}^{*},{K}_{z{\varphi }_{y}}^{*},{K}_{{\varphi }_{y}z}^{*}\) calculated by the two models are approximately equal to zero for different spiral angles.

Figure 14
figure 14

Influence of turbulence effect on the water film stiffness coefficient for different spiral angles (\(\omega =18000\,\mathrm{r}/\mathrm{min}\), \({h}_{s}=15 \, {\upmu}\mathrm{m}\), \({h}_{g}=40 \,{\upmu}\mathrm{m}\))

Full size image

Figures 15 and 16 show the influence of turbulence effect on the water film stiffness coefficients for different groove depths and rotating speeds. It can also be seen that the \({K}_{zz}^{*},{K}_{{\varphi }_{x}{\varphi }_{x}}^{*}, {K}_{{\varphi }_{y}{\varphi }_{y}}^{*}, {K}_{{\varphi }_{x}{\varphi }_{y}}^{*}, {K}_{{\varphi }_{y}{\varphi }_{x}}^{*}\) calculated by the turbulent flow model are also larger than that of the laminar flow model for different groove depths and rotating speeds. And the deviation of the calculation results of the two models decreases with the increase of groove depth, and the deviation of the calculation results of the two models increase with the increase of rotating speed, and the \({K}_{z{\varphi }_{x}}^{*},{K}_{{\varphi }_{x}z}^{*},{K}_{z{\varphi }_{y}}^{*},{K}_{{\varphi }_{y}z}^{*}\) calculated by the two models are also approximately equal to zero for different groove depths and rotating speeds.

Figure 15
figure 15

Influence of turbulence effect on the stiffness coefficient for different groove depths (\(\omega =18000\, \mathrm{r}/\mathrm{min}\), \(\beta \text{=}{20}^{\circ }\), \({h}_{s}=15 \,{\upmu}\mathrm{m}\))

Full size image
Figure 16
figure 16

Influence of turbulence effect on the stiffness coefficient for different rotating speed (\(\beta ={20}^{\circ }\), \({h}_{s}=15 \, {\upmu}\mathrm{m}\), \({h}_{g}=40 \, {\upmu}\mathrm{m}\))

Full size image

5.3.2 Dam** Coefficient

Figures 17 and 18 show the influence of turbulence effect on the water film dam** coefficients for different spiral angles and groove depths.It can also be seen that the \({C}_{zz}^{*},{C}_{{\varphi }_{x}{\varphi }_{x}}^{*},{C}_{{\varphi }_{y}{\varphi }_{y}}^{*}\) calculated by the turbulent flow model are also larger than that of the laminar flow model for different spiral angles and groove depths. And the deviation between \({C}_{zz}^{*},{C}_{{\varphi }_{x}{\varphi }_{x}}^{*},{C}_{{\varphi }_{y}{\varphi }_{y}}^{*}\) calculated by the two models is gradually decreased with the increase of spiral angle. This indicates that the turbulence effect is gradually weakened when the spiral angle increases. And the deviation between \({C}_{zz}^{*},{C}_{{\varphi }_{x}{\varphi }_{x}}^{*},{C}_{{\varphi }_{y}{\varphi }_{y}}^{*}\) calculated by the two modes hardly changes with the increase of groove depth, and this indicates that the turbulence effect is not sensitive to changes in groove depth. In addition, the \({C}_{z{\varphi }_{x}}^{*},{C}_{{\varphi }_{x}z}^{*},{C}_{z{\varphi }_{y}}^{*},{C}_{{\varphi }_{y}z}^{*},{C}_{{\varphi }_{x}{\varphi }_{y}}^{*},{C}_{{\varphi }_{y}{\varphi }_{x}}^{*}\) calculated by the two models are also approximately equal to zero for different spiral angles and groove depth.

Figure 17
figure 17

Influence of turbulence effect on the dam** coefficients for different spiral angles (\(\omega =18000\, \mathrm{r}/\mathrm{min}\), \({h}_{s}=15\, {\upmu}\mathrm{m}\), \({h}_{g}=40 \, {\upmu}\mathrm{m}\))

Full size image
Figure 18
figure 18

Influence of turbulence effect on the dam** coefficients for different groove depths (\(\omega =18000\, \mathrm{r}/\mathrm{min}\), \(\beta \text{=}{20}^{\circ }\), \({h}_{s}=15 \,{\upmu}\mathrm{m}\))

Full size image

Figure 19 shows the influence of turbulence effect on the water film dam** coefficients for different rotating speed. It can be seen that the \({C}_{zz}^{*},{C}_{{\varphi }_{x}{\varphi }_{x}}^{*},{C}_{{\varphi }_{y}{\varphi }_{y}}^{*}\) calculated by the two models increases gently with the increase of rotating speed, it means that \({C}_{zz}^{*},{C}_{{\varphi }_{x}{\varphi }_{x}}^{*},{C}_{{\varphi }_{y}{\varphi }_{y}}^{*}\) is insensitive when rotating speed is increased. And the deviation between \({C}_{zz}^{*},{C}_{{\varphi }_{x}{\varphi }_{x}}^{*},{C}_{{\varphi }_{y}{\varphi }_{y}}^{*}\) calculated by the two modes increase alse with the increase of rotating speed. The \({C}_{z{\varphi }_{x}}^{*},{C}_{{\varphi }_{x}z}^{*},{C}_{z{\varphi }_{y}}^{*},{C}_{{\varphi }_{y}z}^{*},{C}_{{\varphi }_{x}{\varphi }_{y}}^{*},{C}_{{\varphi }_{y}{\varphi }_{x}}^{*}\) calculated by the two models are also approximately equal to zero for different rotating speeds.

Figure 19
figure 19

Influence of turbulence effect on the dam** coefficients for different rotating speed (\(\beta ={20}^{\circ }\), \({h}_{s}=15 \,{\upmu}\mathrm{m}\), \({h}_{g}=40 \,{\upmu}\mathrm{m}\))

Full size image

5.3.3 Bubble Density

Figure 20 shows the influence of turbulence effect on the bubble number for different radius. It can be seen that the bubbles mainly locate at the groove-ridge edges and the outer rim of bearing. This may be explained by the fact that the bubbles are formed due to the pressure drop near the groove-ridge edges. The result also show that the bubbles are approximately evenly distributed in dam region of bearing. In addition, the number of bubbles with laminar flow is more than the number of bubbles with turbulent flow at a specified circumferential position. Because the Reynolds shear stress due to the turbulent flow causes the equivalent viscosity of the turbulent liquid to increase, consequently, the turbulent flow effect on dynamic pressure is enhanced, which contributes to the generation of the bubbles.

Figure 20
figure 20

Influence of turbulence effect on bubbles number for different radius: (a) \(\zeta \text{=}0.2\), (b) \(\zeta \text{=}0.5\) (\(\omega =18000\,\mathrm{r}/\mathrm{min}\), \(\beta \text{=}{20}^{\circ }\), \({h}_{s}=15 \,{\upmu}\mathrm{m}\), \({h}_{g}=40 \,{\upmu}\mathrm{m}\))

Full size image