1 Introduction

The most successful theory of gravity is Einstein’s general relativity (GR), which after decades of careful scrutiny, can describe a broad range of phenomena at solar system scales and beyond. This theory extends Newton’s notion of gravitational force and describes how the mass–energy distribution causes the geometry of space-time to deform. Indeed, a plethora of new discoveries and extremely precise experiments, including SNeIa, LSS, CMB and BAO [1,2,3,4], reveal that the expansion of the universe is accelerating. Furthermore, the unknowable nature of the majority of the universe’s substance was further proven by various recent cosmic observations at astronomical scales [5, 6].

A deeper understanding of the dynamics of the universe may also be gained by studying large-scale structures such as stars, galaxies, and their clusters. The intricate nature of these stellar structures has a significant effect on associated physical variables including energy density, pressure, and heat flow. In this context, researchers have concentrated on the formation and properties of these stellar structures, which are commonly applied to refer to white dwarfs, neutron stars, and black holes. It was long ago realized by Schwarzschild, who obtained the first exact solution to Einstein’s field equation for the interior of a compact stellar structure. The most likely compact stellar structures have been found in pulsars, which are rapidly rotating stars with intense magnetic fields made completely of quark matter. Eventually, Rosat surveys [7], performed in 2006, identified compact stellar structures based on their X-ray emission, revealing that the gravitational energy generated is emitted in X-rays. Hewish et al. [8, 9] revealed the hypothetical emergence of pulsars, which generate a beam of electromagnetic radiation that is truly continuous but pulsed. Therefore, the discovery of pulsars and X-ray bursts motivates researchers to construct theoretical models of compact stellar structures such as neutron stars and quark stars. Several models are occasionally put out to characterize compact stellar structures, despite the fact that the makeup of the particles and the nature of interactions are still unknown.

Currently, considerable efforts are being expended on studying relativistic compact stellar structures. We investigate the static spherically symmetric Einstein’s equations solutions for object modeling under various physical circumstances. These solutions can be described as dust, ideal fluid, and anisotropic fluid. In this context, the majority of the approaches frequently employed by many researchers to study these novel analytic solutions of the field equations impose symmetry requirements such as spherical symmetry, an equation of state relating the pressure and energy density of the stellar fluid, the behavior of the pressure anisotropy or isotropy, vanishing of the Weyl stresses, spacetime dimensionality, and so on, in the attempt to explore exact solutions characterizing static compact stellar structures [10,11,12,13,14,15,16,17]. In this regard, the concept presented by Riemann known as Riemannian geometry is also a useful tool for analyzing the basic geometrical properties of compact stellar systems. These hypotheses make the challenge of obtaining appropriate solutions to the field equations easier and mathematically solvable. Moreover, the relaxation of the isotropy condition boosts the probability of discovering accurate solutions, with the caveat of incorporating imperfect fluids. It is generally recognized that deviations of the isotropy and fluctuations of the local anisotropy in pressures can be induced by a wide range of physical phenomena that we would anticipate to occur in compact stellar objects (see Refs. [18], for an in-depth discussion on this point). In addition, the presence of physical factors such as dissipative fluxes, and/or energy density inhomogeneities, and/or the emergence of shear in the fluid flow will always tend to generate pressure anisotropy, even if the system is originally claimed to be isotropic. These physical factors were pointed out by Herrera in 2020 [19]. However, unequal principle stresses, also termed as anisotropic fluids, might be expected when the self-gravitational fluids’ densities are typically higher than the density of nuclear matter. The concept of anisotropy arises in self-gravitational compact stars due to the occurrence of exotic phase transitions [20], electromagnetic fields, rotations, superfluids or type-A fluids [21], pion and meson condensations [22], core formation and other phenomena have also been investigated extensively by Herrera et al. [18, 23,24,25]. This suggests that the self-gravitational systems have two different kinds of pressure components, namely the radial component (\(p_r\)) and the tangential component (\(p_t\)). Consequently, radial and tangential pressures become unequal (\(p_t \ne p_r\)), and the concept of local anisotropy emerges in the study of self-gravitational fluids. In this context, Herrera and collaborators [13, 26,27,28] explored static anisotropic stars by looking into the effects of Newtonian and general relativistic regimes.

A plethora of exact solutions are known in the literature for nonstatic, radiating stars, including acceleration-free collapse, Weyl-free collapse, vanishing of shear, collapse from/to an initial/final static configuration, and anisotropic collapse models. According to the Buchdahl constraint of ideal fluid distributions, the compactness factor \(u = 2M/R\) should always be \(\le 8/9\) in order to avoid gravitational collapse and the formation of a singularity or black hole. Andréasson [29, 30] generalizes this upper constraint in u by including charge, anisotropy, and even cosmological constant. He considered a straightforward inequality relating pressure and density, \(p_r + 2p_t < \rho \), as the starting point for deriving the new generalized upper constraint in u. More impressively, a generic method described in [31,32,33,34,35,36,37,38,39,40,41] can be attractively applied to find an algorithm for all static and anisotropic solutions with and without charge to Einstein’s equation for the spherically symmetric line element.

A novel method for generating anisotropic solutions to Einstein’s field equations was recently developed [42,43,44,45,46,47]. This novel method known as gravitational decoupling via minimal geometric deformation (MGD) which was intended to enable solutions generated by an isotropic matter distribution to reach anisotropic domains. This approach deforms the object’s geometry while simultaneously modifying its material content, conserving the symmetry of the solution. The number of studies employing this methodology that are now available in the literature has significantly increased during the recent past. To highlight a few instances, applications include studying stellar interiors, black holes, and modified gravity theories [48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76, 78, 79]. Furthermore, in [56] the MGD inverse problem has been developed, i.e. knowing the isotropic counterpart of an anisotropic solution.

The MGD approach aids in the study of the key properties of compact stellar configurations, however, it has significant limitations. For example, geometric deformation can only be achieved if the interplay involving matter sources is purely gravitational. The metric component’s minimal transformation, which only affects the radial coordinate while maintaining the temporal metric potential as an unchanging entity, is likely it has some drawbacks, in particular, it can not explain a stable black hole having a well-defined horizon. In this regard, by utilizing the deformation on both radial and temporal metric functions, Casadio et al. [46] proposed an extended version of the MGD technique and generated a novel solution for spherically symmetric spacetime to overcome this problem. However, the conservation law does not apply in the presence of matter, hence this extension is limited to studying vacuum solutions. Therefore, this extended approach does not allow for analysis of the interior structure or intrinsic characteristics of self-gravitating objects. By manipulating both metric functions (\(g_{rr}\), \(g_{tt}\)), Ovalle [51] put forth the innovative concept of extended geometric deformation or complete geometric deformation (CGD), which remains valid throughout all of the spacetime regardless of the selection of matter distribution. In order to extract the exterior charged BTZ model from the appropriate vacuum solution, Contreras and Bargueno [77] effectively decoupled the field equations in (1 + 2)-dimensional gravity using the CGD approach. In this connection, some notable works using CGD approach can be seen in Refs. [80,81,82,83].

For several years, the notion of complexity of a system has been the topic of extensive study in all fields. Different factors are involved in analyzing the complexity of any system. The main idea is to measure the entropy and information of the configuration contained inside a system. The concept of the complexity of the self-gravitating system is widely analyzed in the studying of heavy configurations. Whereas in physics, isolated gases (which reveal disorder and the greatest quantity of information) are somehow sophisticated systems with vanishing complexity when considering a perfect crystal (which exhibits periodic behavior and is symmetrically dispersed). The concept of disequilibrium was developed by López-Ruiz et al. [84] to analyze the complexity of the system. In general, it is a measurement of “distance” from the system’s achievable form’s equally likely dispersion. They argued that the concept of complexity dissipated in the scenario of an ideal gas and perfect crystal by considering complexity as a mixture of both concepts of “disequilibrium and information”. Next, Herrera [85] established a novel concept of complexity based on fluid constituents including energy density, pressure, and others after observing deficiencies in existing notions of complexity when studying the self-gravitating system. In summary, it is connected to all-inclusive aspects of the fluid’s content. With the help of the complexity factor, which is one of the structural scalars obtained from the orthogonal division of the intrinsic curvature, the complexity is in this case constructed. This concept for dissipative fluid content was extended by Herrera et al. [86]. They did more than only analyze the system’s complexity; they also established the prerequisites for the progression design with the least amount of complexity. They explored that there are several solutions and that the fluid is shearing and geodesic in terms of dissipation.

On the other hand, Herrera et al. [87] were using the axially symmetric geometry to further investigate the effect of complexity on various geometries and identified three different categories of complexity. They showed how complexity and symmetry are interrelated. In this peculiar case, they also obtained some analytical responses. The evolution of spherically symmetric non-static geometry is also investigated by Herrera et al. [88] using the concept of complexity, both in terms of dissipation and non-dissipation. They constructed some models and determined their appropriate implications for understanding evolution by adopting the quasi-homologous condition, which is a relationship between areal radius velocity and areal radius. By using this approach, Contreras and Fuenmayor [89] examined the stability of self-gravitating configurations in terms of gravitational cracking and performed a thorough study to look into the effects of the source’s compactness and changes to the decoupling parameters on the radial force. Taking into account the Misner–Sharp mass and the Tolman mass as well as the involvement of various structural scalars gained via the orthogonal division of the intrinsic curvature, Herrera et al. [90] extended the concept of the complexity factor on the geometry with hyperbolic symmetry. They came to the conclusion that Tolman’s mass in this scenario reflects negative nature. Furthermore, many researchers have effectively employed this complexity approach not only in GR [91,92,93,94,95], but also in the analysis of findings for various geometries in the context of modified theory of gravity [96,97,98].

In this paper, we develop a simple protocol for an anisotropic generalization of the Finch–Skea model by gravitational decoupling satisfying vanishing complexity factor condition. We are using the complete geometric deformation (CGD) scheme, which transforms the gravitational potentials \(g_{rr}\) and \(g_{tt}\) for exploring the physical influence of the generic source \(\Theta ^i_j\) on seed source \(T_{ij}\) and decomposes the system of non-linear field equations into two arrays. One set of these arrays corresponds to the seed source, and the other set provides extra source terms. We would also highlight that the energy transfer between fluid distributions corresponding to the new source (\(\Theta _{ij}\)) and original source (\(\hat{T}_{ij}\)) were analyzed based on the positive and negative values of the energy exchange \(\Delta E\). To be more specific: (i) if \(\Delta E\) is positive, then the new source is supplying energy to the environment, (ii) if \(\Delta E\) is negative, then the original/seed matter distribution is supplying energy.

The article is organized according to the following arrangement. In Sect. 2, we derive the basic field equations for a static sphere containing two sources which are decoupled through the CGD technique. by using the well-behaved Finch–Skea metric potential for the seed spacetime geometry, which ensures a well-defined horizon-free spacetime, we are able to obtain a gravitationally decoupled solution in Sect. 3. In Sect. 4, where we match the decoupled interior solution determined by the anisotropic matter distribution to the exterior Schwarzschild solution at an appropriate boundary, the external spacetime and matching conditions are addressed. The behavior of density, pressures, and anisotropy inside the self-gravitating stellar system, stability of anisotropic solution using adiabatic index, Harrison-Zeldovich-Novikov stability analysis, and energy exchange, which are each covered in Sects. 5.1, 5.2, 5.3, and 5.5, were all considered in Sect. 5 to establish how each solution behaves physically and how it is viable and stable. In Sect. 6, the concluding remarks are given. The Appendix now contains some pertinent lengthy expressions of physical quantities.

2 Einstein’s field equations in the framework of gravitationally decoupled system

In this section, we consider a static fluid with spherical symmetry. This fluid is hypothesized to be anisotropic and constrained by the surface designated by the symbol \(\Sigma \). The analogous line element is represented in Schwarzschild-like ansatz as

$$\begin{aligned} ds^2 = e^{\nu (r)}dt^{2} - e^{\lambda (r)}dr^{2}-r^{2}(\sin ^{2}\theta d \phi ^{2}+d\theta ^{2}), \end{aligned}$$
(1)

where \(\nu (r)\) and \(\lambda (r)\) are functions depending only on the radial coordinate r. Furthermore, the above-mentioned metric complies with the gravitationally decoupled Einstein field equations provided by

$$\begin{aligned}{} & {} \mathcal {R}^i_j-\frac{1}{2}\,\delta ^i_j\,\mathcal {R}= T^i_j, \end{aligned}$$
(2)

where

$$\begin{aligned} T^i_j= \hat{T}^i_j+\beta \Theta ^i_j, \end{aligned}$$
(3)

in which a new source induced by gravitational decoupling is denoted by the symbol \(\Theta ^i_j\). We consider that the space’s physical content consists of an anisotropic distribution of matter with energy density \(\epsilon \), radial pressure \(P_r\), and tangential pressure \(P_\perp \), in order to characterize and explain the underlying structure of the self-gravitating system associated with the source \(T^i_j\). Furthermore, the matter sector may be expressed by the following energy-momentum tensor,

$$\begin{aligned} T^i_j=(\rho ^{\text {eff}}+p^{\text {eff}}_t)\,u^i\,u_j-p^{\text {eff}}_t\,\delta ^i_j+(p^{\text {eff}}_r-p^{\text {eff}}_\perp )\chi ^{i} \chi _j, \end{aligned}$$
(4)

where the index \(i=0,1,2,3\). Moreover, \(u^i\) is called the fluid’s four-velocity vector, and \(\chi ^i\) denotes the radial unit space-like vector that satisfies

$$\begin{aligned} u^i=(e^{-\nu /2},~0,~0,~0) \quad \text {and} \quad \chi ^i=(0,~e^{-\lambda /2},~0,~0), \end{aligned}$$
(5)

such that \(\xi ^i u_j=0\) and \(\chi ^i\chi _j=-1\). Following that, using the spherically symmetric line element (1), the energy-momentum tensor components become as

$$\begin{aligned}{} & {} T^0_0=\rho ^{\text {eff}}, \quad T^1_1=-p^{\text {eff}}_r,\quad T^2_2=T^3_3=-p^{\text {eff}}_t. \end{aligned}$$
(6)

Thus, the gravitationally decoupled Einstein field equations (2) are stated as

$$\begin{aligned}{} & {} \rho ^{\text {eff}}=\frac{1}{8\pi }\bigg [\frac{1}{r^2}-e^{-\lambda }\left( \frac{1}{r^2}-\frac{\lambda ^{\prime }}{r}\right) \bigg ], \end{aligned}$$
(7)
$$\begin{aligned}{} & {} p^{\text {eff}}_{r}=\frac{1}{8\pi }\bigg [-\frac{1}{r^2}+e^{-\lambda }\left( \frac{1}{r^2}+\frac{\nu ^{\prime }}{r}\right) \bigg ], \end{aligned}$$
(8)
$$\begin{aligned}{} & {} p^{\text {eff}}_t=\frac{1}{8\pi }\bigg [\frac{e^{-\lambda }}{4}\left( 2\nu ^{\prime \prime }+\nu ^{\prime 2}-\lambda ^{\prime }\nu ^{\prime }+2\frac{\nu ^{\prime }-\lambda ^{\prime }}{r}\right) \bigg ],~~~ \end{aligned}$$
(9)

where \('\) indicates the derivative with respect to the r coordinate.

Next, using the conservation law \(\nabla _{i}T^{ij}=0\) or by employing Einstein’s equations (7)–(9), we can readily derive the generalized Tolman–Opphenheimer–Volkoff (TOV) (hydrostatic equilibrium) equation [99, 100] for anisotropic matter distribution which reads

$$\begin{aligned}{} & {} \frac{dp^{\text {eff}}_r}{dr}=- \frac{\nu ^\prime }{2} \left( \rho ^{\text {eff}} + p^{\text {eff}}_r \right) + \frac{2 (p^{\text {eff}}_t-p^{\text {eff}}_r)}{r}. \end{aligned}$$
(10)

Alternatively, using the formula for \(\nu ^\prime \) as

$$\begin{aligned} \nu ^\prime =\frac{2m+8\pi \,r^3 p^{\text {eff}}_r}{(r-2m)}, \end{aligned}$$
(11)

Here, the mass function m(r) for the spherically symmetric distribution can be defined by

$$\begin{aligned} R^3_{232}=1-e^{-\lambda }=\frac{2m}{r}, \end{aligned}$$
(12)

or, equivalently [101]

$$\begin{aligned} m(r)=4\pi \int ^r_0 x^2 \rho ^{\text {eff}}(x) dx. \end{aligned}$$
(13)

Furthermore, it is necessary to define the nature of original energy-momentum tensor \(\hat{T}^i_j\) whether this describes either perfect fluid matter distribution or anisotropic matter distribution. Here, we assume \(\hat{T}^i_j\) denotes a perfect fluid matter distribution with spacetime geometry \(\mu \) and \(\xi \) and matter variables \(\rho \) (energy density) and p (pressure), is defined as

$$\begin{aligned} \hat{T}^i_j=\rho \,\alpha ^i\,\alpha _j-p\zeta ^i\,\zeta _j~, \end{aligned}$$
(14)

with \(\alpha ^i\) (four-velocity vector) and \(\zeta ^i\) are given by

$$\begin{aligned} \alpha ^i=(e^{-\xi /2},~0,~0,~0) \quad \text {and} \quad \zeta ^i=(0,~\sqrt{\mu },~0,~0), \end{aligned}$$
(15)

where \(\alpha ^i \zeta _i=0\) and \(\zeta ^i\zeta _i=-1\).

Then effective quantities are written as

$$\begin{aligned} \rho ^{\text {eff}} = \rho +\beta \Theta ^0_0, \quad p^{\text {eff}}_r=p-\beta \Theta ^1_1, \quad p^{\text {eff}}_t = p-\beta \Theta ^2_2. \end{aligned}$$
(16)

and the effective anisotropy depends on,

$$\begin{aligned} \Delta ^{\text {eff}} = \beta (\Theta ^1_1-\Theta ^2_2). \end{aligned}$$
(17)

It is clearly noticed from the above equation that anisotropy can only be introduced in the system when \(\beta \ne 0\). Now, we employ the extended gravitational decoupling approach [51] to modify the gravitational potentials \(e^{\lambda }\) and \(e^{\nu }\) for exploring the physical influence of the generic source \(\Theta ^i_j\) on seed source \(T_{ij}\). The metric functions \(e^{\nu }\) and \(e^{\lambda }\) are effectively deformed via a linear transformation given by

$$\begin{aligned}{} & {} \nu (r) = \xi (r) + \beta ~ h ( r ), \end{aligned}$$
(18)
$$\begin{aligned}{} & {} e^{-\lambda (r)} = \mu (r) + \beta ~ f (r), \end{aligned}$$
(19)

where f(r) and h(r) stand for the geometric deformation functions subject to the radial and temporal coordinates, respectively. The coupling constant \(\beta \) is a real number. Furthermore, the aforementioned transformation includes both the radial and temporal components of the line element and is the extended case of minimal geometric deformation (MGD), also known as an extended geometric deformation or a complete geometric deformation (CGD). The CGD requires that both deformation functions be non-zero, i.e., \(f(r)\ne 0\) and \(h(r)\ne 0\). Therefore, using these transformations, we get the two sets of equations. The first set of equations for the seed source is

$$\begin{aligned}{} & {} 8\pi {\rho }= \frac{1-\mu }{r^2} - \frac{\mu ^ \prime }{r} , \end{aligned}$$
(20)
$$\begin{aligned}{} & {} 8\pi p=\frac{\mu -1 }{r^2} - \frac{\mu \,\eta ^\prime }{r} , \end{aligned}$$
(21)
$$\begin{aligned}{} & {} 8\pi p= \mu \bigg ( \frac{\xi ^{\prime \prime }}{2} + \frac{\xi ^{ \prime 2}}{4} + \frac{\xi ^\prime }{2r} \bigg ) + \bigg ( \frac{\xi ^\prime \mu ^\prime }{4} + \frac{\mu ^\prime }{2r}\bigg ),~~~ \end{aligned}$$
(22)

whose solution can be described by the following line element,

$$\begin{aligned} ds^2 = e^{\xi (r)}dt^{2} - \mu ^{-1} (r)\,dr^{2}-r^{2}(\sin ^{2}\theta d \phi ^{2}+d\theta ^{2}). \end{aligned}$$
(23)

The second set of equations for the extra gravitational source can be given by,

$$\begin{aligned} 8\pi \Theta ^0_0= & {} - ~~\bigg (\frac{f^\prime }{r} + \frac{f}{r^2}\bigg ), \end{aligned}$$
(24)
$$\begin{aligned} 8\pi \Theta ^1_1= & {} - \bigg [ f ~~\bigg ( \frac{\nu ^\prime }{r} + \frac{1}{r^2} \bigg ) + \frac{\mu \,h^\prime }{r} \bigg ], \end{aligned}$$
(25)
$$\begin{aligned} 8\pi \Theta ^2_2= & {} - \bigg [\frac{ f }{2} ~~\bigg ( \nu ^{\prime \prime } + \frac{\nu ^{\prime 2}}{2} + \frac{\nu ^\prime }{r} \bigg ) + \frac{\beta f^\prime }{2} ~~ \bigg (\frac{\nu ^\prime }{2} + \frac{1}{r}\bigg ) \nonumber \\{} & {} - \frac{\mu }{4}\left( 2 h^{\prime \prime } + \beta h^{\prime 2} + \frac{2~h^\prime }{r} + 2 \xi ^\prime h^\prime \right) + \frac{\mu ^\prime ~h^\prime }{4}\bigg ]. \end{aligned}$$
(26)

The corresponding hydrostatic equilibrium equations take the following forms

$$\begin{aligned}{} & {} \frac{dp_r}{dr}=- \frac{m_s+4\pi \,r^3 p}{ (r-2m_s)} \left( \rho + p \right) , ~~ \end{aligned}$$
(27)

and

$$\begin{aligned} -\frac{d \Theta ^1_1}{dr}= & {} -\frac{m+4\pi \,r^3 p^{\text {eff}}_r}{ (r-2m)}\left( \Theta ^0_0-\Theta ^1_1\right) -\frac{2(\Theta ^2_2-\Theta ^1_1)}{r}\nonumber \\{} & {} -\frac{ h^\prime }{2} \left( p + \rho \right) . \end{aligned}$$
(28)

The mass function \(m_s\) is determined by

$$\begin{aligned} m_s(r)=\frac{r}{2} (1-\mu )=4\pi \int ^r_0 x^2\,\rho (x) dx. \end{aligned}$$
(29)

Which implies

$$\begin{aligned} m=m_s-\frac{\beta \,r}{2}\,f(r). \end{aligned}$$
(30)

Moreover, it should be mentioned that the energy exchange between the two sources \(\hat{T}_{ij}\) and \(\Theta _{ij}\) is necessary, to succeed in decoupling between them. The equivalent energy exchange between these sources, denoted by \( \Delta E\), may be provided by [51]

$$\begin{aligned} \Delta E=\frac{h^\prime }{2} \left( p + \rho \right) . \end{aligned}$$
(31)

Next, the gravitationally decoupled mass function m(r), as defined by Herrera [85], may be expressed in terms of the homogeneous energy density and the change caused by density inhomogeneity as

$$\begin{aligned} m(r)=\frac{4\pi }{3} \rho ^{\text {eff}}-\frac{4\pi }{3}\,\int ^r_0 \hat{r}^3\, [\rho ^{\text {eff}}]^{\prime } d\hat{r}. \end{aligned}$$
(32)

Then from Eq. (19), we can get the following relation,

$$\begin{aligned} m(r)=m_s(r)+\beta \,m_{_\Theta } (r), \end{aligned}$$
(33)

where

$$\begin{aligned}{} & {} m_s(r)=\frac{4\pi }{3} \rho \,r^3 -\frac{4\pi }{3}\,\int ^r_0 x^3\, \rho ^{\prime } dx, \end{aligned}$$
(34)
$$\begin{aligned}{} & {} m_{_\Theta } (r)=\frac{4\pi }{3} \Theta ^0_0\, r^3- \frac{4\pi }{3}\,\int ^r_0 x^3\, \left[ \Theta ^0_0\right] ^{\prime } dx. \end{aligned}$$
(35)

The formulation of the mass function for a spherically symmetric static spacetime characterizing the energy content of a fluid stellar structure was also introduced by Tolman [103] as

$$\begin{aligned} m_T=4\pi \,\int ^{r_{_\Sigma }}_0 x^2\,e^{(\nu +\lambda )/2}\,(T^0_0-T^1_1-2T^2_2)\, dx. \end{aligned}$$
(36)

It may be also expressedFootnote 1 as

$$\begin{aligned} m_T= & {} (m_T)_{_\Sigma } \left( \frac{r}{r_{_\Sigma }}\right) ^3-r^3\int ^{r_{_\Sigma }}_r \frac{e^{(\nu +\lambda )/2}}{x} \Bigg [8\pi (p^{\text {eff}}_t-p^{\text {eff}}_r)\nonumber \\{} & {} +\frac{4\pi }{r^3}\,\int ^r_0 x^3\, [\rho ^{\text {eff}}]^{\prime } dx\Bigg ] dx. \end{aligned}$$
(37)

Now we move on to the process of finding the solution for both systems, which requires some points that need to be clarified about what we have so far:

  1. (i).

    We have two systems that depend on the nine unknowns \(\{\xi , \mu , f, h, \rho , p, \Theta ^0_0, \Theta ^1_1\) & \(\Theta ^2_2\}\) with five independent equations. Therefore, we need four auxiliary conditions to solve the system completely.

  2. (ii).

    Whenever spacetime geometry \(\xi \) and \(\mu \) are provided, then it can be seen that Eqs. (20)–(22) are automatically fulfilled. Then, for solving Eqs. (24)–(26), only two auxiliary conditions must be specified in order to close the system of differential equations. These two conditions could be: The mimic constraints for the pressure (\(\Theta ^1_1=p_r\)), density (\(\Theta ^0_0=\rho \)), an equation of state (EoS) operating between the \(\Theta \)-sector, or any other well-known condition. The first three conditions are widely applied to build the interior solutions under the gravitational decoupling system. Furthermore, it is mentioned that the solution of differential equations under the constraints \(\Theta ^1_1=p_r\) is more difficult here because this mimic constraint incorporates the high non-linear term in h and involves both functions f and h together. Therefore, this condition is not suitable to build the solution. Due to this, we need a particular EoS that gives a linear differential equation and involves only the radial deformation function. The best condition is the mimic constraint of the density i.e \(\rho =\Theta ^0_0\) approach.

  3. (iii).

    Finally, we need another condition to close the second system completely. For this purpose, we use the recent condition known as the vanishing complexity factor condition proposed by Herrera [85]. In accordance with Herrera’s concept  [85], we define the complexity factor (\(Y_{TF}\)) formula in the context of Einstein’s field equations (7)–(9) system as

    $$\begin{aligned} Y_{TF} = 8\pi (p^{\text {eff}}_r-p^{\text {eff}}_t)-\frac{4\pi }{2r^3} \int ^r_0 x^3 [\rho ^{\text {eff}}]^{\prime } (x) dx. \end{aligned}$$
    (38)

Then, using Einstein’s set of Eqs. (7)–(9), we can express, \(Y_{TF}\), as

$$\begin{aligned} Y_{TF}=\frac{\nu ^\prime \left[ r (\lambda ^\prime -\nu ^\prime )+2 \right] -2 r \nu ^{\prime \prime }}{4 r e^{\lambda }}. \end{aligned}$$
(39)

Then vanishing of the complexity factor condition, i.e., \(Y_{TF}=0\) provides

$$\begin{aligned} \nu ^\prime \left[ r (\lambda ^\prime -\nu ^\prime )+2 \right] -2 r \nu ^{\prime \prime }=0. \end{aligned}$$
(40)

In terms of total derivative, the aforementioned equation may thus be expressed as

$$\begin{aligned} \frac{d}{dr} \Big ( \log \frac{\nu ^\prime }{r}+ \frac{\nu -\lambda }{2}\Big )=0, \end{aligned}$$
(41)

which leads to

$$\begin{aligned} \log \frac{\nu ^\prime }{r}+ \frac{\nu -\lambda }{2}=\log A, \end{aligned}$$
(42)

where \(\log A_1\) denotes the integration constant.

In this case, the simplified aforementioned equation becomes

$$\begin{aligned} \nu ^\prime \,e^{\nu /2}=A\,r\, e^{\lambda /2}. \end{aligned}$$
(43)

According to the aforementioned equation, \(\nu \) and \(\lambda \) have the following relationship

$$\begin{aligned} e^{\nu }= \left( A_1 \int {r e^{\lambda /2} dr} +B_1\right) ^2 \end{aligned}$$
(44)

with B as an integration constant. It is worth mentioning that the Eq.(43) enables us to derive the deformation function h in terms of the radial deformation function f and the seed metric functions \(\{\xi , \mu \}\) using equations (19) and (44) as [102]

$$\begin{aligned} h(r)=\frac{1}{\beta } \left[ 2\ln \left( A_1\,\int \frac{r}{\sqrt{\mu +\beta f}} dr +B_1 \right) -\xi (r)\right] . \end{aligned}$$
(45)

In order to accomplish this, we must identify the radial deformation function by a particular EoS that only includes f and its derivatives i.e. the mimic constraint of the density (\(\rho =\Theta ^0_0\)) approach, as discussed earlier. It is emphasized that the choice of the seed solution influences the analytical solutions of Eq. (45). In light of the reasoning above, we will employ the following process to obtain the anisotropic interior solutions in the presence of vanishing complexity under gravitational decoupling via extended MGD as:

  1. (i).

    Select the most appropriate seed metric functions: \(\xi \) and \(\mu \).

  2. (ii).

    Start executing the mimic constraint for the density based on a specific EoS \(\rho =\Theta ^0_0\).

  3. (iii).

    By substituting \(\mu \) and f into Eq. (45), one may get the solution for the variable h. once we get f and h, then we can find \(e^{-\lambda }=\mu +\beta \,f\) and \(\nu =\xi +\beta h\) directly, which is our final aim.

Now we are going to present the whole approach mentioned above to find the new anisotropic solution to Einstein’s field equations (7)–(9) having zero complexity by taking the well-known Finch–Skea perfect fluid model and energy exchange between relativistic matter distributions in the next section:

3 Anisotropic generalization of Finch–Skea perfect fluid model

When there are no handy evidences for the source and nature of particle interactions, one must develop a model of the stable content of relativistic compact stellar configurations by formulating the analytical solutions of Einstein’s field equations characterizing the static internal core of relativistic stellar configurations. However, due to the highly non-linear second-order field equations, generating the exact solutions to the gravitational field equations is not at all an easy task. To overcome the issue in this case, a variety of appropriate techniques are frequently applied. In this regard, we specify an explicit metric function corresponding to Finch and Skea [104] spacetime which was employed to model the interiors of relativistic stellar configurations. In this connection, when Duorah and Ray [105] first developed this type of ansatz in 1987, they did not guarantee that it would be fine-tuned to satisfy Einstein’s field equations governing the content of stellar relativistic astrophysical models. Such a form of Finch–Skea solution has aroused great curiosity in the construction of relativistic compact stellar stars since the findings have been well-proven and validate all of the basic and adequate requirements of physical viability [106]. The astrophysical and cosmological backgrounds in GR and as well as higher-order modified gravity theories have been discussed in several outstanding explorations relating to this ansatz [107,108,109,110,111,112]. Motivated by the preceding discussion, we consider the spacetime geometry corresponding to Finch–Skea perfect fluid solution as

$$\begin{aligned} \mu (r)= & {} \frac{1}{1+Cr^2}, \end{aligned}$$
(46)
$$\begin{aligned} \xi (r)= & {} 2\ln \left[ (B-A\sqrt{1+Cr^2}) \cos (\sqrt{1+Cr^2})\right. \nonumber \\{} & {} \left. +(A+B\sqrt{1+Cr^2}) \sin (\sqrt{1+Cr^2})\right] . \end{aligned}$$
(47)

We can easily get the formula for thermodynamic variables like density and pressure by employing these metric functions \(\mu (r)\) and \(\xi (r)\) as

$$\begin{aligned} \rho (r)= & {} \frac{C \left( C r^2+3\right) }{\left( C r^2+1\right) ^2}, \end{aligned}$$
(48)
$$\begin{aligned} p(r)= & {} \frac{C}{(C r^2+1)\,\xi (r)} \Big [-\xi (r)+2 \Big (A \sin \left( \sqrt{C r^2+1}\right) \nonumber \\ {}{} & {} +B \cos \left( \sqrt{C r^2+1}\right) \Big )\Big ]. \end{aligned}$$
(49)

Let us now proceed to the subsequent stage, where we first apply the appropriate EoS, which only contains the deformation function f(r) as an unknown function, in order to identify the deformation function f(r). The mimic constraint for density is, mathematically, the most straightforward EoS involving the deformation function f(r),

$$\begin{aligned} \rho (r)=\Theta ^0_0(r). \end{aligned}$$
(50)

This gives rise to the differential equation shown below

$$\begin{aligned} \frac{df}{dr}+\frac{f}{r}=-\frac{C (3 + C r^2)}{(1 + C r^2)^2}. \end{aligned}$$
(51)

The foregoing equation yields the solution for the deformation function f(r) as

$$\begin{aligned} f(r)=-\frac{C r^2}{C r^2+1}+\frac{D}{r}, \end{aligned}$$
(52)

where D is an arbitrary constant of integration. This arbitrary integration constant D was selected to be zero in order to achieve a non-singular solution and fulfill the constraint \(f(0)=0\). The new metric potential, denoted by the symbol \(e^{\lambda (r)}\), is then known as the deformed metric potential and may be expressed as

$$\begin{aligned} e^{-\lambda (r)}=\frac{1-\beta C r^2}{1+C r^2}. \end{aligned}$$
(53)

Now, plugging the Eq. (53) into Eq. (44) and integrating, we arrive at the following form of potential \(e^{\nu }\),

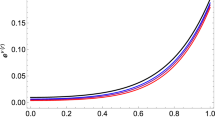
$$\begin{aligned} e^{\frac{\nu (r)}{2}}= & {} \frac{A_1}{2 \beta ^{3/2} C \sqrt{\frac{C r^2+1}{1-\beta C r^2}} \sqrt{1-\beta C r^2}}\left[ \sqrt{\beta } \left( C r^2+1\right) \right. \nonumber \\{} & {} \times \sqrt{1-\beta C r^2}+(\beta +1) \sqrt{C r^2+1}\,\,\nonumber \\{} & {} \times \left. \tan ^{-1}\left( \frac{\sqrt{1-\beta C r^2}}{\sqrt{\beta } \sqrt{C r^2+1}}\right) \right] +B_1, {} \end{aligned}$$
(54)

Now the generalized spacetime geometry for the Finch–Skea model having vanishing complexity factor can be given as

$$\begin{aligned} ds^2 = -\frac{1-\beta C r^2}{1+C r^2}\, dr^2-r^{2}(\sin ^{2}\theta d \phi ^{2}+d\theta ^{2}) + e^{\nu (r)} dt^2,~~~~ \nonumber \\ \end{aligned}$$
(55)

where, \(\nu (r)\) is given by Eq. (54). Now from Eq. (45), we can directly find the second deformation function h(r) as

$$\begin{aligned} h(r)= & {} \frac{1}{\beta }\Bigg [2\ln \Bigg \{\frac{A_1}{2 \beta ^{3/2} C \sqrt{\frac{C r^2+1}{1-\beta C r^2}} \sqrt{1-\beta C r^2}}\Bigg ((\beta +1) \nonumber \\{} & {} \times \sqrt{C r^2+1} \tan ^{-1}\left( \frac{\sqrt{1-\beta C r^2}}{\sqrt{\beta } \sqrt{C r^2+1}}\right) \Bigg )+\sqrt{\beta } \nonumber \\{} & {} \times \left( C r^2+1\right) \sqrt{1-\beta C r^2}+B_1\Bigg \}\nonumber \\{} & {} -\Bigg \{2\ln \left[ (B-A\sqrt{1+Cr^2}) \cos (\sqrt{1+Cr^2}) \right. \nonumber \\{} & {} \left. +(A+B\sqrt{1+Cr^2}) \sin (\sqrt{1+Cr^2})\right] \Bigg \} \Bigg ],~~ \end{aligned}$$
(56)

Now the components of \(\Theta \)-sector are determined by plugging the expressions of f(r) and h(r) along with \(\mu \) and \(\xi \) into the Eqs. (24)–(26) as,

$$\begin{aligned}{} & {} \Theta ^0_0(r)=\frac{C \left( C r^2+3\right) }{\left( C r^2+1\right) ^2}, \end{aligned}$$
(57)
$$\begin{aligned}{} & {} \Theta ^1_1(r)=\frac{C}{\Psi _1(r)}\Bigg [\sqrt{\beta } \sqrt{1-\beta C r^2} \Bigg (\sin \left( \sqrt{C r^2+1}\right) \nonumber \\{} & {} \quad \times \Bigg \{A \Bigg [A_1 (5 \beta +2) \left( C r^2+1\right) \nonumber \\{} & {} \quad +2 \beta (\beta +2)B_1 C \sqrt{\frac{C r^2+1}{1-\beta C r^2}}\Bigg ] \nonumber \\{} & {} \quad +\beta B \sqrt{C r^2+1} \Bigg [5 A_1 \left( C r^2+1\right) +2 \beta B_1 C \sqrt{\frac{C r^2+1}{1-\beta C r^2}}\Bigg ]\Bigg \}\nonumber \\{} & {} \quad +\cos \left( \sqrt{C r^2+1}\right) \Bigg \{A_1 \left( C r^2+1\right) \left( (5 \beta +2) B \right. \nonumber \\{} & {} \quad \times \left. -5 A \beta \sqrt{C r^2+1}\right) +2 \beta B_1 C \sqrt{\frac{C r^2+1}{1-\beta C r^2}} \nonumber \\{} & {} \quad \times \left[ (\beta +2) B-A \beta \sqrt{C r^2+1}\right] \Bigg \}\Bigg )\nonumber \\{} & {} \quad +A_1 (\beta +1) \tan ^{-1}\left( \frac{\sqrt{1-\beta C r^2}}{\sqrt{\beta } \sqrt{C r^2+1}}\right) \nonumber \\{} & {} \quad \times \bigg \{\sin \left( \sqrt{C r^2+1}\right) \left[ A (\beta +2) \sqrt{C r^2+1}\right. \nonumber \\{} & {} \quad \left. +\beta B \left( C r^2+1\right) \right] +\cos \left( \sqrt{C r^2+1}\right) \bigg ((\beta +2) B \sqrt{C r^2+1}\nonumber \\{} & {} \quad -A \beta \left( C r^2+1\right) \bigg )\bigg \}\Bigg ], \end{aligned}$$
(58)
$$\begin{aligned}{} & {} \Theta ^2_2(r)= \frac{C}{2 \beta \Psi _2^2(r) \left( C r^2+1\right) ^{5/2}} \nonumber \\{} & {} \quad \times \Bigg [\frac{1}{y^2(r)}\Bigg \{\sqrt{C r^2+1} \Big (A^2 \Psi _2^2(r) \left( 1-C^2 r^4\right) +2 \beta y^2(r) \nonumber \\{} & {} \quad \times \Big \{2 A_1 \beta \left( C r^2+1\right) \left( \beta C r^2-1\right) \left[ C r^2 \right. \nonumber \\{} & {} \quad \times \left. \left( \beta C r^2-2\right) -1\right] \left( A_1 C r^2+A_1+2 \beta B_1 C \sqrt{\frac{C r^2+1}{1-\beta C r^2}}\right) \nonumber \\{} & {} \quad -2 A_1 \sqrt{\beta } \Psi _2(r) \left( C r^2+1\right) \left( \beta C r^2 \left( C r^2+2\right) -1\right) \nonumber \\{} & {} \quad +\Psi _2^2(r)\Big \}+B^2 \Psi _2^2(r) \left( 1-C^2 r^4\right) \Big )\nonumber \\{} & {} \quad +\Psi _2^2(r) \bigg [\left( C r^2+1\right) \sin \left( 2 \sqrt{C r^2+1}\right) \nonumber \\{} & {} \quad \times \left( -A^2+2 A B \left( C r^2+1\right) ^{3/2}+B^2\right) \nonumber \\{} & {} \quad +2 A y(r) \sqrt{C r^2+1} \sin \left( \sqrt{C r^2+1}\right) \bigg ]\nonumber \\{} & {} \quad -\bigg [\Psi _2^2(r) \left( C r^2+1\right) \cos \left( 2 \sqrt{C r^2+1}\right) \nonumber \\{} & {} \quad \times \left( A^2 \left( C r^2+1\right) ^{3/2}+2 A B \right. \nonumber \\{} & {} \quad \left. -B^2 \left( C r^2+1\right) ^{3/2}\right) \bigg ]+2 B \Psi _2^2(r) y(r) \sqrt{C r^2+1} \nonumber \\{} & {} \quad \times \cos \left( \sqrt{C r^2+1}\right) \Bigg \}\nonumber \\{} & {} \quad -4 \beta ^{3/2} (\beta +1) \left( A_1 C r^2+A_1\right) ^2 \sqrt{1-\beta C r^2} \nonumber \\{} & {} \quad \times \left[ C r^2 \left( \beta C r^2-2\right) -1\right] \cot ^{-1}\left( \frac{\sqrt{\beta } \sqrt{C r^2+1}}{\sqrt{1-\beta C r^2}}\right) \Bigg ]. \end{aligned}$$
(59)
Fig. 1
figure 1

The flow chart shows a simple protocol for generalizing the perfect fluid solution to the anisotropic domain under the vanishing complexity factor

Full size image

The flow chart of this simple protocol for generalizing the perfect fluid solution to the anisotropic domain under the vanishing complexity factor is mentioned in the Fig. 1.

4 Matching conditions

Besides the above, on the boundary surface \(r=R\), the interior metric should be smoothly connected to the exterior metric, hence we need the continuity of the first and second fundamental forms over the boundary surface. The exterior spacetime is described by the exterior Schwarzschild solution, which is

$$\begin{aligned} ds^2 = \left( 1 - \frac{2M}{r}\right) dt^2- \frac{dr^2}{\left( 1 - \frac{2M}{r}\right) } - r^2 (d\theta ^2 + \sin ^2\theta d\phi ^2). \end{aligned}$$
(60)

In order to achieve the above requirements, the first and second fundamentals forms (Israel–Darmois junction conditions [113, 114]) are mathematically expressed as,

$$\begin{aligned}{} & {} 1-\frac{2M}{R}=e^{\nu (R)},~~~ \end{aligned}$$
(61)
$$\begin{aligned}{} & {} 1-\frac{2M}{R}=e^{-\lambda (R)},~~~ \end{aligned}$$
(62)
$$\begin{aligned}{} & {} p^{\text {eff}}_r(R)=0. \end{aligned}$$
(63)

The matching of two spacetime metrics and vanishing of effective pressure (\(p^{\text {eff}}\)) at the boundary surface \(r=R\), the aforementioned requirements (61)–(63) are not independent. These are however sufficient to determine all necessary integration constants involved in the solution. Using the above conditions, we find the expressions for the following constants,

$$\begin{aligned} \frac{A_1}{B1}= & {} -\Bigg [2 \beta ^{3/2} (\beta +1) C \sqrt{\frac{C R^2+1}{1-\beta C R^2}} \left( \beta C R^2-1\right) \Bigg ]\Bigg /\Bigg [\sqrt{\beta } \nonumber \\{} & {} \times (5 \beta +1) \left( C R^2+1\right) \left( \beta C R^2-1\right) -(\beta +1)^2 \nonumber \\{} & {} \times \sqrt{C R^2+1} \sqrt{1-\beta C R^2} \tan ^{-1}\left( \frac{\sqrt{1-\beta C R^2}}{\sqrt{\beta } \sqrt{C R^2+1}}\right) \bigg ],~~~~ \end{aligned}$$
(64)
$$\begin{aligned} M= & {} \frac{(\beta +1) C R^2 R}{2 C R^2+2}, \end{aligned}$$
(65)
$$\begin{aligned} B_1= & {} \sqrt{\frac{(1-\beta \,CR^2)}{(1+CR^2)}} \Bigg [\frac{A1}{B1} \Bigg (\sqrt{\beta } \left( C r^2+1\right) \sqrt{1-\beta C r^2} \nonumber \\{} & {} +(\beta +1) \sqrt{C r^2+1} \tan ^{-1}\left( \frac{\sqrt{1-\beta C r^2}}{\sqrt{\beta } \sqrt{C r^2+1}}\right) \Bigg )\Bigg /\Bigg (2 \beta ^{3/2} \nonumber \\{} & {} \times C \sqrt{\frac{C r^2+1}{1-\beta C r^2}} \sqrt{1-\beta C r^2}\Bigg )+1\Bigg ]^{-1}. \end{aligned}$$
(66)

5 Physical behavior of anisotropic solution

It is generally recognized that a theoretically well-behaved compact star model must meet some fundamental physical and mathematical criteria. The salient characteristics of the anisotropic stellar solution discovered by incorporating the well-known Finch–Skea perfect fluid model with vanishing complexity factor are very helpful in describing the composition of the relativistic compact star. This will be employed to analyze the necessary criteria in the subsections as follows:

5.1 The behavior of physical quantities such as density, pressures, and anisotropy inside the self-gravitating stellar system

In this subsection, based on the graphical plots shown here, we give an in-depth physical analysis of our findings with an emphasis on viability related to the anisotropic generalization of Finch–Skea contributions satisfying the vanishing complexity factor via gravitational decoupling. Figure 2 illustrates the energy density’s behavior. In this graph, we can see how the density profile changes as the deformation parameter \(\beta \) rises. The density, as we can observe, is a monotonically decreasing function with respect to the radial coordinate, r. It is evident that the density of the compact stellar configuration grows gradually when the deformation parameter, \(\beta \), is increased from 0.05 to 0.18. The radial pressure at every inside point of the stellar configuration is shown in Fig. 3. As one goes from the core towards the stellar surface, the radial pressure falls off smoothly until it vanishes at the boundary, as we would expect since there is no energy flux to the surrounding spacetime. The effect caused by the deformation parameter \(\beta \) demonstrates that the radial pressure increases as \(\beta \) grow. The same finding holds true for the tangential pressure with a little change when \(\beta \) assumes tiny values. Additionally, we note that, throughout the stellar configuration, the tangential pressure consistently outweighs its radial counterpart with very small deviations.

Fig. 2
figure 2

The above figure show the behavior of the effective energy density (\(\rho ^{\text {eff}}\times 10^{-4}\,[\text {km}^{-2}]\)) with respect to r for different \(\beta \)

Full size image
Fig. 3
figure 3

The above figure show the behavior of the effective radial pressure (\(p^{\text {eff}}_r\times 10^{-4}\,[\text {km}^{-2}]\)) with respect to r for different \(\beta \)

Full size image

In Fig. 4, we present the behavior of the anisotropy parameter with respect to the radial coordinate, r. We note that at every inside point of the stellar structure, the anisotropy, \(\Delta ^{\text {eff}}\), is positive. A repulsive force comes from anisotropy when the tangential pressure dominates the radial stress. By preventing the stellar configuration from being pulled inward by the gravitational force, this repulsive force aids in stabilizing it. Additionally, we emphasize that the degree of anisotropy can be governed by the deformation parameter \(\beta \), where an increase in \(\beta \) is accompanied by an increase in anisotropy, \(\Delta ^{\text {eff}}\). Generally, we see that when one gets closer to the compact stellar configuration’s surface layers, the anisotropy is the greatest.

Fig. 4
figure 4

The above figure show the behavior of the effective tangential pressure (\(p^{\text {eff}}_t\times 10^{-4}\,[\text {km}^{-2}]\)) with respect to r for different \(\beta \)

Full size image
Fig. 5
figure 5

The above figure shows the behavior of the effective anisotropy (\(\Delta ^{\text {eff}}\times 10^{-4}\,[\text {km}^{-2}]\)) with respect to r for different \(\beta \)

Full size image

5.2 Stability of anisotropic solution using Adiabatic Index

We are mainly interested in discussing the stability of the compact stellar object model using the adiabatic stability criterion defined by Chandrasekhar for isotropic pressure gradients (see [115, 116]). The formula for this adiabatic stability criterion is \( \Gamma = \left( 1+\frac{\rho }{p}\right) \left( \frac{dp}{d\rho }\right) _S\), where \(\frac{dp}{d\rho }\) is the sound speed and the subscript S indicates a constant specific entropy. It establishes that \(\Gamma > 4/3\) for stellar configurations with isotropic pressures, p. It has been shown by Herrera et al. [117, 118] that this criterion modifies when pressure anisotropy is involved, and takes the following form,

$$\begin{aligned} \Gamma < \frac{4}{3} + \left[ -\frac{4}{3}\frac{(p_r - p_t)}{|(p_r)'|r}\right] , \end{aligned}$$
(67)
Fig. 6
figure 6

The above figure shows the behavior of the adiabatic index (\(\Gamma _r\)) with respect to r for different \(\beta \)

Full size image
Table 1 Numerical values of the physical parameters such as: the central density, surface density, central pressure, mass (\(M/M_{\odot }\)), M/R, \(\Gamma _{crit}\), central value of adiabatic index \((\Gamma _{r0})\) and surface redshift \(Z_{s}\) for \(C=0.018~\text {km}^2\), and \(R=11~\text {km}\)
Full size table

where differentiation with respect to radial coordinate, r is shown by the prime. The Newtonian limit, \(\Gamma < \frac{4}{3}\), for unstable areas, emerges from the vanishing of the second component in (67), which originates from relativistic contributions. The adiabatic index can be modified by radial heat flux dissipation or the existence of density inhomogeneities. In this context, stability versus radial perturbations is maintained whenever \(\Gamma > \Gamma _{crit}\), where the critical value for the adiabatic index, \(\Gamma _{crit}\) is defined as \(\Gamma _{crit} = \frac{4}{3} + \frac{19}{21}u\) [119], and \(u = M/R\) indicates the stellar model’s compactness. The behavior of the stability criterion for our model is shown in Fig. 6, and their corresponding central values are shown in Table 1 for all chosen values of \(\beta \). It is noteworthy to note that an increase in the deformation parameter \(\beta \) tends to stabilize the stellar configuration as can be ascertained from Fig. 6. This demonstrates that our model meets the Chandrasekhar stability criterion and is stable under radial adiabatic infinitesimal perturbations, since the adiabatic index (\(\Gamma \)) is growing and greater than 4/3 at the stellar surface for all chosen values of \(\beta \).

5.3 Harrison–Zeldovich–Novikov stability analysis

We also need to investigate the Harrison-Zeldovich-Novikov (HZN) stability criterion in order to confirm the stability of the stellar model. To that end, we analyze the stability of the stellar model corresponding to the relationship between total mass M and central energy density \(\rho ^{\text {eff}}_0\) at the point when \(dM/d\rho ^{\text {eff}}_0 = 0\). According to the HZN stability criterion’s definition, [120, 121], which reveals

$$\begin{aligned} \frac{dM}{d\rho ^{\text {eff}}_0}> & {} 0 \rightarrow \text{ stable } \text{ configuration } \end{aligned}$$
(68)
$$\begin{aligned} \frac{dM}{d\rho ^{\text {eff}}_0}< & {} 0 \rightarrow \text{ unstable } \text{ configuration } \end{aligned}$$
(69)

to be satisfied along with every relativistic compact stellar object. Figure 7 demonstrates that, for our model, \(\frac{dM}{d\rho ^{\text {eff}}_0} > 0\), showing that we have a stable stellar configuration when the deformation parameter is moving from 0.05 to 0.18. In contrast, we show the stellar configuration in Fig. 8 as a function of stellar mass M and the effective central density \(\rho ^{\text {eff}}_0\), which increases with increasing values of \(\beta \) in accordance with the gradient profile shown in Fig. 7. Furthermore, the stellar configuration on the segments \(dM/d\rho ^{\text {eff}}_0 > 0 \) is always stable under radial oscillations, as can be seen from the \(M-\rho (0)\) plot in Fig. 8.

Fig. 7
figure 7

The above figures show the behavior of \(\frac{dM}{d\rho ^{\text {eff}}_0}\) for different \(\beta \)

Full size image
Fig. 8
figure 8

The above figure show the behavior of the mass (\(M/M_{\odot }\)) versus central density (\(\rho ^{\text {eff}}_0\)) for different \(\beta \)

Full size image

5.4 Compactness and surface redshift

According to the formula \(u(r) = m(r)/r\), the compactness factor [122, 123] of a stellar configuration is the ratio of the active gravitational mass to the constraining radius. The upper bound for the maximum possible value permitted for the compactness factor is defined by Buchdahl [124], which is \(u(r)|^{max} \le 8/9\) for a gravitationally confined spherically symmetric fluid. In this connection, Fig. 9 describes the u(r) profile; it is intriguing to notice that u(r) rises with the equilibrium radius, r, for each branch of the deformation parameter, \(\beta \in [0.05,0.18]\), and u(r) stays significantly under the Buchdahl bound.

Fig. 9
figure 9

The above figure describes the compactness (\(u=M/R\)) versus radius (R)

Full size image
Fig. 10
figure 10

The equi-mass contour diagram shows the mass distribution on \(R-\beta \) plane for \(C=0.018~\text {km}^2\)

Full size image

The surface redshift, \(Z_s(R)\), at \(r = R\) is then derived using the radial component of the line element as,

$$\begin{aligned} Z_s(R)=e^{\lambda (R/2)}-1. \end{aligned}$$
(70)

The redshift spectrum is shown in Table 1, it is clearly seen that the surface redshift increases significantly with any increase in \(\beta \) and also Buchdahl bound [124,125,126], \(Z_s < 2\) holds for the surface, \(r = R\) for each branch of the deformation parameter, \(\beta \in [0.05,0.18]\). Furthermore, we plotted the equi-mass contour diagram (10) on \(r-\beta \) plane to observe the effect of \(\beta \) on mass with r. As we can see from Fig.10 that if we fix radius R between 0 to 7.5 and increase \(\beta \), then no effect in mass is observed. But if \(R\ge 7\), then we found that mass (\(M/M_{\odot }\)) is increasing with \(\beta \) and the maximum increment is found near the boundary. On the other hand, if fix \(\beta \), then mass (\(M/M_{\odot }\)) increases with increasing radius R. Finally, we conclude that the decoupling constant (\(\beta \)) introduces an extra packing of mass to the stellar models.

Fig. 11
figure 11

The distribution of energy exchange (\(\Delta E\)) on (\(r-\beta \)) plane for \(A_2=0.5\) (left panel) and \(A_2=1\) (right panel)

Full size image

5.5 Energy exchange

In this section, we discuss the energy exchange between the sources \(T_{ij}\) and \(\Theta _{ij}\). Now using Eq. (31), we find the expression for Energy exchange,

$$\begin{aligned} \Delta E= & {} \frac{C}{\left( 1+C r^2\right) ^2} \Bigg [\left( C r^2+1\right) \Big (\frac{1}{\Delta E_1}\left[ 2 \big \{A_2 \sin \left( \sqrt{C r^2+1}\right) \right. \nonumber \\{} & {} \left. +\cos \left( \sqrt{C r^2+1}\right) \big \}\right] -1\Big )+C r^2+3\Bigg ]\times f_{\Delta E}(r), \end{aligned}$$
(71)

with

$$\begin{aligned} \Delta E_1(r)= & {} \left( 1-A_2 \sqrt{C r^2+1}\right) \cos \left( \sqrt{C r^2+1}\right) \\{} & {} +\left( A_2+\sqrt{C r^2+1}\right) \sin \left( \sqrt{C r^2+1}\right) , \end{aligned}$$

where constant \(A_2\) denotes A/B. The interesting physical feature of an anisotropic solution is the exchange of energy between the relativistic fluids corresponding to the new source (\(\Theta _{ij}\)) and original source (\(\hat{T}_{ij}\)). The energy transfer between fluid distributions can be analyzed based on the positive and negative values of \(\Delta E\). More specifically:

  1. (i)

    If \(\Delta E\) is positive, then the new source is giving energy to the environment.

  2. (ii)

    If \(\Delta E\) is negative, then the original/seed matter distribution is giving the energy.

Since the constant \(A_2\) is independent of the gravitationally decoupled solution but it appears in expression \(\Delta E\). Therefore, it is necessary to see the effect of this constant on the Energy exchange along with the decoupling constant \(\beta \). For this purpose, we plot Figs. 11 and 12 to observe the transitions of the energy exchange between the sources on the \(\beta -r\) plan for different values of constant \(A_2\).

The left panel of Fig. 11 is plotted for \(equi-\Delta E\) contour diagram on the \(\beta -r\) plane for \(A_2=0.5\). It can be observed that the higher value of \(\Delta E\) lies between \(7\le r \le 10\) and \(0.02\le \beta \le 0.03\), which shows that the new source is giving a high amount of energy to the environment in that region. But when we move near the core i.e. \(1.5\le r\le 2.5\), the \(\Delta E\) achieve the highest negative value for the same range of \(\beta \). This implies that the perfect fluid matter distribution is giving a high amount of energy. On the other hand, if we look at the right panel of the Fig. 11, we observe that the higher value of \(\Delta E\) is shifting to \(3\le r \le 6\) for \(\beta =0.21\) when we increase \(A_2\) from 0.5 to 1. Furthermore, the positive range of \(\Delta E\) is shifting towards the boundary when \(A_2\) is increasing.

Fig. 12
figure 12

The distribution of energy exchange (\(\Delta E\)) on (\(r-\beta \)) plane for \(A_2=-0.5\) (left panel) and \(A_2=-0.75\) (right panel)

Full size image

Now we move to Fig. 12, which has been plotted for the negative values of \(A_2=-0.5\) (left panel) and \(A_2=-0.75\) (right panel). From the left panel, we can observe that \(\Delta E\) is positive between \(0.0<r\le 8.5\) for all values of \(\beta \in [0.02,0.2]\) which implies that the new source is giving the energy with the above range. But when \(r \ge 8.5\), \(\Delta E\) stats negative, and values of \(\Delta E\) are ruled out after \(r \approx 9.8\) at \(\beta =0.02\). But when \(\beta \) increases, the negative value of \(\Delta E\) starts shifting near to boundary but the highest negative value exists when \(\beta \le 0.065\). This implies that the perfect fluid matter distribution is giving a high amount of energy near the boundary for all values of \(\beta \le 0.065\). Furthermore, the highest positive value of \(\Delta E\) lies between \(3< r\le 6\) at \(\beta =0.02\). On the other, the right panel of this figure shows that the pattern of energy exchange is the same as the left panel but the negative value of \(\Delta E\) is ruled out for the wide range of r near the surface.

6 Concluding remarks

We now summarise the principal findings of our investigation. A physically viable static anisotropic spherically symmetric stellar model was constructed. The method of gravitational decoupling of the metric components enabled the splitting of the source into a standard Einstein system and an additional system of equations. It was deemed prudent to make use of the well-studied Finch–Skea metric to satisfy the Einstein sector which was assumed to be a perfect fluid. A further condition was necessary to fully determine the new source with pressure anisotropy. To accomplish this it was assumed that the fluid distribution displayed a vanishing complexity factor in the sense of Herrera. The eventual model was carefully examined to check if it satisfied stringent regularity and stability conditions. In particular, the adiabatic stability criteria of Chandrasekar as well as the Harrison–Zeldovich–Novikov condition were all found to be satisfied. Graphical plots using specified parametric values verified that the mass-radius relationships comported with known physical behavior. In addition, a study of the energy exchange between the standard fluid and the anisotropic was exhibited in the form of plots. Moreover, all integration constants that appeared along the way were settled by matching the interior spacetime with the exterior Schwarzschild metric. This experiment has demonstrated the value of the decoupling approach in devising astrophysical models that harmonize with observed phenomena.