Calculation of Two-Boson Exchange with Complex-Valued Masses

Abstract

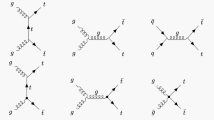
A new method for calculating the contribution of two-boson exchange diagrams (boxes) to the cross section for a four fermion process that involve one and two complex-valued boson masses is described. A detailed numerical analysis of the results obtained by means of this method and their comparison with the asymptotic expressions for the above cross section in the regions of energies below and above the $Z$-resonance energy are performed.

Appendices

Appendix A

CALCULATION OF THREE-BODY FUNCTIONS

The scalar three-body functions $H_{0}$ appearing in Eq. (35) has the form

$$H_{0}^{a}=H_{0}^{a}\left(p_{1},p_{3}\right)$$

(A.1)

$${}=\int\frac{dk}{i\pi^{2}}\frac{1}{\bigl{(}k^{2}-m_{a}^{2}\bigr{)}\bigl{(}k^{2}-2p_{1}k\bigr{)}\bigl{(}k^{2}-2p_{3}k\bigr{)}}.$$

Integrals of this type are readily calculable by the ’t Hooft–Veltman method [2] (for a detailed calculation, see, for example, [18]). For the case of $a=\gamma$, a compact expression that is symmetric with respect to the substitution $m_{q}\leftrightarrow m_{l}$ arises, as a result, in the ultrarelativistic approximation. Specifically, this expression has the form

$$H_{0}^{\gamma}\left(p_{1},p_{3}\right)=\frac{1}{t}\bigg{(}\ln\frac{-t}{\lambda^{2}}\ln\frac{-t}{m_{q}m_{l}}$$

(A.2)

$${}-\frac{1}{2}\ln\frac{-t}{m_{q}^{2}}\ln\frac{-t}{m_{l}^{2}}-\ln^{2}\frac{m_{q}}{m_{l}}-\frac{1}{6}\pi^{2}\bigg{)}.$$

The substitution $t\rightarrow u$ leads to a similar expression for $H_{0}^{\gamma}\left(p_{1},p_{4}\right)$.

The scalar three-body function $F_{0}$ appearing in Eq. (35) is given by

$$F_{0}^{b}=\int\frac{dk}{i\pi^{2}}$$

(A.3)

$${}\times\frac{1}{\bigl{(}(k-q)^{2}-m_{b}^{2}\bigr{)}\bigl{(}k^{2}-2p_{1}k\bigr{)}\bigl{(}k^{2}-2p_{3}k\bigr{)}}.$$

It can readily be reduced to the form (A.1) by means of the substitution $k\rightarrow k+q$ (the equality $F_{0}^{b}=H_{0}^{b}$ is proven in this way) and then be calculated by the method developed in [2]. For the case of $b=Z$, the result has the form of a nontrivial combination of 12 dilogarithms. It will be shown here how the method applied to four-point functions can be used to obtain simple expressions for the case of three-point functions as well.

Thus, the integral in question assumes the following form after the change of integration variable:

$$H_{0}^{Z}=\int\frac{dk}{i\pi^{2}}$$

(A.4)

$${}\times\frac{1}{\bigl{(}k^{2}-m_{Z}^{2}\bigr{)}\bigl{(}k^{2}-2p_{1}k\bigr{)}\bigl{(}k^{2}-2p_{3}k\bigr{)}}.$$

Setting $A=k^{2}-m_{Z}^{2}$, $B=k^{2}-2p_{1}k$, and $C=k^{2}-2p_{3}k$, we obtain

$$H_{0}^{Z}=2\int\limits_{0}^{1}dx\int\limits_{0}^{1}ydy\int\frac{dk}{i\pi^{2}}\frac{1}{E^{3}},$$

(A.5)

$$E=(Ax+B\bar{x})y+C\bar{y}.$$

After some algebra, we arrive at

$$E=k^{2}-2{\mathcal{P}}k+\Delta,$$

$${\mathcal{P}}=\bar{x}y\cdot p_{1}+\bar{y}\cdot p_{3},\quad\Delta=-m_{Z}^{2}\cdot xy.$$

The square of the 4-vector ${\mathcal{P}}$ is positive at any point of the integration domain:

$${\mathcal{P}}^{2}=m_{q}^{2}\cdot\bar{x}y(1-xy)$$

(A.6)

$${}+m_{l}^{2}\cdot\bar{y}(1-xy)-t\cdot\bar{x}y\bar{y}.$$

Removing the integral according to the well-known formula

$$2\int\frac{dk}{i\pi^{2}}\frac{1;k_{\alpha}}{[k^{2}-2{\mathcal{P}}k+\Delta]^{3}}$$

(A.7)

$${}=-\frac{1;{\mathcal{P}}_{\alpha}}{{\mathcal{P}}^{2}-\Delta},$$

we obtain

$$H_{0}^{Z}=-\int\limits_{0}^{1}dx\int\limits_{0}^{1}\frac{ydy}{{\mathcal{E}}-i\epsilon_{Z}\cdot xy},$$

(A.8)

$${\mathcal{E}}={\mathcal{P}}^{2}+m_{Z}^{2}\cdot xy.$$

As a result, we arrive at the following compact expressions:

$${\textrm{Re}}\ H_{0}^{Z}=-\int\limits_{0}^{1}dx\int\limits_{0}^{1}dy\frac{{\mathcal{E}}\cdot y}{{\mathcal{E}}^{2}+\epsilon_{Z}^{2}\cdot x^{2}y^{2}},$$

$${\textrm{Im}}\ H_{0}^{Z}=-\int\limits_{0}^{1}dx\int\limits_{0}^{1}dy\frac{\epsilon_{Z}\cdot xy^{2}}{{\mathcal{E}}^{2}+\epsilon_{Z}^{2}\cdot x^{2}y^{2}}.$$

The analytic result obtained by the method developed in [2] is also given here for the sake of comparison (a detailed derivation of it can be found in [18]). Ultimately (we have maximally sextuple embedding of expressions), it depends on six parameters

$$a=m_{q}^{2},\quad b=m_{q}^{2}+m_{l}^{2}-2p_{1}p_{3},$$

$$c=-2m_{q}^{2}+2p_{1}p_{3},$$

$$d=-f=-m_{Z}^{2}+i\epsilon_{Z},\quad e=0$$

and has the form of combinations of dilogarithms:

$$H_{0}^{Z}=\frac{1}{\beta}\sum_{i=1}^{3}F_{1}^{(i)},$$

(A.9)

$$F_{1}^{(i)}={\textrm{Li}}_{2}\frac{\alpha_{i}}{y^{-}_{i}}-{\textrm{Li}}_{2}\frac{\beta_{i}}{y^{-}_{i}}+{\textrm{Li}}_{2}\frac{\alpha_{i}}{y^{+}_{i}}-{\textrm{Li}}_{2}\frac{\beta_{i}}{y^{+}_{i}}.$$

A dilogarithm, which is a specific form of a polylogarithm, is defined for $z\in{\mathbb{C}}$ as

$${\textrm{Li}}_{2}(z)=-\int\limits_{0}^{z}\frac{\ln(1-t)}{t}dt.$$

(A.10)

In order to calculate dilogarithm values to the required precision, use is made of the following power-series expansion: ${\textrm{Li}}_{2}(z)=\sum_{k=1}^{\infty}\frac{z^{k}}{k^{2}}$. For the argument $z$ to be within the convergence region, the dilogarithm is usually reduced to a combination of a dilogarithm of some other argument and other functions by means of one of the numerous available identities, for example,

$${\textrm{Li}}_{2}(z)=-{\textrm{Li}}_{2}\Bigl{(}\frac{1}{z}\Bigr{)}-\frac{1}{2}\ln^{2}(-z)-\frac{1}{6}\pi^{2}.$$

(A.11)

In expression (A.9) $\beta=c+2\alpha b$ and the remaining coefficients are the following:

$$\alpha_{1}=\beta_{2}={1-\alpha-y_{0}},\quad\alpha_{2}=\beta_{3}={-y_{0}},$$

$$\alpha_{3}=\beta_{1}={-\alpha-y_{0}},\quad y_{0}=-\frac{d+\alpha e}{\beta}.$$

The expression for $\alpha$ is taken to be double-valued, but the ultimate result is independent of the choice of sign:

$$\alpha=\frac{-c\mp\sqrt{c^{2}-4ab}}{2b}.$$

The expressions for $y^{\pm}_{i}$ are roots of the equation $A_{i}y^{2}+B_{i}y+1=0$, where the coefficients depend on $K_{0}$ and $\gamma$ ($K_{0}=by_{0}^{2}+ey_{0}+f$ and $\gamma=2by_{0}+e$), so that we have

$$A_{1}K_{0}=b,$$

$$A_{2}K_{0}=b+\frac{\beta}{1-\alpha},\quad A_{3}K_{0}=b+\frac{\beta}{-\alpha},$$

$$B_{1}K_{0}=\gamma+c+2b\alpha,$$

$$B_{2}K_{0}=\gamma+y_{0}\frac{\beta}{1-\alpha},\quad B_{3}K_{0}=\gamma+y_{0}\frac{\beta}{-\alpha}.$$

Appendix B

TABLE OF INTEGRALS

The calculation involved the following integrals:

$${\mathcal{Y}}_{\mathcal{A}}=\int\limits_{0}^{1}\frac{zdz}{{\mathcal{A}}z+{\mathcal{B}}-i{\mathcal{C}}},$$

(A.12)

$${\mathcal{Y}}_{\mathcal{B}}=\int\limits_{0}^{1}\frac{z^{2}dz}{({\mathcal{A}}z+{\mathcal{B}}-i{\mathcal{C}})^{2}},$$

$${\mathcal{Y}}_{\mathcal{S}}=\int\limits_{0}^{1}\frac{zdz}{({\mathcal{A}}z+{\mathcal{B}}-i{\mathcal{C}})^{2}},$$

$${\mathcal{Y}}_{\mathcal{P}}=\int\limits_{0}^{1}\frac{dz}{({\mathcal{A}}z+{\mathcal{B}}-i{\mathcal{C}})^{2}}.$$

The calculated expressions have the form

$${\textrm{Re}}{\mathcal{Y}}_{\mathcal{A}}=\frac{1}{{\mathcal{A}}^{2}}\Bigl{(}{\mathcal{A}}+{\mathcal{C\ G}}_{\mathcal{A}}-{\mathcal{B\ G}}_{\mathcal{L}}\Bigr{)},$$

(A.13)

$${\textrm{Im}}{\mathcal{Y}}_{\mathcal{A}}=\frac{1}{{\mathcal{A}}^{2}}\Bigl{(}{\mathcal{B\ G}}_{\mathcal{A}}+{\mathcal{C\ G}}_{\mathcal{L}}\Bigr{)},$$

$${\textrm{Re}}{\mathcal{Y}}_{\mathcal{B}}=\frac{1}{{\mathcal{A}}}\Bigl{(}2{\textrm{Re}}{\mathcal{Y}}_{\mathcal{A}}-\frac{\mathcal{A}+\mathcal{B}}{\mathcal{D}}\Bigr{)},$$

$${\textrm{Im}}{\mathcal{Y}}_{\mathcal{B}}=\frac{1}{{\mathcal{A}}}\Bigl{(}2{\textrm{Im}}{\mathcal{Y}}_{\mathcal{A}}-\frac{\mathcal{C}}{\mathcal{D}}\Bigr{)},$$

$${\textrm{Re}}{\mathcal{Y}}_{\mathcal{S}}=\frac{1}{{\mathcal{A}}^{2}}\Bigl{(}-\frac{{\mathcal{A}}({\mathcal{A}}+{\mathcal{B}})}{\mathcal{D}}+{\mathcal{G}_{\mathcal{L}}}\Bigr{)},$$

$${\textrm{Im}}{\mathcal{Y}}_{\mathcal{S}}=\frac{1}{{\mathcal{A}}^{2}}\Bigl{(}-\frac{{\mathcal{A}\ \mathcal{C}}}{\mathcal{D}}-{{\mathcal{G}_{\mathcal{A}}}}\Bigr{)},$$

$${\textrm{Re}}{\mathcal{Y}}_{\mathcal{P}}=\frac{{{\mathcal{B}(\mathcal{A}+\mathcal{B})}}-{\mathcal{C}}^{2}}{({\mathcal{B}}^{2}+{\mathcal{C}}^{2}){\mathcal{D}}},$$

$${\textrm{Im}}{\mathcal{Y}}_{\mathcal{P}}=\frac{({\mathcal{A}}+2{\mathcal{B}}){\mathcal{C}}}{({\mathcal{B}}^{2}+{\mathcal{C}}^{2}){\mathcal{D}}}.$$

Use is made of the following condensed notation:

$${\mathcal{D}}=({\mathcal{A}}+{\mathcal{B}})^{2}+{\mathcal{C}}^{2},\quad{\mathcal{G}_{\mathcal{L}}}=\frac{1}{2}\ln\frac{\mathcal{D}}{{\mathcal{B}}^{2}+{\mathcal{C}}^{2}},$$

(A.14)

$${{\mathcal{G}_{\mathcal{A}}}}=\arctan\frac{\mathcal{B}}{\mathcal{C}}-\arctan\frac{{\mathcal{A}+\mathcal{B}}}{\mathcal{C}}.$$

At the resonance point $q^{2}=m_{Z}^{2}$, we obtain

$${\mathcal{B}}=0,\quad{\mathcal{G}_{\mathcal{L}}}=\ln\frac{\sqrt{{\mathcal{A}}^{2}+{\mathcal{C}}^{2}}}{{\mathcal{C}}},\quad{{\mathcal{G}_{\mathcal{A}}}}=-\arctan\frac{\mathcal{A}}{\mathcal{C}}.$$

Appendix C

ASYMPTOTIC FORMULAS FOR THE LE AND HE MODES

In order to obtain the LE expressions for the $\gamma Z$ box, it is necessary to make use of the general expression in terms of the coefficients and to set to zero all of them, with the exception of $b_{0}$ and the integral $H_{0}^{\gamma}$ from $I_{0}$ (for a proof of this, see, for example, [18] and references therein). For $b_{0}$ (direct box), we use the following asymptotic expression:

$$b_{0}^{\gamma Z,{\textrm{LE}}}=-\frac{1}{4m_{Z}^{2}}\biggl{(}\frac{3}{2}+\log\frac{m_{Z}^{2}}{-t}\biggr{)}.$$

(A.15)

For the $ZZ$ box, only the tensor coefficient $b_{0}$ is of importance:

$$b_{0}^{ZZ,{\textrm{LE}}}=-\frac{1}{4m_{Z}^{2}}.$$

(A.16)

In order to obtain HE formulas, we make use of the asymptotic expressions for the direct boxes (they are applicable for all of the cases: $ab=\gamma\gamma$, $\gamma Z$, $ZZ$, and $WW$):

$${\mathcal{M}}^{ab}_{D}{{\mathcal{M}}_{0}^{c}}^{+}=+\frac{2C_{s}}{s}\Bigl{[}C_{3}^{abc}l_{st}^{2}(3t^{2}+u^{2})$$

(A.17)

$${}+C_{4}^{abc}l_{st}^{2}(u^{2}-t^{2})+2C_{3+4}^{abc}l_{st}su\Bigr{]}$$

$${}-2C_{s}t\Pi^{ab}_{3}(q)H_{ss}^{abc}.$$

For the crossed boxes, we obtain

$${\mathcal{M}}^{ab}_{C}{{\mathcal{M}}_{0}^{c}}^{+}=-\frac{2C_{s}}{s}\Bigl{[}C_{3}^{abc}l_{su}^{2}(t^{2}+3u^{2})$$

(A.18)

$${}+C_{4}^{abc}l_{su}^{2}(u^{2}-t^{2})+2C_{3-4}^{abc}l_{su}st\Bigr{]}$$

$${}+2C_{s}u\Pi^{ab}_{4}(q)H_{ss}^{abc},$$

where $C_{i\pm j}^{abc}=C_{i}^{abc}\pm C_{j}^{abc}$. Also, use is made here of the following condensed notation:

$$H_{ss}^{abc}=2\bigl{[}C_{3}^{abc}(u^{2}+t^{2})+C_{4}^{abc}(u^{2}-t^{2})\bigr{]},$$

(A.19)

$$l_{r_{1}r_{2}}=\ln\frac{|r_{1}|}{|r_{2}|}.$$

The three-point functions in front of the propagator structures factorize; that is,

$$\Pi^{ab}_{3,4}(q)=H_{0}^{a}(p_{1},p_{3,4})D_{b}(q)$$

(A.20)

$${}+H_{0}^{b}(p_{1},p_{3,4})D_{a}(q).$$

We will now write explicitly the infrared-divergent parts of the $\gamma\gamma$ box. We have

$$M_{D}^{\gamma\gamma}{\mathcal{M}}_{0}^{c+}|^{\textrm{IR}}=-16\pi\alpha^{3}Q_{q}Q_{l}$$

(A.21)

$${}\times D_{\gamma}(q)D_{c}^{*}(q)\cdot R_{q}^{\gamma\gamma c}\cdot tH_{0}^{\gamma}(p_{1},p_{3}),$$

$$M_{C}^{\gamma\gamma}{\mathcal{M}}_{0}^{c+}|^{\textrm{IR}}=+16\pi\alpha^{3}Q_{q}Q_{l}$$

$${}\times D_{\gamma}(q)D_{c}^{*}(q)\cdot R_{q}^{\gamma\gamma c}\cdot uH_{0}^{\gamma}(p_{1},p_{4}),$$

where the ‘‘Born’’ term $R_{q}$ [see Eq. (15)] is related to the combinations $C_{3,4}$ by the equations

$$Q_{q}Q_{l}R_{q}^{aac}=2\bigl{[}C_{3}^{a\gamma c}(u^{2}+t^{2})+C_{4}^{a\gamma c}(u^{2}-t^{2})\bigr{]}.$$

(A.22)

The infrared-divergent parts of the $\gamma Z$ box are identical in form to expressions (A.21):

$$M_{D}^{\gamma Z}{\mathcal{M}}_{0}^{c+}|^{\textrm{IR}}=-8\pi\alpha^{3}Q_{q}Q_{l}$$

(A.23)

$${}\times D_{Z}(q)D_{c}^{*}(q)\cdot R_{q}^{ZZc}\cdot tH_{0}^{\gamma}(p_{1},p_{3}),$$

$$M_{C}^{\gamma Z}{\mathcal{M}}_{0}^{c+}|^{\textrm{IR}}=+8\pi\alpha^{3}Q_{q}Q_{l}$$

$${}\times D_{Z}(q)D_{c}^{*}(q)\cdot R_{q}^{ZZc}\cdot uH_{0}^{\gamma}(p_{1},p_{4}).$$

Clearly, the infrared-divergent parts of the $Z\gamma$ box make the same contribution; therefore, doubling occurs in the sum. As a result, the infrared-divergent part of the cross section for the box diagrams has the form

$$\frac{d\sigma_{\textrm{IR}}^{\textrm{Box}}}{dt}=-\frac{2\alpha^{3}}{s^{2}}Q_{q}Q_{l}$$

(A.24)

$${}\times\sum_{a,c=\gamma,Z}\Pi^{ac}R_{q}^{aac}\Bigl{[}tH_{0}^{\gamma,{\textrm{IR}}}(p_{1},p_{3})-(t\leftrightarrow u)\Bigr{]},$$

where

$$tH_{0}^{\gamma,{\textrm{IR}}}(p_{1},p_{3})=\ln\frac{s}{\lambda^{2}}\ln\frac{-t}{m_{q}m_{l}}.$$

Appendix D

COMPENDIUM OF SIMPLIFIED EXPRESSIONS

For the reference purposes, given immediately below is a simplified version of the formulas for the real part of the cross section for the two-boson exchange; that is,

$$\frac{d\sigma^{ab}}{dt}=\frac{2\alpha^{3}}{s^{2}}\int\limits_{0}^{1}dx\int\limits_{0}^{1}dy$$

(A.25)

$${}\times{\textrm{Re}}\!\sum_{c=\gamma,Z}D_{c}^{*}(q)\Bigl{(}C_{3}^{abc}[{\mathcal{K}_{3}^{\mathcal{D}}}+{\mathcal{K}_{3}^{\mathcal{C}}}]+C_{4}^{abc}[{\mathcal{K}_{4}^{\mathcal{D}}}+\mathcal{K}_{4}^{\mathcal{C}}]\Bigr{)},$$

where the coefficients in the cross section (their origin can readily be traced in the main body of the text) are given by

$${\mathcal{K}_{3}^{\mathcal{D}}}={\mathcal{C}_{0}^{\mathcal{D}}}t(t^{2}+u^{2})+2{\mathcal{B}_{0}^{\mathcal{D}}}(4t^{2}+u^{2})$$

(A.26)

$${}-2{\mathcal{C}_{1}^{\mathcal{D}}}st^{2}-{\mathcal{B}_{4}^{\mathcal{D}}}t(2t^{2}+u^{2}),$$

$${\mathcal{K}_{4}^{\mathcal{D}}}={\mathcal{C}_{0}^{\mathcal{D}}}t(u^{2}-t^{2})+2{\mathcal{B}_{0}^{\mathcal{D}}}(u^{2}-4t^{2})$$

$${}+2{\mathcal{C}_{1}^{\mathcal{D}}}st^{2}+{\mathcal{B}_{4}^{\mathcal{D}}}t(2t^{2}-u^{2}),$$

$${\mathcal{K}_{3}^{\mathcal{C}}}=-{\mathcal{K}_{3}^{\mathcal{D}}}|_{t\leftrightarrow u},\quad\mathcal{K}_{4}^{\mathcal{C}}=+{\mathcal{K}_{4}^{\mathcal{D}}}|_{t\leftrightarrow u}.$$

Expressions (A.25) and (A.26) are applicable for all cases ($\gamma Z$ and $ZZ$), but the coefficients ${\mathcal{C}_{0,1}}$ and ${\mathcal{B}_{0,4}}$ are different. They are presented here explicitly. For the $\gamma Z$ box, ${\mathcal{C}_{0,1}}$ and ${\mathcal{B}_{0,4}}$ are given by

$${\mathcal{C}_{0}^{\mathcal{D}}}=y\bigl{[}1-xy-(1+xy)\cdot sD_{Z}\bigr{]}{\mathcal{Y}}_{\mathcal{S}}$$

$${}-D_{Z}\Bigl{[}H_{0}^{\gamma}+\frac{{\mathcal{E}}y}{{\mathcal{E}}^{2}+\epsilon_{Z}^{2}x^{2}y^{2}}\Bigr{]},$$

$${\mathcal{B}_{0}^{\mathcal{D}}}=-\frac{1}{2}y{\mathcal{Y}}_{\mathcal{A}},\quad{\mathcal{C}_{1}^{\mathcal{D}}}=xy^{2}\bigl{[}{\mathcal{Y}}_{\mathcal{S}}+(1-2xy){\mathcal{Y}}_{\mathcal{B}}\bigr{]},$$

$${\mathcal{B}_{4}^{\mathcal{D}}}=\bar{x}y^{2}\bar{y}{\mathcal{Y}}_{\mathcal{B}}.$$

For the direct $ZZ$ box, the expressions for ${\mathcal{C}_{0,1}}$ and ${\mathcal{B}_{0,4}}$ have the form

$${\mathcal{C}_{0}^{\mathcal{D}}}=-y^{2}{\mathcal{Y}}_{\mathcal{S}},\quad{\mathcal{B}_{0}^{\mathcal{D}}}=-\frac{1}{2}y{\mathcal{Y}}_{\mathcal{A}},$$

$${\mathcal{C}_{1}^{\mathcal{D}}}=x\bar{x}y^{3}{\mathcal{Y}}_{\mathcal{B}},\quad{\mathcal{B}_{4}^{\mathcal{D}}}=y\bar{y}\bigl{[}{\mathcal{Y}}_{\mathcal{S}}-{\mathcal{Y}}_{\mathcal{B}}\bigr{]}.$$

The expression for $H_{0}^{\gamma}$ is given by Eq. (A.2), while the expression for ${\mathcal{E}}$ is given by Eq. (A.8). The expressions for $\mathcal{Y}_{\mathcal{A},\mathcal{B},\mathcal{S}}$ are presented in Appendix B. They depend on the coefficients $\mathcal{A}$, $\mathcal{B}$, and $\mathcal{C}$, whose values are given in Table 1 for various boson configurations in the direct diagram.

Table 1 Coefficients $\mathcal{A}$, $\mathcal{B}$, and $\mathcal{C}$ for various boson configurations in the direct box