Simulation of Thermal Surface Waves in a Protoplanetary Disk in a Two-Dimensional Approximation

Abstract

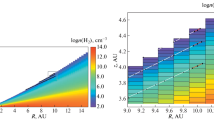
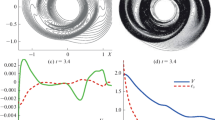
Theoretical models predict that the obscuration of stellar radiation by irregularities on the surface of a protoplanetary disk can cause self-generating waves traveling towards the star. However, this process is traditionally simulated using the 1+1D approach, the key approximations of which—vertical hydrostatic equilibrium of the disk and vertical diffusion of IR radiation—can distort the picture. This article presents a two-dimensional radiative hydrodynamic model of the evolution of an axially symmetric gas and dust disk. Within this model, but using simplified assumptions from 1+1D models, we have reproduced the spontaneous generation and propagation of thermal surface waves. The key conclusion of our work is that taking into account two-dimensional hydrodynamics and diffusion of IR radiation suppresses the spontaneous generation and development of thermal waves observed in the 1+1D approximation. The search for the possibility of the existence of surface thermal waves should be continued by studying the problem for various parameters of protoplanetary disks.

Appendices

APPENDIX A

1.1 FLUX VECTOR COMPONENTS FOR THE FINITE-DIFFERENCE EQUATION OF HYDRODYNAMICS

The components of the flux vectors entering into Eq. (4) for a finite-difference grid in spherical coordinates, taking into account the axial symmetry of the problem, have the following form:

$$\Delta {{F}_{1}} = {{F}_{{1a}}} - {{F}_{{1b}}},$$

$$\Delta {{F}_{2}} = {{F}_{{2a}}} - {{F}_{{2b}}},$$

$$\Delta {{F}_{3}} = {{F}_{{3a}}} - {{F}_{{3b}}},$$

$$\Delta {{F}_{4}} = {{F}_{{4a}}} - {{F}_{{4b}}},$$

$$\Delta {{F}_{5}} = {{F}_{{5a}}} - {{F}_{{5b}}},$$

$$\Delta {{G}_{1}} = {{G}_{{1a}}} - {{G}_{{1b}}},$$

$$\Delta {{G}_{2}} = {{G}_{{2a}}}\cos \theta - {{G}_{{2b}}}\cos \theta + {{G}_{{3a}}}\sin \theta + {{G}_{{3b}}}\sin \theta ,$$

$$\Delta {{G}_{3}} = - {{G}_{{2a}}}\sin \theta - {{G}_{{2b}}}\sin \theta + {{G}_{{3a}}}\cos \theta - {{G}_{{3b}}}\cos \theta ,$$

$$\Delta {{G}_{4}} = {{G}_{{4a}}} - {{G}_{{4b}}},$$

$$\Delta {{G}_{5}} = {{G}_{{5a}}} - {{G}_{{5b}}},$$

$$\Delta {{H}_{1}} = 0,$$

$$\Delta {{H}_{2}} = {{H}_{{4a}}}\sin \varphi \sin \theta + {{H}_{{4b}}}\sin \varphi \sin \theta ,$$

$$\Delta {{H}_{3}} = {{H}_{{4a}}}\sin \varphi \cos \theta + {{H}_{{4b}}}\sin \varphi \cos \theta ,$$

$$\begin{gathered} \Delta {{H}_{4}} = - {{H}_{{2a}}}\sin \varphi \sin \theta - {{H}_{{2b}}}\sin \varphi \sin \theta \\ \, - {{H}_{{3a}}}\sin \varphi \cos \theta - {{H}_{{3b}}}\sin \varphi \cos \theta , \\ \end{gathered} $$

$$\Delta {{H}_{5}} = 0,$$

where

$${{F}_{{1a}}} = (\tilde {\rho }\tilde {u}{{)}_{{ra}}}{\kern 1pt} {{S}_{{ra}}},\quad {{F}_{{1b}}} = (\tilde {\rho }\tilde {u}{{)}_{{rb}}}{\kern 1pt} {{S}_{{rb}}},$$

$${{F}_{{2a}}} = (\tilde {\rho }{{\tilde {u}}^{2}} + \tilde {P}{{)}_{{ra}}}{\kern 1pt} {{S}_{{ra}}},\quad {{F}_{{2b}}} = (\tilde {\rho }{{\tilde {u}}^{2}} + \tilde {P}{{)}_{{rb}}}{\kern 1pt} {{S}_{{rb}}},$$

$${{F}_{{3a}}} = (\tilde {\rho }\tilde {u}\tilde {v}{{)}_{{ra}}}{\kern 1pt} {{S}_{{ra}}},\quad {{F}_{{3b}}} = (\tilde {\rho }\tilde {u}\tilde {v}{{)}_{{rb}}}{\kern 1pt} {{S}_{{rb}}},$$

$${{F}_{{4a}}} = (\tilde {\rho }\tilde {u}\tilde {w}{{)}_{{ra}}}{\kern 1pt} {{S}_{{ra}}},\quad {{F}_{{4b}}} = (\tilde {\rho }\tilde {u}\tilde {w}{{)}_{{rb}}}{\kern 1pt} {{S}_{{rb}}},$$

$${{F}_{{5a}}} = (\tilde {E} + \tilde {P}\tilde {u}{{)}_{{ra}}}{\kern 1pt} {{S}_{{ra}}},\quad {{F}_{{5b}}} = (\tilde {E} + \tilde {P}\tilde {u}{{)}_{{rb}}}{\kern 1pt} {{S}_{{rb}}},$$

$${{G}_{{1a}}} = (\tilde {\rho }\tilde {v}{{)}_{{\theta a}}}{\kern 1pt} {{S}_{{\theta a}}},\quad {{G}_{{1b}}} = (\tilde {\rho }\tilde {v}{{)}_{{\theta b}}}{\kern 1pt} {{S}_{{\theta b}}},$$

$${{G}_{{2a}}} = (\tilde {\rho }\tilde {v}\tilde {u}{{)}_{{ra}}}{\kern 1pt} {{S}_{{\theta a}}},\quad {{G}_{{2b}}} = (\tilde {\rho }\tilde {v}\tilde {u}{{)}_{{rb}}}{\kern 1pt} {{S}_{{\theta b}}},$$

$${{G}_{{3a}}} = (\tilde {\rho }{{\tilde {v}}^{2}} + \tilde {P}{{)}_{{\theta a}}}{\kern 1pt} {{S}_{{\theta a}}},\quad {{G}_{{3b}}} = (\tilde {\rho }{{\tilde {v}}^{2}} + \tilde {P}{{)}_{{\theta b}}}{\kern 1pt} {{S}_{{\theta b}}},$$

$${{G}_{{4a}}} = (\tilde {\rho }\tilde {v}\tilde {w}{{)}_{{\theta a}}}{\kern 1pt} {{S}_{{\theta a}}},\quad {{G}_{{4b}}} = (\tilde {\rho }\tilde {v}\tilde {w}{{)}_{{\theta b}}}{\kern 1pt} {{S}_{{\theta b}}},$$

$${{G}_{{5a}}} = (\tilde {E} + \tilde {P}\tilde {v}{{)}_{{\theta a}}}{\kern 1pt} {{S}_{{\theta a}}},\quad {{G}_{{5b}}} = (\tilde {E} + \tilde {P}\tilde {v}{{)}_{{\theta b}}}{\kern 1pt} {{S}_{{\theta b}}},$$

$${{H}_{{2a}}} = (\tilde {\rho }\tilde {w}\tilde {u}{{)}_{{\varphi a}}}{\kern 1pt} {{S}_{{\varphi a}}},\quad {{H}_{{2b}}} = (\tilde {\rho }\tilde {w}\tilde {u}{{)}_{{\varphi b}}}{\kern 1pt} {{S}_{{\varphi b}}},$$

$${{H}_{{3a}}} = (\tilde {\rho }\tilde {w}\tilde {v}{{)}_{{\varphi a}}}{\kern 1pt} {{S}_{{\varphi a}}},\quad {{H}_{{3b}}} = (\tilde {\rho }\tilde {w}\tilde {v}{{)}_{{\varphi b}}}{\kern 1pt} {{S}_{{\varphi b}}},$$

$${{H}_{{4a}}} = (\tilde {\rho }{{\tilde {w}}^{2}} + \tilde {P}{{)}_{{\varphi a}}}{\kern 1pt} {{S}_{{\varphi a}}},\quad {{H}_{{4b}}} = (\tilde {\rho }{{\tilde {w}}^{2}} + \tilde {P}{{)}_{{\varphi b}}}{\kern 1pt} {{S}_{{\varphi b}}}.$$

In the above expressions, the tilde denotes the quantities found from the solution of the problem of the decay of an arbitrary discontinuity for the corresponding cell’s face, marked with a subscript; ${{S}_{{ra}}}$, ${{S}_{{rb}}}$, ${{S}_{{\theta a}}}$, ${{S}_{{\theta b}}}$, ${{S}_{{\varphi a}}}$, and ${{S}_{{\varphi b}}}$ are the areas of the cell’s faces (see Fig. 2). Note that the trigonometric functions and the mixing of the flux components in the above expressions for the components of $\Delta G$ and $\Delta H$ are associated with the transformation of the local basis (and, accordingly, the coordinates of the velocity vectors) upon the transition between cells in $\theta$ and $\varphi$. At the same time, zero values for $\Delta {{H}_{1}}$ and $\Delta {{H}_{5}}$ are obtained taking into account the assumed axial symmetry of the problem.

APPENDIX B

1.1 METHOD FOR SOLVING THE SYSTEM OF THERMAL RADIATIVE TRANSFER EQUATIONS

The system of equations for the thermal evolution of the medium (10) and (11) is solved using Newton’s iterations; for this, the equations are linearized using the approximation

$${{T}^{4}} \approx 4{\kern 1pt} T_{k}^{3}T - 3{\kern 1pt} T_{k}^{4},$$

where ${{T}_{k}}$ is the temperature value at the previous ($k$th) iteration, after which Eqs. (10) and (11) can be reduced to

$$T = \frac{{{{b}_{{\text{d}}}} + {{\omega }_{{\text{P}}}}\Delta t{\kern 1pt} {{E}_{{\text{r}}}}}}{{{{c}_{{\text{d}}}} + {{c}_{{\text{r}}}}}},$$

(B.1)

$$\left[ {1 + \frac{{{{c}_{{\text{d}}}}}}{{{{c}_{{\text{d}}}} + {{c}_{{\text{r}}}}}}{{\omega }_{{\text{P}}}}\Delta t - \Delta t{\kern 1pt} \hat {\Lambda }} \right]{{E}_{{\text{r}}}} = g.$$

(B.2)

The coefficients ${{c}_{{\text{d}}}}$, ${{\omega }_{{\text{P}}}}$, ${{c}_{{\text{r}}}}$, ${{b}_{{\text{d}}}}$, and $g$ in these equations are calculated as follows:

$${{c}_{{\text{d}}}} = \rho {{c}_{{\text{V}}}},$$

$${{\omega }_{{\text{P}}}} = c\rho {{\kappa }_{{\text{P}}}},$$

$${{c}_{{\text{r}}}} = 4aT_{k}^{3}{{\omega }_{{\text{P}}}}\Delta t,$$

$${{b}_{{\text{d}}}} = {{c}_{{\text{d}}}}{{T}^{n}} + \frac{3}{4}{{c}_{{\text{r}}}}{{T}_{k}} + \rho S\Delta t,$$

$$g = E_{{\text{r}}}^{n} - \frac{3}{4}{{c}_{{\text{r}}}}{{T}_{k}} + \frac{{{{c}_{{\text{r}}}}{{b}_{{\text{d}}}}}}{{{{c}_{{\text{d}}}} + {{c}_{{\text{r}}}}}}{\kern 1pt} .$$

We approximate the differential operator $\hat {\Lambda }$ in spherical coordinates in the following finite difference form:

$$\begin{gathered} \hat {\Lambda }{{E}_{{\text{r}}}} = \frac{1}{{\Delta V}} \\ \times \;\left( {{{S}_{{ra}}}{{F}_{{{\text{r}},ra}}} - {{S}_{{rb}}}{{F}_{{{\text{r}},rb}}} + {{S}_{{\theta a}}}{{F}_{{{\text{r}},\theta a}}} - {{S}_{{\theta b}}}{{F}_{{{\text{r}},\theta b}}}} \right), \\ \end{gathered} $$

(B.3)

where $\Delta V$ is the cell volume and ${{S}_{{ra}}}$, ${{S}_{{rb}}}$, ${{S}_{{\theta a}}}$, and ${{S}_{{\theta b}}}$ are the current cell faces’ areas (see Fig. 2). The fluxes through the cell’s faces are found by the formulas

$${{F}_{{{\text{r}},ra}}} = - \frac{1}{{{{\sigma }_{{ra}}}}}{\kern 1pt} \frac{{{{E}_{{\text{r}}}}(i,j) - {{E}_{{\text{r}}}}(i - 1,j)}}{{\Delta {{r}_{a}}}},$$

$${{F}_{{{\text{r}},rb}}} = - \frac{1}{{{{\sigma }_{{rb}}}}}{\kern 1pt} \frac{{{{E}_{{\text{r}}}}(i + 1,j) - {{E}_{{\text{r}}}}(i,j)}}{{\Delta {{r}_{b}}}},$$

$${{F}_{{{\text{r}},\theta a}}} = - \frac{1}{{{{\sigma }_{{\theta a}}}}}{\kern 1pt} \frac{{{{E}_{{\text{r}}}}(i,j) - {{E}_{{\text{r}}}}(i,j - 1)}}{{{{r}_{c}}\Delta {{\theta }_{a}}}},$$

$${{F}_{{{\text{r}},\theta b}}} = - \frac{1}{{{{\sigma }_{{\theta b}}}}}{\kern 1pt} \frac{{{{E}_{{\text{r}}}}(i,j + 1) - {{E}_{{\text{r}}}}(i,j)}}{{{{r}_{c}}\Delta {{\theta }_{b}}}},$$

where ${{E}_{{\text{r}}}}(i,j)$ is the energy in the current cell with indices $(i,j)$, ${{r}_{c}}$ is the radial coordinate of the center of the current cell, the values of $\sigma = 3\rho {{\kappa }_{{\text{r}}}}{\text{/}}c$ are calculated based on the gas density and medium temperature for the corresponding faces by interpolating the central values, and $\Delta r$ and $r\Delta \theta$ are the distances from the center of the current cell to the centers of adjacent cells for the corresponding faces (see Fig. 2). With this, Eq. (B.2) can be rewritten in the following operator form:

$$\hat {\Omega }{{E}_{{\text{r}}}} = {\mathbf{g}},$$

(B.4)

where $\hat {\Omega } = \left( {1 + \frac{{{{c}_{{\text{d}}}}}}{{{{c}_{{\text{d}}}} + {{c}_{{\text{r}}}}}}{{\omega }_{{\text{P}}}}\Delta t} \right)\hat {I} - \Delta t{\kern 1pt} \hat {\Lambda }$ and $\hat {I}$ is the unit tensor. Equation (B.4) is a compact representation of a system of linear algebraic equations with a sparse five-diagonal matrix. We solve this system of equations using the GMRES method [22] or the alternating direction implicit (ADI) method [23], depending on the complexity of the problem. Our numerical experiments with this model show that the GMRES method has good stability, but is several times slower than the ADI method. For the ADI method, the choice of iterative parameters is important, which we find based on the closeness of the results to the solution of the system by the GMRES method.