Ultrabroadband valley transmission and corner states in valley photonic crystals with dendritic structure

Abstract

In photonic crystal systems, topologically protected edge states and corner states can be achieved by breaking spatial inversion symmetry, which is expected to be applied to topologically protected lasers, optical communication and integrated photonics. However, designing ultrabroadband topological photonic crystals is still a challenge. In this work, we propose a valley photonic crystal composed of dendritic structures, which can realize valley transmission with a relative bandwidth up to 59.65%. Compared with the previously reported two-dimensional broadband photonic crystals with 32.02% bandwidth, the relative bandwidth of the proposed valley transmission is increased by almost 100%. Theoretical analysis, numerical simulation and experimental measurement all confirm flexible manipulation of electromagnetic wave propagation paths. Ultrabroadband topological waveguides with the zigzag and armchair interface are demonstrated, which can achieve experimentally 58.71% and 36.78% relative bandwidth, respectively. In addition, several topological channel intersections are designed. Finally, two types of corner states with valley switchability and selectivity are demonstrated.

Introduction

With the rapid development of wireless communication, the fifth-generation mobile communication technology (5 G) has been intensive researched. Topological insulators offer a new approach of wireless communication since they have edge states where electromagnetic wave can be transmitted without backscattering^1,2,3,4,5. Inspired by this discovery, topological physics in classical systems have attracted considerable attention, such as phononics^6,7,8, mechanics^9,10, and photonic^11,12,13,14. Several main mechanisms of two-dimensional topological systems including Hall effect^11,12, spin Hall effect^13,14,15 and valley Hall effect^{16,17,18,19,20,21} are demonstrated. Recently, higher-order topological insulators as a new research field can realize low-dimensional corner and hinge states, which provides an important basis for realizing higher-dimensional robust topological waveguides^22,23,24,25. Among them, corner states in valley insulators have valley switchability and selectivity, garnering considerable attention in a variety of physical systems^26,27,28. However, it is rare to study the valley switchability and selectivity of the multi-type corner states in the previously reported photonic valley topological insulators.

In photonic system, topological insulators utilize photonic crystals and metamaterials to engineer the topological band structure with emergence of topologically protected edge states and corner states^{13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37}. However, the limited bandwidth of the photonic topological insulators hinders the potential applications of photonic devices in high-speed and multichannel photonic systems. It is a challenge to improve the bandwidth of topological edge states due to the lack of bandwidth enhancement mechanism. Recently, broadband topological insulators have been actively pursued in photonic systems^{29,30,31,32,33,34,35,36,37}. Shalaev et al. design an optical valley topological insulator with a 5.5% relative bandwidth²⁹. Han et al. theoretically presented a valley photonic crystal composed of all-dielectric silicon-based triangular air holes with a relative bandwidth of 15.53%³⁰. Kumar et al. designed a valley photonic crystal waveguide with bearded interface, which can achieve topological edge states with a 30.77% relative bandwidth³². Zhang et al. realized a broadband photonic topological insulator based on triangular-holes array. The topological edge state can be up to 32.02%³³. Although great progress has been made in broadening the bandwidth of topological states in two-dimensional systems, the previously reported maximum bandwidth of edge states is 32.02%. In addition, most of the broadband photonic topological insulators have been demonstrated in simulations. It is rarely to realize ultrabroadband edge states in experiments.

In this paper, we propose a valley photonic crystal composed of dendritic structures, and experimentally realize ultrabroadband valley transmission and higher-order corner states. Two interfaces including zigzag and armchair interfaces are constructed by using arrays of dendritic unit cell. The theoretical relative bandwidths of the edge states in the zigzag and armchair interfaces are 59.65% and 44.66%, respectively. Ultrabroadband topological waveguides are designed based on the different interfaces. The measured relative bandwidths of the topological waveguides with the zigzag and armchair interface are up to 58.71% and 36.78%, respectively. Next, we demonstrate topological channel intersections where the transport paths are determined by the geometries of the intersections. Finally, the traditional corner states based on bulk topology, and the new corner states caused by the long-range interactions are realized. Our results can promote the applications of tunable broadband electromagnetic wave transmission.

Results and discussion

Ultrabroadband valley photonic crystal. In order to obtain broadband valley photonic crystals, we discuss the bulk dispersion around the Brillouin zone boundary by focusing on K valley. As in any uniaxial structure, the eigenmodes propagating in the xoy plane can be classified as TE (E_⊥, H_z) and TM (H_⊥, E_z). Here we discuss TE modes. Based on Maxwell’s equations, a 3$\times$3 equation of the Fourier component of H_z at K point can be obtained and shown as^30,33

$$\hat{{{{{\alpha }}}}}\widetilde{{{{{H}}}}}={{{{{\omega }}}}}^{{{{{2}}}}}{{{{{\mu }}}}}_{{{{{0}}}}}{{{{{\varepsilon }}}}}_{{{{{0}}}}}\hat{{{{{\beta }}}}}\widetilde{{{{{H}}}}}$$

(1)

Here $\hat{{{{{\alpha }}}}}{{{{=}}}}{{{{{K}}}}}^{{{{{2}}}}}{{{{+}}}}{{{{K}}}}{{{{\delta }}}}{{{{{k}}}}}_{{{{{x}}}}}\left(\begin{array}{ccc}{{{{2}}}} & {{{{0}}}} & {{{{0}}}}\\ {{{{0}}}} & {{{{-}}}}{{{{{\bf{1}}}}}} & {{{{0}}}}\\ {{{{0}}}} & {{{{0}}}} & {{{{-}}}}{{{{{\bf{1}}}}}}\end{array}\right){{{{+}}}}{{{{K}}}}{{{{\delta }}}}{{{{{k}}}}}_{{{{{y}}}}}\left(\begin{array}{ccc}{{{{0}}}} & {{{{0}}}} & {{{{0}}}}\\ {{{{0}}}} & {{{{-}}}}\sqrt{{{{{3}}}}} & {{{{0}}}}\\ {{{{0}}}} & {{{{0}}}} & \sqrt{{{{{3}}}}}\end{array}\right)$, $\hat{{{{{\beta }}}}}{{{{=}}}}\left(\begin{array}{ccc}{{{{{\beta }}}}}_{{{{{{G}}}}}_{{{{{0}}}}}} & {{{{{\beta }}}}}_{{{{{{G}}}}}_{{{{{2}}}}}} & {{{{{\beta }}}}}_{{{{{{G}}}}}_{{{{{1}}}}}}\\ {{{{{\beta }}}}}_{{{{{{G}}}}}_{{{{{1}}}}}} & {{{{{\beta }}}}}_{{{{{{G}}}}}_{{{{{0}}}}}} & {{{{{\beta }}}}}_{{{{{{G}}}}}_{{{{{2}}}}}}\\ {{{{{\beta }}}}}_{{{{{{G}}}}}_{{{{{2}}}}}} & {{{{{\beta }}}}}_{{{{{{G}}}}}_{{{{{1}}}}}} & {{{{{\beta }}}}}_{{{{{{G}}}}}_{{{{{0}}}}}}\end{array}\right)$, $\widetilde{{{{{H}}}}}{{{{=}}}}\left[\begin{array}{ccc}{{{{{H}}}}}_{{{{{{G}}}}}_{{{{{0}}}}}} & {{{{{H}}}}}_{{{{{{G}}}}}_{{{{{1}}}}}} & {{{{{H}}}}}_{{{{{{G}}}}}_{{{{{2}}}}}}\end{array}\right]$, where ${{{{K}}}}{{{{=}}}}{{{{4}}}}{{{{\pi }}}}{{{{/}}}}{{{{3}}}}{{{{a}}}}$. By converting Eq. (1), the photonic effective Hamiltonian for the minimum band model of bulk dispersions is

$$\hat{H}={v}_{D}\left({\hat{\sigma }}_{x}{{\hat{\tau }}_{z}\delta k}_{x}+{\hat{\sigma }}_{y}{\hat{\tau }}_{0}\delta {k}_{y}\right)+{\omega }_{D}\Delta p{\hat{\tau }}_{0}{\hat{\sigma }}_{z}$$

(2)

where ${v}_{D}$ is the Dirac velocity, ${\hat{\sigma }}_{x,y,z}$ and ${\hat{\tau }}_{z}$ act on the orbital and valley state vector, respectively. ${\hat{\tau }}_{0}$ is identity matrix, $({\delta k}_{x},{\delta k}_{y})$ is the distance measured from the Dirac points, ${\omega }_{D}$ is the Dirac frequency, and $\Delta p$ is the perturbation strength. According to Hamiltonian $\hat{H}$, bandgap is written as ${\Delta \omega =2\omega }_{0}|\Delta {p|}\approx {2\omega }_{D}|\Delta {p|}$. Therefore, the relative bandwidth ${\gamma =\Delta \omega /\omega }_{0}\approx 2|\Delta {p|}$ is proportional to the perturbation strength $\Delta p$. According to the first-order perturbation theory, $\Delta p$ can be written as

$$\Delta p=\frac{i\sqrt{3}{\mu }_{0}{\varepsilon }_{0}{\omega }_{0}}{4\times {\left(K\right)}^{2}}\left({\beta }_{{G}_{1}}-{\beta }_{{G}_{2}}\right)\propto {\int }_{v}\Delta \varepsilon \left({\left\lfloor {E}_{R}\left(K\right)\right\rfloor }^{2}-{\left\lfloor {E}_{L}\left(K\right)\right\rfloor }^{2}\right){dv}$$

(3)

where ${E}_{R,L}(K)$ represent the normalized electric field of the pseudospin states at K point, and $v$ is the geometric perturbation area.

Figure 1a shows a valley photonic crystal composed of arrays of first-order dendritic unit cells with Y-shape, where the black solid lines indicate the rhombic lattice, and the black dashed lines divide the rhombic lattice into regions I and II. Schematic and band structure of the first-order dendritic unit cell is shown in Fig. 1b. Perturbation strength ∆p depends on the difference between the geometric perturbation area in region I and region II. As the geometric perturbation area in region I is equal to that of region II, the bandgap is zero and a degeneracy point appears at point K/K’. The band diagram is shown in Fig. 1b presented by black solid lines. As the geometric perturbation area of the region I and region II are different, the degeneracy points are opened to form a topological bandgap. The corresponding band diagram is shown by the red solid lines in Fig. 1b.

Fig. 1: Schematic and band structure of the valley photonic crystal.

a Valley photonic crystal composed of first-order dendritic unit cell arranged periodically along a triangular lattice. Solid black lines label the rhombic lattice, where the black dashed lines divide the rhombic lattice into regions I and II. Light orange shaded regions represent the geometric perturbation region. b Schematics and the band structures of the first-order, second-order and third-order fractal dendritic unit cell. Yellow-shaded regions represent the topological bandgaps. Geometric parameters of the first-order dendritic unit cell are a = 30 mm, w = 2.1 mm, θ = -30°, l = 12.15 mm. The lengths of the three branches are the same indicated by l, and the angle between each branch is 120°. Geometric parameters of the second-order dendritic unit cell are α = 60°, b₁ = 6 mm, b₂ = 7.1 mm, l = b₁ + $\frac{\sqrt{3}}{2}$b₂. Geometric parameters of the third-order dendritic unit cell are b₁ = 6 mm, b₂ = 0.75b₁, b₃ = 0.5b₁, l = b₁ + $\frac{\sqrt{3}}{2}$(b₂ + $\frac{\sqrt{3}}{2}$b₃). c Electric field distribution of the valley states at the K point for the different fractal dendritic unit cells. White arrows represent the Poynting vectors. d Variation of the relative bandwidth γ and ΔE at the K point versus l and w for the first-order dendritic unit cell.

All full-wave numerical simulations are accurately calculated by the commercial finite element software (COMSOL Multiphysics). The proposed first-order dendritic configuration can open a topological nontrivial bandgap by breaking the C_3v lattice mirror symmetry. The relative bandwidth γ of the bandgap is proportional to the perturbation strength ∆p. For the proposed valley photonic crystal, $\Delta p\propto \Delta E={\int }_{s}\left({\lfloor {E}_{R}(K)\rfloor }^{2}-\right.\left.{\lfloor {E}_{L}(K)\rfloor }^{2}\right)dS$, where S is the geometric perturbation area shown in the light orange shaded region in Fig. 1a. It is shown that the perturbation strength ∆p depends on ΔE. The simulated electric field distribution of the valley states for the first-order dendritic unit cell is shown in Fig. 1c. Thus, we can calculate ΔE by integrating the normalized electric field over the geometric perturbation region. Figure 1d shows the calculated ΔE and the relative bandwidth γ at the K point versus l and w. The results indicate that ΔE and the relative bandwidth γ increases with the increasing of l, and it increases firstly and then decreases with the increasing of w. It can be seen that the curves of ΔE and the relative bandwidth γ is basically the same, which also agrees with theory. The stronger perturbation strength ∆p makes the greater relative bandwidth γ. The maximum relative bandwidth γ of the first-order dendritic unit cell is 50.06%.

Besides the conventional geometric perturbations, we can also enhance inter-cell coupling to broaden the relative bandwidth γ by increasing the fractal order. Therefore, the second-order and third-order dendritic unit cells are constructed, as shown in Fig. 1b. Their electric field distributions are displayed in Fig. 1c, which shows that $\left\lfloor {E}_{R}\left(K\right)\right\rfloor$ in region I is enhanced with the increasing of fractal order, indicating the strong inter-cell coupling. The relative bandwidth γ of the second-order and third-order dendritic unit cells is up to 52.27% and 59.65%, respectively.

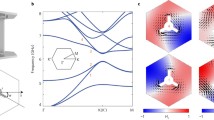
We employ the third-order dendritic unit cell to study topological states since it has wider bandgaps as compared with other unit cells. As θ = 0°, the band structure is shown in Fig. 1b presented by black solid lines, which shows a Dirac cone at 3.8 GHz at the high symmetric point K. By rotating the dendritic structure θ, the mirror symmetry is broken, resulting in opening a new bandgap. The band structure of θ = ±30° is shown in Fig. 1b presented by red solid lines, which displays a broadband bandgap from 2.8 GHz to 5.18 GHz, with a relative bandwidth γ of 59.65%.

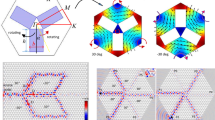
The topological phase diagram of the third-order dendritic photonic crystal is illustrated in Fig. 2a, where the inset is the magnetic field distributions and Poynting vectors at the K point. Obviously, the states p₁ (p₂) and q₁ (q₂) carry opposite vertex chirality centered at the high symmetric points p and q, respectively. The vertex chirality is an important characteristic of valley photonic crystals. Here, the third-order photonic crystal with θ = −30° and θ = +30° are indicated as photonic crystal A and photonic crystal B, respectively. It is observed that the vertex chirality of the pseudospin states in the first (second) band of the photonic crystal A is consistent with the second (first) band of the photonic crystal B, indicating the topological phase transition occurs. The topological bandgap can be characterized by Dirac mass, ${{{{\mathrm{sgn}}}}}({{{{{\rm{m}}}}}})={{{{\mathrm{sgn}}}}}({{{{{{\rm{p}}}}}}}_{1}^{+}-{{{{{{\rm{q}}}}}}}_{1}^{-})$. As θ crosses through 0° (i.e. the transition point), the sign of m changes from positive to negative, the bandgap closes and then reopens, and the frequency order of the two bands is inverted. This is a feature of the topological phase transition. Due to the C₃ symmetry of valley photonic crystal, topological phase transition can occur at any integer of 60° and the phase diagram has a period of 120°. The Berry curvature of the valley photonic crystal A is shown in Fig. 2b. Since the valley photonic crystals have time-reversal symmetry, the Berry curvatures around the K point are opposite to those of K’ point.

Fig. 2: Topological phase transition and Berry curvature.

a Topological phase diagram and magnetic field distribution. Red and blue hollow points are q and p points, respectively. Green arrows represent the Poynting vectors. b Distributions of the Berry curvatures of the photonic crystal A.

Ultrabroadband valley transmission

According to the Jackiw–Rebbi theory, the interface formed by valley photonic crystals with distinct nontrivial topological phase has a “soliton state” localized at the interface that leads to gapless edge states propagating along the interface. The Hamiltonian around the K point can be written as ${{{H}}}_{{{K}}}{{=}}{{\hslash }}{{v}}\left({{{q}}}_{{{x}}}{{{\sigma }}}_{{{x}}}{{+}}{{{q}}}_{{{y}}}{{{\sigma }}}_{{{y}}}\right){{+}}{{\hslash }}{{m}}{{{\sigma }}}_{{{z}}}$³⁷.

We combine the photonic crystal A and photonic crystal B with distinct nontrivial topological phases to form a supercell. Figure 3a presents the zigzag interfaces containing two different domain walls of BA and AB. For the domain wall BA, the solution of the edge states is written as ${{{{{\rm{\psi }}}}}}(K)\propto {e}^{i{q}_{x}x}{e}^{-\frac{1}{v}|{\int }_{0}^{y}d{y}^{{\prime} }m\left({y}^{{\prime} }\right)|}\left(\begin{array}{c}{1}\\ {1}\end{array}\right)$, the corresponding spectrum is $E\left(K\right)=\hslash v{q}_{x}$. For the domain wall AB, the solution of the edge states is written as $\psi (K)\propto {e}^{i{q}_{x}x}{e}^{-\frac{1}{v}{\int }_{0}^{y}d{y}^{{\prime} }m({y}^{{\prime} })}\left(\begin{array}{c}{1}\\ {-1}\end{array}\right)$, and the corresponding spectrum is $E\left(K\right)=-\hslash v{q}_{x}$. The band structure of the supercell with the zigzag interface is shown in Fig. 3a, where the black dots represent bulk states, and the blue and red lines represent the edge states. It can be seen that the frequency ranges of the edge states with the BA domain wall and AB domain wall are 2.7–5.18 GHz and 2.75–4.41 GHz, respectively. Four symmetrical points of the two edge bands are chosen to study the magnetic field distribution and energy flow, as shown in Fig. 3a. The red and blue curves indicate forward- and backward-propagating edge states, respectively. The results indicate that the propagating directions of the two valley edge states bounded to different valleys are exactly opposite, exhibiting valley-locked chirality.

Fig. 3: Valley edge states with zigzag interfaces and armchair interfaces.

Band structures and magnetic field distributions for a zigzag interfaces and b armchair interfaces. Black dots represent the bulk states. Red and blue curves indicate the forward- and backward-propagating edge states, respectively. Dashed and the solid lines represent the edge states of the BA and AB domain walls, respectively. Gray curves through the edge state curves are due to the result of the long-period approximation. Green arrows represent the direction of the energy flow. c Electric field distributions for the straight waveguides with the armchair interfaces in the narrow bandgap.

In addition, we construct an armchair interface supercell with AB domain wall, as shown in Fig. 3b. The solution of the edge states is written as $\psi (K)\propto {e}^{i{q}_{y}y}{e}^{-\frac{1}{v}{\int }_{0}^{x}d{x}^{{\prime} }m({x}^{{\prime} })}\left(\begin{array}{c}{1}\\ {i}\end{array}\right)$, and the corresponding spectrum is $E\left(K\right)=\hslash v{q}_{y}$. Figure 3b presents the band structure and magnetic field distributions of the supercell. It can be seen that the edge states represented by the red and blue curves propagate in opposite directions along the domain wall. There are three edge states with frequencies ranging from 2.76 to 3.50 GHz, 3.70 to 4.41 GHz and 5.11 to 5.15 GHz, respectively. Actually, there is an avoided crossing bandgap in the narrow bandgap of 3.50–3.70 GHz at the k_x = 0 between the two counter-propagating edge states. This bandgap is similar to the bandgap of the edge states in photonic topological insulators with C₆ symmetry, which is caused by breaking C_6v symmetry in the armchair interface³⁸. The width of the bandgap is determined by the degree of geometric symmetry breaking at the interface. The wider the bandgap, the stronger breaking geometric symmetry. In order to prove that there are edge states in this narrow bandgap region, the electric field distributions of the armchair interfaces are presented in Fig.3c. It is shown the energy is confined around the interface, confirming the existence of the edge states in the narrow bandgap. The band structure of the armchair interface supercell with the BA domain wall is same as that the AB domain wall.

Based on the valley edge states of the zigzag and armchair interfaces, two kinds of ultrabroadband waveguides are designed. Figure 4a shows the schematic and electric field distributions of the topological straight waveguide with the zigzag interface. It can be seen that the electromagnetic wave propagates smoothly along the interface and decays exponentially into the bulk. In order to verify the simulations, we fabricated the sample by using wire cutting machine. Figure 4b shows the experimental setup. The measured normalized transmission spectrums for the zigzag interface waveguide are presented in Fig. 4c. High transmissions are observed for the topological waveguide at the edge state frequencies, whereas the transmissions of the bulk states are ultralow. The measured relative bandwidth of the topological zigzag interface waveguide is up to 58.71%. The slight deviation of the relative bandwidth between the simulation and experimental result is due to the tolerance of the sample fabrication.

Fig. 4: Robust electromagnetic transport in topological straight waveguides.

Zigzag interface: a schematic and electric field distributions for the waveguide, b experimental setup, c measured normalized transmission spectrums. Armchair interface: d schematic and electric field distributions for the waveguide, e fabricated sample, f measured normalized transmission spectrums. Schematics and electric field distributions for the g zigzag and h armchair waveguides with disorder and bend defects. Blue stars and red dotted lines indicate the excitation source and the interface, respectively. Blue rectangular lines represent the defects. Yellow-shaded regions represent the edge state frequencies.

Figure 4d shows the schematic and the electric field distributions of the topological straight waveguide with the armchair interface. The electric field distributions show that electromagnetic waves are confined at the interface. Figure 4e, f shows the fabricated sample and measured normalized transmission spectrums, respectively. It is shown that the high transmission is observed in the edge state frequencies. The measured relative bandwidth of the topological waveguide with the armchair interface is up to 36.78%. The robust transmission to defect immunity is a physical property of topological edge states. By introducing two kinds of defects including disorder and bend, the robustness of the valley edge states in the zigzag and armchair interface is verified, as shown in Fig. 4g, h. As expected, electromagnetic waves can still transmit without being affected by the disorder and bend.

Figure 5a–c presents the schematics and electric field distributions for three different cross-shaped channel intersections composed of the zigzag interface, armchair interface and a combination of the zigzag and armchair interface, respectively. It shows that electromagnetic waves emitted along  path 1 (path 2) and are forbidden to transmit along path 3 (path 4) as passing through the intersection. This is due to the fact that the edge states at the path 1 (path 2) and path 3 (path 4) have different valley pseudospins. It is notable that the domain wall AB changes to the domain wall BA through the intersection, and the edge modes of the two distinct domain walls have opposite chirality. As a result, electromagnetic waves only transmit along the paths of the same valley freedom in the channels. In the experiments, a source antenna emits electromagnetic wave along the path 1 (path 2) of the sample, whereas probe antennas are placed at the other three paths. Figure 5d–f presents the measured normalized transmissions. The results show that the transmissions S21 and S41 are much higher than S31, whereas the transmissions S12 and S32 are much higher than S42 within the edge state frequencies. These observations confirm that the valley edge states transmit at the channel intersections are dependent on the geometries.

Fig. 5: Topological channel intersections.

Schematics and electric field distributions for transmission along a zigzag interface, b armchair interface and c a combination of zigzag and armchair interfaces. Blue and red arrows represent the propagating directions of the edge states carrying K and K’ valleys, respectively. Measured normalized transmissions of the topological channel intersections with d zigzag interface, e armchair interface and f a combination of zigzag and armchair interfaces. Yellow-shaded regions represent the edge state frequencies.

Higher-order corner states

Higher-order topological photonic crystal with special topological phase provides an effective method for realizing higher-dimensional topological waveguides. Based on the proposed valley photonic crystals, topologically switchable and valley selective corner states are realized. The higher-order topological phase is characterized by the bulk polarization³⁹. The numerical calculation of the bulk polarization is carried out through a Wilson-loop method as

$${P}_{\alpha }=-\frac{1}{2\pi }{\int }_{L}d{W}_{\alpha ,{k}_{\beta }},\;\alpha ={{{{\mathrm{1,2}}}}};\beta ={{{{\mathrm{1,2}}}}}$$

(4)

where ${W}_{a,{k}_{\beta }}$ is the Berry phase along the loop ${k}_{{{{{{\rm{\beta }}}}}}}$ for a fixed ${k}_{\alpha }$, and ${W}_{\alpha ,{{{\mbox{k}}}}_{\beta }}=-{Im}\left(\log {\prod}_{{k}_{\beta }}\langle {u}_{({k}_{\alpha },{k}_{\beta })}(r)|{u}_{({k}_{\alpha },{k}_{\beta +1})}(r)\rangle \right)$. k_α and k_β are the two directions of the triangular lattice vector, u(r) is the periodic function of the lattice, and L is the projection length of the Brillouin region along the k_β direction. In order to facilitate calculation, a rhombus Brillouin region is adopted, as shown in Fig. 6a. Figure 6b, c shows the Berry phase W₁ of the valley photonic crystal A and crystal B, respectively. Similar calculations on W₂ obtain the same results due to W₁ = W₂ bounded by the C₃ symmetry. Using Eq. (4), the bulk polarization of the valley photonic crystal A and crystal B is P = (−1/3, −1/3) and P = (1/3, 1/3), respectively. The Wannier centers indicated by the gray dots in the insets of Fig. 6b, c demonstrate a valley-locking property. This is important for the valley switchability and selectivity of subsequent corner states.

Fig. 6: Bulk polarization and Wannier center representations.

a Rhombus Brillouin zone in the calculations of the bulk polarization. Berry phase W₁ as a function of k₂ for b photonic crystal A and c crystal B. Blue and black dotted lines indicate the exact value of the bulk polarization and the Berry phase W₁, respectively. Inset is the Wannier center configuration of the unit cell, where the Wannier centers are marked by the gray dots.

In order to study the valley locking property of the corner states in the proposed valley photonic crystals, triangular corner structure with zigzag interface, and hexagonal corner structure with armchair interface are constructed, as shown in Fig. 7. Figure 7a–c presents the schematic and fabricated sample, eigenspectra and measured normalized transmission for the triangular corner structure consisting of the crystal A surrounded by the crystal B, respectively. Eigenspectra shows that the frequency range of the edge states is 2.83–4.41 GHz, and the corner states appear around 4.73 GHz. The measured normalized transmission has a good agreement with the eigenspectra. Figure 7d–f presents the schematic and fabricated sample, eigenspectra and measured normalized transmission for the triangular corner structure consisting of the crystal B surrounded by the crystal A, respectively. The eigenspectra diagram shows the frequency range of the edge states is 2.82–5.16 GHz. It is notable that only edge states exist, and no corner states is observed. This is due to the fact that the three angular points of the triangular structure accurately terminate in the Wannier centers, indicating the presence of corner states. Otherwise, there are no corner states. Therefore, the corner states of the proposed higher-order topological photonic crystals have topological switchability.

Fig. 7: Valley switchability and selectivity of corner states.

Triangular corner structures consisting of the crystal A surrounded by the crystal B: a schematic diagram and fabricated sample, b eigenspectra and c measured normalized transmissions. Triangular corner structures consisting of the crystal B surrounded by the crystal A: d schematic diagram and fabricated sample, e eigenspectra and f measured normalized transmissions. Hexagonal corner structures consisting of the crystal A surrounded by the crystal B: g schematic diagram and fabricated sample, h eigenspectra. Hexagonal corner structures consisting of the crystal B surrounded by the crystal A: i schematic diagram and fabricated sample, j eigenspectra. The insets in the eigenspectra represent the magnetic field distributions of the edge states. Red dots represent the excitation source, and white, blue, black, and yellow dots represent the position of the probe to measure the type-I corner states, type-II corner states, edge states, and bulk states, respectively. k Measured normalized transmissions of the hexagonal corner structures. l Magnetic field distributions of the type-I corner states and type-II corner states.

Next, we investigate hexagonal corner structures with armchair interface to further verify the valley selectivity. Figure 7g–j presents the schematics, fabricated sample and eigenspectra for the hexagonal corner structures. The two hexagonal corner structures can be converted into each other by rotating 180°. Therefore, the corresponding eignspectra of these two corner structures are completely consistent. It can be seen that the frequency range of the edge states is 2.83–4.41 GHz, and the corner states appear around 4.73 GHz and 5.01 GHz. In order to verify the simulations, we measure the transmission spectra, as presented in Fig. 7k. The measured results agree with the simulated eigenspectra. Figure 7l shows the magnetic field distributions of the corner states, indicating two types of corner states. Type-I corner states are the traditional corner states originated from the bulk topology. Type-I corner states are located on the corners within the topological domain. Type-II corner states are the new corner states due to the long-range couplings between the adjacent edge states, which are located on both sides of the corner within the topological domain⁴⁰. Type-I corner states (type-II corner states) appear at the top (bottom), lower-left (upper-left) and lower-right (upper-right) corners for the hexagonal structure consisting of the crystal A surrounded by the crystal B. While in the hexagonal structure with the crystal B surrounded by the crystal A, the type-I corner states (type-II corner states) emerge at the bottom (top), upper-left (lower-left) and upper-right (lower-right) corners, revealing the engaging valley selectivity of the corner states.

Two types of corner states are proved in the proposed third-order dendritic valley photonic crystal. Type-I corner states are located on the corners within the topological domain, which can be predicted by the Wannier centers. Type-I corner states are the traditional corner states originated from the bulk topology. Type-II corner states are located on both sides of the corner within the topological domain, and their appearance cannot be predicted by Wannier centers. To study the generation mechanism of type-II corner states, the hexagonal corner structure composed of first-order dendritic unit cells is discussed. Figure 8a, b presents the schematic diagram and eigenspectra for the hexagonal corner structure composed of first-order dendritic unit cells, respectively. The result indicates that there is no type-II corner states, which is due to the weak inter-cell coupling of the first-order dendritic structure. The inter-cell coupling can be enhanced by introducing fractal. Therefore, third-order dendritic structure is introduced to increase the inter-cell coupling. Figure 8c presents the illustrate of the couplings of the third-order dendritic structure, where t represents intra-cell coupling and j is nearest-neighbor inter-cell coupling. By varying the geometric parameters, the coupling coefficient $j/t$ can be adjusted⁴⁰. Figure 8d presents the variation of the eigenspectra versus b₁. With the increase of b₁, type-II corner states appear that follow closely the eigenspectra of the topological edge states. This is caused by the strong coupling coefficient $j/t$ due to the increase of b₁. Therefore, type-II corner states originate from long-range couplings.

Fig. 8: Localization mechanism of type-II corner states.

a Schematic diagram and b eigenspectra for the hexagonal corner structure composed of first-order dendritic unit cell. The inset represents the magnetic field distribution of the type-I corner states. c Illustrate of the coupling between third-order dendritic cells. d Variation of the eigenspectra for the hexagonal corner structure composed of third-order dendritic unit cells versus b₁.

Conclusions

A valley photonic crystal consisting of third-order dendritic structures with C₃ symmetry is proposed, which can realize ultrabroadband valley transmission and higher-order corner states. The results show that the bandwidth of the photonic crystal can be improved by designing multi-order structures to increasing the perturbation strength ∆p, which provides a new idea for broadening the bandwidth of the valley photonic crystals. The theoretical relative bandwidth of the edge states with the zigzag and armchair interfaces are 59.65% and 44.66%, respectively. Based on topological edge states, two kinds of ultrabroadband topological waveguides with zigzag and armchair interfaces are designed, and the measured relative bandwidths are 58.71% and 36.78%, respectively. In addition, we design topological channel intersections where transport paths are determined by the geometries of the intersections. Finally, the corner states with topological switchability and valley selectivity are proved. Two types of corner states including the type-I corner state based on bulk topology and the type-II corner state caused by long-range interactions are observed. The results of this work are of great significance in the fields of sub-6GHz 5G communication.

Methods

Simulations

All of the numerical simulations for the proposed photonic crystal were performed by COMSOL Multiphysics, which is based on the finite element method. Eigenvalue solver was employed to calculate the bulk, edge, and corner band structures. Periodic boundary condition was set in calculating band structures. Frequency domain simulations were performed to calculate the electric field distributions of the edge and corner states in the different topological photonic crystal. Scattering boundary condition was set in calculating the electric field distribution of the topological photonic crystal.

Experiments

The experiment was performed in an anechoic chamber. The experimental devices are composed of an AV 3629 vector network analyzer and two monopole antennas. One monopole antenna connected to port 1 of the vector network analyzer serves as the source to excite electromagnetic waves. Another monopole antenna connected to port 2 of the vector network analyzer serves as the probe to measure the transmission curve. The samples were fabricated by wire cutting machine. The material of the samples is copper. The rectangle-shaped sample with 20 × 16 unit cells shown in Figs. 4 and 5 is used for measuring the transmission amplitude for the topological edge states. The sample with 20 × 19 unit cells shown in Fig. 7 is used for measuring the transmission amplitude for the bulk, edge and corner states.