Tunable Dirac points in a two-dimensional non-symmorphic wallpaper group lattice

Abstract

Non-symmorphic symmetries protect Dirac nodal lines and cones in lattice systems. Here, we investigate the spectral properties of a two-dimensional lattice belonging to a non-symmorphic group. Specifically, we look at the herringbone lattice, characterized by two sets of glide symmetries applied in two orthogonal directions. We describe the system using a nearest-neighbor tight-binding model containing horizontal and vertical hop** terms. We find two nonequivalent Dirac cones inside the first Brillouin zone along a high-symmetry path. We tune these Dirac cones’ positions by breaking the lattice symmetries using on-site potentials. These Dirac cones can merge into a semi-Dirac cone or unfold along a high-symmetry path. Finally, we perturb the system by applying a dimerization of the hop** terms. We report a flow of Dirac cones inside the first Brillouin zone describing quasi-hyperbolic curves. We present an implementation in terms of CO atoms placed on the top of a Cu(111) surface.

Introduction

Since the isolation of single-layer graphene, there has been a growing interest in analyzing two-dimensional (2D) systems with low-energy physics described by a Dirac-like electronic dispersion^1,2. In addition to graphene, systems of interest are also 3D topological insulators^1,3,4 and other 2D materials beyond graphene^5,6. The quest for systems hosting Dirac-like features is not only within condensed matter but extended to cold-atoms⁷ and electronic quantum simulators^8,9. Most of these systems share the property of having an underlying crystal structure characterized by a symmorphic space group¹⁰. However, there has been an increasing research interest in Dirac-like physics in non-symmorphic crystalline systems^{10,11,12,13,14,15,16,17,18,19}. A non-symmorphic crystalline system contains a fractional lattice translation combined with either a mirror reflection (glide plane) or a rotation (screw axis). This results in a band-folding with crossings inside the first Brillouin zone (FBZ) boundaries that are protected against hybridization^{17,20,21,22,23,24}. In general, a peculiar property of Dirac cones (DCs) is that they can merge into a so-called semi-Dirac (SD) point^{2,25,26,27,28}. These points are distinguished by an energy dispersion linear in one direction and parabolic in the other. They are particularly interesting for their topological²⁹ and anisotropic transport properties³⁰.

In this work, we investigated the spectral properties of a non-symmorphic wallpaper group lattice: the herringbone lattice (HL)³¹, characterized by a pair of DCs. By breaking some of the system’s symmetries, we can tune the position of these DCs within the FBZ to merge them into an SD one and eventually gap them. We achieve similar results by modifying the internal strength of the hop** terms. Moreover, we show that this type of modification leads to the appearance of features similar to a system characterized by a set of parallel Su-Schrieffer-Heeger (SSH) chains^32,33,34,35. In refs. ^33,34, the authors consider inclined SSH chains in a square lattice model. For a certain choice of parameters, the system presents a non-symmorphic symmetry^33,34. However, the HL already possesses non-symmorphic symmetries for homogeneous hop** terms, which introduces additional constraints to the bands of the system. Specifically, it possesses band degeneracies along high-symmetry paths. We also find that the SD unfolds along a high-symmetry path for a specific set of parameters. This unfolding results in a nodal line presenting linear and parabolic dispersion along parallel lines in the FBZ.

Results

Model Hamiltonian and spectrum

The HL contains four sites in its unit cell, all with coordination number 3 (Fig. 1a). The lattice vectors are a₁ = (1, 1) a₀ and a₂ = (−2, 2) a₀, where a₀ is the interatomic distance. We label each unit cell by (m, n) = ma₁ + na₂. The HL can be regarded as a square lattice with each site missing a link; thus, we classify the four sites in the unit cell according to the remaining link: r_mn and l_mn along the horizontal direction with a link to the right and left, respectively, and u_mn and d_mn along the vertical direction with a link upwards and downwards, respectively. Placing s-like orbitals, the HL nearest-neighbor tight-binding Hamiltonian reads

$$\hat{{{{{{{{\mathcal{H}}}}}}}}}=\mathop{\sum}\limits_{\begin{array}{c}\langle m,n\rangle \\ \langle \alpha ,{\alpha }^{{\prime} }\rangle \in \left\{r,d,u,l\right\}\end{array}}\left({t}_{\alpha ,{\alpha }^{{\prime} }}\,{c}_{\alpha ,mn}^{{{{\dagger}}} }{c}_{{\alpha }^{{\prime} },mn}+{\varepsilon }_{\alpha }{c}_{\alpha ,mm}^{{{{\dagger}}} }{c}_{\alpha ,mm}\right)$$

(1)

where ${t}_{\alpha ,{\alpha }^{{\prime} }}$ is the hop** amplitude between nearest-neighboring sites, and c_α,mn(${c}_{\alpha ,mn}^{{{{\dagger}}} }$) annihilates (creates) an electron on a lattice site $\alpha ,{\alpha }^{{\prime} }\in \{r,d,u,l\}$ at unit cell (m, n). In Eq. (1), the symbol 〈…〉 indicates nearest-neighbor lattice sites. The last term is the on-site ε_α: we will use it to break some of the HL symmetries selectively. The hop** terms can be classified into intra-cell, where we only find horizontal terms, and inter-cell hop**s, where we find both horizontal and vertical terms.

Fig. 1: Herringbone lattice in real, reciprocal, and energy space.

a Herringbone lattice unit cell with the naming of the lattice sites (r, d, u, l), direct lattice vectors a₁ and a₂, and the two sets of glides: the dashed blue lines correspond to ${{{{{{{{\mathcal{G}}}}}}}}}_{1\alpha }$ while the red ones to ${{{{{{{{\mathcal{G}}}}}}}}}_{2\alpha }$. The red and blue diamonds represent the 2a and 2b maximal Wyckoff positions, respectively. The Su-Schieffer-Heeger-like chains have been highlighted by two different densities of the dashing. b First Brillouin zone, reciprocal lattice vectors b₁ and b₂, and high-symmetry points, plus the position of the Dirac cones appearing in the irreducible Brillouin zone. c Energy spectrum (E in units of t₀) along the high-symmetry path, in the fully symmetric case (dashed red) and with mass term ${{{{{{{{\mathcal{M}}}}}}}}}_{1}({\delta }_{1}=0.5)$ (solid blue). d, e Berry curvature Ω_z(k) inside the first Brillouin zone for δ₁ = ± 0.5.

Neglecting the on-site energies and introducing k_i = k ⋅ a_i, we can Fourier transform the HL Hamiltonian (1) as follows $\hat{{{{{{{{\mathcal{H}}}}}}}}}={\sum }_{{{{{{{{\bf{k}}}}}}}}}{\hat{{{\Psi }}}}_{{{{{{{{\bf{k}}}}}}}}}^{{{{\dagger}}} }h({{{{{{{\bf{k}}}}}}}}){\hat{{{\Psi }}}}_{{{{{{{{\bf{k}}}}}}}}}$, where

$$h({{{{{{{\bf{k}}}}}}}})=\left(\begin{array}{ll}0&q({{{{{{{\bf{k}}}}}}}})\\ q{({{{{{{{\bf{k}}}}}}}})}^{{{{\dagger}}} }&0\end{array}\right),$$

(2a)

$$q({{{{{{{\bf{k}}}}}}}})={t}_{0}\left(\begin{array}{ll}1+{{{{{{{{\rm{e}}}}}}}}}^{-{{{{{{{\rm{i}}}}}}}}{k}_{1}}&{{{{{{{{\rm{e}}}}}}}}}^{{{{{{{{\rm{i}}}}}}}}{k}_{2}}\\ {{{{{{{{\rm{e}}}}}}}}}^{-{{{{{{{\rm{i}}}}}}}}{k}_{1}}&1+{{{{{{{{\rm{e}}}}}}}}}^{-{{{{{{{\rm{i}}}}}}}}{k}_{1}}\end{array}\right).$$

(2b)

We have set ${t}_{\alpha ,{\alpha }^{{\prime} }}={t}_{0}$ for simplicity. Figure 1b shows the reciprocal space associated with the HL. With the following choice of basis ${{{\Psi }}}_{{{{{{{{\bf{k}}}}}}}}}={({\psi }_{r},{\psi }_{d},{\psi }_{u},{\psi }_{l})}^{{{{{{{{\rm{T}}}}}}}}}$ the Hamiltonian in (2a) fulfills the chiral-symmetry operator ${{{{{{{\mathcal{C}}}}}}}}={\tau }_{z}\otimes {\sigma }_{0}$. This operator hints at an interpretation of the HL as two coupled SSH chains, each with its chiral symmetry^33,34. The chains are formed by pairs of r, u and d, l, respectively. The chains are connected along the horizontal direction via u, d atoms and along the vertical direction via r, l atoms (Fig. 1a). Thus, in the operator ${{{{{{{\mathcal{C}}}}}}}}$, the τ_x,yz represent the intrachain degrees of freedom, while σ_x,y,z represent the interchain ones. This will be addressed further in the text when breaking the various symmetries. The energy spectrum associated with Eq. (2a) reads:

$${{{{{{{{\mathcal{E}}}}}}}}}_{\alpha ,\beta }({{{{{{{\bf{k}}}}}}}})=\alpha {t}_{0}\sqrt{3\,+\,2\cos {k}_{1}\,+\,4\beta \cos \left(\frac{{k}_{1}}{2}\right)\cos \left(\frac{{k}_{2}}{2}\right)}$$

(3)

with α, β = ±. It presents four energy-symmetric bands with several features (Fig. 1c). To start, it displays DCs between bands 2 and 3 located at K^± = ±b₁/3, along a high-symmetry path¹⁷. These cones are characterized by a ±π Berry phase. Additionally, we observe flat nodal lines along SXS lines and dispersive ones along SYS, both between bands 1 and 2 and 3 and 4. All these features are rooted in the symmetries of the HL: it belongs to the pgg wallpaper group³¹. This group is non-symmorphic, meaning that some symmetry operators do not leave any point of the space invariant since they include fractional translations along lattice vectors, called glide symmetries. There are two sets of glides acting on different sites; thus, we name them with two indices, ${{{{{{{{\mathcal{G}}}}}}}}}_{i\alpha }$, where i corresponds to the index of the lattice translation involved, and α = {A, B} depending on whether the r lattice site is closest to the mirror (see Fig. 1a). Using Seitz, symbols³⁶, these glides are ${{{{{{{{\mathcal{G}}}}}}}}}_{1\alpha }=\left\{{m}_{01}| \frac{1}{2}0\right\}$ and ${{{{{{{{\mathcal{G}}}}}}}}}_{2\alpha }=\left\{{m}_{10}| 0\frac{1}{2}\right\}$ (Fig. 1a). The unit cell of the HL contains four maximal Wyckoff positions, and none of the glide planes go through them. However, glides $\left\{{{{{{{{{\mathcal{G}}}}}}}}}_{2\alpha }\right\}$ do go through the lattice sites, while $\left\{{{{{{{{{\mathcal{G}}}}}}}}}_{1\alpha }\right\}$ do not (Fig. 1a). This affects how lattice sites transform under these symmetries: when applying the set of glides $\left\{{{{{{{{{\mathcal{G}}}}}}}}}_{1\alpha }\right\}$, no matter which symmetry operation is performed first (mirror or half translation), the lattice site falls on empty space, whereas for $\left\{{{{{{{{{\mathcal{G}}}}}}}}}_{2\alpha }\right\}$ the half translation already maps r into d, and u into l. These properties affect how the spectrum behaves after breaking $\left\{{{{{{{{{\mathcal{G}}}}}}}}}_{2\alpha }\right\}$ vs. $\left\{{{{{{{{{\mathcal{G}}}}}}}}}_{1\alpha }\right\}$.

Strategies for tuning the Dirac cones

Here, we show how to gap the cones, move them within the FBZ and eventually merge them into an SDC cone. All the on-site perturbations respect Tr h(k) = 0. However, they all commute with ${{{{{{{\mathcal{C}}}}}}}}$, and as a consequence, this is not anymore a well-defined chiral symmetry. We will perturb the bands according to the SSH-like interpretation, meaning we will differentiate between chains and between lattice sites inside each chain in several ways.

To gap the cones, we fix opposite on-site energies at lattice sites r and u, d and l, i.e., (ε_r, ε_d, ε_u, ε_l) = δ₁(1, 1, −1, −1)t₀. This configuration differentiates between the inside of each chain respecting the chiral symmetry, and it can be expressed by the $\left\{{{{{{{{{\mathcal{G}}}}}}}}}_{1\alpha }\right\}$-breaking mass term

$${{{{{{{{\mathcal{M}}}}}}}}}_{1}({\delta }_{1})={\delta }_{1}\left({\tau }_{z}\otimes {{\mathbb{I}}}_{2}\right){t}_{0}.$$

(4)

For δ₁ = 0 (critical point), the spectrum is gapless and energy symmetric (see Fig. 1c). Away from this value, the band structure splits into two gapped composite sets of bands. The rest of the spectral features (flat and degenerate lines) are shifted in energy, preserving the degeneracy.

The spectrum is symmetric with respect to δ₁ = 0, but the eigenfunctions behave differently after a change in sign of δ₁: the Berry curvature^37,38 reveals the exchange of the charge at the K^± points (Fig. 1d, e). Having only two DCs inside the FBZ, once gapped, the Berry curvature displays a dipolar distribution with a fixed length. Given $\{{{{{{{{{\mathcal{G}}}}}}}}}_{{1}_{\alpha }}\}$ involves the mirror m₀₁ in real space, the same mirror in reciprocal space is conserved, and the dipolar distribution is oriented along b₁.

The breaking of $\left\{{{{{{{{{\mathcal{G}}}}}}}}}_{1\alpha }\right\}$ can also be studied from symmetry eigenvalues of $\left\{{{{{{{{{\mathcal{G}}}}}}}}}_{2\alpha }\right\}$ before and after the closing of the gap. We observe that the eigenvalues of bands 2 and 3 invert before and after the gap’s closing, which reflects a band inversion (see Supplementary Note 2).

Next, we show the first strategy to move the DCs. We fix opposite on-site energies at lattice sites r and d, u and l, i.e., (ε_r, ε_d, ε_u, ε_l) = δ₂(1, −1, 1, −1)t₀. Now, we are differentiating between chains by placing the same energy in chiral-symmetric lattice sites. This corresponds to the following $\left\{{{{{{{{{\mathcal{G}}}}}}}}}_{2\alpha }\right\}$-breaking mass term

$${{{{{{{{\mathcal{M}}}}}}}}}_{2}({\delta }_{2})={\delta }_{2}\left({{\mathbb{I}}}_{2}\otimes {\sigma }_{z}\right){t}_{0}.$$

(5)

We recover the unperturbed gapless phase for δ₂ = 0. However, the band structure remains gapless within the interval $| {\delta }_{2}| \le \sqrt{3}$ (degeneracy interval) but differs from the fully symmetric case. The band structure is symmetric with respect to a change in the sign of δ₂, so as soon as δ₂ ≠ 0, the DCs move away from K^± towards Γ. We can find their position as a function of δ₂ by solving ${E}_{3}[{\delta }_{2},{{{{{{{{\bf{k}}}}}}}}}_{2}^{{{{{{{{\rm{D}}}}}}}}}({\delta }_{2})]=0$, where E₃ is the third band, corresponding to (α, β) = (+, −). It yields:

$${{{{{{{{\bf{k}}}}}}}}}_{2}^{{{{{{{{\rm{D}}}}}}}}}({\delta }_{2})=\frac{1}{{a}_{0}}\arccos \left(\frac{1}{2}{\sqrt{1+{\delta }_{2}}}^{2}\right)\frac{{{{{{{{{\bf{b}}}}}}}}}_{1}}{| {{{{{{{\bf{{b}}}}}}}_{1}| }}}.$$

(6)

The motion of the DCs is shown in Fig. 2a. For $| {\delta }_{2}| =\sqrt{3}$ (limits of the degeneracy interval), the DCs have shifted away from K^± (at δ₂ = 0), merging at Γ into an SDC. Figure 2c, d shows the SDC at Γ with the parabolic/linear behavior explicitly displayed. For $| {\delta }_{2}|\, > \,\sqrt{3}$, the SD is gapped away, and the band structure again splits into two detached composite sets of bands, with the flat degeneracy untouched but the dispersive lifted up. The Berry curvature of this situation is shown in Fig. 2f, k, where we observe a band inversion at Γ depending on the sign of δ₂. Figure 6 displays the trajectory of the DCs for increasing δ₂, starting at K^± as DCs for δ₂ = 0, shifting towards Γ at $| {\delta }_{2}| =\sqrt{3}$ merging into an SDC.

Fig. 2: Spectral properties of the Herringbone lattice under ${{{{{{{{\mathcal{M}}}}}}}}}_{1}({\delta }_{1})+{{{{{{{{\mathcal{M}}}}}}}}}_{2}({\delta }_{2})$.

a Energy spectrum (E in units of t₀) with ${{{{{{{{\mathcal{M}}}}}}}}}_{2}({\delta }_{2})$ for several values of δ₂. b Energy spectrum (E in units of t₀) with ${{{{{{{{\mathcal{M}}}}}}}}}_{{{{{{{{\rm{T}}}}}}}}}({\delta }_{1}=-1/2,{\delta }_{2})={{{{{{{{\mathcal{M}}}}}}}}}_{1}(-1/2)+{{{{{{{{\mathcal{M}}}}}}}}}_{2}({\delta }_{2})$ for the same values of δ₂ in (a). c, d Dispersion of bands 2 and 3 displaying a semi-Dirac cone along two different orientations. e Phase diagram of the Herringbone lattice under ${{{{{{{{\mathcal{M}}}}}}}}}_{{{{{{{{\rm{T}}}}}}}}}({\delta }_{1},{\delta }_{2})$ according to the position of the gap. f–l Berry curvature distributions for different sets of parameters (δ₁, δ₂). The colorbar helps to distinguish peaks and valleys in the Berry curvature distributions.

There is another way in which we can gap the band structure, and it is by adding a ${{{{{{{{\mathcal{M}}}}}}}}}_{1}({\delta }_{1})$ term to the already existing ${{{{{{{{\mathcal{M}}}}}}}}}_{2}({\delta }_{2})$. The behavior of the bands under ${{{{{{{{\mathcal{M}}}}}}}}}_{{{{{{{{\rm{T}}}}}}}}}({\delta }_{1},{\delta }_{2})={{{{{{{{\mathcal{M}}}}}}}}}_{1}({\delta }_{1})+{{{{{{{{\mathcal{M}}}}}}}}}_{2}({\delta }_{2})$ is shown in Fig. 2b, where we have added a ${{{{{{{{\mathcal{M}}}}}}}}}_{1}({\delta }_{1}=0.5)$ to the bands in Fig. 2a. The unperturbed case has also been added as a guide to the eye. The overall effect is to gap the four bands everywhere, but more interestingly, to gap the DCs appearing at generic positions. With this total mass term, we are able to shrink the Berry curvature dipolar distribution (Fig. 2i) as well as to visualize the Berry curvature of a gapped SDC, Fig. 2h, j. Here we present some remarks after combining ${{{{{{{{\mathcal{M}}}}}}}}}_{1}({\delta }_{1})+{{{{{{{{\mathcal{M}}}}}}}}}_{2}({\delta }_{2})$: (1) a change in the sign of δ₁ always produces a band inversion (Fig. 2f–l) only displays the Berry curvature for negative δ₁, the ones for positive δ₁ differ in an overall sign; (2) the gap cannot be closed by using ${{{{{{{{\mathcal{M}}}}}}}}}_{1}({\delta }_{1})$ when δ₂ falls outside the interval of degeneracy, so the gap at zero between the solid blue lines in Fig. 2b cannot be closed; (3) the flat degeneracies along SXS remain flat but are completely lifted up by a nonzero value of δ₁, so these two degeneracies are protected by both glides. Figure 2e displays all the gapped/metallic phases of the HL under ${{{{{{{{\mathcal{M}}}}}}}}}_{{{{{{{{\rm{T}}}}}}}}}({\delta }_{1},{\delta }_{2})$ depending on the position of the gap. The values of the parameters for bands in Fig. 2a, b are explicitly shown. At δ₁ = 0, we find the phase diagram of ${{{{{{{{\mathcal{M}}}}}}}}}_{2}({\delta }_{2})$, which is an interval, and for δ₂ = 0, we find the phase diagram of ${{{{{{{{\mathcal{M}}}}}}}}}_{1}({\delta }_{1})$, which is just the critical point.

The breaking of these glides can also be studied from symmetry eigenvalues of $\left\{{{{{{{{{\mathcal{G}}}}}}}}}_{1\alpha }\right\}$ for different values of δ₂. We observe that the eigenvalues of bands 2 and 3 remain different for all values of δ₂, so the crossing is still protected by the first set of glides (as soon as we add ${{{{{{{{\mathcal{M}}}}}}}}}_{1}({\delta }_{1})$, we gap the band structure). See Supplementary Note 2.

Now, we present another strategy to tune the cones at different positions: simultaneously breaking both glides while respecting inversion symmetry. The origin of the unit cell represents the inversion center of the lattice, so in order to define this perturbation, we make (ε_r, ε_d, ε_u, ε_l) = t₀δ_I(1, −1, −1, 1), or

$${{{{{{{{\mathcal{M}}}}}}}}}_{{{{{{{{\rm{I}}}}}}}}}(\delta )={\delta }_{{{{{{{{\rm{I}}}}}}}}}\left({\tau }_{z}\otimes {\sigma }_{z}\right){t}_{0}$$

(7)

This perturbation again commutes with the chiral operator ${{{{{{{\mathcal{C}}}}}}}}$. The spectrum displays common features between the two previous cases (Fig. 3a). Bands 2 and 3 touch for ∣δ_I∣ ≤ 1. Outside of it, the four bands are detached. For ∣δ_I∣ = ± 1, bands 2 and 3 are degenerated at zero energy along SXS, forming a nodal line showing two different regimes: along the path XΓX, the dispersion is locally parabolic around the X point. At the same time, it is locally linear around the S points along SYS. This is represented in Fig. 3b; the SDC is unfolded (UnSDC) along SXS, forming the nodal line. Shifting δ_I from −1 to 1, DCs appear from X (where the UnSDC is placed), shifting towards K^± points at δ_I = 0 and going back to X.

Fig. 3: Spectral properties of the Herringbone lattice under ${{{{{{{{\mathcal{M}}}}}}}}}_{1}({\delta }_{1})+{{{{{{{{\mathcal{M}}}}}}}}}_{{{{{{{{\rm{I}}}}}}}}}({\delta }_{{{{{{{{\rm{I}}}}}}}}})$.

a Energy spectrum (E in units of t₀) with ${{{{{{{{\mathcal{M}}}}}}}}}_{{{{{{{{\rm{I}}}}}}}}}({\delta }_{{{{{{{{\rm{I}}}}}}}}})$ for different values of δ_I. b Bands 2 and 3 with the nodal line, where the parabolic/linear behavior around X/S points is highlighted. c Energy spectrum of the Herringbone lattice with ${{{{{{{{\mathcal{M}}}}}}}}}_{{{{{{{{\rm{T}}}}}}}}}^{{{{{{{{\rm{A}}}}}}}}}({\delta }_{{{{{{{{\rm{I}}}}}}}}},{\delta }_{1}=-0.7)={{{{{{{{\mathcal{M}}}}}}}}}_{{{{{{{{\rm{I}}}}}}}}}({\delta }_{{{{{{{{\rm{I}}}}}}}}})+{{{{{{{{\mathcal{M}}}}}}}}}_{1}(-0.7)$. d Robust nodal line. e Phase diagram of the Herringbone lattice with ${{{{{{{{\mathcal{M}}}}}}}}}_{{{{{{{{\rm{T}}}}}}}}}^{{{{{{{{\rm{A}}}}}}}}}({\delta }_{{{{{{{{\rm{I}}}}}}}}},{\delta }_{1})$ according to the position of the gap. f–j Berry curvatures for the selected set of parameters. Band inversions occur for the positive value of δ₁. The colorbar helps to distinguish peaks and valleys in the Berry curvature distributions.

We obtain the analytical position of the DCs by solving ${E}_{3}[{\delta }_{{{{{{{{\rm{I}}}}}}}}},{{{{{{{{\bf{k}}}}}}}}}_{{{{{{{{\rm{I}}}}}}}}}^{{{{{{{{\rm{D}}}}}}}}}({\delta }_{{{{{{{{\rm{I}}}}}}}}})]=0$. It yields:

$${{{{{{{{\bf{k}}}}}}}}}_{{{{{{{{\rm{I}}}}}}}}}^{{{{{{{{\rm{D}}}}}}}}}({\delta }_{{{{{{{{\rm{I}}}}}}}}})=\frac{1}{2{a}_{0}}\arccos \left(-\frac{1+{\delta }_{{{{{{{{\rm{I}}}}}}}}}^{2}}{2}\right)\frac{{{{{{{{\bf{{b}}}}}}}_{1}}}}{| {{{{{{{\bf{{b}}}}}}}_{1}}}| }$$

(8)

Figure 6 displays the trajectory of the DCs for increasing δ_I. With this perturbation, we achieve the splitting of all degeneracies, which we have already seen after consecutively breaking both glide symmetries. However, here we are breaking both sets of glides at the same time while preserving inversion symmetry; thus, the results are different. Since we preserve time-reversal symmetry, the Berry curvature is zero in the FBZ for all δ_I values and bands.

We now combine the inversion-symmetric mass term ${{{{{{{{\mathcal{M}}}}}}}}}_{{{{{{{{\rm{I}}}}}}}}}({\delta }_{{{{{{{{\rm{I}}}}}}}}})$ with the two previous mass terms, i.e., ${{{{{{{{\mathcal{M}}}}}}}}}_{1}({\delta }_{1})$ and ${{{{{{{{\mathcal{M}}}}}}}}}_{2}({\delta }_{2})$. We show in Fig. 3c the behavior of the band structure with the total mass term ${{{{{{{{\mathcal{M}}}}}}}}}_{{{{{{{{\rm{T}}}}}}}}}^{{{{{{{{\rm{A}}}}}}}}}({\delta }_{{{{{{{{\rm{I}}}}}}}}},{\delta }_{1})={{{{{{{{\mathcal{M}}}}}}}}}_{{{{{{{{\rm{I}}}}}}}}}({\delta }_{{{{{{{{\rm{I}}}}}}}}})+{{{{{{{{\mathcal{M}}}}}}}}}_{{{{{{{{\rm{1}}}}}}}}}({\delta }_{1})$. This choice gaps the DCs at generic positions given by expression (8), as shown in Fig. 3c. Band inversions are detected using the distribution of the Berry curvature inside the FBZ, which has stretched with respect to Figs. 1d and 3j. Robust degenerate flat bands along SXS are found by setting ${{{{{{{{\mathcal{M}}}}}}}}}_{{{{{{{{\rm{T}}}}}}}}}^{{{{{{{{\rm{A}}}}}}}}}({\delta }_{{{{{{{{\rm{I}}}}}}}}})={{{{{{{{\mathcal{M}}}}}}}}}_{{{{{{{{\rm{T}}}}}}}}}^{{{{{{{{\rm{A}}}}}}}}}({\delta }_{{{{{{{{\rm{I}}}}}}}}},{\delta }_{{{{{{{{\rm{I}}}}}}}}})={{{{{{{{\mathcal{M}}}}}}}}}_{{{{{{{{\rm{I}}}}}}}}}({\delta }_{{{{{{{{\rm{I}}}}}}}}})+{{{{{{{{\mathcal{M}}}}}}}}}_{{{{{{{{\rm{1}}}}}}}}}(\pm \sqrt{{\delta }_{{{{{{{{\rm{I}}}}}}}}}^{2}-1})$ for any δ_I > 1 (see Fig. 3d).

Now that inversion has been broken, bands acquire a finite Berry curvature (Fig. 3f–j). There is a line at which the flat features of the Berry curvature start to appear. In this situation, the gapped DCs merge into the band, reaching the same value of the energy along the nodal line. We look for the relation between (δ₁, δ_I) that makes the energy at ${{{{{{{{\bf{k}}}}}}}}}_{{{{{{{{\rm{I}}}}}}}}}^{{{{{{{{\rm{D}}}}}}}}}({\delta }_{{{{{{{{\rm{I}}}}}}}}})$ equal to the energy along SXS since δ₁ does not change the position of the DCs. We obtain:

$${\delta }_{1}({\delta }_{{{{{{{{\rm{I}}}}}}}}})=\pm \frac{\sqrt{9-10{\delta }_{{{{{{{{\rm{I}}}}}}}}}^{2}+{\delta }_{{{{{{{{\rm{I}}}}}}}}}^{4}}}{4{\delta }_{{{{{{{{\rm{I}}}}}}}}}}$$

(9)

All this information is displayed in the phase diagram of Fig. 3e. The three colored regions represent different gapped phases. As in the previous case, for δ₁ = 0, we recover the phase diagram of ${{{{{{{{\mathcal{M}}}}}}}}}_{{{{{{{{\rm{I}}}}}}}}}({\delta }_{{{{{{{{\rm{I}}}}}}}}})$, which is an interval. Setting δ_I = 0, we recover the phase diagram of ${{{{{{{{\mathcal{M}}}}}}}}}_{1}({\delta }_{1})$ (same as before). The Berry curvature distribution is shown for different sets of parameters. Along the line δ_I = −2, the band inversion has been explicitly displayed since the Berry curvature changes sign without a gap closing. This is due to the fact that at δ₁ = 0, δ_I > 1, inversion symmetry is recovered while the bands are fully gapped, and thus the Berry curvature is zero. Figure 3g has been rescaled to match the colorbar.

We now study the mass term ${{{{{{{{\mathcal{M}}}}}}}}}_{{{{{{{{\rm{T}}}}}}}}}^{{{{{{{{\rm{B}}}}}}}}}({\delta }_{{{{{{{{\rm{I}}}}}}}}},{\delta }_{2})={{{{{{{{\mathcal{M}}}}}}}}}_{{{{{{{{\rm{I}}}}}}}}}({\delta }_{{{{{{{{\rm{I}}}}}}}}})+{{{{{{{{\mathcal{M}}}}}}}}}_{{{{{{{{\rm{2}}}}}}}}}({\delta }_{2})$. Figure 4a shows the band structure for different values of (δ₂, δ_I). Figure 4b shows the phase diagram of this choice of mass term. It describes the physics of ${{{{{{{{\mathcal{M}}}}}}}}}_{2}({\delta }_{2})$ by making δ_I = 0 and the physics of ${{{{{{{{\mathcal{M}}}}}}}}}_{{{{{{{{\rm{I}}}}}}}}}({\delta }_{{{{{{{{\rm{I}}}}}}}}})$ by making δ₂ = 0. Starting from these two setups, we can expand the phase diagram in the following way. The vertical axis is delimited by the point where the gap closes at Γ forming an SDC, so we solve E₃[δ₂, δ_I, Γ] = 0. We obtain:

$${\delta }_{2}({\delta }_{{{{{{{{\rm{I}}}}}}}}})=\pm \sqrt{3+{\delta }_{{{{{{{{\rm{I}}}}}}}}}^{2}}$$

(10)

Fig. 4: Spectral properties of the Herringbone lattice under ${{{{{{{{\mathcal{M}}}}}}}}}_{2}({\delta }_{2})+{{{{{{{{\mathcal{M}}}}}}}}}_{{{{{{{{\rm{I}}}}}}}}}({\delta }_{{{{{{{{\rm{I}}}}}}}}})$.

a Energy spectrum (E in units of t₀) of the Herringbone lattice with ${{{{{{{{\mathcal{M}}}}}}}}}_{{{{{{{{\rm{T}}}}}}}}}^{{{{{{{{\rm{B}}}}}}}}}({\delta }_{2},{\delta }_{{{{{{{{\rm{I}}}}}}}}})={{{{{{{{\mathcal{M}}}}}}}}}_{2}({\delta }_{2})+{{{{{{{{\mathcal{M}}}}}}}}}_{{{{{{{{\rm{I}}}}}}}}}({\delta }_{{{{{{{{\rm{I}}}}}}}}})$. The values of (δ₂, δ_I) are shown in (b). b Phase diagram of the Herringbone lattice with ${{{{{{{{\mathcal{M}}}}}}}}}_{{{{{{{{\rm{T}}}}}}}}}^{{{{{{{{\rm{B}}}}}}}}}({\delta }_{2},{\delta }_{{{{{{{{\rm{I}}}}}}}}})$ according to the position of the gap. c–e Berry curvatures for the choices of parameters. The colorbar helps to distinguish peaks and valleys in the Berry curvature distributions.

When δ_I ≠ 0, the SDC is formed just by the two intermediate bands. This new SDC can be gapped by adding a ${{{{{{{{\mathcal{M}}}}}}}}}_{1}({\delta }_{1})$. However, with the three mass terms, the bands are no longer symmetric in energy by pairs since the four on-site energies are in general different (see Supplementary Note 3).

We can split the new SDC into DCs moving across the whole FBZ. The position of the DCs is now governed by:

$${{{{{{{{\bf{k}}}}}}}}}_{{{{{{{{\rm{I}}}}}}}}+2}^{{{{{{{{\rm{D}}}}}}}}}({\delta }_{{{{{{{{\rm{I}}}}}}}}},{\delta }_{2})=\frac{1}{2{a}_{0}}\arccos \left(\frac{{\delta }_{2}^{2}-{\delta }_{{{{{{{{\rm{I}}}}}}}}}^{2}-1}{2}\right)\frac{{{{{{{{{\bf{b}}}}}}}}}_{{{{{{{{\bf{1}}}}}}}}}}{| {{{{{{{{\bf{b}}}}}}}}}_{1}| }.$$

(11)

By making δ₂ = ± ∣δ_I∣ the new DCs always locates at K^±. Figure 6 displays the trajectory of these DCs moving across the whole FBZ from X, where an SDC splits into two DCs that move towards Γ, merging again into an SDC.

In order to expand the horizontal axis, at (δ₂, δ_I) = (0, ±1), the gap closes along SXS in an UnSDC, so we solve E₃[δ₂, δ_I, X] = 0 to find the extension of the UnSDC for nonzero δ₂. We obtain:

$${\delta }_{2}({\delta }_{{{{{{{{\rm{I}}}}}}}}})=\pm \sqrt{{\delta }_{{{{{{{{\rm{I}}}}}}}}}^{2}-1}$$

(12)

The band structure is gapless at zero energy inside the region

$${{{{{{{\mathcal{R}}}}}}}}=\left\{({\delta }_{2},{\delta }_{{{{{{{{\rm{I}}}}}}}}}):\,{\delta }_{2}^{2}-{\delta }_{{{{{{{{\rm{I}}}}}}}}}^{2} < | 3| \cup {\delta }_{{{{{{{{\rm{I}}}}}}}}}^{2}-{\delta }_{2}^{2} < 1\right\}$$

(13)

Outside this gapless region, the bands are gapped, and thus, the associated Berry curvature can be nonzero inside the FBZ. Figure 4c–e shows the Berry curvature for the selected cases. With this, we complete the phase diagram and our study of the on-site energies. In Supplementary Note 1, we present a low-energy theory³⁹ for all the cases studied so far.

Finally, we present a completely different strategy for tuning the DCs. It is based on differentiating between the horizontal and vertical hop** amplitudes in a breathing form t_h/v = t₀(1 ± δ_D)^34,40. Figure 5a shows the real space interpretation of this choice of breathing. There are several other choices to distort the system that also preserve some of the glides, but we studied the breathing one since it is the one yielding corner modes in certain geometries³⁵. This breathing distortion breaks both glides while preserving inversion symmetry. We add to Eq. (2b) the matrix:

$${q}_{{{{{{{{\rm{B}}}}}}}}}({{{{{{{\bf{k}}}}}}}})={t}_{0}{\delta }_{{{{{{{{\rm{D}}}}}}}}}\left(\begin{array}{rc}1-{{{{{{{{\rm{e}}}}}}}}}^{-{{{{{{{\rm{i}}}}}}}}{k}_{1}}&-{{{{{{{{\rm{e}}}}}}}}}^{{{{{{{{\rm{i}}}}}}}}{k}_{2}}\\ {{{{{{{{\rm{e}}}}}}}}}^{-{{{{{{{\rm{i}}}}}}}}{k}_{1}}&1-{{{{{{{{\rm{e}}}}}}}}}^{-{{{{{{{\rm{i}}}}}}}}{k}_{1}}\\ \end{array}\right).$$

(14)

After diagonalizing the Hamiltonian, SDCs appear at the S_2,4 points for ${\delta }_{{{{{{{{\rm{D}}}}}}}}}=-1/\sqrt{5}$. For increasing δ_D, these cones split into DCs moving out from the S points towards the K^± for δ_D = 0, where the fully symmetric case is recovered. For positive δ_D, the cones keep moving continuously until they reach S_1,3, where they merge into SDC points with the ones coming from the neighboring reciprocal unit cells. The trajectory of the cones is quasi-hyperbolic. Figure 5b shows the two Dirac cones outside of the high-symmetry path for ${\delta }_{{{{{{{{\rm{D}}}}}}}}}={(2\sqrt{5})}^{-1}$. If we now add on-site potentials according to (4) or (5), the overall effect is to gap the cones at the arbitrary positions along the quasi-hyperbolic curve. This translates into an arbitrary orientation and length of the Berry curvature dipolar distribution, as shown in Fig. 5c. We show the trajectory of the DCs as a function of δ_D in Fig. 6.

Fig. 5: Spectral properties of the dimerized Herringbone lattice.

a Sketch of the chosen dimerized implementation of the Herringbone lattice in real space. b Bands 2 and 3 of the dimerized Herringbone lattice for ${\delta }_{{{{{{{{\rm{D}}}}}}}}}={(2\sqrt{5})}^{-1}$. The Dirac cones are now inside the first Brillouin zone and not along a high-symmetry point or line. Their position as a function of δ_D is displayed. c Berry curvature for the dimerized Herringbone lattice after gap** the Dirac cones with ${{{{{{{{\mathcal{M}}}}}}}}}_{1}({\delta }_{1})$. The colorbar helps to distinguish peaks and valleys in the Berry curvature distributions.

Fig. 6: Summary of the positions of the Dirac cones according to the different perturbations.

Representation of all trajectories of the Dirac cones as they move across the first Brillouin zone as a function of the different perturbations (only showing positive values of k_x, k_y).

In this work, we have shown how to tune the position of the DCs of the non-symmorphic HL. We have proposed several strategies for merging the cones into an SDC one and eventually opening an energy gap in the system. We have summarized all the possible positions of the DCs within the BZ in Fig. 6. In addition to tuning the position of the DCs, we can manipulate the orientation of the Berry curvature dipolar distribution, from being parallel to the reciprocal lattice vectors to having a generic length and orientation. Table 1 summarizes the action of the on-site perturbations studied so far in the system. As mentioned above, the combination of breathing plus on-site only gaps the spectrum, so it has not been added to the table.

Table 1 Summary of the main features of the combination of mass terms.

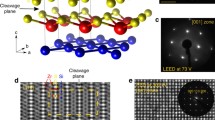
Conclusions

The moving and merging of the DCs has already been experimentally observed in black phosphorous^41,42: a 2D layered material characterized by non-symmorphic symmetries. We propose here a realization of the HL within the synthetic platform known as the artificial electron lattice⁴³. Here the two-dimensional electron gas hosted on the (111) surface state of Cu is confined to a potential well designed with a set of CO molecules, which are placed with atomic precision at certain positions with the help of the tip of a scanning tunneling microscope^{8,9,35,44,45,46,47,48}. We present the design of the HL in Fig. 7a. Symmetry plays a crucial role: if the space groups of the substrate and the simulated lattice have common generators (one is a subgroup of the other), then the electronic structure of the lattice is very well recovered. However, if this condition is not met, it is more difficult to describe a lattice with this technique⁹. In our case, we expect something similar for our proposal. First of all, Fig. 7b shows the lower bands obtained for the unit cell depicted in Fig. 7a. Only the lowest four bands come from the inner electronic levels of the artificial electronic lattice, and so they represent the bands closer to our spectrum presented in the results section. Figure 7c shows bands 2 and 3 inside the FBZ, and we can see how two DCs appear at opposite k points. From the discussion in the previous section, we can already see that the proposed unit cell will show some dimerization plus some on-site energies that will return to the position of the DCs. To fit these bands to a tight-binding Hamiltonian, next-nearest neighbors may be included, and even longer range hop**s, since the nearly free electron method does not involve atomic orbitals or species, nor chemical bonds between them. The lattice sites are built with artificial interacting quantum dots (also known as artificial atoms⁴⁸) connected by hop** amplitudes which are always long-range and modeled by potential wells or barriers. We present further details about the calculation of the spectrum in the “Methods” section. In conclusion, we have presented the spectral properties of a 2D non-symmorphic lattice. We have shown that the system is characterized by two DCs along a high-symmetry line that can either gap or move within the FBZ. We also achieve the possibility of merging these DCs into an SDC one or, in a special case, into an UnSDC that respects the nodal line degeneracy imposed by a glide symmetry.

Fig. 7: Spectral properties of the simulated Herringbone lattice.

a Proposal for the unit cell of the Herringbone lattice in the nearly free electron simulator. b Energy spectrum along a high-symmetry path for the Herringbone lattice according to the proposal. c Bands 2 and 3 of the proposal, underlining the presence of the Dirac cones outside a high-symmetry path.

Methods

Berry curvature

We have classified the topological character of the bands below the Fermi level using the Berry curvature as a topological marker. It is important to note that there are always two bands below zero energy that can be degenerated or not. To evaluate the Berry curvature, we made use of the Kubo formula³⁸, provided the occupied set of bands is well separated from the unoccupied one:

$${\Omega }_{\gamma }({{{{{{{\bf{k}}}}}}}})={{{{{{{\rm{i}}}}}}}}{\epsilon }_{\alpha \beta \gamma }\mathop{\sum}\limits_{n}\mathop{\sum}\limits_{m}\frac{\langle {u}_{n}| {v}_{\alpha }| {u}_{m}\rangle \langle {u}_{m}| {v}_{\beta }| {u}_{n}\rangle }{{({E}_{m}-{E}_{n})}^{2}}\,,$$

(15)

where ${v}_{\mu }={\partial }_{\mu }{{{{{{{\mathcal{H}}}}}}}}$ are electron velocity along the μ-direction, $\left\vert {u}_{n}\right\rangle$ are the periodic parts of the Bloch wave functions, and ϵ_αβγ is the Levi-Civita antisymmetric tensor.

Energy spectrum for the artificial electron lattice

The solution to the bulk problem for the artificial electron lattice is obtained within the nearly free electron method^35,43,49. We model each CO molecule as a cylindrical potential barrier placed at position r₀:

$$V(r-{r}_{0})=\left\{\begin{array}{ll}{V}_{0} & r \le {r}_{0} \hfill \\ 0 \hfill & r > {r}_{0}\end{array}\right..$$

(16)

The complete lattice V_latt(r) is given by the superposition of such potential barrier in Eq. (16). Then, we expand the periodic potential in Fourier components

$${V}_{{{{{{{{\rm{latt}}}}}}}}}({{{{{{{\bf{r}}}}}}}})=\mathop{\sum}\limits_{{{{{{{{\bf{G}}}}}}}}}{V}_{{{{{{{{\bf{G}}}}}}}}}{{{{{{{{\rm{e}}}}}}}}}^{{{{{{{{\rm{i}}}}}}}}{{{{{{{\bf{G}}}}}}}}\cdot {{{{{{{\bf{r}}}}}}}}},$$

(17)

which are

$${V}_{{{{{{{{\bf{G}}}}}}}}} =\frac{1}{\sqrt{2\pi }}{\int}_{{{{{{{{\rm{unit}}}}}}}}{{{{{{{\rm{cell}}}}}}}}}d{{{{{{{\bf{r}}}}}}}}\,\,{{{{{{{{\rm{e}}}}}}}}}^{-{{{{{{{\rm{i}}}}}}}}{{{{{{{\bf{G}}}}}}}}\cdot {{{{{{{\bf{r}}}}}}}}}{V}_{{{{{{{{\rm{latt}}}}}}}}}({{{{{{{\bf{r}}}}}}}})\,\\ ={V}_{0}{r}_{0}\mathop{\sum}\limits_{{\alpha }_{0}}{{{{{{{{\rm{e}}}}}}}}}^{-{{{{{{{\rm{i}}}}}}}}{{{{{{{\bf{G}}}}}}}}\cdot {{{{{{{{\bf{R}}}}}}}}}^{\alpha }}\frac{{{{{{{{{\mathcal{J}}}}}}}}}_{1}(| {{{{{{{\bf{G}}}}}}}}| {r}_{0})}{| {{{{{{{\bf{G}}}}}}}}| },$$

(18)

where R^α are the positions of the molecules inside the unit cell, and ${{{{{{{{\mathcal{J}}}}}}}}}_{1}(| {{{{{{{\bf{G}}}}}}}}| {r}_{0})$ is the Bessel function of the first kind.

The stationary Schrödinger equation is transformed into a set of linear equations for the coefficients {c_n,q}, which expand the wave function in plane waves ∣ and the energy of the system,

$$\left(\frac{{\hslash }^{2}{\left\vert {{{{{{{\bf{q}}}}}}}}-{{{{{{{\bf{G}}}}}}}}\right\vert }^{2}}{2m}-{{{{{{{\mathcal{E}}}}}}}}\right){c}_{{{{{{{{\bf{q}}}}}}}}-{{{{{{{\bf{G}}}}}}}}}+\mathop{\sum}\limits_{{{{{{{{\bf{{G}}}}}}}^{{\prime} }}}}{V}_{{{{{{{{{\bf{G}}}}}}}}}^{{\prime} }-{{{{{{{\bf{G}}}}}}}}}\,{c}_{{{{{{{{\bf{q}}}}}}}}-{{{{{{{\bf{G}}}}}}}}}=0,$$

(19)

solving this equation for the energy ${{{{{{{\mathcal{E}}}}}}}}$ results in the energy spectrum artificial electron lattice in the nearly free electron approximation. From the coefficients {c_n,q} that are used to obtain the periodic part of the wave function as

$${u}_{n,{{{{{{{\bf{q}}}}}}}}}({{{{{{{\bf{r}}}}}}}})=\mathop{\sum}\limits_{{{{{{{{\bf{G}}}}}}}}}{{{{{{{{\rm{e}}}}}}}}}^{{{{{{{{\rm{i}}}}}}}}{{{{{{{\bf{G}}}}}}}}\cdot {{{{{{{\bf{r}}}}}}}}}{c}_{n,{{{{{{{\bf{q}}}}}}}}-{{{{{{{\bf{G}}}}}}}}}.$$