Introduction

The ability to tune the twist angle between different layers of two-dimensional materials has led to a paradigm shift in quantum band engineering. The low-energy electronic structure of twisted heterostructure is determined by the moiré potential originating from the rotational misalignment of the constituent layers. Alternatively, superlattices can also be realized based on the mismatch between the lattice constants of these layers. After the initial discovery of correlated insulating states1 and superconductivity2 in twisted bilayer graphene, the field of twistronics has expanded to various moiré systems, such as ABC-stacked trilayer graphene (TLG) with hexagonal boron nitride (TLG/h-BN)3,4, twisted double bilayer graphene (TDBLG)5,6,7, twisted monolayer-bilayer graphene8,9, twisted trilayer graphene10,11, twisted tetralayer and pentalayer graphene12, and transition metal dichalcogenide (TMD) heterostructures13,14. A plethora of broken-symmetry phases, including but not limited to correlated insulators1,5, superconductivity2,10,15 quantum anomalous Hall effect16, ferromagnetism8,17,18, strange metal19,20, and Wigner crystals21,22 have been discovered in various moiré systems.

Twisted double trilayer graphene (TDTLG), which has only scarcely been explored to date, is a natural extension of the world of moiré materials. In particular, TDTLG fabricated with two ABC-stacked TLG layers (Fig. 1a, b) provides an appealing platform to tune the band structure of the hybrid system as single ABC-stacked TLG features van Hove singularities at or near the band edge where the density of states (DOS) diverges23. Moreover, the recent observation of ferromagnetism24 and superconductivity1a). As a result, in part of the channel, n and D cannot be controlled.

Electric field tunable bandgap

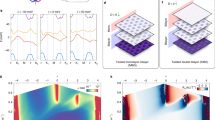
Figure 2a shows the resistance R measured in device S1 with θ = 1. 8∘ as a function of VTG and VBG. The phase space exhibits multiple resistive features in the entire range of VTG and VBG. The central diagonal resistance line corresponds to the charge neutrality point (CNPDG) of the dual-gated TDTLG region, which is underneath the top gate. In contrast, the two diagonal resistance lines at the top-right and bottom-left correspond to the full filling of the moiré superlattice bands (±ns), which allows us to calculate the twist angle (see Methods). We also observe three additional, horizontal, resistive features, which we identify as the CNP and the superlattice peaks of the singly-gated regions of the sample, which are not affected by the top gate. The different peaks become more apparent when plotting a line cut of R as a function of n at D/ϵ0 = 0, as shown in Fig. 2b.

Fig. 2: Electrical characterization.
figure 2

a Two-probe resistance R as a function of VTG and VBG measured at T = 300 mK for device S1 with θ = 1.8∘. b R as a function of n at D/ϵ0 = 0. The peaks corresponding to the CNP and full fillings of the bands (±ns) in the dual-gated region are marked for clarity. c High-resolution map showing the R as a function of D and n near the CNP. d R as a function of D at n = 0 showing the insulator-semimetal-insulator transition. e Schematic illustration of the band structure of TDTLG at three different electric fields. The gap closes at a finite electric field D0/ϵ0 ~0.1 V/nm and opens again as the D is increased further.

Full size image

Further, to understand the effect of the displacement field on the band structure of TDTLG, we show a high-resolution resistance map (separate measurement from Fig. 2a) as a function of n and D field in Fig. 2c. We find that TDTLG shows an intrinsic bandgap in the absence of a displacement field. The absence of a bandgap at zero field in the underlying TLG suggests that the gap emerges due to the intrinsic superlattice structure. However, when a displacement field is applied in either direction, the gap gradually fades out and disappears at a finite field, indicating an insulator-to-semimetal phase transition in this region. More strikingly, when the D is increased further, the gap opens again with increasing width.

To better visualize the evolution of the bandgap as a function of the displacement field, we plot R as a function of D at n = 0 in Fig. 2d. Here, an insulator-semimetal transition is observed at around D/ϵ0 = 0 ± 0.1 V/nm and a semimetal-insulator transition at around D/ϵ0 = ± 0.2 ± 0.3 V/nm. In contrast, the resistive peaks at ± ns show an insulating behavior in the investigated range of D. Based on these experimental observations, we schematically show the expected low-energy band structure of TDTLG at three different values of D (Fig. 2e). The figure shows a bandgap that is finite at D/ϵ0 = 0, closes at D = D0, where D0/ϵ0 ~ 0.1 V/nm, and then opens again for D > D0. We note that all three devices show similar characteristics with intrinsic single-particle gaps at the CNP and insulating states at ±ns. Meanwhile, the insulator-semimetal-insulator transition is observed in all devices (Supplementary Figs. 2, 4) and, thus, is intrinsic to TDTLG.

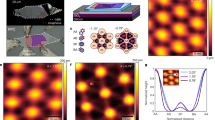
The electric field tunable electronic states, especially the intrinsic gap state in TDTLG, is interesting from a fundamental point of view. To gain further insight into the intrinsic gap state of TDTLG, we measured the differential conductance (dI/dV) at T = 255 mK as a function of source-drain bias VBias and VBG at three fixed VTG (marked with three dashed lines in Fig. 2a), as shown in Fig. 3a–c. We find that the differential conductance map for VTG = 0.16 V (Fig. 3a) reveals a large diamond-like structure centered at the CNP. The line cut of dI/dV at D/ϵ0 = 0 as a function of VBias is plotted in Fig. 3d (blue color). For VBias < 3 mV, dI/dV remains close to 0, while it rises sharply when VBias is increased further to 5 mV, and finally shows a linear increase with further increment of VBias. This “U” shape feature demonstrates the presence of an intrinsic bandgap in TDTLG.

Fig. 3: Differential conductance and temperature dependence of resistance.
figure 3

a–c Differential conductance dI/dV of the device S1 as a function of VBias and VBG at a fixed top gate voltage of 0.16, 0.4, and 1.32 V, respectively (marked in Fig. 2a). The device exhibits diamond-like structure for VTG = 0.16 V, which almost vanishes at VTG = 1.32 V, suggesting the closing of the bandgap. d dI/dV as a function of VBias for three different values of D, marked by dashed lines in (a–c). e–g Arrhenius plots presenting the T-dependence of resistance recorded at three different values of D. The solid lines show the Arrhenius-like fits to the data, where Δ is the extracted bandgap of the device.

Full size image

Next, the stability diagram for VTG = 0.4 V (Fig. 3b) shows a much smaller diamond-like structure centered at the CNP. The corresponding dI/dV curve at the center of the diamond (or at D/ϵ0 = 0.05 V/nm) (yellow color in Fig. 3d) presents a “V” shape feature, revealing a smaller gap at D/ϵ0 = 0.05 V/nm than the gap at D/ϵ0 = 0. Finally, no diamond-like structure is seen for the stability diagram measured at D/ϵ0 = 0.15 V/nm, and the dI/dV is predominantly independent of bias (as shown in the corresponding dI/dV curve in Fig. 3d) and gate, suggesting the gap closes at a larger D field of D/ϵ0 = 0.15 V/nm.

Temperature dependence

To further quantify the magnitude of intrinsic bandgap in TDTLG, we performed a detailed study of the temperature dependence of the resistance. Figure 3e–g show Arrhenius plots of the temperature dependence of resistance at the CNP for the dual-gated region at three different values of the D/ϵ0 field (0.043, 0, and −0.041 V/nm). In all three cases, the experimental data above 15−20 K follow the behavior expected for thermally-activated transport, according to \(R={R}_{0}\exp (\Delta /2{k}_{B}T)\), where kB is the Boltzmann constant and R0 and Δ are fitting parameters. A maximum energy gap Δ = 37 meV is extracted for D/ϵ0 = 0 V/nm, and two reduced energy gaps Δ = 21 meV for D/ϵ0 = 0.043 V/nm and Δ = 17 meV for D/ϵ0 = − 0.041 V/nm. At lower values of T, the deviation from the thermally-activated behavior to a much weaker T-dependence can be attributed to a combination of the Mott variable-range hop** conduction mediated by localized states and quantum tunneling through a short-channel semiconductor29. We note that the insulating state near the CNP survives up to temperatures as high as 40 K. (Supplementary Fig. 3). In an additional device S4 (Supplementary Fig. 4), we measure the T-dependence of resistance over a wide range of D fields. At CNP and large D fields, the device behaves like an insulator as the resistance decreases as T goes up, which agrees well with the literature ref. 30. At the critical field D = D0=0.21 V/nm, the resistance first slightly decreases and then increases after T drops down to a critical point (10 K), suggesting a semimetal behavior31,32. A detailed discussion on device S4 can be found in Supplementary Fig. 4.

Theoretical calculation

Finally, we have performed tight-binding calculations to rationalize the observed charge-transport behavior and get insights into the band structure. The band structures of TDTLG as a function of twist angles and displacement field were calculated using the tight-binding model implemented in WannierTools33. The tight-binding Hamiltonian was built using orbital distance-dependent Slater–Koster parameters and considers second-nearest-neighbor interactions. For the relaxed band structures, the atomic positions of TDTLG were relaxed using the classical force field approximation implemented in LAMMPS34. The ABC-CAB domains display the largest out-of-plane relaxation of atomic positions, while the ABC-ABC domains have the least (Supplementary Fig. 5). This behavior minimizes the repulsion between “C-C” regions at the twisted layer.

Figure 4a shows the band structure of unrelaxed (blue) and relaxed (orange) ABC-ABC stacked TDTLG at a twist angle of θ = 1.8∘. The calculations show that TDTLG is intrinsically an insulator—with a bandgap of ~0.01 eV, as observed experimentally in Fig. 2a. The intrinsic bandgap at the CNP may be attributed to the absence of inversion symmetry in twisted ABC-ABC stacked TDTLG. This behavior is similar to that reported for TDBLG for the same twist angle35. A comparison of the unrelaxed/rigid and relaxed bands shows that lattice relaxation has a negligible effect on the band structure around the Fermi energy, again similar to that reported for TDBLG35.

Fig. 4: Theoretical calculations.
figure 4

a Calculated band structure of ABC-ABC stacked TDTLG with θ = 1. 8∘ in the absence of an external electric field. The blue (orange) lines denote the bands of an unrelaxed (relaxed) TDTLG. b, c Calculated band structure in the presence of an external field. The displacement field D has been calculated using the dielectric constant of h-BN and screening effects have been ignored. d Bandgap as a function of D for both the relaxed (red curve) and unrelaxed (green curve) structure of ABC-ABC stacked TDTLG. e Bandgap as a function of twist angle for unrelaxed ABC-ABC stacked TDTLG in the absence of an external displacement field.

Full size image

Figure 4a–c show the closing and reopening of the bandgap with increasing displacement field, indicating an insulator-semimetal-insulator transition, consistent with our experimental observation. This is in contrast with the behavior of twisted ABA-ABA stacked graphene, which is an intrinsic insulator in the absence of an external field, becomes metallic in the presence of low external fields, but does not revert to insulating behavior upon a further increase of the external field (Supplementary Fig. 6). However, as illustrated in ref. 26, the device can exhibit several stacking configurations. To correlate the charge-transport behavior with stacking configuration, we have performed the calculations on Thirty-two sliding configurations, as discussed in ref. 26 (Supplementary Fig. 7). We find that there are eight configurations that exhibits a variation in the bandgap similar to ABC-ABC stacking. In all other configurations, the system either remains semimetallic or shows a very small bandgap upon crossing a critical displacement field. Based on the symmetry arguments, we can narrow down the possible configurations in our devices to ABC-ABC, CAB-ABC, CAB-ACB, and CBA-BCA (see Supplementary Information for discussion). Further, as demonstrated in ref. 26, CAB-ABC/BCA-BCA are energetically the least favorable configurations with respect to the configuration with no sliding and are therefore unlikely to exist in our devices. Additionally, theoretical calculations show that CAB-ACB, and CBA-BCA have large stacking energy26, but it is impossible to rule out these possibilities as stacking energy data are not available for all configurations. In conclusion, while the ABC-ABC stacking configuration is more likely to exist in our devices, CAB-ACB, CAB-ABC, or CBA-BCA configurations, or a combination thereof, may also exist.

Further, a comparison of Fig. 4b, c to Fig. 4a shows that the presence of a displacement field leads to a splitting in the valence bands, as well as the conduction bands. The position and dispersion of valence bands below −0.02 eV remain largely unaffected by the external field, while the increased dispersion and splitting of both the degenerate conduction and valence bands around 0 eV lead to the closing of the bandgap at displacement fields around 0.074 V/nm, as observed in panel Fig. 4b. A similar behavior has been reported in TDBLG35 and was attributed to layer polarization and correlation effects. It was demonstrated that the displacement field in the +z direction leads to an asymmetry in the layer contribution to the bands around the Fermi energy in TDBLG. The valence bands become confined within the top layer, while the conduction bands become confined to the bottom layer. In addition to layer polarization, there is an enhancement in the density of states in the conduction bands around the Fermi energy. This makes the correlation effects stronger in the conduction bands than in the valence bands, leading to an electron-hole asymmetry in the external fields.

As shown in Fig. 4d, lattice relaxation has a negligible effect on the overall trend of the bandgap as a function of the displacement field. Both the unrelaxed and relaxed ABC-ABC stacked TDTLG are intrinsic insulators in the absence of an external displacement field. An insulator-to-semimetal transition is observed for a displacement field slightly below 0.1 V/nm, and a semimetal-to-insulator transition is observed for a displacement field slightly above 0.1 V/nm. The bandgap increases monotonically for D/ϵ0 > 0.1 V/nm. The displacement fields required to observe insulator-metal-insulator transitions are slightly lower than that those observed experimentally. We attribute this to the absence of screening effects in the tight-binding model36.

Figure 4e shows the bandgap of ABC-ABC stacked TDTLG as a function of twist angle in the absence of an external displacement field. Without a twist, the system has no bandgap and behaves like an ABC-stacked trilayer graphene37. The bandgap increases with twist angle to a maximum around θ ≈ 2.5∘ and then decreases for larger twist angles. We speculate that this non-monotonic behavior originates from an interplay between the reduced coupling in some regions of the trilayer-trilayer interface and the periodicity of those regions due to angle-induced lattice mismatch.

Conclusions

In summary, we have performed the first electrical measurements on twisted double trilayer graphene for small twist angle devices (~1.7−2.0∘). Our measurements show the presence of an intrinsic bandgap in this heterostructure, which is supported by tight-binding calculations. In addition, we also observe an insulator-semimetal-insulator transition, which results from the closing and reopening of the bandgap upon an increase of the displacement field. The presence of an intrinsic bandgap in TDTLG opens up the possibility of exploiting such devices for optoelectronic applications38, in particular, because its size is highly tunable by the applied displacement field. Moreover, we anticipate that further tuning of devices with twist angle closer to ~1.2−1.5∘ will lead to stronger correlation effects and, in turn, symmetry-broken many-body phases.

Methods

Device fabrication

The TDTLG devices were fabricated following a typical “tear and stack” technique27,28. Trilayer graphene, h-BN (20−35 nm thick) and graphite flakes were mechanically exfoliated on SiO2/Si (100 nm oxide thickness). The heterostructure was assembled using standard dry-transfer techniques39. We used poly bisphenol A carbonate (PC) supported by polydimethylsiloxane (PDMS) on a glass slide to first pick up h-BN and then tear and pick up the trilayer graphene. A commercial micromanipulator was used to control the rotation angle. The graphite flake was finally picked up as a bottom gate. The fabrication of the metal top gate and electrodes followed a standard electron-beam lithography process and electron-beam metal evaporation. The devices were designed into a four-terminal structure shaped by traditional reactive ion etching with a CHF3 and O2 gas mixture. Finally, all the contacts were shaped as 1D edge contacts with Cr/Au electrodes39.

Electronic measurements

Transport measurements were performed in a He3 cryostat with a base temperature of 255 mK. We applied standard lock-in techniques to measure the resistance, with 17.777 Hz excitation frequency and 1 nA excitation current. Although the devices had four contacts, they were not patterned in a four-terminal Hall-bar or van der Pauw geometry for accurate four-terminal measurements. Hence, we conducted measurements in a two-terminal configuration to avoid artifacts that can arise from a “pseudo” four-terminal geometry.

Twist angle extraction

To estimate the twist angle, we used the relation \({n}_{s}=8{\theta }^{2}/\sqrt{3}{a}^{2}\) (including valley and spin degeneracies), where a = 0.246 nm is the lattice constant of graphene and ns is the charge carrier density corresponding to a fully filled superlattice unit cell1.

Band structure calculations

Tight-Binding Model Calculations—The tight-binding model Hamiltonian for carbon atoms in WannierTools considers only the pz orbitals.

$$H=\mathop{\sum}\limits_{ij}{\varepsilon }_{i}{a}_{i}^{{\dagger} }{a}_{j}+\mathop{\sum}\limits_{i\ne j}{V}_{ij}{a}_{i}^{{\dagger} }{a}_{j}$$
(1)

with \({\varepsilon }_{i}={E}_{{z}_{i}}\), where E is the strength of the electric field, zi is the atomic z-axis coordinate, and \({a}_{i}^{{\dagger} }\) and aj are the creation and annihilation operators.

$${V}_{ij}={V}_{pp\pi }{\sin }^{2}\theta +{V}_{pp\sigma }{\cos }^{2}\theta$$
(2)

where Vppσ and Vppπ are σ-type and π-type Slater–Koster parameters, θ is the angle between the orbital axes and Rij = Ri − Rj connecting the two orbital centers. The Slater–Koster parameters depend on the distance r between two orbitals as

$${V}_{pp\pi }(r)={V}_{pp\pi }^{0}{e}^{{q}_{\pi }(1-\frac{r}{{a}_{\pi }})}{F}_{c}(r)$$
(3)
$${V}_{pp\sigma }(r)={V}_{pp\sigma }^{0}{e}^{{q}_{\sigma }(1-\frac{r}{{a}_{\sigma }})}{F}_{c}(r)$$
(4)

where aπ is the first nearest neighbor distance in the plane, aσ is the interlayer distance, and \({V}_{pp\pi }^{0}\) and \({V}_{pp\sigma }^{0}\) are the corresponding coupling values. The smooth cutoff function that takes into account the distance between orbitals is given by

$${F}_{c}(r)={\left(1+{e}^{\frac{r-{r}_{c}}{{l}_{c}}}\right)}^{-1}=\left\{\begin{array}{lr}1&r\,\ll\, {r}_{c}\\ 0&r\,\gg\, {r}_{c}\\ \end{array}\right\}$$
(5)

The on-site energy of pz orbitals is set to ϵi = − 0.78 eV to adjust the reference. The following constants have been used in the above equations; \({V}_{pp\pi }^{0}=-2.81\) eV, \({V}_{pp\sigma }^{0}=0.48\) eV, qσ = 7.428, aπ = 1.418 Å, qπ = 3.1451, lc = 0.265 Å, aσ = 3.5 Å, and rc = 6.165 Å36,40.

Classical Force—Field Simulations—The second generation REBO potential41 and the Kolmogorov– Crespi potential42 were used to describe the intralayer and interlayer interactions respectively in the lattice relaxation of TDTLG in LAMMPS. The relaxation was performed until the total force acting on each atom was less than 10−6 eV/atom using the FIRE algorithm43.