Introduction

Epilepsy is a neurological disorder in which transient alteration of brain functions due to hyperexcitable neurons and their network causes seizures1,2. Patients with epilepsy suffer from recurrent paroxysmal symptoms, such as loss of consciousness, tonic‒clonic seizures, and behavioral changes3, as well as persistent comorbidities, such as depression and anxiety. Thus, epilepsy is a highly burdensome disease. The causes of epilepsy include nutritional status during pregnancy, complications during childbirth, head injury, exposure to toxic substances, brain infections, tumors, strokes, and degenerative changes in the brain4,5,6.

Antiseizure medication (ASM) is an initial option and the mainstay in epilepsy treatment7. While more than 30 ASMs have been developed and utilized8, approximately one-third of epilepsy patients are still medically refractory9,10,11. Among medically refractory patients, surgically remediable patients undergo resection of the seizure focus area. The International League Against Epilepsy (ILAE) defines medically refractory epilepsy as the persistence of seizures even after adequate trials of two ASMs12. However, given the paucity of information regarding seizures induced by cognitive problems, nocturnal seizures, and amnesia after seizures40,41.

Additionally, the EEG modulation in the gamma band was reflected in the kurtosis and the maximum value. One phenomenon—namely, sharp wave ripples—may account for the processes assessed by kurtosis and maximum values. Sharp wave ripples, which support the consolidation of recently acquired memories or the planning of future actions, consist of several spectral components: a slow sharp wave (5–15 Hz), a high-frequency “ripple” oscillation (150–200 Hz), and a slow “gamma” oscillation (20–40 Hz). The fusion of sharp wave ripples could also be reflected as increased power in the slow gamma band42. These prior findings lend credibility to our results with respect to the importance of low gamma and Feature 2.

Limitations and future work

Our study has several limitations. First, our analysis was based on individual EEG segments for each patient. We only drew segments once for all window lengths because we were comparing performance across window lengths, and thus, we suspected that having different numbers of epochs for different window lengths might affect the results. The use of only one segment per patient might not fully capture the variability inherent in EEG signals. This approach may limit the generalizability of our findings, as multiple segments could provide a more comprehensive view of each patient's EEG characteristics. Second, the highest frequency bands that can be observed through scalp EEG signals are only approximately 50 Hz43. Therefore, it is necessary to investigate frequency ranges higher than 50 Hz through another modality through an additional method. Third, most patients were already taking ASMs at the time of the EEG study. Fourth, because the dataset used in this study consisted of patients receiving mono- or polytherapy, it is difficult to characterize the effect of a particular ASM on the EEG signal. Finally, this retrospective study was conducted using a limited dataset, which could introduce bias in the characteristics of epilepsy patients. Future research should apply more sophisticated methods that can aggregate multiple frequency bands and multiple time segments using resting-state EEG signals.

Conclusion

This study shows that the application of spectral and temporal filters to resting-state EEG signals enhanced the prediction of long-term patient outcomes when the spectral and temporal filters were simultaneously optimized. In particular, an EEG window length of greater than 2 min and the gamma band substantially impacted the prediction performance. This optimization strategy can be applied for the early identification of patients with drug-resistant epilepsy, as they are potential candidates for nonpharmacologic intervention.

Materials and methods

Patients and data collection

We retrospectively analyzed the medical records and EEG data of patients with TLE who visited Seoul National University Hospital between 2014 and 2021. All included patients had experienced at least one clinical seizure and were confirmed as having TLE based on seizure semiology, EEG, and/or 3.0-Tesla magnetic resonance imaging throughout the follow-up period. All patients received ASM during the follow-up period. We included patients whose initial EEG data were obtained using the NicoletOne® EEG system (Natus, San Carlo, CA, USA). Demographic and clinical characteristics, including baseline and final seizure frequencies, were obtained through a retrospective review of medical records. A total of 46 patients with TLE were selected and divided into two groups according to the final outcome: the SF group (seizure-free for the last year of follow-up, n = 22) and the NSF group (at least one seizure in the last year of follow-up, n = 24). In our capacity as a tertiary referral hospital, we identified only one treatment-naïve patient with TLE, while all other patients were already using ASMs at the time of EEG study. None of the patients had undergone ketogenic diet therapy. This study was conducted in accordance with the Declaration of Helsinki. This study was approved by the Institutional Review Board of Seoul National University Hospital (IRB No. H-2109-005-1251), and the need for informed consent was waived by the Institutional Review Board of Seoul National University Hospital due to the retrospective nature of the study. Detailed patient information can be found in Table 2.

Table 2 Demographic and clinical characteristics of the seizure-free and non-seizure-free groups.
Full size table

EEG recording

All EEG data were acquired with the NicoletOne® EEG system using the modified international 10–20 electrode placement system (electrodes: Fp1, Fp2, T1, F7, F3, Fz, F4, F8, T2, T3, C3, Cz, C4, T4, T5, P3, Pz, P4, T6, O1, and O2), with a sampling rate of 250 Hz, a hardware high-pass filter of 0.1 Hz, and a hardware low-pass filter of 500 Hz. All electrode impedances were maintained below 10 kΩ. After photic stimulation and hyperventilation, the patients were asked to close their eyes to collect resting-state EEG data. The first 5 min of resting-state EEG data were processed for further analysis. Among the participants, 1 out of 22 SF patients (4.5%) and 4 out of 24 NSF patients (16.7%) exhibited interictal epileptiform discharges within the first 5 min of EEG recordings (p = 0.349).

Preprocessing

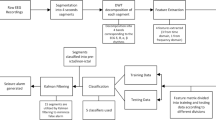
The resting-state EEG signals, recorded from 20 to 320 s, were epoched and then scaled by 106 to convert the measurements from volts to microvolts (µV), thus enhancing both the relevance and clarity of the data44. Data from all 21 channels were used in further analysis. However, data referencing was conducted only with the following EEG channels: F3, Fz, F4, C3, Cz, C4, P3, Pz, P4, O1, and O245.

Analysis strategy

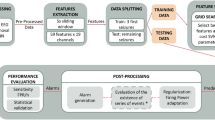
To determine the effect of appropriate spectral and temporal ranges in predicting SF outcomes of TLE patients, the following three strategies were compared. (1) In the OTS strategy, a grid search was applied to optimize the temporal range of the EEG signals in a fixed frequency band (0.1–51 Hz). The temporal segments were extracted only once with different durations. All segments started precisely at the 0-s mark of the resting-state EEG data. The target temporal range was set at 1-s intervals from 1 to 30 s and 30-s intervals from 30 to 300 s (thus yielding a total of 39 temporal segments, 1, 2, 3, …, 27, 28, 29, 30, 60, …, 90, 120, 150, …, 300 s). (2) In the OFS strategy, a grid search was applied to optimize the spectral range of EEG signals from 0.1 Hz (low cut) to 2 Hz (high cut) up to 49 Hz (low cut) to 51 Hz (high cut) (a total of 50 bands spanning 2 Hz) for the total resting state (300 s). (3) In the OFTS strategy, a two-grid search was applied to 50 spectral and 39 temporal ranges to optimize the spectral and temporal ranges simultaneously. Then, bandpass filtering, standardization46 and segmentation were sequentially performed. Figure 4 shows the analysis pipeline for OFTS. In the case of NS, total resting state (300 s) and fixed-frequency bandpass cutoff from 0.1 Hz (low cut) to 51 Hz (high cut) were applied.

Figure 4
figure 4

Analysis strategy for determining the optimal spectral and temporal range.

Full size image

Feature extraction

Among the many EEG features, four types of features were selected based on the following three questions (1) Is it a time-domain feature? (The analysis pipeline included a narrow bandpass filter). (2) Has it ever been used in an EEG-based epilepsy study? (3) What is the computational cost? (Supplementary Table 4). The selected features were as follows: Hjorth parameters (Feature group A), statistical parameters (Feature group B), energy (Feature group C), zero-crossing rate (Feature group D), interchannel correlation (ICC) (Feature group E), interchannel phase locking value (ICPLV) (Feature group F), spectral power (Feature group G), Stockwell transform (ST) (Feature group H), and wavelet transform (WT) (Feature group I).

Hjorth parameters (Feature group A)

Hjorth parameters consist of activity, mobility, and complexity, which represent the signal power, mean frequency, and change in frequency, respectively47. In many epilepsy studies, these parameters have been used to detect and diagnose seizures48,49 or to predict seizure recurrence after ASM withdrawal50. A total of 63 Hjorth parameters were acquired using Eqs. (1)–(3) and used as ML inputs.

$$ {\text{Activity}}\left( {\text{X}} \right) = {\text{var}}\left( {{\text{X}}\left( {\text{t}} \right)} \right) $$
(1)
$$ {\text{Mobility}} = \frac{{\sqrt {{\text{var}}\left( {{{{\text X}^{\prime}}}\left( {\text{t}} \right)} \right)} }}{{\sqrt {{\text{var}}\left( {{\text{X}}\left( {\text{t}} \right)} \right)} }} $$
(2)
$$ {\text{Complexity}} = \frac{{\sqrt {{\text{var}}\left( {{{{\text X}^{\prime\prime}}}\left( {\text{t}} \right)} \right)} /\sqrt {{\text{var}}\left( {{{{\text X}^{\prime}}}\left( {\text{t}} \right)} \right)} }}{{\sqrt {{\text{var}}\left( {{{{\text X}^{\prime}}}\left( {\text{t}} \right)} \right)} /\sqrt {{\text{var}}\left( {{\text{X}}\left( {\text{t}} \right)} \right)} }} $$
(3)

Statistical parameters (Feature group B)

In many EEG-based epilepsy studies, statistical parameters have been used as features to detect seizures51, distinguish healthy participants from epilepsy patients52 and predict LEV treatment responses17,51. We selected six of the most commonly used statistical indicators (i.e., skewness, kurtosis, and the mean, median, minimum, and maximum values) as Feature group B. Variance, which is one of the most commonly used statistical indicators, was excluded from Feature group B because it was included in Feature group A (Hjorth parameters). A total of 126 statistical parameters were acquired using Eqs. (4)–(9) and used as ML inputs.

$$ {\text{Skewness}}\left( {\text{X}} \right) = {\text{E}}\left[ {\left( {\frac{X\left( t \right) - \mu }{\sigma }} \right)^{3} } \right], $$
(4)
$$ {\text{Kurtosis}}\left( {\text{X}} \right) = {\text{E}}\left[ {\left( {\frac{X\left( t \right) - \mu }{\sigma }} \right)^{4} } \right] $$
(5)
$$ {\text{Mean}}\left( {\text{X}} \right) = \frac{1}{n}\mathop \sum \limits_{t = 1}^{n} X\left( t \right) $$
(6)
$$ {\text{Median}}\left( {\text{X}} \right) = \left\{ {\begin{array}{*{20}l} {X\left( {\left( {t + 1} \right)/2} \right)} \hfill & { if\; t\; is\; odd} \hfill \\ {\left( {X\left( \frac{t}{2} \right) + X\left( {\frac{t}{2} + 1} \right)} \right)/2} \hfill & {if\; t\; is\; even} \hfill \\ \end{array} } \right. $$
(7)
$$ {\text{Min}}\left( {\text{X}} \right) = X\left( {t_{0} } \right),\;\; if\left( {\forall {\text{t}} \in {\text{T}}} \right) X\left( {t_{0} } \right) \le X\left( t \right) $$
(8)
$$ {\text{Max}}\left( {\text{X}} \right) = X\left( {t_{0} } \right),\;\; if\left( {\forall {\text{t}} \in {\text{T}}} \right) X\left( {t_{0} } \right) \ge X\left( t \right) $$
(9)

Energy (Feature group C)

Many studies have used energy as an indicator of brain activity18,19. Therefore, the linear and nonlinear energy of the EEG signals were included in Feature group C52. A total of 42 energy parameters were acquired using Eqs. (10), (11) and used as ML inputs.

$$ Energy_{Linear} \left( {\text{X}} \right) = \frac{1}{n}\mathop \sum \limits_{t = 1}^{n} X\left( t \right)*X\left( t \right) $$
(10)
$$ Energy_{Non - linear} \left( {\text{X}} \right) = \frac{1}{n - 2}\left( {\mathop \sum \limits_{t = 2}^{n - 1} X\left( t \right)*X\left( t \right) - \mathop \sum \limits_{t = 3}^{n} X\left( t \right)*X\left( t \right)} \right) $$
(11)

Zero-crossing rate (Feature group D)

The zero-crossing rate is the rate at which a signal changes from positive to zero to negative or from negative to zero to positive53. This parameter has been used to detect or classify seizures from normal EEG signals in many studies54,55. In this study, the zero-crossing rate and its first derivative were included in Feature group D52. A total of 42 zero-crossing parameters were acquired using Eqs. (12), (13) and used as ML inputs.

$$ {\text{Zero}} - {\text{crossing rate }}\left( {\text{X}} \right) = \frac{1}{2}\mathop \sum \limits_{t = 2}^{n} \left| {sign(X\left( t \right) - sign(X\left( {t - 1} \right)} \right| $$
(12)
$$ {\text{Zero}} - {\text{crossing}}_{derivative} \left( {\text{X}} \right) = \frac{1}{2}\mathop \sum \limits_{t = 2}^{n} \left| {sign(X^{\prime}\left( t \right) - sign(X^{\prime}\left( {t - 1} \right)} \right| $$
(13)

ICC (Feature group E)

In the context of EEG analysis, cross-correlation is a powerful tool56,57 that offers unique insights into the functional connectivity and relationships between different brain regions. We used the Pearson correlation coefficient as the correlation coefficient in Eq. (14), which is a measure of the linear correlation between two variables X and Y. A total of 210 ICC were acquired using Eq. (14) and 20 graph measurements23,58 were used as ML inputs. Graph measurements were performed using NetworkX59 and nilearn60 Python libraries.

$$ {\text{Inter}} - {\text{channel}}_{correalation} \left( {{\text{X}},{\text{Y}}} \right) = \frac{{\mathop \sum \nolimits_{t = 1}^{T} \left( {X\left( t \right) - \overline{X}} \right)\left( {Y\left( t \right) - \overline{Y}} \right)}}{{\sqrt {\mathop \sum \nolimits_{t = 1}^{T} \left( {X\left( t \right) - \overline{X}} \right)^{2} \left( {Y\left( t \right) - \overline{Y}} \right)^{2} } }} $$
(14)

ICPLV (Feature group F)

In the context of EEG analysis, ICPLV is a powerful tool for investigating phase synchronization between brain regions. Its ability to provide insights into the timing and coordination of brain activities makes it invaluable in both research and clinical settings61,62. A total of 210 ICPLVs were acquired using Eq. (15), and 20 graph measurements23,58 were used as ML inputs.

$$ {\text{Inter}} - {\text{channel}}_{plv} \left( {{\text{X}},{\text{Y}}} \right) = \left| {\frac{1}{{\text{T}}}\mathop \sum \limits_{t = 1}^{T} e^{{i\left( {\emptyset_{X\left( t \right)} - \emptyset_{Y\left( t \right)} } \right)}} } \right| $$
(15)

Spectral parameters (Feature group G)

Spectral power and phase, which are acquired using fast Fourier transform (FFT) (Eq. 16), are crucial components of EEG signal analysis, These parameters provide deep insights into brain function and neural activity.63,64 We extracted five spectral parameters: mean, median, minimum, maximum, skewness and standard deviation of power and phase. A total of 126 spectral parameters were acquired using Eq. (16) and used as ML inputs.

$$ Spectral - power\left( {\text{X}} \right) = \mathop \sum \limits_{t = 1}^{T - 1} X\left( t \right)*e^{{\frac{i2\pi }{T}kt}} $$
(16)

ST parameters (Feature group H)

The ST is a linear transform that combines elements of the wavelet transform and the Fourier transform. It provides a time–frequency representation of a signal, similar to the wavelet transform, but it exhibits properties more akin to the Fourier transform65,66. We extracted five ST parameters mean, median, minimum, maximum, skewness and standard deviation. The stockwell python package was used to estimate ST. A total of 126 ST parameters were used as ML inputs.

WT (Feature group I)

Wavelet coefficients derives from the application of a wavelet transform to a signal. The wavelet transform decomposes the signal into components that vary in both time and frequency, unlike the Fourier transform, which only provides frequency information67,68. The wavelet coefficient of the continuous wavelet transform was acquired using the pywt.cwt function in Python (‘wavelet = db4’)69. We extracted five wavelet coefficient parameters: mean, median, minimum, maximum, skewness and standard deviation of square of absolute values of WT. A total of 126 WT parameters were used as ML inputs.

Classification and statistical analysis

The classification was performed using the RF model26 in the main experiment, and LDA27, XGB28, and CATB29 were used for the additional experiment. We treated each EEG channel as a separate input and only used a single segment of the temporal range. The area under the receiver operating characteristic curve, accuracy, F1 score, true positive rate, true negative rate, positive predictive value, and negative predictive value for each feature were compared through five-fold nested cross-validation with grid search, in which the number of patients in the test dataset was 9 or 10. The hyperparameter of each fold of each model was set based on grid-search (Supplementary Table 5). The Mann‒Whitney U test and Cliff’s delta were used for all statistical analyses, including the comparison of each feature’s performance.

Conflict of interest/ethical publication statement

None of the authors has any conflict of interest to disclose. We confirm that we have read the Journal’s position on issues involved in ethical publication and affirm that this report is consistent with those guidelines. This study was approved by the Institutional Review Board of Seoul National University Hospital (IRB No. H-2102-178-1200), and the need for informed consent was waived because of the retrospective design.