Alternating twisted multilayer graphene: generic partition rules, double flat bands, and orbital magnetoelectric effect

Abstract

Recently the alternating twisted trilayer graphene is discovered to exhibit unconventional superconductivity, which motivates us to study the electronic structures and possible correlation effects for this class of alternating twisted multilayer graphene (ATMG) systems. In this work we consider generic ATMG systems with M-L-N stacking configurations, in which the M (L) graphene layers and the L (N) layers are twisted by an angle θ (−θ). Based on analysis from a simplified k⋅p model approach, we derive generic partition rules for the low-energy electronic structures, which exhibit various band dispersions including two pairs of flat bands and flat bands co-existing with various gapless Fermionic excitations. For a mirror-symmetric ATMG system with doubled flat bands, we further find that Coulomb interactions may drive the system into a state with intertwined electric polarization and orbital magnetization orders, which can exhibit an interaction-driven orbital magnetoelectric effect.

Introduction

The recent discoveries of some phenomena, such as superconductivity^{1,2,3,4,5,6,7,8}, quantum anomalous Hall effect^{9,10,11,12,13,14,15}, and correlated insulator states^{4,5,6,7,9,16,17,18,19,20,21} in magic-angle twisted bilayer graphene (TBG) have aroused great interest. In magic-angle TBG²², the interlayer moiré potential generates pseudo magnetic fields, which are coupled with the Dirac fermions from the two layers, leading to topological nontrivial flat bands with eightfold degeneracy with valley, spin, and sublattice degrees of freedom^{23,24,25,26,27,28}. Such degeneracy can be split by strong Coulomb interactions, leading to symmetry-breaking states reminiscent of quantum Hall ferromagnetism. The interplay between nontrivial topology and strong Coulomb interaction gives rise to fruitful physics in magic-angle TBG^{29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57}.

The flat-bands physics is not unique for magic-angle TBG. It has been theoretically proposed and experimentally observed that topologically nontrivial flat bands with strong correlation effects can also exist in twisted multilayer systems such as twisted bilayer-monolayer graphene and twisted double bilayer graphene^{16,58,59,60,61,62,63,64,65,66,67,68}. Moreover, recently unconventional superconductivity has been observed in alternating twist trilayer graphene^69,70,71,72, which is a new type of twisted graphene system with topologically nontrivial flat bands co-existing with dispersive Dirac cone around the charge neutrality point (CNP)^73,74,75. This motivates us to study the electronic structures and correlation effects of alternating twisted multilayer graphene systems. One would expect that the extra twist may fundamentally change the low-energy electronic structures, and the extra layers may introduce additional degrees of freedom that may give rise to interesting interaction effects^76,77,78.

In this work, we theoretically study the alternating twisted multilayer graphene (ATMG): a class of twisted graphene systems consisting of three sequences of graphene multilayers with alternating twist angles. We describe the non-interacting band structures of the ATMG system using extended continuum model Hamiltonians of the Bistritzer-MacDonald type²². The low-energy band dispersions of the ATMG system (for each valley each spin) can be classified into three types, including one pair of flat bands, two pairs of flat bands, as well as flat bands co-existing with E(k) ~ k^J dispersive bands (J is positive integer). Based on an analytic analysis from a simplified k⋅p model approach, we find that the low energy band structures can be described by a generic partition rule. According to the partition rule, there must be double flat bands for mirror-symmetric ATMG with more than one layers in the middle sequence. Lastly, we consider Coulomb interaction effects in a mirror-symmetric ATMG system with two pairs of flat bands for each spin and valley. We have theoretically studied the ground states at each integer filling of the double flat bands based on unrestricted self-consistent Hartree–Fock calculations including the screening effects from the remote bands. At certain fillings, we find that Coulomb interactions may drive the system into a state breaking both time-reversal and mirror symmetries, which can exhibit orbital magnetoelectric effect due to the intertwining of electric polarization and orbital magnetization orders in the symmetry-breaking state.

Results and discussion

Continuum model

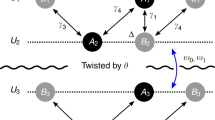
We consider a class of ATMG, which consist of three sets of graphene multilayers with the number of layers denoted by M, L, and N, respectively. The stacking sequence within each set of multilayers can be Bernal (ABA), rhombohedral (ABC), or a mixture of the two. These multilayers are stacked from bottom to up in the M-L-N sequence, where the N (L) layers and the L (M) layers are twisted by an angle θ (−θ) as schematically shown in Fig. 1a. Such a system forms a moiré pattern in real space with the moiré superlattice constant ${L}_{s}\,=\,a/(2\sin \theta /2)$, where a = 2.46 Å is the graphene lattice constant. The corresponding moiré Brillouin zone is shown in Fig. 1b. Similar to twisted bilayer graphene (TBG), the low energy states of the ATMG system are contributed by those from the atomic K and $K^{\prime}$ valleys, which are approximately decoupled from each other at the non-interacting level for small twist angles. Thus, it is generally assumed that the system preserves valley charge conservation at small twist angles²². Therefore, we generalize the Bistritzer-MacDonald continuum model²² to describe the low-energy states of the ATMG system for each valley and each spin, assuming the states from the K and $K^{\prime}$ valleys are completely decoupled. The continuum model for valley μ (μ = ∓ for K and $K^{\prime}$ valleys) is expressed as

$$\begin{array}{rc}&{H}_{ATMG}^{\mu }=\left(\begin{array}{ccc}{H}_{N}^{\mu }&{{\mathbb{U}}}_{\mu }^{{\dagger} }{e}^{-i\mu {{\Delta }}{{{\bf{K}}}}\cdot {{{\bf{r}}}}}&0\\ {{\mathbb{U}}}_{\mu }{e}^{i\mu {{\Delta }}{{{\bf{K}}}}\cdot {{{\bf{r}}}}}&{H}_{L}^{\mu }&{{\mathbb{U}}}_{\mu }{e}^{i\mu {{\Delta }}{{{\bf{K}}}}\cdot {{{\bf{r}}}}}\\ 0&{{\mathbb{U}}}_{\mu }^{{\dagger} }{e}^{-i\mu {{\Delta }}{{{\bf{K}}}}\cdot {{{\bf{r}}}}}&{H}_{M}^{\mu }\end{array}\right)\end{array}$$

(1)

where ${H}_{N}^{\mu }$, ${H}_{L}^{\mu }$ and ${H}_{M}^{\mu }$ denote the k⋅p Hamiltonians of the untwisted graphene multilayers, which consist of the Dirac fermions of each monolayer graphene and the interlayer hop** terms. ${{\mathbb{U}}}_{\mu }{e}^{i\mu {{\Delta }}{{{\bf{K}}}}\cdot {{{\bf{r}}}}}$ stands for the moiré potential term for valley μ, which arises from the mutual twist between two sets of adjacent multilayers. ΔK = (0, 4π/(3L_s)) is a vector characterizing the shift of Dirac points due to the twist.

Fig. 1: Schematic and single particle band structures of ATMG systems.

a Lattice structure of alternating twist multilayer graphene. b Brillouin zones of M, L and N layers and Moiré Brillouin zone with high symmetry points. Band structure of c A-A-A and d A-ABA-A at K valley(solid line) and ${K}^{\prime}$ valley(dashed line) in the chiral limit, considering nearest neighbor interlayer hop** with zero displacement field.

One can obtain various types of low-energy band structures from the Hamiltonian given by Eq. (1). A careful study reveals that the ATMG systems can be roughly divided into three types based on their low-energy band dispersion: for type (i) there is only one pair of flat bands for each valley and spin, which is similar to TBG; for type (ii) there is one pair of flat bands co-existing with some low-energy bands characterized by the dispersion E(k) ~ k^J(J is positive integer); and for type (iii) there are two pairs of flat bands. In Fig. 1c, d we show the band structures of two typical ATMG systems with A-A-A and A-ABA-A stacking, where the solid and dashed lines denote energy bands from the K and $K^{\prime}$ valleys respectively in chiral limit, i.e., the intrasublattice coupling between twisted layers vanishes. For the A-A-A system, there is one pair of flat bands co-existing with a Dirac cone (per valley per spin), which can be categorized as type (ii) ATMG; while there are two pairs of flat bands for each valley and spin for the A-ABA-A system, which is the simplest example of type (iii) ATMG. In what follows we will explain the origin of such low-energy dispersion and derive partition rules for generic ATMG systems.

Generic partition rules and the simplified k⋅p model

To better illustrate the origin of these low-energy dispersions, we first consider the chiral limit in which all the intrasublattice couplings are turned off. Within the chiral limit, we first analyze the low-energy states of the untwisted multilayers, then discuss the effects of the moiré potentials at the twisted interfaces. It has been proposed that a multilayer graphene with arbitrary stacking sequence and with the total number of layers N can be decomposed into S_N chiral segments⁷⁹, within each of which the stacking chirality is unchanged. Then the low-energy states contributed by the ith chiral segment with the number of layers J_i consists of a chiral doublet described by the following effective Hamiltonian⁷⁹

$${H}_{{J}_{i}}^{\mu }({{{\bf{k}}}})\propto {k}^{{J}_{i}}[\cos ({J}_{i}{\phi }_{{{{\bf{k}}}}}){\sigma }_{x}\pm \sin ({J}_{i}{\phi }_{{{{\bf{k}}}}}){\sigma }_{y}]$$

(2)

where $\tan {\phi }_{{{{\bf{k}}}}}={k}_{y}/{k}_{x}$, and σ_x,y denote Pauli matrices in the sublattice space. Then the low-energy Hamiltonian of the untwisted N layers from valley μ can be written as a direct sum of those of the S_N chiral segments: ${H}_{N}^{\mu }\approx {H}_{{J}_{1}}^{\mu }\oplus {H}_{{J}_{2}}^{\mu }...\oplus {H}_{{J}_{{S}_{N}}}^{\mu }$. Each segment contributes to a chiral doublet with the dispersion $E \sim {k}^{{J}_{i}}$ around K^μ point (μ = ± is the valley index). Then we consider the N layers are stacked with the other M layers and are twisted by angle θ. The moiré potential at the interface would couple the topmost chiral segment of the N layers with the bottom-most segment of the M layers, giving rise to a pair of flat bands for each spin and each valley. These flat bands would co-exist with the dispersive chiral doublets contributed by the remaining uncoupled chiral segments (if any) of the two sets of multilayers⁸⁰. The ATMG system introduces additional complexity due to the additional multilayers (L layers) and the additional twist. It turns out that the situations with the number of middle layers L = 1 and L > 1 need to be treated separately.

To evaluate the difference between ATMG systems with L = 1 and L > 1, we first consider alternating twisted trilayer graphene (TTG), i.e., M = L = N = 1. In TTG, three alternating twisted graphene monolayers are coupled together. The Hamiltonian of TTG can be decoupled into a TBG-like Hamiltonian and a free Dirac-fermion Hamiltonian through a proper unitary transformation. The TBG part and Dirac fermion part are completely decoupled from each other, which contribute to one pair of flat bands co-existing with a Dirac cone as shown in Fig. 1c. For L = 1 but M, N > 1, one can apply the chiral decomposition rule to the M layers and N layers. The topmost chiral segment from the M layers and the bottom-most segment from the N layers are coupled with the L = 1 middle layer through the moiré potentials, contributing to one pair of flat bands co-existing with either a Dirac cone or a pair of quadratic bands. The remaining chiral segments (if any) in the N layers and M layers would contribute to additional E(k) ~ k^J dispersive bands. On the other hand, when L > 1, one needs to apply the chiral decomposition rule to the L multilayers as well, and carefully study how the chiral doublets contributed by the M, L, and N layers are coupled to each other through the moiré potentials at the two twisted interfaces.

After a comprehensive theoretical analysis based on a simplified k⋅p model approach (see Methods and Supplementary Information for more details), we have derived a set of generic partition rules describing the low-energy band structures of ATMG systems in the chiral limit. First, the M, L, and N multilayers are divided into S_M, S_L, and S_N chiral segments, and the number of layers of the ith segment, say, in N multilayer is denoted as J_N,i (i = 1, . . . , S_N). We also need to keep the chiral segments that are closest to the twisted interfaces to be as long as possible, i.e., we need to make a choice of chiral decomposition to make ${J}_{M,{S}_{M}}$, J_L,1, ${J}_{L,{S}_{L}}$ and J_N,1 as large as possible. Based on the above choice of chiral segments, we reach the following partition rules for the low-energy dispersion in the chiral limit:

• (a) For L = 1: the ${J}_{M,{S}_{M}}$, J_L,1 and J_N,1 chiral segments are coupled through the moiré potential generated by the alternating twisted structure. When the stacking chirality of ${J}_{M,{S}_{M}}$ and J_N,1 are the same, there are one pair of flat bands and one Dirac cone co-existing near K_μ point (per spin per valley); while if ${J}_{M,{S}_{M}}$ and J_N,1 have opposite stacking chiralities, there are one pair of flat bands and one pair of quadratic bands co-existing near K_μ point. The remaining chiral segments in the M (N) multilayers would contribute to additional chiral doublets with the dispersion $E({{{\bf{k}}}})\, \sim \,{k}^{{J}_{M,i}}$ ($E({{{\bf{k}}}})\, \sim \,{k}^{{J}_{N,i}}$) near K_μ point.

• (b) For L > 1: if the L multilayer can be divided into more than one chiral segments (S_L > 1), there are two pairs of flat bands (double flat bands) around CNP; while if the L multilayer is in the chiral (rhombohedral) stacking sequence with S_L = 1, there is only one pair of flat bands. When S_L > 1, the remaining chiral segment {J_L,i, 2 ≤ i ≤ S_L − 1} that are decoupled from the M and N multilayers would contribute to dispersive bands $E({{{\bf{k}}}}) \sim {k}^{{J}_{L,i}}$ around CNP. Similarly, the remaining chiral segments {J_M,i, 1 ≤ i ≤ S_M − 1} ({J_N,i, 2 ≤ i ≤ S_N}) from the M (N) multilayer that are not coupled the middle L multilayer would contribute to the low-energy dispersive bands with $E({{{\bf{k}}}}) \sim {k}^{{J}_{M,i}}$ ($E({{{\bf{k}}}}) \sim {k}^{{J}_{N,i}}$).

In Table 1, we illustrate some ATMG systems as typical cases and apply the partition rules described above to these systems to characterize their low energy band structures, where the notation (m, n) means that there are m pairs of bands with dispersion E(k) ~ kⁿ around K_s or $K^{\prime}_s$ points. For example, for A-A-ABAC system, it can be divided into two parts including the alternating twisted layers A-A-AB and untwisted layers AC. The twisted layers would contribute one pair of flat bands co-existing with a Dirac cone around K_μ point, while the untwisted layers give rise to a pair of quadratic bands(E(k) ~ k²) centered at K_μ point.

Table 1 Typical cases for generic partition rules.

The partition rules presented above can be derived using a simplified k⋅p model approach. In this approach, we write a k⋅p model within the moiré Brillouin zone by expanding the flat bands and the Dirac cones around the moiré K_s or $K^{\prime}_s$ points including the coupling terms between them. In the chiral limit both the flat bands and the Dirac cone can be solved exactly²³, then we can analytically construct a greatly simplified k⋅p model on the basis of the zero modes (flat-band wavefunctions) and the Dirac fermions, and solve it exactly. From the analytic solutions of the simplified k⋅p model, we derive the partition rules for generic ATMG systems presented above. Such an approach can capture the essential low-energy physics, while neglecting the irrelevant high-energy bands obtained from a direct numerical diagonalization of the original continuum Hamiltonian. More details and examples about the k⋅p model approach are presented in Methods and Supplementary Information.

It is worthwhile to note that the simplified k⋅p model is constructed in the chiral limit neglecting all the intrasublattice couplings. Consequently, the partition rules derived from the simplified k⋅p model and the above discussions about double flat bands are rigorous only in the chiral limit. In a more realistic situation, one needs to include the intrasublattice component of the moiré potential and the further neighbor interlayer hop** within the untwisted layers (see Supplementary Information), which break chiral symmetry. With these additional coupling terms, the otherwise exactly flat bands at the magic angle may acquire nonzero bandwidths, and the E(k) ~ k^J bands may have slightly modified dispersion. However, despite these perturbative changes, the main conclusions sketched by the partition rules are unchanged.

Symmetry-breaking ground states in mirror-symmetric ATMG system

It follows from the previous arguments that a mirror-symmetric ATMG system with L > 1 must satisfy the condition of S_L > 1 (S_L denotes the total number of chiral segments within the L multilayer), thus there must be two pairs of flat bands for mirror-symmetric ATMG with L > 1. The double flat bands can be classified by the opposite mirror eigenvalues ± 1 for ATMG with mirror (m_z) symmetry^{1d, in the realistic situation two of the four flat bands become more dispersive with the bandwidth ~25 meV, while the other pair of flat bands remain flat with very small bandwidth ~10 meV. Second, we note that the weight of the middle layer for the pair of flat bands lower in energy with small bandwidth is vanishing, while the upper pair of flat bands with relatively large bandwidth have significant contributions from the middle-layer states. This is because the two flat bands lower/upper in energy have mirror eigenvalues ∓ 1, and the Bloch states with −1 mirror eigenvalue must have zero contribution from the middle layer. In the presence of Coulomb interactions, the m_z symmetry could be broken spontaneously at certain filling factors.}

Fig. 2: Band structures and orbital magnetoelectric effect in A-ABA-A system.

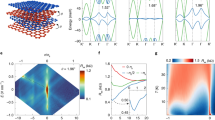
The band structure of A-ABA-A for two valleys including intrasublattice moiré potential and the further neighbor interlayer hop**. a The non-interacting band structures with weight projected to the middlemost layer. b The Hartree–Fock band structure for two valleys. c The vertical polarization, and d the valley polarization and the corresponding orbital magnetization of the symmetry-breaking ground state at -3 filling as a function of vertical electrostatic potential drop U_d.

The ubiquitous flat bands in ATMG make these systems strongly susceptible to Coulomb interactions. Moreover, unlike magic-angle TBG, in magic-angle ATMG typically there are flat bands co-existing with other dispersive bands (such as Dirac cone) or double flat bands. The extra low-energy dispersive bands (e.g., Dirac cone) may be coupled with the flat bands under weak displacement fields and display different correlated states from those in magic-angle TBG at certain filling factors^77,78. On the other hand, in mirror-symmetric ATMG with double flat bands, e.g., in A-ABA-A system, the extra pair of flat bands marked by opposite mirror eigenvalues introduce additional degrees of freedom. What are the correlated ground states in such double-flat-band systems at different filling factors of the flat bands, how the extra degrees of freedom (mirror eigenvalues) would play a role, and how the correlated states would differ from those of TBG, are all open questions. We try to answer these questions by studying the correlated states at different integer fillings of ATMG with A-ABA-A stacking, the simplest mirror-symmetric ATMG system with double flat bands.

We consider intravalley Coulomb interactions in this work, which are orders of magnitude greater than intervalley Coulomb scatterings at small twist angles. The Coulomb interactions are considered to be screened by single metallic gate (see Methods). We further project the Coulomb interactions onto the double flat bands and perform unrestricted self-consistent Hartree–Fock calculations within the subspace of the double flat bands. Besides, the Coulomb interactions between electrons in the double flat bands can be further screened by virtual particle-hole excitations in the remote energy bands, and such screening effects in our calculation are treated with the constrained random phase approximation(cRPA)^40,81. The details of the Hartree–Fock and cRPA methods are presented in Methods and Supplementary Information.

We first calculate the ground states at different integer fillings of the double flat bands using the Hartree–Fock and cRPA methods described above. The filling factor is counted with respect to the CNP, i.e., the filling factor is defined as ν = n − 8 when n out of the 16 flat bands (including valley and spin degeneracy) are filled. Then we calculate the expectation values of the order parameters of the Hartree–Fock ground states at each integer filling, and figure out the dominant ones which are presented in Table 2, where τ, s, and σ denote Pauli matrices defined in valley, spin, and sublattice space respectively. For example, the ground state at filling -3 is a gapped spin-valley polarized state. In order to depict the spontaneous m_z symmetry breaking, we also calculate the vertical electric polarization at different filling factors. The vertical electric polarization per moiré supercell p_z is defined as: ${p}_{z}\,=\,\mathop{\sum }\nolimits_{l = 1}^{5}\,(l-3)\,{q}_{l}{d}_{0}$, where d₀ = 3.35 Å is the interlayer distance of Bernal bilayer graphene, ${q}_{l}=e\left\langle {\tau }_{0}{{{{\rm{s}}}}}_{0}{{\mathbb{L}}}_{l}{\sigma }_{0}\right\rangle$ is the layer resolved charge density, where ${{\mathbb{L}}}_{l}$ is the projection operator onto layer l, a 5 × 5 matrix with the lth diagonal element identity and all other elements being zeros. The unit of the electric polarization is e ⋅ Å per moiré supercell. We also evaluate the orbital magnetization and valley polarization. The valley polarization ξ_z is defined as: ${\xi }_{z}\,=\,\mathop{\sum }\nolimits_{l = 1}^{5}{\xi }_{z}(l)\,=\,\mathop{\sum }\nolimits_{l = 1}^{5}\left\langle {\tau }_{z}{s}_{0}{{\mathbb{L}}}_{l}{\sigma }_{0}\right\rangle$, where ξ_z(l) is defined as the valley polarization projected onto layer l. A finite valley polarization would give rise to non-vanishing net orbital magnetization. In Table 2, we present the calculated vertical electric polarization and valley polarization of the spontaneous symmetry-breaking states at different integer filling factors. We find that m_z symmetry is spontaneously broken by Coulomb interactions at all integer fillings, which generate small but nonzero electric polarization.

Table 2 Gaps, main order parameters, electric polarization, and valley polarization of the Hartree–Fock ground states at different integer filling factors.

Orbital magnetoelectric effect through intertwined orders

In order to characterize the effects of vertical displacement field, we calculate both the vertical electric polarization and valley polarization of the Hartree−Fock ground states for the A-ABA-A system at filling factor −3 with increasing displacement fields. The displacement field (D) is introduced by applying a homogeneous vertical electrostatic potential difference U_d between the topmost and bottommost layers, i.e., U_d = 4eDd₀/ϵ_BN, where ϵ_BN ≈ 4 is the dielectric constant of the BN substrate. Our calculations indicate that the dominant order parameters of the ground states at filling −3 are unchanged for 0 ≤ U_d≤ 0.02 eV, i.e., the system always stays in the spin-valley polarized state with broken m_z symmetry, suggesting that no phase transition occurs at least for 0 ≤ U_d ≤ 0.02 eV. However, by virtue of the m_z symmetry and the additional layer degrees of freedom, the valley polarization acquires nontrivial layer distributions as shown by the ξ_z(l) (l = 1, . . . , 5) values in Table 3. We see that ξ_z(1) and ξ_z(2) are approximately the same, while ξ_z(4) and ξ_z(5) are approximately the same, which are all different from ξ_z(3). As a result, the layer-resolved valley polarization can be approximately decomposed into three terms:

$$\hat{{\xi }_{z}}\approx {\xi }_{z}^{s}\,{{\mathbb{1}}}_{5\times 5}+{\xi }_{z}^{a}{\hat{P}}_{z}+{\xi }_{z}^{a}{\hat{Q}}_{z}$$

(3)

where

$$\begin{array}{r}{\hat{P}}_{z}=\left(\begin{array}{ccccc}-2&0&0&0&0\\ 0&-1&0&0&0\\ 0&0&0&0&0\\ 0&0&0&1&0\\ 0&0&0&0&2\end{array}\right)\ ,\ \ {\hat{Q}}_{z}=\left(\begin{array}{ccccc}1&0&0&0&0\\ 0&0&0&0&0\\ 0&0&0&0&0\\ 0&0&0&0&0\\ 0&0&0&0&-1\end{array}\right)\end{array}$$

(4)

and ${\hat{\xi }}_{z}$ is a 5 × 5 matrix with its lth diagonal element denoting the valley polarization contributed by layer l, i.e., ${\hat{\xi }}_{z,ll}={\xi }_{z}(l)$. ${\xi }_{z}^{s}$ and ${\xi }_{z}^{a}$ denote the layer-symmetric and layer anti-symmetric components of the valley polarization, with ${\xi }_{z}^{s}=\mathop{\sum }\nolimits_{l = 1}^{5}{\xi }_{z}(l)/5$, and ${\xi }_{z}^{a}={\sum }_{l\ne 3}{{{\rm{sgn}}}}[(l-3)]({\xi }_{z}(l)-{\xi }_{z}^{s})/4$. In other words, ${\xi }_{z}^{s}=\langle {\tau }_{z}\otimes {{\mathbb{1}}}_{5\times 5}\rangle /5$ is the layer average of valley polarization (${{\mathbb{1}}}_{5\times 5}$ denotes identity matrix in layer space), and ${\xi }_{z}^{a}=\langle {\tau }_{z}\otimes ({\hat{P}}_{z}+{\hat{Q}}_{z})\rangle /4$, where $\langle \hat{O}\rangle$ denotes the expectation value of operator $\hat{O}$ evaluated with respect to the symmetry-breaking ground state. The layer-symmetric and layer anti-symmetric valley polarization for the ground states at filling − 3 with different U_d are presented in the last two rows of Table 3.

Table 3 Layer resolved valley polarization for the ground states at filling -3 under different U_d. ${\xi }_{z}^{s}=\mathop{\sum }\nolimits_{l = 1}^{5}{\xi }_{z}(l)/5$, and ${\xi }_{z}^{a}={\sum }_{l\ne 3}{{{\rm{sgn}}}}[(l-3)]({\xi }_{z}(l)-{\xi }_{z}^{s})/4$.

We note that ${\hat{P}}_{z}$ is exactly the vertical electric polarization operator ${\hat{p}}_{z}\,=\,e{d}_{0}{\hat{P}}_{z}$, which couples linearly to external electric field; while the valley polarization operator is proportional to the orbital magnetization operator ${\hat{M}}_{z}\,=\,{g}_{z}{\mu }_{B}{\tau }_{z}$ which couples linearly to external magnetic field, where g_z is introduced as an effective g factor and μ_B is the Bohr magneton. Given the above discussions, we introduce an effective mean-field Hamiltonian to describe how the symmetry-breaking state at filling -3 would respond to external electric and magnetic fields

$$\begin{array}{ll}H({{{\bf{k}}}})=&{H}_{0}({{{\bf{k}}}})+{{{\Delta }}}_{z0}\,{\tau }_{z}\otimes {{\mathbb{1}}}_{5\times 5}+{{{\Delta }}}_{zz}\,{\tau }_{z}\otimes ({\hat{P}}_{z}+{\hat{Q}}_{z})\\ &-{g}_{z}{\mu }_{B}{B}_{z}\,{\tau }_{z}\otimes {{\mathbb{1}}}_{5\times 5}+\frac{1}{4}{U}_{d}\,{\tau }_{0}\otimes {\hat{P}}_{z}\ ,\end{array}$$

(5)

where Δ_z0 and Δ_zz are the “mean fields” that are self consistently generated by Coulomb interactions which are coupled with the ${\tau }_{z}\otimes {{\mathbb{1}}}_{5\times 5}$ operator and ${\tau }_{z}\otimes ({\hat{P}}_{z}+{\hat{Q}}_{z})$ operator respectively, while B_z is the vertical magnetic field and U_d is the vertical electrostatic energy drop. As the electric polarization operator and the valley polarization operator are intertwined together, Eq. (5) implies a tunable electric polarization by magnetic field and conversely a tunable valley polarization (orbital magnetization) by electric field. To be specific, a vertical electric field is coupled to the ${\hat{P}}_{z}$ operator, which is in turn intertwined with the layer anti-symmetric component of the valley polarization operator, thus would change the valley polarization and orbital magnetization of the system. Conversely, a vertical magnetic B_z is coupled to orbital magnetization (valley polarization), and the valley polarization operator is intertwined with the electric polarization operator, which would change electric polarization of the system. It is clearly seen from Table 3 that the layer symmetric valley polarization is larger than the layer anti-symmetric one, implying that the orbital magnetization still has the strongest coupling to magnetic field, but can be tuned by electric field. In Fig. 2c, d, we present the calculated electric polarization and valley polarization of the symmetry-breaking states at filling -3 under different U_d. As U_d increases, clearly the electric polarization is linearly enhanced as shown in Fig. 2c. On the other hand, the valley polarization and the corresponding orbital magnetization are also dramatically enhanced with the increase of U_d as shown by the blue and red dots in Fig. 2d. This indicates orbital magnetoelectric effect driven by Coulomb interactions in mirror-symmetric ATMG system with double flat bands.

We note that structural relaxations are usually significant in moiré graphene systems^{82,83,84,85,86}, which may have substantial effects on the electronic structures. Therefore, we have performed the structural relaxation calculations for the A-ABA-A ATMG system based on a realistic elastic model proposed by Koshino et al.⁸⁷, and we have further calculated the band structures of the A-ABA-A ATMG system with the fully relaxed lattice structures. The main conclusion is that, depending on the twist angles, the structural relaxations can either enhance or reduce the bandwidth of the double flat bands. In particular, we find θ ≈ 0. 9 ^∘ seems to be an “optimal" angle at which the double flat bands have a total bandwidth ~25 meV, and are energetically separated from the remote bands by gaps ~10 meV. In the meanwhile, the topological properties of the double flat bands are unchanged by the structural relaxations. Therefore, it is expected that the intertwined polarization-magnetization orders and the interaction-driven orbital magnetoelectric effect are more likely to be realized at θ ≈ 0. 9^∘. On the other hand, in experiments the two twist angles at the interfaces of the ATMG system may not be exactly equal in amplitudes. Thus, we also consider the inequality in the amplitudes of the two twist angles, and find that it has very weak effects on the electronic structure. We refer the readers to Supplementary Material for more details about the structural relaxation calculations and the effects of inequality of the two twist angles.

To summarize, in this work we have theoretically studied the electronic structures and interaction effects of alternating twisted multilayer graphene (ATMG) systems. We find that these ATMG systems exhibit various non-interacting band dispersions including one pair of flat bands, one pair of flat bands co-existing with Dirac cones or more generally E(k) ~ k^J(J is positive integer) dispersion, as well as two pairs of flat bands which may also co-exist with E(k) ~ k^J(J is positive integer)dispersion. Based on an analysis from a simplified k⋅p model approach, we find that the low energy band structures of the ATMG system can be described by a set of generic partition rules. We have also considered Coulomb interaction effects in ATMG with A-ABA-A stacking, the simplest mirror-symmetric ATMG system having two pairs of flat bands. We have studied the symmetry-breaking ground states at different integer filling factors under zero external fields based on unrestricted Hartree–Fock calculations. We find that at certain fillings both time-reversal symmetry and the mirror symmetry can be broken spontaneously by Coulomb interactions, leading to gapped states with intertwined electric polarization and orbital magnetization. As a result of such intertwined ordering, the system can exhibit orbital magnetoelectric effect with the orbital magnetization (electric polarization) being highly tunable by external electric (magnetic) field. Our work is a significant step forward in understanding the electronic structures and correlation effects of alternating twisted graphene systems, and will provide useful guidelines for future experimental and theoretical studies.

Methods

The continuum model for alternating twisted multilayer graphene

We define the atomic structure of ATMG starting from three sets of graphene multilayers, denoted as M, L, and N. These multilayers are stacked from bottom to top, where the N(L) layers and the L(M) layers are twisted by an angle θ(−θ). For small twist angles, the slight mismatch between layers gives rise to a long-period moiré supercell. The lattice vectors of the moiré superlattice are: ${{{{\bf{t}}}}}_{1}=(\sqrt{3}{L}_{s}/2,{L}_{s}/2),{{{{\bf{t}}}}}_{2}=(0,{L}_{s})$, where ${L}_{s}=a/(2\sin (\theta /2))$ is the moiré lattice constant, a is the atomic lattice constant of graphene. Like TBG, we consider corrugation effects in AMTG systems, which would lead to a difference between intrasublattice and intersublattic moiré potential parameters.

The low-energy electronic structure of ATMG can be well described based on the Bistritzer-MacDonald continuum model²². The free Dirac fermions from the atomic K and ${K}^{\prime}$ valleys contribute to the low energy states of ATMG. We may consider the low energy states from two different atomic valleys as decoupled at small twist angle, i.e., the total Hamiltonian is block-diagonalized into the two independent valleys. The continuum model of the μ = ∓ ($K/K^{\prime}$) valley is:

$$\begin{array}{rc}&{H}_{ATMG}^{\mu }=\left(\begin{array}{ccc}{H}_{N}^{\mu }&{{\mathbb{U}}}_{\mu }^{{\dagger} }{e}^{-i\mu {{\Delta }}{{{\bf{K}}}}\cdot {{{\bf{r}}}}}&0\\ {{\mathbb{U}}}_{\mu }{e}^{i\mu {{\Delta }}{{{\bf{K}}}}\cdot {{{\bf{r}}}}}&{H}_{L}^{\mu }&{{\mathbb{U}}}_{\mu }{e}^{i\mu {{\Delta }}{{{\bf{K}}}}\cdot {{{\bf{r}}}}}\\ 0&{{\mathbb{U}}}_{\mu }^{{\dagger} }{e}^{-i\mu {{\Delta }}{{{\bf{K}}}}\cdot {{{\bf{r}}}}}&{H}_{M}^{\mu }\end{array}\right)\end{array}$$

(6)

where ${H}_{N}^{\mu }$, ${H}_{L}^{\mu }$, and ${H}_{M}^{\mu }$ denote the k⋅p Hamiltonians of the untwisted graphene multilayers, which consist of the Dirac fermions of each monolayer graphene and the interlayer hop** terms. ${{\mathbb{U}}}_{\mu }{e}^{i\mu {{\Delta }}{{{\bf{K}}}}\cdot {{{\bf{r}}}}}$ stands for the moiré potential term for valley μ (μ = ∓ for $K/K^{\prime}$ valley), which arises from the mutual twist between two sets of adjacent multilayers. ΔK = (0, 4π/(3L_s)) is a vector characterizing the shift of Dirac points due to the twist. The details of the continuum Hamiltonian are presented in Supplementary Information.

The ATMG system introduces additional complexity due to the additional twist. We will show that for TTG, i.e., M = L = N = 1, the continuum Hamiltonian for each valley can be decomposed into a TBG-like Hamiltonian and a free Dirac fermion Hamiltonian. For the sake of convenience, we first apply a gauge transformation to the basic functions of the ATMG system: ${\widetilde{\psi }}_{ls,{{{\bf{k}}}}}^{\mu }({{{\bf{r}}}})={\psi }_{ls,{{{\bf{k}}}}}^{\mu }({{{\bf{r}}}}){e}^{i{{{{\bf{K}}}}}_{l}^{\mu }\cdot {{{\bf{r}}}}}$, where ${{{{\bf{K}}}}}_{l}^{\mu }$ denotes the Dirac point of valley μ and layer l, and s is the sublattice index. Such a gauge transformation would remove the phase factor e^i±μΔK⋅r in the moiré potential term, and would move the Dirac points of the different twisted layers to the same origin. Then we apply a unitary transformation to the alternating TTG Hamiltonian, ${\tilde{H}}_{TTG}^{\mu }={W}^{{\dagger} }{H}_{TTG}^{\mu }W$. The Hamiltonian after the unitary transformation ${\tilde{H}}_{TTG}^{K}$ is expressed as

$$\begin{array}{r}\begin{array}{l}{\tilde{H}}_{TTG}^{\mu }=\left(\begin{array}{ccc}{h}^{\mu }({{{\bf{k}}}})&0&\sqrt{2}\,{{\mathbb{U}}}_{\mu }\\ 0&{h}^{\mu }({{{\bf{k}}}})&0\\ \sqrt{2}\,{{\mathbb{U}}}_{\mu }^{{\dagger} }&0&{h}^{\mu }({{{\bf{k}}}})\end{array}\right)\ ,\end{array}\end{array}$$

(7)

where h^μ(k) = − $\hslash$_Fk⋅σ_μ, with the Pauli matrices σ_μ = (μσ_x, σ_y) defined in the sublattice space, and the unitary transformation matrix W is expressed as

$$\begin{array}{r}\begin{array}{l}W=\left(\begin{array}{ccc}0&-\frac{1}{\sqrt{2}}&\frac{1}{\sqrt{2}}\\ 1&0&0\\ 0&\frac{1}{\sqrt{2}}&\frac{1}{\sqrt{2}}\end{array}\right)\ .\end{array}\end{array}$$

(8)

From Eq. (7) it is immediately seen that the total Hamiltonian of alternating twisted trilayer graphene consists of a TBG-like part with the moiré potential rescaled by $\sqrt{2}$ and a free Dirac fermion part. Moreover, since the magic angle is determined by the ratio between the intersublattice component of the moiré potential and the Fermi velocity, the re-scaled moiré potential in Eq. (7) implies that the magic angle for the TTG system is rescaled by the same factor, i.e., the new magic angle should be $\sqrt{2}\times 1.0{5}^{\circ }\approx 1.{5}^{\circ }$.

The simplified k⋅p model

We write a simplified k⋅p model to capture the essential low-energy physics, while neglecting the irrelevant high-energy bands obtained from a direct numerical diagonalization of the original continuum model. To construct such a simplified k⋅p model for a generic ATMG system (in the chiral limit), we should first find proper unitary transformations to the original continuum Hamiltonian to decompose it into a form consisting of a TBG-like continuum Hamiltonian and free Dirac fermions, e.g., as illustrated in Eq. (7). For each of the TBG-like terms, we can obtain the zero-mode solution of magic-angle TBG in the chiral limit. The analytical wave functions for the zero modes in magic-angle TBG in the chiral limit are expressed as²³:

$$\begin{array}{rcl}{{{\Psi }}}_{lA,{{{\bf{k}}}}}({{{\bf{r}}}})&=&{f}_{{{{\bf{k}}}}}(z){{{\Psi }}}_{lA,{{{\bf{K}}}}}({{{\bf{r}}}}),\\ {{{\Psi }}}_{lB,{{{\bf{k}}}}}({{{\bf{r}}}})&=&{f}_{{{{\bf{k}}}}}^{* }(-z){{{\Psi }}}_{lB,{{{\bf{K}}}}}({{{\bf{r}}}})\end{array}$$

(9)

where $l=\bar{\alpha },\bar{\gamma }$ refers to the two mix-layer indices, Ψ_ls,K(r) refers to the s (s = A, B) sublattice component of the zero-mode solution at the Dirac point K²³. ${f}_{{{{\bf{k}}}}}(z)={\vartheta }_{{a}_{1},{b}_{1}}(z)/{\vartheta }_{{a}_{2},{b}_{2}}(z)$, where ϑ_a,b(z) is the theta function defined in the previous work²³. For the untwisted layers, we take the k⋅p Hamiltonians of the Dirac fermions and expand them around the Dirac points within the moiré Brillouin zone. The coupling between the zero modes from the twisted layers and the Dirac fermions from the untwisted layers can be evaluated by re-expressing the original interlayer hop** matrix on the basis of the zero-mode wavefunctions and the free Dirac-fermion states. We provide details of the simplified k⋅p model and two examples in Supplementary Information.

Hartree–Fock and constrained random phase approximation

We have performed unrestricted self-consistent Hartree–Fock calculations for the A-ABA-A system within the subspace of the double flat bands.

$${H}_{C}^{{{{\rm{intra}}}}}=\frac{1}{2{N}_{s}}\mathop{\sum}\limits_{{{{{\bf{k}}}}}_{a}{{{{\bf{k}}}}}_{a}^{\prime}{{{{\bf{q}}}}}_{a}}\mathop{\sum}\limits_{\mu {\mu }^{\prime},\sigma {\sigma }^{\prime},\alpha {\alpha }^{\prime}}\,V({{{{\bf{q}}}}}_{a}){\hat{c}}_{{{{{\bf{k}}}}}_{a}+{{{{\bf{q}}}}}_{a},\mu \alpha \sigma }^{{\dagger} }\,{\hat{c}}_{{{{{\bf{k}}}}}_{a}^{\prime}-{{{{\bf{q}}}}}_{a},{\mu }^{\prime}{\alpha }^{\prime}{\sigma }^{\prime}}^{{\dagger} }\,{\hat{c}}_{{{{{\bf{k}}}}}_{a}^{\prime},{\mu }^{\prime}{\alpha }^{\prime}{\sigma }^{\prime}}\,{\hat{c}}_{{{{{\bf{k}}}}}_{a},\mu \alpha \sigma }$$

(10)

where $\mu ,{\mu }^{\prime}=\pm$ are the valley indices, $\alpha ,\alpha ^{\prime}$ are the layer/sublattice indices, and now the wavevectors k_a, ${{{{\bf{k}}}}}_{a}^{\prime}$, and q_a are expanded around the Dirac point of valley μ (K^μ), which can decomposed as k_a = k + Q, where k is the moiré wavevector in moiré Brillouin zone, and Q is the moiré lattice vector. ${\hat{c}}^{{\dagger} }$ and $\hat{c}$ operators in the above equation are the electron creation and annihilation operators. A single-gate screened Coulomb interaction V(q_a) is adopted in this work,

$$V({{{{\bf{q}}}}}_{a})={e}^{2}(1-{e}^{-2| {{{{\bf{q}}}}}_{a}| {d}_{s}})/(2{{{\Omega }}}_{M}{\epsilon }_{{{{\rm{BN}}}}}| {{{{\bf{q}}}}}_{a}| )$$

(11)

where Ω_M is the area of moiré primitive cell, d_s ≈ 40 nm is the distance between the ATMG system and the metallic gate, ϵ_BN ≈ 4 is the dielectric constant of the BN substrate. The Coulomb interactions are further projected onto the double-flat bands, i.e., we can project the electron creation/annihilation operator on the subspace of the double flat bands: ${\hat{c}}_{{{{{\bf{k}}}}}_{a},\mu \alpha \sigma }={\sum }_{n}{C}_{\mu \alpha {{{\bf{G}}}},n}({{{\bf{k}}}}){\hat{c}}_{\mu \sigma ,n{{{\bf{k}}}}}$, where C_μαG,n(k) is the non-interacting wavefunction of the nth Bloch eigenstate at moiré wave vector k from valley μ, and the summation of band index n is restricted to the subspace of the double flat bands. We make Hartree–Fock approximations to Eq. (10) to decompose the two-particle interactions into a superposition of the Hartree and Fock mean-field single-particle Hamiltonians, and find self-consistent solutions. Besides, the Coulomb interactions between electrons in the flat bands can be further screened by virtual particle-hole excitations from the remote energy bands, and such screening effects in our calculation are treated with the constrained random phase approximation(cRPA)^40,81, where the cRPA dielectric constant is expressed as: $\epsilon ({{{\bf{q}}}}+{{{\bf{Q}}}})={\epsilon }_{{{{\rm{BN}}}}}{({\mathbb{1}}+{\hat{\chi }}^{0}({{{\bf{q}}}})\hat{V}({{{\bf{q}}}}))}_{{{{\bf{Q}}}},{{{\bf{Q}}}}}$. Here ${\hat{\chi }}^{0}({{{\bf{q}}}})$ is the zero-frequency bare susceptibility at moiré wavevector q, and $\hat{V}({{{\bf{q}}}})$ is the Coulomb interaction matrix defined in the space of reciprocal moiré lattice vector Q, with $\hat{V}{({{{\bf{q}}}})}_{{{{\bf{Q}}}},{{{\bf{Q}}}}}=V({{{\bf{q}}}}+{{{\bf{Q}}}})$. We provide more details of the Hartree–Fock and cRPA methods in Supplementary Information.