Emerging opportunities and challenges for the future of reservoir computing

Abstract

Reservoir computing originates in the early 2000s, the core idea being to utilize dynamical systems as reservoirs (nonlinear generalizations of standard bases) to adaptively learn spatiotemporal features and hidden patterns in complex time series. Shown to have the potential of achieving higher-precision prediction in chaotic systems, those pioneering works led to a great amount of interest and follow-ups in the community of nonlinear dynamics and complex systems. To unlock the full capabilities of reservoir computing towards a fast, lightweight, and significantly more interpretable learning framework for temporal dynamical systems, substantially more research is needed. This Perspective intends to elucidate the parallel progress of mathematical theory, algorithm design and experimental realizations of reservoir computing, and identify emerging opportunities as well as existing challenges for large-scale industrial adoption of reservoir computing, together with a few ideas and viewpoints on how some of those challenges might be resolved with joint efforts by academic and industrial researchers across multiple disciplines.

Introduction

At the core of today’s technological challenges is the ability to process information at massively superior speed and accuracy. Despite large-scale success of deep learning approaches in producing exciting new possibilities^{1,2,3,4,5,6,7}, such methods generally rely on training big models of neural networks posing severe limitations on their deployment in the most common applications⁸. In fact, there is a growing demand for develo** small, lightweight models that are capable of fast inference and also fast adaptation - inspired by the fact that biological systems such as human brains are able to accomplish highly accurate and reliable information processing across different scenarios while costing only a tiny fraction of the energy that would have been needed using big neural networks.

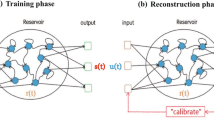
As an alternative direction to the current deep learning paradigm, research into the so-called neuromorphic computing has been attracting significant interest⁹. Neuromorphic computing generally focuses on develo** novel types of computing systems that operate at a fraction of the energy comparing against current transistor-based computers, often deviating from the von-Neumann architecture and drawing inspirations from biological and physical principles¹⁰. Within the broader field of neuromorphic computing, an important family of models known as reservoir computing (RC) has progressed significantly over the past two decades^11,12. RC conceptualizes how a brain-like system operates, with a core three-layer architecture (see Box 1 and Box 2): An input (sensing) layer which receives information and performs some pre-processing, a middle (processing) layer typically defined by some nonlinear recurrent network dynamics with input signals acting as stimulus and an output (control) layer that recombines signals from the processing layer to produce the final output. Reminiscent of many biological neuronal systems, the front end of an RC network, including its input and processing layers, is fixed and non-adaptive, which transforms input signals before reaching the output layer; in the last, output part of an RC the signals are combined in some optimized way to achieve the desired task. An important aspect of the output layer is its simplicity, where typically a weighted sum is sufficient, reminding a great deal of how common mechanical and electrical systems operate - with a complicated core that operates internally and a control layer that enables simple adaptation according to the specific application scenario.

Can such an architecture work? This inquiry was attempted in the early 2000s by Jaeger (echo state networks (ESNs)¹¹) and Maass (liquid state machines (LSMs),¹²), achieving surprisingly high level of prediction accuracy in systems that exhibit strong nonlinearity and chaotic behavior. These two initially distinct lines of work were later reconciled into a unified, reservoir computing framework by Schrauwen and Verstraeten¹³, explicitly defining a new area of research that touches upon nonlinear dynamics, complex networks and machine learning. Research in RC over the past twenty years has produced significant results in the mathematical theory, computational methods as well as experimental prototypes and realizations, summarized in Fig. 1. Despite successes in those respective directions, large-scale industry-wide adoption of RC or broadly convincing “killer-applications” beyond synthetic and lab experiments are still not available. This is not due to the lack of potential applications. In fact, thanks to its compact design and fast training, RC has long been sought as an ideal solution in many industry-level signal processing and learning tasks including nonlinear distortion compensation in optical communications, real-time speech recognition, active noise control, among others. For practical applications, an integrated RC approach is much needed and can hardly be derived from existing work that focuses on either the algorithm or the experiment alone. This perspective offers a unified overview of the current status in theoretical, algorithmic and experimental RCs, to identify critical gaps that prevents industry adoption of RC and to discuss remedies.

Fig. 1: Selected research milestones of RC encompassing system and algorithm designs, representing theory, experimental realizations as well as applications.

For each category a selection of the representative publications were highlighted.

Box 1 Comparison bettwen deep learning and reservoir computing

Box 2 Schematic representation of the reservoir computing (RC) framework

Theory and algorithm design of RC systems

The core idea of RC is to design and use a dynamical system as reservoir that adaptively generates signal basis according to the input data and combines them in some optimal way to mimic the dynamic behavior of a desired process. Under this angle, we review and discuss important results on representing, designing and analyzing RC systems.

Mathematical representation of an RC system

The mathematical abstraction of an RC can generally be described in the language of dynamical systems, as follows. Consider a coupled system of equations

$$\left\{\begin{array}{l}\Delta {{{{{{ x}}}}}}=F({{{{{{ x}}}}}};{{{{{{ u}}}}}};{{{{{{ p}}}}}}),\quad \\ {{{{{{ y}}}}}}=G({{{{{{ x}}}}}};{{{{{{ u}}}}}};{{{{{{ q}}}}}}).\quad \end{array}\right.$$

(1)

Here the operator Δ acting on x becomes $\frac{{{{{{{{\rm{d}}}}}}}}x}{{{{{{{{\rm{d}}}}}}}}t}$ for a continuous-time system, x(t + 1) − x(t) for a discrete-time system, and a compound of these two operations for a hybrid system. Additionally, ${{{{{{ u}}}}}}\in {{\mathbb{R}}}^{d}$, ${{{{{{ x}}}}}}\in {{\mathbb{R}}}^{n}$, and ${{{{{{ y}}}}}}\in {{\mathbb{R}}}^{m}$ are generally referred to as the input, internal state and output of the system, respectively, with vector field F, output function G and parameters p (fixed) and q (learnable) representing their functional couplings. Once set up by fixing the vector field F and the output function G and the parameters p, one can utilize the RC system to perform learning tasks, typically in time-series data. Given a time series ${\{{{{{{{ z}}}}}}(t)\in {{\mathbb{R}}}^{m}\}}_{t\in {\mathbb{N}}}$, an optimization problem is usually formulated to determine the best q:

$$\mathop{\min }\limits_{{{{{{{ q}}}}}}}{\int}_{t}\left(\parallel\! G({{{{{{x(t)}}}}}};{{{{{{u(t)}}}}}};{{{{{{ q}}}}}})-{{{{{{ z}}}}}}(t){\parallel }^{2}+\beta R({{{{{{ q}}}}}})\right)dt,$$

(2)

where R(q) is a regularization term.

Also, when z(t) is seen as a driving signal, the optimization problem can be regarded as a driving-response synchronization problem finding appropriate parameters q¹⁴. Since RC is often simulated on classical computers, most commonly used RC takes discrete time steps:

$$\left\{\begin{array}{l}{{{{{{ x}}}}}}(t+1)=(1-\gamma ){{{{{{ x}}}}}}(t)+\gamma f(W{{{{{{ x}}}}}}(t)+{W}^{(in)}{{{{{{ u}}}}}}(t)+{{{{{{ b}}}}}}),\quad \\ {{{{{{ y}}}}}}(t)={W}^{(out)}{{{{{{ x}}}}}}(t),\quad\hfill \end{array}\right.$$

(3)

which is a special form of (1), but now with time steps and network parameters more explicitly expressed. In this form, f is usually a component-wise nonlinear activation function (e.g., $\tanh$), the input-to-internal and internal-to-output map**s are encoded by the matrices W⁽ⁱⁿ⁾ and W^(out), whereas the internal network is represented by the matrix W. The additional parameters b and γ are used to ensure that the dynamics of x is bounded, non-diminishing and (ideally) exhibits rich patterns that enable later extraction. Given some training time series data {z(t)} (assumed to be scalar for notational convenience), once the RC system is set up by fixing the choice of f, γ, b, W⁽ⁱⁿ⁾ and W, the output weight matrix W^(out) can be obtained by attempting to minimize a loss function. A commonly used loss function is

$${W}^{(out)\top }=\arg \mathop{\min }\limits_{{{{{{{ w}}}}}}}\left(\parallel\! X{{{{{{ w}}}}}}-{{{{{{ z}}}}}}{\parallel }^{2}+\beta \parallel\! {{{{{{ w}}}}}}{\parallel }^{2}\right),$$

(4)

where $X={({{{{{{ x}}}}}}{(1)}^{\top },\,{{{{{{ x}}}}}}{(2)}^{\top },\ldots,\,{{{{{{ x}}}}}}{(T)}^{\top })}^{\top }$, z = (z(1), z(2), …, z(T))^⊤ and β ∈ [0, 1] is a prescribed parameter. This problem is in a special form of Tikhonov regularization and yields an explicit solution ${W}^{(out)\top }={\left({X}^{\top }X+{\beta }^{2}I\right)}^{-1}{X}^{\top }{{{{{{ z}}}}}}$.

Common RC designs

Designing is a crucial step for acquiring a powerful RC network. There are still no complete instructions on how to design optimal RC networks based on various necessities. With the unified forms Eqs. (1) and (2) in mind, a standard RC system as initially proposed contains everything random and fixed including the input and internal matrices W⁽ⁱⁿ⁾ and W, leaving the choice of parameters γ and β according to some heuristic rules. Based on this default setting, we show how different RC designs can generally be interpreted as optimizing in one and/or multiple parts along the following directions. Firstly, in RC coupling parameter search, with the goal of selecting a good and potentially optimal coupling parameter γ to maintain the RC dynamics bounded and produces rich pattern that allow for the internal states to form a signal bases that can later be combined to approximate the desired series {z(t)}. Empirical studies have shown that γ chosen so that the system is around the edge of chaos¹⁵ typically produces the best outcome, which is supported by a necessary but not sufficient condition - imposed on the largest singular value of the effective stability matrix W_γ = (1 − γ) + γW. Then, in RC output training, whose design commonly amounts to two aspects. One is to determine the right optimization objective, for instance the one in Eq. (4) with common generalizations include to change the norms used in the objective in particular the term ∥w∥ to enforce sparsity or to impose additional prior information by changing β∥w∥ into ∥Lw∥ with some matrix L encoding the prior information. On the other hand, (upon choice of the objective) to further determine the parameter, e.g., β as in Eq. (4). Although there is no general theoretically guaranteed optimal choice, several common methods can be utilized, e.g., cross-validation techniques that had been well-developed in the literature of computational inverse problems. RC network design is crucial to determine the dynamic characteristics. With the goal of determining a good internal coupling network W. This has received much attention and has attracted many novel proposals, which include structured graphs with random as well as non-random weights^16,17, and networks that are layered and deep or hierarchically coupled^18,19,20. Furthermore, sometimes those designs are themselves coupled with the way the input and output parts of the system are used, for example in solving partial differential equations (PDEs)^21,22 or representing the dynamics of multivariate time series²³. Finally, as for RC input design, although received relatively little attention until recently, it turns out that the input part of an RC can play very important roles in the system’s performance. Here input design is generally interpreted to include not only the design of the input coupling matrix W⁽ⁱⁿ⁾ but also potentially some (non)linear transformation on the input u(t) and/or target variable z(t) prior to setting up the rest of the RC system. The so-called next-generation RC (NG-RC) is one such example²⁴, showing great potential of input design in improving the data efficiency (less data required to train) of an RC.

In addition to the separate designs of the individual parts of an RC, the novel concept of neural architecture search (NAS) has motivated the research of hyperparmeter optimization¹¹. Ref. ¹¹ considers RC network with sigmoid nonlinearity and unit output function and showed that if the largest singular value of the weight matrix W is less than one then the system has ESP, and if the spectral radius of W is larger than one then the system is asymptotically unstable and thus cannot has ESP. Tighter bounds were subsequently derived in⁴¹. In particular, the spectral radius condition provides a practical way of ruling out bad RCs and can be seen a necessary condition for RC to properly function.

The second category is about memory capacity. Defined by the summation of delay linear correlations of the input sequence and output states, was shown to not exceed N for under iid input stream⁴², can be approached with arbitrary precision using simple linear cyclic reservoirs¹⁶, and can be improved using the time delays in the reservoir neurons⁴³.

Universal approximation theorems can be regarded as a single category. Prior to the research of RC, universal representation theorems by Boyd and Chua showed that any time-invariant continuous nonlinear operator can be approximated either by a Volterra series or alternatively by a linear dynamical system with nonlinear readout⁴⁴. RC’s representation power has attracted significant recent interest: ESNs are shown to be universally approximating for discrete-time fading memory processes that are uniformly bounded⁴⁵ and further that the approximating family can be associated with networks with ESP and fading memory⁴⁶. For discrete-time stochastic inputs, linear reservoir systems with either polynomial or neural network readout maps are universal and so are ESNs with linear outputs under further exponential moment constraints imposed on the input process⁴⁷. For structurally stable systems, they can be approximated (upon topological conjugacy) by a sufficiently large ESN⁴⁸. In particular, ESNs whose output states are trained with Tikhonov regularization are shown to approximate ergodic dynamical systems⁴⁹. Also rigorously, the dynamics of RC is validated as a higher-dimensional embedding of the input nonlinear dynamics⁴³. In addition, explicit error bounds are derived for ESNs and general RCs with ESP and fading memory properties under input sequences with given dependency structures⁵⁰. Finally, according to conventional and generalized embedding theories, the RCs with time delays are established with significantly-reduced network sizes, and sometimes can achieve dynamics reconstruction even in the reservoir with a single neuron⁴³.

The last category includes research about linear versus nonlinear transformations and next-generation RC. Focusing on linear reservoirs (possibly upon pre-transformations of the input states), recent work showed that the output states of an RC can be expressed in terms of a controllability matrix together with the network encoded inputs¹⁷. Moreover, a simplified class of RCs are shown to be equivalent to general vector autoregressive (VAR) processes⁵¹ - with possible nonlinear basis expansions it forms theoretical foundations for the recently coined concept of next-generation RC²⁴.

Research of how to design RC architectures, how to train them and why they work have, over the past two decades following the pioneering works of Jaeger and Maass, led to much evolved view of the capabilities as well as limitations of the RC framework for learning. On the one hand, simulation and numerical research has produced many new network architectures improving the performance of RC beyond purely random connections; future works can either adopt a one-fits-all approach to investigate very large random RCs or perhaps more likely to follow the concept of domain-specific architecture (DSA)⁵² to explore structured classes of RCs that achieve optimal performance for particular types of applications, with Bayesian optimization^26,

Box 3 Schematic diagram of physical reservoir computing

Application benchmarks of RC

Applications of RC are quite diverse and can be mainly divided into several categories: signal classification (e.g., spoken digit recognition), time series prediction (e.g., chaos prediction such as in the Mackey-Glass dynamics), control of system dynamics (e.g., learning to control robots in real-time) and PDE computations (e.g., fast simulation of Kuramoto-Sivashinsky equations), which we discuss below respectively.

In signal classification tasks, the input of RC are usually broadly-interpreted (physical) signals such as audio, image or temporal waves. The target output are the corresponding labels which can be spoken digits16,28,29,34,35,65,68,82,83,84, image labels^{33,35,85,86,87}, bit-symbols^{16,29,68,88,89,90,91,92,93} and so on. The effectiveness of traditional neural networks in classification tasks has been verified in lots of work. However, dealing with temporal input signal is still a challenge. Compared with traditional neural networks, RC can map temporal signals with multiple timescales to high dimension, encoding these signals with its various internal states. Furthermore, RC network has much less parameters thus requiring less training resources. Therefore, RC can be a good candidate to be utilized in temporal signal classification tasks. The signals are in various types (audio, image or temporal waves), and usually require some preprocessing before injecting to RC network. For example, in the spoken-digit recognition task, the raw signal is first transformed to frequency domain in terms of multiple frequency channels via Lyon’s passive ear model, as shown in Fig. 2a. Then the 2-D signals can be directly mapped to the RC network as input u(t) via input mask, or can be transformed to 1-D input sequence u(t) by connecting each row successively. The targets are a vector of size ten corresponding to digit number from 0 to 9. The state-of-the-art of RC currently can reach a word error rate (WER) of 0.4% from memristor chip RC³⁵, and 0.2% from electronic RC⁹⁴.

Fig. 2: Example applications of RC.

Flow diagrams showing how RC is applied in different types of applications, here referring to as signal classification, nonlinear time series prediction, dynamical control and PDE computing, respectively. a RC for spoken-digit recognition^{16,28,29,34,35,65,68,82,83,84}, when the targets are a vector of digit numbers corresponding to 0–9. b RC for time series prediction with Mackey-Glass equations^{11,31,34,51,95} as an example. In method 1 with off-line training, the training sequence starts with the first point (black point), while the target sequence starts with the second one (orange point). In method 2 with on-line retraining, the training and testing are alternately presented. c RC acts as the prediction optimizer in the general model predictive control (MPC)^{104,105,106,107,108,11,31,34,51,95}, Lorenz system^{22,26,49,51,95,96,97}, Santa Fe Chaotic time series^16,86,89,95, Ikeda system⁹⁵, auto-regressive moving average (NARMA) sequence^{16,28,29,93,94,97} and wind power¹⁰³. Given a training time series ${\{{{{{{{ z}}}}}}(t)\}}_{t\in {\mathbb{Z}}}$ and prescribed prediction horizon τ, the input sequence of RC can be defined as u(t) = z(t) while the target output as y(t) = z(t + τ). (For one-step prediction we use τ = 1.) Once the parameters of RC is learned, it can be used as a predictive model, taking a temporal input and predicts its next steps. In particular, RC trained with one-step prediction can nevertheless be used to make multi-step predictions, in the following way. Suppose that a finite-length time series {u(t)}_t=1,…,T is provided, we feed it into RC to compute a state y(t + 1) as a one-step prediction. We then append this state to the end of the input effectively defining u(t + 1) = y(t + 1) and through RC to compute a next state y(t + 2), and so on and so forth to obtain a series of next steps y(t + 1, t + 2, …, t + h). A schematic example of nonlinear time series prediction task is shown in Fig. 2b. In order to realize long-term prediction, there is another training scheme in which the target sequence is inserted periodically. In particular, the input to the RC now comes from its feedback or target sequence alternately, as shown in Fig. 2b (method 2). Compared with the previous case which can be regarded as an offline training scheme, here RC can acquire target data periodically, then retraining and updating the output weights regularly. This is an online training scheme. Since RC has access to target data during its evolution, it can adjust the output weights to prevent the predictive output data from diverging. Therefore, the online training typically yields longer prediction period and better prediction performances.

RC can play important roles in the control of nonlinear dynamical systems^{104,105,106,107,108,Intelligent robots}

Opportunities. Robots are becoming increasingly important in today’s information society due to their ability to take many forms, including intelligent physical manifestations. One example of this is large-scale commercial swee** robots used in smart homes115, which have replaced traditional manual operations in various scenarios, improving both production efficiency and living standards. With advances in technology, more types of intelligent robots are expected to emerge over the next decade, capable of completing complicated tasks through autonomous perception, calculation, optimization, and control in complex environments like failure detection, medical diagnosis, and search-and-rescue operations. Biological intelligence serves as inspiration for achieving robot intelligence, which relies on three key elements: real-time intensive information collection and perception capabilities (made possible by technologies such as flexible sensing, electronic skin, and multi-dimensional environment modeling), fast information processing capabilities (enabled by technologies like decision-making optimization and dynamic control), and physical control capabilities (facilitated by nonlinear modeling and electromechanical control). Challenges. Due to physical constraints such as battery capacity and deployment environment uncertainty, the core modules supporting robot intelligence are expected to be embedded in the physical entity of the robot in an offline manner rather than relying on cloud and network capabilities to provide potential large model capabilities. Similar to the IoT scenario, machine learning that is widely relied on in robot intelligence must have the characteristics of miniaturization, low energy consumption, and easy deployment, while requiring the ability to recognize, predict, calculate, and control dynamic processes. This presents an excellent application field for RC systems to play a role. In MPC, since the role of RC merely replaces a linear predictor the overall controller architecture remains transparent and intact. In principle, it is possible to adopt RC for general controller design beyond usage in the MPC framework, e.g., directly learning control rules from data together with (some) prior model knowledge. However, the main challenge would be to pose theoretical guarantees on error and convergence neither of which have been resolved by existing works of RC.

AI for science and digital twins

Opportunities. To fully realize the ongoing information revolution, it is essential to rethink and reshape crucial aspects of industrial manufacturing through the innovative framework of AI for science and digital twins. This involves achieving full perception and precise control of physical systems through interactions and iterative feedback between digital models and entities in the physical world. Essentially, digital twins establish a synchronous relationship between physical systems and their digital representations. Using this synchronous function, simulations can be run in the digital world, and optimized designs can repeatedly and iteratively be imported into the physical system, ultimately leading to optimization and control. For systems with clear and complete physical mechanisms, synchronization models that digital twins rely on are usually sets of ODEs/PDEs. For example, simulating full three-dimensional turbulence, weather forecasting, laser dynamics, etc. Preliminary studies suggest that reservoir computing can be used to reduce the computational resources required for these expensive simulations. Arcomano et al.¹¹¹ developed a low-resolution global prediction model based on reservoir computing and investigated the applicability of RC in weather forecasting. They demonstrated that a parallel ML model based on RC can predict the global atmospheric state in the same grid format as the numerical (physics-based) global weather forecast model. They also found that the current version of the ML model has potential in short-term weather forecasting. They further discovered that when full-state dynamics are available for training, RC outperforms the time-based backpropagation through time (BPTT) method in terms of prediction performance and capturing long-term statistical data while requiring less training time. Challenges. Calculations of these physics-inferred equations can be challenging. In more complex industrial applications, multiple coupling modules are often present, and interactions between the system and the open environment cannot be fully described by physical mechanisms or mathematical functions. Therefore, it is necessary to consider fast calculation techniques, but also find ways to build synchronization models for non-white-box complex dynamic systems. Mathematical modeling of fusion between physical mechanisms and data-driven techniques has been significantly developed in the past decade. For instance, Physics-inspired Neural Networks (PINN) embed the structure and form of physical equations into neural network loss functions, which guides the neural network to approximate provided physics equations during parameter training¹²⁴. Another type of physics-inspired computing system, RC, inherently provides an embedding method of the mechanism model, which is expected to provide a powerful supplement to the solver for basic physical models of industrial simulation, focusing on offering a dynamic modeling framework for the fusion of mechanisms and data. However, for reduced-order data, large-scale RC models may be unstable and more likely to exhibit bias than the BPTT algorithm. In another example of research on nonlinear laser dynamics, the authors found that RC methods have simpler training mechanisms and can reduce training time compared to deep neural networks¹²⁵. For practical problems involving complex nonlinear physical processes, we have reason to believe that RC methods may provide us with solutions for computational acceleration.

Outlook

In summary, although RC has the potential for large-scale application in terms of functions, in order to truly solve the technical problems in the above-mentioned various major applications, there are still many key challenges in the existing RC system in various aspects. For example, in theoretical research, although the universal approximation theory of RC has advanced significantly in recent years, most of the theoretical results focus on existence proofs and lack structural design. Hence, the current approximation theory has not yet played an important guiding role in RC network architecture design, training methods, etc., nor can it quantitatively evaluate the approximation potential of a specific RC scheme for dynamic systems or time series. An important reason to further advance the mathematical theory of RC is for data-driven control applications. In most of those applications, rigorous theory on control error and convergence are necessary for the corresponding controller to be considered usable in an industrial setting. However, so far very little work has been done to address these important problems. As for algorithmic challenges, most industrial applications do not require a universal approximator, but in the same field, the approximation model needs to be generalizable. Existing RC research has very little exploration in domain-specific architecture optimization. Problems in the industrial field are divided into scenarios and categories. Therefore, it is important to construct general-purpose RC models possibly by means of architecture search. In addition, leaving aside the practicality of RC for the time being, past research has turned its advantages into constraints, such as small size, simple training, and so on. However, how strong is RC’s learning ability (whether there is an RC architecture that can compare with GPT’s ability), it is still unknown.

At the experimental level, there are still some gaps when map** RC models to physical systems. The first is timescale problem of physical substrate RC: Matching the timescales between the computational challenge and the internal dynamics of the physical RC substrate is a key issue in reservoir computing. If the timescale of the problem is much faster than the response time of the physical system, the response of the reservoir will be too small or the fading memory of the reservoir will not be properly utilized, rendering the physical reservoir computing system ineffective. One intuitive solution is to adjust the physical parameters of the reservoir to match the timescale of the computational problem. This poses high requirements for the design of RC network structures and training algorithms. Using other technologies such as super-resolution and compressive sensing to overcome the resolution problem of single-point measurement and processing in RC systems may be a viable solution. The second is the real-time data processing problem: One of the significant advantages of reservoir computing is lightweight and fast computation. However, in practical physical systems, it is often unrealistic to sample and store a large number of node responses to a certain input due to limitations such as sampling bandwidth, storage depth and bandwidth, or their combinations. It is simply not feasible in many cases to probe a system with a large number of probes (10s–1000s) interfaced with AD converters. In addition to these practical challenges, hardware drift often requires regular repetition of calibration procedures, hence it cannot be a one-of optimization. Furthermore, data preprocessing and postprocessing also limit the overall computational speed of the physical RC system. One approach to address this issue is to use hardware-based readout instead of software-based readout^{126,127,128,129}.

Moving forward, it is crucial that we thoroughly explore the potential of intelligent learning machines based on dynamical systems. In the realm of theoretical and algorithmic research, it is necessary to continuously push the boundaries of performance and offer guidance for experimental design. Reservoir computing (RC) research can take root in theory and algorithms, with experiments serving as approximations to theoretical and algorithmic results. However, one disadvantage of this approach is that it can be challenging to identify equivalent devices in experiments that can achieve the nonlinear properties of RC in theory, which can lead to reduced accuracy. Alternatively, researchers can focus on building physical RC system as the ultimate goal, which requires close collaboration between theoretical and experimental teams to optimize the system jointly. This approach has the advantage of considering physical constraints and application characteristics when designing algorithms, making it more likely to achieve better solutions at the implementation level. This also raises the bar for interdisciplinary research, as participants will need to possess cross-disciplinary communication skills and knowledge, along with an openness towards multi-module complex coupling optimization.

Looking ahead, unlocking the full potential of RC and neuromorphic computing in general is critical yet challenging. In fact, this goes beyond just putting out open-source codes or solve a few specific problems. Innovative ideas and interdisciplinary research formats are much needed. As concrete suggestions, researchers of the applied mathematics and nonlinear dynamics communities who have been the main players in RC will need to get close(r) to the mainstream AI applications and try to develop next-generation RC systems to compete in these scenarios where the value of application has been established and recognized by the industry. A good starting point can be open-source tasks and datasets such as Kaggle, and more generally to directly partner with industrial research labs to put RC into real applications. On the other hand, raising awareness of the (potential) utility of RC requires attracting interest from researchers and decision-makers who are traditionally outside of the field. For instance, themed conferences and workshops may be organized to foster such discussions among scientists and researchers from diverse fields across academia and industry. Despite the many challenges, with persistence and innovations a new and future paradigm of intelligent learning and computing may possibly emerge from the works of RC and neuromorphic computing.