Abstract
Within a short period of time, COVID-19 grew into a world-wide pandemic. Transmission by pre-symptomatic and asymptomatic viral carriers rendered intervention and containment of the disease extremely challenging. Based on reported infection case studies, we construct an epidemiological model that focuses on transmission around the symptom onset. The model is calibrated against incubation period and pairwise transmission statistics during the initial outbreaks of the pandemic outside Wuhan with minimal non-pharmaceutical interventions. Mathematical treatment of the model yields explicit expressions for the size of latent and pre-symptomatic subpopulations during the exponential growth phase, with the local epidemic growth rate as input. We then explore reduction of the basic reproduction number R0 through specific transmission control measures such as contact tracing, testing, social distancing, wearing masks and sheltering in place. When these measures are implemented in combination, their effects on R0 multiply. We also compare our model behaviour to the first wave of the COVID-19 spreading in various affected regions and highlight generic and less generic features of the pandemic development.
Similar content being viewed by others
Introduction
The Coronavirus Disease 2019 (COVID-19) is a new contagious disease caused by the novel coronavirus (SARS-COV-2)1, which belongs to the genera of betacoronavirus, the same as the coronavirus that caused the SARS epidemic between 2002 and 20032. COVID-19 has spread to more than 200 countries/regions, with over 102 million confirmed cases and 2.2 million lives claimed as of January 31, 20213. The outbreak has been declared a pandemic and a public health emergency of international concern4.
As the specific symptoms of COVID-19 are now well-publicised, symptomatic transmissions are being contained in most countries. However, disease transmission by pre-symptomatic and asymptomatic viral carriers is seen to be extremely difficult to deal with due to its hidden nature5. Clinical data reveals that viral load becomes significant before the symptom onset6,7,8. Epidemiological investigations have identified clear cases of pre-symptomatic transmission soon after the initial outbreak9,10,11,12. Estimates vary greatly among experts on the percentage of total transmission due to this group of viral carriers, ranging from as low as 18% to over 50%13,14,15. An early model-based study by Ferretti et al.16 suggested that pre-symptomatic transmission alone could yield a basic reproduction number R0,p = 0.9, close to the critical value of 1.0 that sustains epidemic growth. Under intense surveillance of the pandemic, pre-symptomatic and asymptomatic transmissions become the main focus in outbreak control5.
While the actual viral shedding is influenced by many factors, patient viral load during the course of disease progression is more universal. This suggests a modelling approach that starts with clinical observations of symptom onset, and treats disease transmission as a dependent process that is further shaped by living and social conditions, including control measures to reduce physical contact. Following this strategy, we first introduce a model for an unprotected population and calibrate the model parameters against clinical case reports during the initial outbreak. Subsequently, we estimate the percentage reduction in the basic reproduction number (estimated to be around 3.87 at an exponential growth rate of 0.3/day) due to contact tracing, mask wearing and other measures, individually or in combination. Additionally, we present our findings against the epidemic development curves around the world to highlight the level of social mobilisation required to contain COVID-19 spreading.
Results
A renewal process centred on symptom onset
In epidemiological studies, the central quantity is the average number of secondary infections per unit time r(t) by a viral carrier on day t since the individual’s own infection17,18. In the case of COVID-19, disease transmission peaks around the symptom onset time of the individual7,8, as illustrated by the infectiousness curve shown in Fig. 1a (left panel). This property, when averaged over the population, gives an r(t) (Fig. 1a, right panel) that closely resembles the symptom onset time distribution, which we denote by pO(t) (Fig. 1a, middle panel). In fact, when the time window of transmission is narrowly centred around the symptom onset, we have approximately
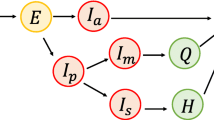
a The mean reproduction rate r(t) (black curve) of a patient on day t since infection is expressed as a convolution of the symptom onset time distribution pO(t) (red curve) and the infectiousness curve REpI(Δt) (blue curve), where Δt is measured from the symptom onset. The mean reproduction number RE sets the overall level of the epidemic. The peak of the normalised infectiousness function pI(Δt) is shifted from the symptom onset by an amount θP, which takes a positive value on the pre-symptomatic side. The peak of the mean reproduction rate r(t) is shifted from the peak of the symptom onset time distribution pO(t) by θS. b A compartmentalised model. A person infected first goes through a non-infectious latent phase (L) until tL, followed by an infectious period that spans across symptom onset at tO. In the pre-symptomatic phase A, the person is infectious without symptoms. The A phase is further split into two subphases, A1 with a constant transmission rate (orange region) and A2 with a declining transmission rate (blue region). At the symptom onset time tO, the person enters the S phase, and continues to be infectious (light blue region). Contact tracing brings an infected person out of the transmission cycle at the point of isolation, while testing does so only when the result is positive.
The mean reproduction number RE sets the overall level of disease transmission in the population, and equals the basic reproduction number R0 when the infectious disease first breaks into a community. Its actual value could change over time due to factors such as the intervention and containment measures considered below. The shift parameter θS (Fig. 1a, right panel) accommodates the actual shape of the infectiousness curve as well as effects resulting from intervention measures, e.g., isolation delays of infected cases.
To link up Eq. (1) with actual transmission data, we developed a compartmentalised epidemic spreading model as illustrated in Fig. 1b. A total of four phases are introduced to accommodate the infectiousness curve in Fig. 1a, left panel. Three of these phases reside in the pre-symptomatic period: a non-infectious latent phase L, followed by infectious phases A1 and A2 before and after the infectiousness peak. Starting from the day of infection, an individual first stays in the latent phase L. Transition to phase A1 takes place at a rate αL(t) that depends on the elapsed time t since infection. Once in phase A1, the individual is infectious with a daily transmission rate βA. Duration of the A1 phase is variable and follows Poisson statistics with an exit rate constant αA. On the other hand, duration of the succeeding phase A2 is fixed at θP, after which symptoms develop and the person enters the symptomatic phase S. Upon entering A2, the patient’s disease transmission rate βB(τ) weakens with the elapsed time τ = t−tO + θP to match the right-wing of the infectiousness curve. Note that, due to the variable duration of A1, the population-averaged infectiousness of this phase rises towards the symptom onset.
Applying the above rules of disease transmission to a large and well-mixed population, the number of new infections per unit time JL(T) on day T satisfies the renewal equation
where the kernel function is given by
with \(q_{\mathrm{L}}\left( t \right) = {\mathrm{e}}^{ - {\int}_0^t {\alpha _{\mathrm{L}}\left( {t_1} \right){\mathrm{d}}t_1} }\) being the probability that an individual remains in the latent phase t days after infection. Derivation of these results are presented in Supplementary Section 1, together with dynamic equations governing the size of each subgroup.
Equations (2) and (3) can be solved by performing the Laplace transform. In this respect our model is equally tractable mathematically as the susceptible-exposed-infectious-recovered (SEIR) type models defined by a set of rate equations19. As we show below, the explicit representation of the temporal structure for disease progression and transmission in the present case facilitates direct model calibration from clinical data and also quantitative evaluation of intervention measures against epidemic development.
In Supplementary Section 1.3, we show that the mean reproduction number of the model is given by \(R_{\mathrm{E}} = R_{\mathrm{E}}^{\mathrm{A}} + R_{\mathrm{E}}^{\mathrm{S}}\), with \(R_{\mathrm{E}}^{\mathrm{A}} = \beta _{\mathrm{A}}/\alpha _{\mathrm{A}} + {\int}_0^{\theta _{\mathrm{P}}} {\beta _{\mathrm{B}}\left( \tau \right){\mathrm{d}}\tau }\) and \(R_{\mathrm{E}}^{\mathrm{S}} = {\int}_{\theta _{\mathrm{P}}}^\infty {\beta _{\mathrm{B}}\left( \tau \right){\mathrm{d}}\tau }\) being reproduction numbers associated with pre-symptomatic and symptomatic transmissions, respectively. When the right wing of the infectiousness curve in Fig. 1a takes the form of an exponentially decaying function \(\beta _{\mathrm{B}}\left( \tau \right) = \beta _{\mathrm{A}}{\mathrm{e}}^{ - \alpha _{\mathrm{B}}\tau }\) with a sufficiently large decay rate αB, we recover Eq. (1) which was initially proposed on heuristic grounds. The shift parameter is given approximately by
Parameter calibration
By combining three data sets7. Result of the MLE is given by two exponential functions meeting at −0.68 days (red solid line). Also shown are distributions with a constant bridge (dash line), or with a dome cap (dash-dotted line), with slightly lower likelihood values (see Supplementary Section 2.2). Thin grey curves are from bootstrap** for model #1 (see the “Methods” section). c Serial interval statistics outside the Hubei province in China from January 9 to February 13, 202022,23: whole period (solid circles), first two weeks (open squares), and last two weeks (open triangles). The grey dashed line on the right indicates exponential decay at a rate −0.31/day. The red curve is the convolution of the two red curves shown in a and b.
Alternatively, viewing the data as samples of a common underlying probability distribution, we estimated pO(t) by likelihood maximisation (see the “Methods” section and Supplementary Section 2.1). Within the class of functions considered, the log-normal distribution combined with an exponential tail yields the largest likelihood value (Fig. 2a, red line). From day 6 onward, pO(t) follows an exponential decay with a rate of −0.31/day, with a 95% confidence interval (CI) of (−0.35, −0.27) per day. We have also examined other values (from day 4 to day 8) for the switch. In all cases, exponential tail decay rates are found to be round −0.31/day (see Supplementary Section 2.1).
A data set of 77 pairwise transmissions in several eastern and southeastern Asian countries and regions during their initial COVID-19 outbreak was compiled by He et al. 7 We took 66 pairs with unique symptom onset of the primary case to estimate the transmission probability pI(∆t), with ∆t measured from the symptom onset of the primary case. The results are shown in Fig. 2b (see the “Methods” section and Supplementary Section 2.2 for details). Under a maximum-likelihood estimation scheme, we considered three alternative forms for pI(∆t). All have exponential tails far away from the transmission peak, but differ in the way the two wings are joined together in the peak region. In the first case, the two exponential tails join directly to produce a cusp in the middle. In the second case, a flat top of variable width is introduced. In the third case, the flat top is replaced by a parabolic cap to give a more rounded peak. It turns out that the cusp function, with its peak located at 0.68 days before the symptom onset, is the most probable for this data set (Fig. 2b). Decay rates for the left and right wings are given by 0.46/day and 0.54/day, respectively (see Supplementary Section 2.2.2).
Duration of the A1 phase follows a Poisson process and is hence exponentially distributed. This gives rise to an exponential tail of the population-averaged infectiousness curve prior to entering the A2 phase. We therefore set the model parameters to αA = 0.46/day, θP = 0.68 days, and \(\beta _{\mathrm{B}}\left( \tau \right) = \beta _{\mathrm{A}}{\mathrm{e}}^{ - \alpha _{\mathrm{B}}\tau }\) with αB = 0.54/day. These values were used in our numerical calculations, with the corresponding CIs given in Table 1.
Serial interval
Xu et al. 22 compiled a database of 1407 COVID-19 transmission pairs outside the Hubei province in China between early January till mid-February 2020. Among them, 677 pairs have the symptom onset dates and social relationships of infector–infectees. A detailed analysis of the data set, stratified before, during and one week after the Wuhan lockdown on 23 January 2020, was carried out by Ali et al. 23 which showed reduction of the serial interval of symptom onsets by a factor of 3 over the 5 weeks. In Fig. 2c, we show the distribution of the serial interval data for the whole period (solid circles) and separately for the first (open squares) and last two weeks (open triangles) of the period. The red line gives the predicted serial interval distribution
using our estimated values for pO(t) and pI(∆t) (see Supplementary Section 2). While the overall agreement with the unstratified data is good especially on the positive side, it is also evident that serial intervals can be affected by travel and prevention measures, such as the percentage of imported cases among the infectors, the typical length of isolation delays, etc., which changed substantially before and after the Wuhan lockdown. Such temporal effect on the serial interval can be simulated simply with a shape function that masks pI(∆t). For example, imported index cases who spent part of their infectious period outside the region shift pSI(tSI) to the right. On the other hand, vigorous contact tracing shortens isolation delays significantly, which in turn shifts pSI(tSI) to the left.
The long-time tail of both pO(t) and pSI(tSI) decays slower than the rates αA and αB associated with the infectiousness curve. We have computed the tail of the probability qL(t) to remain in the latent phase, whose decay rate matches that of pO(t) (see Supplementary Section 2.4). According to Eq. (1), the long-time tail of the mean reproduction rate r(t) can also be attributed to infected cases who have a long incubation period in their disease progression.
Mean reproduction number
Under Eq. (1), the well-known Lotka–Euler estimating equation24 yields
where \({\tilde {p}}_{\mathrm{O}}\left( \lambda \right) = {\int}_0^\infty {p_{\mathrm{O}}\left( t \right){\mathrm{e}}^{ - \lambda t}{\mathrm{d}}t}\) is the Laplace transform of pO(t) (see Supplementary Sections 1.3 and 3.1). Using the estimated values above, we obtain from Eq. (6) the RE versus λ curve shown in Fig. 3a, which covers both the growth (λ > 0) and declining (λ < 0) phases of the epidemic. The slope of the curve at RE = 1 is given by 1/τg, where τg is the mean generation time and equals τO−θS = 6.19 days under Eq. (6). The intercept of the curve at RE = 0 gives an ultimate epidemic decay rate of −0.31/day when disease transmission comes to a complete halt.
a The relationship between the epidemic growth rate λ and the mean reproduction number RE. The grey lines, generated using the data shown in Fig. 2 with bootstrap**, give the range of uncertainty in the estimated function. At λ = 0.3/day, RE = R0 = 3.87. CI stands for confidence interval. b Probabilities for an infected individual being in each of the four phases on day t after infection. The thick red line indicates the boundary between the pre-symptomatic and symptomatic phases. c Percentage of the infected population in each of the phases when the epidemic is growing at a rate λ. The thick red curve indicates the boundary between the pre-symptomatic and symptomatic population.
To estimate the uncertainty in the computed RE−λ curve, we performed bootstrap analysis of the data used to obtain pO(t) and pI(∆t). The detailed procedure is described in Supplementary Section 2, with the result shown in Fig. 3a. At a growth rate of λ = 0.3/day, our estimated value for the basic reproduction number R0 is 3.87 (95% CI [3.38, 4.48]).
Composition of the infected population
As we demonstrate in the Supplementary Information, the convolutional form of our main Eq. (2) enables many analytic results to be derived and evaluated with the calibrated parameters. Figure 3b shows the probabilities that a given individual is in one of the four phases on day t after infection, computed using the formula in Supplementary Table 1. The red line marks the boundary between the pre-symptomatic and symptomatic phases. The width of the orange-coloured region (A1 phase), on the other hand, is proportional to \(\alpha _{\mathrm{A}}^{ - 1} \approx\) 2 days.
Figure 3c, obtained from the Laplace transforms of these curves, gives the percentage of the infected population in each of the four phases on a given day when the epidemic is growing at a rate λ. These curves allow for estimation of the hidden population in L, A1 and A2 phases from the knowledge of S in real-time. They form the basis for quantitative assessment of intervention measures discussed below. Note that at high growth rates, a larger percentage of the infected population is in the latent and pre-symptomatic phases, so that suppressing transmission by this group through, say mask wearing and social distancing, assumes a greater priority.
Testing and contact tracing
To break the transmission chain in the community, governments around the world have adopted two measures with varying levels of intensity: (1) testing and isolating infected individuals and (2) tracing and quarantining contacts of infected individuals.
For testing control, persons who were in close proximity to a confirmed infection case are asked to undergo voluntary or mandatory testing for infection, and quarantined when the result is positive. From Fig. 3b we see that, if the test is conducted shortly after infection, the individual has a high probability to still be in the latent phase, hence the test result is likely to be negative. On the other hand, if the test is conducted too late, the person may have already infected others so that the reduction of r(t) given by Eq. (1) is small. Therefore, there is an optimal window between the infection date and the test date, which we analyse in Supplementary Section 4.1.2. In Fig. 4a, we show the reduction of the basic reproduction number R0 as a function of the reporting delay, assuming all suspected contacts are tested. At R0 = 3.87, if the results become available immediately after testing, the reduction of R0 is shown as the blue curve, better than the testing outcomes with one day delay (red curve). The largest reduction is obtained when the test is performed 3 days after the contact. This corresponds to the day when the width of the orange plus dark blue region in Fig. 3b is the widest.
a Testing. Results are given for testing with 0 or 1 day reporting delay (blue and red curves), respectively. CI confidence interval. b Contact tracing and isolation. Results are shown for 100% (blue) and 80% (red) success rates, respectively. The 95% CIs of the estimated quantities in a and b (shaded areas) were obtained through bootstrap resampling with 1000 replications symptom onset times of 347 cases27,28,29,30 the aggregate impact of mask wearing at the population level is not yet clearly quantified. Given the now established risk of pre-symptomatic transmission, and the dominant role of droplet-mediated COVID-19 infections31, masks with relatively low efficacy for personal protection may nevertheless reduce the overall infections in a population32. Based on a previous study on influenza aerosols33, we constructed a semi-quantitative model to show that mask-wearing reduces r(t) and hence RE by a factor (1−e ⋅ pm)2, where e is the efficacy of trap** viral particles inside the mask, and pm is the percentage of the mask-wearing population (see Supplementary Section 4.2). According to this model, even for masks with intermediate efficacy (e = 50%), population-wide mask-wearing at pm = 98% alone could bring down RE from its basic value R0 = 3.87 to 1, assuming no social segregation of mask-wearing and non-mask-wearing groups.
When combined with contact tracing (Fig. 4c), the two effects multiply. Figure 4c shows a heatmap of the reduced RE when contact tracing and isolation is completed within 5 days of infection. The solid black line indicates that the reduced RE reaches 1. For example, the combination of tracing of close contacts at 60% efficiency within 5 days and 60% of the general public wearing masks achieves the same purpose. This target line can be reached with lower percentages when close contacts can be found within 2 days of possible infection (dash-dotted line), but the numbers need to be higher when the time frame is relaxed to 8 days (dashed line).
Provincial outbreaks and containment in China
We examined the temporal progression of COVID-19 outbreaks in different parts of the world using the data available from the Johns Hopkins CSSE Repository34, with the aim to extract more universal aspects of the pandemic development in light of our model studies. In the case of China, we focused on the daily confirmed cases from various provinces since the Wuhan lockdown on January 23, 2020. Broadly speaking, the ascending and descending curves follow very similar exponential laws, while the time it took to achieve the crossover was affected by the overall extent of the epidemic as well as occurrences of smaller outbreaks. From the data, we define three phases of epidemic development.
Phase I is characterised by an exponential growth of the epidemic. In the first week after the Wuhan lockdown, nearly all provinces registered a growth rate of ~0.3/day (Fig. 5, region shaded in pink) in the newly confirmed cases. Reports indicate that most of the growth during this period was driven by imported cases from Hubei province, whose own growth continued at this rate for a longer period (Fig. 5a). The fraction of local infections during import-driven growth can be calculated and the result depends on the local value of RE through its mean reproduction rate Eq. (1) (see Supplementary Section 4.3).
Daily confirmed cases in Hubei and other provinces since the Wuhan lockdown on January 23, 2020. a Hubei province. The three phases of the epidemic development are shaded with different colours: exponential growth (red), crossover (yellow), and descent phase (green). Early exponential growth reached a rate λ at ~0.3/day (left dashed line). Growth slowed and entered the crossover phase in the middle of the second week, and reached the third phase nearly 4 weeks later. The final descent that began in the beginning of March is characterised by λ = −0.31/day (right dashed line). The incubation period distribution is shown in open circles (reported data of 347 casesFull size image
The surging pandemic triggered an emergency response by public health authorities and governments at all levels. Towards the end of March, countries that adopted stringent intervention measures have seen a significant reduction of the pandemic growth rate (Fig. 6b). The government of Italy imposed a national quarantine on March 9, 202040, after which growth in the number of newly confirmed cases slowed down34. On the other hand, South Korea implemented aggressive contact tracing and testing policies41,42, enabling the country to bring the outbreak to a much-reduced level at RE ≈ 1.0.
In Fig. 6d we show the estimated epidemic growth rate λ(T) against the cumulative number of confirmed cases N(T) in five representative countries. We computed the growth rate from the local slope of the ln N(T) against T curve, i.e., λ(T) = ln [N(T)/N(T−ΔT)]/ΔT, using a time window ΔT = 3 days. The interval between a few tens to a few thousands cumulative cases can be taken as the first phase of local outbreaks in these countries, where the estimated values of λ(T) remain approximately stable. Three of the five countries exhibited growth rates of ~0.3/day during this period, while Iran and Japan assumed values above 0.4/day and around 0.1/day, respectively. It is evident that epidemic preparedness and cultural aspects significantly affected COVID-19 spreading in the local population, before government intervention and containment measures took effect. A more complete discussion of growth rates during the exponential phase in different countries and regions can be found in Supplementary Section 5.
Discussions
We have succeeded in develo** a directly calibratable model for COVID-19 transmission by both pre-symptomatic and symptomatic viral carriers. This was made possible by focusing on transmission around the symptom onset, which is a prominent feature of the disease. Explicit mathematical expressions for the size of subpopulations in various phases of disease progression and the associated transmission risks are obtained. These results facilitate assessment of control measures, either to break the transmission chain or to reduce the overall level of social contacts in the community. For example, contact tracing, in combination with mask wearing in public places, can have a strong and immediate effect in bringing down epidemic growth. In reality, governments often take incremental steps in intervention measures to ease their impact on the economy and on people’s livelihood. The quantitative treatment of epidemic control carried out in this study can serve as a reference in the decision-making process.
On a technical level, the modelling framework presented here is intuitive and flexible, and allows easy association of clinical features with population level pandemic development. This can be a significant advantage when the need arises to adapt the epidemic model to specific social environments and demographic composition. Our estimated incubation period distribution is in excellent agreement with other studies (see Table 1 for a comparison of key statistical features) and furthermore is not expected to change significantly over time. This places Eq. (1) as a convenient starting point for exploring temporal structures of epidemic development. The shift parameter θS in the equation embodies, in an explicit form, changing patterns of disease transmission from symptomatic to the pre-symptomatic viral carriers, and hence can serve as an important index for epidemic control.
With regard to the quantitative predictions under specific intervention measures, the main uncertainty comes from estimation of their efficacy in reducing transmission from the infectious subpopulations identified in this study. As a baseline study, we estimated the infectiousness function pI(∆t) based on a relatively small data set of 66 transmission pairs which led to a sizable CI at 95% for its wings. This could improve as more carefully curated transmission cases during the initial outbreak become available. Response of the public to specific intervention measures is a complex topic that deserves extensive research in the future.
Finally, as with other epidemic models that assume a well-mixed population, our current modelling framework does not treat epidemic spreading in a heterogeneous population that exhibits complex spatio-temporal dynamics, nor does it consider significant differences in disease progression and transmission in different age groups. Some of the basic questions in COVID-19 epidemiological studies, such as whether pre-symptomatic spread constitutes a major contributor to disease transmission43,44, cannot have definitive answers without considering these additional factors. In a large population, while individual outbreaks in specific communities may still follow the dynamics proposed here with suitable values of RE, transmission across communities requires a separate treatment.
Methods
Key variables and parameters
We collect key variables and parameters of the compartmentalised model together with the estimated values in Table 1 for easy reference.
Incubation period distribution
We analysed incubation periods of a total of N = 347 cases by combining three datasets11,20,21. For most cases, the infection date can only be assigned to a time window of more than one day. Therefore, the actual incubation period falls between IPli and IPui, i = 1, …, N, where IPli and IPui are the lower and upper bounds for case i. We perform maximum-likelihood estimation of the underlying symptom onset time distribution pO(t), following a scheme proposed by Reich et al. 47 Considering the exponential tail observed in the real data, we write
where A is the normalisation factor and θ denotes the set of parameters to be estimated. Transition to the exponential decay (with rate γ) takes place at te. Following common practice in the epidemiological literature, we take pleft(t) to be a truncated log-normal or Weibull distribution with two parameters in each case
Continuity of derivatives at te yields
Thus we are left with a set of three independent parameters. To estimate these parameters from the data, we consider the likelihood function
with
We performed optimisation and sensitivity analyses by scanning te values from 4 to 8, and infinity for log-normal distribution and from 3 to 7, and infinity for Weibull distribution. The best estimate is obtained when pleft(t) is a truncated log-normal distribution with te = 6 (see Supplementary Sec. 2.1 for details).
We also performed bootstrap analysis to determine uncertainties in the estimated pO(t). This is done by generating 1000 re-sampled copies of the original dataset with 347 cases. The maximum-likelihood estimation of pO(t) is then performed for each of the re-sampled copies. The 95% CIs were obtained from the 1000 replications (see Table 1).
Infectiousness profile
Disease transmission is quantified by the infectiousness function pI(t), the probability density function for pairwise transmission at time t since the symptom onset of the infector. We infer pI(t) by maximum-likelihood estimation, using the infector–infectee pairs published by He et al. 7. In this dataset, the infectee exposure windows were documented in addition to the symptom onset dates of both infectors and infectees (77 pairs in total). Among them, 66 pairs have a unique symptom onset date (see Source Data), which are used here.
Given the general form and the limited temporal resolution of the dataset, we adopted simple exponentials for the two wings of the infectiousness function joined in the middle by a cap function,
where A is the normalisation factor. The infectiousness function transits to the left exponential tail at θA and to the right exponential tail at θB. Between θA and θB, it takes the form of f(t). We consider three different forms of f(t):
-
Model 1: f(t) = 1 and θA = θB = θP (two exponential tails directly join at θP); Independent parameters θ = (αA,αB,θP).
-
Model 2: f(t) = 1 and θA < θB (two exponential tails with a flat cap of length ϵ = θB− θA, centred at tP); Independent parameters θ = (αA,αB,ϵ, θP).
-
Model 3: f(t) = [1−χ(t−θP)2] and θA < θB (two exponential tails with a rounded cap peaked at tθP, whose shape is characterised by χ); Independent parameters θ = (αA,αB,χ, θP) (θA and θB are determined by the smoothness condition).
We perform maximum-likelihood estimations using the dataset mentioned above, where each transmission pair i is associated with an exposure window Wi = [Wli,Wui] relative to the symptom onset of the infector. The likelihood function is constructed as follows:
where
Sensitivity analysis is performed at a set of values for ϵ (Model 2) and χ (Model 3), respectively. In both cases, the best estimate degenerates into Model 1 (see Supplementary Section 2.2 for details).
The uncertainty in the estimated pI(t) is determined through bootstrap** with 1000 replications, with which the 95% CIs were obtained (see Table 1).
Reporting summary
Further information on research design is available in the Nature Research Reporting Summary linked to this article.
Data availability
The COVID-19 pandemic and clinical data used in this work are all from published studies or datasets: confirmed case numbers in selected countries/regions (COVID-19 Data Repository by the Center for Systems Science and Engineering at Johns Hopkins University: https://github.com/CSSEGISandData/COVID-19), confirmed cases number for the Diamond Princess cruise ship13, incubation period (three datasets11,20,21), exposure window of transmission pair (one dataset7), and serial interval (one dataset22,23). These datasets are included in Source Data for easy reference, together with the parametrised distributions and the RE−λ relation from this work.
Code availability
MATLAB codes for the analyses presented are deposited at: https://github.com/hkbu-covid19group/Calib-covid1948.
References
World Health Organization. Coronavirus Disease 2019 (COVID-19) Situation Report-71 (World Health Organization, accessed 31 March 2020); https://www.who.int/docs/default-source/coronaviruse/situation-reports/20200331-sitrep-71-covid-19.pdf?sfvrsn=4360e92b_8.
Wu, F. et al. A new coronavirus associated with human respiratory disease in China. Nature 579, 265–269 (2020).
World Health Organization. Coronavirus disease (COVID-19) Weekly Epidemiological Update-15 December 2020 https://www.who.int/publications/m/item/weekly-epidemiological-update---15-december-2020.
World Health Organization. WHO Director-General’s opening remarks at the media briefing on COVID-19—11 March 2020 (World Health Organization, accessed 13 March 2020); https://www.who.int/dg/speeches/detail/who-director-general-s-opening-remarks-at-the-media-briefing-on-covid-19---11-march-2020.
Anderson, R. M. et al. How will country-based mitigation measures influence the course of the COVID- 19 epidemic? Lancet 395, 931–934 (2020).
Zou, L. et al. SARS-CoV-2 viral load in upper respiratory specimens of infected patients. New Engl. J. Med. 382, 1177–1179 (2020).
He, X. et al. Temporal dynamics in viral shedding and transmissibility of COVID-19. Nat. Med. 26, 672–675 (2020).
To, K. K. et al. Temporal profiles of viral load in posterior oropharyngeal saliva samples and serum antibody responses during infection by SARS-CoV-2: an observational cohort study. Lancet Infect. Dis. 3099, 1–10 (2020).
Du, Z. et al. Serial Interval of COVID-19 among publicly reported confirmed cases. Emerg. Infect. Dis. 26, 1341–1343 (2020).
Nishiura, H., Linton, N. M. & Akhmetzhanov, A. R. Serial interval of novel coronavirus (COVID-19) infections. Int. J. Infect. Dis. 93, 284–286 (2020).
**a, W. et al. Transmission of corona virus disease 2019 during the incubation period may lead to a quarantine loophole. Preprint at medRxiv https://doi.org/10.1101/2020.03.06.20031955 (2020).
Huang, R. et al. A family cluster of SARS-CoV-2 infection involving 11 patients in Nan**g, China. Lancet Infect. Dis. 20, 534–535 (2020).
Mizumoto, K. et al. Estimating the asymptomatic proportion of coronavirus disease 2019 (COVID-19) cases on board the Diamond Princess cruise ship, Yokohama, Japan, 2020. Eur. Surveill. 25, 2000180 (2020).
Dong, Y. et al. Epidemiological characteristics of 2143 pediatric patients with 2019 coronavirus disease in China. Pediatrics 145, e20200702 (2020).
Wang, H. et al. Phase-adjusted estimation of the number of coronavirus disease 2019 cases in Wuhan, China. Cell Discov. 6, 10 (2020).
Ferretti, L. et al. Quantifying SARS-CoV-2 transmission suggests epidemic control with digital con- tact tracing. Science 368, eabb6936 (2020).
Fraser, C. et al. Factors that make an infectious disease outbreak controllable. Proc. Natl Acad. Sci. USA 101, 6146–6151 (2004).
Grassly, N. C. & Fraser, C. Mathematical models of infectious disease transmission. Nat. Rev. Microbiol. 6, 477–487 (2008).
Becker, N. G. & Britton, T. Statistical studies of infectious disease incidence. J. R. Stat. Soc. Ser. B 61, 287–307 (1999).
Men, K. et al. Estimate the incubation period of coronavirus 2019 (COVID-19). Preprint at medRxiv https://doi.org/10.1101/2020.02.24.20027474 (2020).
Bi, Q. et al. Epidemiology and transmission of COVID-19 in Shenzhen China: analysis of 391 cases and 1,286 of their close contacts. Lancet Infect. Dis. 20, 911–919 (2020).
Xu, X.-K. et al. Reconstruction of transmission pairs for novel coronavirus disease 2019 (COVID- 19) in Mainland China: estimation of superspreading events, serial interval, and hazard of infection. Clin. Infect. Dis. ciaa790 (2020) https://doi.org/10.1093/cid/ciaa790
Ali, S. T. et al. Serial interval of SARS-CoV-2 was shortened over time by nonpharmaceutical interventions. Science 369, 1106–1109 (2020).
Wallinga, J. & Lipsitch, M. How generation intervals shape the relationship between growth rates and reproductive numbers. Proc. R. Soc. B 274, 599–604 (2007).
Howard, J. et al. An evidence review of face masks against COVID-19. PNAS 118, e2014564118 (2020).
Christopher, T. L. et al. Association of country-wide coronavirus mortality with demographics, testing, lockdowns, and public wearing of masks. Am. J. Trop. Med. Hyg. 103, 2400–2411 (2020).
Leung, N. H. L. et al. Respiratory virus shedding in exhaled breath and efficacy of face masks. Nat. Med. 26, 676–680 (2020).
Chan, J. F. -W. et al. Surgical mask partition reduces the risk of non-contact transmission in a golden Syrian hamster model for Coronavirus Disease 2019 (COVID-19). Clin. Infect. Dis. ciaa644 (2020) https://doi.org/10.1093/cid/ciaa644.
Jung, H. et al. Comparison of filtration efficiency and pressure drop in anti-yellow sand masks, quarantine masks, medical masks, general masks, and handkerchiefs. Aerosol Air Qual. Res. 14, 991–1002 (2014).
World Health Organization. Advice on the Use of Masks in the Context of COVID-19—Interim Guidance (World Health Organization, accessed 2 April 2020); https://www.who.int/publications/i/item/advice-on-the-use-of-masks-in-the-community-during-home-care-and-in-healthcare-settings-in-the-context-of-the-novel-coronavirus-(2019-ncov)-outbreak.
World Health Organization. Modes of transmission of virus causing COVID-19: implications for IPC precaution recommendations. (World Health Organization, accessed 2 April 2020); https://www.who.int/news-room/commentaries/detail/modes-of-transmission-of-virus-causing-covid-19-implications-for-ipc-precaution-recommendations.
ASTM F2101-19. Standard Test Method for Evaluating the Bacterial Filtration Efficiency (BFE) of Medical Face Mask Materials, Using a Biological Aerosol of Staphylococcus aureus (ASTM International, West Conshohocken, PA, 2019).
Milton, D. K. et al. Influenza virus aerosols in human exhaled breath: particle size, culturability, and effect of surgical masks. PLoS Pathog. 9, e1003205 (2013).
Dong, E., Du, H. & Gardner, L. An interactive web-based dashboard to track COVID-19 in real time. Lancet Infect. Dis. 3099, 19–20 (2020).
CNBC News. China says More than 500 Cases of the New Coronavirus Stemmed from Prisons. https://www.cnbc.com/2020/02/21/coronavirus-china-says-two-prisons-reported-nearly-250-cases.html (accessed 25 March 2020).
Chong, K. C. et al. Transmissibility of coronavirus disease 2019 (COVID-19) in Chinese cities with different transmission dynamics of imported cases. PeerJ 8, e10350 (2020).
Sina News. Wuhan Lockdown https://news.sina.com.cn/c/2020-02-15/doc-iimxxstf1526561.shtml (accessed 10 March 2020).
Chen, S. et al. Fangcang shelter hospitals: a novel concept for responding to public health emergencies. Lancet 395, 1305–1314 (2020).
Shim, E. et al. Transmission potential and severity of COVID-19 in South Korea. Int. J. Infect. Dis. 93, 339–344 (2020).
NY Post. Italy’s Coronavirus Lockdown Extended to Entire Country. https://nypost.com/2020/03/09/italys-coronavirus-lockdown-extended-to-entire-country (accessed 25 March 2020).
Guardian. South Korea took rapid, intrusive measures against Covid-19—and they worked https://www.theguardian.com/commentisfree/2020/mar/20/south-korea-rapid-intrusive-measures-covid-19 (accessed 20 March 2020).
Observers. Food, Water and Masks: South Korea’s COVID-19 Quarantine Kits https://observers.france24.com/en/20200305-south-korea-coronavirus-COVID-19-kits-masks (accessed 25 March 2020).
Slifka, M. K. & Gao, L. Is presymptomatic spread a major contributor to COVID-19 transmission? Nat. Med. 26, 1531–1533 (2020).
Lau, E. H. Y. & Leung, G. M. Reply to: is presymptomatic spread a major contributor to COVID-19 transmission? Nat. Med. 26, 1534–1535 (2020).
Backer, J. A., Klinkenberg, D. & Wallinga, J. Incubation period of 2019 novel coronavirus (2019-nCoV) infections among travellers from Wuhan, China, 20–28 January 2020. Eur. Surveill. 25, 2000062 (2020).
Lauer, S. A. et al. The incubation period of coronavirus disease 2019 (COVID-19) from publicly reported confirmed cases: estimation and application. Ann. Intern. Med. 172, 577–582 (2020).
Reich, N. G. et al. Estimating incubation period distributions with coarse data. Stat. Med. 28, 2769–2784 (2009).
Tian, L. et al. Calibrated Intervention and Containment of the COVID-19 Pandemic, Calib-covid19. https://doi.org/10.5281/zenodo.4431829 (2021).
Acknowledgements
The work is supported in part by the NSFC under Grant Nos. 11635002, 32000886, and U1930402, and by the Research Grants Council of the Hong Kong Special Administrative Region (HKSAR) under Grants HKBU 12324716 and 12304020. Any views expressed by Jiang Liu and Viola Tang are not as a representative speaking for or on behalf of his/her employer, nor do they represent his/her employer’s positions, strategies or opinions.
Author information
Authors and Affiliations
Contributions
L.-H.T., X.F.L. and J.L. formulated and analysed the mathematical model. L.T. performed MLE and other statistical analyses of the data. Z.L. constructed and analysed the facemask model. L.-H.T., L.T., X.F.L., V.T., Z.L., H.L., F.Q., and J.L. wrote the paper. L.-H.T. coordinated the project. All authors participated in the pandemic and clinical data collection and initial analysis, and the discussion of results.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information Nature Communications thanks Sheikh Taslim Ali, Tom Britton, Odo Diekmann and the other, anonymous, reviewer(s) for their contribution to the peer review of this work. Peer reviewer reports are available.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Tian, L., Li, X., Qi, F. et al. Harnessing peak transmission around symptom onset for non-pharmaceutical intervention and containment of the COVID-19 pandemic. Nat Commun 12, 1147 (2021). https://doi.org/10.1038/s41467-021-21385-z
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-021-21385-z
- Springer Nature Limited