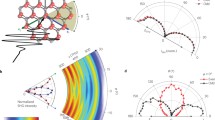
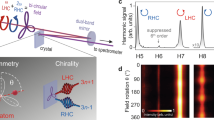
Abstract
Attosecond metrology sensitive to sub-optical-cycle electronic and structural dynamics is opening up new avenues for ultrafast spectroscopy of condensed matter. Using intense lightwaves to precisely control the fast carrier dynamics in crystals holds great promise for next-generation petahertz electronics and devices. The carrier dynamics can produce high-order harmonics of the driving field extending up into the extreme-ultraviolet region. Here, we introduce polarization-state-resolved high-harmonic spectroscopy of solids, which provides deeper insights into both electronic and structural sub-cycle dynamics. Performing high-harmonic generation measurements from silicon and quartz, we demonstrate that the polarization states of the harmonics are not only determined by crystal symmetries, but can be dynamically controlled, as a consequence of the intertwined interband and intraband electronic dynamics. We exploit this symmetry-dynamics duality to efficiently generate coherent circularly polarized harmonics from elliptically polarized pulses. Our experimental results are supported by ab-initio simulations, providing evidence for the microscopic origin of the phenomenon.
Similar content being viewed by others
Introduction
The study of lightwave-driven electronic dynamics occurring on sub-optical-cycle time scales in condensed matter and nanosystems is a fascinating frontier of attosecond science originally developed in atoms and molecules1. Adapting attosecond metrology techniques2 to observe and control the fastest electronic dynamics in the plethora of known solids and novel quantum materials3 is very promising for studying correlated electronic dynamics (e.g., excitonic effects, screening) on atomic length and time scales, thereby potentially impacting future technologies such as emerging petahertz electronic signal processing2,4 or strong-field optoelectronics5,6.
The nonlinear process of high-order harmonic generation (HHG) in gases is one of the cornerstones of attosecond science and is well understood by the semiclassical three-step model1. In solids, nonperturbative HHG up to 25th harmonic order without irreversible damage was first reported in ref. 7. This work triggered extensive research activities aimed at unraveling the microscopic interband and intraband dynamics underlying HHG from crystals (for a comprehensive overview, see ref. 8), thereby extending attoscience techniques to solids. The prevailing strong-field dynamics were successfully identified in specific cases, even if a global picture has not yet emerged. Other works demonstrated isolated attosecond extreme ultraviolet (XUV) pulses emitted from thin SiO2 films9, or investigated HHG from two-dimensional (2D) materials such as graphene10, 2D transition-metal dichalcogenides10,11, and monolayer hexagonal boron nitride12.
Elucidating the complex microscopic electronic dynamics producing HHG without making a priori severe assumptions poses a challenge for theory. Indeed, the theory must capture at the same time the transitions between discrete electronic bands, and the ultrafast motion of electrons within the bands; two mechanisms usually decoupled in the description of either optical properties or transport in semiconductors and insulators. An effective way to account for the full interacting many-body electronic dynamics and real crystal structure is using ab-initio time-dependent density functional theory (TDDFT) simulations13,14,15. Some of us recently used this theoretical framework to reveal how the microscopic mechanisms governing HHG in solids depend on the ellipticity of the driving field and the underlying band structure15. That work predicted that different harmonics react differently to the driver ellipticity, as they can either originate mainly from intraband contributions or from coupled interband and intraband dynamics14.
The symmetry properties of the light-matter interaction Hamiltonian distinguishes HHG in crystals from atoms and molecules, with major ramifications for the selection rules of different harmonics and their polarization states. HHG from atoms driven by propeller-shaped bichromatic waveforms produces circular harmonics16 (for convenience, we often use the terminology linear/circular/elliptical instead of linearly/circularly/elliptically polarized to refer to the polarization state). In molecules, both the point group and the driving field determine the symmetries of the coupled light-matter system. Consequently, depending on the molecular symmetries and the molecule’s orientation with respect to the light polarization direction, elliptical high-order harmonics can be produced by linear17 or elliptical driver pulses18. For bichromatic bicircular driver fields, circular harmonics with alternating helicities can be obtained, provided that the molecule’s symmetries are compatible with that of the driving field19. In crystals, several recent works studied the high-harmonic response on driver pulse ellipticity ε, which can strongly differ qualitatively from the atomic and molecular cases. Whereas earlier work20 looked exclusively at the harmonic yield, later research also investigated the polarization states and selection rules of the higher harmonics from various solids of different crystal symmetries15,2). The pulses are focused onto the sample with a 25-cm CaF2 lens, resulting in a 1/e2 focus diameter of 2w0 = 95 μm. After 50 cm of propagation, an iris is used to spatially suppress the otherwise very strong third harmonic. A curved UV-enhanced Al mirror is used to direct the output light to an Ocean Optics UV-VIS HR4000 spectrometer with a slit width of 10 μm. To determine the ellipticities and major axes of the generated harmonics, a Rochon polarizer is placed between sample and iris and rotated in total by 360°, measuring a spectrum every 18°. To detect the helicity of the circular harmonics, a tunable zero-order QWP (from Alphalas) is placed between sample and polarizer. For post-processing the polarizer scans, the harmonic intensities are fitted with a sin-square curve offset from zero, the ellipticity calculated as \(|\varepsilon _{{\mathrm{HH}}}| = \sqrt {I_{{\mathrm{min}}}/I_{{\mathrm{max}}}}\) and the major-axis rotation as ϕHH = arctan(Iy/Ix). The driving-intensity scan in Supplementary Figure 3 is performed employing reflective neutral-density filters.
Ab-initio TDDFT simulations of high-harmonic generation in solids
Within the framework of TDDFT, the evolution of the wavefunctions and the evaluation of the time-dependent current are computed by propagating the Kohn–Sham equations
where ψn,k is a Bloch state, n a band index, k a point in the first Brillouin zone (BZ), and HKS is the Kohn–Sham Hamiltonian given by
The different terms correspond to the kinetic energy, the ionic potential, the Hartree potential, that describes the classical electron–electron interaction, and exchange-correlation potential, which contains all the correlations and nontrivial interactions between the electrons. The latter needs to be approximated in practice34.
We perform the calculations using the Octopus code35, employing the TB0936 meta generalized gradient approximation (MGGA) functional to approximate the exchange-correlation potential using the adiabatic approximation. To ensure the stability of our time-propagation, we solved the time-dependent Kohn–Sham equations self-consistently at every time step using the enforced time-reversal symmetry propagator37. The c-value entering in the TB09 functional is recomputed at each time step using the gauge-invariant kinetic energy density. We employ norm-conserving pseudo-potentials. We emphasize that within TB09 MGGA, the experimental bandgap of common semiconductors and insulators is well reproduced38, which is an important improvement over the local-density approximation (LDA) used in refs. 14,15, permitting direct comparison between experiment and theory. As shown in ref. 14 for adiabatic LDA (ALDA), local-field effects and dynamical correlations (at the level of the ALDA functional) do not seem to affect the HHG spectra of Si. The excitonic effects in Si mainly come from the long-range part of the exchange-correlation potential39, i.e., a renormalization of the Hartree term (which does not play any role in HHG from Si14); therefore, excitonic effects are not expected to modify the HHG spectra of materials such as Si. We note that this is not necessarily true for all materials, in particular materials with strongly localized excitons, for which bound states will form in the bandgap, or in strongly correlated materials23,24.
All calculations for bulk Si are performed using the primitive cell of bulk Si, using a real-space spacing of 0.484 atomic units, corresponding to 15 points along each primitive axis. We consider a laser pulse of 50-fs FWHM duration with a sin-square envelope and a carrier wavelength λ of 2.08 μm, corresponding to 0.60 eV carrier photon energy. We employ an optimized 36 × 36 × 36 grid shifted four times to sample the BZ, and we use the intensity corresponding to the experimental intensity, using the value for the optical index n of ~3.4 for computing the intensity in matter. The four shifts of the k-point grid are (in reduced coordinates) (0.5, 0.5, 0.5), (0.5, 0.0, 0.0), (0.0, 0.5, 0.0), (0.0, 0.0, 0.5). We use the experimental lattice constant a leading to a MGGA bandgap (direct) of silicon of 3.09 eV. In all our calculations, we assume a CEP of ϕ = 0.
We compute the total electronic current j(r, t) from the time-evolved wavefunctions, the HHG spectrum is then directly given by
where FT denotes the Fourier transform.
Supplementary Figure 5 shows a comparison of a computed HHG spectrum to a corresponding experimental spectrum. Note that, as mentioned above, in our experiments we only detect harmonics up to HH9 due to the spectrometer used (Ocean Optics UV-VIS HR4000). Our TDDFT calculations predict that harmonics up to HH19 in the XUV spectral region are generated for our experimental conditions.
Code availability
The OCTOPUS code is available from http://www.octopus-code.org.
Data availability
The data that support the findings of this study are available from the corresponding authors upon reasonable request, and will be deposited on the NoMaD repository (https://doi.org/10.17172/NOMAD/2019.03.04-1).
References
Krausz, F. & Ivanov, M. Attosecond physics. Rev. Mod. Phys. 81, 163–234 (2009).
Krausz, F. & Stockman, M. I. Attosecond metrology: from electron capture to future signal processing. Nat. Phot. 8, 205–213 (2014).
Basov, D. N., Averitt, R. D. & Hsieh, D. Towards properties on demand in quantum materials. Nat. Mater. 16, 1077–1088 (2017).
Mashiko, H., Oguri, K., Yamaguchi, T., Suda, A. & Gotoh, H. Petahertz optical drive with wide-bandgap semiconductor. Nat. Phys. 12, 741–745 (2016).
Schiffrin, A. et al. Optical-field-induced current in dielectrics. Nature 493, 70–74 (2013).
Sivis, M. et al. Tailored semiconductors for high-harmonic optoelectronics. Science 357, 303–306 (2017).
Ghimire, S. et al. Observation of high-order harmonic generation in a bulk crystal. Nat. Phys. 7, 138–141 (2011).
Huttner, U., Kira, M. & Koch, S. W. Ultrahigh off-resonant field effects in semiconductors. Laser Photonics Rev. 11, 1700049 (2017).
Garg, M. et al. Multi-petahertz electronic metrology. Nature 538, 359–363 (2016).
Yoshikawa, N., Tamaya, T. & Tanaka, K. High-harmonic generation in graphene enhanced by elliptically polarized light excitation. Science 356, 736–738 (2017).
Liu, H. et al. High-harmonic generation from an atomically thin semiconductor. Nat. Phys. 13, 262–265 (2017).
Tancogne-Dejean, N. & Rubio, A. Atomic-like high-harmonic generation from two-dimensional materials. Sci. Adv. 4, eaao5207 (2018).
Otobe, T. First-principle description for the high-harmonic generation in a diamond by intense short laser pulse. J. Appl. Phys. 111, 093112 (2012).
Tancogne-Dejean, N., Mücke, O. D., Kärtner, F. X. & Rubio, A. Impact of the electronic band structure in high-harmonic generation spectra of solids. Phys. Rev. Lett. 118, 087403 (2017).
Tancogne-Dejean, N., Mücke, O. D., Kärtner, F. X. & Rubio, A. Ellipticity dependence of high-harmonic generation in solids originating from coupled intraband and interband dynamics. Nat. Commun. 8, 745 (2017).
Kfir, O. et al. Generation of bright phase-matched circularly-polarized extreme ultraviolet high harmonics. Nat. Phot. 9, 99–105 (2015).
Mairesse, Y. et al. High harmonic spectroscopy of multichannel dynamics in strong-field ionization. Phys. Rev. Lett. 104, 213601 (2010).
Cireasa, R. et al. Probing molecular chirality on a sub-femtosecond timescale. Nat. Phys. 11, 654–658 (2015).
Bandrauk, A. D., Mauger, F. & Yuan, K.-J. Circularly polarized harmonic generation by intense bicircular laser pulses: electron recollision dynamics and frequency dependent helicity. J. Phys. B 49, 23LT01 (2016).
You, Y. S., Reis, D. A. & Ghimire, S. Anisotropic high-harmonic generation in bulk crystals. Nat. Phys. 13, 345–349 (2017).
Klemke, N. et al. Circularly polarized high-order harmonics from solids driven by single-color infrared pulses. Talk presented at ATTO 2017, **’an, China, July 2–7 (2017).
Saito, N. et al. Observation of selection rules for circularly polarized fields in high-harmonic generation from a crystalline solid. Optica 4, 1333–1336 (2017).
Tancogne-Dejean, N., Sentef, M. A. & Rubio, A. Ultrafast modification of Hubbard U in a strongly correlated material: ab initio high-harmonic generation in NiO. Phys. Rev. Lett. 121, 097402 (2018).
Silva, R. E. F., Blinov, I. V., Rubtsov, A. N., Smirnova, O. & Ivanov, M. High-harmonic spectroscopy of ultrafast many-body dynamics in strongly correlated systems. Nat. Phot. 12, 266–270 (2018).
Silva, R. E. F., Jiménez-Galán, Á., Amorim, B., Smirnova, O. & Ivanov, M. Topological strong field physics on sub-laser cycle time scale. Preprint at https://arxiv.org/abs/1806.11232v2 [physics.optics] (2018).
Zhang, G. P., Si, M. S., Murakami, M., Bai, Y. H. & George, T. F. Generating high-order optical and spin harmonics from ferromagnetic monolayers. Nat. Commun. 9, 3031 (2018).
Corkum, P. B., Burnett, N. H. & Ivanov, M. Y. Subfemtosecond pulses. Opt. Lett. 19, 1870–1872 (1994).
Tang, C. L. & Rabin, H. Selection rules for circularly polarized waves in nonlinear optics. Phys. Rev. B 3, 4025–4034 (1971).
Barreau, L. et al. Evidence of depolarization and ellipticity of high harmonics driven by ultrashort bichromatic circularly polarized fields. Nat. Commun. 9, 4727 (2018).
Veyrinas, K. et al. Molecular frame photoemission by a comb of elliptical high-order harmonics: a sensitive probe of both photodynamics and harmonic complete polarization state. Faraday Discuss. 194, 161–183 (2016).
Cerullo, G., Baltuška, A., Mücke, O. D. & Vozzi, C. Few-optical-cycle light pulses with passive carrier-envelope phase stabilization. Laser Photonics Rev. 5, 323–351 (2011).
Rossi, G. M. et al. CEP dependence of signal and idler upon pump-seed synchronization in optical parametric amplifiers. Opt. Lett. 43, 178–181 (2018).
Mücke, O. D. et al. Toward waveform nonlinear optics using multimillijoule sub-cycle waveform synthesizers. IEEE J. Sel. Top. Quantum Electron. 21, 8700712 (2015).
Marques, M. A. L., Maitra, N. T., Nogueira, F. M. S., Gross, E. K. U. & Rubio, A. (eds). Fundamentals of Time-Dependent Functional Theory (Springer, Berlin, 2012).
Andrade, X. et al. Real-space grids and the Octopus code as tools for the development of new simulation approaches for electronic systems. Phys. Chem. Chem. Phys. 17, 31371–31396 (2015).
Tran, F. & Blaha, P. Accurate band gaps of semiconductors and insulators with a semilocal exchange-correlation potential. Phys. Rev. Lett. 102, 226401 (2009).
Castro, A., Marques, M. A. L. & Rubio, A. Propagators for the time-dependent Kohn-Sham equations. J. Chem. Phys. 121, 3425–3433 (2004).
Waroquiers, D. et al. Band widths and gaps from the Tran-Blaha functional: Comparison with many-body perturbation theory. Phys. Rev. B 87, 075121 (2013).
Botti, S. et al. Long-range contribution to the exchange-correlation kernel of time-dependent density functional theory. Phys. Rev. B 69, 155112 (2004).
Acknowledgements
We acknowledge support by the cluster of excellence “Advanced Imaging of Matter” (EXC 2056—project ID 390715994) and the priority program QUTIF (SPP1840 SOLSTICE) of the Deutsche Forschungsgemeinschaft, as well as financial support from the European Research Council (ERC-2015-AdG-694097), Grupos Consolidados (IT578-13), and European Union’s H2020 program under GA no. 676580 (NOMAD). N.T.-D., A.R., and O.D.M. thank M. Altarelli for very fruitful discussion. We thank M. Spiwek for help with the Laue X-ray diffraction characterization of samples.
Author information
Authors and Affiliations
Contributions
N.T.-D., A.R., F.X.K., and O.D.M. conceived, designed, and coordinated the project. G.M.R. and R.E.M. implemented the IR-OPA driver source. N.K., Y.Y., G.D.S., and O.D.M. conceived the setup and performed the HHG experiments. F.S. and N.K. performed the 2DSI characterization. N.T.-D. carried out the code implementation and numerical calculations. N.K., N.T.-D., and O.D.M. analyzed and interpreted the experimental and theoretical results. N.K., N.T.-D., A.R., F.X.K., and O.D.M. participated in the discussion of the results and contributed to the manuscript with revisions by all.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Journal peer review information: Nature Communications thanks Yasushi Shinohara and the other anonymous reviewer(s) for their contribution to the peer review of this work. Peer reviewer reports are available
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Klemke, N., Tancogne-Dejean, N., Rossi, G.M. et al. Polarization-state-resolved high-harmonic spectroscopy of solids. Nat Commun 10, 1319 (2019). https://doi.org/10.1038/s41467-019-09328-1
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-019-09328-1
- Springer Nature Limited