Introduction

In the optical regime, a light wave’s spatial wavelength λ = 2πc/ωn is at the micro- or nanoscale, resulting in rapid variations in spatial phase over the medium in which light propagates. These variations limit the performance of many optical devices. For example, in guided-wave optics, fibers and waveguides are usually much longer than the spatial wavelength and so they are limited to smooth curvilinear lines without sharp bending, restricting their integration in photonic integrated circuits. In nonlinear optics, the short spatial wavelength makes it challenging to achieve a desired phase relationship between the interacting waves over a long interaction distance, necessitating the use of various phase-matching techniques that restrict the configuration of nonlinear optical elements. In quantum optics, collective emission phenomena require that the linear size of an assembly of atoms or ions be smaller than the emission wavelength, limiting the number of atoms/ions in the assembly and the spatial extent of collective emission phenomena.

In a medium with a refractive index of zero n = 0, the effective wavelength becomes infinite, λ = 2πc/ωn → ∞, and the spatial phase distribution of a propagating wave becomes uniform over the entire medium1,2, overcoming many limitations imposed by the short spatial wavelength in the optical regime. In guided-wave optics, a zero-index waveguide can achieve high transmission regardless of shape, significantly improving the prospect of integration of integrated photonic circuits3,4,5,6. In nonlinear optics, as the spatial wavelength approaches infinity, phase mismatch–free nonlinear generation becomes possible7. In quantum optics, collective emission can be realized with an infinite spatial wavelength at the emission frequency with many atoms/ions in a highly extended sample8.

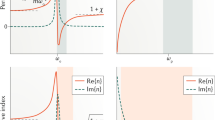
Because of causality, an index of zero of a passive medium can only be realized at a single frequency and so in this review, we will focus on the low refractive index near a zero crossing. According to the ultra-low-loss purely dielectric zero-index metamaterials, the bandwidth in which |neff| ≤ 0.1 can be as wide as ~5%9. Based on the definition of refractive index \(n = \sqrt {\varepsilon _{{{\mathrm{r}}}}\mu _{{{\mathrm{r}}}}}\), a near-zero index can be achieved in three ways: permittivity near zero (ENZ), permeability near-zero (MNZ), and permittivity and permeability near-zero (EMNZ)10,16,17,18,19,20, or in all-dielectric metamaterials supporting a Dirac-like cone dispersion at the center of the Brillouin zone (“Comparison of Dirac-like cone-based zero index....” section)21,22,23,24,25,26.

Dirac-like cone dispersion is formed by the accidental 3-fold degeneracy of two linear bands with conical dispersion and a quadratic dispersive band (which is flat near k = 0) at the center of the Brillouin zone. The group velocities of the two linear dispersive bands change sign at their crossing point. From an effective medium point of view, the change in sign of group velocity implies that the effective refractive index changes sign at the Dirac point, which in turn means that the effective refractive index is zero at the Dirac-point frequency. The zero effective refractive index implies the existence of a quasi-longitudinal solution to the Maxwell equation from a macroscopic point of view, and this is consistent with the existence of the flat band cutting through the Dirac point, giving rise to a 3-fold degeneracy. Using rigorous effective medium homogenization approaches, it can be shown that the metamaterial’s effective permittivity and permeability cross zero simultaneously and linearly at the Dirac-point frequency under certain conditions (“Relationship between a Dirac-cone dispersion at the...” section). The zero effective refractive index of such systems is of special interest as the “double zero” (both permittivity and permeability are zero) means that the impedance can be tuned to match that of the external medium.

Dirac cones typically refer to the conical dispersion of electronic states at the corner of Brillouin zone of materials such as graphene27. These electronic states manifest themselves as massless fermions with unique transport properties. Here, we discuss another type of Dirac cone—a Dirac-like cone dispersion at the Brillouin zone center of some photonic crystals. Different from Dirac cones of graphene, which are 2-fold degeneracies at the Dirac point, the Dirac-like cones at zone center are 3-fold degeneracies21. And, Dirac-like cones’ transport properties are distinctly different from those of massless fermions. The photonic states of the Dirac-like cone transport as they are traveling in a medium with a refractive index of zero. According to the slope of bands near Dirac point, Dirac cones can be categorized into type-I, II, and III, which show opposite signs of group velocities, identical signs of group velocities and zero group velocities, respectively, at the Dirac-point frequency28. Dirac-like cone corresponds to the type-I photonic Dirac cone with an additional flat band.

Time reversed symmetry mandates that isolated bands must have a dispersion that obey ∂ω/∂k = 0 at k = 0 and hence Dirac cones with linear dispersion cannot be realigned. However, if there are accidental degeneracies, a Dirac-like cone dispersion with linear dispersion is permitted in some high symmetry lattices. If an effective medium theory can be applied to those systems, the effective ε(ω) and μ(ω) pass through zero simultaneously at the Dirac-point frequency where impedance is determined by the ratio of ∂μeff/∂ω and ∂εeff/∂ω and can be tuned to match that of the input medium (“Relationship between a Dirac-cone dispersion at the...” section). The group velocity of the modes on the Dirac-like cone can likewise be tuned by changing the microstructure topology. In contrast, an ENZ or MNZ material has near-zero group velocity and extreme impedances when the material is lossless and spatially unbounded29. Such extreme impedances can be tuned to finite by engineering the height of a waveguide filled with ENZ or MNZ medium3,30.

In Dirac-like cone-based zero-index metamaterials (DCZIMs), the two curl equations of the Maxwell equations, which couple electric and magnetic phenomena, become zero \(\nabla \times \vec E = 0,\nabla \times \vec H = 0\), decoupling the average electric and magnetic fields over the metamaterial. EMNZ also leads to a zero wavevector \(\left| {\vec k} \right| = \omega n/c\mathop { \to }\limits^{n = 0} 0\), corresponding to a momentum with zero amplitude and undefined direction. The zero wavevector results in an infinite spatial wavelength \(\lambda = 2\pi /\left| {\vec k} \right|\mathop { \to }\limits^{\left| {\vec k} \right| = 0} \infty\) and a zero spatial phase \(\vec k \cdot \vec r\mathop { \to }\limits^{\left| {\vec k} \right| = 0} 0\), leading to a uniform spatial phase distribution throughout the metamaterial31. This phenomenon can be understood from the viewpoint of phase velocity: the wavefront is able to travel through the metamaterial instantaneously, indicating an infinite phase velocity \(v_{{{\mathrm{p}}}} = \omega /\left| {\vec k} \right|\mathop { \to }\limits^{\left| {\vec k} \right| = 0} \infty\). However, DCZIMs still show an energy velocity lower than the velocity of light in a vacuum, satisfying causality. To efficiently excite the zero-index modes of DCZIMs, the incident plane wave has to satisfy the normal incidence condition. Oblique incidence at certain angles excites the “flat band” of the Dirac-like cone (“Homogenization of DCZIMs” section), which does not correspond to zero-index behavior32,33. As summary, in a DCZIM excited by a normally incident plane wave, an electromagnetic wave propagates in all directions with an infinite phase velocity, whose corresponding electric and magnetic fields oscillate in unison throughout the metamaterial.

This review provides an overview of the significant progress in the fundamental physics, design, experimental implementations, and potential applications of photonic DCZIMs. We first explain the relationship between a Dirac-cone dispersion at the center of the Brillouin zone and EMNZ. We then analyze the homogenization of DCZIMs as bulk media with effective constitutive parameters. We note that the zero-index materials are realized using dielectric photonic crystals. As the conical dispersion is at k = 0 and the dispersion originates from lowest order resonances, effective medium theories can be rigorously applied to extract effective constitutive parameters34. In this sense, we can call the photonic crystal a metamaterial even though we are not considering the ω → 0 limit. Then, we compare the optical properties of DCZIMs with those of other mechanisms for achieving a near-zero refractive index. We review the design of DCZIMs for various zero-index properties. We then introduce several experimental realizations of DCZIMs in the form of either bulk metamaterials (out-of-plane configuration) or on-chip metamaterials (in-plane configuration). We summarize DCZIMs’ potential applications in electromagnetic waveguides, free-space wave manipulation, metrology, nonlinear optics, lasers, and quantum optics. We finally discuss the pros and cons of DCZIMs in comparison with other mechanisms for achieving zero index and envision DCZIMs’ future development in applications in optical interconnects, nonlinear optics, lasers, and quantum optics.

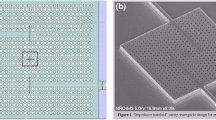
A good recent review provided a comprehensive summary of the fundamental physics of homogeneous zero-index materials, history of DCZIMs from the metallic EMNZ metamaterials to the all-dielectric EMNZ metamaterials, and challenges of DCZIMs35. In contrast, our review focuses on the fundamental physics of DCZIMs, comparison of DCZIM with zero-index materials based on volume plasmon, fishnet metamaterials and doped ENZ medium, classification of DCZIMs, demonstration of optical DCZIMs, and promising potential applications of DCZIMs. In addition to photonic metamaterials, the concept of DCZIMs has already been adopted by other kinds of metamaterials including acoustic36,

Comparison of Dirac-like cone-based zero index with spatially continuous zero index provided by volume plasmon, and zero indices achieved by fishnet metamaterial and photonic do**

To understand the underlying physics of the Dirac-like cone-induced zero index, we compare its optical properties with those of spatially continuous zero index provided by bulk metals—volume plasmons and macroscopic zero index achieved by fishnet metamaterials and by do** an ENZ medium with dielectric dopants.

When a uniform electric field is applied to a thin slab of metal at the plasma frequency ωp, all the electrons in the metal slab will show in-phase oscillation in the longitudinal direction (i.e., the wavevector direction). Such a collective longitudinal oscillation of free electrons is called a volume plasmon. It leads to the cancellation of the left two terms of the wave equation \(\mathop{k}\limits^{\rightharpoonup} \left( {\mathop{k}\limits^{\rightharpoonup} \cdot \mathop{E}\limits^{\rightharpoonup} } \right) - k^2\mathop{E}\limits^{\rightharpoonup} = - \varepsilon \omega ^2\mathop{E}\limits^{\rightharpoonup} /c^2\), resulting in a zero permittivity and hence a refractive index of zero. As a result, based on the constitutive relationship \(\mathop{D}\limits^{\rightharpoonup} = 0 = \varepsilon _0\mathop{E}\limits^{\rightharpoonup} + \mathop{P}\limits^{\rightharpoonup}\), polarization within the metal slab cancels out the applied electric field. The longitudinal nature of the volume plasmon prevents it from coupling to transverse electromagnetic waves, decoupling the time-harmonic electric and magnetic fields. This phenomenon can also be explained by zero permittivity. The zero permittivity and refractive index provided by the volume plasmon is continuous over a volume. Such a zero refractive index can also be observed in the dispersion diagram, in which the volume plasmon corresponds to a zero wavenumber at ωp.

Although the longitudinal nature of the volume plasmon prevents it from coupling to transverse waves and disables almost all the potential light-matter interactions within the bulk metal, the bulk metal can still show ENZ behavior around the ωp. At frequencies ω > ωp, the bulk metal has a positive refractive index and behaves like transparent dielectrics, enabling the propagation of transverse waves inside the metal. In this region, the metal’s dispersion curve is inside the radiation continuum above the light line, indicating a good coupling to free space via transverse waves. Although most metals’ ωp are in the ultraviolet regime, some other materials’ ωp are in various frequency regimes. For example, some doped semiconductors, such as indium tin oxide, have ωp in the telecom regime and their ωp can even be tuned by controlling the do** level68,69. These materials enable ENZ-based light-matter interactions in various frequency regimes.

Distinct from the longitudinal wave supported by volume plasmons, DCZIMs can support the propagation of TM and/or TE waves. Using TM-polarized DCZIMs as an example, the electric field of the TM-polarized wave oscillates between an electric monopole mode and a transverse magnetic dipole mode, corresponding to zero effective permittivity (εzz = 0) and permeability (μxx = μyy = 0), respectively. Such an EMNZ behavior is essentially different from the ENZ behavior of volume plasmons. From the viewpoint of the impedance matching, EMNZ induces a finite intrinsic impedance \(Z = \sqrt {\mu _{{{{\mathrm{eff}}}}}/\varepsilon _{{{{\mathrm{eff}}}}}}\) instead of the infinite impedance of ENZ. Consequently, EMNZ can be better impedance-matched with a regular medium, such as free space, optical fibers, and waveguides. From the viewpoint of losses, Dirac-like cone’s good coupling to free space brings large radiation losses, resulting in a short propagation length. A Dirac-like cone can provide a macroscopic refractive index of zero by averaging the electric and magnetic responses over the plane of the 2D photonic crystal. On the other hand, volume plasmons can provide a continuous zero refractive index over a bulk metal. The Dirac-like cone-based zero index can only replace the continuous zero refractive index for certain light-matter interactions, such as the normal incidence of transverse waves and the interactions of many dipoles which are randomly distributed throughout the zero-index medium.

EMNZ can be achieved by engineering a typical traditional metamaterial—metal-dielectric-metal fishnet structure15. Different from fishnet metamaterials, DCZIMs can be realized via purely dielectric structures, avoiding the ohmic losses. Fishnet structure can be simply fabricated in the out-of-plane configuration (light propagates perpendicular to the substrate) which can couple to free-space light efficiently, making it suitable for free-space-optical applications. On the other hand, the 2D-array structure of DCZIM can be easily fabricated in the in-plane configuration (light propagates parallel to the substrate) which can couple to integrated photonic waveguides efficiently, enabling applications in integrated photonics. Both DCZIM and fishnet metamaterial can be designed to show EMNZ behavior to arbitrary polarized incident light at normal incidence. And, both DCZIM and fishnet metamaterial are periodic structures consisting of subwavelength unit cells, showing macroscopic EMNZ behavior (“Homogenization of DCZIMs” section).

An arbitrarily shaped 2D ENZ medium doped with several 2D macroscopic nonmagnetic dielectric dopants is equivalent to a 2D homogeneous medium with the same shape, a near-zero effective permittivity, and an effective permeability determined by the geometric and material parameters of the dopants16,17,18,19. When the dopants’ parameters equal to certain values, the effective permeability equals to zero, leading to an EMNZ behavior near the plasma frequency of the ENZ host. The effective permittivity of the doped ENZ medium behaves the same as that of the ENZ host—a volume plasmon showing zero permittivity at the plasma frequency (Table 1). In the dispersion diagram, this EMNZ behavior corresponds to the dispersion curve crossing zero wavenumber at the plasma frequency, leading to a continuous change of the effective refractive index from a negative value at lower frequencies to a positive value at higher frequencies. This EMNZ phenomenon can be excited by a transverse electric (TE) polarized wave, enabling a transmission of such a wave through the doped ENZ medium without any spatial phase advance. Even the losses and dispersion of the ENZ host limit the performance of photonic do**, the desired zero permeability can still exist with moderate losses. And, because the EMNZ behavior corresponds to the dispersion curve in the radiation continuum above the light line, doped ENZ medium can couple to free space via transverse wave, resulting in radiation losses.

Table 1 Comparison of optical properties of volume plasmon, fishnet metamaterials, photonic do**, and DCZIMs
Full size table

Both doped ENZ media and DCZIMs show macroscopic EMNZ behavior—uniform field distribution outside the media and non-uniform field distribution inside the media. Distinct from the arbitrarily shaped ENZ media doped with dielectric dopants, DCZIMs consist of periodic structures, having less flexibility in forming an arbitrary-shaped geometry, especially when the local feature of the geometry is comparable to the size of the unit cells of the metamaterials. In contrast to the doped ENZ media which show EMNZ response to TE wave only, DCZIMs can show EMNZ response to both TE and/or TM waves. Because the ENZ hosts of doped ENZ media are usually made from metals, doped ENZ media always show a certain amount of ohmic losses, especially in the optical regime. On the other hand, DCZIMs can be made by purely dielectric structures, avoiding ohmic losses completely. Both DCZIMs and doped ENZ media correspond to dispersion curves in the radiation continuum above the light line, leading to radiation losses.

Classification of DCZIMs

DCZIMs were originally realized by engineering the radius and lattice constant of 2D photonic crystals consisting of a square or triangular lattices of dielectric rods21 (Fig. 3a). These DCZIMs can show an impedance-matched and isotropic zero refractive index for TM-polarized light. Such a metamaterial can also be realized via a photonic quasicrystal of dielectric rods without translational symmetry (Fig. 3b)70. By changing the cross-section of the rods from a circle to an ellipse in a square lattice, an anisotropic semi-Dirac-like cone can be achieved with EMNZ in one direction and ENZ in the orthogonal direction (Fig. 3c)71,72. The semi-Dirac-like cone is useful for applications in directional emission73, asymmetric transmission74, beam deflection, beam splitting, and light focusing75. As most 2D DCZIMs are designed for either TM or TE polarization, full-polarization Dirac-like cones induced by the degeneracy of a TM Dirac-like cone and a TE Dirac-like cone at the same frequency can show zero-index behavior regardless of the polarization of the incident light. Full-polarization Dirac-like cones can be achieved via photonic hyper-crystals consisting of dielectric rods in an elliptic metamaterial (Fig. 3d)76, photonic crystals inversely designed by using topology optimization (Fig. 3e)52, a square lattice of dielectric veins54, or a square lattice of dielectric rods (Fig. 3f)77.

Fig. 3: Photonic bandstructure and schematic of different types of DCZIMs.
figure 3

Dirac-like cones based on a a 2D photonic crystal with a square lattice of dielectric rods and b a 2D photonic quasicrystal of dielectric rods. c semi-Dirac-like cone based on a square lattice of elliptical dielectric rods. Full-polarization Dirac-like cones based on d a hyper-crystal consisting of dielectric rods in an elliptic metamaterial, e a photonic crystal designed by using topology optimization, f a square lattice of dielectric rods. Figure adapted with permission from: a ref. 21, Springer Nature Limited; b ref. 70, APS; c ref. 71, © The Optical Society; d ref. 76, Springer Nature Limited; e ref. 52, APS; f ref. 54, © The Optical Society

Full size image

Optical DCZIMs

Based on the original theoretical design of DCZIM (Fig. 4a), most optical DCZIMs are implemented by using standard planar processes in two configurations: out-of-plane configuration in which light propagates in the direction perpendicular to the substrate (Fig. 4b), and in-plane configuration where light propagates in the direction parallel to the substrate (Fig. 4d). The out-of-plane configuration can couple to free-space light efficiently, making it suitable for free-space-optical applications. The in-plane configuration can be fabricated over a large area in arbitrary shapes and can efficiently couple to integrated photonic circuits, enabling various zero index-based devices for integrated photonics.

Fig. 4: Development of optical DCZIMs.
figure 4

a Original theoretical design of DCZIM consists of a square array of 2D silicon pillars21. b Out-of-plane configuration of DCZIM with the plane of periodicity perpendicular to substrate. c First optical DCZIM realized in the out-of-plane configuration56. d In-plane configuration of DCZIM with the plane of periodicity parallel to substrate. e In-plane DCZIM consists of a square array of silicon pillars embedded within a SU-8 matrix and clad by gold mirrors57. f In-plane DCZIM shows robustness against the fabrication imperfection in the radii of pillars79. g In-plane CMOS-compatible DCZIM consists of a square array of air holes in a 220-nm silicon on insulator51. h In-plane 1D DCZIM waveguide31. i In-plane DCZIM achieves ultra-low propagation loss via bound states in the continuum (BIC)53,55

Full size image

The first optical DCZIM was realized in an out-of-plane configuration by patterning 11 alternating layers of amorphous silicon and silica, forming 5 layers of silicon rods in the out-of-plane direction (Figs. 4c and 5a)56. This metamaterial’s transmission measurement shows an impedance-matched low index at 1409 nm followed by a bandgap near 1460 nm, corresponding to a continuous spectrum with both εeff and μeff positive, εeff negative and μeff positive, and both εeff and μeff negative. This result is further confirmed by the measured transmission in a small angular regime of the Fourier plane at the low-index wavelength, which is due to the small critical angle at the interface between air and a low-index medium (Fig. 5b). To further verify the near-zero index of the metamaterial, emissions from the quantum dots, whose luminescence peak is around the near-zero-index wavelength, embedded in the metamaterial and an un-patterned PMMA film were measured. When compared with the un-patterned sample, the metamaterial significantly enhances both the angular confinement and the emission in the direction normal to the interface (Fig. 5c). The enhanced angular confinement is due to the small critical angle at the interface between air and the near-zero-index medium. The enhanced emission is caused by the constructive interference of the emitted light over the almost uniform spatial phase distribution throughout the metamaterial.

Fig. 5: Optical DCZIMs’ structures, theoretical and experimental results.
figure 5

a Scanning electron microscopy (SEM) image of an out-of-plane zero-index metamaterial with the experimental demonstration of this metamaterial’s small angular selectivity b and directional emission from quantum dots within this metamaterial (c). d SEM images of an in-plane zero-index metamaterial and e the waveguides and metamaterial for measuring the zero index with f the simulated and measured effective indices. g In-plane zero-index lens with its optical microscope image (h), effective refractive index (top), and longitudinal spherical aberration (bottom) i. j SEM image of an in-plane zero-index waveguide with its measured interference patterns at different wavelengths (k). l SEM images of in-plane resonance-trapped (top) and symmetry-protected (bottom) BIC zero-index metamaterials with their measured quality factors and effective refractive indices, respectively (m, n). Figure adapted with permission from a–c ref. 56, Springer Nature Limited; d–f ref. 57, Springer Nature Limited; g–i ref. 78, American Chemical Society; j–k ref. 31, American Chemical Society; l–n ref. 55, American Chemical Society

Full size image

An in-plane DCZIM was achieved by sandwiching low-aspect-ratio silicon pillars between two gold films based on a silicon-on-insulator chip (Figs. 4e and 5d)57. According to imaging theory, the two gold films serve as mirrors to extend the optical height of the silicon pillars, realizing effective 2D silicon pillars with infinite height. To experimentally measure the zero index of this metamaterial, a prism consisting of 8 by 8 metamaterial unit cells was fabricated. Light is guided into this prism via a silicon tapered waveguide operating in the fundamental TM mode, and refracted into a semicircular SU-8 slab waveguide (Fig. 5e). The refraction angle is obtained by measuring the scattered light at the semicircular edge of the SU-8 slab waveguide. Measured results show that the effective refractive index of this metamaterial crosses zero linearly near 1570 nm, corresponding to a Dirac-like cone dispersion at the center of the Brillouin zone (Fig. 5f).

Another in-plane DCZIM was realized by fabricating high-aspect-ratio silicon pillars from a single crystalline silicon substrate78. This metamaterial was fabricated over a large area to form a planar concave lens with wavelength-scale thickness (Fig. 5g). As light transmitting through a zero-index medium is always refracted in the direction normal to the interface, the zero-index concave lens can focus all the refracted ray on the concave center (Fig. 5h), eliminating the longitudinal spherical aberration induced by the difference between the focal spots of paraxial and off-axial light. Such an extraordinary focusing effect was measured by probing the light scattered by the irregular silicon substrate. The effective refractive index of the metamaterial can be retrieved from the measured position of the focal point. Experimental results show that the effective index continuously changes from a positive value at short wavelengths to a negative value at longer wavelengths, indicating a zero crossing at 1490 nm (Fig. 5i, top). Results also show that the zero-index lens has a longitudinal spherical aberration of −28.3 ± 3.7 dB at the zero-index wavelength, which is at least 10 dB smaller than that at other wavelengths (Fig. 5i, bottom).

The impedance-matched zero index provided by a DCZIM is not robust against fabrication imperfections because the Dirac-like cone dispersion is formed by an accidental degeneracy that can only exist for a particular combination of geometric parameters. Even a small change in the geometric parameters can break the accidentally degenerated Dirac-like cone into a bandgap. To overcome this drawback, an in-plane all-dielectric DCZIM whose Dirac-like cone dispersion is robust against changes in the radius of pillars was demonstrated (Fig. 4f)79. Radius was chosen because its fabrication error is much larger than those associated with the lattice constant and the height of pillars. Considering that the Dirac-like cone is induced by the degeneracy of an electric monopole mode and a transverse magnetic dipole mode at the Γ point, the pitch and height were designed to guarantee that the Γ point wavelengths and equivalent indices, respectively, of monopole and dipole modes are equal to each other over a large range of radii. Experimental results show that zero-crossing of the effective refractive index redshifts from ~1560 to ~1620 nm as the radius increases from 229.5 to 251.5 nm, verifying the robustness of this design against changes in the pillar radius.

An in-plane, monolithic, CMOS-compatible DCZIM was achieved by fabricating a square lattice of air holes in a standard 220-nm-thick silicon-on-insulator (SOI) (Fig. 4g)51. This metamaterial can be patterned on a photonic chip in a single step together with other components of a photonic integrated circuit. The measured effective refractive index of this metamaterial linearly changes from 0.51 ± 0.04 at 1480 nm to −0.21 ± 0.05 at 1680 nm, crossing zero at 1625 nm. This metamaterial enables the mass production of zero-index-based devices at low cost and with high quality via CMOS fabrication techniques.

To reduce zero-index metamaterials’ cross-section in the transverse plane for applications in nonlinear optics and integrated photonics, one row of the CMOS-compatible DCZIM51 was taken to realize a zero-index waveguide (Figs. 4h and 5j)31. To measure the near-zero effective index of this waveguide, a standing wave is formed in the waveguide by illuminating it from both ends simultaneously. Because the distance between successive nodes or antinodes of a standing wave in a low-index medium is above the diffraction limit, this distance can be resolved in the far-field by measuring the out-of-plane radiation from the zero-index waveguide (Fig. 5k). The effective wavelength and effective refractive index of the waveguide can be extracted from the measured distance between successive antinodes of the standing wave, showing an effective refractive index of zero near 1627 nm.

Because the transverse dipole mode forming the Dirac-like cone is in the radiation continuum above the light line, in-plane DCZIMs have large radiation losses in both the in-plane and out-of-plane directions, resulting in a propagation loss as high as 1.12 dB μm−151. Such a large out-of-plane radiation loss can be mitigated using the concept of bound states in the continuum (BIC)—photonic modes in the radiation continuum above the light line but are confined in the photonic crystal slab with an infinite quality factor80,81. BIC DCZIMs have been implemented in at least two ways: eliminating the out-of-plane radiation of the transverse dipole mode via resonance-trapped BIC which causes destructive interference in the far-field9,82,83; and, forming Dirac-like cone dispersion via symmetry-protected modes without out-of-plane radiation53,55. The resonance-trapped BIC zero-index metamaterial consists of a square lattice of air holes in 570-nm-thick SOI whereas the symmetry-protected BIC zero-index metamaterial consists of a hexagonal lattice of daisy-shaped air holes in 370-nm-thick SOI (Figs. 4i and 5l). Experimental results show that resonance-trapped and symmetry-protected BIC zero-index metamaterials have quality factors of 2.6 × 103 and 7.8 × 103, respectively, near the zero-index wavelengths at 1548.0 nm and 1558.0 nm (Fig. 5m, n). The symmetry-protected BIC zero-index metamaterial shows a propagation loss that is one-order of magnitude smaller than the previous design51.

BIC zero-index metamaterials have several limitations. The resonance-trapped BIC zero-index metamaterials only show a low propagation loss when the thickness of the photonic crystal slab equals to a certain value, which is due to the resonance-trapped BIC’s high sensitivity to the variation in the thickness of photonic crystal slab9. In contrast, the low propagation loss of symmetry-protected BIC zero-index metamaterials is robust against the variations in geometric parameters due to the fact that symmetry-protected BIC modes show high-quality factors because of their intrinsic mode symmetry53,55. Because BIC only show a high quality factor (a low out-of-plane radiation loss) at a certain wavelength, BIC zero-index metamaterials only show high quality factors (low out-of-plane radiation losses) near the zero-index wavelengths (Fig. 5m, n).

Applications

By fully leveraging DCZIMs’ unique electromagnetic property—the infinite effective spatial wavelength, promising potential applications of DCZIMs have been demonstrated in electromagnetic waveguides, free-space wave manipulation, metrology, nonlinear optics, lasers and quantum optics (Fig. 6). In this section, we review DCZIMs’ applications whose performances are or may go beyond the state of the arts. For example, compared with the state-of-the-art direction-independent phase matching in a fishnet metamaterial over an interaction length (800 nm) shorter than the free-space wavelength (1510 nm)7, DCZIM waveguide achieved, at similar wavelengths, the direction-independent phase matching over an interaction length almost 10 free-space wavelengths (14.8 μm)87.

Free-space wave manipulation

By taking advantage of the out-of-plane radiation of the in-plane DCZIMs, we can achieve leaky-wave antennas for continuous beam scanning through broadside by varying the operating frequency88. Such continuous beam scanning is enabled by the linear dispersion of the gapless Dirac-like cone in the radiation continuum above the light line, corresponding to the continuity of the direction of the beam’s wavevector across the broadside. The leaky-wave antennas can be implemented in the microwave and terahertz regimes as dielectric-filled, parallel-plate waveguides with the top perfect-electric-conductor plate perforated to allow out-of-plane radiation out of the waveguide (Fig. 6: leaky-wave antennas, top). Simulation results show that in this design, the beam can be steered from 61° to −37° as the frequency is varied from 8.3 to 11.12 THz with a gain variation less than 2 dB (Fig. 6: leaky-wave antennas, bottom). To avoid metal’s ohmic losses in the optical regime, another leaky-wave antenna is designed in the form of in-plane DCZIMs in the telecom regime. The beam in this design can be steered from 86° to 93° as the frequency is varied from 198 to 204 THz.

Because the cloaking effect of waveguide filled with a DCZIM is induced by resonant tunneling instead of transformation optics89, scattering can be eliminated for normal incident wave only. Such a limitation can be overcome by coating the DCZIM with a transparent metasurface (Fig. 6: cloaking in free space, top), which redirects the wavefront of the incident wave to the direction normal to the surface of the metamaterial (Fig. 6: cloaking in free space, middle)90. This hybrid cloak was experimentally realized in the microwave regime and showed a good cloaking effect (Fig. 6: cloaking in free space, bottom), featuring an almost arbitrary shape. Moreover, this hybrid cloak can achieve a subwavelength thickness by replacing DCZIMs with other thin zero-index materials such as volume plasmon and fishnet metamaterials.

Metrology

DCZIMs can be used in measuring subwavelength displacement91. As shown in Fig. 6: displacement measurement, by sending a continuous wave to a reflector, a standing wave can be formed via the interference between the incident and reflected waves. To measure a quarter free-space wavelength displacement of the reflector, we need to measure the spatial distance between a node and its neighboring antinode, which equals to a quarter free-space wavelength and is smaller than the diffraction limit. To measure this spatial distance in free space, we have to use super-resolution imaging techniques. If a zero-index metamaterial is placed where the standing wave’s antinode interfaces with the metamaterial’s input facet (right-hand-side facet in Fig. 6: displacement measurement, top), the amplitude of the uniform field would be maximized throughout the metamaterial. If the reflector is then moved by a distance equivalent to a quarter of the free-space wavelength, the node of the standing wave will interface with the metamaterial’s input facet (right-hand-side facet in Fig. 6: displacement measurement, bottom), minimizing the amplitude of the uniform field throughout the metamaterial. Hence, we can measure the displacement of the reflector by observing the intensity of the field within the metamaterial, whose size can be much larger than the diffraction limit. Such a displacement measurement method can provide a resolution better than a quarter of the free-space wavelength without using super-resolution imaging techniques. Experimental results show that the contrast of the measured field intensity is as large as ~55%, corresponding to a displacement of ~5 mm, which is approximately a quarter of the operating wavelength, 20.7 mm.

Nonlinear optics

In general, DCZIMs can be used in nonlinear optics for phase matching and nonlinear enhancement. To generate a nonlinear signal efficiently over a long light-matter interaction length, the phase-matching condition Δk = 0 must be met92. For four-wave mixing in zero-index metamaterials, the phase-matching condition Δk = 2γPpump − ΔkL can be satisfied when the pump, signal, and idler are all in the near-zero-index regime near the Dirac-point frequency, in which the phase mismatch due to linear dispersion ΔkL = 2kpump − ksignal − kidler compensates for the phase mismatch due to self-phase modulation and cross-phase modulation 2γPpump7,18, DCZIMs consist of periodic structures, limiting its flexibility in forming an arbitrarily shaped geometry, especially when the local feature of the geometry is comparable to the size of the unit cell. Hence, we should choose the mechanism to achieve a near-zero refractive index according to the particular application.

So far, most potential applications of DCZIMs are only predicted by theoretical results while a few are demonstrated through proof-of-concept experiments. To further develop those potential applications and even achieve performance beyond the state of the arts, such as zero-index waveguides whose overall performance is better than that of silicon waveguides, we envision “customized” DCZIMs designed to satisfy the particular requirements of certain applications. In the following sections, we try to provide the design methodology of DCZIMs for their applications in optical interconnects, nonlinear optics, lasers, and quantum optics.

Optical interconnects

The most intriguing application of DCZIMs in linear optics may be super-couplers whose minimum bending radius could be smaller than that of silicon waveguides (around 5 μm at 1500 nm107). This feature could increase the density of photonic integration of optical interconnects significantly. However, a super-coupler is made by filling a metallic waveguide with a zero-index medium, hampering the realization of optical super-couplers due to the high losses of metals in the optical regime. To achieve super-couplers with low propagation losses at optical frequencies, we envision zero-index waveguides consisting of a linear array of unit cells of the DCZIMs—a periodic dielectric waveguide showing a Dirac-cone dispersion at k = 0. Such a zero-index waveguide’s radiation losses could be eliminated by introducing a BIC in both the out-of-plane and in-plane directions80 or by inversely designing Dirac-like cone dispersion with modes without out-of-plane and in-plane radiations108. This zero-index waveguide’s bending losses could be decreased via structures with the connected dielectric region along the propagation direction, such as fishbone31.

Nonlinear optics

Because only a Dirac-cone dispersion at a long wavelength can rigorously correspond to the EMNZ behavior (“Relationship between a Dirac-cone dispersion...” section), it may unrealistic to achieve zero index-based phase-matching for nonlinear processes whose interacting waves’ frequencies are further away from each other, such as second-harmonic generation and third-harmonic generation. For second-harmonic generation, to satisfy the phase-matching condition Δk = 2k1 − k2 = 0, the zero index-based phase matching requires the metamaterial showing zero-index behaviors at both the fundamental frequency ω1 and the second-harmonic frequency ω2. Even we can design a metamaterial with two Dirac-cone dispersions at ω1 and ω2, respectively, the metamaterial won’t behave as a bulk homogeneous medium with an effective refractive index of zero at ω2 because the size of unit cell a is comparable to the free-space wavelength at ω2 (for a metamaterial consisting of a square array of 2D silicon pillars, a/λ0 ≈ 0.55 at ω1 and a/λ0 ≈ 1.1 at ω2).

Based on DCZIMs, we can realize zero index-based phase-matching for nonlinear processes whose interacting waves’ frequencies are closing to each other, such a four-wave mixing84,93. To improve the nonlinear conversion efficiency, we shall design a zero-index waveguide with a low propagation loss and a small effective mode area. To increase the frequency range of the interacting waves, we could design a zero-index waveguide with a low-loss near-zero index over a relatively large bandwidth. However, DCZIMs are always dispersive and can only show a near-zero index in the vicinity of the Dirac-point frequency, but the bandwidth may be improved by designing the metamaterial to approach the ENZ bandwidth of the Drude model—the widest bandwidth of a near-zero index of passive low-loss media.

Lasers

Further development of Dirac-like cone-based PCSELs is limited by the following constraints: the index contrast between the pattern and semiconductor cladding is too low to design a DCZIM, and the quality factors of Dirac-like cone modes are too close to each other to provide enough mode selection for single-mode lasing109,110. The first constraints might be overcome by carefully selecting materials for the pattern and cladding. We may overcome the second constraint by engineering quality factors of all the modes near the Dirac-cone wavelength using inverse design52.

Quantum optics

Although extended superradiance could be realized in a DCZIM with a large number of emitters over a large spatial extent8, it may be better to achieve superradiance in a purely dielectric ENZ metamaterial. Such an ENZ metamaterial could be realized by breaking the accidental degeneracy of modes forming the Dirac-cone dispersion (“Relationship between a Dirac-cone dispersion....” section), resulting in a monopole mode at the center of the Brillouin at a long wavelength. Such a monopole mode could show ENZ behavior. The advantages of this ENZ metamaterial over DCZIM includes: first, the huge impedance mismatch between the ENZ metamaterial and the ambient media confines most of the light within the metamaterial; second, the large impedance of ENZ metamaterial corresponds to a slow-light effect, leading to an enhancement in the spontaneous emission111,112. Furthermore, this purely dielectric ENZ metamaterial is also advantageous over metallic ENZ systems such as plasmonic channels113 and ENZ nanoscale waveguides114 due to its low propagation losses and arbitrary shapes over the plane of the pattern.