Abstract
A topological insulator1,2,3,4,5,6,7,8,9 is a new state of quantum matter that is characterized by a finite energy gap in the bulk and gapless modes flowing along the boundaries that are robust against disorder scattering. The topological protection of the surface state could be useful for both low-power electronics10 and error-tolerant quantum computing11,12. For a thin slab of three-dimensional topological insulator, the boundary modes from the opposite surfaces may be coupled by quantum tunnelling, so that a small, thickness-dependent gap is opened up13,14,15. Here we report such results from angle-resolved photoemission spectroscopy on Bi2Se3 films of various thicknesses grown by molecular beam epitaxy. The energy gap opening is clearly seen when the thickness is below six quintuple layers. The gapped surface states also exhibit sizeable Rashba-type spin–orbit splitting because of the substrate-induced potential difference between the two surfaces. The tunable gap and the spin–orbit coupling make these topological thin films ideal for electronic and spintronic device applications.
Similar content being viewed by others
Main
Bi2Se3, along with the congeneric Bi2Te3 and Sb2Te3, is theoretically predicted16, a, Thickness dependence of the binding energies of the Dirac point (⩾6 QL)(open black squares), the spin-degenerate point (<6 QL) (open blue triangles) and the mid-gap position E0 of the surface states (<6 QL) measured at room temperature (RT; open green circles) and 150 K (low temperature (LT); filled red circles). b, Thickness-dependent energies of QWS peaks at the  point relative to the mid-gap energy E0. c, Real-space weight of the surface states at 5 QL. The green and blue colours represent the states that mainly localize at the surface and interface, respectively. The inset shows a schematic illustration of the surface states of a Bi2Se3 film above (right) and below (left) 6 QL. The solid and dashed lines represent the surface states that mainly localize at the surface and interface of the Bi2Se3 film, respectively. The red and blue colours of the lines represent different spins. d, Thickness dependence of the measured gap size of the surface states. e, ARPES EDCs of the 3 QL Bi2Se3 film measured at 150 K.
point relative to the mid-gap energy E0. c, Real-space weight of the surface states at 5 QL. The green and blue colours represent the states that mainly localize at the surface and interface, respectively. The inset shows a schematic illustration of the surface states of a Bi2Se3 film above (right) and below (left) 6 QL. The solid and dashed lines represent the surface states that mainly localize at the surface and interface of the Bi2Se3 film, respectively. The red and blue colours of the lines represent different spins. d, Thickness dependence of the measured gap size of the surface states. e, ARPES EDCs of the 3 QL Bi2Se3 film measured at 150 K.
Besides the surface states, above 2 QL, there are other features either above the upper surface states or below the lower surface states. With increasing thickness, these bands move up or down towards the surface states, and more bands emerge. In Fig. 3b we summarize the energies of these bands at the  point with respect to the mid-gap energies of the surface states. The mid-gap energies are used as a reference to remove the influence of chemical potential change. The energy evolution shows a typical QWS behaviour. Therefore, these bands can be attributed to QWSs of conduction and valence bands.
point with respect to the mid-gap energies of the surface states. The mid-gap energies are used as a reference to remove the influence of chemical potential change. The energy evolution shows a typical QWS behaviour. Therefore, these bands can be attributed to QWSs of conduction and valence bands.
When the thickness of a film is reduced to only several nanometres, overlap** between the surface-state wavefunctions from the two surfaces of the film becomes non-negligible, and hybridization between them has to be taken into account. For a freestanding and symmetric Bi2Se3 film, the spin-polarized surface states at one surface will be mixed up with the components of opposite spin from the other surface when the thickness is small enough. It will lead to a hybridization gap at the Dirac point to avoid crossing of bands with the same quantum numbers. The observed gap opening below 6 QL can preliminarily be attributed to this effect. The band and spin structures of a 3D topological insulator such as Bi2Se3 near the Fermi level are well described by the four-band effective model16. In the ultrathin limit15, the 3D topological insulator model of ref. 11 reduces to the Bernevig–Hughes–Zhang model3 of the 2D QSH insulator, and the in-plane dispersions of the surface states can be written as15:

The term including the Fermi velocity vF is the Dirac component of the bands, and Δ represents the gap size. The definition of the parameters D and B can be found in ref. 15. For a 1 QL film, only one band can be observed. The absence of the lower surface states may be due to the bonding with the substrate. The ARPES spectra of 2 QL can be well fitted by equation (1). The pink dashed lines in Fig. 2b depict the fitted curves with the parameters listed in Table 1. However, starting from 3 QL, the surface states exhibit Rashba-type splitting. The splitting cannot be obtained with equation (1), and neither by previous first-principles calculation16. Both the effective model and the first-principles calculation are based on a free-standing symmetric topological insulator film, whereas the existence of substrate breaks the structural inversion symmetry, which can result in a Rashba-type spin splitting in the ultrathin-film regime.
To model the substrate effect, we invoke an effective electrical potential V (z) along the film normal direction. From this modified model, we can obtain the dispersions25:

The  term represents the effect of the potential V (z). Each spin-degenerate dispersion in equation (1) is now split into two sub-bands of opposite spins (σ=±1) that shift away from each other along the k// axis. If
term represents the effect of the potential V (z). Each spin-degenerate dispersion in equation (1) is now split into two sub-bands of opposite spins (σ=±1) that shift away from each other along the k// axis. If  , equation (2) degenerates into equation (1), which corresponds to the 2 QL case discussed above. The splitting of the upper surface states is very well reproduced in the fitting with equation (2) (see the dashed lines in Fig. 2c–e). When Δ is zero, the dispersions obtained from equation (2) evolve into two sets of Dirac cones centred at the
, equation (2) degenerates into equation (1), which corresponds to the 2 QL case discussed above. The splitting of the upper surface states is very well reproduced in the fitting with equation (2) (see the dashed lines in Fig. 2c–e). When Δ is zero, the dispersions obtained from equation (2) evolve into two sets of Dirac cones centred at the  point. The two Dirac points are shifted in energy by
point. The two Dirac points are shifted in energy by  . In the ARPES data, at 6 QL only one Dirac cone was observed. The outer branches of the Rashba-split upper surface states, which are expected to evolve into part of the other Dirac cone, are nearly invisible. In Fig. 3c, the calculated weights in real space of the surface states at 5 QL are shown with the colours of the lines. It is clear that near critical thickness the outer and inner branches of the Rashba-split surface states localize at different surfaces of the film. The two Dirac cones obtained from equation (2) correspond to the two sets of gapless surface states from the surface and interface sides of the film, respectively. The absence of one Dirac cone in the ARPES spectra is due to its localization at the interface side, which is beyond the detection depth of ARPES. In this context, the observed Rashba splitting can also be understood as a result of the hybridization of the two sets of gapless surface states with different Dirac points from the two surfaces of the film.
. In the ARPES data, at 6 QL only one Dirac cone was observed. The outer branches of the Rashba-split upper surface states, which are expected to evolve into part of the other Dirac cone, are nearly invisible. In Fig. 3c, the calculated weights in real space of the surface states at 5 QL are shown with the colours of the lines. It is clear that near critical thickness the outer and inner branches of the Rashba-split surface states localize at different surfaces of the film. The two Dirac cones obtained from equation (2) correspond to the two sets of gapless surface states from the surface and interface sides of the film, respectively. The absence of one Dirac cone in the ARPES spectra is due to its localization at the interface side, which is beyond the detection depth of ARPES. In this context, the observed Rashba splitting can also be understood as a result of the hybridization of the two sets of gapless surface states with different Dirac points from the two surfaces of the film.
The breaking of structural inversion symmetry of the system can originate from the band bending induced by the substrate, as suggested in Fig. 3a, or alternatively from different environments of the two surfaces. In the former case, when the film is much thinner than the thickness of the band-bending region, that is, the Debye length, which is determined by the dielectric constant and carrier density of the material, the potential variation along the z direction of the film will be negligible. So the Rashba effect is weaker in thinner films. In the latter case, the structural asymmetry is more significant in thinner films, and thus the Rashba effect is stronger. Our observation of reduced Rashba splitting with decreasing film thickness suggests that the former case dominates in Bi2Se2 films. In an epitaxial film, band bending can be modified by the surface photovoltage (SPV) effect, which takes place in a p–n or Schottky junction in which the photon-excited electrons and holes are driven in opposite directions by a space charge layer26,27. As a result, the band bending is reduced and even completely removed. The SPV effect is more prominent at low temperature because of less electron–hole recombination. The epitaxial Bi2Se3 films show a strong SPV effect at 150 K, which is confirmed by the 0.06 eV shift of the Fermi edge compared with the room-temperature spectra26. In Fig. 3e, we show EDCs of ARPES spectra of 3 QL Bi2Se3 at 150 K. Rashba splitting cannot be distinguished any more, whereas other features, for example the gap size, are basically similar to the room-temperature data. The thickness dependence of energies of the Dirac point (⩾6 QL) and mid-gap position (<6 QL) measured at low temperature is also shown in Fig. 3a. The variation of chemical potential with thickness is largely reduced, suggesting a nearly flat band. The quench of the Rashba splitting by the SPV effect demonstrates that the splitting is mainly contributed by substrate-induced band bending.
The above conclusion implies that the Rashba splitting can be controlled by modifying band bending, which can be easily realized by applying a gate voltage. It is of great significance for spintronic devices, especially the Datta–Das spin field-effect transistor28, in that the spin structure can be tuned electrically. In Table 1, the fitted Rashba parameter αR values are listed. The Bi2Se3 films (3–6 QL) show at least one order of magnitude larger Rashba splitting than semiconductor heterostructures29, and the splitting can be removed by changing the band bending by ∼0.3 eV. Therefore, ultrathin films of topological insulators provide a new kind of spintronic materials that may realize high-efficiency electrical spin manipulation.
A thickness-dependent oscillatory transition with a periodicity of 3 QL between QSH and ordinary insulator phases was predicted theoretically14. The oscillation mostly refers to the sign of the gap, but could also lead to an oscillation in the magnitude of the gap size13,14,15. In Fig. 3d, we show the measured gap size as a function of thickness, which is more or less monotonic. According to refs 15, 25, if Δ and B in equation (2) have the same sign, the film is in the QSH phase, otherwise, it is a trivial insulator. From the fitted parameters listed in Table 1, we can see that from 2 to 5 QL, Δ and B have the same sign. Therefore, it illustrates that the films are in the QSH regime. However, because band dispersion can be influenced by other non-universal factors, further experiments by STM and electrical transport measurement with and without external magnetic field, similar to those carried out in ref. 4, are needed to clarify this issue.
Methods
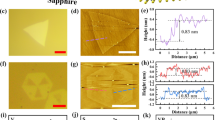
All experiments were carried out in an ultrahigh-vacuum system (Omicron), equipped with MBE, an STM and ARPES. The base pressure of the system is 1.5×10−10 torr. In the ARPES measurement, photoelectrons are excited by an unpolarized He-Iα light (21.21 eV), and collected by a Scienta SES-2002 analyser (15 meV). Bi2Se3 films were grown under Se-rich conditions on a double-layer-graphene-terminated 6H-SiC (0001) substrate at 220 °C by MBE. Bi (99.9999%) and Se (99.999%) were both evaporated from standard Knudsen cells. The growth rate was calibrated by a real-time RHEED intensity oscillation measured on the (00) diffraction. The Se4(Se2)/Bi flux ratio was between 10 and 15, which leads to a growth rate of ∼0.3 QL min−1 when the Bi source temperature was set at 550 °C.