1 Introduction

Poor cash flow planning is one of the main causes of business failures for many businesses globally [1]. This problem is exacerbated by the fact that most Enterprise Resource Planning (ERP) systems are designed for medium-sized and large businesses, while smaller businesses are left with few tools that are suitable for their needs. These systems typically have complex synchronization processes, which makes them difficult for business owners to adopt. Since cash flow is the lifeblood of any business, effective cash management strategies play a vital role in ensuring the growth and survival of companies. Accurate cash flow forecasting, particularly of receivables and inflows, is more important than ever before in the current volatile business environment. Without an accurate forecast, businesses must manage larger variations in cash and keep a higher balance to avoid cash outs, which can inhibit business efficiency and growth.

Major events, such as the COVID-19 pandemic, have caused significant shifts in consumer behaviour and economic trends, leading to erratic fluctuations in the cash flow positions of businesses. According to a survey conducted by the International Labor Organization, inadequate cash flow management was the major cause of retrenchment during the pandemic [2]. Other black swan events, such as the 2021 Suez Canal obstruction, the Russia-Ukraine war, rising tensions in the South China Sea and adverse climate conditions, have also significantly disrupted global supply chains and impacted the ability of corporates to optimise their working capital and cash flow planning. The looming worldwide economic downturn will present an additional challenge to businesses, compelling them to implement sophisticated strategies to project and manage their cash flow, thereby ensuring their survival.

Inaccurate cash flow forecasting is a common issue in many businesses. Spreadsheet-based approaches and legacy systems are widely used, but are not flexible and cannot easily adapt to dynamic changes in cash flow positions. Account Receivables (AR) play an important role in cash flow forecasting, as the variability of customer paying along with credit terms as well as raising invoices in time makes it difficult to predict incoming cash. AR are often difficult and unpredictable due to factors such as varying customers behaviours, changes in business cycles and seasonal variations due to calendar events.

AR forecasts at the invoice level for open and late invoices based on past customer behaviour can help identify settlement dates of the invoices by the customer more accurately. This would ultimately lead to more efficient cash flow management.

In this study, we introduce a discrete survival framework for predicting the time to payment of invoices. In this setting, we are interested in modelling the probability of a customer making a payment at a specific time. The statistical strategy is based on generalized linear mixed effects models [3] which also allow incorporating company- and invoice-specific covariate information. To capture customer heterogeneity in payment behaviour, we introduce customer-specific random effects. The baseline hazard, i.e. the baseline risk of payment at time t given that the customer has not paid until time t, is modelled flexibly through B-splines. Time-varying effects of covariates are also accommodated.

The paper is organized as follows: in Sect. 2, we introduce the business problem and current approaches. In Sect. 3, we detail the statistical strategy. In Sect. 4, we describe the two example data sets. In Sect. 5, we present the analysis results. Section 6 concludes the paper.

2 Background and literature review

The objective of this study is to obtain accurate and timely account receivables estimations which can feed into a Cash Flow Forecast (CFF), particularly in the context of a generic supply chain company. The main components of the CFF are AR, Account Payables (AP) and Working Capital (WC). The focus of this work is on AR, with specific emphasis on how they contribute to the overall cash flow forecasting. Additionally, AR predictions can support the prioritization of collections, indicating to the user which invoices are less likely to be paid on time. This allows for better planning and prompting of further actions towards ensuring that the amounts can be collected.

Depending on the specific motivation, CFFs have different time horizons, even though the reporting is normally done at monthly level. Short-term forecasts concentrate on the upcoming 30–60 days and are conducted at daily or weekly granularity. They can leverage the most detailed data available, such as invoice data and effects of calendar events. Medium-term forecasts run through the months and quarters, generally until the end of the fiscal year or rolling 12 months. They are conducted at weekly or monthly level and can leverage external data such as daily news or projections of economic changes or similar aspects. Long-term forecasts have a more strategic nature. They run through the quarters and up to 3–5 years and include projections on business targets and goals, and expected socio-economic changes.

In this work, we focus on short-term forecasting and we exploit discrete survival analysis techniques to predict when each invoice will be paid, reducing the uncertainty of the overall account receivables estimations. It is important to note that this approach does not consider invoices that are not yet generated and sent to the customers, which would also have an impact on the cash flow predictions. While out of scope for this study, considerations of future invoices depend on the type of company, products or services offered and the buying patterns of customers in the next 30–60 days. We remark that the modelling strategy would be able to accommodate such information.

To accurately predict AR, it is important to employ techniques which allow the identification of late or unpaid invoices and the estimation of time to payment of each invoice. These tasks have often been been framed as classification problems in the literature. For instance, Zeng et al. [4] use supervised machine learning methods, with payment times treated as “classes”, while Hu [5] formulates the problem as a binary classification problem, and the focus is on whether the invoices are paid late or on time. Similarly, Appel et al. [6, 7] propose a method to predict whether invoices are paid within five days of being due or not, in order to support collection agents. These approaches based on machine learning methods do not incorporate time-related information, which limits their ability to make accurate predictions of account receivables.

In this work, we propose the use of discrete survival analysis techniques to predict the time to payment of each invoice, exploiting all available information. This strategy allows us to properly account for the payment time horizon, ultimately leading to more accurate forecasts of account receivables. Such methods have been successfully employed to tackle similar problems in the credit data domain. For example, Narian [8], Banasik et al. [9], Cao et al. [10], Dirick et al. [11] and Rychnovský [12] apply survival analysis methods (e.g. Cox proportional hazards model) to predict the debtor’s repayment date. In the context of time to payment for AR, Smirnov [13] use Random Survival Forests [14] to estimate payment probability using right-censored invoice data. Moore and van Vuuren [15] develop Survival Boost, a framework for AR prediction that combines survival analysis and machine learning. The aforementioned approaches highlight the potential of survival methods for AR prediction, but still treat time to payment as a continuous variable. This is a drawback as often time to payment data are recorded on a discrete scale, such as number of days to default for payment.

3 Discrete survival approach

Discrete survival models [16] are applied to time-to-event data when the times are recorded on a discrete scale, i.e. the events they mark refer to an interval rather than an instant. As such, they are particularly suitable to estimate the probability of account receivable payments being made within a specific time period, or predicting the likelihood of customer churn within a certain time frame.

Let \(T_{ij}\) be the time to payment of invoice j for customer i. Let \(b_i\) denote the customer-specific random effect and \(\varvec{x}_{i}\) a covariate vector. The hazard function is given by:

$$\begin{aligned}&P(T_{ij} =t \mid T_{ij} \ge t, \varvec{x}_{i}, b_i) = \lambda ( t \mid \varvec{x}_{i}, b_{i}) \nonumber \\&\quad =h( b_{i}+\gamma _{t} +\varvec{x}_{i}^{\top } \varvec{\beta }) \end{aligned}$$
(1)

where \(t= 1, 2,\ldots , \tau\) and \(\tau\) is the maximum observed time. Here, \(\gamma _{t}\) denotes a time-varying intercept and can be interpreted as a baseline hazard [16]. The function \(h(\cdot )\) is the link function, for example a log-log or logit link. In our applications, all the invoices are paid. Thus, there is no censoring and the likelihood contribution of each transaction is given by:

$$\begin{aligned} L_{ij} = \lambda ( T_{ij} \mid \varvec{x}_{i}, b_{i}) \prod _{s=1}^{T_{ij} - 1} (1 - \lambda ( s \mid \varvec{x}_{i}, b_{i}) ) \end{aligned}$$
(2)

The estimation of the model is performed through maximum likelihood by reformulating the problem as a binary response model. Each \(T_{ij}\) is represented by a vector \(y_{ij}\) of length \(T_{ij}\), whose elements are all zeros except the last one which is equal to one, denoting that the event has occurred. In this way, for each customer i and and invoice j, we can recognize the likelihood in (2) as coinciding with that of a binary response model with \(T_{ij}\) independent observations, and we can employ generalized linear mixed effects models to perform inference. Here, we choose h as the inverse of the complementary log-log function, i.e.

$$\begin{aligned} h(\eta )= 1-\exp (- \exp (\eta )), \end{aligned}$$

since this choice corresponds to a discretisation of the Cox proportional hazards model [17]. As Chen et al. [18] recommend, an asymmetric link function may be more appropriate than a symmetric link function when the number of 1’s and 0’s are very different (unbalanced data), as in our case.

The random effect \(b_{i}\) follows a normal distribution, \(b_{i} \sim N( 0, \sigma ^{2})\). The variance \(\sigma ^{2}\) captures the heterogeneity in the population. The baseline function \(\gamma _t\) is estimated using a general non-parametric smoothing method called B-spline. We use cubic B-splines with no inner knots and boundary knots at the extremes \(t=1\) and \(t = \tau = \max _{ij} T_{ij}\). Specifically, the spline basis elements used are \(B_m(t) = \left( {\begin{array}{c}3\\ m\end{array}}\right) (t - 1)^m (\tau - t)^{3 - m} / (\tau - 1)^3\) for \(m=1,2,3\). Then, \(\gamma _t = \theta _0 + \theta _1 B_1(t) + \theta _2 B_2(t) + \theta _3 B_3(t)\) for an intercept \(\theta _0\), and coefficients \(\theta _1\), \(\theta _2\) and \(\theta _3\). Moreover, we include in the model the continuous covariate \(\log (\text {Amount} + 1)\) and an interaction effect of amount and the B-splines \(B_m(t)\). The latter term captures time-varying effect of amount. This implies that the effects for the covariate vary smoothly over time (see Section 5.3 of [16]). Further covariates are discussed in Sect. 4. Model fitting is performed in R version 4.3.2 using the package lme4 version 1.1\(-\)35.1 [19] with more details on the software environment provided in Online Resource 1.

From the model estimate, we can derive quantities of interest, such as the probability distribution of the time to payment for each invoice \(T_{ij}\). The predicted time to payment, \(\hat{T}_{ij}\), can be obtained as the expectation of \(T_{ij}\):

$$\begin{aligned} \hat{T}_{ij} = \mathbb {E} {(} T_{ij} {)} = \sum _{t=1}^\tau t\cdot \hat{\mathbb {P}}(T_{ij}=t). \end{aligned}$$

where \(\hat{\mathbb {P}}\) is the estimated probability distribution.

4 Data description

We demonstrate the methodology in two applications involving account receivables invoices. We refer to the data sets under investigation as “Data I” and “Data II”. Note that Data I includes a proportion of invoices that present part or the total amount written off. Because large write-offs generally include situations that are outside the normal payment cycle, such as products not delivered or returned, or customer not willing to pay, we only keep invoices with no or negligible write-off, which represent 98% of the total amount and 96% of the transactions. We also exclude invoices paid on the same day they were issued: the objective is to predict when open invoices will be settled with the model being run on a weekly or monthly basis to forecast multiple months ahead. Specifically, only invoices that are still open at the end of the day, when the model is run, are considered. Thus, invoices paid on their issue date are not of interest. Additionally, we restrict our analysis to customers with a minimum of three invoices for both data sets, to obtain more stable estimates of customer-specific random effect. Finally, we exclude the 0.5% of invoices with the longest time to payment in Data I to limit the range of times in the discrete survival model: a high maximum observed time \(\tau\) poses a challenge for discrete survival methods due to the associated large number of parameters [16]. Furthermore, we focus on forecasting weeks or months, rather than years, ahead, and the 0.5% longest payment times are greater than 300 days.

At the end of the cleaning process, Data I includes 9932 invoices issued to 401 customers, spanning the period from February 2018 to July 2020. Data II contains 35,192 invoices issued to 1351 customers, covering the time period between January 2009 and September 2017. Invoice information used in the survival regression is:

  • Customer A specific identification number assigned to a customer, which can refer to either a company or an individual.

  • Amount The total amount of each invoice, which reflects the cost of the goods or services provided.

  • Issue date The date on which the invoice is issued by the seller.

  • Payment terms The expected number of days within which payment is expected from the customer, as outlined in the agreement between buyer and seller.

  • Due date The expected date on which payment is due, which can be derived from the payment terms and issue date.

  • Closed date The actual date on which payment is received, completing the transaction. On this information, we build the response variable, time to payment.

  • Customer type The type of customer, whether a company or an individual. This information is only included in Data I.

  • Tax Whether the invoice includes a tax or not. It is important to note that most of the transactions do not include a tax, and this information is only contained in Data II.

We now specify the covariates that are used in (1) in addition to those already mentioned in Sect. 3. We include the quarter of issue date as a categorical predictor. Since the payment terms are fixed in Data I and vary for each transaction in Data II, we only include them as a covariate in the model for Data II. Similarly, customer type is a predictor only for Data I and tax only for Data II. The included covariates represent the variables available in the data, and no further model or variable selection is performed.

5 Results

5.1 Data I

Table 1 contains the coefficient estimates, standard errors, confidence intervals (CIs) and p-values for the covariates of the model. Positive coefficient estimates imply that the corresponding covariates have a positive effect on hazards (and hence correspond to forecasting an invoice to be paid earlier). Furthermore, individuals are more likely than companies to pay early. In addition, invoices issued outside of the first calendar quarter, particularly those issued in the second and third quarter, are also expected to be paid earlier compared to those issued in the first quarter.

Table 1 Data I: Estimated regression coefficients of the covariates
Full size table
Fig. 1
figure 1

Data I: Estimated survival function (solid curve) for six companies with 95% confidence bands (shaded area), as well as the empirical survival function (dashed curve). The points mark the median survival time of each survival function

Full size image
Table 2 Data I: Median survival times of the estimated and empirical survival functions in Fig. 1
Full size table

Figure 1 displays survival functions averaged across all invoices for six companies selected from those with at least 10 invoices. Companies 5 and 6 are those with the lowest and highest median time to payment, respectively. Table 2 contains the corresponding median survival times. Median time to payment can be used, for example, to rank companies on the basis of their risk.

We report the amount paid per month and per day in Figs. 2, 3, respectively, which is compared with amounts deriving from the due date, the proposed survival model, a Cox proportional hazards model which treats survival times as continuous, and results obtained by a moving average, the theta method [20] and an error, trend and seasonality (ETS) model [21].

The estimated survival functions provide distributions on payment dates. To obtain the shaded bands in Fig. 2, we take \(10^5\) draws from these distributions to obtain \(10^5\) scenarios of the amount received in each month. For each month, we show the lowest (i.e. worst) and highest (i.e. best) payment amounts from these possible scenarios. This is an important feature of our modelling approach as it allows for better cashflow planning. We summarise the predictive performance of the model in Table 3. The predictions based on invoice-level data capture the variation in amount received better than the moving average, the theta method or the ETS model. Moreover, the discrete survival approach yields more accurate predicted amounts for most days and also in terms of cumulative prediction error across time per Table 3.

Fig. 2
figure 2

Data I: Amount received per month based on each invoice’s actual payment date, due date, predicted date by the Cox proportional hazards model and the discrete survival model, and predicted amount by a moving average, the theta method and an ETS model on the daily amount received. The shaded areas mark the worst and best case scenarios from the survival model

Full size image
Fig. 3
figure 3

Data I: Amount received per day based on each invoice’s actual payment date, due date, and predicted date by the Cox proportional hazards model and the discrete survival model for a subset of six months before (top) and after (bottom) COVID

Full size image
Table 3 Data I: Accuracy of predictions
Full size table

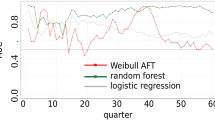
An alternative and more common, but more limited, approach to analysis of such data is to use classification methods, such as logistic regression. We compare our results with those obtained fitting a logistic regression model, using as binary response whether the invoice is paid by the due date or not. We use the probability of on-time payment derived from the discrete survival or the logistic regression model to determine whether an invoice is paid on time. We summarise the classification performance of each in Fig. 4 and Table 4. Even though it is not the main focus of our model, it can still be used for classification. Still we note that methods that specifically target the task of determining which invoice is paid on time generally perform better in this regard as has been reported before [15].

Fig. 4
figure 4

Data I: Receiver operating characteristic (ROC) curves for the comparison with logistic regression

Full size image
Table 4 Data I: The area under the curves (AUCs, higher is better) and the Brier scores (lower is better) for the classification problem of whether an invoice is paid on time, using the discrete survival model and logistic regression
Full size table

5.2 Data II

Table 5 reports the estimates of the regression coefficients. Longer payment term in days may result in later payments. The effects of the issue quarters are slightly different from those in the previous analysis. Although the effect of quarters 2, 3 and 4 results in a higher probability of early payment compared to the first quarter, the effect is stronger for the third and fourth quarters.

Table 5 Data II: Estimated regression coefficients of the covariates
Full size table

Figs. 5, 6 and 7, and Tables 6, 7 and 8 are analogous to the corresponding figures in Sect. 5.1. Like for Data I, the use of invoice-level data results in more accurate prediction of the amount received compared to the moving average, the theta method or the ETS model. Furthermore, the discrete survival model is able to capture patterns, e.g. seasonal fluctuations, that prediction from the due date omits. As a result, the discrete survival approach provides predictions closer to the actual amount than those obtained from the due date. Finally, the discrete survival model outperforms the Cox proportional hazards model in terms of AR prediction per Table 7.

Fig. 5
figure 5

Data II: Estimated survival function (solid curve) for six companies with 95% confidence bands (shaded area), as well as the empirical survival function (dashed curve). The points mark the median survival time of each survival function

Full size image
Table 6 Data II: Median survival times of the estimated and empirical survival functions in Fig. 5
Full size table
Fig. 6
figure 6

Data II: Amount received per month based on each invoice’s actual payment date, due date, predicted date by the Cox proportional hazards model and the discrete survival model, and predicted amount by a moving average, the theta method and an ETS model on the daily amount received. The shaded areas mark the worst and best case scenarios from the survival model

Full size image
Table 7 Data II: Accuracy of predictions
Full size table
Fig. 7
figure 7

Data II: Receiver operating characteristic (ROC) curves for the comparison with logistic regression

Full size image
Table 8 Data II: The area under the curves (AUCs, higher is better) and the Brier scores (lower is better) for the classification problem of whether an invoice is paid on time, using the discrete survival model and logistic regression
Full size table

6 Conclusions

In this paper, we propose the use of discrete survival models for AR forecasting. We show that such approach presents many advantages as compared to standard methods, in particular the ability to derive quantities of interest (for example at invoice or company level) based on the distribution of time to payment of each invoice, which are fundamental to ensure effective account receivable planning. Furthermore, the method compares favourably with Cox proportional hazards modelling which is a survival method that treats time to payment as continuous.

The benefits of the discrete survival approach to AR forecasting are accompanied by some limitations. Firstly, classification methods such as logistic regression outperform prediction methods for determining whether an invoice will be paid on time [15], which was also true in our applications. Other limitations stem from the use of invoice-level data. While such use aids prediction, it also means that our method requires such data. Furthermore, any issues with them, e.g. uncertainty about future invoices or incompleteness of invoice data, will directly affect forecasts.

The results show that account receivable forecasts are mainly affected by the time of the year in which the invoice is issued, the customer that is paying the invoice and the amount, which indicates that payment behaviours can be predicted to a good extent. The model can be easily extended to incorporate other factors. For instance, we could investigate the effects on the forecast of receiving the money in the next k days to better understand what provides the best compromise between accuracy and usability from a business perspective. It is important to also add predictions on invoices not yet received but expected based on past customers behaviours.

The implications of this work on the practice of cash flow forecasting and financial management in wholesale scenarios within supply chain companies are significant: (i) using discrete survival methods with a time-varying baseline hazard function improves the precision of predicting invoice payment times, enhancing cash flow forecasting accuracy; (ii) more accurate AR predictions contribute to reliable Cash Flow Forecasting (CFF), aiding in strategic financial planning and decision-making; (iii) enhanced AR predictions enable better management of Working Capital (WC), ensuring efficient allocation of resources and minimizing the need for excessive borrowing; (iv) precise AR forecasts help identify potential cash flow gaps and payment delays, allowing proactive risk mitigation strategies and improved financial stability; (v) accurate predictions streamline collection processes, reducing costs associated with chasing overdue payments and improving operational efficiency; (vi) companies with better cash flow management gain a competitive advantage, enabling quicker responses to market changes, investment in growth and overall financial stability.