1 Introduction

Mechanical vibrations from earthquakes, land transport, and building construction not only reduce the safety of buildings, but also interfere with the operation of precision instruments in laboratories or hospitals, and adversely affect the physical and mental health of residents. Such vibration hazards are essentially caused by the propagation of waves. Commonly, elastic waves caused by traffic and civil engineering activities include both bulk waves, propagating mainly in the underground, and elastic surface waves, propagating along the ground surface which have a greater impact on the buildings and structures [1, 2]. Therefore, this work focuses on the attenuation of elastic surface waves.

In order to reduce the damaging effects of elastic surface waves, various methods such as open, in-filled, and stiff wave barriers have been proposed [3,4,5,6,7]. However, these traditional methods have the disadvantages of low vibration reduction efficiency, narrow operating frequency, and inability to design according to practical needs. Acoustic metamaterials are artificial structural materials consisting of sub-wavelength elements that exhibit extraordinary wave properties such as isolation [8,9,10,11,12], cloaking [13,14,15,16], and topological insulators [17,18,25,26,27,28]. Such metastructures can isolate vibration waves by reflection, refraction, and conversion effects to protect targeted objects.

The first experimental study on seismic metamaterials was carried out by Brule et al. by considering a periodic array of cylindrical holes with finite depth (5 m) in the soil to isolate the elastic surface waves around 50 Hz [29]. Colombi et al. regarded forests as natural metamaterials to study the Rayleigh wave bandgaps [30]. Miniaci et al. explored different metamaterial configurations (ross-like cavity, hollow cylinder and coated cylinder in the soil), and revealed that both surface and bulk seismic waves can be considerably attenuated [31]. Huang and Shi investigated the isolation effectiveness of periodic pile barriers, and found that elastic surface waves in the range of attenuation zones can be strongly reduced [32, 33]. Zeng et al. contrasted results on the dispersion curves of metamaterials with different numbers of tubes and found that an added tube creates new band gaps [34]. Wu et al. presented a new gradient metamaterial consisting of a gradient combination of above-ground pillars and embedded core–shell inclusions and they proved that such structure is capable of broadening the bandgap and shifting it to lower frequencies [35].

Most previous studies on elastic surface wave isolation are established on the assumption that the soil is a single-phase media. In reality, soil properties are complex, such as layered and saturated. Different soil properties need to be considered in investigating the elastic surface wave attenuation of metastructures [36,37,38]. Pu and Shi arranged periodic pile foundations in layered soil and revealed that Rayleigh and Love waves could be effectively attenuated. By further varying the column spacing and the lattice constants, it was found that the attenuation zones of the overall structure can be modulated [39]. Muhammad et al. investigated the propagation of elastic surface waves through a periodically arranged built-up steel section in a single and six-layered soil and found that wider bandgaps could be achieved in the case of a layered soil medium [40]. Amanat et al. studied three different configurations of periodic barriers consisting of finite and infinite lattices to mitigate seismic surface waves in layered soil [41]. Zeng et al. theoretically and numerically investigated the dispersion relations of Rayleigh waves propagating through vertical oscillators periodically distributed on stratified media [42]. Cai et al. analyzed the complex band structures and transmission spectra and investigated the propagation and attenuation of the Rayleigh and pseudo surface waves in two types of viscoelastic seismic metamaterials [43]. Wang et al. analyzed wave propagation in 1D fluid-saturated porous metamaterials and revealed that by increasing viscosity the attenuation in the passing bands is first enhanced and then reduced [44]. Chen et al. used multi-layered soil with different mechanical properties to design new seismic metamaterials and validated the effect of the seismic metamaterials on the attenuation of surface wave transmission experimentally and numerically [45]. Zeighami et al. conducted an experimental study on metabarrier design within the frequency range of 50-100 Hz [46], analyzed the embedded depth of metastructures and the mechanical parameters of the soil on the surface wave attenuation capability of the metastructures [47, 48]. Almost all ahead studies designed metastructures with local resonant mechanism to generate low-frequency hybridized bandgap to attenuate elastic surface waves for different soil conditions. Whether metastructures with Bragg bandgap mechanism also work, it remains unclear. In this work, we verify that non-resonant metastructures in layered soil with Bragg bandgap mechanism can attenuate low frequency elastic surface waves efficiently, showing a remarkable relative bandgap width value.

In this study, we calculate the elastic surface wave dispersion and transmission curves of metastructures in layered soil. Then, the influence of the embedded depth of the metastructures, the depth of the vibrating source, soil density, arrangement order, and soil viscosity on the isolation effect are discussed. The outline of the paper is as follows. After the introduction in "Introduction" section, the method of calculations and numerical simulation are presented in "Basic theory and numerical simulation" section. In "Analysis of influencing factors" section, we further investigate the factors that influence the attenuation efficiency. "Conclusion" section summarizes the work.

2 Basic theory and numerical simulation

2.1 Bloch theory and dispersion equation

Assuming that the medium is homogeneous, isotropic and linear, the equation of motion for elastic wave propagation in this medium can be expressed as [49]

$$\frac{E}{2\left(1+v\right)\left(1-2v\right)}\nabla \left(\nabla \cdot \boldsymbol{u}\right)+\frac{E}{2\left(1+v\right)}{\nabla }^{2}{\varvec{u}}={-\rho \omega }^{2}{\varvec{u}}$$
(1)

Where \(\nabla\) is a differential operator, E, ν, and ρ are the Young’s modulus, the Poisson’s ratio, and the mass density, respectively, and u = u(r) is the displacement vector, r is the position vector, ω is the angular frequency.

By applying the Bloch theorem [49], the displacement field of waves in periodic media can be represented as

$${\varvec{u}}\left({\varvec{r}},t\right)={{\varvec{u}}}_{k}\left({\varvec{r}}\right){e}^{i\left(\boldsymbol{k}\cdot \boldsymbol{r}-\omega t\right)}$$
(2)

where k is the wave vector, \(i=\sqrt{-1}\) , uk is a modulation function of the displacement vector. Periodic boundary condition can be further obtained by combining the periodicity of uk

$${\varvec{u}}\left({\varvec{r}}+a,t\right)={\varvec{u}}\left({\varvec{r}},t\right){e}^{{{i}}{\varvec{k}}\cdot a}$$
(3)

where a is the lattice constant.

Substituting Eq. (3) into Eq. (1), the dispersion equation can be obtained as

$$\left({\varvec{K}}-{\omega }^{2}{\varvec{M}}\right)\cdot {\varvec{u}}=0$$
(4)

where K is the stiffness matrix and M is the mass matrix. Scanning the wave vector k along the boundary of the first irreducible Brillouin zone, the corresponding eigenfrequency ω can be found to obtain the dispersion relation of the periodic structure.

2.2 Introduction of viscosity

If materials are considered linear elastic materials in the absence of viscosity, the constitutive relations of the material can be expressed as

$${\sigma }_{ij}={\lambda \theta \delta }_{ij}+{2\mu \varepsilon }_{ij}$$
(5)
$${\delta }_{ij}=\left\{\begin{array}{c}1\left(i=j\right)\\ 0\left(i\ne j\right)\end{array}\right.$$
(6)

where σij is the stress tensor, \(\theta\) is the volumetric strain, δij is the Kronecker symbol, and εij is the strain tensor.

However, ideal materials without dam** do not exist in practical applications, so dam** terms need to be introduced to modify the constitutive relations. At room temperature, the viscosity loss of many materials may be described by a viscous dam** term. Considering time-harmonic waves, the ideal Hooke’s law can be modified as

$${\sigma }_{ij}=\left(\lambda +\eta \frac{\partial }{\partial t}\right){\theta \delta }_{ij}+2\left(\mu +\eta \frac{\partial }{\partial t}\right){\varepsilon }_{ij}=\left(\lambda +i\omega \eta \right){\theta \delta }_{ij}+2\left(\mu +i\omega \eta \right){\varepsilon }_{ij}$$
(7)

where η is the viscosity factor. Here, we introduce the same viscosity in λ and μ [50].

$$\begin{array}{cc}\lambda ={\lambda }_{0}+i\omega \eta & \mu ={\mu }_{0}+i\omega \eta \end{array}$$
(8)

2.3 Modeling

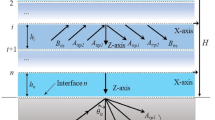
We propose metastructures consisting of periodic inclusions in 6-layers soil as shown the configuration in Fig. 1(a) with the parameters of the layed soil listed in Table 1 whose data are taken from the reference [51]. The inclusions of the metastructures are chosen as flyash with mass density of 500 kg/m3, Young’s modulus E of 25 MPa, Poisson ratio of 0.35 [39]. Previous study using finite element and boundary element methods shows that 2D models provide results that qualitatively agree with those of 3D models at most frequencies and physical phenomena like bandgap will conserve, so we choose a 2D model to reduce the computation cost [52]. The unit cell of the metastructure is shown in Fig. 1(b) with periodic boundary condition applied to the two edges in x direction and low-reflection boundary applied to the bottom edge to avoid wave reflection from the bottom surface. The width of the inclusion is chosen as b = 0.6 m, and b1 = b2 = 0.2 m, the embedded depth of the metastructure is h0 and the lattice constant a is set to 1.0 m [41, 53].

Fig. 1
figure 1

Schematic diagram of metastructures in layered soil: a 3D model; b The unit cell model used for dispersion analysis; c The transmission configuration used for harmonic response analysis

Full size image
Table 1 Soil properties [51]
Full size table

The dispersion curve describes the wave properties of infinite period metastructures. However, the metastructures are finite in practical applications, so the transmission curve of finite metastructures needs to be calculated to verify their vibration isolation properties. The finite periodic model is established to study the transmission properties of finite metastructures as shown in Fig. 1(c) where the low-reflection boundaries are applied on the bottom and side edges to avoid reflection of waves by the boundaries. A load P is applied at yellow point A at a distance d from the ground to model an incident wave as the source. The output area B with length l3 = 8 m is located behind the last column of pile barriers at a distance l4 = 2 m. The total length of the model is l = 40 m and the total depth is H = 30 m.

In order to evaluate the vibration attenuation effect of the metastructures, we introduce the amplitude reduction factor (AR) in terms of the ratio between surface displacement amplitude with and without metastructures [54]. Since the amplitude reduction factors are not uniform over the output zone B, the averaged amplitude reduction factor \(\overline{{A }_{R}}\) is defined and the transmission coefficient T is thus introduced,

$${A}_{R}=\frac{{u }_{1}}{{u }_{2}}$$
(9)
$$\overline{{A }_{R}}=\frac{{\int }_{0}^{S}{u}_{1}dS}{{\int }_{0}^{S}{u}_{2}dS}$$
(10)
$$T=20{{\text{log}}}_{10}\stackrel{-}{\left({A}_{R}\right)}$$
(11)

where u1 denotes the normal displacement at the evaluation point located after the metastructures and u2 denotes the normal displacement at the same point without the metastructures, S is the area of the output zone. The smaller the value of the transmission, the stronger the elastic surface wave attenuation effect of the metastructures.

2.4 Results of numerical simulations

First, we investigate the dispersion relations of metastructure in layered soil. The embedded depth of the metastructure is set as h0 = 9 m. By scanning the wave vector k along x direction, we can obtain the dispersion relation containing both bulk and surface wave dispersion curves. To sort out elastic surface waves, a concept based on energy distribution along the z-axis of each mode is used [55]. The energy distribution is quantitatively given by normalized depth of energy (ξ):

$$\xi =\frac{1}{H}\frac{{\int }_{0}^{H}z\cdot {E}_{p}dS}{{\int }_{0}^{H}{E}_{p}dS}$$
(12)

where H is the total depth of the unit cell, Ep is the elastic potential energy density. The value of ξ varies from 0 to 1. A smaller value (close to zero) indicates bulk modes, while the larger value of ξ implies surface modes. In this paper, ξ = 0.95 is taken as a threshold to distinguish surface and bulk modes. The dispersion relation of elastic surface waves along x direction is shown in Fig. 2(a) where the bandgap is presented in gray with a range [40, 57] Hz. To further reveal the properties of the elastic surface waves in the presence of 10 columns of units, we calculate the corresponding transmission spectrum in Fig. 2(b). One can see that there is an attenuation area marked as the gray area with a range [40, 57] Hz which is consistent with the bandgap in Fig. 2(a). The relative bandgap width ∆f/fc = 35%, where ∆f is the gap width and fc is the center frequency of the gap, showing a remarkable advantage with Bragg bandgap mechanism.

Fig. 2
figure 2

a The dispersion relations of elastic surface waves along ΓX direction of the metastructure in layered soil; b Transmission spectrum of 10 columns of units; Elastic strain energy density field at c point C and d point D

Full size image

We further select point C at 28 Hz (below the bandgap) and point D at 47 Hz (inside the bandgap) and plot the distribution of the elastic strain energy density with embedded depth of metastructure h0 = 9 m in Fig. 2(c) and (d), respectively. For point C at 28 Hz, it’s outside the bandgap locating at the passing bands, so that the metastructure allows elastic surface wave propagation, as seen the field distribution in Fig. 2(c). However, for point D at 47 Hz, it’s inside the bandgap meaning that incident elastic surface waves are mainly reflected and converted into bulk waves by the metastructures, resulting in a low transmission value, as seen the field in Fig. 2(d). It shows that the finite metastructures can effectively attenuate the propagation of elastic surface waves in the bandgap frequency range, thus playing the role of vibration reduction. To be noted that the frequency of the Bragg bandgap will slightly deviate along other propagating directions in practice.

3 Analysis of influencing factors

As mentioned above, the bandgap and the attenuation zones play key roles in the isolation of elastic surface waves by the metastructure and are of primary interest in this work. Therefore, a detailed parametric study will be carried out, using the single variable method, in order to investigate the effect of the main parameters on the bandgap (from dispersion curves) and attenuation zones (from transmission spectrum) of elastic surface waves.

In order to further investigate the influence of geometric and material parameters on the elastic surface wave isolation effect of the metastructure, the average transmission coefficient \(\overline{T }\) is defined [56]

$$\overline{T }={\int }_{{f}_{1}}^{{f}_{2}}Tdf/\left({f}_{2}-{f}_{1}\right)$$
(13)

where f1 and f2 are the elastic surface wave frequencies corresponding to the lower and upper bounds of the bandgap.

3.1 Effect of embedded depth of metastructures

The embedded depth of the metastructure is one of the important factors affecting the isolation effect, and its clarification is of great significance for the engineering applications. Kee** other parameters fixed, change the embedded depth of metastructures h0 as h0 = 2 m, h0 = 5 m, h0 = 9 m, h0 = 15 m, then obtain the corresponding elastic surface wave bandgaps and transmission curves, as the results shown in Fig. 3.

Fig. 3
figure 3

a Transmission with different h0, the bandgaps are denoted by the shaded areas; b Influence of h0 on the lower and upper bound of surface wave bandgap frequencies f1 and f2, as well as the width of the bandgap zone (∆f = f2–f1)

Full size image

As seen from Fig. 3(a), when h0 is 2 m or 5 m, the average transmission coefficient \(\overline{T }\) keeps about -23 dB. It can be seen that the attenuation of elastic surface waves by the metastructure is enhanced when h0 increases to 9 m. Notably, \(\overline{T }\) reaches -31.9 dB when h0 increases to 15 m. The bandgap property almost keeps stable when h0 increases to 5 m as shown in Fig. 3(b). Although increasing the embedded depth of the metastructures contributes to the improvement of the vibration reduction effect, it will bring more cost. Therefore, the embedded depth of the inclusions should be well-balanced in practice.

3.2 Effect of source depth

Practically, the source of vibration may locate at a certain depth below the ground surface so it is necessary to consider the effect of source depth on vibration reduction. Kee** the other parameters fixed and the depth of the metastructure taken as h0 = 9 m, the transmission curves for different values of source depth d as d = 0 m, d = 1 m, d = 2 m, d = 3 m, with the results shown in Fig. 4(a). It can be seen that the transmission coefficient firstly decreases when the depth of the source d increases from 0 to 1 m, then increases significantly when d increases to 2 m and 3 m.

Fig. 4
figure 4

a Transmission with different d, the bandgap zone are denoted by the shaded areas; b Elastic strain energy density field at point E in (a)

Full size image

However, as shown in Fig. 4(b), the metastructures still deflect the incident waves when the source depth reaches 3 m. This is due to the fact that as the depth of the source increases, a metastructure with bulk wave bandgaps is required to attenuate the vibration, but this metastructure has no bulk wave bandgap.

3.3 Effect of the density of the first-layer soil

Kee** other parameters fixed, the embedded depth of the metastructures is set as h0 = 15 m, and the depth of the source is set as d = 0 m. The transmission curves and surface wave bandgaps are obtained for the three different values of the first layer density ρ as ρ2 = 0.9 ρ1 = 1647 kg/m3, ρ1 = 1830 kg/m3, and ρ3 = 1.1 ρ1 = 2013 kg/m3, as the results shown in Fig. 5. It can be seen that increasing the density of the first layer actually decreases a bit the value of the transmission coefficient and has small influence on the position of the elastic surface wave bandgap. This can be attributed to the fact that the increased density of the first layer results in a denser soil, which decreases the amplitude of the displacement caused by vibration and provides a certain degree of vibration isolation.

Fig. 5
figure 5

a Transmission with different ρ, the bandgaps are denoted by the shaded areas; b Influence of ρ on the lower and upper bound of surface wave frequencies f1 and f2, as well as the width of the bandgap zone (∆f = f2–f1)

Full size image

3.4 Effect of the sequence of the layered soil

Since the elastic surface wave energy is mainly concentrated near the free surface, we consider the effect of the different order of the first four layers on the vibration isolation effect. As can be seen in Table 1, Young’s modulus of the fourth layer is quite different from that of the other three layers. Therefore, we primarily focus on the effect of different locations of the fourth layer on the vibration isolation. Keep other parameters fixed, the embedded depth of the metastructure is set as h0 = 20 m, the source depth is set as d = 0 m, and only the location of the fourth layer is changed. The layer is denoted by "1", "2", "3", "4" to represent the original first, second, third, and fourth layer, respectively. We consider the sequences of layers as "1234", "2341", "3412", "4123" and obtain the corresponding dispersion and transmission curves, as shown results in Fig. 6, where the horizontal coordinate D in (b) is the distance between the upper surface of the fourth layer and the free surface. It can be seen that as the fourth layer gradually moves upward, both of the position and width of the elastic surface wave bandgap increase, and the value of the transmission coefficient decreases. Since the Young’s modulus of the fourth layer is large, the shallower the depth of the fourth layer, the smaller the surface displacement response caused by the vibration on the ground.

Fig. 6
figure 6

a Transmission with different sequence, the bandgaps are denoted by the shaded areas. 1,2,3 and 4 represent the first, second, third, and fourth layer, respectively. b Influence of the sequence on the lower and upper bound of surface wave frequencies f1 and f2, as well as the width of the bandgap zone (∆f = f2–f1), D is the distance from the fourth layer of soil to the surface

Full size image

3.5 Effect of the soil viscosity

In all the previous studies, the soil was treated as linear elastic materials in the absence of viscosity. In this section soil viscosity is introduced and its effect on the vibration reduction of the metastructure is studied.

Firstly, we consider the effect of introducing viscosity to certain layer at different locations. The variation of the transmission spectra in view of introducing viscosity as η = 1 × 10−4μs to the certain layer is shown in Fig. 7(a). The solid and dashed lines represent the transmission spectra with and without the metastructure, respectively. It can be seen from Fig. 7(a) that the attenuation degree increases with the introduction of viscosity in any layer, regardless of the presence or absence of metastructures. Particularly, the viscosity of the first layer has the greatest impact on the vibration attenuation coefficient. When the viscosity of the first layer is introduced, the transmittance coefficient decreases even in the absence of the metastructure as seen the purple dashed line in Fig. 7(a). In the presence of metastructures, both the attenuation degree and the attenuation range increase compared to the case without viscosity, as seen the purple solid line in Fig. 7(a). Therefore, it is necessary to analyze the effect of different viscosity of the first layer on the vibration isolation. We consider different values of viscosity η for the first layer, as shown in Table 2, while setting η = 0 for the other layers. The corresponding transmission curves are shown in Fig. 7(b), demonstrating that the introduction of viscosity in the first layer increases the attenuation with or without the metastructure. With the increasing of the viscosity in the first layer, both of the transmission curves with and without the metastructure decrease, indicating an enhanced vibration isolation effect.

Fig. 7
figure 7

a The variation of the transmission spectra in view of introducing viscosities to the certain layer; b The variation of the transmission spectra in view of introducing different viscosities to the first layer; c The variation of the transmission spectra in view of introducing viscosities to certain layers. The solid and dashed lines represent the transmission spectra of the model with (W) and without (WO) metastructures, respectively

Full size image
Table 2 Value of the first layer viscosity
Full size table

In the above analyses, we have only considered the effect of viscosity in a single layer. Here the impact of introducing viscosity to multiple layers on the attenuation effect is further investigated. We set the viscosity value as η = 1 × 10−4μs, and the transmission curves are calculated for different scenarios: without introducing viscosity, introducing viscosity to the first layer, the first two layers, the first three layers, and the first four layers, respectively, as results shown in Fig. 7(c). In the plot, "0" represents the case that viscosity is not considered, while "1", " 12", "123", and "1234" indicate the number of layers where viscosity is introduced, respectively. From Fig. 7(c), we can see that as the number of layers introducing viscosity increases, the transmission curves shift towards low values, indicating an enhanced vibration isolation effect. It is easy to see that the difference between the results considering the viscosity of the first four layers and those considering the viscosity of the first three layers is relatively small. This suggests that considering the viscosity of the first three layers is already indicative of the problem in this work.

4 Conclusion

The isolation of elastic surface waves by metastructures with Bragg bandgap mechanism in layered soil is investigated in this work. Based on dispersion and transmission calculations, the effects of the embedded depth of the metastructure, source depth, soil density, arrangement order and soil viscosity on the elastic surface wave attenuation are further discussed. The results show that metastructures in layered soil can effectively attenuate elastic surface waves in the bandgaps. Increasing the embedded depth of the metastructure contributes to the improvement of the vibration reduction effect. An increase in the density of the first layer and a decrease in the burial depth of the harder layer will increase the frequency position and width of the bandgap, with enhanced vibration reduction effect. After the introduction of soil viscosity, the attenuation effect is generally enhanced. Especially, the viscosity of the first layer has the greatest influence on the attenuation coefficient, and the vibration reduction effect is gradually enhanced with the increase in the number of viscous soil layers. However, when the source is located at a certain depth, the attenuation efficiency decreases significantly due to the lack of bulk wave bandgap. The results of this work may retain a large potential for the design and optimization of metastructures in layered soil for applications in attenuating elastic surface waves. In the future, the effect of groundwater, the model of metastructures in other soil types, and the design for lower frequency and wider bandgaps can be further explored.