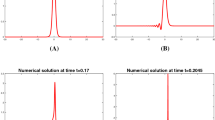
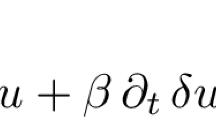Abstract
We study the periodic problem for the Korteweg–de Vries equation with Landau dam**, linear pum** and a higher-order convective nonlinearity
where, \(\alpha ,\beta >0,\) \(\lambda \in \mathbb {R},\) \(\Omega =\left[ -\pi ,\pi \right] .\) We assume that the initial data \(\psi \left( x\right) \) are \(2\pi \) - periodic. We prove the global existence of solutions and analyze their large-time asymptotics.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Our aim is to study the periodic problem for the for the Korteweg-de Vries equation with Landau dam**, linear pum** and a higher-order convective nonlinearity
where \(t,\alpha ,\beta >0\), \(\lambda \in \mathbb {R}\), \(\Omega =\left[ -\pi ,\pi \right] \), \(w=w(x,t)\) is the function that describes the wave amplitude as a function of position x and time t, \(w_{t}=\) \(\partial w/\partial t\) is the partial derivative of w with respect to time t, \(w_{xx}=\) \(\partial w^{2}/\partial x^{2}\) is the second order partial derivative of w with respect to position x, \(w_{xxx}=\) \(\partial w^{3}/\partial x^{3}\) is the third partial derivative of w with respect to position x, \(\alpha \) corresponds to effects of Landau dam**, \(\beta \) represents linear pum** \((\beta >0)\). The case of \(\beta <0,\) the \(\beta \) term converts to Landau dam** and \(w_{x}^{2}w_{xx}\) is the term associated with convective non linearity.
Equation (1) arises in various physical contexts, including the propagation of undular bores in shallow water [1], the flow of liquids containing gas bubbles [17], the propagation of waves in an elastic tube filled with a viscous fluid [9], weakly nonlinear plasma waves with certain dissipative effects [4, 8], and turbulence [13, 16].
Local well-posedness was established in [11, 12] using the weighted Sobolev spaces. Blowup results in the case of the Cauchy problem were obtained in [15], and global well-posedness was studied in [3, 7, 16]. The large time asymptotic behavior of solutions to the Cauchy problem for the Korteweg–de Vries-Burgers equations with different dissipative terms was extensively studied (see [5] and references cited therein). However, to the best of our knowledge, the large-time asymptotics for the periodic problem (1) with pum** and convective nonlinearity have not been previously considered. In this paper, we fill this gap and determine the asymptotic profile of solutions for large time. Our approach builds upon the work initiated in [2, 6, 10] and [14], with the present paper closely following the method presented in [2].
The main challenge in proving global existence of solutions lies in obtaining a priori estimates. In comparison to [2], we have to consider estimates in higher order Sobolev spaces. Notably, the energy-type estimates in our case turn out to be simpler than those in [2]. For \(\lambda >0\), we are able to eliminate the requirement of small initial data to obtain decay estimates for the solution with respect to time. However, when calculating the asymptotics of solutions for large times, we have to assume that the initial data are sufficiently small.
Changing the dependent variable \(w=e^{\beta t}v,\) we obtain
Denote the mean value \(\widehat{v}_{0}\left( t\right) =\frac{1}{2\pi } \int _{\Omega }v\left( t,x\right) dx.\) By equation (2) we have \(\widehat{v}_{0}^{\prime }=0.\) Hence \(\widehat{v}_{0}\left( t\right) =\widehat{\phi }_{0},\) where the mean value of the initial data \(\widehat{\phi }_{0}=\frac{1}{2\pi }\int _{\Omega }\psi \left( x\right) dx.\)
We now change the dependent variable \(u=v-\widehat{\phi }_{0},\) thus we get the following periodic problem
where the initial data \(\phi \left( x\right) =\psi \left( x\right) -\widehat{\phi }_{0},\) have zero mean value. We consider the solutions u of periodic problem (3), which have a zero mean value.
We give some notations. Denote the Sobolev space for the case of periodic functions
for any \(s\in \mathbf {R.}\) Here and below \(\left\langle k\right\rangle =\sqrt{1+k^{2}}\) and \(\widehat{\phi }_{k}=\frac{1}{2\pi }\int _{\Omega } e^{-ikx}\phi \left( x\right) dx\) are the Fourier coefficients of the \(2\pi \) - periodic function \(\phi \left( x\right) .\) For the functions with zero mean value we introduce the homogeneous Sobolev space \(\mathbf {\mathring{H}} ^{s}=\left\{ \phi \in \textbf{H}^{s}:\widehat{\phi }_{0}=0\right\} ,\) and homogeneous Lebesgue space \(\mathbf {\mathring{L}}^{2}=\left\{ \phi \in \textbf{L}^{2}:\widehat{\phi }_{0}=0\right\} ,\) so we have
By \(\textbf{C}\left( \textbf{I};\textbf{B}\right) \) we denote the space of continuous functions from a time interval \(\textbf{I}\) to the Banach space \(\textbf{B}\).
We state the main results of this paper.
Theorem 1
Let \(\lambda >0.\) Suppose that the initial data \(\phi \in \mathbf {\mathring{H}}^{1}\). Then there exists a unique solution \(u\in \textbf{C}\left( \left[ 0,\infty \right) ;\mathbf {\mathring{H}}^{1}\right) \) of the periodic problem (3). Moreover the time decay estimate \(\left\| u\left( t\right) \right\| _{\mathbf {\mathring{H}}^{1}}\le \left\| \phi \right\| _{\mathbf {\mathring{H}}^{1}}e^{-\alpha t}\) is true for all \(t\ge 0.\)
Proposition 2
Let \(\lambda >0.\) Suppose that \(\psi \in \textbf{H}^{1}\). Then there exists a unique solution \(w\in \textbf{C}\left( \left[ 0,\infty \right) ;\textbf{H}^{1}\right) \) of the periodic problem (1). Moreover the time growth estimate \(\left\| w\left( t\right) \right\| _{\textbf{H}^{1}}\le Ce^{\beta t}\) is fulfilled for all \(t\ge 0.\)
For the case of the equation (1) in view of the relation \(w=e^{\beta t}\left( u+\widehat{\phi }_{0}\right) \) we find the following result.
Theorem 3
Let \(\lambda <0,\) \(\alpha >\beta .\) Suppose that the initial data \(\phi \in \mathbf {\mathring{H}}^{2}\), and the norm \(\varepsilon =\left\| \phi \right\| _{\mathbf {\mathring{H}}^{2}}\) is small. Then there exists a unique solution \(u\in \textbf{C}\left( \left[ 0,\infty \right) ;\mathbf {\mathring{H}}^{2}\right) \) of the periodic problem (3). Moreover the time decay estimate \(\left\| u\left( t\right) \right\| _{\mathbf {\mathring{H}}^{2}}\le \left\| \phi \right\| _{\mathbf {\mathring{H}}^{2}}e^{-\beta t}\) is valid for all \(t\ge 0.\)
As a consequence we find the solutions of equation (1).
Proposition 4
Let \(\lambda <0,\) \(\alpha >\beta .\) Suppose that \(\psi \in \textbf{H}^{2}\) with small \(\varepsilon =\left\| \psi \right\| _{\mathbf {\mathring{H}}^{2}}\). Then there exists a unique solution \(w\in \textbf{C}\left( \left[ 0,\infty \right) ;\textbf{H}^{2}\right) \) of the periodic problem (1). Moreover the estimate \(\left\| w\left( t\right) \right\| _{\textbf{H}^{2}}\le C\varepsilon \) is true for all \(t\ge 0.\)
In order to calculate the large time asymptotic behavior of solutions we need estimates in higher-order Sobolev spaces. Denote \(L_{k}=\alpha k^{2}-ik^{3}.\)
Theorem 5
Let \(\lambda \in \mathbb {R},\) \(\alpha >2\beta .\) Assume that \({\text {Re}}L_{N}<2\left( \alpha -\beta \right) \) for some \(N\ge 1.\) Suppose that the initial data \(\phi \in \mathbf {\mathring{H}}^{4}\) with small \(\varepsilon =\left\| \phi \right\| _{\mathbf {\mathring{H}}^{4}}\).
Then there exists a unique solution \(u\in \textbf{C}\left( \left[ 0,\infty \right) ;\mathbf {\mathring{H}}^{4}\right) \) of the periodic problem (3). Moreover the time decay estimate \(\left\| u\left( t\right) \right\| _{\mathbf {\mathring{H}}^{2}}\le C\varepsilon e^{-\alpha t}\) is valid for all \(t\ge 0.\) Furthermore there exist \(\widehat{b_{k}}\) (which are defined below by formula (12)) such that the asymptotics
is true for \(t\rightarrow \infty \) uniformly with respect to \(x\in \Omega \), where \(\delta >0.\)
We can reformulate this result in terms of the equation (1) as follows.
Proposition 6
Let \(\lambda \in \mathbb {R},\) \(\alpha >2\beta .\) Assume that \({\text {Re}}L_{N}<2\left( \alpha -\beta \right) \) with \(N\ge 1.\) Suppose that the initial data \(\psi \in \textbf{H}^{4}\) have a small norm \(\varepsilon =\left\| psi\right\| _{\mathbf {\mathring{H}}^{4}}\). Then there exists a unique solution \(w\left( t,x\right) \in \textbf{C}\left( \left[ 0,\infty \right) ;\textbf{H}^{4}\right) \)of the periodic problem (1). Moreover the time growth estimate \(\left\| w\left( t\right) \right\| _{\mathbf {\mathring{H}}^{2}}\le C\varepsilon e^{\beta t}\) is fulfilled for all \(t\ge 0.\) Furthermore there exist \(\widehat{b_{k}}\) (which are defined below by formula (12)) such that the asymptotics
is true for \(t\rightarrow \infty \) uniformly with respect to \(x\in \Omega \), where \(\delta >0.\)
We organize the rest of our paper as follows. In the next two sections we prove Theorem 1 and Theorem 3, respectively. Section 4 is devoted to estimates of the Green operator corresponding to the linear periodic problem for the Korteweg-de Vries-Burgers equation. Then we prove Theorem 5 in Sect. 5.
2 Proof of Theorem 1
First we state the local existence result (see papers [11, 12] for the proof.)
Theorem 7
Suppose that the initial data \(\phi \in \mathbf {\mathring{H}}^{s}\), \(s\ge 0.\) Then there exists a time \(T>0,\) such that there exists a unique solution \(u\in \textbf{C}\left( \left[ 0,\infty \right) ;\mathbf {\mathring{H}}^{s}\right) \) of the periodic problem (3).
To get the estimate for the solution we multiply equation (3) by \(u_{xx}\) and integrate over \(\mathbf {\Omega }\). Then we obtain
where
and
Since the solution u has the zero mean value \(\widehat{u}_{0}=0,\) we have the estimate
Since \(\lambda >0\) we obtain \(H\ge 2\alpha \left\| u_{xx}\right\| _{\textbf{L}^{2}}^{2}\ge 2\alpha \left\| u_{x}\right\| _{\textbf{L}^{2} }^{2},\) therefore
Integration in time yields \(\left\| u_{x}\left( t\right) \right\| _{\textbf{L}^{2}}^{2}\le e^{-2\alpha t}\left\| \phi \right\| _{\textbf{L}^{2}}^{2}.\) Then using the local existence Theorem 7 we get the result of Theorem 1.
3 Proof of Theorem 3
To find the estimate for the higher-order energy, we multiply equation (3) by \(u_{xxxx}\) and integrate over \(\mathbf {\Omega }\)
We estimate the last two terms on the right-hand side of the above equation
and
Then we get
Lets us prove the estimate \(\left\| u_{x}\right\| _{\textbf{L}^{\infty }}<C\varepsilon e^{-\beta t}\) for all \(t\ge 0.\) By the contrary we can find a time \(T>0\) such that \(\left\| u_{x}\right\| _{\textbf{L}^{\infty }}=C\varepsilon e^{-\beta t}\) for \(t=T.\) Then we obtain
Using the fact that the solution u has a zero mean value, we obtain the estimate \(\left\| u_{xx}\right\| _{\textbf{L}^{2}}\le \left\| u_{xxx}\right\| _{\textbf{L}^{2}}.\) If \(\varepsilon >0\) is small enough, such that \(2\alpha -C\varepsilon ^{2}\ge 2\beta ,\) we get \(\frac{d}{dt}\left\| u_{xx}\right\| _{\textbf{L}^{2}}^{2}\le -2\beta \left\| u_{xx}\right\| _{\textbf{L}^{2}}^{2}.\) Integration in time yields \(\left\| u\right\| _{\textbf{H}^{2}}\le \left\| \phi \right\| _{\textbf{H}^{2}}e^{-\beta t}.\) Hence \(\left\| u_{x}\right\| _{\textbf{L}^{\infty }}<C\varepsilon e^{-\beta t}.\) We arrive to a contradiction. Therefore the estimate \(\left\| u_{x}\right\| _{\textbf{L}^{\infty }}<C\varepsilon e^{-\beta t}\) is fulfilled for all \(t\ge 0.\) Thus via Theorem 7 we get the result of Theorem 3.
4 Green Operator
Consider the linear periodic problem
where the force \(f\left( t,x\right) ,\) and the initial data \(\phi \left( x\right) ,\) are periodic : \(f\left( t,2\pi +x\right) =f\left( t,x\right) ,\) \(\phi \left( 2\pi +x\right) =\phi \left( x\right) ,\) for all \(x\in \mathbb {R}\textbf{,}\) \(t>0\) and have zero mean value.
We represent the solution by the Fourier series \(u=\sum _{\left| k\right| \ge 1}\widehat{u}_{k}e^{ixk},\) where the Fourier coefficients \(\widehat{u}_{k}=\frac{1}{2\pi }\int _{\Omega }e^{-ikx}u\left( x\right) dx.\) Then from equation (5) we get \(\widehat{u}_{k}^{\prime }-ik^{3}\widehat{u}_{k}+\alpha k^{2}\widehat{u}_{k}=\widehat{f}_{k}.\) Solving this equation we define the Green operator \(\mathcal {G}\left( t\right) \psi =\sum _{\left| k\right| \ge 1}\widehat{\psi }_{k}e^{ixk-L_{k}t},\) where the symbol \(L_{k}=\alpha k^{2}-ik^{3}.\) Thus we write the solution of the periodic problem (5) in the form
Also we define the projectors
and
for \(N\ge 1.\)
Next we obtain the estimates for the Green operator in the Sobolev space \(\mathbf {\mathring{H}}^{s}\).
Proposition 8
The following estimates are true
and
for all \(t>0,\) if \(\Lambda >{\text {Re}}L_{N},\) \(N\ge 1.\)
Proof
By the Parseval equality we obtain
Consequently, we find
Similarly
Hence we obtain
Lemma 8 is proved. \(\square \)
5 Proof of Theorem 5
Let us prove the estimates
for all \(t\ge 0.\) We argue by a contradiction. Assume that there exists a maximal time T such that \(\left\| u\right\| _{\mathbf {\mathring{H}}^{4}}\le C\varepsilon ,\) \(\left\| u\right\| _{\mathbf {\mathring{H}}^{2}}\le C\varepsilon e^{-\alpha t}\) for all \(t\in \left[ 0,T\right] .\) To get the estimate for the solution we multiply equation (3) by \(\partial _{x}^{8}u\) and integrate over \(\mathbf {\Omega }\). We get
Then we obtain
Hence
since \(\alpha \ge \beta \) and \(\varepsilon \) is small. Therefore \(\left\| u\right\| _{\mathbf {\mathring{H}}^{4}}<C\varepsilon \) for all \(t\in \left[ 0,T\right] .\)
We rewrite problem (3) in the form of the integral equation
Using estimates of Lemma 8 with \(N=1\) we find from equation (10)
for all \(t\in \left[ 0,T\right] ,\) if \(\alpha >2\beta .\) We obtain a contradiction. Hence estimates (9) are valid for all \(t\ge 0.\)
To prove the asymptotics, we define \(u_{N}\left( t\right) =\mathcal {P}_{N}u\) and \(r_{N+1}\left( t\right) =\mathcal {R}_{N+1}u,\) \(N\ge 1.\) Then we get \(u=u_{N}+r_{N+1}.\) By the integral equation (10) we find
Let us prove the estimate
for all \(t\ge 0.\) By the estimates of Lemma 8 with \(s=2\) we get
and
By the Sobolev imbedding inequality and estimates (9) we have
Hence
since \({\text {Re}}L_{N}+\delta <\Lambda \le 2\left( \alpha -\beta \right) \) with some small \(\delta >0.\) Thus we get estimate (11).
To calculate the asymptotics of solutions we define
and write the representation
By the last estimate of Lemma 8 we find
for all \(t>0,\) since \(\Lambda >{\text {Re}}L_{N}.\) As above we have
Hence
since \({\text {Re}}L_{N}+\delta <\Lambda \le 2\left( \alpha -\beta \right) \). Also we have
Hence we find the asymptotics (4). Note that the Fourier coefficients \(\widehat{b_{k}}\) of the function b can be estimated approximately by solving integral equation (10) via successive approximations. Let \(u^{\left( 0\right) }\left( t\right) =\mathcal {G}\left( t\right) \phi \) and define
for \(m\ge 0.\) Then the function b can be calculated approximately by
for sufficiently large \(m\ge 0.\) Theorem 5 is proved.
Data Availability
The study has no data.
References
Benney, D.J.: Long waves on liquid films. J. Math. Phys. 45, 150–55 (1966)
Carreño-Bolaños, R., Juárez-Campos, B., Naumkin, P.I.: Periodic problem for the nonlinear damped wave equation with convective nonlinearity. Stud. Appl. Math. 145(1), 137–149 (2020)
Constantin, P., Saut, J.-C.: Local smoothing properties of dispersive equations. J. Amer. Math. Soc. 1(2), 413–439 (1988)
Grad, H., Hu, P.N.: Unified shock profile in a plasma. Phys. Fluids 10, 2596–2602 (1967)
Hayashi, N., Kaikina, E.I., Naumkin, P.I., Shishmarev, I.A.: Asymptotics for dissipative nonlinear equations. Lecture Notes in Mathematics, vol. 1884. Springer-Verlag, Berlin (2006)
Hayashi, N., Naumkin, P.I., Rodriguez-Ceballos, J.A.: Asymptotics of solutions to the periodic problem for the nonlinear damped wave equation. NoDEA Nonlinear Differential Equations Appl. 17(3), 355–369 (2010)
Hirayama, H., Kinoshita, S., Okamoto, M.: Well-posedness for KdV-type equations with quadratic nonlinearity. J. Evol. Equ. 20(3), 811–835 (2020)
Hu, P.N.: Collisional theory of shock and nonlinear waves in a plasma. Phys. Fluids 15, 854–64 (1972)
Johnson, R.S.: A nonlinear equation incorporating dam** and dispersion. J. Fluid Mech. 42, 49–60 (1970)
Kaikina, E.I., Naumkin, P.I., Shishmarëv, I.A.: Asymptotic expansion of solutions of a periodic problem for a nonlinear equation of Sobolev type. Izv. Ross. Akad. Nauk Ser. Mat. 77(2), 97–108 (2013)
Kenig, C.E., Ponce, G., Vega, L.: Higher-order nonlinear dispersive equations. Proc. Amer. Math. Soc. 122(1), 157–166 (1994)
Kenig, C.E., Staffilani, G.: Local well-posedness for higher order nonlinear dispersive systems. J. Fourier Anal. Appl. 3(4), 417–433 (1997)
Liu, S.D., Liu, S.K.: KdV-Burgers equation modelling of turbulence. Sci. Sinica (Ser. A) 35, 576–586 (1992)
Naumkin, P.I., Rojas-Milla, C.J.: Asymptotics of solutions to the periodic problem for a Burgers type equation. J. Evol. Equ. 11(1), 107–119 (2011)
Pilod, D.: On the Cauchy problem for higher-order nonlinear dispersive equations. J. Differential Equations 245(8), 2055–2077 (2008)
Saut, J.-C.: Quelques generalisations de l’equation de Korteweg-de Vries. J. Differential Equations 33(3), 320–335 (1979)
van Wijngaarden, L.: On the motion of gas bubbles in a perfect fluid. Ann. Rev. Fluid Mech. 4, 369–73 (1972)
Acknowledgements
We are grateful with the referees for many useful suggestions and comments.
Funding
This research was carried out in support of Tecnológico Nacional de México/Instituto Tecnológico de Morelia and CONAHCYT.
Author information
Authors and Affiliations
Contributions
All authors carried out the analysis of the equation and drafted manuscript, read and approved the final manuscript.
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no competing interests.
Ethical approval and Consent to participate
Not applicable.
Consent for publication
Authors declare the consent for manuscript publication.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Juárez-Campos, B., Villela-Aguilar, J. & Carreño-Bolaños, R. Asymptotics of Solutions for Periodic Problem for the Korteweg-de Vries Equation with Landau Dam**, Pum** and Higher Order Convective Non Linearity. J Nonlinear Math Phys 30, 1316–1326 (2023). https://doi.org/10.1007/s44198-023-00131-7
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s44198-023-00131-7