The nth-Darboux Transformation and Explicit Solutions of the PT-Symmetry Second-Type Derivative Nonlinear Schrödinger Equation

Abstract

Non-local problems have become one of the research hotspots in recent years since Ablowitz–Musslimani constructed an integrable non-local nonlinear $\hbox {Schr}\ddot{\mathrm{o}}\hbox {dinger}$ (NLS) equation in 2013. In this paper, we first derive the PT-symmetry second derivative nonlinear $\hbox {Schr}\ddot{\mathrm{o}}\hbox {dinger}$ (PT-DNLSII) equation. Then we present the nth-Darboux transformation (DT) of the PT-DNLSII equation. As applications, starting from the zero seed solution and non-zero periodic seed solution, the explicit expressions of the multi-soliton solutions, bright soliton solution, dark soliton solution and breather soliton solution of the PT-DNLSII equation are worked out.

1 Introduction

Usually, many physical problems will occur in two or more places, and are related to each other, it is called multi-point problems. In order to work on such multi-point problems, the Alice–Bob system [1] is proposed. The Alice–Bob system describes that if A(x,t) is the state of Alice and B(x,t) is the state of Bob, then there will be an operator f that can describe the state of Alice and Bob. The relationship between

$$\begin{aligned} B(x_0,t_0) = fA(x,t), A(x,t) = f^{-1}B(x_0,t_0). \end{aligned}$$

(1)

Equivalently, the operator is required to satisfy the condition $f^2=1$. Generally, (x, t) is far away from $(x_0,t_0)$, so the two-point system, or Alice–Bob system, is a non-local system. Some special non-local models have been proposed. For example, in 2013, Ablowitz and Musslimani proposed a nonlinear Schr$\ddot{ o}$dinger equation (NLS) with $f=PC$ transformation [2], where P is the spatial inversion transformation and C is the charge conjugate transformation. After the pioneering work of Ablowitz-Musslimani, various non-local integrable models have been proposed. For example, the non-local AKNS model obtained by the Ablowitz–Kaup–Newell–Segur (AKNS) system [3], local KdV model [4], non-local NLS model obtained from discrete non-local NLS model [5, 6], coupled non-local NLS model [7, 8], non-local MKdV model [9] and so on, are still in the rapid development stage. These existed results inspire us to study the non-local equation further.

In 1979, the Chen–Lee–Liu (CLL) equation, also called the second derivative nonlinear $\hbox {Schr}\ddot{o}\hbox {dinger}$ equation (DNLSII), was proposed and proved to be integrable. In 2007, the physical meaning of the DNLSII equation was experimentally proved in optics aspect: this equation controls the propagation of the optical pulse which only has the self-steepening effect but without the self-phase-modulation. Also, this equation has a wide range of applications in the fields of weakly nonlinear dispersive water waves, nonlinear optics, etc. Therefore, it is interesting to study the PT-symmetry DNLSII equation.

In this paper, based on the coupled CLL equation, we construct the PT-symmetry DNLSII equation

$$\begin{aligned} iq_t+q_{xx}+iqq(-x+x_0,-t+t_0)q_x=0 \end{aligned}$$

in Sect. 2. Then, the nth-DT of the PT-symmetry DNLSII equation are constructed in Sect. 3. In Sect. 5, the multi-soliton solutions, periodic solution, bright soliton, dark soliton and breather solution are obtained. A conclusion is given in the last section.

2 PT-Symmetry DNLSII Equation

After Chen–Lee–Liu equated the linearisation equation of the nonlinear Hamilton system with the Lax pair time part [10] and started to find the Lax pair of the given equations, many equations have been obtained. One of them is an integrable coupled derivative NLS equation

$$\begin{aligned} \begin{array}{ll} &{}q_t=q_{xx}+qrq_{x},\\ &{}r_t=-r_{xx}+qrr_{x}.\\ \end{array} \end{aligned}$$

(2)

Let $r=q^*$, the DNLSII equation can be obtained

$$\begin{aligned} iq_t+q_{xx}+i|q|^2q_x=0. \end{aligned}$$

(3)

First, we construct an integrable coupled CLL system [11], as shown below

$$\begin{aligned} \begin{array}{ll} &{}q_t=q_{xx}+2(p+q)^{2}(r+s)(pr-qs)+2q(r+s)(p_x+q_x)+2[(p+q)(qs-pr)]_{x},\\ &{}p_t=p_{xx}-2(p+q)^{2}(r+s)(pr-qs)+2p(r+s)(p_x+q_x)+2[(p+q)(pr-qs)]_{x},\\ &{}r_t=-r_{xx}+2(p+q)(r+s)^{2}(pr-qs)+2r(p+q)(r_x+s_x)+2[(r+s)(pr-qs)]_{x},\\ &{}s_t=-s_{xx}-2(p+q)(r+s)^{2}(pr-qs)+2s(p+q)(r_x+s_x)+2[(r+s)(qs-pr)]_{x}. \end{array} \end{aligned}$$

(4)

If $p=q$, $s=r$, coupled CLL system can be obtained from the coupled system (4).

Then let $t = it$, $x = -ix$ and $r = \frac{r}{8}$, we can get

$$\begin{aligned} \begin{array}{ll} &{}iq_t+q_{xx}+qrq_{x}=0,\\ &{}ir_t - r_{xx}+qrr_{x}=0.\\ \end{array} \end{aligned}$$

(5)

The integrability of the coupled CLL system (4) can be guaranteed by the following Lax pairs:

$$\begin{aligned} \begin{array}{ll} \Psi _x=M\Psi ,\\ \Psi _t=N\Psi ,\,\,\,\,\Psi =(\psi _1,\psi _2)^{T} \end{array} \end{aligned}$$

(6)

$$\begin{aligned} M= & {} \left[ \begin{array}{cccc} -\frac{1}{2}(\lambda ^{2}-(p+q)(r+s)) &{} (q+q)\lambda &{}0&{}0\\ (r+s)\lambda &{} \frac{1}{2}(\lambda ^{2}-(p+q)(r+s))&{}0&{}0 \\ 0&{} (p-q)\lambda &{} -\frac{1}{2}(\lambda ^{2}-(p+q)(r+s))&{} (q+q)\lambda \\ (r-s)\lambda &{}0 &{}(r+s)\lambda &{}\frac{1}{2}(\lambda ^{2}-(p+q)(r+s)) \end{array} \right] ,\\ N= & {} \left[ \begin{array}{cccc} n_{11} &{} n_{12}&{}0 &{}0\\ n_{21}&{} -n_{11} &{}0 &{}0\\ n_{31}&{} n_{32}&{}n_{11} &{} n_{12}\\ n_{41}&{} -n_{31}&{} n_{21} &{}-n_{11} \end{array} \right] , \end{aligned}$$

with

$$\begin{aligned}n_{11}&=\alpha \lambda ^4+(p+q)(r+s)\lambda ^2-\frac{1}{2}(p+q)^2(r+s)^2-\frac{1}{2}(r+s)(p_x+q_x)+\frac{1}{2}(p+q)(r_x+s_x),\\n_{12}&=(p+q)\lambda ^{3}+[-(p+q)_{x}-(p+q)^{2}(r+s)]\lambda ,\,n_{21}=(r+s)\lambda ^{3}+[(r+s)_{x}-(p+q)(r+s)^{2}]\lambda ,\\n_{31}&=\beta \lambda ^{4}+2(pr-qs)\lambda ^2+8(p+q)(r+s)(qs-pr)-2rp_x+2sq_x+2pr_x-2qs_x,\\n_{41}&=(r-s)\lambda ^{3}+[r_x-s_x-4(r+s)(pr-qs)-(p+q)(r+s)(r-s)]\lambda . \end{aligned}$$

For the CLL system (4), let $p=q$, $s=r$, $r = \frac{r}{8}$, and then take the reduced condition $r = q( -x+x_0,-t+t_0)$, we get the DNLSII equation of the non-local system with PT-symmetry condition

$$\begin{aligned} iq_t+q_{xx}+iqq(-x+x_0,-t+t_0)q_x=0. \end{aligned}$$

(7)

3 Darboux Transformation of the PT-Symmetry DNLSII Equation

In this section, we will construct the DT of the PT-symmetry DNLSII equation. We first briefly review the DT of the coupled DNLSII equation

$$\begin{aligned} \begin{array}{ll} &{}iq_t+q_{xx}+iqrq_{x}=0,\\ &{}ir_t-r_{xx}+irqr_{x}=0,\\ \end{array} \end{aligned}$$

(8)

which has the following Lax pair:

$$\begin{aligned} \begin{array}{ll} \Phi _x=U\Phi =(-i\lambda ^2+\frac{i}{4}qr)J\Phi +\lambda Q\Phi , \\ \Phi _t=V\Phi =(-2i\lambda ^4+iqr\lambda ^2+\frac{1}{4}(qr_x-rq_{x})-\frac{i}{8}q^2r^2)J\Phi +2\lambda ^3Q\Phi +\lambda W\Phi , \end{array} \end{aligned}$$

(9)

with

$$\begin{aligned}&\Phi (x,t,\lambda )=(f(x,t,\lambda ),g(x,t,\lambda ))^{T},\\&J=\left( \begin{array}{cc} 1 &{} 0\\ 0 &{} -1 \end{array} \right) , Q=\left( \begin{array}{cc} 0 &{} q\\ -r &{} 0 \end{array} \right) , W=\left( \begin{array}{cc} 0 &{} iq_x-\frac{1}{2}q^2r\\ ir_x+\frac{1}{2}r^2q &{} 0 \end{array} \right) . \end{aligned}$$

Then, we suppose

$$\begin{aligned} T(\lambda )= \left( \begin{array}{cc} a_1 &{} b_1\\ c_1 &{} d_1 \end{array} \right) \lambda + \left( \begin{array}{cc} a_0 &{} b_0\\ c_0 &{} d_0 \end{array} \right) \end{aligned}$$

(10)

is the first-order DT of the coupled DNLSII equation, which transform U and V into $U^{[1]}$ and $V^{[1]}$ with q and r replaced by the new potentials $q^{[1]}$ and $r^{[1]}$. Taking the gauge transformation [12]

$$\begin{aligned} \Phi ^{[1]}=T^{[1]}\Phi , \end{aligned}$$

(11)

the Eq. (9) turns into

$$\begin{aligned} \begin{array}{ll} \Phi _{x}^{[1]}=(T_{x}^{[1]}+T^{[1]}U)(T^{[1]})^{-1}\Phi ^{[1]}=U^{[1]}\Phi ^{[1]},\\ \Phi _{t}^{[1]}=(T_{t}^{[1]}+T^{[1]}V)(T^{[1]})^{-1}\Phi ^{[1]}=V^{[1]}\Phi ^{[1]}, \end{array} \end{aligned}$$

(12)

i.e.

$$\begin{aligned} T_{x}+TU=U^{[1]}T,T_{t}+TV=V^{[1]}T. \end{aligned}$$

(13)

To determine $a_0$, $b_0$, $c_0$, $d_0$, $a_1$, $b_1$, $c_1$, $d_1$, the functions of x and t,we compare the coefficients of $\lambda ^{j},(j=0,1,2,3)$ of Eq. (12). In order to obtain non-trival solutions, we take $a_0=d_0=b_1=c_1=0$. After that we get the relationship between the new potentials $q^{[1]}$, $r^{[1]}$ and the old ones

$$\begin{aligned} \begin{array}{ll} q^{[1]}=\frac{1}{d_1}(a_1q+2ib_0),\\ r^{[1]}=\frac{1}{a_1}(d_1r+2ic_0). \end{array} \end{aligned}$$

(14)

From the relation $q(x,t)=r(-x+x_0,-t+t_0)$, we obtain the following constraints:

$$\begin{aligned} \begin{array}{ll} \frac{d_1(x,t)}{a_1(x,t)}=\frac{a_1(-x+x_0,-t+t_0)}{d_1(-x+x_0,-t+t_0)},\\ \frac{c_0(x,t)}{a_1(x,t)}=\frac{b_0(-x+x_0,-t+t_0)}{d_1(-x+x_0,-t+t_0)}. \end{array} \end{aligned}$$

(15)

In the same way, from correlation relationship $q^{[n]}=r^{[n]}(-x+x_0,-t+t_0)$, we can get the following relationships:

$$\begin{aligned} \begin{array}{ll} \frac{d_n(x,t)}{a_n(x,t)}=\frac{a_n(-x+x_0,-t+t_0)}{d_n(-x+x_0,-t+t_0)},\\ \frac{c_{n-1}(x,t)}{a_n(x,t)}=\frac{b_{n-1}(-x+x_0,-t+t_0)}{d_n(-x+x_0,-t+t_0)}.\,\,\,\,\,\,\,\,\,\, \end{array} \end{aligned}$$

(16)

Lemma 1

If $H=e^{\int _{(x_0,t_0)}^{(x,t)} \frac{1}{2}iqrdx-\frac{1}{4}(i q^2 r^2-2qr_x+2rq_x)dt}$,and $\frac{\partial H}{\partial x}=\frac{1}{2}iHqr$,$\frac{\partial H}{\partial t}=-\frac{1}{4}H(iq^2r^2-2qr_x+2rq_x)$,then $a_1b_0=\eta H.$

Suppose the eigenfunctions corresponding to the seed solutions are

$$\begin{aligned} \Phi _i=(f_i,g_i)^{T},i=1,2,\ldots ,n \end{aligned}$$

(17)

where $f_i$, $g_i$ are the functions of x, t and $\lambda _i$ respectively.

From the equation $T_1 \Phi _1=0$, we can obtain the following equation

$$\begin{aligned} a_1\lambda _1 f_1+b_0g_1=0,\,c_0f_1+d_1\lambda _1 g_1=0. \end{aligned}$$

(18)

Let $\eta =-\lambda _1$ in Lemma 1, the coefficients of $T_1$ can be expressed as the functions of $\lambda _1$

$$\begin{aligned} a_1=\sqrt{\frac{H}{h_1}},\,d_1=\sqrt{\frac{h_1}{H}},\,b_0=-\lambda _1 \sqrt{Hh_1},\,c_0=\frac{-\lambda _1}{\sqrt{Hh_1}}, \end{aligned}$$

(19)

where $h_1=\frac{f_1}{g_1}$.

Remark 1

In some cases, H can be solved. For example, when $q=r=0$, H is a constant. When $r(x,t)=q(-x+x_0,-t+t_0)=c e^{i(ax+bt)}$, $H=e^{-\frac{1}{4}ic^2(4aht+c^2h^2t-2hx)}$, where $h=e^{i(ax_0+bt_0)},b=-a^2-ac^2$.

Thus, the matrix of $T_1$ can be written as follows

$$\begin{aligned} T_1= \left( \begin{array}{cc} \sqrt{H} &{} \\ &{} \frac{1}{\sqrt{H}} \end{array} \right) \left( \begin{array}{cc} \frac{\lambda }{\sqrt{h_1}} &{} -\lambda _1 \sqrt{h_1}\\ -\frac{\lambda _1}{\sqrt{h_1}} &{}\lambda \sqrt{h_1} \end{array} \right) . \end{aligned}$$

(20)

From the explicit form of $T_1$ above, the recursive form of $q_1$ starting from q can be expressed as

$$\begin{aligned} q_1=\frac{H}{h_1}(q-2i\lambda _1 h_1),\,r_1=\frac{h_1}{H}\left( r-2i\frac{\lambda _1}{h_1}\right) . \end{aligned}$$

(21)

Remark 2

Compared with the classical DT for the Kaup-newell spectral problem [13], the Darboux matrix in our paper is more general and the determination of the the pending coefficients in the Darboux matrix depends on Lemma 1 rather than the symmetry relations.

Same as above, we can obtain the explicit form of $T_n$,

$$\begin{aligned} T_n=\sum_{l=0}^n P_{l}\lambda ^l \end{aligned}$$

(22)

where

$$\begin{aligned} P_n=\left( \begin{array}{cc} a_n^n &{} 0 \\ 0 &{} d_n^n \end{array} \right) ,\,P_{n-1}=\left( \begin{array}{cc} 0 &{} b_{n-1}^n \\ c_{n-1}^n &{} 0 \end{array} \right) . \end{aligned}$$

(23)

According to the article [12], the recursive solution of $q_n$ can be get from the matrix form of $T_n$ above.

$$\begin{aligned} q_n=\left\{ \begin{array}{c} \frac{\mid W_n^{'}\mid }{\mid W_n \mid }q-2i\frac{\mid M_n \mid }{\mid W_n \mid },n=2k \\ H\left( \frac{\mid W_n^{'}\mid }{\mid W_n \mid }q-2i\frac{\mid M_n \mid }{\mid W_n \mid }\right) ,n=2k-1 \end{array} k=1,2,3,\ldots \right. \end{aligned}$$

(24)

When $\hbox {n}=2\hbox {k}+1$,

$$\begin{aligned}&W_n=\left( \begin{array}{cccccccc} \lambda _1^{n-1}f_1 &{} \lambda _1^{n-2}g_1 &{} \lambda _1^{n-3}f_1 &{} \lambda _1^{n-4}g_1 &{} ...&{} \lambda _1^{2}f_1 &{} \lambda _1 g_1 &{} f_1 \\ \lambda _{2}^{n-1}f_2 &{} \lambda _2^{n-2}g_2 &{} \lambda _2^{n-3}f_2 &{} \lambda _2^{n-4}g_2 &{} ...&{} \lambda _2^{2}f_2 &{} \lambda _2 g_2 &{} f_2 \\ . &{} .&{}.&{}.&{}. &{} .&{}.\\ . &{} .&{}.&{}.&{}. &{} .&{}.\\ . &{} .&{}.&{}.&{}. &{} .&{}.\\ \lambda _n^{n-1}f_n &{} \lambda _n^{n-2}g_n &{} \lambda _n^{n-3}f_n &{} \lambda _n^{n-4}g_n &{} ...&{} \lambda _n^{2}f_n &{} \lambda _n g_n &{} f_n \end{array} \right) , \end{aligned}$$

(25)

$$\begin{aligned}&W_n^{'}=\left( \begin{array}{cccccccc} \lambda _1^{n-1}g_1 &{} \lambda _1^{n-2}f_1 &{} \lambda _1^{n-3}g_1 &{} \lambda _1^{n-4}f_1 &{} ...&{} \lambda _1^{2}g_1 &{} \lambda _1 f_1 &{} g_1 \\ \lambda _{2}^{n-1}g_2 &{} \lambda _2^{n-2}f_2 &{} \lambda _2^{n-3}g_2 &{} \lambda _2^{n-4}f_2 &{} ...&{} \lambda _2^{2}g_2 &{} \lambda _2 f_2 &{} g_2 \\ . &{} .&{}.&{}.&{}. &{} .&{}.\\ . &{} .&{}.&{}.&{}. &{} .&{}.\\ . &{} .&{}.&{}.&{}. &{} .&{}.\\ \lambda _n^{n-1}g_n &{} \lambda _n^{n-2}f_n &{} \lambda _n^{n-3}g_n &{} \lambda _n^{n-4}f_n &{} ...&{} \lambda _n^{2}g_n &{} \lambda _n f_n &{} g_n \end{array} \right) , \end{aligned}$$

(26)

$$\begin{aligned}&M_n=\left( \begin{array}{cccccccc} \lambda _1^n f_1 &{} \lambda _1^{n-2} f_1 &{} \lambda _1^{n-3} g_1 &{} \lambda _1^{n-4} f_1 &{}...&{} \lambda _1^2 g_1 &{} \lambda _1 f_1 &{} g_1 \\ \lambda _2^n f_2 &{} \lambda _2^{n-2} f_2 &{} \lambda _2^{n-3} g_2 &{} \lambda _2^{n-4} f_2 &{}...&{} \lambda _2^2 g_2 &{} \lambda _2 f_2 &{} g_2 \\ . &{} .&{}.&{}.&{}. &{} .&{}.\\ . &{} .&{}.&{}.&{}. &{} .&{}.\\ . &{} .&{}.&{}.&{}. &{} .&{}.\\ \lambda _n^n f_n &{} \lambda _n^{n-2} f_n &{} \lambda _n^{n-3} g_1 &{} \lambda _1^{n-4} f_1 &{}...&{} \lambda _1^2 f_1 &{} \lambda _1 g_1 &{} f_1 \\ \lambda _2^n f_2 &{} \lambda _2^{n-2} f_2 &{} \lambda _2^{n-3} g_2 &{} \lambda _2^{n-4} f_2 &{}...&{} \lambda _2^2 f_2 &{} \lambda _2 g_2 &{} f_2 \\ . &{} .&{}.&{}.&{}. &{} .&{}.\\ . &{} .&{}.&{}.&{}. &{} .&{}.\\ . &{} .&{}.&{}.&{}. &{} .&{}.\\ \lambda _n^n f_n &{} \lambda _n^{n-2} f_n &{} \lambda _n^{n-3} g_n &{} \lambda _n^{n-4} f_n &{}...&{} \lambda _n^2 f_n &{} \lambda _n g_n &{} f_n \\ \end{array} \right) . \end{aligned}$$

(27)

When $n=2k$,

$$\begin{aligned}&W_n=\left( \begin{array}{cccccccc} \lambda _1^{n-1}f_1 &{} \lambda _1^{n-2}g_1 &{} \lambda _1^{n-3}f_1 &{} \lambda _1^{n-4}g_1 &{} ...&{} \lambda _1^{2}g_1 &{} \lambda _1 f_1 &{} g_1 \\ \lambda _{2}^{n-1}f_2 &{} \lambda _2^{n-2}g_2 &{} \lambda _2^{n-3}f_2 &{} \lambda _2^{n-4}g_2 &{} ...&{} \lambda _2^{2}g_2 &{} \lambda _2 f_2 &{} g_2 \\ . &{} .&{}.&{}.&{}. &{} .&{}.\\ . &{} .&{}.&{}.&{}. &{} .&{}.\\ . &{} .&{}.&{}.&{}. &{} .&{}.\\ \lambda _n^{n-1}f_n &{} \lambda _n^{n-2}g_n &{} \lambda _n^{n-3}f_n &{} \lambda _n^{n-4}g_n &{} ...&{} \lambda _n^{2}g_n &{} \lambda _n f_n &{} g_n \end{array} \right) , \end{aligned}$$

(28)

$$\begin{aligned}&W_n^{'}=\left( \begin{array}{cccccccc} \lambda _1^{n-1}g_1 &{} \lambda _1^{n-2}f_1 &{} \lambda _1^{n-3}g_1 &{} \lambda _1^{n-4}f_1 &{} ...&{} \lambda _1^{2}f_1 &{} \lambda _1 g_1 &{} f_1 \\ \lambda _{2}^{n-1}g_2 &{} \lambda _2^{n-2}f_2 &{} \lambda _2^{n-3}g_2 &{} \lambda _2^{n-4}f_2 &{} ...&{} \lambda _2^{2}f_2 &{} \lambda _2 g_2 &{} f_2 \\ . &{} .&{}.&{}.&{}. &{} .&{}.\\ . &{} .&{}.&{}.&{}. &{} .&{}.\\ . &{} .&{}.&{}.&{}. &{} .&{}.\\ \lambda _n^{n-1}g_n &{} \lambda _n^{n-2}f_n &{} \lambda _n^{n-3}g_n &{} \lambda _n^{n-4}f_n &{} ...&{} \lambda _n^{2}f_n &{} \lambda _n g_n &{} f_n \end{array} \right) , \end{aligned}$$

(29)

$$\begin{aligned}&M_n=\left( \begin{array}{cccccccc} \lambda _1^n f_1 &{} \lambda _1^{n-2} f_1 &{} \lambda _1^{n-3} g_1 &{} \lambda _1^{n-4} f_1 &{}...&{} \lambda _1^2 f_1 &{} \lambda _1 g_1 &{} f_1 \\ \lambda _2^n f_2 &{} \lambda _2^{n-2} f_2 &{} \lambda _2^{n-3} g_2 &{} \lambda _2^{n-4} f_2 &{}...&{} \lambda _2^2 f_2 &{} \lambda _2 g_2 &{} f_2 \\ . &{} .&{}.&{}.&{}. &{} .&{}.\\ . &{} .&{}.&{}.&{}. &{} .&{}.\\ . &{} .&{}.&{}.&{}. &{} .&{}.\\ \lambda _n^n f_n &{} \lambda _n^{n-2} f_n &{} \lambda _n^{n-3} g_n &{} \lambda _n^{n-4} f_n &{}...&{} \lambda _n^2 f_n &{} \lambda _n g_n &{} f_n \\ \end{array} \right) . \end{aligned}$$

(30)

Theorem

Let $g_k = f_k(-x+x_0,-t+t_0).$ Then the nth order solutions $(q_n,r_n)$ satisfy the reduction condition $r_n = q_n(-x+x_0,-t+t_0).$

Proof

For $n = 1$, let $g_1 = f_1(-x+x_0,-t+t_0)$. According to Eq. (14), we get

$$\begin{aligned}&q_1(-x+x_0,-t+t_0) = \frac{H\left( -x+x_0,-t+t_0\right) }{h_1(-x+x_0,-t+t_0)}\\&\quad [q(-x+x_0,-t+t_0)-2i\lambda _1h_1(-x+x_0,-t+t_0)]. \end{aligned}$$

Putting the expressions of $b_0$, $c_0$ into Eq. (16) to get

$$\begin{aligned} HH(-x+x_0,-t+t_0)=1, \end{aligned}$$

then

$$\begin{aligned} q_1(-x+x_0,-t+t_0) = \frac{h_1}{H}\left( r-2i\frac{\lambda _1}{h_1}\right) = r_1(x,t). \end{aligned}$$

For $n = 2$, let $g_1 = f_1(-x+x_0,-t+t_0)$, $g_2 = f_2(-x+x_0,-t+t_0)$. According to Eq. (24), we get

$$\begin{aligned}&q_2=q\frac{\left| \begin{array}{cc} \lambda _1 g_1 &{} f_1 \\ \lambda _2 g_2 &{} f_2 \end{array} \right| }{\left| \begin{array}{cc} \lambda _1 f_1 &{} g_1 \\ \lambda _2 f_2 &{} g_2 \end{array} \right| }-2i \frac{\left| \begin{array}{cc} \lambda _1^2 f_1 &{} f_1 \\ \lambda _2^2 f_2 &{} f_2 \end{array} \right| }{\left| \begin{array}{cc} \lambda _1 f_1 &{} g_1 \\ \lambda _2 f_2 &{} g_2 \end{array} \right| }, \end{aligned}$$

(31)

$$\begin{aligned}&r_2=r\frac{\left| \begin{array}{cc} \lambda _1 f_1 &{} g_1 \\ \lambda _2 f_2 &{} g_2 \end{array} \right| }{\left| \begin{array}{cc} \lambda _1 g_1 &{} f_1 \\ \lambda _2 g_2 &{} f_2 \end{array} \right| }-2i \frac{\left| \begin{array}{cc} \lambda _1^2 g_1 &{} g_1 \\ \lambda _2^2 g_2 &{} g_2 \end{array} \right| }{\left| \begin{array}{cc} \lambda _1 g_1 &{} f_1 \\ \lambda _2 g_2 &{} f_2 \end{array} \right| }, \end{aligned}$$

(32)

and

$$\begin{aligned} q_2(-x+x_0,-t+t_0)=r\frac{\left| \begin{array}{cc} \lambda _1 f_1 &{} g_1 \\ \lambda _2 f_2 &{} g_2 \end{array} \right| }{\left| \begin{array}{cc} \lambda _1 g_1 &{} f_1 \\ \lambda _2 g_2 &{} f_2 \end{array} \right| }-2i \frac{\left| \begin{array}{cc} \lambda _1^2 g_1 &{} g_1 \\ \lambda _2^2 g_2 &{} g_2 \end{array} \right| }{\left| \begin{array}{cc} \lambda _1 g_1 &{} f_1 \\ \lambda _2 g_2 &{} f_2 \end{array} \right| }. \end{aligned}$$

(33)

That is, $r_2 = q_2(-x+x_0,-t+t_0)$.

The same can be proved, in the case $n>2$, $r_n = q_n(-x+x_0,-t+t_0)$ can be proved. $\square$

4 Soliton Solutions of the PT-Symmetry DNLSII Equation

In this section, we will present some exact solutions of the PT-symmetry DNLSII equation, including the single-soliton solution, two-soliton solution, periodic solution, dark and bright-soliton solutions and breather solution.

4.1 One-Soliton Solution and Two-Soliton Solution from Zero Seed

Starting from the zero solution, according to the recursive form of the solution obtained by Darboux Transformation, we can find some explicit solution expressions.

When $q=r=0$, the eigenfunctions $\Phi _k=(f_k,g_k)^T$ obtained by solving the Lax pair (9) can be written as:

$$\begin{aligned} \left\{ \begin{array}{c} f_k=\gamma _{1k}e^{-i\lambda _k^2 x-2i\lambda _k^4 t},\\ g_k=\gamma _{2k}e^{i\lambda _k^2 x+2i\lambda _k^4 t}. \end{array} \right. \end{aligned}$$

(34)

Next, substituting $a_1=\sqrt{\frac{H}{h_1}},d_1=\sqrt{\frac{h_1}{H}}$ into Eq. (16), we can get the following relationship between $h_1$ and H,

$$\begin{aligned} \frac{h_1(x,t)}{H(x,t)}=\frac{H(-x+x_0,-t+t_0)}{h_1(-x+x_0,-t+t_0)}, \end{aligned}$$

(35)

that is

$$\begin{aligned} \frac{f_1(x,t)f_1(-x+x_0,-t+t_0)}{g_1(x,t)g_1(-x+x_0,-t+t_0)}= H(x,t)H(-x+x_0,-t+t_0). \end{aligned}$$

(36)

After that, put the expressions of $b_0,c_0$ into Eq. (16) to get

$$\begin{aligned} H(x,t)H(-x+x_0,-t+t_0)=1. \end{aligned}$$

(37)

Hence, it can be easily obtained by Eqs. (36) and (37) that

$$\begin{aligned} \frac{f_1(x,t)f_1(-x+x_0,-t+t_0)}{g_1(x,t)g_1(-x+x_0,-t+t_0)}=1. \end{aligned}$$

(38)

From Eq. (38) we can get that $\gamma _{11}$ and $\gamma _{21}$ should satisfy

$$\begin{aligned} \frac{\gamma _{11}^2}{\gamma _{21}^2}=e^{2i\lambda _1^2 x_0+4i\lambda _1^4 t_0}. \end{aligned}$$

(39)

In the same way, the following relationship holds for order k

$$\begin{aligned} \frac{\gamma _{1k}^2}{\gamma _{2k}^2}=e^{2i\lambda _k^2 x_0+4i\lambda _k^4 t_0}. \end{aligned}$$

(40)

Therefore, the eigenfunctions $f_k, g_k$ at order k satisfy

$$\begin{aligned} \frac{g_k}{f_k}=\frac{\gamma _{2k}}{\gamma _{1k}}e^{2i\lambda _k^2 x+4i\lambda _k^4 t}=e^{i\lambda _k^2[2x-x_0 +(4t-2t_0)\lambda _k^2]}. \end{aligned}$$

(41)

For n = 1, according to Eq. (21), we obtain

$$\begin{aligned} q_1=2\beta , \end{aligned}$$

(42)

which is a trivial solution of the PT-symmetry DNLSII equation.

Fig. 1

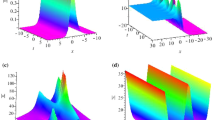
Display of the structures for four kinds of solution with $\lambda _1 = 0.3+0.2i$, $\lambda _2 = -0.3+0.2i,\, t_0=5,\,x_0=-3$; $\lambda _1 = 0.2i$, $\lambda _2 = 0.2+0.2i,\,t_0=5,\,x_0=-3$; $\lambda _1 = 0.05i$, $\lambda _2 = 0.2+0.2i,\,t_0=0,\,x_0=0$ and $\lambda _1 = 1-i$, $\lambda _2 = 0.8i,\,t_0=40,\,x_0=-1$ respectively

When $\hbox {n}=2$, one-soliton solution is worked out

$$\begin{aligned}&q_2=q\frac{\left| \begin{array}{cc} \lambda _1 g_1 &{} f_1 \\ \lambda _2 g_2 &{} f_2 \end{array} \right| }{\left| \begin{array}{cc} \lambda _1 f_1 &{} g_1 \\ \lambda _2 f_2 &{} g_2 \end{array} \right| }-2i \frac{\left| \begin{array}{cc} \lambda _1^2 f_1 &{} f_1 \\ \lambda _2^2 f_2 &{} f_2 \end{array} \right| }{\left| \begin{array}{cc} \lambda _1 f_1 &{} g_1 \\ \lambda _2 f_2 &{} g_2 \end{array} \right| }\nonumber \\&\quad =-2i(\lambda _1^2-\lambda _2^2)\frac{1}{\frac{\lambda _1}{h_2}-\frac{\lambda _2}{h_1}}\nonumber \\&\quad =\frac{2i(\lambda _2^2-\lambda _1^2)}{ \lambda _1 e^{\xi _2-\frac{1}{2}\xi _2(x_0,t_0)}- \lambda _2 e^{\xi _1-\frac{1}{2}\xi _1(x_0,t_0)}},\nonumber \\&\quad \xi _{j}(x,t)=2i\lambda _j^2(x+2\lambda _j^2 t),j=1,2. \end{aligned}$$

(43)

Then for $\hbox {n} = 3$, it is still a single-soliton solution. The structure of $|q_2|^{2}$ is shown in Fig. 1. The first column is a standard left propagating single-soliton. The second column shows a stationary soliton whose amplitude changes with time. The third column shows a rightward propagating soliton-like solution with time-varying amplitude and the fourth column reveal a kink-shape solution.

Fig. 2

a The two-soliton solutions from zero seed with $x_0=t_0=0$, $\lambda _1 = 0.3+0.4i$, $\lambda _2=-0.3+0.4i$, $\lambda _3 = 0.36+0.5i$, $\lambda _4 = -0.36+0.5i.$ b The process of two-soliton interaction

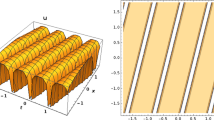
Figure 2 shows that, the two-soliton solutions are obtained from zero seed when $n=4$. The first two solitons will meet and then separate over time. And there is no change in the waveform before and after the encounter, which is in line with the characteristics of solitons. Taking special values of $\lambda _j$, two kinds of periodic solutions are presented, as shown in Fig. 3.

Fig. 3

a The periodic solution with $\lambda _1 = 0$, $\lambda _2 = 0.8i$, $\lambda _3 = -0.2i$, $\lambda _4 = 0.4i$, $x_0=2$, $t_0=1.$ b The periodic solution with $\lambda _1 = 0.5$, $\lambda _2 = 0.2$, $\lambda _3 = 0.5i$, $\lambda _4 = -0.5i$, $x_0 = 0.1$, $t_0 = 0.$

4.2 Dark and Bright-Soliton Solutions and Breather Solution from Periodic Seed

Here, we will discuss the solutions generated from a periodic seed solution. Set a periodic seed

$$\begin{aligned} q = c e^{i\rho }, \qquad \rho = ax+bt, \qquad b=-a^2-c^2a, \qquad a,c\in R \end{aligned}$$

(44)

According to Remark 1, $H =e^{-\frac{1}{4}ic^2(4aht+c^2h^2t-2hx)}$, $h =e^{i(ax_0+bt_0)}$. Solving the Lax pair (9) with this seed solution and separating variables, we get a solution corresponding to an eigenfunction $\lambda$ as

$$\begin{aligned} \left( \begin{array}{c} f(x,t,\lambda )\\ g(x,t,\lambda ) \end{array} \right) = \left( \begin{array}{c} e^{i\{\frac{\rho }{2}-\frac{s}{4}x+[\frac{2a+c^2h-4\lambda ^2}{8}s+\frac{1}{2}ac^2(1-h)]t\}}\\ \frac{i(2a-s+4\lambda ^2-c^2h^2)}{4c\lambda }e^{i\{-\frac{\rho }{2} -\frac{s}{4}x+\left[ \frac{2a+c^2h-4\lambda ^2}{8}s+\frac{1}{2}ac^2(1-h)\right] t\}}\ \end{array} \right) \end{aligned}$$

(45)

with

$$\begin{aligned} s = \sqrt{4a^2+16a\lambda ^2-4ac^2h+c^4h^2+8c^2h\lambda ^2+16\lambda ^4}, \qquad h =e^{i(ax_0+bt_0)}. \end{aligned}$$

(46)

In the condition of $q = r(-x+x_0,-t+t_0)$, it is obviously that $\left( \begin{array}{c} g(-x+x_0,-t+t_0,\lambda )\\ f(-x+x_0,-t+t_0,\lambda ) \end{array} \right)$ is also a solution of the Lax pair (9). To satisfy the Eq. (38) we need to construct a new solution of the Lax pair. Let

$$\begin{aligned} \left( \begin{array}{c} F_j(x,t,\lambda _j)\\ G_j(x,t,\lambda _j) \end{array} \right) = \left( \begin{array}{c} f_j(x,t,\lambda _j)+g_j(-x+x_0,-t+t_0,\lambda _j)\\ g_j(x,t,\lambda _j)+f_j(-x+x_0,-t+t_0,\lambda _j) \end{array} \right) . \end{aligned}$$

(47)

Obviously, this is a solution of the Lax pair (9). Next, we will use this eigenfunction to construct the new solutions of PT-DNLSII equation.

Let $n = 1$, $\lambda = i\beta$, the first-order solution is obtained by Eq. (21).

$$\begin{aligned} q_1 = e^{-\frac{i}{4}c^2(4aht+c^2h^2t-2hx)}\frac{2\lambda u(2a-s+4\lambda ^2-c^2h^2+2c^2h)+ic\sqrt{h}(2a-s-4\lambda ^2-c^2h^2)\Gamma ^2}{4c\lambda \sqrt{h}\Gamma ^2+i(2a-s+4\lambda ^2-c^2h^2)u} \end{aligned}$$

(48)

with

$$\begin{aligned}&\Gamma ^2 = e^{2i\{-\frac{s}{4}x+[\frac{2a+c^2h-4\lambda ^2}{8}s+\frac{1}{2}ac^2(1-h)]t\}},\\&u = e^{i\{-\frac{s}{4}x_0+[\frac{2a+c^2h-4\lambda ^2}{8}s+\frac{1}{2}ac^2(1-h)]t_0\}}. \end{aligned}$$

It can generate a dark soliton and a bright soliton as showed in Fig. 4.

Fig. 4

a A bright soliton with $a = 0.3$, $c= 0.3$, $x_0 = 0.2$, $t_0 = 0.5$, $\lambda = 0.5i$. b A dark soliton with $a = 0.3$, $c=0.3$, $x_0=0.2$, $t_0=0.5$, $\lambda = -0.5i$

Let $\hbox {n} = 2$. In order to get breather solution of the equation, let

$$\begin{aligned} a = -2\alpha _1^2+2\beta _1^2-\frac{1}{2}c^2=-2\alpha _2^2+2\beta _2^2-\frac{1}{2}c^2, \qquad ax_0+bt_0 = 0 \end{aligned}$$

(49)

so that the imaginary part of $4a^2+16a\lambda _j^2-4ac^2h+c^4h^2+8c^2h\lambda _j^2+16\lambda _j^4$ equals 0 so that $s= 2\sqrt{c^4+4c^2\alpha _j^2-4c^2\beta _j^2-16\alpha _j^2\beta _j^2}=2k_j$, $j = 1,2.$ Then, the second-order solution is obtained by Eq. (31)

$$\begin{aligned} q_2=q\frac{\left| \begin{array}{cc} \lambda _1 G_1 &{} F_1 \\ \lambda _2 G_2 &{} F_2 \end{array} \right| }{\left| \begin{array}{cc} \lambda _1 G_1 &{} F_1 \\ \lambda _2 F_2 &{} G_2 \end{array} \right| }-2i \frac{\left| \begin{array}{cc} \lambda _1^2 F_1 &{} F_1 \\ \lambda _2^2 F_2 &{} F_2 \end{array} \right| }{\left| \begin{array}{cc} \lambda _1 F_1 &{} G_1 \\ \lambda _2 F_2 &{} G_2 \end{array} \right| }. \end{aligned}$$

(50)

Let $k_j^2>0$

$$\begin{aligned} \left( \begin{array}{c} F_j\\ G_j \end{array} \right) = \left( \begin{array}{c} L e^{\theta _{2j}} e^{i\theta _{1j}}+\frac{v_j}{L^o}e^{\theta _{2j}^o}e^{i\theta _{1j}^o}Le^{-\theta _{2j}}e^{-i\theta _{1j}}\\ L^oe^{\theta _{2j}^o}e^{i\theta _{1j}^o}\frac{1}{L}e^{-\theta _{2j}}e^{-i\theta _{1j}}+\frac{v_j}{L}e^{\theta _{2j}}e^{i\theta _{1j}} \end{array} \right) \end{aligned}$$

(51)

with

$$\begin{aligned}&L =e^{\frac{i\rho }{2}}, \, \theta _{1j} = -\frac{k_j}{2}x+2k_j(\beta _j^2-\alpha _j^2)t,\,\theta _{2j} = 2k_j\alpha _j\beta _j t,\\&L^0 =e^{\frac{i(ax_0+bt_0)}{2}}, \, \theta _{1j}^0 = -\frac{k_j}{2}x_0+2k_j(\beta _j^2-\alpha _j^2)t_0,\, \theta _{2j}^0 = 2k_j\alpha _j\beta _j t_0,\\&v_j = \frac{-\beta _j(c^2+k_j+4\alpha _j^2)+i\alpha _j(-c^2-k_j+4\beta _j^2)}{2c(\alpha _j^2+\beta _j^2)}, \, j = 1,2. \end{aligned}$$

In order to satisfy the Eq. (49), let $\alpha _2 = -\alpha _1$, $\beta _2 = \beta _1$. Then it can generate the breather solution of PT-DNLSII equation as showed in Fig. 5.

Fig. 5

a A breather with $\alpha _1 = 0.4$, $\beta _1 = 0.2$, $x_0 = 0$, $t_0=0, c = 3.$ b The corresponding density profile

5 Conclusion

The study of analytical solutions to nonlinear equations is one of the important issues studied by mathematical physicists in recent years. This article introduces the PT symmetric DNLSII equation studied in this article on the basis of the research significance and background. Firstly, the recursive form of the n-th order solution of the general DNLSII equation is derived with the help of the Darboux transformation matrix. Then, according to the constraints of PT symmetry, the conditions that the parameters of the solution need to meet are deduced, and the solution of the PT-symmetry DNLSII equation is obtained. Finally, starting from zero and non-zero solutions, the expressions of explicit solutions are given.

It is found that the PT-symmetry DNLSII equation possesses abundant solution structures. Starting from the zero solution, the standard multi-soliton solution, the soliton-like solution, kink-shape solution and periodic solutions are obtained. Among them, the two-soliton solution have no molecular structure [14] because it will be reduced to a single soliton when the velocities of two solitons are the same. Starting from the periodic seed solution, bright soliton, dark soliton and breather solution are obtained. Based on the breather solution, the rogue wave [15] can be obtained by series expansion and taking the limit [16]. We will study this problem in detail in another paper.