1 Introduction

Vibration control plays a critical role in industrial productions and has become one of the most important research topics in the field of nonlinear dynamics. Many types of vibration control techniques and efficient devices have been developed over the years. Dynamic vibration absorber (DVA), as one of the common devices for vibration control, has been widely used in engineering practice such as transportation, earthquake and civil engineering due to it’s simple structure and low cost.

A dynamic vibration absorber is a device that reduces the vibration of a primary vibration system by absorbing the vibration energy of the primary system through control structures attached to the primary system. In recent decades, various structural forms and working methods of the DVA have been proposed. The first DVA without dam** was invented by Frahm [1] in 1909. In 1928, Ormondroyd and Den Hartog [2, 3] found that a DVA with dam** element could suppress the amplitude of the primary system in a broader frequency range, which had been recognized as the typical Voigt type DVA. Den Hartog and Ormondroyd also proposed the optimization principle of the damped DVA in terms of minimizing the maximum amplitude response of the primary system. This optimum design method of the dynamic vibration absorber is called the fixed-points theory, which was well documented in the textbook by Den Hartog [3]. In 2001, Ren [4] presented a DVA where the dam** element was not connected to the primary system, but to the earth or the base structure. The result indicated it could present better control performance than Voigt type DVA under the same parameters condition. Thereafter, Asami et al. [5,6,7] derived the exact series solutions for the optimum frequency and dam** ratios of the DVA attached to damped linear systems.

The general definition of stiffness is the load that an elastic element bears when it produces a unit deformation. If the deformation increases with the increase of load, the stiffness is positive. If the load increases and the deformation decreases, the stiffness is negative. Devices made up of a number of basic components exhibit negative stiffness characteristics under certain conditions, such as inverted pendulum, magnetic device, pressure bar device, etc. Negative stiffness element has been widely used in system vibration reduction in recent years because of its advantages of large bearing capacity, small deformation and good controllability, and the parallel use of positive stiffness element can effectively solve the contradiction between low stiffness and high static load shape variables. Thus, it is necessary and meaningful to draw into the negative stiffness to the vibration control system. In 2013, Acar et al. [8] analyzed and experimentally studied an adaptive passive DVA with a negative stiffness mechanism and found that it can suppress the amplitude of the system by appropriately adjusting the parameters. Yang et al. [19] discussed the advantages and disadvantages of the inerter in the vibration isolation system, and proposed a simple method to improve the high frequency performance of the system. De Domenico et al. [20] proposed a vibration control system that combines a traditional foundation isolation scheme with an inertial foundation device. When inertiators are mounted in series with spring and damper elements, a lower mass and more efficient alternative to conventional tuned mass damper where device inertia plays a role in tune mass damper is obtained. Based on the sensitivity analysis, the effect of detuning is discussed.These studies show that the introduction of inerter has a potential advantage in improving the performance of the DVA. Kim et al. [21] proposed and analyzed the optimal design of friction multi-tuned mass dampers, studied the use of statistical linearization to replace the original nonlinear system and the equivalent linear system, and found a primary structure of optimal design to minimize the root mean square displacement. Sun et al. [22] studied a vibration isolation system of n-layer scissor structure, analyzed and designed nonlinear stiffness, friction and dam** characteristics, and it is easy to achieve better vibration isolation performance and loading capacity by designing structural parameters. Bian et al. [23] designed a novel tunable nonlinear tuned mass damper using a bionic X-type structure. Compared with traditional absorbers, X absorbers can significantly improve the robustness of system parameters, expand anti-resonance and expand vibration suppression bandwidth. These studies showed that the introduction of inerter has a potential advantage in improving the performance of the DVA.

As described above, inerter can change the inertia characteristics of the system without changing the physical mass of the structure, grounding stiffness can adjust the stiffness characteristics of the system. Both devices can change the natural frequency of the system, and improve the performance of the vibration absorber. The control performance of the dynamic vibration absorber can be improved by using the grounded negative stiffness and inertial vessel simultaneously, but most of the current researches only introduce inertial vessel or the grounded negative stiffnes into the dynamic vibration absorber.

In this paper the effect of the negative stiffness and inerter on the amplitude of the primary system is studied by introducing inerter and the negative stiffness which is connected the DVA with the earth. Section 2 presents the model and optimizes the system parameters based on the fixed-point theory. Section 3 compares the present DVA with other typical DVAs under harmonic and random excitations, the results verify the DVA in this paper has more significant control performance. The conclusion is drawn finally in Sect. 4.

2 The Model of DVA and Parameters Optimization

2.1 Dynamic Model of DVA

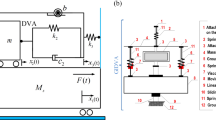
Figure 1 shows the dynamic vibration absorber model proposed in this paper, where \(m_1\), \(m_2\), \(k_1\) and \(k_2\) are the masses, linear stiffness coefficients of the primary system and the DVA respectively. c is the dam** coefficient of the absorber, b is the inertance and k is the negative stiffness coefficient. \(x_1\) and \(x_2\) are the displacements of the primary system and the DVA respectively. F and \(\omega\) are the amplitude and frequency of the force excitation.

Fig. 1
figure 1

The model of DVA with negative stiffness and inerter-mass

Full size image

According to Newton’s second law, the motion equation of the system with negative stiffness can be established as

$$\begin{aligned}&m_1\ddot{x}_1+(k_1+k_2) x_1-k_2 x_2+b\ddot{x}_1-b\ddot{x}_2=F\cos {(\omega t)}\nonumber \\&m_2\ddot{x}_2+(k+k_2) x_2-k_2 x_1+c\dot{x}_2-b\ddot{x}_1+b\ddot{x}_2=0 \end{aligned}$$
(1)

Using the following parametric transformation

$$\begin{aligned} \omega _1&=\sqrt{\frac{k_1}{m_1}}, \quad \omega _2=\sqrt{\frac{k_2}{m_2}}, \quad \xi =\frac{c}{2 m_2 \omega _2} \\\mu&=\frac{m_2}{m_1}, \quad \alpha =\frac{k}{k_2}, \quad f=\frac{F}{m_1}, \quad h=\frac{b}{m_2} \end{aligned}$$

Eq. (1) becomes

$$\begin{aligned}&\ddot{x}_1 + (\omega _1^2+\mu \omega _2^2) x_1-\mu \omega _2^2 x_2 + \mu h \ddot{x}_1 - \mu h \ddot{x}_2=f \cos {(\omega t)} \nonumber \\&\ddot{x}_2 + (\alpha \omega _2^2+ \omega _2^2) x_2 - \omega _2^2 x_1 + 2 \omega _2 \xi \dot{x}_2 - h \ddot{x}_1 + h\ddot{x}_2=0 \end{aligned}$$
(2)

2.2 The Analytical Solution

Letting \(f \cos {(\omega t)}\) in Eq. (2) be represented by \(f e^{j\omega t}\), the steady state solutions take the forms as

$$\begin{aligned} x_1=X_1 e^{j\omega t}, \quad x_2=X_2 e^{j\omega t} \end{aligned}$$
(3)

Substituting (3) into (2), one could obtain

$$\begin{aligned} X_1=\frac{A_2 f}{A_1 A_2-B_1 B_2},\quad X_2=-\frac{B_2 f}{A_1 A_2-B_1 B_2} \end{aligned}$$
(4)

where

$$\begin{aligned} A_1&=-\omega ^2+\omega _1^2+\mu (\omega _2^2-h \omega ^2) \nonumber \\ A_2&=-(h+1)\omega ^2+\omega _2^2(\alpha +1)+2j\omega \omega _2 \xi \nonumber \\ B_1&=\mu (h \omega ^2-\omega _2^2) \nonumber \\ B_2&=h \omega ^2-\omega _2^2 \end{aligned}$$
(5)

Introducing the parameters

$$\begin{aligned} \lambda =\frac{\omega }{\omega _1},\quad \nu =\frac{\omega _2}{\omega _1},\quad X_{st}=\frac{F}{k_1} \end{aligned}$$

Based on the above analysis, the amplitude amplification factor of the primary system should be

$$\begin{aligned} A= \Bigg \vert \frac{X_1}{X_{st}} \Bigg \vert =\sqrt{\frac{A_3^2+B_3^2 \xi ^2}{C_3^2+D_3^2 \xi ^2}} \end{aligned}$$
(6)

where

$$\begin{aligned} A_3&=\beta _1-\lambda ^2 (h+1),\quad B_3=2 \lambda \nu , \quad D_3=2 \lambda \nu (\beta _2-\lambda ^2\beta _3) \nonumber \\ C_3&=\big (\beta _1-\lambda ^2 (h+1)\big ) (\beta _2-\lambda ^2\beta _3) - \mu (h \lambda ^2 - \nu ^2)^2 \nonumber \\ \beta _1&=\nu ^2(\alpha +1),\quad \beta _2=\mu \nu ^2 +1,\quad \beta _3=\mu h+1 \end{aligned}$$
(7)

2.3 Parameters Optimization

By simple deduction of (6), it can be found that the normalized amplitude-frequency curve under the different dam** ratios as 0.1, 0.2 and 0.4 given in Fig. 2 will pass through two points which are independent of the dam** ratio. And it could be clearly seen that there exist two commonly fixed points P and Q on all the curves, which are independent of the dam** ratio. Thus, based on fixed point theory, the optimum natural frequency ratio can be obtained by adjusting the responses at P and Q to the same level. Then making P and Q as the maximum values of the amplitude-frequency curve to obtain the optimum dam** ratio.

Fig. 2
figure 2

The normalized amplitude-frequency curves

Full size image

Due to the fixed-point theory, there exist two equal values if \(\xi \rightarrow \infty\) and \(\xi \rightarrow 0\) in Eq. (6)

$$\begin{aligned} \Bigg \vert \frac{A_3}{C_3} \Bigg \vert = \Bigg \vert \frac{B_3}{D_3} \Bigg \vert \end{aligned}$$
(8)

i.e.

$$\begin{aligned} \frac{\beta _1-\lambda ^2 (h+1)}{\big (\beta _1-\lambda ^2 (h+1)\big ) (\beta _2-\lambda ^2\beta _3) - \mu (h \lambda ^2 - \nu ^2)^2}=\pm \frac{1}{\beta _2-\lambda ^2\beta _3} \end{aligned}$$
(9)

It could be found that there is no meaning when the right part of (9) is positive. Accordingly, taking the negative one and simplifying the equation, one can get

$$\begin{aligned} \lambda ^4+a_1 \lambda ^2+a_2 =0 \end{aligned}$$
(10)

where

$$\begin{aligned} a_1&=\frac{2(\mu \nu ^2 h - \beta _1 \beta _3 - \beta _2 (h+1))}{2 (h+1) \beta _3-\mu h^2} \\ a_2&=\frac{\mu \nu ^4-2 \beta _1 \beta _2}{2 (h+1) \beta _3-\mu h^2} \end{aligned}$$

Supposing the roots of Eq. (10) are \(\lambda _P\) and \(\lambda _Q\), one can get the following equation

$$\begin{aligned} \lambda _P^2+\lambda _Q^2=-\frac{2(\mu \nu ^2 h - \beta _1 \beta _3 - \beta _2 (h+1))}{2 (h+1) \beta _3-\mu h^2} \end{aligned}$$
(11)

In order to get the optimum natural frequency ratio, adjusting the values at P and Q to be the same

$$\begin{aligned} \frac{1}{\beta _2-\beta _3 \lambda _P^2}=-\frac{1}{\beta _2-\beta _3 \lambda _Q^2} \end{aligned}$$
(12)

Simplifying Eq. (12) leads to

$$\begin{aligned} \lambda _P^2+\lambda _Q^2=\frac{2 \beta _2}{\beta _3} \end{aligned}$$
(13)

Combining Eqs.(11) and (13), the optimum natural frequency ratio can be obtained

$$\begin{aligned} \nu _{opt}=\sqrt{\frac{\beta _3+h}{b_1}} \end{aligned}$$
(14)

where \(b_1=\alpha \beta _3^2-\mu \beta _3+1\). For convenience, we denote

$$\begin{aligned} b_2=\alpha \beta _3+1, \quad b_3=(h+2)\beta _3+h, \quad b_4=\beta _3 (1-h \alpha ) \end{aligned}$$

Then the two fixed points can be obtained

$$\begin{aligned} \lambda _P^2=\frac{b_2 b_3-b_4 \sqrt{\mu b_3}}{b_1 b_3}, \quad \lambda _Q^2=\frac{b_2 b_3+b_4 \sqrt{\mu b_3}}{b_1 b_3} \end{aligned}$$
(15)

Based on the optimum natural frequency ratio, the amplitude amplification factor at P and Q can be obtained

$$\begin{aligned} A\big \vert _{\lambda _P, \lambda _Q}=\frac{b_1 b_3}{\beta _3 b_4 \sqrt{\mu b_3}} \end{aligned}$$
(16)

Next, to make the maximum amplitude of the primary system at the fixed points, the dam** ratio is adjusted. The condition can be achieved when the derivatives of the amplitude amplification factor are zero at the two fixed points

$$\begin{aligned} \frac{\partial A^2}{\partial \lambda _P^2}=0, \quad \frac{\partial A^2}{\partial \lambda _Q^2}=0 \end{aligned}$$
(17)

Solving Eq. (17) and substituting the optimum natural frequency ratio into the results one can get

$$\begin{aligned} \xi _P^2&=\frac{\mu (1-\alpha h)^2 (2b_3-\beta _3-h+2h \sqrt{\mu b_3})}{4 (b_2 b_3-b_4\sqrt{\mu b_3})} \nonumber \\ \xi _Q^2&=\frac{\mu (1-\alpha h)^2 (2b_3-\beta _3-h-2h \sqrt{\mu b_3})}{4 (b_2 b_3+b_4\sqrt{\mu b_3})} \end{aligned}$$
(18)

Taking an average of \(\xi _P\) and \(\xi _Q\), one can get the optimum dam** ratio

$$\begin{aligned} \xi _{opt}=\sqrt{\frac{\xi _P^2+\xi _Q^2}{2}}=\frac{1-\alpha h}{2}\sqrt{\frac{\mu b_2(2b_3-\beta _3-h)+2\mu ^2 h b_4 }{b_2^2 b_3-\mu b_4^2}} \end{aligned}$$
(19)

From the above analysis, we can see that this result cannot exactly make the points P and Q as the maximum values of the amplitude-frequency curve. But this approximation can be accepted as a simple design law. Considering Eqs. (14) and (19), there still exist adjustable parameters in the optimum natural frequency ratio and dam** ratio. According to the characteristics of the negative stiffness system, it can be achieved when the negative stiffness material is applied by preload, which could be realized by pre-compressed member or inverted pendulum. The preload will cause a pre-displacement of the primary system, therefore, an approximation method is adopted to select the pre-displacement as the amplitude at the fixed point, which means the response to zero-frequency excitation is the same as the response at the fixed points.

$$\begin{aligned} A=\Big \vert \frac{X_1}{X_{st}}\Big \vert =\frac{b_1 b_3}{\beta _3 b_4 \sqrt{\mu b_3}}=\frac{b_1(1+\alpha )}{b_1+\alpha \beta _3 (\alpha \beta _3+1)} \end{aligned}$$
(20)

Solving Eq. (20), we can obtain

$$\begin{aligned} \alpha _1&=-\frac{\beta _3-\sqrt{\mu b_3}}{\beta _3}, \quad \alpha _2=-\frac{\beta _3+\sqrt{\mu b_3}}{\beta _3} \nonumber \\ \alpha _3&=-\frac{\beta _3+1-\sqrt{\mu b_3}}{2 \beta _3}, \quad \alpha _4=-\frac{\beta _3+1+\sqrt{\mu b_3}}{2 \beta _3} \end{aligned}$$
(21)

Considering Eqs. (14) and (19), one can find that taking \(\alpha _2\) and \(\alpha _4\) as the negative stiffness ratio will make the optimum natural frequency ratio as imaginary number and taking \(\alpha _3\) as the negative stiffness will make the optimum dam** ratio infinity. So \(\alpha _1\) is choosed as the optimum negative stiffness ratio, namely

$$\begin{aligned} \alpha _{opt}=-\frac{\beta _3-\sqrt{\mu b_3}}{\beta _3} \end{aligned}$$
(22)

Then according to the parameter optimization procedures, the three adjustable parameters of the DVA are analytically obtained.

Fig. 3
figure 3

The relationship between mass ratio and optimum parameters

Full size image

Actually, in terms of practicality, we give the relationships between the optimum parameters in Eqs.(14), (19), and (22) with the mass ratio in Fig. 3. Based on the analysis of the figure, we can find that the negative stiffness ratio plays a small role in the consideration of the system stability.

2.4 The Best Working Range of Inerter

According to the calculation, when the inerter-mass ratio is not appropriate, the optimal solution will cause system instability, so it can be deduced that in the optimal design process of dynamic vibration absorber, under the premise of ensuring system stability, there is an optimal working range of inerter-mass ratio. The coefficients of existing inerter-mass ratio elements are all positive and the mass ratio is positive. Considering each optimal parameter and its calculation process, the working range of inerter-mass ratio should satisfy that the denominator of each expression is not equal to 0, the part under the square root is greater than 0, and the optimal frequency ratio \(\nu _{opt}\) and optimal dam** ratio \(\xi _{opt}\) are greater than 0.

Substituting negative stiffness ratio \(\alpha _{opt}\) into optimal frequency ratio, yields

$$\begin{aligned} \nu _{opt}=\sqrt{\frac{\beta _3+h}{\beta _3 \sqrt{\mu b_3}-\mu (b_3-\beta _3)}} \end{aligned}$$
(23)

From above analysis, inerter-mass ratio h should simultaneously satisfy

$$\begin{aligned} \alpha _{opt}<0, \quad \nu _{opt}>0, \quad \xi _{opt}>0 \end{aligned}$$
(24)

Solving equation (24), one can obtain

$$\begin{aligned} 0<h<\frac{1-2\mu }{2\mu ^2} \end{aligned}$$
(25)

3 Comparisons of the Control Performances

In order to verify the vibration reduction effect of the dynamic vibration absorber model proposed in this paper, a comparison was made between the classic Voigt dynamic vibration absorber, Ren-type dynamic vibration absorber and IR1 dynamic vibration absorber with inerter-mass element attached in reference [14]. The three comparative vibration absorber models are shown in Fig. 4, and the optimal parameter formula corresponding to each model is shown in Table 1 [4, 17].

Fig. 4
figure 4

Three typical models of DVAs: a The type by Den Hartog; b The type by Ren; c The type by Reference 14

Full size image
Table 1 The formulas of the three typical models of DVAs
Full size table

3.1 The Comparison with Other DVAs Under Sinusoidal Excitation

Many equipment in engineering, especially rotating machinery, is often subjected to harmonic excitation, therefore the vibration reduction effect of each model under different excitation frequencies is firstly compared. The mass ratio is taken \(\mu =0.1\) and \(\mu =0.05\) for all models, and the inerter-mass ratio is taken \(h=0.1\) for the model in reference [14] and this paper. Relevant parameters are calculated according to the optimal parameter design formula previously deduced and existing in Table 1, and the displacement response of the primary system under different frequency harmonic excitation is simulated. The normalized displacement amplitude-frequency curves of each model are obtained, as shown in Fig. 5.

Fig. 5
figure 5

The comparison with other DVAs

Full size image

It must be pointed out that we adopt approximation in the optimum dam** ratio, thus the three amplitudes on zero-frequency excitation, fixed point P and Q are not exactly the same.

Through the above analysis, we can draw conclusions:

  1. (1)

    According to the comparison, we can clearly find that the DVA presented in this paper can not only broaden the frequency range of vibration absorption, but also greatly reduce the amplitude of the primary system.

  2. (2)

    By comparing with the traditional Den Hartog and Ren DVA, we can find that the negative grounding stiffness and inerter play a greater role in vibration absortion. Furthermore, compared with DVA in reference [14], it is found that the negative grounding stiffness is more beneficial to reduce the amplitude of the primary system.

  3. (3)

    The presented DVA is not so sensitive to the mass ratio, which means one can get a better control performance using a smaller absorber mass.

3.2 The Comparison with DVAs Under Random Excitation

It is more important and meaningful to investigate the system response under random excitation, especially when DVA is applied in earthquake and civil engineering. A further study is conducted on the DVA under random excitation in this subsection. When a single degree-of-freedom system (SDOF, the primary system) shown in Fig. 6 is subjected to random excitation with zero mean and power spectral density as \(S(\omega )=S_0\), the mean square response of the SDOF system can be got as [3]

$$\begin{aligned} \sigma ^2=\frac{\pi S_0}{2\omega _1^3\xi } \end{aligned}$$
(26)
Fig. 6
figure 6

A single degree system under random excitation

Full size image

Considering Eq. (26), one can find that the mean square response will become infinity if the dam** coefficient approaches zero. Therefore, it is necessary to connect a DVA to reduce the system response.

Considering the primary system subjected to white noise excitation with zero mean value and constant power spectral density \(S(\omega )=S_0\). Then, the power spectral density function of the displacement response of the above four models is as follows.

$$\begin{aligned}&S_V(\omega )=\vert X_{V_1}\vert ^2 S_0, \quad S_R(\omega )=\vert X_{R_1}\vert ^2 S_0 \nonumber \\&S_{IR1}(\omega )=\vert X_{IR1_1}\vert ^2 S_0, \quad S_N(\omega )=\vert X_{N_1}\vert ^2 S_0 \end{aligned}$$
(27)

where the subscript V, R, IR1 and N represent for the Den Hartog type DVA, the model by Ren, the model by reference [14] and the DVA in this paper respectively. According to the optimal parameters in literatures [4, 17], the mean square response of the primary system of these DVAs can be deduced as

$$\begin{aligned} \sigma _V^2=\int _{-\infty }^{+\infty }S_V(\omega )\mathrm{d}\omega&=S_0\int _{-\infty }^{+\infty }\big \vert X_{V_1}\big \vert ^2\mathrm{d}\omega =\frac{\pi S_0 Y_V}{2\omega _1^3 \mu \xi \nu } \nonumber \\ \sigma _R^2=\int _{-\infty }^{+\infty }S_R(\omega )\mathrm{d}\omega&=S_0\int _{-\infty }^{+\infty }\big \vert X_{R_1}\big \vert ^2\mathrm{d}\omega =\frac{\pi S_0 Y_R}{2\omega _1^3 \mu \xi \nu ^5} \nonumber \\ \sigma _{IR1}^2=\int _{-\infty }^{+\infty }S_{IR1}(\omega )\mathrm{d}\omega&=S_0\int _{-\infty }^{+\infty }\big \vert X_{{IR1}_1}\big \vert ^2\mathrm{d}\omega \nonumber \\&=\frac{\pi S_0 Y_{IR1}}{2\omega _1^3 \mu \xi \nu (\nu ^2-h_{IR1})^2} \nonumber \\ \sigma _N^2=\int _{-\infty }^{+\infty }S_N(\omega )\mathrm{d}\omega&=S_0\int _{-\infty }^{+\infty }\big \vert X_{N_1}\big \vert ^2\mathrm{d}\omega \nonumber \\&=\frac{\pi S_0 Y_N}{2\omega _1^3 \mu \xi \nu (\nu ^2-h)^2(\alpha \mu \nu ^2+\alpha +1)} \end{aligned}$$
(28)

where

$$\begin{aligned} Y_V= & \, \nu ^4(1+\mu )^2+\nu ^2\big (4\xi ^2(1+\mu )-\mu -2\big )+1 \nonumber \\ Y_R= & \, \nu ^4+\nu ^2(4\xi ^2+\mu -2)+1 \nonumber \\ Y_{IR1}= & \, \nu ^4+\nu ^2\big (4\xi ^2(1+\mu h_{IR1}) +\mu -2(1+h_{IR1})\big )+(1+h_{IR1})^2 \nonumber \\ Y_N= & \, \nu ^4 \gamma _1+\nu ^2 \gamma _2+(1+h)^2(\alpha +1) \nonumber \\ \gamma _1= & , (\mu h+1)^2\alpha ^3+\big (2(1-\mu )(\mu h+1)+1\big )\alpha ^2 \nonumber \\&+\big (4\mu \xi ^2(\mu h+1)+(\mu -1)^2+2\big )\alpha +1 \nonumber \\ \gamma _2= & \, -\big ((\mu h+1)(h+2)+h \big )\alpha ^2 +\big (4\xi ^2(\mu h+1)-4(h+1)+2\mu \big )\alpha \nonumber \\&+4\xi ^2(\mu h+1)-2(h+1)+\mu \end{aligned}$$
(29)

The mean square response of the primary system under the optimal parameters can be respectively obtained for \(\mu =0.1\), \(h=0.1\), \(h_{IR1}=0.1\) as follows

$$\begin{aligned} \sigma _R^2&=\frac{5.780\pi S_0}{\omega _1^3},\quad \sigma _V^2=\frac{6.401\pi S_0}{\omega _1^3} \nonumber \\ \sigma _{IR1}^2&=\frac{5.958\pi S_0}{\omega _1^3},\quad \sigma _N^2=\frac{1.595\pi S_0}{\omega _1^3} \end{aligned}$$
(30)

It is shown that the DVA with negative stiffness and inerter-mass in this paper has the minimum mean square response, which means the presented model can get a better performance than other DVAs even under the random excitation. Moreover, the presented model is still superior to other three DVAs if different mass ratios are selected.

Fig. 7
figure 7

The time history of the random excitation

Full size image
Fig. 8
figure 8

Comparison of time domain dynamic responses for the primary system with different DVAs

Full size image

Furthermore, we construct the \(50\,\mathrm {s}\) random excitation, which is composed of 5000 normalized random numbers with zero mean and unit variance. The time history of random excitation is shown in Fig. 7. We take the primary mass \(m_1=1 \,\mathrm {kg}\), the stiffness \(k_1=100 \,\mathrm {N/m}\), the mass of the vibration absorber is \(m_2=0.1 \,\mathrm {kg}\) , according to Tab. 1 and the derivation process of this paper, the optimal parameters can be obtained. Based on the fourth-order Runge-Kutta method, the response of the primary systems without DVA and with different DVAs can be obtained. Figure 8 shows the displacement response of the four different dynamic vibration absorbers attached to the primary system.

From Fig. 8, it could be concluded that DVA in this paper could present better control performance than other DVAs, even when the primary system is subjected to random excitation. Comparing with the traditional Den Hartog and Ren DVA, we can find that the negative grounding stiffness and inerter play a greater role in vibration absortion. Furthermore, when the DVA is attached with the negative grounding stiffness, compared with DVA in reference [14], it is found that the DVA presented in this paper has better control performance under random excitation.

4 Conclusions

In this paper, a novel dynamic vibration absorber model with inerter-mass and grounding negative stiffness is proposed. Based on the fixed point theory, the optimal frequency ratio, approximate optimal dam** ratio and optimal negative stiffness ratio are obtained. It is found that when inerter-mass and negative grounding stiffness act together, the system will be unstable when the improper inerter-mass coefficient is used in the optimal design process, thus the optimum working range of inerter-mass is obtained, which provides reference for the design of new vibration absorber in practical production. Compared with other types of dynamic vibration absorbers, the proposed DVA can greatly reduce the resonance amplitude and broaden the vibration frequency range.