Integration of the Non-linear Time Series GARCH Model with Fuzzy Model Optimized with Water Cycle Algorithm for River Streamflow Forecasting

Abstract

For managing water resources and operating reservoirs in dynamic contexts, accurate hydrological forecasting is essential. However, it is difficult to track complex hydrological time series with highly non-linear and non-stationary characteristics. The intricacy of the issue is further increased by the risk and uncertainty that are brought about by the dependence of several factors on the hydrological system’s output. To hydrologically model river outflows, a hybrid GARCH time series model technique has been applied in this study. To improve the precision of the proposed model estimation, this hybrid model employs a controllable fuzzy logic system to explore the impact of various input variables and an Archimedean detail function to account for the uncertainty in the dependence of the variables. The prediction error in this model is minimized by utilizing weighting factors and problem analysis parameters that are calculated using the water cycle algorithm. It was found that the minimum root-mean-square error values for the training and testing modeling stages are RMSE = 1.89 m and 1.92 m, respectively, by looking at the hydrological modeling results for a watershed of the Karaj dam. For extended lead (i.e., a 6-month rainfall lag), the weakest forecasting capacity was found. The modeling of the copula function using a higher percentage of answers in the confidence band and a smaller bandwidth resulted in less uncertainty for the estimation of the suggested model, according to the uncertainty analysis.

1 Introduction

Simulating and predicting flow at various time steps, such as daily flow in catchment areas, requires the use of rainfall–runoff conceptual models of soil moisture. These models must be used with recorded rainfall and flow information. However, it is not feasible to have enough and accessible historical information to provide all the necessary information in the majority of watersheds. One of these variables that is typically unavailable for information and requires estimation is soil moisture level. The values of the parameters specified in the models are also unknown and need to be found using developed techniques, optimization, or simulation.

Stream flow forecasting, agriculture, risk management, flood control, and reservoir operation are just few of the many uses for precipitation–runoff models to estimate stream flow. Over the past 40 years, a large range of hydrological models with varied degrees of complexity have been developed and deployed globally [1] thanks to widespread computer accessibility. However, there are problems with using a lot of these models, particularly in an educational setting. The first issue is that most models’ source code is not freely available, restricting users to only modifying the model at the component level. Another issue is that most models are not user-friendly while having a very straightforward structure. It can take a long time (months or even years) to master the most complicated models. This is a major flaw in the current system for providing education. Complex models like HEC-HMS are available for free but are not easily modified, and others like HBV [2] necessitate coding skills that not everyone possesses. The uncertainty affecting rainfall–runoff models needs to be taken into account. Uncertainty in these models stems from three distinct areas: the input data used the desired model’s structure and the models’ parameters. The uncertainty and risk associated with employing rainfall–runoff models have been the focus of significant recent work [3, 4].

Significant advancements have been made in the study of satellite motion and robotics thanks to the invention and deployment of sequential data update systems. These techniques offer a high-level framework for integrating forecasts with uncertainty and observational data while also taking into account the uncertainty of input data, outputs, model structure, and more. Unlike traditional approaches of calibrating rainfall–runoff models, which only determine the model’s parameters through optimization, the updating approach regularly adjusts the model’s state variables in light of fresh measurements of the water flow. It is worth noting that it can also provide reliable forecasts.

The primary goal of the hydrological model is to provide experts, engineers, researchers, and operators of water resources systems with an efficient and straightforward modeling tool. Despite its straightforward design, the model must successfully simulate flow in the catchment under investigation. Several intercomparison studies [5, 6] have demonstrated that for flow prediction at catchment outlets, lumped models perform just as well as their more sophisticated dispersed equivalents.

The regional and temporal distribution of ecosystem water availability and sustainability is altered as a result of global changes, such as climate and land use [7, 8]. The conflict of anabatic water resources in the context of decreasing water supply is a challenge to environmental and human sustainability [9, 10], brought on by rising water demand and shifts in the natural environment. Due to the effects of global warming and shifting patterns of land use, effective management of water supplies is more difficult than ever.

Individual stochastic approaches typically fall short of the complexity and resilience of managing water resources. Water resource optimization may be aided by the integration of many uncertain methodologies [11]. Additionally, prior attempts to optimize water resources focused primarily on meeting domestic, industrial, and agricultural water demands rather than taking ecosystem water demands into account, which led to unsustainable development and environmental degradation. Further, some studies have demonstrated that ensembles of general circulation models (GCMs) are preferable to individual GCMs for hydrological forecasting [12, 13]. This is because the effect of aggregation of approaches enhances the bias and downscaling of uncertainties. More creative approaches are needed to carry over uncertainties in hydrological models from climate projections to analyses of water resource uncertainty. As a result, this research aims to create an Integrated Simulation–Optimization Modeling System (ISOMS) strategy to explore various adaptive strategies in light of the accumulated consequences of climate change and the associated uncertainties. The ISOMS framework used a combined hydrological model to predict hydrological changes, including input from a cross-combination of four climate ensembles based on 31 GCMs. To forecast river flow and manage available water resources, a fuzzy system model has been combined with the time series model approach, with the use of copula functions to account for the uncertainties inherent in hydrological modeling. To better understand how to establish a connection between the hydrological model in the natural system and the applied analysis of the social system under the changing environment, a case study of the catchment area of Amir Kabir Dam on the Karaj River was conducted. The results of this investigation demonstrate the generalizability of the suggested framework, which is the first attempt to apply such a framework to a mountainous region with substantial spatial variability. Decision-makers can use the findings to create adaptable water distribution strategies for stochastic, interval, and phase uncertainty, which in turn can increase the accuracy of hydrological forecasts by overcoming the individual inputs of environmental change in earlier research. To achieve sustainable development in the Karaj River’s water resources, society, economics, and ecosystem, this study is crucial.

In regards to the proposed compression and reconstruction design of medical images, this article’s key contribution is as follows:

• Outlining coupled hydrological modeling methods with the goal of calculating river flow in the case study’s catchment area.

• Applying the GARCH model to a non-linear time series system.

• Investigating how various meteorological factors affect river flow using a fuzzy logic forecasting system.

• Using the water cycle algorithm (WCA) to define model parameters to lower estimated inaccuracy.

This article is structured as follows. In Sect. 2, we quickly recap the context of relevant works and the underlying ideas. In Sect. 3, the enhanced hybrid hydrological modeling framework and its components are introduced. In Sect. 4, we compare the results of our technique to those obtained by other codecs when applied to a variety of climatic data sets collected over a 19-year time span. Section 5 contains the summary and analysis.

2 Concepts and Review of Related Works

2.1 Related Works

Recently, the idea of representative parameter sets (RPSs) was suggested to describe modeling uncertainty in flow frequency space with minimal computing expense and using a chosen group of model parameters. This idea is modified in [14] to evaluate the risks associated with three flow indices: the yearly mean flow, the annual low flow average during the preceding seven days, and the annual maximum flow. The applicability of the RPS to other flow indicators and to hydrological consequences is also thoroughly examined. By choosing parameter sets at random, benchmarks for RPS-based simulations are created. The findings indicate that (a) RPSs can successfully be switched between flow indices with a negligible loss in model performance. (b) Modeling uncertainty in hydrological effects can be represented using RPSs. To map the modeling uncertainty of any environmental model, the RPS approach offers a lot of potential.

In the article [15], experts are polled on their predictions for a new monthly Combined Terrestrial Evapotranspiration Index (CTEI) in the Ganges River Basin (GRB) for a period of 14 years as a measure for all three types of drought (meteorological, hydrological, and agricultural). Eleven input variables were used as part of a combination of hydro-meteorological and satellite data for this purpose. The best input combinations were discovered using a new Artificial Neural Network (ANN) linked with a Whale Optimization Algorithm (WOA-ANN) and a feature selection technique based on Relief algorithm-based Feature Selection (FS) for simulation CTEI monthly index. To verify the effectiveness of WOA-ANN, independent ANN and Least Square Support Vector Regression (LSSVR) models were examined. With (R = 0.9391), (RMSE = 0.241), (WI = 0.968), and (U95% = 0.669), the results demonstrated that WOA-ANN has a great capacity to predict CTEI. The RMSE of the ANN and LSSVR models is also decreased by 27% and 30%, respectively.

To enhance the reliability of hydrological time series forecasts, researchers [16] examined a hybrid model that combines meta-heuristic optimization with Compete Ensemble Empirical Mode Decomposition with Adaptive Noise (CEEMDAN) and Twin Support Vector Machine (TSVM). Step one involves using the CEEMDAN program to break down the primary runoff data into numerous stable sub-components at various resolutions and frequencies. The emergent cooperative search method is then utilized to look for suitable parameter combinations, and a TSVM prediction model is created to extract the deep features of each subset. By adding the results from each TSVM model, a final prediction for the original hydrological time series can be made. Several hydrological stations along China’s Yangtze River collect long-term streamflow data that are utilized for modeling purposes. The experimental results show that compared to the conventional support vector machine, the suggested method reduces the mean square root of the error by about 36.5% and the mean value of the absolute error by about 41.6%.

Sunflower Optimization (SO) was used with an Adaptive Neuro-Fuzzy Inference System (ANFIS) and Multilayer Perceptron (MLP) models in the study [17] to model the lake’s water level. Advanced Artificial Intelligence (AI) models are used to make predictions and assessments on the water level in Lake Urmia. The Sunflower optimization method has been used to determine the best configuration settings. Using all three delays of rainfall and temperature as input features, the ANFIS-SO model achieved the best predictive performance.

Hourly, researchers in the study [18] evaluate the efficacy of two AI-based data-driven approaches: a multilayer perceptron neural network (MLP-NN) and an adaptive neural fuzzy inference system (ANFIS) for predicting river levels. The suggested models are trained and tested using hourly measurements of the Muda River’s water level collected over a 10-year period in northern Malaysia. To verify the accuracy of the models, numerous statistical indicators have been implemented. Both models’ hyperparameters have been studied for optimization purposes. The next step is to conduct a sensitivity and uncertainty analysis. Finally, the models’ ability to forecast the river level 1, 3, 6, 9, 12, and 24 h in advance is examined.

For any watershed’s ecological and geomorphological evaluation of soil erosion, river sediment is a crucial indication. Therefore, sediment movement in a river basin is both a dynamic and multidimensional process in the natural world. Features, such as high randomness, non-linearity, non-stationarity, and redundancy, are indicative of this phenomenon. Several AI modeling frameworks have been implemented to address sedimentation issues in rivers. This article [19] aims to provide a comprehensive overview of the most recent AI-based sediment transport modeling applications for river basin systems.

Reference evapotranspiration (ET0) is an integral part of agricultural water management strategies for making effective use of scarce water supplies through efficient and meaningful irrigation event planning. Predicting ET0 early and accurately can help with agricultural water management and serve as the basis for good irrigation planning. The purpose of this research [20] is to examine the efficacy of several models of the Adaptive Neural Fuzzy Inference System (ANFIS) in conjunction with optimization techniques for the daily prediction of ET0. Daily ET0 values were estimated using historical weather data collected from a meteorological station in Bangladesh and analyzed using the FAO-Penman–Monteith method. Hybrid ANFIS models are trained using input–output patterns based on the acquired climatic variables and the estimated ET0 values. These modified ANFIS models were evaluated alongside the original ANFIS model using the Gradient Descent and Least-Squares Estimate (GD-LSE) adjustment methods. With the use of Shannon’s entropy (SE), the variation coefficient (VC), and gray relationship analysis (GRA), eight statistical variables were used to rank the performance of these ANFIS models. While the weights may be different in absolute terms, the results suggest that SE and VC-based decision theories provide comparable rankings. However, GRA issued its ranks in a slightly different order. The Firefly ANFIS (FA-ANFIS) algorithm was chosen as the top performing particle swarm optimization-ANFIS model by both SE and VC.

Specifically, this article [21] reviews the evolution of copula models and their implementations in the energy, fuel cell, forestry, and environmental research industries. In terms of static and dynamic applications, this study analyzes recent papers on a range of copula models, including Gumbel, Clayton, Frank, Gaussian, vine, and the theoretical development of mixtures of bivariate and multivariate distributions. In contrast to Copula, comparative analysis of articles is conducted utilizing the ARMA, DCC, and GARCH models.

Based on hybrid and LVaR models, the article [22] creates a novel method to assess the optimization of Liquidity-Adjusted Value-at-Risk (LVaR) of multi-asset portfolios. Under a variety of practical operating and budgetary limitations, the outcomes demonstrate that the current strategy is superior to the standard Markowitz portfolio mean–variance approach in terms of optimal portfolio selection. Using Geographic Information System (GIS) technology, researchers in this study [23] implemented three groundwater vulnerability assessment indicators called DRASTIC (depth to water surface, net nutrition, aquifer environment, soil environment, topography, influence of vadose zone, and hydraulic conductivity), SINTACS (Soggicenza, Infiltrazione), Non saturo, Tipologia della covertura, Acquifero, Conducibilit’a, and Superficie topografica. The hybrid PSO-GA approach is a powerful optimization algorithm that combines the best features of PSO and GA while omitting their drawbacks. The PSO-GA optimization technique is used to fine-tune the DRASTIC weighting system. The rates and weights employed by DRASTIC can also be adjusted using the Multi-Attribute Decision Making (MADM) technique known as Step-wise Weight Assessment Ratio Analysis (SWARA).

The study [24] used a combination of data pre-processing, permutation entropy, and artificial intelligence (AI) methods to create a hybrid model for point and interval forecasting of the short-term to long-term series of the standardized precipitation index in northwest Iran, based on the estimation of upper and lower limits. The years 1983–2017 were used for this analysis of ground precipitation and remote-sensing data. During the first stage of the modeling procedure, we looked into the efficacy of Variational Mode Decomposition (VMD), Empirical Mode Decomposition (EMD), and Permutation Entropy (PE) in predicting drought points. To deal with this new level of uncertainty and still give enough information for actionable operational decisions, time-frame forecasting was implemented. The simulation results demonstrated that the suggested combined models can outperform their component parts.

In [25], researchers combine time series models with AI techniques to create novel hybrid models. Monthly streamflow time series data from the Ocmulgee River in Georgia and the Umpqua River in Oregon, USA, were modeled using these integrated models. Gene Expression Programming (GEP), Multivariate Adaptive Regression Splines (MARS), and Multiple Linear Regression (MLR) were combined with Fractionally Autoregressive Moving Average (FARIMA) and Self-Exciting Threshold Auto-Regressive (SETAR) time series models to create an AI-based solution. The outcomes highlighted the superiority of time series models over MLR and AI methods.

One of the most crucial aspects of operational hydrology is flow forecasting. Different watersheds have different responses to runoff because of different climatic conditions and watershed features. In [26], a non-linear and dynamic rainfall–runoff model called stepwise cluster analysis hydrological (SCAH) is devised. At Yichang Station, Hankou Station, and Datong Station on the Yangtze River Basin in China, the suggested method is used for runoff forecasting under local weather patterns. Important findings include: (1) Both deterministic and probabilistic models place a high value on SCAH performance. In SCAH with a robust cluster tree topology, (2) SCAH is insensitive to the value of p. (3) Water resources in the lower parts of the Yangtze River are influenced by water flowing in from the upstream due to high correlations, as shown by a case study conducted in the Yangtze River watershed. This research demonstrated that SCAH’s statistical hydrological model method is capable of characterizing complicated hydrological processes with non-linear and dynamic interactions and making accurate forecasts. SCAH is a useful technique for showing precipitation–runoff interactions because of its low data needs, quick calibration, and consistent performance. Several researches have been presented for modeling climate and precipitation issues in the catchment area and various optimizations [27,28,29,30,31,32,33,34].

After reading and analyzing the articles, the following stand out as primary goals of the proposed method:

• (a) Water resources monitoring and management systems include hydrological modeling of climatic data from watersheds and long-term water plan predictions.

• (b) Hydrological estimations contain risk and uncertainty, which increases the model’s complexity and poses significant problems to the design of the underlying system.

• (c) Prediction errors can be minimized by combining a time series model with an analysis of the elements that influence that model.

• (d) A modified strategy, which may be represented with the aid of copula functions, can be presented to explain the reliance of various components and parameters in the problem.

2.2 Concepts

2.2.1 Water Cycle Algorithm

The proposed water cycle algorithm is based on real-world observations of the water cycle and the natural direction of water flow (from rivers and streams to the ocean). It is the movement of water from one location to another that creates rivers and streams. This means that the majority of rivers originate high in the mountains, from the melting of snow and glaciers. Rivers never stop moving. Water from rain and other streams flows into rivers and then to the ocean. A simplified representation of the hydrological cycle is shown in Fig. 1. The water in rivers and lakes evaporates, and plants release water through the process of photosynthesis. Evaporation causes clouds, which eventually rain water back down from the colder atmosphere of space. Hydrological cycle [35] describes this process.

Fig. 1

A A simple diagram of the hydrological cycle (water cycle) [35]. B Schematic representation of hydrologic cycle

Most of the water that falls as rain or snow really ends up in the aquifer. Underground water reserves cover large areas. Underground water is referred to as an aquifer (Fig. 1). There is also a downward flow of water in the aquifer beneath the earth’s surface. An underground water source may eventually end up in a lake or stream. More clouds and rain are brought to these regions because water evaporates from streams and rivers as well as trees and other agricultural plants [35].

Water movement between the land, seas, and atmosphere is shown in a simplified flowchart in Fig. 1b. However, the real hydrological process is extremely complicated and necessitates a thorough comprehension of how each step works in concert with the others, how energy is transformed between the various phases of water (solid, liquid, and gas), how water moves and is distributed on Earth, and how all of this impacts water resources.

The raindrops serve as the beginning population in the water cycle algorithm, as they do in other metacognitive algorithms. At first glance, it appears that rain is inevitable. The best individual (the best raindrop) is picked to represent the ocean. Then, a certain quantity of the best raindrops is chosen to serve as a river, while the others are categorized as streams that eventually join rivers and the ocean. Each river takes in water from streams at a different rate, which is detailed in greater detail below according to the respective rivers’ flow volumes. In actuality, rivers and the sea have different water volumes than other streams. The rivers that receive the most precipitation also run to the sea.

2.2.1.1 Creating the Initial Population

To find an optimal solution, “Particle Position” employs metaphysical techniques based on a population. A solution is thus referred to as “Raindrop” in the proposed approach. The raindrop represents an array of 1 × N_VARs in an N_var dimensional optimization problem. This array’s matrix has the following definition:

$$ {\text{Raindrop}} = \left[ {x_1 , \, x_2 , \, x_3 , \, . \, . \, . \, , \, X_n } \right]. $$

(1)

The optimization procedure begins with the generation of an N_pop × N_var raindrop matrix. As a result, below is how the randomly generated X-matrix looks like (the rows and columns represent the total number of populations and the variables in the design, respectively)

$$ \begin{aligned} {\text{Population of raindrops}} & = \left[ {\begin{array}{*{20}c} {{\text{Raindrop}}_1 } \\ {{\text{Raindrop}}_2 } \\ {\begin{array}{*{20}c} {{\text{Raindrop}}_3 } \\ {\begin{array}{*{20}c} \vdots \\ {{\text{Raindrop}}_{N_{{\text{pop}}} } } \\ \end{array} } \\ \end{array} } \\ \end{array} } \right] \\ & = \left[ {\begin{array}{*{20}c} {x_1^1 } & {x_2^1 } & {x_3^1 } & \ldots & {x_{N_{{\text{Var}}} }^1 } \\ {x_1^2 } & {x_2^2 } & {x_3^2 } & \ldots & {x_{N_{{\text{Var}}} }^2 } \\ \vdots & \vdots & \vdots & \vdots & \vdots \\ {x_1^{N_{{\text{POP}}} } } & {x_2^{N_{{\text{POP}}} } } & {x_3^{N_{{\text{POP}}} } } & \cdots & {x_{N_{{\text{Var}}} }^{N_{{\text{POP}}} } } \\ \end{array} } \right]. \\ \end{aligned} $$

(2)

For both continuous and discrete situations, the decision variable Þ $x_{N_{\text{var}} }$ can take on either a floating point (actual value) or a preset set representation. Based on the cost performance (C) analysis, the cost of a single raindrop can be calculated as follows:

$$ C_{i } = {\text{Cost}}_i = f\left( {x_1^i ,x_2^i , \ldots , x_{N_{\text{var}} }^i } \right)\quad i = 1,2,3, \ldots ,N_{{\text{pop}}} , $$

(3)

where N_pop is the initial population size and N_var is the total number of design parameters. Npop raindrops are made for the first time. The best candidates (minimum values) for the roles of sea and river N_sr are then chosen. When comparing raindrops, the one with the lowest value is equated to the ocean. In fact, the number of rivers (a user parameter) plus the unit sea (Eq. 4) equals N_sr. Equation 4 is used to compute the remaining population (raindrops that produce streams that run into rivers or the ocean directly)

$$ N_{{\text{sr}}} = {\text{Number of River}} + \underbrace 1_{{\text{sea}}} $$

(4)

$$ N_{{\text{Raindrops}}} = N_{{\text{pop}}} - N_{{\text{sr}}} . $$

(5)

The following equation is provided to determine/allocate raindrops to rivers and the sea based on the magnitude of the flow:

$$ N_{{\text{sn}}} = {\text{round}}\left\{ {\left| {\frac{\cos t_n }{{\sum_{i = 1}^{N_{sr} } \cos t_i }}} \right| \times N_{{\text{Raindrops}}} } \right\},\quad n = 1,2, \ldots ,N_{{\text{sr}}} , $$

(6)

where N_Sn is the total number of flows that are sent to the sea or rivers.

Raindrops generate stream which then converge to produce further rivers. It is possible that some streams could be sent straight into the ocean. The best part is that all rivers eventually empty into the ocean. Figure 2 depicts the orderly progress of drops along a predetermined watercourse. A flow to the river through the connecting line between them at a randomly chosen distance is as indicated in Fig. 2

$$ X\varepsilon \left( {0, \, C \, \times \, d} \right);C > 1, $$

where C is a number between one and two, relatively near to two. The optimal value of C could be 2. The symbol d represents the present distance from the vapor drop to the river. In Eq. (6), the value of X represents a random number drawn from a distribution (uniform or otherwise) between 0 and (C d). If C is bigger than 1, the water will move in opposite directions toward the rivers.

Fig. 2

Schematic representation of the flow of droplets to a specific river (star and circle represent the river and drop, respectively)

The process through which rivers eventually empty into the ocean is another use of this idea. As a result, the revised arrangement for the river and steam can be as follows:

$$ X_{{\text{Stream}}}^{i + 1} = X_{{\text{Stream}}}^i + {\text{rand}} \times C \times \left( {X_{{\text{River}}}^i - X_{{\text{Stream}}}^i } \right) $$

(7)

$$ X_{{\text{River}}}^{i + 1} = X_{{\text{River}}}^i + {\text{rand}} \times C \times \left( {X_{{\text{Sea}}}^i - X_{{\text{River}}}^i } \right). $$

(8)

Rand is a uniformly distributed random number between 0 and 1. The roles of the river and the vapor droplet are swapped if the solution provided by the former is superior to that of the latter (i.e., the vapor becomes the river and the river becomes vapor). Likewise, a trade between rivers and oceans is possible. Figure 3 depicts the optimal option for the exchange of flow between other vapor droplets and the river.

Fig. 3

Exchange droplet and river positions where the star represents the river and the black circle indicates the best vapor among other vapors to exchange [65]

One of the main obstacles to the algorithm reaching rapid convergence (immature convergence) is evaporation. Water is lost through evaporation from rivers and lakes and is returned to the environment by plants through the process of photosynthesis. Water vapor rises into the atmosphere, condenses into clouds, and eventually falls back to Earth as rain after combining with other particles in the chilly air. The rain gives birth to new streams, which eventually join the rivers that empty into the ocean [35, 36].

In the suggested method, the seawater is returned to the ocean via rivers or vapors caused by the evaporation process. To prevent being stuck at a single solution, this hypothesis is put forth. The steps below explain how to figure out if a river empties into the ocean

$$ \begin{aligned} & {\text{if}}\quad \left| {X_{{\text{Sea}}}^i - X_{{\text{River}}}^i } \right| < d_{\max } \quad i = 1,2, \ldots ,N_{{\text{sr}}} - 1 \\ & \quad \quad {\text{Evaporation and raining process end,}} \\ \end{aligned} $$

where d_max is a tiny positive integer near zero. This means that the river has reached the sea if the distance between them is less than the maximum allowed (d_max). The process of evaporation is used in this case, and after enough water has evaporated, rain begins to fall. By contrast, setting d_max to a lower amount facilitates a thorough search in coastal areas. As a result, d_max determines how thoroughly searches are conducted in coastal areas (best answer). Adaptively, d_max is lowered to the following values:

$$ d_{\max }^{i + 1} = d_{\max }^i - \frac{{d_{\max }^i }}{{\max \,{\text{iteration}}}}. $$

(9)

The precipitation process is implemented once the evaporation process has been resolved. The process of raining is analogous to the genetic algorithm’s mutation operator in that new raindrops form streams at various sites. The following equation is used to find the new positions of newly created streams:

$$ X_{{\text{Stream}}}^{{\text{new}}} = LB + {\text{rand}} \times \left( {UB - LB} \right), $$

(10)

where LB and UB are the problem-specific lower and upper bounds.

Again, the most ideal freshly created drop of rain travels as a river to the ocean. The balance of the fresh precipitation probably forms new streams that eventually join larger waterways or drain into the ocean.

Equation 11 is employed solely for the currents that flow directly to the sea to increase the algorithm’s convergence speed and computing performance for constrained issues. To promote near-sea exploration (the optimal solution) in the relevant region for constrained situations, this equation is offered

$$ X_{{\text{stream}}}^{{\text{new}}} = X_{{\text{sea}}} + \sqrt {\mu } \times {\text{rand}}n\left( {1.N_{\text{var}} } \right), $$

(11)

where μ is a coefficient that shows the scope of the search area near the sea. A random number with a normal distribution is denoted by Randn. A larger value for μ increases the probability of exiting the feasible region. On the other hand, a smaller value for μ leads the algorithm to search in a smaller area near the sea. The appropriate value for μ is set to 0.1.

The mathematical definition of variance is the square root term μ in Eq. (11), which stands for the standard deviation. With these ideas in mind, the droplets with variance are evenly dispersed about the ideal (sea) center.

Streams and rivers in the search space may conflict with certain problem constraints or design variable constraints. The following four guidelines allow for a modification-based mechanism to be implemented in this work, which is then used to deal with the problem’s particular restrictions [37].

• Rule 1: Any feasible option should be chosen over any unfavorable one.

• Rule 2: Inappropriate solutions with minor violations of limitations are accepted (from 0.01 in the first iteration to 0.001 in the final iteration).

• Rule 3: When choosing between two potential solutions, go with the one that has a higher objective function value.

• Rule 4: If there are two impossible solutions, choose the one that has a smaller defect set than the constraint.

Applying the first and fourth rules, one is led to believe that the search for the feasible region should be conducted in the impossible zone. The search is narrowed to a workable region containing good options by applying the third law [37]. The minimum value for most structural optimization issues is typically described in terms of a range that lies on or near a relevant design space. With the help of the second law, vapor droplets and rivers have a better chance of reaching the global minimum as they approach the borders [38].

The optimal solution (the minimum of the objective function) is found to satisfy the convergence criterion, which is typically stated as the maximum number of iterations, the maximum amount of CPU time, or ɛ the constant. Minimal values are non-negative ones. In this section, the objective function is to minimize the time of sitting down and the time of going up and down. The maximum number of iterations, which serves as a convergence criterion, is reached after the water cycle algorithm has finished its search.

Figure 4 provides a high-level perspective of the suggested technique, with circles representing steam, stars representing rivers, and rhombuses representing the ocean. Figure 4 shows where rivers and vapor droplets have found new locations by the white (empty) shapes. The content of Fig. 4 continues that of Fig. 2. A watershed is the area of land that stretches from the start of the branches to the end of the lowlands. Put another way, when it rains on the earth’s highlands and lowlands, the water runs in the direction of the earth’s slope and then joins to form rivers that flow toward the sea, lakes, etc. The shape of this river is straight or spiral based on the slope of the river (Fig. 4a). Rivers have two types of slopes: straight for steep slopes and spirals for low slopes. A catchment area is a region in which surface runoff concentrates at a single location and flows in a particular direction. Our work in defining the WCA algorithm’s performance is based on this notion. The outcomes of the algorithm design for a watershed and its very accurate behavioral modeling will be used by looking at this operational area.

Fig. 4

A Display the progress of droplets along a predetermined watercourse. B Schematic view of WCA [65]

2.2.1.2 Steps and Flowchart of Water Cycle Algorithm

The algorithm’s steps are outlined in the following manner [39]:

• Step 1: Choose the water cycle algorithm’s initial parameters, including N_sr, d_max, N_pop, and max_iteration in step one.

• Step 2: Using Eqs. (2), (4), and (5), gather the initial random population and produce the first flows (red rains), rivers, and the sea.

• Step 3: Apply Eq. 3 to determine each raindrop’s value (cost).

• Using Eq. 6, step 4 determines the strength of river and ocean flow.

• Using relation 7, perform step 5 to transform steam into rivers.

• Step 6: Using Eq. 8, determine where the rivers flow into the sea and where the most precipitation occurs.

• Step 7: Reposition the river to achieve the best possible outcome, as shown in Fig. 9-3.

• Step 8: In a manner similar to step 7, if a river finds a more advantageous solution than the sea, the positions of the two are switched (see Fig. 9-3).

• Using the conditional statement, step 9 is to verify the evaporation condition.

• Step 10: Eqs. 10 and 11 are used to simulate the precipitation process if the evaporation conditions are favorable.

• Step 11: Decrease the value of dmax, a parameter that the user determined using Eq. (9).

• Step 12: Verify the convergence requirements. The algorithm will terminate if the stop** requirement is met; else, it will proceed to step 5 again.

Figure 5 depicts the suggested WCA method’s flowchart. Only individuals (particles) in PSO, in contrast, are able to identify the optimum solution and search strategy based on their unique and superior experiences. The “evaporation and precipitation conditions” used in the proposed WCA are comparable to the mutation operator in the genetic algorithm. Conditions for evaporation and precipitation can prevent the WCA algorithm from being stuck in local solutions. However, it does not appear that PSO has a similar standard or process.

Fig. 5

Proposed WCA flowchart [65]

In the proposed method, rivers [a number of selected best answers except the final best answer (i.e., the sea)] are used as “answers” to guide other people in the population to better positions (as shown in Fig. 4). The work here seeks to reduce the likelihood of, or completely avoid, becoming trapped in suboptimal portions of the solution space [see Eq. (7)]. Also, rivers are not static answers; they flow ultimately toward the sea. Indirectly approaching the optimal solution by this strategy (directing the flow to rivers and then connecting the rivers to the ocean) is possible.

2.2.2 Introduction of Fuzzy Logic

Fuzzy set theory is a method for making decisions using imprecise or incomplete data. Comparison of criteria weight and the linguistic values indicated by fuzzy numbers are published, together with the merit of substitution. To quantify fuzziness, the fuzzy set maps linguistic variables onto quantitative ones. Unit intervals are used instead of logical real numbers in the decision-making process [40]. In mathematics, a set is a collection of elements that can either be counted or is infinite in size. In each case, each element or member of a set is or is not. With fuzzy systems, however, this element could exist either within or outside of the collection. As a result, there is no one correct response to the statement “X is a member of a set A” [41].

2.2.2.1 Fuzzy Set

A fuzzy set A defined in the global discourse. It is characterized by a membership function μ_A: U → [0, 1] given by the following relation [42]:

$$ A = \left\{ {\left( {x, \mu_A (x)} \right)| x {{\epsilon }}U \wedge \mu_A \left( x \right){{\epsilon }}[0,1]} \right\}. $$

(12)

For each x member of the set X; μ_A(x) indicates the degree of connection of x in A

$$ x{{\epsilon }} \left( {A, \mu } \right) \Leftrightarrow x \in A \wedge \mu \left( x \right) \ne 0. $$

(13)

In addition, the membership function expresses the likelihood that an element x of member U belongs to set A by expressing the degree of relatedness between element x and each set A. A degree of zero indicates that an element is not part of the fuzzy set, whereas a degree of one indicates that it is entirely part of the fuzzy set [43].

2.2.2.2 Fuzzification

The triangle membership function was chosen, because it best suits the needs of the context in which this work will be used. The matching function for a triangular fuzzy integer A is provided by Eq. (14) [42]

$$ \mu_A \left( x \right) = \left\{ {\begin{array}{*{20}l} {0,} \hfill & {se x \le a;} \hfill \\ {\frac{x - a}{{b - a}},} \hfill & {se a \le x \le b;} \hfill \\ {\frac{c - x}{{c - b}}, } \hfill & {se b \le x \le c;} \hfill \\ {0,} \hfill & {se x \ge c.} \hfill \\ \end{array} } \right. $$

(14)

2.2.2.3 Fuzzy Inference

In fuzzy logic, defuzzification is the process by which fuzzy numbers are transformed into a single number using a variety of criteria. The maximum typical load is calculated here to be equal to (15)

$$ Z_0 = \frac{\mu (x)_i w_i }{{\mu (x)_i }}, $$

(15)

According to Eqs. (2, 3), Z₀ is the defuzzification output, μ(x)_i is the correlation degree, and w_i is the weight value of the fuzzy output [42].

2.2.3 Time Series

As seen here, a time series is a set of observations that have been organized according to time (or another quantity)

$$ Xt1,Xt2, \ldots ,Xtn{:} $$

Several objectives can be pursued in time series analysis, and they fall into the following categories [44, 45]:

• (A) As an initial step in analyzing a time series, a simple description of the data in the form of a graph and some descriptive terms is typically provided.

• (B) Explanation: It is possible to explain changes in one time series using changes in another series when observations are made on two or more variables. Multivariate regression models may be helpful in these circumstances.

• (C) Prediction: Assuming a time series, we are expected to forecast the series’ future values. This work is crucial for forecasting and interpreting hydrological time series.

• (D) Control: Process control might be the goal of a time series analysis, because it evaluates the “quality” of a production process. The controller in statistical control makes decisions based on the findings of studies and maps after drawing observations on control charts.

• (E) Model fitting: Model fitting entails calculating and determining the parameters of the models chosen in the first step as well as determining whether or not each model’s parameters are significant. In other words, if any model’s parameters are not significant at this point, that model is eliminated from the list of models that were chosen. One of the most vital phases of modeling is parameter estimation.

In the case of a time series with N observations drawn from an infinite population, the resulting model is a random model, generated by a random process. Time series models can be classified as autoregressive, moving average, or composite. Some processes not only exhibit autocorrelation, but also display features typical of moving averages. Autoregressive moving average and autoregressive cumulative moving average models are utilized in such circumstances. Determining or identifying the model based on the characteristics of the observation series is the first stage in modeling. Some aspects of the model may become apparent after first analyzing the evolution of serial statistical parameters like mean, standard deviation, and skewness [45].

3 Presenting the Techniques Used in the Proposed Hybrid Modeling

This section describes the modeling methods used to estimate the watershed’s runoff and discharge of river flow. The proposed estimating methods, as well as their combination and optimization, are depicted in a simple flowchart (Fig. 6).

Fig. 6

Hydrological modeling flowchart display of the proposed plan

In this suggested approach, we estimate runoff using three different time intervals from the hydrology model. Risk modeling and twofold uncertainty of factors affecting river flow estimation by defining Frank's Archimedean copula function are two examples of these techniques. Another is the use of fuzzy systems to account for the dependency of runoff amount on independent variables. Each model and its specifications are outlined below. Finally, the river flow estimation function is defined through modeling based on the following connection:

$$ Q_{{\text{est}}} = Y_{{\text{TSM}}} *\left( {Y_{{\text{FLS}}} + Y_{{\text{COPM}}} } \right). $$

(16)

This effective error between the observed and estimated flow rates is then used to derive the goal function using the following formula:

$$ E_{{\text{rms}}} = \sqrt {{\frac{{\sum_{k = 1}^n \left( {Q_{{\text{est}}} \left( k \right) - Q_{{\text{obs}}} \left( k \right)} \right)^2 }}{n}}} , $$

(17)

where n represents the total number of samples taken at various periods.

The final phase involves optimizing the objective function with the help of a water cycle algorithm to lower the effective error. Through arriving at a solution, the modeling parameters of each modeling approach are quantified. The goal function will be the optimized version of the function using the parameters found by the algorithm.

3.1 GARCH Time Series Modeling

Physical phenomenon modeling and signal processing are only two of the many applications for time series. For instance, in signal processing, the Auto-Regressive Moving Average (ARMA) model is widely utilized. Heteroscedastic models are offered for modeling unstable phenomena [46, 47], and this is one of the time series we are looking at. The time-variance change causes instability in such models. For instance, interest rate and stock price series can be modeled using variations on the fundamental Autoregressive Conditional Heteroscedasticity (ARCH) and Generalized Autoregressive Conditional Heteroscedasticity (GARCH) models [48]. The GARCH model explains a return mechanism that draws on past observations by combining the concepts of Heteroscedasticity (varying variance with time) and Conditional Instability (dependency on prior observations). Generalized also refers to a generic approach. Therefore, as is evident from the name of this model, GARCH is a mechanism in which past variances are taken into account while attempting to explain future variance. In other terms, GARCH is a method for modeling time series in which past variances are employed to predict future variances. Time series that exhibit instability (such as those involving the economy and hydrology) have found a home in GARCH models throughout the past decade. Belerself [49] initially proposed the GARCH model as a generalization of the GARCH model's fundamental approach [50]. Because of this, he was able to conduct the required modeling with fewer inputs. There is some similarity between the relationships (Auto-Regressive) of AR and ARMA and ARCH and GARCH.

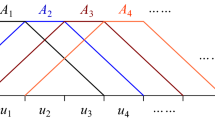
The main use that the creators of these techniques had in mind was the modeling of time series pertaining to economic activities like interest rates and stock prices. The heavy tail of the probability density function and volatility clustering are the two key characteristics of GARCH models. Figure 7 illustrates the probability distribution functions for the GARCH model and Gaussian processes, with the second distribution function (full line) having a greater degree of sequence. Being serial is referred to as Excess Kurtosis. Unstable clustering (a form of Heteroscedasticity) is also characterized by the fact that significant changes follow tiny changes in these processes. This feature may originate from non-Gaussianity in the distribution of random processes and also be modified by variance variability. After a brief introduction to Heteroscedastic models and the generalized GARCH model, we will delve into the mathematical relations that underpin this distribution. If n(t) denotes a discrete random process in time, then for a GARCH(p, q) process, the following relations hold [49]:

$$ \left( {i = 1, \ldots ,q \, } \right)\alpha i \ge 0\quad \alpha > 0 \quad \left( { \, j = 1, \ldots , \, p \, } \right)\quad \beta \, j \ge 0. $$

β j and α i coefficients are called ARCH coefficients, respectively. If p = 0, the obtained model is ARCH(q), and if p = q = 0, n(t) will be a white noise. From the above relationships, the relationship between the conditional variance and the variance of the previous times has been clearly defined. Figure 8 shows some examples of this model. As mentioned in this figure, changing the coefficients in this model makes it flexible in modeling all kinds of series.

Fig. 7

Comparison of sequence in Gaussian and GARCH density functions

Fig. 8

GARCH(1,1) time series with different coefficients

3.2 Fuzzy Logic System Modeling to Investigate the Effect of Independent Variables

To improve the precision of river flow estimation, a fuzzy logic system has been utilized in this work to examine the effects of each of the four independent meteorological variables in the primary model. The following equation describes how this system applies to each variable to derive the fuzzy estimation function:

$$ Y_{{\text{FLS}}} = \mathop \sum \limits_{i = 1}^M W_i \times {\text{Fuzzy}}_{vi,ui} \left( {**,Zi} \right). $$

(18)

The fuzzy optimum system for each of the four independent meteorological variables included in the objective function is represented by the parameters Wi, vi, ui, and Zi. The water cycle algorithm is used to calculate these values of each fuzzy variable's influence on the suggested estimation model. The overview of this fuzzy system is depicted in Fig. 9. Figure 9b, c depicts the fuzzy system's parameters. The fuzzy rules that control this estimating model are displayed in Table 1.

Fig. 9

a Fuzzy system. b Input and output membership functions. c Input and output characteristics

Table 1 Fuzzy rules governing the fuzzy system model

Fuzzy rules are presented to create a dispersion of input information to increase the accuracy of system estimation. Therefore, by optimally determining the parameter values by optimization algorithms, a fuzzy non-linear map** is performed on each meteorological variable. This map** makes the system to an optimal flexibility for the input data to correctly estimate the objective function. To shape the data and improve the estimation accuracy, these rules are defined in accordance with Table 1 to produce a distinct scatter in accordance with Fig. 9c for the rules of different membership functions of LAW 1, 2.

3.3 Using Copula Functions to Model Risk and Uncertainty of Dependencies Between Independent Variables

Joint statistical distributions with various marginal distribution functions can be easily generated using copula functions, which are quite versatile. The copula is a statistical distribution function that can be used to create bivariate or multivariate distributions by combining the distribution functions of univariate margins. Joints are multivariate distribution functions with uniformly distributed one-dimensional margins between (1 and 0). Sklar [51, 52], who discusses in a theory how univariate distribution functions can be coupled to create multivariate distributions, is credited with the invention and presentation of the joint. Scalar demonstrated the existence of a CU1, …, Ud such that: For d-dimensional continuous random variables X1, …, Xd with marginal CDFs u j = FXj (x j) where j = 1, …, d is a joint, d is one-dimensional

$$ C_{U_1 , \ldots ,U_d } \left( {u_1 , \ldots ,u_d } \right) = H_{X_1 , \ldots ,X_d } \quad \left( {X_1 , \ldots ,X_d } \right), $$

(19)

where u j, j is the marginal margin and HX1, …, Xd is the CDF of {X1, …, Xd}. Because the margins from 0 to 1 are non-decreasing for continuous random variables of the CDF function, the joint Cu1, …, ud can be defined as the transformation of HX1, …, Xd [− ∞, ∞]^d to [0, 1]^d in commented. The result of this transformation is that marginal distributions are separated from HX1, …, Xd, and therefore, Cu1, …, ud are only related to the relationship between variables and provide a complete description of the overall dependence structure [53]

$$ {\text{Frank}}\quad C\left( {u,v} \right) = - \frac{1}{\theta } \ln \left[ {1 + \frac{{\left( {{\text{e}}^{ - \theta u} - 1} \right)\left( {{\text{e}}^{ - \theta v} - 1} \right)}}{{{\text{e}}^{ - \theta } - 1}}} \right] \theta \ne 0. $$

(20)

The Joint function can generally be thought of as a multivariate function that has been transformed from [− ∞,∞]^d to [0, 1]^d. The Joint function C is only connected to the reliance between the variables as a result of this transformation, which separates the marginal distributions from the F function. This completes the description of the internal dependency structure. In other words, the scalar theorem demonstrates that for multivariate distributions, the internal dependence structure between the variables and the distribution functions of a marginal variable can be separated from one another, and the Joint function can fully explicate the dependence structure. Archimedean Joint functions are one of the most frequently used functions in the multivariate analysis of hydrological events and have explicit relationships in their cumulative distribution functions, which are an advantage over using some other functions, such as Elliptic joint functions, which do not have an explicit cumulative distribution. This research employed Frank’s Joint function to examine the Karaj drainage basin's multivariate river flows. Below, we display the corresponding relation for the applied specific functions [53].

Finding the level of correlation between the two variables under examination is the first stage in fitting and choosing the Joint function.

Estimating the joint parameter (θ) is the second and most crucial stage in the application of joint functions. Researchers have developed a number of methods, each of which has benefits and drawbacks, to estimate the joint dependence parameter, including the method of moments, the Maximum-Likelihood Method, the Canonical Maximum-Likelihood method, and meta-exploration methods (such as the genetic algorithm) [54, 55]. Kendall’s rank correlation is used to compute the copula function's parameter (θ). TAU is the result of the RHO linear correlation parameter for a Gaussian pair with the Kendall rank correlation. RHO is a scalar correlation coefficient that corresponds to a bivariate copula if TAU is a scalar correlation coefficient [56].

This investigation applies the uncertainties governing the river flow estimation relationship using the following mathematical formula:

$$ Y_{{\text{copm}}} = \mathop \sum \limits_{i \ne j = 1}^M W_{ij} \times {\text{copula}}_{{\text{frank}}} \left( {**,Xj} \right) \times ** \times Xj. $$

(21)

The values of the weather variables are multiplied by the value of the copula function M = 4, where M is the number of weather variables defined in the meteorological data of the research area. The water cycle algorithm incorporates uncertainty and risk into the objective function by applying this function to the system with a weighted W_ij.

4 Simulation, Results and Discussion

4.1 Introduction of the Study Area

The modeling of non-linear systems faces various challenges that require new combined methods for control and modeling in recent works [57,58,59,60,61,62]. The Karaj River has been selected for hydrology modeling and river flow calculation in the central Alborz highlands of the Karaj Dam basin. According to Fig. 10, this basin is situated geographically between the cities of 35 degrees 54 min and 36 degrees 9 min north latitude and 51 degrees 3 min and 51 degrees 34 min east longitude in the northwest of Tehran Province. It may be found in Tehran, Nowshahr, and Chalus. The watershed surrounding the Karaj Dam covers 764 square kilometers. With a maximum height of 4747 m and a minimum height of 1676 m, this basin is entirely mountainous. This basin is traversed by the significant Karaj–Chalus route, which links the provinces of Mazandaran and Tehran. The basin's socioeconomic structure is rural, and the inhabitants utilize its pastures and natural resources all year long.

Fig. 10

Location of the study area

4.2 Performance Evaluation Indicators of the Proposed Model

The accuracy of the simulated behavior of a hydrological model in comparison to observational data must be estimated to assess the performance of the model. In this work, the performance of the suggested ALSIS-HBV model is evaluated using 4 objective functions. The statistics employed include the root-mean-square error to standard deviation of the measurement data (RSR), the coefficient of explanation (R²), the Nash–Sutcliffe efficiency coefficient (NSE), bias (BIAS), and the Nash–Sutcliffe efficiency coefficient to the bias

$$ R^2 = \left( {\frac{{\sum_{i = 1}^N \left( {Q_{{\text{obs}},i} - \overline{Q}_{{\text{obs}}} } \right)\left( {Q_{{\text{sim}},i} - \overline{Q}_{{\text{sim}}} } \right)}}{{\left[ {\sum_{i = 1}^N \left( {Q_{{\text{obs}},i} - \overline{Q}_{{\text{obs}}} } \right)^2 } \right]^{0.5} \left[ {\sum_{i = 1}^N \left( {Q_{{\text{sim}},i} - \overline{Q}_{{\text{sim}}} } \right)^2 } \right]^{0.5} }}} \right)^2 , $$

(22)

where N is the number of Q_sim and Q_obs observations, simulated and observed flow, and Q_sim and Q_obs are the average observed and simulated flow for the entire time period.

The NSE index ranges from minus infinity to one, and it is a normalized value that assesses the significance of the residual variance. If the NSE is greater than zero, the model predictions are more accurate than the average of the observations, and if it is equal to one, the model forecasts and the observations are identical. The NSE statistic is commonly used in hydrological modeling to assess the level of concordance between two independent variables [63]

$$ {\text{NSE}} = 1 - \frac{{\sum_{i = 1}^N \left( {Q_{{\text{obs}},i} - Q_{{\text{sim}},i} } \right)^2 }}{{\sum_{i = 1}^N \left( {Q_{{\text{obs}},i} - \overline{Q}_{{\text{obs}}} } \right)^2 }}. $$

(23)

The overall level of agreement between two variables is shown by BIAS [64]. Zero BIAS denotes a lack of general bias in the result of the simulation when compared to the observations. Overestimation and underestimating of the model, respectively, are indicated by positive and negative skewness scores

$$ {\text{BIAS}} = \frac{{\sum_{i = 1}^N \left( {Q_{{\text{sim}},i} - Q_{{\text{obs}},i} } \right)}}{{\sum_{i = 1}^N \left( {Q_{{\text{obs}},i} } \right)}}. $$

(24)

RSR ranges from 0 to a significant positive value. The better the model performs, the smaller this statistic is

$$ {\text{PSR}} = \frac{{{\text{RMSE}}}}{{{\text{STDEV}}_{{\text{obs}}} }} = \frac{{\sqrt {{\sum_{i = 1}^N \left( {Q_{{\text{obs}},i} - Q_{{\text{sim}},i} } \right)^2 }} }}{{\sqrt {{\sum_{i = 1}^N \left( {Q_{{\text{obs}},i} - \overline{Q}_{{\text{obs}}} } \right)^2 }} }}. $$

(25)

4.3 Experimental Results

The outcomes of applying the proposed hybrid hydrological modeling approaches are described here. In this evaluation, we used a 2.90 GHz Intel Core i5 processor with 8.00 GB of RAM. For 19 years of weather records, the proposed method has been implemented in the 64-bit Windows environment using the MATLAB program. The MATLAB application on Windows has been used to implement the proposed method for estimating river flow and runoff in the Karaj Dam catchment area. We measure the efficiency of the suggested method in terms of modeling time and other relevant parameters.

Weather data, including the amount of rainfall and snowfall, air temperature, and humidity, over a period of 19 years (2014 September 23 to 2023 September 22) were selected for training and testing to model the daily flow of the Karaj River using a hydrological modeling to estimate the river water flow optimized with the water cycle algorithm. To conform to the time series modeling of the river flow, a total of 85% of the data were used for training and 15% was used for testing.

Selecting a variety of primary random populations in a phenomenon (termed educational data in water cycle planning) with the intent of imparting knowledge about the mechanism governing the phenomenon increases not only the complexity of the model and the amount of memory required, but also decreases the accuracy of the pattern. This means that the best observational data should be used as training data when attempting to model river flow. With a population of 5, the algorithm can only go through a maximum of 300 optimization cycles. There are a total of 28 members in the objective function's response parameters, including 6 members in the weighting model of copula functions two by two variables, 16 members in the time series model, and 6 members in the fuzzy system model. The analysis results for the water cycle algorithm to determine the optimal solution are displayed in Fig. 11. The findings of the comparison model for various methods on a variety of test data are also displayed in Fig. 12.

Fig. 11

Performance results of the water cycle algorithm. a ATS. b Comap-FLS-TS. c FLS-TS

Fig. 12

Modeling results for observed and estimated samples with different techniques. a TS. b FLS-TS. c CopM-FLS-TS

The results of applying the water cycle algorithm planning approach to model the daily flow of the river for different input patterns are compared statistically, as shown in Table 2. This table shows that the model that was discharged 3 days ago had the least error and the highest accuracy, making it the best model created for planning the water cycle. Additionally, the proposed method has shown better results when compared to previous time series models, and in the best case scenario, it was able to forecast the daily flow rate of the investigated river.

Table 2 Comparison of the proposed work's evaluation criteria results

In this section, the optimal solutions for the various proposed models are presented in Table 3. According to the results of the objective function in Fig. 11, the best solutions after the 50 iteration period for all three models have been obtained approximately by the WCA algorithm. Despite having 28 different parameters and a more intricate search than the other two models, the CopM + FLSM + TS model was able to follow a more accurate approximation and achieve the lowest objective function.

Table 3 Introduction of optimal parameters calculated by WCA algorithm for different models

A visual representation of the error is provided in Fig. 13. Error values (the difference between observed and anticipated values over the statistical period) are always between zero and one, and smaller error values suggest the existence of fewer differences. All of the model's input variables have been double-checked in the prediction test over the course of a year using a t test. As can be seen in Figs. 12 and 13, the simulated and observed values are quite close to one another across the 19-year period, with most falling within a 20% confidence interval of the true value. Therefore, the ability of the model in simulating and generating climate data for the next few years was confirmed.

Fig. 13

Modeling error with the proposed technique

4.4 Discussion

Before introducing the model effects of each parameter with the aid of the fuzzy system, the authors define global sensitivity analysis to identify the uncertainty of the sensitive parameters of the model in accordance with the Frick copula function. For the Karaj River runoff estimation over a period of 1 month, the sensitivity and accuracy findings demonstrate a good improvement (Table 2). Time series (TS) modeling, fuzzy logic and support vector machines (FLSM + TS), and copula function modeling (CoPM + FLSM + TS) are some of the methodologies compared. Also, the results of these proposed models are compared with two other models from recent articles in Table 2. According to the compared criteria, the TS model has a better estimation speed than other models, but the combined CoPM + FLSM + TS model performs very well in terms of accuracy and error compared to other methods and models mentioned in Table 2. To show the difference in Fig. 14, the results of the criteria of different models are compared. As shown by the results, the best solutions are produced using the CopM + FLSM + TS method. This method shows an improvement of 98.3% and 96.3%, respectively, in the RMSE criterion compared to TS and FLSM + TS models.

Fig. 14

Bar chart display of benchmark results for different modeling

5 Conclusion

One of the crucial and significant factors in the catchment basin's water resource management is determining how rivers flow. There are several applications for the study of this hydrological phenomenon, including flood predictions. However, in the short term, particularly daily, the river flow mechanism appears to be non-linear. The non-linearity of short-term climatic processes like precipitation and temperature is the main cause of non-linearity in the daily short-term flow process, and the non-linearity of the reaction of precipitation and runoff also complicates the river process.

The integrated non-linear model of time series, copula function, and fuzzy logic system in water resources is one of the applications of this research. The results of this study indicate that this model is more accurate than linear models and is compatible with time series of river flow. Due to the copula function’s consideration of risk and uncertainty, fuzzy modeling of each of the important factors in estimating river runoff, and the GARCH time series model, this model has a good resilience to climate change.

The findings of this study also demonstrated that the Abriz Karaj River's discharge could be predicted using a non-linear model that had higher accuracy and lower error than comparable models based on conventional time series. The scientific community and users have access to a wide variety of hydrological models; however, the suggested models will be straightforward but effective. In the next phase of our research, we intend to utilize this model to calculate the input flow rate, calculate the height and volume of water behind the Amirkabir dam, and assess how evaporation and transpiration would affect the suggested model.