1 Introduction

The broader context of this research is the significant progress made in recent decades in finding analytical methods to solve nonlinear partial differential equations. These equations are pivotal in understanding nonlinear physical processes that are integral to various scientific and engineering fields, such as plasma physics, fluid mechanics, neurobiology, optical fibers, and porous media. The inverse scattering approach [2], HI Rota’s bilinear method [11], the Painlevé expansion technique [29], the first integral approach [28], and the tanh technique [18] are notable examples of such analytical procedures.

The tanh method is particularly highlighted for its effectiveness in solving travelling wave problems, offering solutions mainly in the form of profiles of solitary waves by defining them as a finite power series in tanh. Malfliet [18] simplified this method by expressing tanh as a new variable, making it applicable to a wider range of nonlinear evolution equations. Afterwards, this method was improved by determining the velocity through asymptomatic and combining boundary conditions with the resultant expansion [14, 16, 19, 20]. Other generalizations have been introduced as well; see for example [1, 6, 7, 13, 26, 27].

Our study applies the tanh method [18] to derive accurate solutions for the travelling wave to the two-dimensional Allen-Cahn equation with multiplicative noise given as

$$\begin{aligned} v_t=v_{xx}+v_{yy}+v-v^3+\delta v dB(t), \end{aligned}$$
(1.1)

where B(t) is a standard \(\mathcal {Q}\)-Brownian motion defined on filtered probability space \((\Omega , \mathcal {F},\mathcal {F}_t,\mathbb {P})\), and \(\delta\) stands for the noise strength. The Brownian motion B(t) in our work is considered in time only.

Allen and Cahn originally developed this equation (for \(\delta =0\)) [3] as a model for non-conserved order fields in binary alloys. The equation has found applications in a variety of scientific disciplines such as mathematical biology, quantum mechanics, and plasma physics. Its travelling wave solutions have been extensively researched both analytically and numerically, using techniques such as the first integral method [28], the tanh function approach [30, 31], the double exp-function technique [5], and the method of the Haar wavelet [10]. The uncertainty in applications of mean curvature flow connected to the Allen-Cahn equation due to heat fluctuations [8] requires the study of the influence of randomness on the solutions to the stochastic Allen-Cahn model. Many analytical techniques have been presented to study those stochastic effects, as shown in [12, 21,22,23].

This work builds on Mohammed et al.’s research [24], which found analytical solutions for travelling waves for the one-dimensional stochastic Allen-Cahn equation. We extend their work to cover the case of two dimensions using the classical tanh method. The novelty of our work is to provide analytical solutions for Eq. (1.1) since the previous studies focused only on approximate and numerical solutions of such an equation.

The influences of multiplicative noise on the generation of travelling waves in excitable media are diverse and significant, as shown in various studies [9, 17, 25]. Specifically, we aim to explore how multiplicative noise affects the travelling wave solutions of the Allen-Cahn equation and wave propagation in excitable media, with a focus on propagation failure phenomenon as in the case of high noise levels. The increase of noise decreases the amplitude of the travelling wave that the model exhibits. When the noise becomes strong enough, the wave is completely annihilated, leading to the phenomenon of propagation failure.

The article is organized as follows. Section 2 explores the analytical solutions for travelling waves in Eq. (1.1), employing the tanh approach combined with a technique of wave transformation. Section 3 is dedicated to examining the influence of multiplicative noise on the behaviour of such solutions, featuring visual representations to highlight the occurrence of propagation failure. The paper concludes with our final observations and insights in the last section.

2 Exact solutions for travelling waves

It’s important to note before moving forward with the derivation of exact travelling wave solutions using the tanh method for Eq. (1.1), that the existence and uniqueness of solutions for such equations have been thoroughly investigated in previous studies, as detailed in references like [4, 15] and others cited therein.

2.1 Derivation of exact solutions for travelling waves

We suppose that the solution of the Eq. (1.1) is written as a wave transformation given by [24]

$$\begin{aligned} v(t,x,y)=\varphi (\rho )e^\eta , \end{aligned}$$
(2.1)

where \(\rho =\lambda (x+y-ct)\) and \(\eta =\delta B(t)-\frac{\delta ^2}{2}t\). The parameters \(\lambda\) and c stand for the number and speed of wave, respectively. We now have

$$\begin{aligned} v_t= & {} -c\lambda \varphi ^{\prime } +\delta \varphi dB(t)-\frac{1}{2}\delta ^2 \varphi \\\nonumber v_{xx}= \,& {} \lambda ^2 \varphi ^{\prime \prime } e^\eta \\\nonumber v_{yy}= \,& {} \lambda ^2 \varphi ^{\prime \prime } e^\eta . \end{aligned}$$
(2.2)

Substituting Eqs. (2.1) and (2.2) into Eq. (1.1) leads to

$$\begin{aligned} (c\lambda \varphi ^{\prime }-\delta \varphi dB(t)+\frac{\delta ^2}{2}\varphi +2\lambda ^2\varphi ^{\prime \prime }+\varphi +\delta \varphi dB(t))e^\eta -\varphi ^3 e^{3\eta }=0. \end{aligned}$$
(2.3)

Thus

$$\begin{aligned} 2\lambda ^2\varphi ^{\prime \prime }+c\lambda \varphi ^{\prime }-\varphi ^3 e^{2\eta }+\left(1+\frac{\delta ^2}{2}\right)\varphi =0. \end{aligned}$$
(2.4)

Note that

$$\begin{aligned} E(e^{2\eta })= \,& {} E(e^{2(\delta B(t)-\frac{\delta ^2}{2}t})\\= \,& {} e^{-\delta ^2 t}E(e^{2(\delta B(t)}), \end{aligned}$$

where E stands for the expectation with respect to Brownian motion B(t). Since \(\delta B(t)\) distributed like \(\delta \sqrt{t} \omega\) for normally distributed random variable \(\omega\), we obtain \(E(e^{(\delta B(t)})=e^{\frac{\delta ^2}{2}t}\). Apply the expectation on the Eq. (2.4), we get

$$\begin{aligned} 2\lambda ^2\varphi ^{\prime \prime }+c\lambda \varphi ^{\prime }-\varphi ^3 +\left(1+\frac{\delta ^2}{2}\right)\varphi =0. \end{aligned}$$
(2.5)

2.1.1 Tanh function technique

The possible solution of Eq. (2.5) is supposed to be a finite tanh power series written as [18]

$$\begin{aligned} \varphi (\rho )=\sum _{r=0}^{N} \beta _{r} \tanh ^{r}(\rho ). \end{aligned}$$
(2.6)

To determine N, we balance the highest derivative \(\varphi ^{\prime \prime }\) with the highest order of the non-linear term \(\varphi ^3\). Thus, \(N+2=3N\), which yields that \(N=1\). Hence, the solution of Eq. (2.5) is given as

$$\begin{aligned} \varphi (\rho )=\beta _{0}+\beta _{1} \tanh (\rho ), \end{aligned}$$
(2.7)

which yields

$$\begin{aligned} \varphi ^{\prime }(\rho )=\beta _{1}sech^2(\rho )=\beta _{1}(1-\tanh ^2(\rho )), \end{aligned}$$

and

$$\begin{aligned} \varphi ^{\prime \prime }(\rho )=-2\beta _{1}sech^2(\rho )\tanh (\rho )=-2\beta _{1}(1-\tanh ^2(\rho ))\tanh (\rho ). \end{aligned}$$

Substituting for \(\varphi\), \(\varphi ^{\prime }\) and \(\varphi ^{\prime \prime }\) into Eq. (2.5), we obtain

$$\begin{aligned} -4\lambda ^2\beta _{1}(1-\tanh ^2(\rho ))\tanh (\rho )+c\lambda \beta _{1}(1-\tanh ^2(\rho ))\\\nonumber -(\beta _{0}+\beta _{1}\tanh (\rho ))^3 +\left(1+\frac{\delta ^2}{2}\right)(\beta _{0}+\beta _{1}tanh(\rho ))=0. \end{aligned}$$
(2.8)

Thus

$$\begin{aligned}{} & {} (4\lambda ^2\beta _{1}-\beta _{1}^3)\tanh ^3(\rho )-(c\lambda \beta _{1}+3\beta _{0}\beta _{1}^2)\tanh ^2(\rho )\\\nonumber{} & {} \quad +\left(-4\lambda ^2\beta _{1}-3\beta _{0}^2\beta _{1}+\beta _{1}+\frac{\beta _{1}\delta ^{2}}{2}\right)\tanh (\rho )\\\nonumber{} & {} \quad +c\lambda \beta _{1}-\beta _{0}^3+\beta _{0}+\frac{\beta _{0}\delta ^{2}}{2}=0. \end{aligned}$$
(2.9)

Setting the value of each coefficient of \(\tanh ^{r}, r=0,1,2,3\) to zero, we get the following system of algebraic equations for unknown \(\beta _{0},\beta _{1}\), and \(\lambda\):

$$\begin{aligned} 4\lambda ^2\beta _{1}-\beta _{1}^3= \,& {} 0\\\nonumber c\lambda \beta _{1}+3\beta _{0}\beta _{1}^2= \,& {} 0\\\nonumber -4\lambda ^2\beta _{1}-3\beta _{0}^2\beta _{1}+\beta _{1}+\frac{\beta _{1}\delta ^{2}}{2}= \,& {} 0\\\nonumber c\lambda \beta _{1}-\beta _{0}^3+\beta _{0}+\frac{\beta _{0}\delta ^{2}}{2}=\, & {} 0. \end{aligned}$$
(2.10)

Solving such a system, we obtain

$$\begin{aligned} \beta _{1}= & {} \pm 2\lambda \\\nonumber \beta _{0}= & {} \mp \frac{c}{6}\\\nonumber \lambda= & {} \pm \sqrt{\frac{\delta ^{2}+2}{8}-\frac{c^2}{48}}. \end{aligned}$$
(2.11)

The solution of Eq. (2.5), therefore, is in the form

$$\begin{aligned} \varphi (\rho )=\mp \frac{c}{6} \pm 2\lambda \tanh (\rho ). \end{aligned}$$
(2.12)

Hence, the exact solutions for travelling waves of Eq. (1.1) can be written as

$$\begin{aligned}{} & {} v(t,x,y)=\left(- \frac{c}{6}+2\sqrt{\frac{\delta ^{2}+2}{8}-\frac{c^2}{48}} \, \tanh \left(\sqrt{\frac{\delta ^{2}+2}{8}-\frac{c^2}{48}}(x+y-ct)\right)\right)e^{\delta B(t)-\frac{\delta ^2}{2}t}, \end{aligned}$$
(2.13)

and

$$\begin{aligned}{} & {} v(t,x,y)=\left(+ \frac{c}{6}-2\sqrt{\frac{\delta ^{2}+2}{8}-\frac{c^2}{48}}\, \tanh \left(\sqrt{\frac{\delta ^{2}+2}{8}-\frac{c^2}{48}}(x+y-ct)\right)\right)e^{\delta B(t)-\frac{\delta ^2}{2}t}. \end{aligned}$$
(2.14)

3 The multiplicative noise effects on the solutions for the travelling waves

We employ a variety of graphical representations to analyse the influence of multiplicative noise on the dynamics of travelling waves as depicted in the stochastic Allen-Cahn Eq. (1.1).

3.1 Propagation of travelling waves

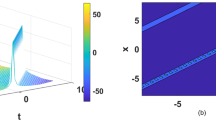
Figure 1 illustrates the noiseless case (\(\delta =0\)), while Fig. 2 shows the scenario when \(\delta = 0.8\), both utilizing the exact solution of travelling wave from Eq. (2.13) to highlight the effect of multiplicative noise on the physical characteristics of travelling waves. The simulations are conducted with a spatial step size of \(\Delta x=\Delta y=h=0.01\) across a square domain of \([-5, 5]^2\). The progression of travelling wave propagation is captured in these figures at various time intervals, namely \(t = 0\), \(t = 10\), \(t = 15\), and \(t = 25\).

From Fig. 1, it is evident that in a deterministic setting (\(\delta = 0\)), the travelling wave maintains its key physical properties, such as width, amplitude, and speed, embodied the characteristics of solitary waves [11]. In contrast, with the introduction of even a small amount of noise ( \(\delta = 0.8\)), there is a notable reduction in the amplitude of the travelling wave over time. More precisely, when \(\delta = 0\), the peak value of the solution for the travelling wave remains approximately at 1 over time. However, with the presence of multiplicative noise (\(\delta = 0.8\)), the peak value starts at around 1 but significantly diminishes to about 0.0028 by \(t = 25\).

Fig. 1
figure 1

Plot of the exact solution for travelling wave of Eq. (1.1) on the range \([-5,5]^2\), taking at levels of times: \(t=0\), \(t=10\), \(t=15\) and \(t=25\), with parameters chosen as \(h=0.01\), \(c=0.3\) representing the spatial step size and the wave speed, respectively. The noise intensity is fixed as \(\delta =0\) which refers to the noiseless case

Full size image
Fig. 2
figure 2

Plot of the exact solution for travelling wave of Eq. (1.1) on the range \([-5,5]^2\), taking at levels of times: \(t=0\), \(t=10\), \(t=15\) and \(t=25\), with parameters chosen as \(h=0.01\), \(c=0.3\), and \(\delta =0.8\), representing the spatial step size, the wave speed, and the noise intensity, respectively

Full size image

3.2 Propagation failure of waves

Figure 3 showcases the travelling wave solution for \(\delta =0.5\), and Fig. 4 demonstrates the case at \(t=1\), aiding in the explanation of the mechanism behind propagation failure. For these simulations, we set the parameters as \(c=1\) and \(h=0.01\) over the range \([-5, 5]^2\). Figure 3 uses different time frames for the simulation: \(t = 0\), \(t = 10\), \(t = 30\), and \(t = 50\). It is observed that the waveform begins to deteriorate over time, losing its characteristic shape and completely vanishing by \(t = 50\), even with a moderate level of noise (\(\delta = 0.5\)). Conversely, Fig. 4 displays the solution of the travelling wave at \(t = 1\) under various noise intensities, specifically \(\delta = 0\), \(\delta = 5\), \(\delta =20\), and \(\delta =40\). In the absence of noise (\(\delta = 0\)), the peak value of the solution for travelling wave remains close to 1. However, this value drops dramatically to 0.0002 when noise intensity increases to \(\delta =5\). At higher noise levels (\(\delta =20\) and \(\delta =40\)), the travelling wave is completely obliterated, underscoring the detrimental impact of noise on wave propagation.

Fig. 3
figure 3

Plot of the exact solution for travelling wave of Eq. (1.1) on the range \([-5,5]^2\), taking at levels of times: \(t=0\), \(t=10\), \(t=30\) and \(t=50\), with parameters chosen as \(h=0.01\), \(c=1\), and \(\delta =0.5\), representing the spatial step size, the wave speed, and the noise intensity, respectively. The figure shows that the wave fails to propagate at high levels of times

Full size image
Fig. 4
figure 4

Plot of the exact solution for travelling wave of Eq. (1.1) on the range \([-5,5]^2\), taking at levels of noise \(\delta =0\), \(\delta =5\), \(\delta =20\) and \(\delta =40\), with parameters chosen as \(h=0.01\), \(c=1\), and \(T=1\), representing the spatial step size, the wave speed, and the time, respectively. The figure shows that the wave fails to propagate when the noise becomes large enough

Full size image

4 Conclusion

We have effectively used the tanh function approach to analytically solve the stochastic Allen-Cahn equation in a two-dimensional space with multiplicative noise. This approach successfully yielded exact solutions for travelling waves. A significant aspect of this research has been the investigation of propagation failure of wave, specifically focusing on the influences of multiplicative noise on the dynamics of these travelling waves. We noted that elevated noise levels can disrupt the travelling waveform, ultimately leading to the nullification of solutions for the governing equation. This highlights the critical impact of noise on the dynamics of wave solutions in these stochastic systems.