Variational autoencoder-based techniques for a streamlined cross-topology modeling and optimization workflow in electrical drives

Abstract

The generation and optimization of simulation data for electrical machines remain challenging, largely due to the complexities of magneto-static finite element analysis. Traditional methodologies are not only resource-intensive, but also time-consuming. Deep learning models can be used to shortcut these calculations. However, challenges arise when considering the unique parameter sets specific to each machine topology. Building on two recent studies (Parekh et al. in IEEE Trans. Magn. 58(9):1–4, 2022; Parekh et al., Deep learning based meta-modeling for multi-objective technology optimization of electrical machines, 2023, ar**v:2306.09087), that utilized a variational autoencoder to cohesively map diverse topologies into a singular latent space for subsequent optimization, this paper proposes a refined architecture and optimization workflow. Our modifications aim to streamline and enhance the robustness of both the training and optimization processes, and compare the results with the variational autoencoder architecture proposed recently.

1 Introduction

The realm of electrical drives has seen unprecedented advances over the past decades. These advances, however, have also given rise to challenges in simulation and optimization of the diverse machine topologies involved. One core challenge is to deal with the complexities inherent to magneto-static finite element analysis (FEA). Traditional FEA methods are notably resource-intensive and time-consuming, constraining rapid advances in design and optimization [3]. Different ideas to counteract this issue with large computational complexities have been discussed, for example in [4].

Machine learning, and in particular deep learning, has emerged as a promising solution with the idea to approximate the complex FEA with a surrogate model based on machine learning [5]. The trained surrogate model can then be used within the optimization workflow to effectively search for the best electric machine (EM) designs given certain requirements. This general process, also adapted in our paper, is showcased in Fig. 1 and follows the general idea introduced in [6].

Figure 1

Complete workflow for the topology optimization process in this work. A surrogate model, in the form of a machine learning model, approximates the complex FEA calculations. This surrogate model is then used within the optimization workflow to find the best possible design parameters given some requirements

Surrogate modeling in electrical machine design can be primarily categorized into two distinct directions based on the data representation used for training. The first direction leverages image-based representations of the motor cross-sections, transforming complex geometrical and material properties into a visual format that can be processed using convolutional neural networks (CNNs). This method has been shown to effectively capture spatial dependencies and geometric features in order to output key performance indicators, as first demonstrated in [7]. With [8] another method was introduced to apply generative adversarial networks (GAN) to efficiently generate novel image representations and subsequently predict motor KPIs of the motors. Conversely, the second direction focuses on parameterization, where the motor’s design variables are directly given to the model. This method facilitates direct manipulation of design parameters, offering a more straightforward integration with optimization algorithms, and is the primary focus of this paper.

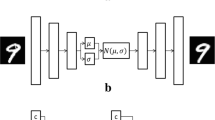
A challenge within the parameterization approach is that different motor topologies require unique surrogate models because of different parameter used. While the topologies can be modeled and optimized individually, a recent study proposed to use the variational autoencoder (VAE) [1] in the process of topology optimization. The idea behind that is to map the different electric machine topologies into a common latent space, as illustrated in Fig. 2. This essentially provides two advantages for the optimization process: Firstly, the optimizer is capable of simultaneously exploring all topologies. Secondly, it efficiently compresses the original input data into a lower-dimensional latent space, retaining most of the crucial information. This compact representation significantly accelerates the optimization process by reducing the need to operate over the entire original input space, thereby offering considerable time savings.

Figure 2

Overview of the proposed surrogate model architecture in [1] with a standard VAE and a KPI prediction network

In this paper, we introduce a range of methods and techniques designed to enhance and streamline the topology optimization workflow, utilizing VAE-based surrogate modeling. To confirm the benefits of these improvements, we provide a comparative analysis of our newly introduced techniques with the approach previously proposed in [1], which was further developed in [2].

The structure of this paper is as follows: In Sect. 2 all the fundamentals leading to the results shown in Sect. 3 are introduced and explained. This includes the introduction of the used data, the proposed adaptions in the surrogate modeling process and in the optimization process. Sect. 3 summarizes the results obtained from using the adapted workflow in comparison to the previous work. Sect. 4 discusses the found results and concludes this paper with a summary and possible future research directions.

2 Background

2.1 Dataset

This study focuses on two topologies of the permanent magnet synchronous machine: the Single-V (SV) topology and Double-V (DV) topology. An example image for both topologies can be seen in Fig. 3. A total of 2411 SV designs and 2819 DV designs were sampled using the motor data engine, as outlined in [9]. Tables 1 and 2 present the design parameters and their respective boundaries utilized for data generation for the SV ($\mathbf{p}_{\text{sv}}$) and DV ($\mathbf{p}_{\text{dv}}$) designs, respectively. For every sampled design, its KPIs were computed using FEA, providing quantifiable measures to evaluate its performance. These KPIs encompass crucial aspects of an electric drive, such as its power, torque, efficiency, and even economic factors like its total cost. All KPIs are normalized throughout this study.

Figure 3

Depiction of the two topologies from the permanent magnet synchronous machine used in this paper: (a) Single-V topology. (b) Double-V topology. Due to symmetries, the topologies are depicted as only an excerpt of the full e-machine. The dark blue parts describe magnets, cyan are the stator windings, the lower gray part is the rotor and the upper gray part is the stator

Table 1 Complete overview of the parameters describing the Single-V topology ($\mathbf{p}_{\text{sv}}$). Discrete=Disc., Continuous=Cont

Table 2 Complete overview of the parameters describing the Double-V topology ($\mathbf{p}_{\text{dv}}$). Discrete=Disc., Continuous=Cont

To enable cross-topology optimization using a single model, it is necessary to merge the two designs into one unified dataset. Table 3 shows that not every design parameter is relevant to both topologies; each has unique parameters absent in the other. Following the approach in [1], any missing values were assigned a default value of zero (“0”). Additionally, a binary parameter (0/1) was added to identify the topology type (SV/DV) of each sample.

Table 3 SV and DV topology datasets combined into one unified cross-topology dataset. Marked blue columns are SV specific parameters, marked orange columns are DV specific parameters. $\mathbf{p}_{\text{discrete}}$ are the discrete parameters and $\mathbf{p}_{\text{continuous}}$ are the continuous parameters of the complete feature vector

2.2 Surrogate modeling

As mentioned in the Introduction, differing from the research in [1] and [2] we introduce two modifications of the surrogate modeling process with the VAE. Whereas the previous studies used the complete parameter vector p from Table 3 as input data for the VAE, this study adapts the architecture such that continuous and discrete parameters are handled differently. Furthermore, an adaption in the form of the so-called Masked Learning Process for training the model will be introduced.

2.2.1 Overall model architecture

The modified model architecture, termed CD-VAE (Continuous Discrete-VAE) in this study, is depicted in Fig. 4. The core concept involves separating continuous and non-continuous input parameters. This separation of the input data in the VAE framework is motivated by the challenges highlighted in handling mixed-type datasets. VAEs, traditionally tailored for continuous data, struggle with heterogeneous data comprising varied types, such as continuous and discrete. This mismatch can lead to suboptimal results, as different likelihood functions are required for diverse data types. These contribute unevenly during training, often favoring certain dimensions over others [10]. With the CD-VAE approach, only continuous parameters ($\mathbf{p}_{ \text{continuous}}$) are processed for compression into the latent space z and subsequent reconstruction. Discrete parameters ($\mathbf{p}_{\text{discrete}}$), such as topology or the maximum AC line current, are concatenated to the compressed latent space z, which is then used to predict the KPIs of the samples.

Figure 4

Overview of the proposed CD-VAE adaption. The complete input feature vector is split up into continuous and discrete features before being processed

In our implementation, all three networks – the encoder $f(\cdot )$, decoder $g(\cdot )$, and the KPI prediction network $k(\cdot )$ – are modeled as Multilayer Perceptrons (MLPs). The encoder $f(\cdot )$ comprises an input layer of size 7 (all continuous parameters $\mathbf{p}_{\text{continuous}}$ from Table 3), followed by two hidden layers with ReLU activation functions, and ends with two distinct output layers, where the mean and variance of samples in the latent space $\mathbf{z} \in \mathbb{R}^{5}$ are determined individually. The decoder $g(\cdot )$, on the other hand, accepts samples from the latent space z at its input layer, processes them through two hidden layers with again ReLU activation functions, and then yields the reconstructed values of the continuous input parameters in a single output layer.

For KPI prediction $k(\cdot )$, the network takes the latent vector z concatenated with the discrete variables from the input vector $\mathbf{p}_{\text{discrete}}$ as its input, funnels it through two hidden layers with ReLU activation functions, and ultimately predicts the KPIs in its final output layer. The complete model architecture, i.e., the VAE together with the KPI prediction, is trained jointly by minimizing the standard VAE loss together with the KPI reconstruction loss:

$$ L=L_{\text{recon}}+L_{\text{kl}}+L_{\text{kpi}}, $$

(1)

where

$$\begin{aligned}& L_{\text{recon}}(\mathbf{p},\hat{\mathbf{p}})= \Vert \mathbf{p}- \hat{\mathbf{p}} \Vert _{2}^{2}, \end{aligned}$$

(2)

$$\begin{aligned}& L_{\text{kl}}=D_{\text{kl}}\bigl(N\bigl(\mu ,\sigma ^{2}\bigr)\Vert N(0,I)\bigr) \end{aligned}$$

(3)

and

$$ L_{\text{kpi}}(\mathbf{y},\hat{\mathbf{y}})= \Vert \mathbf{y}- \hat{\mathbf{y}} \Vert _{2}^{2}. $$

(4)

$L_{\text{recon}}$ represents the mean squared error (MSE), which quantifies the discrepancy between the actual parameter inputs and their reconstructed counterparts. Furthermore, $L_{\text{kl}}$ is the KL-divergence of the VAE between the learned latent space distribution (i.e., μ and $\sigma ^{2}$) and a standard normal distribution. Finally, $L_{\text{kpi}}$ is the MSE of the KPI prediction.

2.2.2 Masked learning process

Another proposed enhancement solves the problem of input parameters specific to one topology and missing in the other. Replacing these missing values with an arbitrary fixed constant (zeros in our case) forces the autoencoder to learn to reconstruct these values, though they carry no real meaning (they are irrelevant for the topology). This wastes the capacity of the model and makes the learning more difficult. Instead, we propose a Masked Learning Process for the VAE training, whereby only the relevant parameters of the respective topology are considered in the reconstruction loss. We split the reconstruction loss defined in Equation (2) into two parts, one for each topology, as follows:

$$ L_{\text{recon}} = L_{\text{sv}\_\text{recon}} + L_{\text{dv}\_\text{recon}}, $$

(5)

where

$$\begin{aligned} L_{\text{sv}\_\text{recon}} & = \Vert \mathbf{p}_{\text{sv}} - \hat{ \mathbf{p}}_{\text{sv}} \Vert _{2}^{2}, \end{aligned}$$

(6)

$$\begin{aligned} L_{\text{dv}\_\text{recon}} & = \Vert \mathbf{p}_{\text{dv}} - \hat{ \mathbf{p}}_{\text{dv}} \Vert _{2}^{2}. \end{aligned}$$

(7)

The impact of this adaptation on the reconstruction of parameter samples is discussed in detail in Section 3.1. Essentially, a comparison between the standard VAE approach and the adapted learning process reveals a significant difference. In the standard VAE approach, the model attempts to reconstruct zero values for nonsensical parameters that are not present in the given topology. In contrast, the adapted learning process allows the model to predict any value for these variables without being penalized by the loss function during training.

2.3 Optimization

The target for our KPI optimization is the maximization of the axle power and minimization of the total cost ($y_{2}$ and $y_{10}$ in Table 4). In our surrogate-modelling approach, we formulate the multi-objective optimization as follows:

$$ \begin{aligned} &\operatorname*{arg\,min}_{\mathbf{p}} [- \hat{y}_{2}, \hat{y}_{10}] \\ &\quad \text{s.t. } p_{i}^{(\min )} \leq p_{i} \leq p_{i}^{(\max )} , \end{aligned} $$

(8)

where $\hat{y}_{2}$ and $\hat{y}_{10}$ are the outputs of the surrogate predictor $k(\cdot )$, and $p_{i}^{(\min )}$ and $p_{i}^{(\max )}$ are the minimum/maximum admissible values for the input parameters as listed in Tables 1 and 2. These boundaries ensure that the optimizer searches within a space where designs are mostly geometrically valid. Additional constraints, such as requiring the designs to have a maximum torque of over 3000, could be introduced here depending on the specific use case but were not considered for this study.

Table 4 Complete overview of the KPIs characterizing the EM designs

We have introduced two additional modifications to the optimization process, leading to an overall better performance:

2.3.1 Feasibility classifier

Despite the min/max admissibility constraints for the parameter values, the optimization process may yield parameter combinations that are not feasible in real world applications. Specifically, we have observed that certain SV topology feature combinations yielded infeasible designs. A mechanism to preemptively identify such infeasible solutions is crucial to ensure an efficient optimization process.

We trained the feasibility classifier, denoted as $\phi (\mathbf{p_{\text{geom}}})$, using only the geometric design parameters $\mathbf{p}_{\text{geom}}$ (stator outer diameter, magnet spread, magnet inclination, and relative magnet width) from 1150 designs. We obtained these designs through Latin Hypercube Sampling (LHS) [11], specifically for the SV topology. The feasibility of each design is verified with FEA, with 493 designs ($\approx 43\%$) deemed feasible. Considering the simplicity of this problem, we tested several standard algorithms and ultimately selected a Logistic Regression (LR) model for its high accuracy of 99%. This model effectively classifies the geometric feasibility of designs.

Additionally, we integrated this classifier as an extra constraint in the optimization formulation, as specified in Equation (8).

$$ \begin{aligned} & \text{s.t.} \quad \phi ( \mathbf{p_{\text{geom}}})=1. \end{aligned} $$

(9)

This integration of the feasibility classifier in the optimization loop, as shown in Fig. 5, ensures the optimizer only identifies designs that are practical for real-world use.

Figure 5

Proposed inclusion of the Feasibility Classifier and the Biased Population Initialization within the workflow of electric machine optimization with a surrogate model

2.3.2 Biased population initialization

In our study, we employed the NSGA-II genetic algorithm for optimization [12]. However, during our VAE optimization experiments, one topology consistently dominated the population, sidelining samples from the other topology. This dominance effect was particularly pronounced when a significant gap existed between the two topologies in the optimization space. To counter this imbalance and foster a more equally distributed representation of both topologies, we implement a strategy of biased population initialization.

To ensure more consistent outcomes in the optimization process, we take an initial step of identifying all the extreme points in the original dataset for the given objective space, which includes axle power and total cost, for each topology. This preliminary step involves pinpointing eight extreme points — four per topology — which represent the upper and lower bounds of the objective space within the dataset (see Fig. 6).

Figure 6

KPIs of the initial population, initialized with a bias. Eight extreme points (four per topology) are identified and bolstered with additional samples through adding random noise

To enhance population density and reliability, we derive additional samples in the latent space based on the eight identified extreme points. This is achieved by introducing normally distributed noise to each point, which was repeated for each extreme point n times. In our study, we set $n=100$, resulting in an initial population of 800, as depicted in Fig. 6. The number n of additional samples per extreme point and their standard deviation were determined through a trial and error process, and further tests may reveal opportunities for additional improvements.

In our optimization approach, samples initialized in regions near the extreme points that do not align with the overarching optimization objective are quickly dismissed during the optimization procedure due to their inferiority. The core aim here is to ensure that the remaining population consistently represents segments of the Pareto front. By focusing on this objective, we facilitate a more efficient establishment of the Pareto frontier in the optimization process. This targeted initialization strategy effectively mitigates the issue of one topology disproportionately dominating the population and ensures a balanced exploration of the design space across different topologies. In other words, this strategy of biased population initialization ensures that each topology is represented equally at the start of the optimization process. Consequently, if one topology inherently possesses superior designs for certain regions of the objective space, these designs are reliably included within the population. This approach guarantees a comprehensive exploration of all potential design configurations, providing a robust foundation for identifying the most optimal solutions across varying topologies.

3 Results

In this section, we contrast the performance of the conventional VAE framework, as introduced in [1], with that of our modified implementation, the CD-VAE.

3.1 Sample reconstruction and KPI prediction

Both model architectures were trained over a span of 1000 epochs. For the training, the dataset (5227 samples) was divided into three subsets: training (80%), validation (10%), and testing (10%). The complete models are trained and optimized using the Adam optimizer, with a learning rate of 0.0001. For evaluating the performances, the mean absolute error (MAE)

$$ \mathrm{MAE} = \frac{1}{n} \sum_{i=1}^{n} \vert x_{i} - \hat{x}_{i} \vert $$

(10)

and the mean relative error (MRE)

$$ \mathrm{MRE} = \frac{1}{n} \sum_{i=1}^{n} \biggl\vert \frac{x_{i} - \hat{x}_{i}}{x_{i}} \biggr\vert \times 100 $$

(11)

are used. These formulas are applied for both the model’s KPI predictions y and the reconstruction of parameters p.

Figure 7 showcases two of the parameters that were reconstructed for both the standard VAE approach (upper figures) and the proposed method (lower figures) in this paper.. It can be seen that for the stator outer diameter parameter, both architectures are more or less equal in the shown reconstructed and true values. The results of both are aligning with the identity line. For $p_{6}$, which is the magnet spread angle, the effects of the masked learning process can be seen for the CD-VAE approach. While the standard VAE reconstructs also the fictional zero values for the DV topology, the CD-VAE predicts these in the range of the SV designs, albeit the actual values being irrelevant for the DV topology.

Figure 7

Reconstructed parameter samples. Upper: VAE. Lower: CD-VAE

The correctness of reconstruction for both architectures is also re-confirmed by the numerical results shown in Table 5. Both exhibit very low reconstruction errors across all parameters, with the CD-VAE being slightly better. Table 5 also shows that for the CD-VAE the first two discrete parameters $p_{1}$ and $p_{2}$ are not subject to reconstruction, as discussed in Sect. 2.2.

Table 5 Reconstruction errors of the VAE and CD-VAE for all nine cross-topology dataset parameters given by the MAE and MRE

Similar to the reconstruction, Fig. 8 shows the network’s predictions for two out of the ten KPIs (the ones used in the optimization) in comparison to the actual KPI values. Additionally, Table 6 presents the specific numerical errors.

Figure 8

Predicted KPI samples. Upper: VAE. Lower: CD-VAE

Table 6 KPI prediction errors of the VAE and CD-VAE across all ten KPIs given by the MAE and MRE

Upon closer examination of the Figure, it is notable that the KPI prediction results for the CD-VAE (lower row) demonstrate a slightly narrower spread from the identity line. This observation is further confirmed by the results displayed in the table. Although the margin is not substantial, the CD-VAE model consistently exhibits lower errors across all ten KPIs. This indicates that the proposed model architecture slightly outperforms the existing method in its ability to predict the KPIs.

3.2 Optimization results

For both the standard VAE and the CD-VAE approaches, one surrogate model was trained and subsequently employed in the optimization loop to address the multi-objective problem defined in (8). In our implementation, the optimization procedure relies on the functionalities of the Python library pymoo [13]. More specifically, we have used the genetic optimization algorithm NSGA-II [12]. The configuration for both surrogate models and optimization algorithm was as follows:

• Population size: 100

• Offsprings: 10

• Generations: 2000

• Crossover: Simulated Binary Crossover (SBX)

• Mutation: Polynomial Mutation (PM).

Figure 9 shows the Pareto fronts we obtained using both the standard VAE and the CD-VAE approaches. We further validated the design parameter configurations of these samples through FEA to determine their true KPIs. In our evaluation of the design quality, we again employed the MAE and MRE. Although the overall results display only minor differences, the CD-VAE approach’s predicted KPIs align more closely with the FEA-validated samples for both SV and DV topology samples. We observed a disparity in the standard VAE approach, especially where the initial data sample density is lower (mostly in the range of 0.6-0.8 in Axle Power Max). This observation is further supported by the concrete numerical data in Table 7, demonstrating that the CD-VAE approach consistently results in lower error rates when directly comparing predicted and validated samples, as opposed to the standard VAE approach.

Figure 9

Optimized Pareto fronts obtained through the usage of the VAE (upper) and CD-VAE (lower) as surrogate models

Table 7 Comprehensive overview of the KPI errors between the predicted optimized Pareto samples and the FEA validated ones

It’s important to mention that the expected Pareto front for the SV samples is not always completely represented in our results. Theoretically, a greater number of SV samples could be identified. Although the precise reason for this shortfall requires further analysis, one potential factor could be the size of the sample population, which we limited to 100 in our experiment. By increasing this population limit, there’s a possibility that we might uncover and retain a larger array of SV designs in the final Pareto front. This approach could potentially enhance the comprehensiveness of our Pareto front representation for SV samples.

3.3 Runtime results

Given the significance of both performance and runtime in electric machine design optimization, we conducted an examination of both model training and optimization times, as presented in Table 8. For all experiments we used the following hardware setup: a Dell Precision 7550 Laptop equipped with an Intel Core i7-10850H @ 2.7GHz, 32GB RAM, and an NVIDIA Quadro T2000 GPU. The reported optimization times are the average runtimes of the optimization processes with the previously introduced configuration over five trials each. The training time for the CD-VAE is slightly longer, but it excels in efficiency during the optimization loop. This efficiency stems from the CD-VAE’s ability to bypass the reconstruction of discrete values and subsequent correction within the optimization loop. Although the training duration is marginally extended, there is potential for further improvements in the implementation, such as vectorizing the split loss calculation for various topologies, to align the training time with that of the standard VAE.

Table 8 Overview of the runtimes for model training and optimization for both the VAE and CD-VAE

4 Discussion and conclusion

In this study, we introduced several key adaptations to the Variational Autoencoder approach as proposed in [1, 2], aiming to enhance surrogate modeling and optimization in electric machine design. Our methodology demonstrated improvements in parameter reconstruction, KPI prediction, and Pareto optimization over previous research. These advancements are crucial, as even slight enhancements in Pareto-optimized accuracy greatly impact the quality of simulations for optimal electric machine design, bridging the gap between predicted and validated objectives.

The adaptations involved separating discrete and continuous input parameters during training and implementing a masked learning process. These changes, along with the introduction of a feasibility classifier and a biased initial sampling strategy within the optimization process, contributed to improved results. Specifically, these modifications led to superior outcomes in generating predicted Pareto samples that align closely with validated ones. These improvements underscore the value of the proposed methodological tweaks, highlighting their role in achieving more accurate and feasible electric machine designs.

The initial setup for the CD-VAE, being the separation of continuous and discrete parameters, is a straightforward and easily extendable process. This aspect of our methodology ensures that adapting to new topologies or electric machine architectures can be done with little additional effort in data preparation. While the initial training time for our approach is marginally longer, it offers an advantage in terms of optimization run time. This improvement is particularly beneficial when conducting multiple optimization runs, where the efficiency of the run time becomes a more critical factor than the one-time increase in training duration. Furthermore, despite the greater complexity of our approach, it does not demand substantial computational resources for routine operations. As highlighted in our introduction, this capability is essential for an exhaustive search for the most optimal electric machine designs.

It is also important to note that our experiments were conducted on a dataset with limited complexity, involving only nine parameters. This limitation suggests the need for future research to test our methodology on a broader range of topology parameters and various electric machine topologies. Such extended testing will help evaluate the robustness and applicability of our proposed approach under more complex and diverse conditions.

Compared to other methodologies currently under research, particularly those using image-based modeling and optimization, the VAE approach offers a distinct advantage by sidestep** the inherent complexities associated with high-dimensional data management. Image-based methods, while powerful in capturing spatial and geometric dependencies, often require significant computational power to process and optimize due to the large volumes of data involved. The VAE approach, on the other hand, manages these challenges more efficiently, focusing on a streamlined and practical application of data.

Building on the strengths of the existing VAE architecture, our introduced workflow not only enhances the simplicity and standardization of the modeling and optimization processes but also ensures that all topologies are equally represented and that only valid electric machine designs are considered during optimization. This methodological improvement is crucial, as it significantly enhances the efficiency of identifying the most optimal topologies and designs for electric machines.

In summary, while our approach entails some initial setup effort, the enhancements in Pareto electric machine designs and the methodological insights provided are noteworthy. Our approach introduces novel enhancements in the workflow of using the VAE as a surrogate model, which have not been previously utilized in this manner. The results demonstrate promising outcomes, suggesting that this methodology could offer practically relevant contributions to the field of optimized electric machine performance. Our findings pave the way for further research and development in the field, aiming for even more efficient and precise electric machine designs.