Performance and Efficiency Exploration of Hardware Polynomial Multipliers for Post-Quantum Lattice-Based Cryptosystems

Abstract

The significant effort in the research and design of large-scale quantum computers has spurred a transition to post-quantum cryptographic primitives worldwide. The post-quantum cryptographic primitive standardization effort led by the US NIST has recently selected the asymmetric encryption primitive Kyber as its candidate for standardization and indicated NTRU, as a valid alternative if intellectual property issues are not solved. Finally, a more conservative alternative to NTRU, NTRUPrime was also considered as an alternate candidate, due to its design choices that remove the possibility for a large set of attacks preemptively. All the aforementioned asymmetric primitives provide good performances, and are prime choices to provide IoT devices with post-quantum confidentiality services. In this work, we present a comprehensive exploration of hardware designs for the computation of polynomial multiplications, the workhorse operation in all the aforementioned cryptosystems, with a thorough analysis of performance, compactness and efficiency. The presented designs cope with the differences in the arithmetics of polynomial rings employed by distinct cryptosystems, benefiting from configurations and optimizations that are applicable at synthesis time and/or run time. In this context, we target a use case scenario where long-term key pairs are used, such as the ones for VPNs (e.g., over IPSec), secure shell protocols and instant messaging applications. Our high-performance design variants exhibit figures of latency comparable to the ones needed for the execution of the symmetric cryptographic primitives also included in the Post-Quantum schemes. Notably, the performance figures of the designs proposed for NTRU and NTRU Prime surpass the ones described in the related literature.

Introduction

Public-key cryptography (PKC) plays a fundamental role in today’s technology providing the properties of confidentiality, data and origin authentication, and non-repudiability; indeed, its diffusion is witnessed by the number of widely used communication protocols that rely on it, such as the IETF Transport Layer Security (TLS) and IP Security (IPsec) Internet standard protocols. PKC primitives are in wide use to encrypt data between two parties (without a pre-shared secret) over an insecure channel, or to build a Public Key Infrastructure, and to guarantee the integrity and authenticity of data in form of digital signatures.

Currently, the most used algorithms, RSA and Elliptic Curve cryptography, rely on the hardness of integer factoring and the hardness of computing discrete logarithm in finite cyclic groups, respectively. However, in 1994, Peter Shor designed an algorithm for quantum computers that solve both the prime factoring and discrete logarithm problem with an exponential speedup with respect to classical computers, effectively breaking the corresponding cryptosystems.

Due to the long-term confidentiality and data/origin authentication guarantees required from asymmetric cryptographic primitives, and in sight of the recent advancements in the implementation of quantum computers, a significant effort in standardizing quantum-resistant algorithms for public-key cryptography is required. For that reason, the National Institute of Standards and Technology (NIST) in 2016 started the Post-Quantum Cryptography (PQC) standardization process to assess viable candidates for both Public Key Encryption (PKE) functionalities, in form of Key Encapsulation Mechanisms (KEMs), and digital signatures. The process refined its 69 candidate algorithms, reducing them to a single KEM and three digital signatures for immediate standardization at the end of the third round [1]. Furthermore, NIST provided a list of candidates that are still under investigation as alternates, as they rely on different computationally hard problems. Arguably, the the most successful class of algorithms of this standardization process is the one of lattice-based algorithms, being attractive in terms of computational latency and with practically acceptable key and ciphertext sizes.

Besides the candidate selected for immediate standardization, Kyber [2], three other schemes were deemed particularly interesting in the contest: NTRU [3], NTRU Prime [4] and Saber [5]. NTRU was officially recommended as the fallback alternative in case patent issues cannot be solved by the end of 2023 [6]. As a further testimony of NTRU’s security and efficiency, Google LLC adopted it as the key encapsulation method of choice in its internal infrastructure [7, 8]. NTRU Prime is an NTRU variant with conservative choices in the underlying algebraic structure, which prevent a number of attacks preemptively. Thanks to its conservative design choices, it has been adopted, and employed by default in hybrid mode by OpenSSH [9], the most widely diffused implementation of the Secure SHell (SSH) protocol suite. Saber [5] is based on a slightly different algebraic problem with respect to Kyber (i.e., the Module Ring-learning with roundings problem instead of Module Ring-learning with errors problem), which is at least as computationally hard as the one of Kyber.

The four aforementioned lattice-based cryptosystems rely on the arithmetic of polynomials with integer coefficients modulo q, where q is either a power of two, or a small prime number; all considered modulo a polynomial with a low number of terms. Depending on the choices, the polynomial ring obtained in such a way, may be more or less friendly to sub-quadratic multiplication techniques. Among such techniques, the Number Theoretic Transform (NTT) is the most efficient way to perform a multiplication, provided that the maximum degree of the polynomial generating the ring is a power of two and that the ring of coefficients is modulo a prime: given an n degree polynomial, it runs in $\mathcal {O}(n\log _2(n)))$ sequential steps. By contrast, efficient versions of the schoolbook algorithm, which runs in $\mathcal {O}(n^2)$, such as the one by Comba [10], can always be applied, leading to extremely compact designs but also reduced throughput. Software and hardware implementations of the multiplication algorithms also rely on divide-et-impera techniques such as Karatsuba [11] or Toom-Cook decompositions [12]: these techniques trade off an increased design complexity and larger constants hidden in the $\mathcal {O}$ notation for a constant decrease in the complexity exponent.

An emerging hardware design approach is the one known in the literature as x-net or LFSR-based multiplier. Its underlying idea is to perform n coefficient-wise multiplications per clock cycle, resulting in a total computation time that is $\mathcal {O}(n)$. While x-net-based multipliers require a non-negligible amount of resources, their very good performance and flexibility prompted this work, in which we provide results on a unified multiplier design for Kyber, NTRU, NTRU Prime and Saber. We note that the specification of Kyber states that the private and public keys are represented in the NTT-transformed domain, in order to save NTT computations, in the encryption and decryption primitives. Doing so, obtains an advantage in computation speed, at the cost of sacrificing cryptographic agility. Indeed, devising accelerators that are able to speed up the computation of Kyber employing the key pair in the specified transport format, i.e., in the NTT-transformed domain, would result in the design not being compatible with lattice-based cryptosystems where the underlying polynomial ring is not NTT friendly, e.g., NTRU.

To this end, in our work, we consider that our unified multiplier is employed in cryptographically agile components, where the transport format of the Kyber key pairs is first converted back into the canonical domain upon key pair loading. This scenario fits appropriately all the cases where long-term key pairs are used, and cryptographic agility is desired, such as in smartcards, IPSec-based VPNs, instant messaging protocols, and the SSH transport layer protocol [13].

Contributions

Our work aims to show that it is possible to have a unified design for an hardware accelerator computing the polynomial multiplications in all polynomial rings of the four lattice-based cryptosystems: Kyber, NTRU, NTRU Prime, and Saber. The structure of such an accelerator stems from an architecture able to achieve efficiency results beyond the state of the art for NTRU-like cryptosystems. We provide efficiency results of a synthesis-time specialized accelerator for the arithmetic used by the NTRU (both NTRU HPS and NTRU HRSS variants), NTRU Prime, Saber and Kyber cryptoschemes, namely every round-3 lattice-based KEM proposals at NIST’s Post-Quantum standardization contest. Subsequently, we provide a unified design supporting all the polynomial rings, for all security levels of the KEMs, allowing cryptographic agility without the need of replacing the hardware component. We validated the correctness of the results and gathered the performance and resource figures for every parameter set specified by the latest specifications available, for an FPGA design flow. Our design does not depend on FPGA specific resources, allowing for simple portability across different FPGA manufacturers, and retargeting toward ASIC designs. We note that our design uses a sequential memory layout to store polynomial coefficients in memory, and accesses them in a single sweep; therefore, our design is eligible to be used also in a pipelined fashion, a feature not achievable with current NTT-based multipliers. This work is the result of an extension of the one presented in [14]: in particular, we studied further design trade-offs, adding the resource constrained designs, and further exploring the advantages coming from the unified multiplier architecture when a specific NIST security level is specified at design time.

Preliminaries

Table 1 Summary of the features of the polynomial rings $\mathcal {R}_p = \mathbb {Z}_p\left[ x\right] /\left\langle p(x) \right\rangle$ and $\mathcal {R}_q = \mathbb {Z}_q\left[ x\right] /\left\langle p(x) \right\rangle$ for each KEM

In this section, we provide a summary of the polynomial arithmetic for the polynomial rings employed in Kyber, NTRU, NTRU Prime and Saber. Subsequently, we provide a summary of linear time hardware modular multipliers obtained with the x-net technique for speed-oriented designs, as well as an outline of generic modular multipliers minimizing the memory accesses obtained with the Comba’s strategy for size-oriented designs. In the following, we will denote polynomials of degree n with lowercase letters as $a(x) = \sum _{i=0}^{n-1} a_i x^i$.

The aforementioned cryptosystems consider the arithmetic over two quotient polynomial rings $\mathcal {R}_{q}$ and $\mathcal {R}_{p}$, which are defined as $\mathbb {Z}_q\left[ x\right] /\left\langle p(x) \right\rangle$ and $\mathbb {Z}_p\left[ x\right] /\left\langle p(x) \right\rangle$, respectively. The differences in the ring structures arise from the choice of the values p, q, n, and p(x), of which a summary is reported in Table 1. Each cryptosystem specifies multiple parameter sets guaranteeing a security margin equivalent to the one provided by AES-128 (security level 1), AES-192 (security level 3), and AES-256 (security level 5). In particular, p is always chosen to be a small odd number between 3 and 11; q is either a small power of two (between $2^{11}$ and $2^{13}$) or a prime number of the same order of magnitude. The latter choice yields polynomials with coefficient over a field, $\mathbb {Z}_p$, while the former choice allows a trivial modular reduction $\bmod \ q$, via truncation of the most significant bits.

The polynomial, p(x), employed to obtain the quotient ring, gives $\mathcal {R}_{q}$ and $\mathcal {R}_{p}$ a nega-cyclic algebraic structure, as in Kyber and Saber, (i.e., with $p(x) = x^n+1$) or a cyclic algebraic structure, as in NTRU, (i.e., with $p(x) = x^n-1$). The latter structure name stems from the fact that, given an element $a(x)\in R_p$, computing the result of $x\cdot a(x)$ is equivalent to cyclically shifting its coefficients toward the higher degrees, by one position. Similarly, the nega-cyclic structure implies that the same cyclic shift takes place, but a sign flip of the constant term is also performed after the cyclic shift. The authors of NTRU Prime chose $x^n-x-1$ as the polynomial modulus p(x), thus obtaining polynomial field algebraic structures for $\mathcal {R}_{q}$ and $\mathcal {R}_{p}$: this removes the need to introduce further constraints on the parameters of the structure (which are indeed present in Kyber and Saber), preventing future attacks that may exploit the specific properties of finite fields. To align our notation with the one of the cipher specifications, we will consider the representatives of the residue classes modulo q or modulo p, to which the coefficients of polynomials belong, as the integers balanced around the zero element, for example between $-\big \lceil (q-1)/2\big \rceil$ and $\left\lfloor (q-1)/2 \right\rfloor$.

Modular Polynomial Multiplication Algorithms

Modular Polynomial multiplications with large operands are extremely common in cryptographic primitives, and have seen significant efforts in their optimization. A first classification criterion is the strategy that is employed to perform the modular polynomial reduction: indeed, it is sometimes possible to interleave the reduction operation with the intermediate steps of the multiplication algorithm, saving on the memory elements required for the computation. The second classification criterion is the asymptotic complexity of the multiplication method, counted as the number of coefficient-wise multiplications, which in turn is a function of the number of coefficients of the operands, n.

As shown in Algorithm 1, the operand-scanning, schoolbook method for polynomial multiplications involves $\mathcal {O}(n^2)$ coefficient-wise multiplications as it adds together all the results of multiplying the first polynomial factor by each one of the monomials composing the second factor.

Algorithm 1

Schoolbook Multiplication Algorithm

The sub-quadratic methods, pioneered by Karatsuba [11], provide algorithms to compute the polynomial multiplication in $\mathcal {O}(n^{\log _{a}(2a-1)})$ coefficient-wise multiplications, where $a\ge 2$. In particular, Karatsuba proposed the algorithmic variant for $a=2$, while Toom and Cook [12] generalized the result for $a>2$. The reason for avoiding the ubiquitous application of such methods is that, while the number of coefficient-wise application decreases, they require an increasing number of polynomial additions and subtractions to compute the result. While additions and subtractions have a linear cost in n, their overhead offsets the gains coming from saving multiplications for small values of n. Given that the ratio between the absolute values of the computational costs of multiplications and additions/subtractions varies depending on the underlying computational platform, it is commonplace to determine the break-even value for the parameter a through an exhaustive evaluation when designing a specific instance of a cryptographic scheme. In our context, Karatsuba was used in [15] instantiating three parallel Comba multipliers, while the design in [16] involved a 3-way Toom-Cook computing five parallel multiplications recursively with the Karatsuba method.

Algorithm 2

Parallel Schoolbook Algorithm

Finally, it is possible to compute polynomial multiplications in $\mathcal {O}(n\log _2(n))$ exploiting Fourier transformations. The method relies on the fact that multiplying two polynomials yields the same result computed by the convolution of their coefficients, interpreted as integer sequences. This allows to perform the multiplication computing the discrete-time Fourier transform of the sequences, performing the element-wise multiplication of the results and computing the inverse Fourier transform of such an outcome. The total cost of the operation depends on the cost of computing the Fourier transform, to which a linear amount of coefficient-wise multiplications must be added. For the special case where n is a power of two, computing the Fourier transform takes $\mathcal {O}(n\log _2(n))$, thus resulting in a $\mathcal {O}(2(n\log _2(n))+n) = \mathcal {O}(n\log _2(n))$ cost for the entire multiplication. This technique is applied fruitfully to polynomials in a ring $\mathbb {Z}_q\left[ x\right] /\left\langle p(x) \right\rangle$, provided that the degree of p(x) is a power of two, and that $\mathbb {Z}_q$ is a field, (to make use of all the required roots of unity), and goes by the name of Number Theoretic Transform (NTT) [16]. As it is the case for the sub-quadratic multiplication techniques, also the NTT requires some linear time operations to be computed, and thus the break-even point for the value of n is sought experimentally. Of the four cryptosystems we are considering, only Kyber has a parameter choice that may benefit from the use of NTT-based techniques.

Linear-time Modular Multiplication

An orthogonal approach to the redesign of a multiplication algorithm is the one that exploits the inherent parallelism of the schoolbook strategy. Indeed, all the coefficient-wise multiplications involved in a product of a single monomial coefficient by the entire other factor, can be computed independently. This observation leads to the design of a linear time multiplication algorithm that exploits n computation units and n coefficient-wide memories to compute the entire product in $\mathcal {O}(n)$ following the operative pattern shown in Algorithm 2.

The first proposal of a linear time modular multiplication algorithm specialized for the NTRUEncrypt polynomial ring comes from [17]. The work achieves the multiplication in n clock cycles using n parallel multiply-and-accumulate (MAC) units. Furthermore, to reduce the area of each MAC unit, the work replaces the multiplier with a multiplexer, which selects one of the three possible coefficient-wise multiplication outcomes, thanks to the small size of the coefficients of the $\mathcal {R}_p$ operand, with $p$ $=$ $3$. This approach was then separately adapted for the realization of the arithmetic of the different polynomial rings of Saber, NTRU, and NTRU Prime cryptoschemes [16, 18, 19]. The authors of [18] proposed a centralized way to compute the few possible results of a coefficient-wise multiplication, and distribute them to every MAC unit. In [20], the authors proposed to postpone the reduction $\bmod \ q$ of the coefficients of the multiplication result to the end of the multiplication. This approach entails larger accumulators to store the coefficients of the resulting polynomial, while allowing to save area as only a single modular reduction unit is required.

Algorithm 3

Comba’s Multiplication Algorithm

Resource Constrained Modular Multiplication

Employing a schoolbook multiplier to perform the polynomial modular multiplication in an operand-scanning fashion results in the smallest amount of computational and memory resources. Indeed, in a software-based implementation, the operand-scanning approach has the minimum code size and register pressure, while in a hardware implementation the compact design of the multiplier and the simple control logic, which in turn reduces the size of the driver Finite State Machine (FSM), yield area savings. A notable alternative to the plain schoolbook multiplier design is represented by the Comba’s method [10] reported in Algorithm 3. Such a strategy can be seen an optimization of the schoolbook algorithm, aiming at minimizing the number of memory accesses to compute each coefficient of the result, even if it still involves $\mathcal {O}(n^2)$ coefficient-wise multiplications. This optimization has the additional benefit of requiring a minimal amount of computational resources, in the same fashion as the schoolbook method. The intuition in Comba’s method is to reorder the single-coefficient multiplications with respect to the operative pattern of the schoolbook algorithm by performing additions of properly shifted intermediate polynomials (which in turn are obtained multiplying the first polynomial factor by each coefficient of the second one). Comba’s method computes and writes the final value of each coefficient of the resulting polynomial into the corresponding memory space only once (proceeding from the least significant coefficient to the most significant one, or vice versa). From an implementation standpoint, such a feature is particularly advantageous because it allows to perform only $2n-1$ read/write accesses to the memory holding the result, instead of $2n^2$ read/write accesses required by the schoolbook strategy. To achieve a modular multiplication with an operand-scanning Comba multiplier, it is sufficient to accumulate the coefficient of the result in the corresponding appropriate position: in case the computed coefficient is within the maximum degree of the polynomial ring elements, it is added as reported in Algorithm 3, lines 2–7; in case the coefficient belongs to a monomial of higher degree (lines 8–13), it is added or subtracted to a set of monomials of lower degrees, corresponding to the non-null coefficients of the polynomial ring modulus.

Our Unified Multiplier Design

In this section, we provide the description of our digital designs to implement the x-net approach and the Comba approach to polynomial multiplication, for a generic polynomial modulus p(x). In particular, we employ our framework to describe the x-net multiplier design, specialize its structure for each one of the four polynomial rings required in Kyber, Saber, NTRU and NTRU Prime, and describe a unified multiplier architecture. Subsequently, we describe the Comba approach to polynomial multiplication, which can be applied to all polynomial rings needed for Kyber, Saber, NTRU and NTRU Prime, and similarly describe another unified multiplier architecture.

In the following, we consider the case of the multiplication of two polynomials where the first one has coefficients in $\mathbb {Z}_p$, while the second one has coefficients in $\mathbb {Z}_q$, with $p$ $q$, and the product has coefficients in $\mathbb {Z}_q$, which is the polynomial multiplication taking place in all the cryptosystems at hand. The operation is intended to be computed lifting the coefficients of the first polynomial $\mathbb {Z}_p$ simply reconsidering their values as being in $\mathbb {Z}_q$. We note that NTRU also requires a multiplication between two polynomials with coefficients in $\mathbb {Z}_q$. The described multiplier structure also covers this case, enlarging the width of the signals carrying coefficients in $\mathbb {Z}_p$ to hold the coefficients in $\mathbb {Z}_q$. In the following, we will assume that the polynomial modulus p(x) is monic, as it is always the case in practice.

Algorithm 4

x-net polynomial multiplier

The main idea of the x-net multiplication is to rewrite the computation of the polynomial ring multiplication, i.e., the multiplication of the between a(x) and b(x), and the subsequent modular reduction $\bmod \ p(x)$, as described in Algorithm 4. The modular polynomial multiplication, $a(x) \cdot b(x) = c(x) \bmod p(x)$, is decomposed as a sequence of coefficient-by-polynomial multiplications and polynomial additions involving a single coefficient of the second factor and the entire first factor (line 3), and multiplications by x followed by modular reductions of the first factor (line 4). This decomposition of the modular multiplication operation allows an efficient hardware implementation; indeed, the coefficient-wise multiplications of line 3 expose a large amount of data parallelism, while the modular multiplication by x and the subsequent reduction can be implemented by means of an LFSR structure.

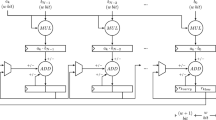
The hardware structure of a generic x-net modular multiplier for a monic p(x) is depicted in Fig. 1.

The coefficient-by-polynomial multiplication (line 3 in Algorithm 4) is computed with n independent Multiply and Accumulate (MAC) elements that compute the product of the coefficient $b_i$ by each coefficient of polynomial a(x), and add the result to the corresponding coefficient of c(x). The corresponding portion of the circuit in Fig. 1 is the bottom half, where one MAC element is highlighted in gray. A single MAC element is composed by an integer multiplier, an adder, a modular reducer $\bmod \ q$, and a register containing the value of the coefficient $C_i, 0\le i < n$.

The computation of the multiplication of the first factor by x, $a(x)\leftarrow a(x) \cdot x$ is efficiently done by storing the coefficients of a(x) in a shift register, as the multiplication by x acts shifting the coefficients by one position toward higher degree monomials (to the right, in Fig. 1). Since the degree of a(x) is at most $n-1$ before the multiplication by x, the modular reduction $a(x)\leftarrow a(x) \cdot x \bmod p(x)$ can be efficiently computed. Indeed, since p(x) is monic, computing the remainder of $a(x)\cdot x \bmod p(x)$ is equivalent to the subtraction from $a(x) \cdot x$ of the polynomial $A_{n-1}\cdot (p(x)-x^n)$.

The multiplication and modular reduction are performed in the same clock cycle by the the portion of the x-net multiplier managing the operation (top portion of Fig. 1). This circuit, structured as a shift register with feedback, performs the $a(x)\cdot x$ shifting the contents of the registers containing $(A_{0}, \ldots A_{n-1})$ toward right. The same circuit also subtracts $A_{n-1}\cdot (p(x)-x^n)$ from $a(x) \cdot x$ by adding the coefficients of $-A_{n-1}\cdot (p(x)-x^n)$ to the ones of $a(x)\cdot x$. This is done inserting the adders on the shift lines between any two elements of the shift register that contains a(x). This feedback network structure will thus need as many multipliers and adders as the number of non-null coefficients in p(x), benefiting from values of p(x) with a very small number of coefficients, as it is the case in the four considered cryptosystems. Finally, we note that the shift register structure also allows to perform the loading of a(x) with minimal additional hardware. Indeed, a(x) in our design is loaded coefficient-wise from $A_{n-1}$ to $A_0$, inserting a single mux (represented on the left in Fig. 1).

Fig. 1

Structure of an x-net multiplier computing the product $r(x) = (a(x) \cdot b(x))\bmod p(x)$. The top portion of the modular multiplier takes care of computing $x^i\cdot a(x)\bmod p(x)$ at the i-th clock cycle, while the bottom part performs the coefficient-by-polynomial multiplication

Structural x-net Optimizations

The first observation leading to an optimization is that the topmost portion of the x-net multiplier may operate entirely with values $\bmod \ p$, leading to a significant saving in the resource consumption for the cases where $p\ll q$. The lifting required to multiply coefficient in $\mathbb {Z}_p$ by coefficients in $\mathbb {Z}_q$ is efficiently realized within the multiplier units in the MAC elements by sign-extending the two’s complement representation of the $\mathbb {Z}_p$ elements.

The second observation leading to an optimization is that, in case p is very small, as it is the case in our cryptosystems, the multiplier in the MAC can be substituted by a multiplexer that selects among a small set of fixed multiples of $B_i$, which are in turn computed by a small number of additions. Taking as an example $p=5$, the multiplier is substituted by a multiplexer selecting among the values $\{-2B_i,-B_i,0,B_i,2B_i\}$, depending on the value of the coefficient of the a(x) polynomial. The values can be either precomputed only once, and distributed, or computed within the MAC unit and selected in place. The first approach requires a larger amount of resources for each single MAC unit, while obtaining a reduction in the wiring congestion, which is particularly beneficial for FPGA targeted implementations.

A final point concerning the optimization of the x-net multiplier is the trade-off between performing modular reductions in the MAC complex managing the coefficients of the result, and performing the reductions upon result readout. Choosing to perform the modular reductions at readout requires wider accumulator registers for C(x); in particular, their size grows from $\big \lceil \log _2 \left( q\right) \big \rceil$ to $\big \lceil \log _2 \left( npq\right) \big \rceil$ bits, as n values $\bmod \ q$ will be multiplied by a value $\bmod \ p$ and added by the x-net multiplier during its operation. This increase in area is however compensated by the removal of n modular reducers $\bmod \ q$ from each multiply and accumulate complex, enacting a trade-off that typically gains in area consumption, unless the reduction by q is trivial (e.g., when q is a power of two). We explored both strategies devising modular reducers as follows. In the former case, each accumulator register has $\log _2(q)$ bits size, and we perform the $\bmod \ q$ operation by conditionally applying additions and subtractions. Since the distance between each integer multiplication result and a valid $\mathbb {Z}_{q}$ element is at most $\left( q-1\right) \cdot \big \lceil \left( p-1\right) /2 \big \rceil$, then $\big \lceil \left( p-1\right) /2 \big \rceil$ additions and subtractions are carried out in parallel with values multiple of q and the only valid result in $\mathbb {Z}_{q}$ is selected. In case of the reduction operation performed during the readout, a single Barrett reduction module is used.

Fig. 2

x-net architectures specifically tailored for each polynomial ring. The readout circuit of the accumulators is omitted for clarity. The $\bmod \ q$ reducer is not present whenever the reduction is performed upon result readout

Specialized and Unified x-net Designs

We now describe the specializations of the x-net designs that can be performed to optimize its resource consumption according to the specific polynomial ring for NTRU, Saber, NTRU Prime and Kyber. The specialized designs are depicted in Fig. 2. For the case of the NTRU polynomial ring, we have that the large modulus q is a power of two, while the modulus polynomial is $p(x)=x^n-1$. This in turn allows us to perform the structural optimizations depicted in Fig. 2a: we perform implicitly the modular reduction as it is a simple bitwise truncation; therefore, no explicit reducers modulo q are present; the addition of $-A_{n-1}\cdot (p(x)-x^n)$ becomes the addition of $A_{n-1}$ alone, since $p(x)-x^n=-1$. Given that this element should be added to the $A_0$ coefficient of the $a(x)\cdot x$ product, no adder is needed, as the product $a(x)\cdot x$ has always $A_0=0$. Therefore, the value of $A_{n-1}$ is simply fed back into the first register by the feedback line on top of Fig. 2a.

For the case of Saber, depicted in Fig. 2b, the modulus q is still a power of two, therefore allowing modular reduction $\bmod \ q$ with a simple bit truncation as for NTRU, while the polynomial modulus is $p(x)=x^n+1$. The value of the polynomial modulus implies that adding $-A_{n-1}\cdot (p(x)-x^n)$ is equivalent to adding $-A_{n-1}$ to the null $A_0$ coefficient of $a(x)\cdot x$. As a consequence, a subtractor is added on the feedback line, fed with 0 as the minuend and $A_{n-1}$ as the subtrahend.

The x-net design for Kyber, depicted in Fig. 2c, manages the fact that the large modulus q is a prime value, therefore requiring modular reduction units between the output of the MAC operation and the input of the register storing $C_i, 0\le i < n$. The value of the polynomial modulus for Kyber matches the one of Saber, i.e., $p(x)=x^n+1$. As a consequence, the computation of $-A_{n-1}\cdot (p(x)-x^n)$ to be added back as a result of the modular reduction $a(x)\cdot x \bmod \ p(x)$ results again in $-A_{n-1}$ being added to the null $A_0$ coefficient of $a(x)\cdot x$.

Finally, the design of the x-net multiplier for NTRU Prime, depicted in Fig. 2d, also requires to employ a value of q which is a prime number, in turn requiring a $\bmod \ q$ reducer for each MAC complex. The modulus value for NTRU prime is $p(x)=x^n-x-1$, which in turn implies that adding $-A_{n-1}\cdot (p(x)-x^n)$ is equivalent to adding $-A_{n-1}\cdot (-x-1)= A_{n-1}x + A_{n-1}$ to $a(x)\cdot x$. While adding $A_{n-1}$ does not require an actual adder, as the $A_0$ coefficient of $a(x)\cdot x$ is null, adding $A_{n-1}x$ requires an actual coefficient-wise addition $A_{n-1}+A_1$, where $A_1$ is the coefficient of x in $a(x)\cdot x$. Therefore, the feedback network for the x-net design of NTRU Prime has an adder taking as inputs $A_{n-1}$ and $A_0$ from a(x), which is indeed $A_1$ in the $a(x)\cdot x$ product.

Providing a single unified design for all the four cryptosystems was achieved postponing the modulo reduction of resulting coefficients upon readout and considering the largest among all the register sizes required by the four designs, and inserting multiplexers regulating which multiply-add elements are active on the feedback network of the register containing a(x), and whether or not the sign of $A_{n-1}$ should be flipped. We provide a graphical depiction of the selection multiplexer to support the inverted feedback coefficient selection in Fig. 3.

Fig. 3

Multiplexers introduced by the unified x-net multiplier

This approach required a Barrett reduction module compatible with multiple modulus, which was achieved through storing the pre-computed constants in a small read-only memory.

Multiplying in Less Than 3n Cycles

In our design, we also explored the possibility of reducing the multiplication time under 3n cycles. Indeed, the described architecture uses n clock cycles to load the a(x) from memory, n cycles to compute the result of the modular multiplication (potentially without coefficient-wise modular reduction), and n cycles to read out the final polynomial multiplication result and store it into the memory. This process can be sped up devising a memory bus transferring multiple polynomial coefficients at once. Transferring $\alpha$, $\beta$ and $\gamma$ coefficients for respectively the small, large and result polynomials, the overall latency of a polynomial multiplication is $\big \lceil n/\alpha \big \rceil + \big \lceil n/\beta \big \rceil + \big \lceil n/\gamma \big \rceil$. Loading $\alpha$ coefficients of a(x) for each clock cycle is achieved transferring them in parallel from main memory, and having the shift register containing a rotate by $\alpha$ positions at each clock cycle through appropriate connections. The same approach is applied for reading out $\gamma$ coefficients of the result from the accumulator registers, possibly instantiating $\gamma$ parallel Barrett modules when performing the reductions-at-readout approach. To compute the multiplication of $\beta$ $\mathbb {Z}_{q}$ coefficients in parallel, we need a total of $\beta \cdot n$ MACs. Indeed, to compute the result of $\beta$ multiplication steps, $\beta$ multiplications and sums need to be computed at each clock cycle, to obtain the result which is to be stored $\beta - 1$ cells to the right of each MAC unit. Furthermore, it is to be noted that $\beta$ steps of the update of a(x) should be computed in a single step. This in turn requires to perform $\beta -1$ sign flips of the $\mathbb {Z}_{p}$ coefficient for specific MAC units of Kyber and Saber, and additional $2(\beta -1)$ multiply and additions for specific MAC units of NTRU Prime.

Fig. 4

Datapath of the Comba multiplier

Comba Multiplication

Realizing a Comba multiplier requires a remarkably small datapath that is only in charge of performing a single MAC operation between polynomial coefficients per clock cycle, and store the result in an accumulator register. The datapath, depicted in Fig. 4 requires, in addition to a multiplier and an adder, an additional reducer modulo q, which can be omitted in case the value of q is a power of two, as the modular reduction amounts to a simple bit truncation of the output of the MAC. This datapath allows to compute one of the iterations of the loops of Algorithm 3, lines 3–5 and lines 9–11 per clock cycle, while retaining the value of the $\texttt{tmp}$ variable within the local accumulator. The writeback of the correctly computed value $C_{\texttt{rIdx}}$ onto the memory holding the result is thus done only once at the end of each iteration of the outer loops of Algorithm 3, lines 2–7 and lines 8–13.

Performing a regular multiplication, followed by a polynomial reduction with Comba’s approach would produce a result with a maximum degree up to $2n-1$, which would in turn double the size of the required memory to contain it. We optimized the regular Comba algorithm taking care of saving the result of a single outer loop iteration of lines 8–13 of Algorithm 3, while taking care of the effects of the modular reduction. This entails either adding or subtracting the coefficient of the monomials with degree higher than $n-1$ in the result of the plain multiplication to the appropriate coefficient of the modular multiplication result. We note that such an approach is non-trivial to realize for the case of the NTRU Prime cryptographic scheme, as coefficients of monomials with degree higher than $n-1$ have to be added twice, to two subsequent coefficients in the modular multiplication result. We also note that, before depositing the result of the sum/subtraction of the coefficient of the monomial with degree higher than $n-1$ and the one present in the result accumulator, a modular reduction is required. Since we know that the maximum value admissible as the result of the accumulation is smaller than $2q-2$, it is possible to perform the modular reduction together with the accumulation through a simple selection of the result of a short chain of adders and subtractors, even when the modulus q is not reduction friendly (i.e., a power of two).

Experimental Evaluation

Table 2 Number of $\mathcal {R}_p \times \mathcal {R}_q$ multiplications in key generation, encapsulation and decapsulation primitives of each cryptographic scheme

In this section, we present the results of our synthesis campaign on specialized x-net multipliers for all the four cryptosystems we considered, and compare them with the current state of the art solutions. In addition, we show the results for the design based on the Comba algorithm, optimized for the NTRU, Kyber, and Saber schemes. Furthermore, we report the figures of merit for our unified multiplier designs.

The correctness of the results of our multipliers was tested through test benches obtained with a synthetic computation model written in SageMath, which generated known answer tests according to the reference implementations of the ciphers. We tested the correctness of the polynomial multiplication for every ring defined by the parameter sets of Kyber, Saber, NTRU, and NTRU Prime cryptographic schemes.

We conducted our syntheses for the **linx UltraScale+ ZCU106 FPGA (target xczu7ev-ffvc1156-3-e) using Vivado 2021.1 with Flow_AlternateRoutability and Performance_NetDelay_high strategies for synthesis and implementation, using out-of-context synthesis mode and fixing the clock source cell in order to produce a realistic timing analysis.

Considering the x-net architecture, we explored four different choices of the amount of coefficients being loaded, namely, loading either one or four $\mathcal {R}_{p}$ coefficients, and one or two $\mathcal {R}_{q}$ coefficients. Our systematic exploration led us to discover that the x-net configurations loading four $\mathcal {R}_{p}$ coefficients per clock cycle achieve better performance figures (when transferring two $\mathcal {R}_{q}$ coefficients) and better area–time product (when transferring one $\mathcal {R}_{q}$ coefficient) than their alternatives, we therefore report their results alone for the sake of brevity. We thus have that the first operand, i.e., the one on $\mathbb {Z}_p/\langle p(x) \rangle$ is loaded into the registers 4 coefficients at a time, with a data transfer of 8 to 16 bits per clock cycle depending on the cryptographic scheme and parameter set. Moreover, we report the resulting data when the modulo reduction operation is performed every clock cycle or upon readout. By contrast, the design based on Comba algorithm performs a modular reduction at each single coefficient MAC, aiming for extreme compactness and low circuit complexity. Finally, we report the results of our unified multiplier designs, able to support the NIST security levels 1, 3 and 5, which are equivalent to the security margin provided by AES-128, AES-192, and AES-256, respectively. In providing overall latency figures for the computations accelerated by our designs in the four considered cryptosystems, we take into account the number of accelerated multiplications per primitive, as reported in Table 2. We consider, in all cases, the sequential executions of the required multiplication operations to provide the latency figures. We note that the area-time product does not change if multiple parallel multipliers are instantiated whenever data parallelism is available in the scheme.

Net Performance Results

We conducted an exploration for the x-net optimized designs and gathered detailed data of the resource consumption, in terms of Cell Logic Blocks (CLBs), employed by each multiplier, the number of clock cycles taken for an entire modular multiplication, and the maximum target frequency that the design was able to reach. Furthermore, we also computed the total latency taken by all $\mathcal {R}_p\times \mathcal {R}_q$ multiplications in the key generation, key encapsulation (encryption) and key decapsulation (decryption) primitives of the scheme, as some schemes require more than a single multiplication (see Table 2). We evaluated the two coefficient ring reduction strategies described in Sect. Potential function (i.e., the one acting at each clock cycle, and the one acting upon readout) for NTRU Prime and Kyber to determine which solution is to be preferred when targeting an FPGA design. We noted that delaying the reduction to the readout phase yields an important gain in the designs of Kyber and NTRU Prime in terms of utilization of resources and increase of the working frequency, although at the cost of a moderate increase in the number of needed Flip Flops. As a consequence we selected the said reduction strategy to realize Kyber and NTRU Prime multipliers. As far the multipliers employed in Saber and NTRU scheme are concerned, as their parameter set exhibit a value of q that is a power of 2, the most convenient reduction strategy is to reduce the result of the multiplication between two polynomial coefficients at each clock cycle (see Sect. Potential function).

In the following, we employ the Area-Time (AT) product as an efficiency indicator, computing it as the number of occupied CLBs times the execution time in milliseconds.

Fig. 5

Efficiency comparison of x-net-based designs. Blue, yellow and orange markers refer to parameters of security level 1, 3, and 5, respectively. Red markers denote parameters above security level 5. Dashed lines exhbit the same area-time (AT) product (lower is better)

Figure 5 allows to compare the designs of the encapsulation module of Kyber, Saber, NTRU, and NTRU Prime, employing the x-net-based multipliers that realize for each of them the more suitable reduction strategy. A blue marker represents a design with a parameter set corresponding to the NIST security level 1, a yellow marker refers to security level 3, an orange marker corresponds to security level 5, while the red ones refer to security levels above level 5. The figure also shows as dashed lines the design space points that exhibit the same area-time (AT) product (lower is better) to the end of easing the evaluation of the efficiency of the encapsulation modules with the parameter sets recommended in the official specification of each cryptographic scheme.

Figures with similar trends were also obtained for decapsulation modules and key generation modules, employing the data in Appendix A, which shows the detailed and complete set of results we obtained from our design space exploration.

In Fig. 5 and in the data referring to decapsulation and key generation modules, by comparing the designs with an equivalent security level, it can be noted that the time spent in polynomial multiplications is larger in Kyber (a module RLWE scheme) and Saber (a module RLWR) than in NTRU-based schemes (right-most values on the x axis of Fig. 5). Moreover, such a difference increases with the security level. The only exception to such a trend is the latency of polynomial multiplications for the key generation of NTRU HPS and HRSS for the parameter sets ranked with security level 1 and 3 due to the large number of operations carried out. Nonetheless, this penalty is compensated by the flexibility of Kyber and Saber schemes, which have an almost identical polynomial multiplier usable in every parameter set (almost constant value on the y axis of the figure). As it can be clearly seen, given the large amount of parameter sets for NTRU Prime, the latency of the multiplication for our design and this cryptographic scheme is linear in the degree of the polynomials. As a consequence the performance penalty imposed by larger security levels grows more slowly than for Kyber and Saber.

When considering various parameter sets of equivalent security level, it becomes evident that NTRU Prime stands out as having the least efficient implementation among them. Comparing NTRU-based parameters with those of Kyber and Saber, we can see that the former exhibit a considerably lower degree of variability in terms of efficiency when increasing the security level with respect to the latter. The gathered data suggests that the x-net architecture is from 4 to 8 times more efficient when employed to compute polynomial multiplications during encapsulations in NTRU rings, as shown by the marks in Fig. 5 which are close to the origin of the chart. This fact however does not hold anymore for the keygen and decapsulation operations, having fewer multiplications to perform than NTRU. Finally, it is worth noting that Kyber lags significantly behind the efficiency achieved by the Learning With Errors (LWE) scheme Saber. In fact, Kyber’s design efficiency is approximately two times worse than the one of Saber (Tables 3, 4).

The full results of our design space exploration of the x-net architecture design are reported in Tables 5, 6, 7, 8 in the Appendix section.

Comba Performance Results

Considering the results of the synthesis campaign of the Comba-based multipliers, the design shows a remarkably small area requiring almost two orders of magnitude less CLBs with respect to the x-net design. This compactness in turn allows to further improve the working frequency up to 36% for NTRU parameter sets.

Fig. 6

Efficiency comparison of Comba-based designs. Blue, yellow and orange markers refer to parameters of security level 1, 3, and 5, respectively. Red markers denote parameters above security level 5. Dashed lines exhbit the same area–time (AT) product (lower is better)

From the chart depicted in Fig. 6 obtained with analogous conditions of the Fig. 5, see similar trends than the ones obtained with the x-net architecture: Kyber is the slowest cryptoscheme, NTRU has the fastest and most efficient implementation during the encapuslation and decapsulation procedures, and Saber is showing the same results for the key generation.

These results proved that an extremely compact solution requiring almost two order of magnitude less area than the low-latency solution based on x-net still maintains competitive efficiency. In scenarios where the extra incurred cost of a large low-latency design is not feasible, a compact design with competitive efficiency presents an appealing solution when a latency of few milliseconds is admissible.

We report the complete results of the synthesis campaign in Table 9 in the Appendix.

Table 3 Comparing results of our x-net and $x^2$-net with [19], and [21] with multiplier architectures adaptable to multiple cryptographic schemes targeting a UltraScale+ target

Comparison with the State-of-the-Art Results

Table 3 reports the comparison of our cryptosystem-specialized designs with the existing state of the art on NTRU and NTRU Prime linear time multipliers. We note that our design achieves a 30–40% reduction in the required CLBs for both cryptosystems, when comparing our solution which loads a single $\mathcal {R}_{q}$ coefficient (x-net) with the one in [19]. Furthermore, we also obtain a 28–96% gain in working frequency with respect to the same design, therefore achieving also a higher area-time efficiency. We compare our solution loading two $\mathcal {R}_{q}$ coefficients at once, with the only currently available data point in the public technical report [21]. The solution reported in the technical report, where it is denoted as $x^2$-net, is 10% larger in area a $2.2\times$ slower in the working frequency for the design for NTRU. These results show how the x-net design is a remarkable fit for the $\mathcal {R}_p\times \mathcal {R}_q$ multiplications in NTRU and NTRU Prime.

Unified Design Performance Figures

We now analyze the results of the unified architecture supporting polynomial multiplications for all four cryptographic schemes at hand. The results are reported in Table 4.

When considering a unified x-net design capable of adapting at run time to the required polynomial ring, we basically need to instantiate the longest LFSR among the ones for the the supported parameter sets, pre-compute $2p+1$ integer multiplication outcomes for the largest value of p in use across all schemes, and insert multiplexers to propagate the correct data to the functional units. By contrast, obtaining a unified Comba design is less demanding on FPGA resources, since the only accumulator which is present in the Comba datapath has a size depending uniquely on the value of the large modulus q. As a consequence, we report the synthesis results of the Comba unified design for the highest security level alone, as they match the ones for all other security levels.

Table 4 Results of the synthesis targeting an **linx UltraScale+ ZCU106 FPGA for the unified designs compatible with the specified parameter sets

Analyzing the results in Table 4, we observe that, while raising the security level from 1 to 3 (5) the unified designs require $\approx 15$% ($\approx 30$%, respectively) more FPGA resources to be implemented. In particular, we also observe that omitting Saber from the supported cipher set allows for a consistent FPGA resource saving, such that the design compatible with parameters up to security level 5 is more compact than the smaller one which only has compatibility with lightsaber parameters. Raising the desired security level for the integrated design also has a negative impact on the maximum working frequency; however, such an impact is quite limited ($\approx 10$%). Finally, we note that the FPGA resource requirements for the unified Comba design are approximately two orders of magnitude smaller with respect to the x-net design, therefore providing an extremely appealing optimization corner for resource constrained environments.

Fig. 7

Comparison of the area of the designs of different cryptoschemes (security level 1)

By looking at the area comparison of the unified design with the ones specialized to a specific parameter set depicted in Fig. 7, the design providing complete run time flexibility takes around 50% more area resources than the largest tailored component (NTRU Prime) required to run the most demanding cipher of the same security level set, and when support to Saber is dropped, the area penalty drops to almost negligible values. Furthermore, the achieved running frequency is only 5 to 22% slower than the slowest component it encompasses, while taking no penalty on the number of clock cycles used to compute any of the multiplications with respect to a dedicated design.

The $x^2$-net designs specialized for the NTRU HPS/HRSS parameters are more compact than the ones tailored for Saber parameter sets, suggesting that the increasing of the size of $\mathcal {R}_{p}$ coefficients is more impactful than the increase of the length of polynomials.

Unsurprisingly, those high-performance designs require $2\times$ the area than the x-net designs processing just one $\mathcal {R}_{q}$ coefficient. However, this is not the case for the designs tailored for the parameters of NTRU Prime and Kyber which, delaying the modulo of the coefficient at readout phase, use only $1.45\times$ ($1.71\times$, respectively) more resources.

The unified design implemented by means of a Comba-based multiplier needs to drop support for NTRU Prime ciphers, but shows an even greater flexibility supporting all security levels with a single design with no area penalties incurred. This peculiarity is due to the fact that supporting higher security levels for the investigated cryptographic schemes translates into smaller values of the parameter p (decreasing the complexity of the MAC unit) and larger values of n or k (increasing the latency of the operation for the Comba algorithm).

Ultimately this multiplier requires only 10% more area with respect to the largest tailored component (kyber512), and does not manifest a decrease in maximum working frequency.

Fig. 8

Comparison of the efficiency of the multipliers among the encapsulation algorithms (security level 1)

When comparing the area–time (AT) product of all our designs in Fig. 8, we can see that for NTRU parameters both the x-net and Comba designs have higher efficiency than the other proposed schemes, suggesting a remarkable fit for the task. In particular, for the x-net design performing the coefficient modulo operation each clock cycle shows an order of magnitude difference. During the keygen and decapsulation, this no longer holds, and we recall that one of the three multiplications during decapsulation specified in round 3 submission of NTRU does not have one operand with $\mathcal {R}_{p}$ coefficients, thus requiring an additional cost.

Moreover, considering the Saber parameters, we see an almost equivalent AT product of the Comba and x-net designs.

For the unified x-net design supporting parameters up to security level 1, its efficiency is matching the one produced by the specialized design supporting the NTRU Prime parameter, suggesting that its support is the limiting factor leading to a $9.6\times$ decrease of efficiency when compared with the specialized design supporting only the NTRU HPS parameter.

Similarly, when considering the unified Comba design and the specialized one for Kyber parameters we can determine a matching area-time product, signaling that the coefficient modulo operation is limiting the maximum frequency and increasing the area requirements.

The $x^2$-net designs performing the coefficient modulo each clock cycle shows a drastic reduction of efficiency with respect to the design processing a single $\mathcal {R}_{q}$ coefficient. This fact suggests that the design is too large for our FPGA target design, probably congesting the routing resources and sparsely occupying the CLBs. This is not the case when the modulo operation is performed during the readout: we see an identical area–time product, suggesting that this technique is a viable solution for increasing the performance.

An important detail is that our unified design based on the Comba algorithm achieves substantial better efficiency than the security level 5 unified solutions based on the x-net architecture. When Kyber’s parameter sets are in use, the gain is between $2\times$ and $5.5\times$.

Finally, we want to highlight the fact that our x-net-based unified solutions would not perfectly suit a power-efficient scenario, particularly when considering the results of the design specialized for the NTRU parameter sets.

The Comba-based unified solution mitigates this drawback, and the efficiency improvement has profound implications for applications where power efficiency and cryptographic agility is paramount, such in case of low-power edge devices in a cloud computing architecture deployed in remote locations. Although, this solution exhibits a significant latency of few milliseconds, which could pose challenges for certain class of applications.

Concluding Remarks

In this work, we analyzed a flexible design for linear time polynomial multiplications, applicable to accelerate four post-quantum cryptographic primitives: Kyber, Saber, NTRU, and NTRU Prime. We reported quantitative results of the efficiency of primitive-tailored designs, obtaining area savings (10–40%) and significant frequency gains (96–120%) with respect to the state of the art of NTRU and NTRU Prime multipliers. Our unified design provides the first hardware implementation of a polynomial multiplier able to accelerate the computation of Kyber, Saber, NTRU, and NTRU Prime at all security levels in a single component with a frequency reduction in the range of 5–22%, and only a 50% multiplier area increase.

Furthermore, we presented a simpler and compact multiplier based on the Comba algorithm specialized for NTRU, Saber and Kyber schemes, in some cases able to achieve a comparable design efficiency than the x-net-based solutions, and proposing a more efficient unified design able to adapt at run time to the different polynomial rings using only 10% more resources and without a frequency drop compared to its specialized solution.

Appendices

Appendix A

Design Space Exploration Results

This section includes the results of our comprehensive design space exploration.

These tables are meant to strengthen the reproducibility of our designs and trade-offs. The complete dataset is also available in CSV format at https://doi.org/10.5281/zenodo.8337625.

Table 5 Results of the synthesis targeting an **linx UltraScale+ ZCU106 FPGA specialized for each supported parameter sets

Table 6 Results of the synthesis targeting an **linx UltraScale+ ZCU106 FPGA specialized for each supported parameter sets

Table 7 Results of the synthesis targeting an **linx UltraScale+ ZCU106 FPGA specialized for each supported parameter sets

Table 8 Results of the synthesis targeting an **linx UltraScale+ ZCU106 FPGA specialized for each supported parameter sets

Table 9 Results of the synthesis targeting an **linx UltraScale+ ZCU106 FPGA specialized for each supported parameter sets