Byzantine-resilient decentralized network learning

Abstract

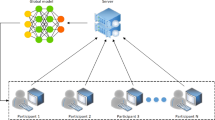
Decentralized federated learning based on fully normal nodes has drawn attention in modern statistical learning. However, due to data corruption, device malfunctioning, malicious attacks and some other unexpected behaviors, not all nodes can obey the estimation process and the existing decentralized federated learning methods may fail. An unknown number of abnormal nodes, called Byzantine nodes, arbitrarily deviate from their intended behaviors, send wrong messages to their neighbors and affect all honest nodes across the entire network through passing polluted messages. In this paper, we focus on decentralized federated learning in the presence of Byzantine attacks and then propose a unified Byzantine-resilient framework based on the network gradient descent and several robust aggregation rules. Theoretically, the convergence of the proposed algorithm is guaranteed under some weakly balanced conditions of network structure. The finite-sample performance is studied through simulations under different network topologies and various Byzantine attacks. An application to Communities and Crime Data is also presented.

Appendix

Lemma 1

Assume that $\{\mathcal {A}_n\}_{n\in \mathcal {N }}$ in Algorithm 1 satisfy (1). Under A1–A3 and a constant step size $\alpha \le {1/(6\,L)}$, it holds that

$$\begin{aligned} \max _{n \in \mathcal {N}}\big \Vert \widehat{\theta }_n^{t+\frac{1}{2}}-\overline{\theta }^{t+\frac{1}{2}}\big \Vert ^2 \le 2\max _{n \in \mathcal {N}}\big \Vert \widehat{\theta }_n^t-\overline{\theta }^t\big \Vert ^2+9 \alpha ^2\delta ^2, \end{aligned}$$

(2)

$$\begin{aligned} N^{-1} \sum _{n \in \mathcal {N}} \big \Vert \widehat{\theta }_n^{t+\frac{1}{2}}-\overline{\theta }^{t+\frac{1}{2}}\big \Vert ^2 \le \frac{2}{N} \sum _{n \in \mathcal {N}}\big \Vert \widehat{\theta }_n^t-\overline{\theta }^t\big \Vert ^2+9 \alpha ^2\delta ^2. \end{aligned}$$

(3)

Lemma 1 characterizes the connection between $\big \Vert \widehat{\theta }_n^{t+\frac{1}{2}}-\overline{\theta }^{t+\frac{1}{2}}\big \Vert ^2$ and $\big \Vert \widehat{\theta }_n^{t}-\overline{\theta }^{t}\big \Vert ^2$ which is pivotal to show the relation between $\widehat{\theta }_n^{t+1}$ and $\widehat{\theta }_n^{t}$ such that we can establish the convergence rate of $\big \Vert \nabla f\big (\overline{\theta }^t\big )\big \Vert$.

Proof of Lemma 1:

Observe that

$$\begin{aligned} \begin{aligned} \max _{n \in \mathcal {N}}\big \Vert \widehat{\theta }_n^{t+\frac{1}{2}}-\overline{\theta }^{t+\frac{1}{2}}\big \Vert ^2 \le&\frac{3}{2} \max _{n \in \mathcal {N}}\left\| \overline{\theta }_n^t-N^{-1}\sum _{m \in \mathcal {N}}\overline{\theta }^t_m\right\| ^2\\&+ 3\alpha ^2 \max _{n \in \mathcal {N}} \left\| \nabla f_n\big (\overline{\theta }_n^t \big )-N^{-1} \sum _{m \in \mathcal {N}} \nabla f_m\big (\overline{\theta }_m^t \big )\right\| ^2. \end{aligned} \end{aligned}$$

(4)

With Assumptions 1 and 3, the second term at the RHS of (4) can be bounded by

$$\begin{aligned} \begin{aligned}&\max _{n \in \mathcal {N}}\left\| \nabla f_n\big (\overline{\theta }_n^t\big )-N^{-1} \sum _{m \in \mathcal {N}} \nabla f_m\big (\overline{\theta }_m^t\big )\right\| ^2 \\&\le 3 \max _{n \in \mathcal {N}}\left\| \nabla f_n\big (\overline{\theta }_n^t\big )-\nabla f_n\big (\overline{\theta }^t\big )\right\| ^2 \\&\quad + 3 \max _{n \in \mathcal {N}}\left\| \nabla f_n\big (\overline{\theta }^t\big )-N^{-1} \sum _{m \in \mathcal {N}} \nabla f_m\big (\overline{\theta }^t\big )\right\| ^2 \\&\quad +3 \max _{n \in \mathcal {N}}\left\| N^{-1} \sum _{m \in \mathcal {N}} \nabla f_m\big (\overline{\theta }^t\big )-N^{-1} \sum _{m \in \mathcal {N}} \nabla f_m\big (\overline{\theta }_m^t\big )\right\| ^2\\&\le 6L^2 \max _{n \in \mathcal {N}}\big \Vert \overline{\theta }_n^t-\overline{\theta }^t\big \Vert ^2+3 \delta ^2 \le 6L^2 \max _{n \in \mathcal {N}}\big \Vert {\widehat{\theta }}_n^t-\overline{\theta }^t\big \Vert ^2+3 \delta ^2. \end{aligned} \end{aligned}$$

(5)

Substituting (5) and $\alpha \le \frac{1}{6L}$ into (4) yields

$$\begin{aligned} \begin{aligned} \max _{n \in \mathcal {N}}\big \Vert \widehat{\theta }_n^{t+\frac{1}{2}}-\overline{\theta }^{t+\frac{1}{2}}\big \Vert ^2&\le \frac{3}{2} \max _{n \in \mathcal {N}}\left\| \overline{\theta }_n^t-N^{-1}\sum _{m \in \mathcal {N}}\overline{\theta }^t_m\right\| ^2+ 18\alpha ^2L^2 \max _{n \in \mathcal {N}}\big \Vert {\widehat{\theta }}_n^t-\overline{\theta }^t\big \Vert ^2+9 \alpha ^2\delta ^2 \\&\le \frac{3}{2} \max _{n \in \mathcal {N}}\big \Vert {\widehat{\theta }}_n^t-\overline{\theta }^t\big \Vert ^2+ 18\alpha ^2L^2 \max _{n \in \mathcal {N}}\big \Vert {\widehat{\theta }}_n^t-\overline{\theta }^t\big \Vert ^2+9 \alpha ^2\delta ^2 \\&\le 2\max _{n \in \mathcal {N}}\big \Vert \widehat{\theta }_n^t-\overline{\theta }^t\big \Vert ^2+9 \alpha ^2\delta ^2. \end{aligned} \end{aligned}$$

(6)

The deduction from (4) to (6) still holds if we replace $\max _{n \in \mathcal {N}}$ with $N^{-1}\sum _{n\in \mathcal { N }}$, and we can get (3) immediately. $\square$

Define average and maximal consensus errors as

$$\begin{aligned} \begin{aligned} H_\lambda ^t =\Vert (I-N^{-1} \textbf{1 1}{ }^{T}) \widehat{\Theta }^t\Vert ^2, \; H_\beta ^t =\Vert (I-N^{-1} \textbf{1 1}^{T}) \widehat{\Theta }^t\Vert _{2, \infty }^2, \end{aligned} \end{aligned}$$

respectively. To simultaneously analyze the errors, we consider

$$\begin{aligned} H^t=\frac{1}{2} (H_\lambda ^t+H_\beta ^t ). \end{aligned}$$

(7)

Proof of Theorem 1:

By the L-smoothness in Assumption 1, we have

$$\begin{aligned} \begin{aligned} f\big (\overline{\theta }^{t+1}\big ) \le&f\big (\overline{\theta }^t\big )+\big \langle \nabla f\big (\overline{\theta }^t\big ), \overline{\theta }^{t+1}-\overline{\theta }^t\big \rangle +\frac{L}{2} \big \Vert \overline{\theta }^{t+1}-\overline{\theta }^t\big \Vert ^2. \end{aligned} \end{aligned}$$

(8)

With the equality $\langle \theta _1, \theta _2\rangle =\frac{1}{2}\Vert \theta _1+\theta _2\Vert ^2-\frac{1}{2}\Vert \theta _1\Vert ^2-\frac{1}{2}\Vert \theta _2\Vert ^2$, we can rewrite the second term at the RHS of (8) as

$$\begin{aligned} \begin{aligned} \big \langle \nabla f\big (\overline{\theta }^t\big ), \overline{\theta }^{t+1}-\overline{\theta }^t\big \rangle =&\alpha \big \langle \nabla f\big (\overline{\theta }^t\big ),\alpha ^{-1} \big (\overline{\theta }^{t+1}-\overline{\theta }^t\big )\big \rangle \\ =&\frac{\alpha }{2} \big \Vert \nabla f\big (\overline{\theta }^t\big )+\alpha ^{-1} \big (\overline{\theta }^{t+1}-\overline{\theta }^t\big )\big \Vert ^2\\&-\frac{\alpha }{2}\big \Vert \nabla f\big (\overline{\theta }^t\big )\big \Vert ^2 -\frac{\alpha }{2} \big \Vert \alpha ^{-1} \big (\overline{\theta }^{t+1}-\overline{\theta }^t\big )\big \Vert ^2. \end{aligned} \end{aligned}$$

(9)

Because $\alpha \le \frac{1}{6L}$, substituting (9) into (8) yields

$$\begin{aligned} \begin{aligned} f\big (\overline{\theta }^{t+1}\big ) \le&f\big (\overline{\theta }^t\big )+\frac{\alpha }{2} \big \Vert \nabla f\big (\overline{\theta }^t \big )+\alpha ^{-1} \big (\overline{\theta }^{t+1}-\overline{\theta }^t\big )\big \Vert ^2\\&-\frac{1}{2}(\alpha ^{-1} -L) \big \Vert \overline{\theta }^{t+1}-\overline{\theta }^t\big \Vert ^2 -\frac{\alpha }{2}\big \Vert \nabla f\big (\overline{\theta }^t\big )\big \Vert ^2\\ \le&f\big (\overline{\theta }^t\big )+\frac{\alpha }{2} \big \Vert \nabla f\big (\overline{\theta }^t \big )+\alpha ^{-1} \big (\overline{\theta }^{t+1}-\overline{\theta }^t\big )\big \Vert ^2 -\frac{\alpha }{2}\big \Vert \nabla f\big (\overline{\theta }^t\big )\big \Vert ^2. \end{aligned} \end{aligned}$$

(10)

According to the update rule, we expand the second term at the RHS of (10) as

$$\begin{aligned} \begin{aligned}\nabla f\big (\overline{\theta }^t \big )+\alpha ^{-1} \big (\overline{\theta }^{t+1}-\overline{\theta }^t\big ) &= \nabla f\big (\overline{\theta }^t\big )+(\alpha N)^{-1} \sum _{n \in \mathcal {N}}\left( \mathcal {A}_n\left( \widehat{\theta }_n^{t+\frac{1}{2}},\left\{ \tilde{\theta }_{m, n}^{t+\frac{1}{2}}\right\} _{m \in \mathcal {N}_n \cup \mathcal {B}_n}\right) -\overline{\theta }^t\right) \\ &=\nabla f\big (\overline{\theta }^t \big )-N^{-1} \sum _{n \in \mathcal {N}} \nabla f_n\big (\overline{\theta }_n^t \big ) + (\alpha N)^{-1} \sum _{n \in \mathcal {N}}\left( \sum _{m \in \mathcal {N}_n} w_{nm} \widehat{\theta }_m^{t+\frac{1}{2}}-\overline{\theta }^t+\alpha N^{-1} \sum _{n \in \mathcal {N}} \nabla f_n\big (\overline{\theta }_n^t\big )\right) \\&\quad+(\alpha N)^{-1} \sum _{n \in \mathcal {N}}\left( \mathcal {A}_n\left( \widehat{\theta }_n^{t+\frac{1}{2}},\left\{ \tilde{\theta }_{m, n}^{t+\frac{1}{2}}\right\} _{m \in \mathcal {N}_n \cup \mathcal {B}_n}\right) -\sum _{m \in \mathcal {N}_n} w_{nm} \widehat{\theta }_m^{t+\frac{1}{2}}\right) . \end{aligned} \end{aligned}$$

(11)

Denote the $\ell _2$ norms of the three terms at the RHS of (11) as $T_1, T_2$ and $T_3$. We establish their upper bounds as follows.

Upper bound of $T_1$. For $T_1$, it holds that

$$\begin{aligned} \begin{aligned} T_1&=\left\| \nabla f\big (\overline{\theta }^t \big )-N^{-1} \sum _{n \in \mathcal {N}} \nabla f_n\big (\overline{\theta }^t_n\big )\right\| ^2 =\left\| N^{-1} \sum _{n \in \mathcal {N}}\big (\nabla f_n\big (\overline{\theta }^t \big )-\nabla f_n\big (\overline{\theta }^t_n \big )\big )\right\| ^2 \\&\le N^{-1} \sum _{n \in \mathcal {N}} \left\| \nabla f_n\big (\overline{\theta }^t\big )-\nabla f_n\big (\overline{\theta }^t_n \big )\right\| ^2. \end{aligned} \end{aligned}$$

Further, according to Assumption 1, we have

$$\begin{aligned} \big \Vert \nabla f_n\big (\overline{\theta }^t \big )-\nabla f_n\big (\overline{\theta }^t_n\big )\big \Vert ^2 \le L^2\big \Vert \overline{\theta }^t-\overline{\theta }^t_n\big \Vert ^2. \end{aligned}$$

With this inequality, $T_1$ can be bounded by

$$\begin{aligned} \begin{aligned} T_1 \le \frac{L^2}{N} \sum _{n \in \mathcal {N}}\big \Vert \overline{\theta }^t_n-\overline{\theta }^t\big \Vert ^2 \le L^2 \max _{n\in \mathcal { N }}\big \Vert \widehat{\theta }^t_n-\overline{\theta }^t\big \Vert ^2. \end{aligned} \end{aligned}$$

(12)

Upper bound of $T_2$. By $\overline{\theta }^{t+\frac{1}{2}}=N^{-1}\sum _{n\in \mathcal { N }}\overline{\theta }^t_n-\alpha N^{-1} \sum _{n \in \mathcal {N}} \nabla f_n\big (\overline{\theta }^t_n\big )$, we can rewrite the second term at the RHS of (11) as

$$\begin{aligned} \begin{aligned}&(\alpha N)^{-1} \sum _{n \in \mathcal {N}}\left( \sum _{m \in \mathcal {N}_n} w_{nm} \widehat{\theta }_m^{t+\frac{1}{2}}-\overline{\theta }^t+\alpha N^{-1} \sum _{n \in \mathcal {N}} \nabla f_n\big (\overline{\theta }_n^t \big )\right) \\&=(\alpha N)^{-1} \sum _{n \in \mathcal {N}}\left( \sum _{m \in \mathcal {N}_n} w_{nm} \widehat{\theta }_m^{t+\frac{1}{2}}+N^{-1}\sum _{n\in \mathcal { N }}\overline{\theta }^t_n-\overline{\theta }^t-N^{-1}\sum _{n\in \mathcal { N }}\overline{\theta }^t_n+\alpha N^{-1} \sum _{n \in \mathcal {N}} \nabla f_n\big (\overline{\theta }_n^t \big )\right) \\&= (\alpha N)^{-1} \sum _{n \in \mathcal {N}}\left( \sum _{m \in \mathcal {N}_n} w_{m n} \widehat{\theta }_m^{t+\frac{1}{2}}+N^{-1}\sum _{n\in \mathcal { N }}\overline{\theta }^t_n-\overline{\theta }^{t}-\overline{\theta }^{t+\frac{1}{2}}\right) . \end{aligned} \end{aligned}$$

Stacking all local models in $\widehat{\Theta }$ and applying Cauchy–Schwarz inequality, we have

$$\begin{aligned} \begin{aligned} T_2&=\left\| (\alpha N)^{-1} \sum _{n \in \mathcal {N}}\left( \sum _{m \in \mathcal {N}_n} w_{m n} \widehat{\theta }_m^{t+\frac{1}{2}}+N^{-1}\sum _{n\in \mathcal { N }}\overline{\theta }^t_n-\overline{\theta }^{t}-\overline{\theta }^{t+\frac{1}{2}}\right) \right\| ^2\\&= \left\| (\alpha N)^{-1} \sum _{n \in \mathcal {N}}\left( \sum _{m \in \mathcal {N}_n} w_{m n} \widehat{\theta }_m^{t+\frac{1}{2}}-\overline{\theta }^{t+\frac{1}{2}}\right) +(\alpha N)^{-1} \sum _{n\in \mathcal { N }}\left( N^{-1}\sum _{n\in \mathcal {N }}\overline{\theta }^t_n -\overline{\theta }^{t}\right) \right\| ^2 \\&=\left\| (\alpha N)^{-1} \big (\textbf{1}^{T}W \widehat{\Theta }^{t+\frac{1}{2}}-N^{-1}\textbf{1}^{T} \textbf{1} \textbf{1}^{T} \widehat{\Theta }^{t+\frac{1}{2}}\big ) \right. \\& \quad \left. +(\alpha N)^{-1} \left( \sum _{n \in \mathcal {N}}N^{-1}\textbf{1}^{T}W \widehat{\Theta }^{t}-N^{-1} \textbf{1}^{T}\textbf{1} \textbf{1}^{T}\widehat{\Theta }^{t}\right) \right\| ^2\\&=\frac{1}{\alpha ^2 N^2}\big \Vert \big (\textbf{1}^{T} W-\textbf{1}^{T}\big )\big (\widehat{\Theta }^{t+\frac{1}{2}}-N^{-1} \textbf{1} \textbf{1}^{T} \widehat{\Theta }^{t+\frac{1}{2}}\big )+\big (\textbf{1}^{T} W-\textbf{1}^{T}\big )\big (\widehat{\Theta }^{t}-N^{-1} \textbf{1} \textbf{1}^{T} \widehat{\Theta }^{t}\big )\big \Vert ^2 \\&\le \frac{2}{\alpha ^2 N^2}\big \Vert W^{T} \textbf{1}-\textbf{1}\big \Vert ^2\big (\big \Vert \widehat{\Theta }^{t+\frac{1}{2}}-N^{-1} \textbf{1} \textbf{1}^{T} \widehat{\Theta }^{t+\frac{1}{2}}\big \Vert _F^2+\big \Vert \widehat{\Theta }^{t}-N^{-1} \textbf{1} \textbf{1}^{T} \widehat{\Theta }^{t}\big \Vert _F^2\big ) \\&=\frac{2SE^2(W)}{\alpha ^2 N} \sum _{n \in \mathcal {N}}\big (\big \Vert \widehat{\theta }_n^{t+\frac{1}{2}}-\overline{\theta }^{t+\frac{1}{2}}\big \Vert ^2 +\big \Vert \widehat{\theta }_n^{t}-\overline{\theta }^{t}\big \Vert ^2\big ). \end{aligned} \end{aligned}$$

(13)

Upper bound of $T_3$. From the contractive property of robust aggregation rules $\big \{\mathcal {A}_n\big \}_{n \in \mathcal {N}}$, $T_3$ can be bounded by

$$\begin{aligned} \begin{aligned} T_3&=\left\| (\alpha N)^{-1} \sum _{n \in \mathcal {N}}\left( \mathcal {A}_n\left( \widehat{\theta }_n^{t+\frac{1}{2}},\left\{ \tilde{\theta }_{m, n}^{t+\frac{1}{2}}\right\} _{m \in \mathcal {N}_n \cup \mathcal {B}_n}\right) -\overline{\theta }_n^{t+\frac{1}{2}}\right) \right\| ^2\\&\le \frac{1}{\alpha ^2 N} \sum _{n \in \mathcal {N}}\left\| \mathcal {A}_n\left( \widehat{\theta }_n^{t+\frac{1}{2}},\left\{ \tilde{\theta }_{m, n}^{t+\frac{1}{2}}\right\} _{m \in \mathcal {N}_n \cup \mathcal {B}_n}\right) -\overline{\theta }_n^{t+\frac{1}{2}}\right\| ^2 \\&\le \frac{1}{\alpha ^2 N} \sum _{n \in \mathcal {N}} \rho ^2 \max _{m \in \mathcal {N}_n}\left\| \widehat{\theta }_m^{t+\frac{1}{2}}-\overline{\theta }_n^{t+\frac{1}{2}}\right\| ^2. \end{aligned} \end{aligned}$$

With inequality

$$\begin{aligned} \begin{aligned} \big \Vert \widehat{\theta }_m^{t+\frac{1}{2}}-\overline{\theta }_n^{t+\frac{1}{2}}\big \Vert ^2 \le&2\big \Vert \widehat{\theta }_m^{t+\frac{1}{2}}-\overline{\theta }^{t+\frac{1}{2}}\big \Vert ^2 +2\big \Vert \overline{\theta }^{t+\frac{1}{2}}-\overline{\theta }_n^{t+\frac{1}{2}}\big \Vert ^2\\ \le&2\big \Vert \widehat{\theta }_m^{t+\frac{1}{2}}-\overline{\theta }^{t+\frac{1}{2}}\big \Vert ^2+2 \max _{n \in \mathcal {N}}\big \Vert \widehat{\theta }_n^{t+\frac{1}{2}}-\overline{\theta }^{t+\frac{1}{2}}\big \Vert ^2, \end{aligned} \end{aligned}$$

we have

$$\begin{aligned} T_3 \le \frac{4 \rho ^2}{\alpha ^2} \max _{n \in \mathcal {N}}\big \Vert \widehat{\theta }_n^{t+\frac{1}{2}}-\overline{\theta }^{t+\frac{1}{2}}\big \Vert ^2. \end{aligned}$$

(14)

According to the derived upper bounds (12), (13) and (14), from (11) we have

$$\begin{aligned} \begin{aligned}&\big \Vert \nabla f\big (\overline{\theta }^t \big )+\alpha ^{-1} \big (\overline{\theta }^{t+1}-\overline{\theta }^t\big )\big \Vert ^2 \le 3 T_1+3 T_2+3 T_3 \\&\le 3L^2 \max _{n\in \mathcal {N }}\big \Vert \widehat{\theta }^t_n-\overline{\theta }^t\big \Vert ^2+\frac{6 SE^2(W)}{\alpha ^2 N} \sum _{n \in \mathcal {N}}\big (\big \Vert \widehat{\theta }_n^{t+\frac{1}{2}}-\overline{\theta }^{t+\frac{1}{2}}\big \Vert ^2 +\big \Vert \widehat{\theta }_n^{t}-\overline{\theta }^{t}\big \Vert ^2 \big )\\&\quad +\frac{12 \rho ^2}{\alpha ^2} \max _{n \in \mathcal {N}}\big \Vert \widehat{\theta }_n^{t+\frac{1}{2}} -\overline{\theta }^{t+\frac{1}{2}}\big \Vert ^2. \end{aligned} \end{aligned}$$

(15)

Plugging (2) and (3) in Lemma 1 into (15) yields

$$\begin{aligned} \begin{aligned}&\big \Vert \nabla f\big (\overline{\theta }^t\big )+\alpha ^{-1} \big (\overline{\theta }^{t+1}-\overline{\theta }^t\big )\big \Vert ^2 \le \left( \frac{24 \rho ^2}{\alpha ^2}+3L^2\right) \max _{n \in \mathcal {N}}\big \Vert \widehat{\theta }_n^t-\overline{\theta }^t\big \Vert ^2\\& \quad +\frac{18 SE^2(W)}{\alpha ^2 N} \sum _{n \in \mathcal {N}}\big \Vert \widehat{\theta }_n^t-\overline{\theta }^t\big \Vert ^2 \\&\quad +27\big (4 \rho ^2+SE^2(W)\big )\delta ^2 \\&\le \left( \frac{24 \rho ^2}{\alpha ^2}+3L^2\right) H_\beta ^t+\frac{18SE^2(W)}{\alpha ^2 } H_{\lambda }^t+27\big (4 \rho ^2+SE^2(W)\big )\delta ^2. \end{aligned} \end{aligned}$$

(16)

Reorganizing the terms in (10) and then substituting (16), we have

$$\begin{aligned} \begin{aligned} \big \Vert \nabla f\big (\overline{\theta }^t\big )\big \Vert ^2 \le&\frac{2 \big (f\big (\overline{\theta }^t\big )-f\big (\overline{\theta }^{t+1}\big )\big )}{\alpha }+\big \Vert \nabla f\big (\overline{\theta }^t\big )+\alpha ^{-1} \big (\overline{\theta }^{t+1}-\overline{\theta }^t\big )\big \Vert ^2 \\ \le&\frac{2 \big (f\big (\overline{\theta }^t\big )-f\big (\overline{\theta }^{t+1}\big )\big )}{\alpha }+27\big (4 \rho ^2+SE^2(W)^2\big )\delta ^2 \\&+\left( \frac{24 \rho ^2}{\alpha ^2}+3L^2\right) H_\beta ^t+\frac{18 SE^2(W)}{\alpha ^2 } H_{\lambda }^t. \end{aligned} \end{aligned}$$

(17)

Averaging (17) over $t=1, \ldots , T$ gives

$$\begin{aligned} \begin{aligned} \frac{1}{T} \sum _{t=1}^T \big \Vert \nabla f\big (\overline{\theta }^t\big )\big \Vert ^2 \le&\frac{2 \big (f\big (\overline{\theta }^0\big )-f\big (\overline{\theta }^{t+1}\big )\big )}{\alpha T}+27\big (4 \rho ^2+SE^2(W)\big )\delta ^2 \\&+\frac{1}{\alpha ^2 T} \sum _{t=1}^T\big ((24 \rho ^2+3 \alpha ^2 L^2) H_\beta ^t+18 SE^2(W) H_\lambda ^t\big ) \\ \le&\frac{2\big (f\big (\overline{\theta }^0\big )-f^*\big )}{\alpha T}+27\big (4 \rho ^2+SE^2(W)\big )\delta ^2 \\&+\frac{1}{\alpha ^2 T} \sum _{t=1}^T\big ((24 \rho ^2+3 \alpha ^2 L^2) H_\beta ^t+18 SE^2(W) H_\lambda ^t\big ). \end{aligned} \end{aligned}$$

Since we define $H^t=\frac{1}{2} (H_\beta ^t+ H_\lambda ^t),$ we then further show the convergence of $H^t$. Writing the maximal consensus error in a matrix form, we know that for any $u \in (0,1)$, it holds

$$\begin{aligned} \begin{aligned} \max _{n \in \mathcal {N}}\big \Vert \widehat{\theta }_n^{t+1}-\overline{\theta }^{t+1}\big \Vert ^2&=\big \Vert \big (I-N^{-1} \textbf{1} \textbf{1}^{T}\big ) \widehat{\Theta }^{t+1}\big \Vert _{2, \infty }^2 \le \frac{1}{1-u}\big \Vert \big (I-N^{-1} \textbf{1 1}^{T}\big ) W\widehat{\Theta }^{t+\frac{1}{2}}\big \Vert _{2, \infty }^2\\&\quad+\frac{2}{u}\big \Vert \widehat{\Theta }^{t+1}-W \widehat{\Theta }^{t+\frac{1}{2}}\big \Vert _{2, \infty }^2 +\frac{2}{u} \big \Vert N^{-1} \textbf{1} \textbf{1}^{T} \widehat{\Theta }^{t+1}-N^{-1} \textbf{1 1}\big \Vert _{2,\infty }^2, \end{aligned} \end{aligned}$$

(18)

where the inequality comes from $\Vert \theta _1+\theta _2+\theta _3\Vert ^2 \le \frac{1}{1-u}\Vert \theta _1\Vert ^2+$ $\frac{2}{u}\Vert \theta _2\Vert ^2+\frac{2}{u}\Vert \theta _3\Vert ^2$. Since W is a row stochastic matrix, it holds that $W \textbf{1}=\textbf{1}$, with which the first term at the RHS of (18) can be bounded by

$$\begin{aligned} \begin{aligned} \big \Vert \big (I-N^{-1} \textbf{1} \textbf{1}^{T}\big ) W \widehat{\Theta }^{t+\frac{1}{2}}\big \Vert _{2, \infty }^2 =&\big \Vert \big (I-N^{-1} \textbf{1} \textbf{1}^{T}\big ) W\big (I-N^{-1} \textbf{1} \textbf{1}^{T}\big ) \widehat{\Theta }^{t+\frac{1}{2}}\big \Vert _{2, \infty }^2 \\ \le&\big \Vert \big (I-N^{-1} \textbf{1} \textbf{1}^{T}\big ) W\big \Vert _{2, \infty }^2\big \Vert \big (I-N^{-1} \textbf{1} \textbf{1}^{T}\big ) \widehat{\Theta }^{t+\frac{1}{2}}\big \Vert ^2 \\ =&(1-\beta )\big \Vert \big (I-N^{-1} \textbf{1} \textbf{1}^{T}\big )\widehat{\Theta }^{t+\frac{1}{2}}\big \Vert ^2. \end{aligned} \end{aligned}$$

(19)

With the contractive property of robust aggregation rules $\big \{\mathcal {A}_n\big \}_{n \in \mathcal {N}}$ in (1), we can bound the second term at the RHS of (18) by

$$\begin{aligned} \begin{aligned} \big \Vert \widehat{\Theta }^{t+1}-W \widehat{\Theta }^{t+\frac{1}{2}}\big \Vert _{2, \infty }^2 =&\max _{n \in \mathcal {N}}\big \Vert \mathcal {A}_n\big (\widehat{\theta }_n^{t+\frac{1}{2}},\big \{\tilde{\theta }_{m, n}^{t+\frac{1}{2}}\big \}_{m \in \mathcal {N}_n \cup \mathcal {B}_n}\big )-\overline{\theta }_n^{t+\frac{1}{2}}\big \Vert ^2 \\ \le&\rho ^2 \max _{n \in \mathcal {N}} \max _{m \in \mathcal {N}_n}\big \Vert \widehat{\theta }_m^{t+\frac{1}{2}}-\overline{\theta }_n^{t+\frac{1}{2}}\big \Vert ^2\\ \le&4 \rho ^2 \max _{n \in \mathcal {N}}\big \Vert \widehat{\theta }_n^{t+\frac{1}{2}}-\overline{\theta }^{t+\frac{1}{2}}\big \Vert ^2. \end{aligned} \end{aligned}$$

(20)

A similar technique can be applied to the third term at the RHS of (18) to get

$$\begin{aligned} \begin{aligned} \big \Vert N^{-1} \textbf{1} \textbf{1}^{T} \widehat{\Theta }^{t+1}-N^{-1} \textbf{1} \textbf{1}^{T} W\widehat{\Theta }^{t+\frac{1}{2}}\big \Vert _{2, \infty }^2 =&\big \Vert N^{-1} \textbf{1}^{T} \widehat{\Theta }^{t+1}-N^{-1} \textbf{1}^{T} W \widehat{\Theta }^{t+\frac{1}{2}}\big \Vert ^2 \\ \le&N^{-1}\big \Vert \widehat{\Theta }^{t+1}-W \widehat{\Theta }^{t+\frac{1}{2}}\big \Vert _F^2 \\ =&N^{-1} \sum _{n \in \mathcal {N}}\big \Vert \mathcal {A}_n\big (\widehat{\theta }_n^{t+\frac{1}{2}},\big \{\tilde{\theta }_{m, n}^{t+\frac{1}{2}}\big \}_{m \in \mathcal {N}_n \cup \mathcal {B}_n}\big )-\overline{\theta }_n^{t+\frac{1}{2}}\big \Vert ^2 \\ \le&4 \rho ^2 \max _{n \in \mathcal {N}}\big \Vert \widehat{\theta }_n^{t+\frac{1}{2}}-\overline{\theta }^{t+\frac{1}{2}}\big \Vert ^2, \end{aligned} \end{aligned}$$

(21)

where the first equality holds because all rows of the matrix $N^{-1} \textbf{1 1}{ }^{T}\widehat{\Theta }^{t+1}-N^{-1} \textbf{ 1} \textbf{ 1}^{T} W \widehat{\Theta }^{t+\frac{1}{2}}$ are identical. Substituting (19)–(21) back into (18), we have

$$\begin{aligned} \begin{aligned} \big \Vert \big (I-N^{-1} \textbf{1 1}^{T}\big ) \widehat{\Theta }^{t+1}\big \Vert _{2, \infty }^2 \le&\frac{1-\beta }{1-u}\big \Vert \big (I-N^{-1} \textbf{1 1}^{T}\big )\widehat{\Theta }^{t+\frac{1}{2}}\big \Vert ^2 \\&+\frac{16 \rho ^2}{u}\big \Vert \big (I-N^{-1} \textbf{ 1} \textbf{1}^{T}\big ) \widehat{\Theta }^{t+\frac{1}{2}}\big \Vert _{2, \infty }^2.&\end{aligned} \end{aligned}$$

Applying Lemma 1, we have

$$\begin{aligned} \begin{aligned} \big \Vert \big (I-N^{-1} \textbf{1 1}^{T}\big ) \widehat{\Theta }^{t+1}\big \Vert _{2, \infty }^2 \le&2\left( \frac{1-\beta }{1-u}\right) \big \Vert \big (I-N^{-1} \textbf{1 1}^{T}\big ) \widehat{\Theta }^t\big \Vert ^2 \\&+\frac{32 \rho ^2}{u}\big \Vert \big (I-N^{-1} \textbf{1 1}{ }^{T}\big ) \widehat{\Theta }^t\big \Vert _{2, \infty }^2 +\left( \frac{1-\beta }{1-u}+\frac{16 \rho ^2}{u}\right) 9 \alpha ^2\delta ^2 \\ =&2\left( \frac{1-\beta }{1-u}\right) H_{\lambda }^t +\frac{32 \rho ^2}{u}H_{\beta }^t +\left( \frac{1-\beta }{1-u}+\frac{16 \rho ^2}{u}\right) 9 \alpha ^2\delta ^2. \end{aligned} \end{aligned}$$

With similar techniques, we can also prove that

$$\begin{aligned} \begin{aligned} \big \Vert \big (I-N^{-1} \textbf{1 1}^{T}\big ) \widehat{\Theta }^{t+1}\big \Vert ^2 \le 2\left( \frac{1-\lambda }{1-u}\right) H_{\lambda }^t +\frac{32 \rho ^2}{u}H_{\beta }^t +\left( \frac{1-\lambda }{1-u}+\frac{16 \rho ^2}{u}\right) 9 \alpha ^2\delta ^2. \end{aligned} \end{aligned}$$

Then we conclude that

$$\begin{aligned} \begin{aligned} H^{t+1} \le \frac{32\rho ^2}{u} H_\beta ^t +\frac{2-\beta -\lambda }{1-u} H_\lambda ^t +\frac{1}{2}\left( \frac{2-\lambda -\beta }{1-u}+\frac{32\rho ^2}{u}\right) 9 \alpha ^2\delta ^2. \end{aligned} \end{aligned}$$

(22)

Now we are going to designate some constants such that the RHS of (22) contains only $H^t$ and the term of $O\big (\delta ^2\big )$. Choose proper u such that

$$\begin{aligned} \frac{32\rho ^2}{u}=\frac{2-\lambda -\beta }{1-u}, \end{aligned}$$

which means

$$\begin{aligned} u=\frac{32\rho ^2}{32\rho ^2+2-\beta -\lambda }<1. \end{aligned}$$

(23)

With (23), (22) becomes

$$\begin{aligned} \begin{aligned} H^{t+1}&\le (32\rho ^2+2-\beta -\lambda ) H^t + 9 (32\rho ^2+2-\beta -\lambda )\alpha ^2\delta ^2\\&=\gamma _1H^t+9\gamma _1\alpha ^2\delta ^2. \end{aligned} \end{aligned}$$

(24)

Since we have $\rho < \sqrt{\frac{\beta +\lambda -1}{32}}$, then $0<\gamma _1<1$. Using telescopic cancellation on (24) from 0 to k, we deduce that

$$\begin{aligned} H^{t+1} \le \gamma _1^{t+1} H^0+\frac{\gamma _1-\gamma _1^{k+2}}{1-\gamma _1}9\alpha ^2\delta ^2, \end{aligned}$$

which completes the proof. $\square$